MetaTrader 5 / 機械学習
English Русский Español Português
preview
ニューラルネットワークの実践：最初のニューロン

ニューラルネットワークの実践：最初のニューロン

MetaTrader 5 — 機械学習 | 28 4月 2025, 09:19
33 0
Daniel Jose
Daniel Jose

はじめに

みなさんこんにちは。ニューラルネットワークに関する新しい記事へようこそ。前の記事「ニューラルネットワークの実践：ニューロンのスケッチ」では、単純なニューロンを構築するための初歩的なスケッチをおこないました。しかしながら、努力の甲斐あって完成したとはいえ、そのニューロンは実は理想とは少し違っていました。というのも、小さな欠陥と呼べるものが含まれていたからです。それでも、ご安心ください。親愛なる読者の皆さん。私の目標は、ニューラルネットワークの構築プロセスを段階的に、そしてしっかりと理解していただくことです。そして、この小さな欠陥があったとしても、今回のシンプルなニューロンの機能性にはほとんど影響しません。

「何の欠陥ですか。変なことには何も気が付きませんでした。ニューロンは私のテストで完璧に機能しました。」と疑問に思われるかもしれません。私がここで何を言おうとしているのかを理解するには、これまでのニューラルネットワークに関する連載を少し振り返ってみる必要があります。

最初の記事では、機械に線形方程式を作成させる方法について解説しました。その際、方程式はデカルト座標平面の原点、つまり(0, 0)を必ず通るように制約されていました。これは、次の式における定数bをゼロに固定していたためです。

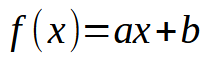
最小二乗法を用いて適切な方程式を導き出し、データベースに保存されたデータセットや既存の知識を数学的に表現できるようにしました。しかし、このモデリング手法では、必ずしも最も適した方程式を見つけ出すことはできませんでした。その理由は、知識ベース内のデータセットによっては、定数bに0以外の値が必要になる場合があるということです。

これまでの記事を注意深く振り返ってみると、傾きを表す定数aと、切片を示す定数bの両方について、最適な値を求めるためにさまざまな数学的テクニックを用いたことがわかるでしょう。これらの調整によって、最も適切な線形方程式を導くことができました。具体的には、微分計算による方法と、行列演算による方法の2通りを検討しました。

しかし、ここから先は、それらの計算手法はもはや有効ではありません。なぜなら、線形方程式の定数を求めるために、新たなアプローチが必要になるからです。前回の記事では、傾きを示す定数の求め方について紹介しました。もしそのコードを実際に試して楽しんでいただけたなら嬉しいです。今回はそれより少しだけ複雑な内容に取り組みますが、その分、多くの可能性が開かれることになります。実際のところ、この記事はこのニューラルネットワーク連載の中で最も興味深い内容になるかもしれません。なぜなら、この記事で紹介する考え方を理解すれば、今後のすべての内容がよりシンプルで、実用的なものになるからです。


人はなぜ物事をそんなに複雑にしてしまうのか

さて、親愛なる読者の皆さん。コードに入る前に、いくつかの重要な概念についてお話ししたいと思います。ニューラルネットワークの学習を始めると、きっと大量の専門用語が、まさに「雪崩」のように押し寄せてくるでしょう。なぜ多くの人が、もともとはシンプルな仕組みを、わざわざ難しく説明してしまうのか、正直私にもわかりません。私の考えでは、そこまで複雑にする必要はまったくないのです。ただし、ここで私がしたいのは、誰かを批判したり揶揄したりすることではありません。本当の目的は、「舞台裏」で何がどう動いているのかを、できるだけわかりやすく伝えることです。

できる限りシンプルにするために、まずはニューラルネットワークに頻繁に登場する基本用語に絞って説明していきましょう。最初のキーワードは「重み」です。これは単に、線形方程式における傾き（係数）を意味しています。どんなに難しく聞こえる説明であっても、「重み」とは本質的に「傾き」のことです。次によく出てくるのが「バイアス」という言葉です。これは決して難解な概念ではなく、ニューラルネットワークやAI特有の用語というわけでもありません。むしろ、バイアスとは「切片」、つまり、線形方程式におけるy軸との交点を指すだけなのです。ここでは割線を扱っているので、この点を混同しないようにしてください。

こうした、一見すると複雑そうな用語をベースにして、さらに多くの技術用語が生まれています。でも実際は、それらはただの言い換えにすぎないことが多いのです。なぜ既知の概念に新しい名前が付けられているのかという話には、ここでは触れませんが、ニューラルネットワークやその関連分野を学んでいる中で、聞き慣れない単語に出会ったら、ぜひその背景にある数学的な式に目を向けてみてください。きっと、意外と単純なことに気づくはずです。

私がこう言うのは、多くの人が物事を不必要に複雑にしてしまう傾向があるからです。

本来は単純な仕組みであるにもかかわらず、余計な装飾や複雑な構造を加えることで、誰でも理解できるはずのことが、かえって難しく見えてしまうのです。プログラミングや理系の分野においては、シンプルであることが非常に重要です。物事に不要な要素が入り始め、話が散漫になったり、細かすぎる情報が加わったりしたときは、いったん立ち止まり、余分な複雑さをすべて取り除いて、核心だけを見直すべきです。多くの人は、「この分野は難しい」、「ニューラルネットワークを使うには専門家でなければならない」、「特定の言語やツールを使わなければできない」などと言い張るでしょう。でも、ここまで読み進めてくれた皆さんなら、もうお気づきのはずです。ニューラルネットワークは、決して複雑なものではありません。実は、とてもシンプルなのです。

さて、それでは次のトピックに進みましょう。今度は「b」と呼ばれる定数、つまり「交点（バイアス）」をどのように式に組み込むかを学んでいきます。これは、ニューロンを訓練するために使うデータセットを、より正確に表現するために、直線の方程式を調整するために必要なステップです。


最初のニューロンの誕生

最初のニューロンを形作るためには、まず私たちが何を扱っているのかを理解する必要があります。そして一度その形が整えば、すぐにわかるように、もう修正する必要はなくなります。現在のニューロンは、下のアニメーションに示されているように動作しています。



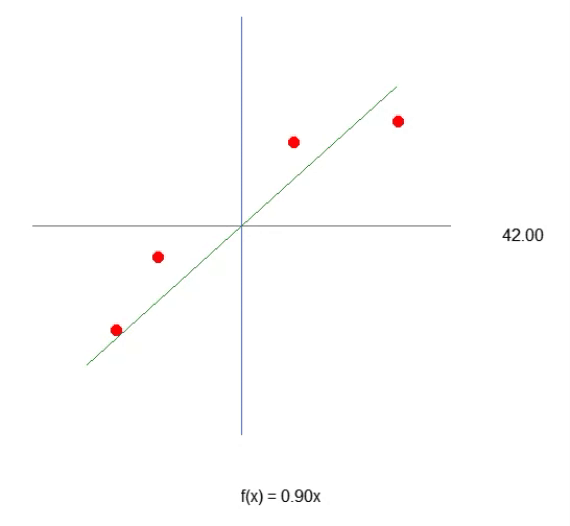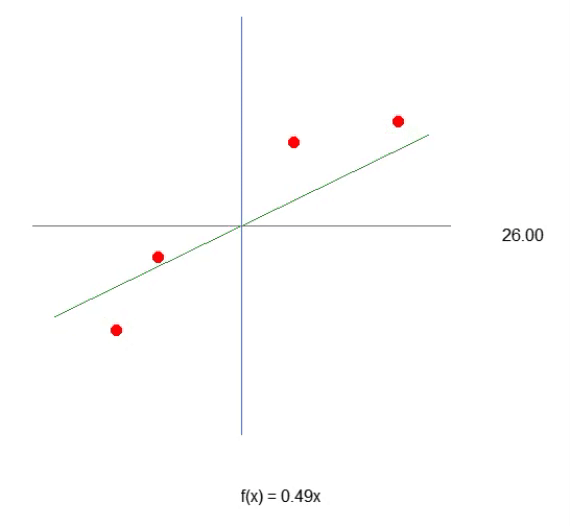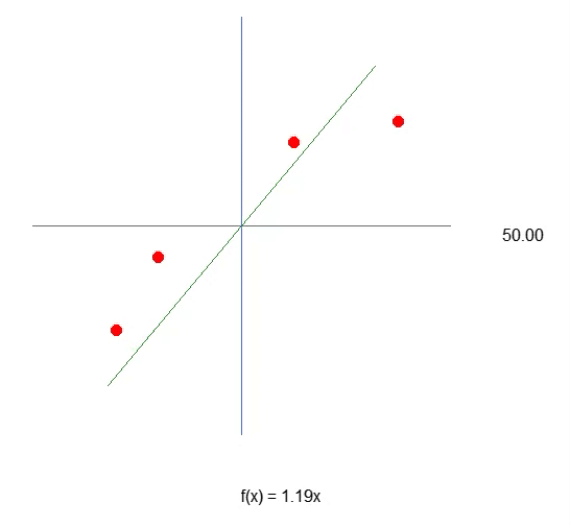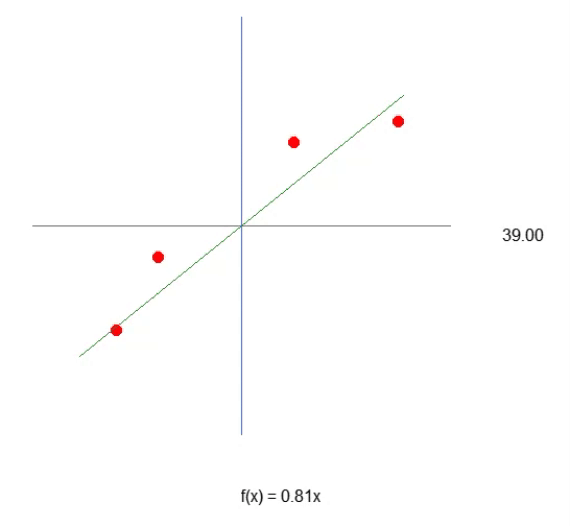
これは記事「ニューラルネットワークの実践：割線」で紹介されているものと同じアニメーションです。言い換えれば、これまでは方向キーを使って手動でおこなっていたタスクを、ニューロンが自動で実行できるようにするための第一歩を、私たちは踏み出したということです。とはいえ、これだけではまだ不十分であることに気づいたかもしれません。この方程式をさらに正確なものにするためには、「交差定数（バイアス）」を追加する必要があります。これをおこなうのは非常に複雑だと思うかもしれませんが、実際には驚くほどシンプルです。あまりにも簡単で、拍子抜けするかもしれません。以下をご覧ください。ニューロンに交差定数を加える方法を、次のコード断片で確認できます。

01. //+------------------------------------------------------------------+
02. double Cost(const double w, const double b)
03. {
04.     double err, fx, x;
05. 
06.     err = 0;
07.     for (uint c = 0; c < nTrain; c++)
08.     {
09.         x = Train[c][0];
10.         fx =  a * w + b;
11.         err += MathPow(fx - Train[c][1], 2);
12.     }
13. 
14.     return err / nTrain;
15. }
16. //+------------------------------------------------------------------+

読者の皆さんが、何がどうおこなわれているのかを細かく理解できるように、コードは小さな断片に分けて紹介していきます。そして最後に、ぜひ教えてください。これは、本当に複雑でしょうか。ニューラルネットワークを語るときに多くの人が付け加えたがる不要な複雑さは本当に必要なのでしょうか。

ここでの複雑さのレベルは、もはや不条理と言ってもいいほどです（笑）。たとえば9行目では、訓練データの値を変数Xに代入しています。そして10行目では、因数分解をしています。ああ、なんと複雑な計算なのでしょう。でも、ちょっと待ってください。これは、最初に見たあの「直線の方程式」と同じです。冗談ですか。このようなものが本当に、AIプログラムに使われるニューロンとして機能するのでしょうか。

落ち着いてください、親愛なる読者の皆さん。このニューロンは、他のどんな人工知能やニューラルネットワークのプログラムと同じように、ちゃんと動作します。どれだけ難しく聞こえる説明をされても、本質的には、どのニューラルネットワークにも共通するごく基本的な概念なのです。違いが出てくるのは、このあとのステップです。それも、皆さんが想像しているほど劇的ではありません。一歩ずつ物事を進めていきましょう。

誤差の計算が更新されたら、コスト関数内で使われている2つのパラメータを調整するコードの断片を、少し変更することができます。これも重要なポイントをしっかり理解できるよう、段階的に紹介していきます。まずは、前回の記事で使用していた元のコードを修正し、以下に示す新しいバージョンへと置き換えましょう。

01. //+------------------------------------------------------------------+
02. void OnStart()
03. {
04.     double weight, ew, eb, e1, bias;
05.     int f = FileOpen("Cost.csv", FILE_COMMON | FILE_WRITE | FILE_CSV);
06. 
07.     Print("The first neuron...");
08.     MathSrand(512);
09.     weight = (double)macroRandom;
10.     bias = (double)macroRandom;
11. 
12.     for(ulong c = 0; (c < ULONG_MAX) && ((e1 = Cost(weight, bias)) > eps); c++)
13.     {
14.         ew = (Cost(weight + eps, bias) - e1) / eps;
15.         eb = (Cost(weight, bias + eps) - e1) / eps;
16.         weight -= (ew * eps);
17.         bias -= (eb * eps);
18.         if (f != INVALID_HANDLE)
19.             FileWriteString(f, StringFormat("%I64u;%f;%f;%f;%f;%f\n", c, weight, ew, bias, eb, e1));
20.     }
21.     if (f != INVALID_HANDLE)
22.         FileClose(f);
23.     Print("Weight: ", weight, "  Bias: ", bias);
24.     Print("Error Weight: ", ew);
25.     Print("Error Bias: ", eb);
26.     Print("Error: ", e1);
27. }
28. //+------------------------------------------------------------------+

これらの変更を加えたスクリプトを実行すると、以下の画像のようなものが表示されます。


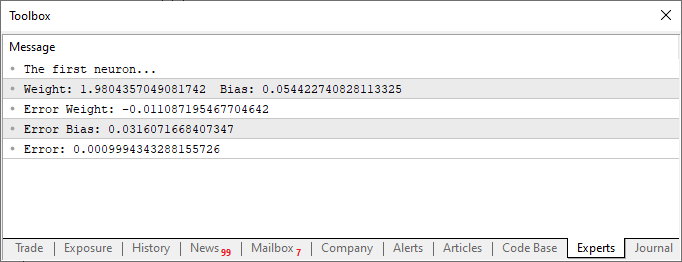
さて、ここではこの2番目のコードフラグメントにだけ注目してみましょう。4行目では、いくつかの変数を追加・変更していますが、特に難しいことはしていません。続いて10行目では、バイアス、つまり「交差定数」にランダムな値を割り当てるようアプリケーションに指示しています。この値は、Cost関数にも渡す必要があります。これは12行目、14行目、そして15行目でおこなっています。注目すべきは、ここで重みに対する誤差とバイアスに対する誤差、2種類の集約された誤差を生成している点です。どちらも同じ方程式の一部ではあるものの、調整の仕方は異なるという点がとても重要です。そのため、それぞれがシステム全体の中でどのような誤差を表しているのか、個別に特定する必要があるのです。

このことを踏まえて、16行目と17行目では、次のforループの反復に向けて値を適切に更新しています。さらに、前回の記事と同様に、これらの値はCSVファイルに記録しています。これによって、グラフを作成し、時間の経過とともに値がどのように変化しているかを視覚的に分析できるようになります。

この時点で、最初のニューロンはついに完成しました。とはいえ、以下に示す完全なコードを見ることで、まだいくつかの細かいポイントを確認することができます。以下は、私が考案したニューロンの完全なコードです。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define macroRandom (rand() / (double)SHORT_MAX)
05. //+------------------------------------------------------------------+
06. double Train[][2] {
07.                     {0, 0},
08.                     {1, 2},
09.                     {2, 4},
10.                     {3, 6},
11.                     {4, 8},
12.                   };
13. //+------------------------------------------------------------------+
14. const uint nTrain = Train.Size() / 2;
15. const double eps = 1e-3;
16. //+------------------------------------------------------------------+
17. double Cost(const double w, const double b)
18. {
19.     double err, fx, a;
20. 
21.     err = 0;
22.     for (uint c = 0; c < nTrain; c++)
23.     {
24.         a = Train[c][0];
25.         fx =  a * w + b;
26.         err += MathPow(fx - Train[c][1], 2);
27.     }
28. 
29.     return err / nTrain;
30. }
31. //+------------------------------------------------------------------+
32. void OnStart()
33. {
34.     double weight, ew, eb, e1, bias;
35.     int f = FileOpen("Cost.csv", FILE_COMMON | FILE_WRITE | FILE_CSV);
36. 
37.     Print("The first neuron...");
38.     MathSrand(512);
39.     weight = (double)macroRandom;
40.     bias = (double)macroRandom;
41. 
42.     for(ulong c = 0; (c < ULONG_MAX) && ((e1 = Cost(weight, bias)) > eps); c++)
43.     {
44.         ew = (Cost(weight + eps, bias) - e1) / eps;
45.         eb = (Cost(weight, bias + eps) - e1) / eps;
46.         weight -= (ew * eps);
47.         bias -= (eb * eps);
48.         if (f != INVALID_HANDLE)
49.             FileWriteString(f, StringFormat("%I64u;%f;%f;%f;%f;%f\n", c, weight, ew, bias, eb, e1));
50.     }
51.     if (f != INVALID_HANDLE)
52.         FileClose(f);
53.     Print("Weight: ", weight, "  Bias: ", bias);
54.     Print("Error Weight: ", ew);
55.     Print("Error Bias: ", eb);
56.     Print("Error: ", e1);
57. }
58. //+------------------------------------------------------------------+

コードと上に表示された画像の結果には、どちらにも興味深い点があります。6行目を見ると、ニューロンの訓練に使われた値がわかります。明らかに、乗数は2であるべきです。ところが、ニューロンは1.9804357049081742と報告しています。同様に、交点は0のはずですが、ニューロンは0.054422740828113325と答えています。さて、15行目で許容誤差を0.001に設定していたことを考えると、これはそこまで悪い結果ではありません。実際、ニューロンが報告した最終的な誤差は0.0009994343288155726で、設定した閾値をきちんと下回っています。

このようなわずかな差異が示しているのが、どれだけ正確に近づけたかという確率的な指標です。これは通常、パーセンテージで表されます。ただし、100%に到達することはありません。どれだけ近づいても、近似誤差のために完全な100%になることはないのです。

ただし、ここで言う「確率指標」は、情報の確実性を示す指標とは異なります。今の段階では、そういった確実性のインデックスを生成するところまでは進んでいません。ここでやっているのは、ただニューロンを訓練して、与えられたデータ同士の相関関係をきちんと学習できているかを確認するだけです。とはいえ、もしかしたらあなたはこう思っているかもしれません。「このニューロンは全部役に立ちません。今の作り方では意味がありません。すでにわかってる数字を見つけてるだけです。私が欲しいのは、もっと役に立つシステムです。例えば、質問に答えてくれるとか、文章を生成するとか、コードを書いてくれるとか。あるいは、金融市場で動いて、必要なときに自動でお金を稼いでくれるプログラムとかです。」

ごもっともです。なかなか壮大な目標です。ただし、もし「AIやニューラルネットワークを使って一発当てたい」「金儲けしたい」という目的だけでこの分野を見ているのだとしたら、少し残念なお知らせがあります。その考え方では、まずうまくいきません。実際にこの分野で儲けているのは、AIやニューラルネットワークを販売している人たちです。彼らは、AIが熟練した専門家よりも優れた成果を出せると他者を納得させようとします。このようなソリューションを販売することで利益を得ている人々を除けば、AIやニューラルネットワークによって直接的に収益を得ている人は、ほとんど存在しません。もし本当に簡単に利益が出せるものであれば、私がこうして仕組みを解説する記事を書く必要などないはずです。他の専門家たちも、これらのメカニズムについて公に共有することはないでしょう。それは意味をなさないでしょう。沈黙を守り、十分に訓練されたニューラルネットワークを利用して利益を得ればよいだけだからです。しかし、現実はそうではありません。したがって、ニューラルネットワークを簡単に構築し、いくつかのコード断片を寄せ集めるだけで、実際の知識なしに収益を上げられるという考えは捨ててください。

とはいえ、読者の皆さんが、たとえば金融市場における売買判断や、あるいは特定の傾向の可視化など、意思決定の支援を目的として小規模なニューラルネットワークを開発しようと考えているのであれば、それを妨げるものは何もありません。それを実現することは可能です。たとえ学習のペースが遅くとも、必要な内容をしっかりと学び、十分な努力と献身をもって取り組めば、目的に沿ったニューラルネットワークを訓練することは可能です。ただし、先ほど述べたように、それには努力が必要です。実現可能であるということと、簡単に達成できるということは別の話です。

ここまでで、私たちは最初のニューロンの構築に成功しました。しかし、すぐに活用方法を考え始める前に、まずその構造をもう少し詳しく見てみましょう。理解を深めるために、以下の図をご覧ください。

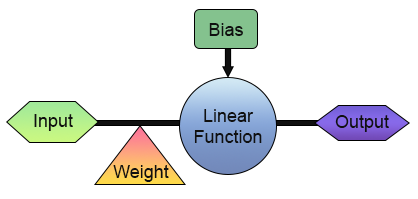
上の画像では、私たちのニューロンがどのように実装されているかを確認することができます。ご覧のとおり、1つの入力と1つの出力で構成されています。この1つの入力は、重みを受け取ります。一見すると、これがあまり実用的ではないように思えるかもしれません。「入力と出力が1つずつだけでは、いったい何の意味があるのか」と疑問に思われることでしょう。そのような疑問を抱かれるのももっともです。しかし、さまざまな分野におけるあなたの背景や知識によっては、デジタルエレクトロニクスの分野において、まさにこのように「入力が1つ、出力も1つ」という構成で動作する回路が存在することをご存じないかもしれません。実際、そのような回路には2種類あり、「インバーター」と「バッファ」と呼ばれています。これらは、より複雑なシステムにおいても基本的かつ不可欠な構成要素です。そして、私たちのニューロンも、それらと同様の挙動を再現できるように訓練することが可能です。そのために必要なのは、以下に示すように、トレーニングマトリックスを適切に変更することだけです。

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
double Train[][2] {
                    {0, 1},
                    {1, 0},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 2;
const double eps = 1e-3;
//+------------------------------------------------------------------+

このコードを使用して、以下の画像に示されるようなものを作成します。


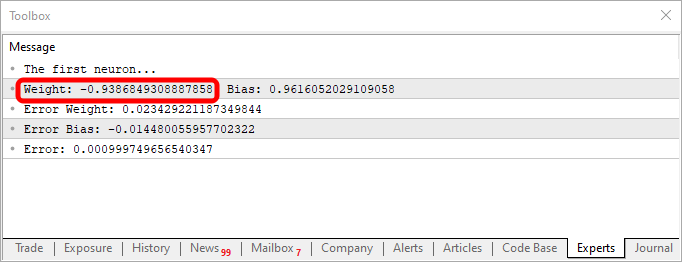
重みの値が負であることに注目してください。これは、入力値が反転されることを意味します。言い換えれば、インバーターがあるということです。以下のコードを使用することで、異なる出力を得ることができます。

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
double Train[][2] {
                    {0, 0},
                    {1, 1},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 2;
const double eps = 1e-3;
//+------------------------------------------------------------------+

この場合の出力は以下の画像に示されています。


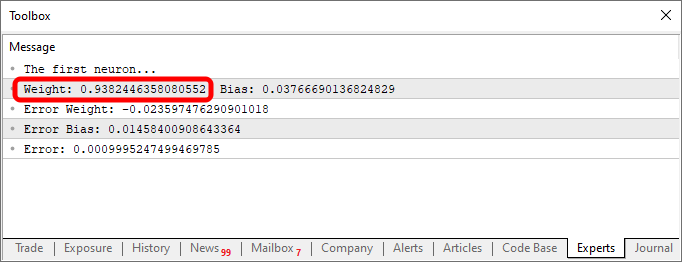
重みの値が正になっていることに注目してください。これは、入力がそのまま出力へとバッファリングされていることを意味します。つまり、バッファとして機能しているということです。こうして実験してみるのはとても楽しいと思いませんか。

知識ベース、つまり今回の例では二次元配列のデータを変更するという、ただそれだけの操作で、同じコードから異なる動作を表す方程式を生成できるのです。だからこそ、プログラミングに関心のある人々がニューラルネットワークの扱いを楽しいと感じるのです。実験のしがいがあるのです。

とはいえ、この最初のニューロンには明確な制限があります。それは構造そのものによるのではなく、入力が1つに限られているという点です。実際のニューラルネットワークにおけるニューロンは、必要に応じて複数の入力を持つことができますし、同じように、タスクを遂行するために必要な数の出力も持つことが可能です。読者の皆さんが圧倒されることのないよう、これらの概念は段階的に紹介しています。私の目的は、この仕組みがどのように、そしてなぜ機能するのかをしっかりと理解していただくことです。もちろん、私や他の誰かがどれほど詳しく説明しようとも、この技術で実現できるすべての可能性を紹介しきることはできません。なぜなら、可能性はあなた自身の創造力によってのみ制限されるものだからです。とはいえ、今は物事をもう少し面白く、さらに楽しくしていきましょう。


シグモイド関数

ここから先に紹介する内容は、すべてほんの氷山の一角に過ぎません。どんなにプログラミングが刺激的で、複雑で、楽しく思えても、これから触れることは、無限に広がる可能性のごく一部を垣間見るにすぎないのです。ですから、親愛なる読者の皆さん、この時点でそろそろこの分野をもう少し主体的に学び始めるべきでしょう。私の目的は、さらなる発見へとつながる道を示し、そのきっかけとなることにあります。これからお見せする内容は、ぜひ自由に試し、探求し、楽しんでみてください。前にも述べたように、唯一の制限はあなた自身の想像力です。

さて、単一のニューロンが複数の入力を学習できるようにするには、ひとつの単純かつ本質的なポイントを理解するだけで十分です。その要点は、以下の図に示されています。

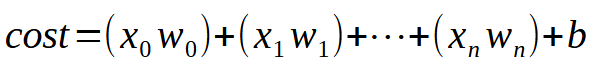
以下は、同じ式です。

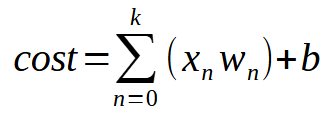
値kは、ニューロンが持つことができる入力の数を表しています。つまり、必要な入力数がいくつであっても、それに応じて入力を追加するだけで、ニューロンはそれぞれの新たな状況に対応する方法を学習できるのです。しかし、2つ目の入力を導入した時点で、関数はもはや線形方程式（直線）ではなくなります。その代わりに、任意の形状を表現できるような方程式へと変化します。この変化は、ニューロンが多様な訓練シナリオに適応できるようにするために不可欠なものです。

ここからが本番です。この調整により、たった1つのニューロンでも複数の異なるパターンを学習できるようになります。ただし、単純な線形方程式を超えると、小さな課題も生じてきます。それを理解するために、以下のようにプログラムを改良してみましょう。

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
double Train[][3] {
                    {0, 0, 0},
                    {0, 1, 1},
                    {1, 0, 1},
                    {1, 1, 1},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 3;
const double eps = 1e-3;
//+------------------------------------------------------------------+
double Cost(const double w0, const double w1, const double b)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow(((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2], 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+
void OnStart()
{
    double  w0, w1, err, ew0, ew1, eb, bias;

    Print("The Mini Neuron...");
    MathSrand(512);
    w0 = (double)macroRandom;
    w1 = (double)macroRandom;
    bias = (double)macroRandom;

    for (ulong c = 0; (c < 3000) && ((err = Cost(w0, w1, bias)) > eps); c++)
    {
        ew0 = (Cost(w0 + eps, w1, bias) - err) / eps;
        ew1 = (Cost(w0, w1 + eps, bias) - err) / eps;
        eb  = (Cost(w0, w1, bias + eps) - err) / eps;
        w0 -= (ew0 * eps);
        w1 -= (ew1 * eps);
        bias -= (eb * eps);
        PrintFormat("%I64u > w0: %.4f %.4f || w1: %.4f %.4f || b: %.4f %.4f || %.4f", c, w0, ew0, w1, ew1, bias, eb, err);
    }
    Print("w0 = ", w0, " || w1 = ", w1, " || Bias = ", bias);
    Print("Error Weight 0: ", ew0);
    Print("Error Weight 1: ", ew1);
    Print("Error Bias: ", eb);
    Print("Error: ", err);
}
//+------------------------------------------------------------------+

このコードを実行すると、次の画像のような結果が得られます。


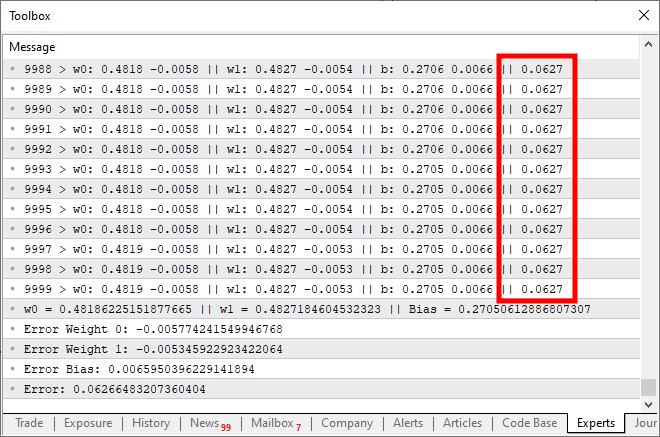
さて、ここで何が問題だったのでしょうか。コードを見れば、複数の入力に対応できるように修正しただけであり、その処理自体は正しくおこなわれていることが分かります。ですが、興味深い現象が確認できます。およそ1万回ほど繰り返したあたりで、コスト関数の値がそれ以上減らなくなっています。あるいは、減少は続いているとしても、そのペースは極めて緩慢です。なぜ、こうなるのでしょうか。その原因は、私たちのニューロンにある要素が欠けていることにあります。これは入力が1つだけの場合には必要のなかったものですが、複数の入力を扱う際には不可欠な要素です。この欠落している要素は、ディープラーニングで用いられる「ニューロンの層」を扱う際にも重要となるものであり、後ほど詳しく説明する予定です。今は、この主な問題に集中しましょう。現在のニューロンは停滞点に達しており、そこから先、誤差（コスト）をこれ以上下げることができなくなっています。この問題を解決するためには、出力に活性化関数を導入する必要があります。どの活性化関数を使うか、またその動作は、解こうとしている問題の種類によって異なります。万能な一つの解決策があるわけではなく、実際にはさまざまな種類の活性化関数が存在します。その中でも最もよく使われている関数のひとつが、シグモイド関数です。理由は非常にシンプルです。シグモイド関数は、負の無限大から正の無限大までの値を、0から1の範囲に変換してくれるからです。場合によっては、-1から1の範囲にマッピングされるよう調整することもありますが、ここでは基本的な形式を使用します。シグモイド関数は、次の数式で定義されます。

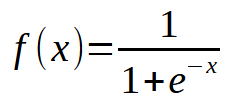
さて、これを実際のコードにどう適用すればよいのでしょうか。最初は少し難しそうに見えるかもしれません。ですが、親愛なる読者の皆さん、安心してください。見た目ほど複雑ではありません。実際には、既存のコードにほんの少し手を加えるだけで十分なのです。その変更点を以下に示します。

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
#define macroSigmoid(a) (1.0 / (1 + MathExp(-a)))
//+------------------------------------------------------------------+
double Train[][3] {
                    {0, 0, 0},
                    {0, 1, 1},
                    {1, 0, 1},
                    {1, 1, 1},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 3;
const double eps = 1e-3;
//+------------------------------------------------------------------+
double Cost(const double w0, const double w1, const double b)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2]), 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+
void OnStart()
{
    double  w0, w1, err, ew0, ew1, eb, bias;

    Print("The Mini Neuron...");
    MathSrand(512);
    w0 = (double)macroRandom;
    w1 = (double)macroRandom;
    bias = (double)macroRandom;

    for (ulong c = 0; (c < ULONG_MAX) && ((err = Cost(w0, w1, bias)) > eps); c++)
    {
        ew0 = (Cost(w0 + eps, w1, bias) - err) / eps;
        ew1 = (Cost(w0, w1 + eps, bias) - err) / eps;
        eb  = (Cost(w0, w1, bias + eps) - err) / eps;
        w0 -= (ew0 * eps);
        w1 -= (ew1 * eps);
        bias -= (eb * eps);
        PrintFormat("%I64u > w0: %.4f %.4f || w1: %.4f %.4f || b: %.4f %.4f || %.4f", c, w0, ew0, w1, ew1, bias, eb, err);
    }
    Print("w0 = ", w0, " || w1 = ", w1, " || Bias = ", bias);
    Print("Error Weight 0: ", ew0);
    Print("Error Weight 1: ", ew1);
    Print("Error Bias: ", eb);
    Print("Error: ", err);
}
//+------------------------------------------------------------------+

上記のコードを実行すると、出力は次の画像のようになります。


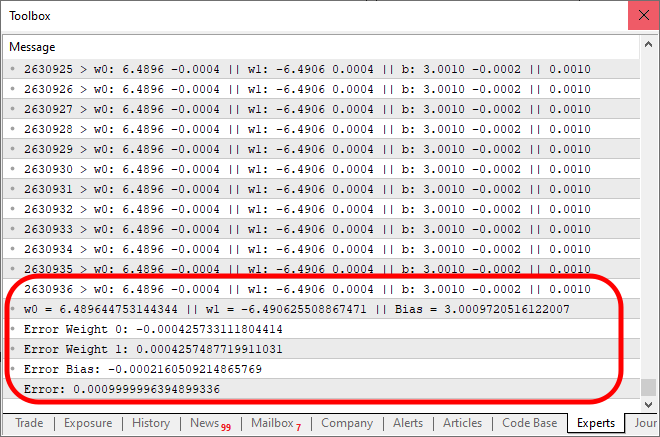
ご注目ください。結果が期待される誤差範囲に収束するまでに、2,630,936回もの反復が必要でした。ですが、これは決して悪い結果ではありません。この時点で、特にCPU上で実行している場合に、プログラムの動作が少し遅く感じられるかもしれません。しかし、その主な原因は、すべての反復でメッセージを出力していることにあります。処理速度を向上させるには、出力方法を見直すだけで十分です。ついでに、このニューロンの性能を評価するための簡単なテストも追加してみましょう。以下に示すのが、最終的なコードバージョンです。

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
#define macroSigmoid(a) (1.0 / (1 + MathExp(-a)))
//+------------------------------------------------------------------+
double Train[][3] {
                    {0, 0, 0},
                    {0, 1, 1},
                    {1, 0, 1},
                    {1, 1, 1},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 3;
const double eps = 1e-3;
//+------------------------------------------------------------------+
double Cost(const double w0, const double w1, const double b)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2]), 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+
void OnStart()
{
    double  w0, w1, err, ew0, ew1, eb, bias;
    ulong count;

    Print("The Mini Neuron...");
    MathSrand(512);
    w0 = (double)macroRandom;
    w1 = (double)macroRandom;
    bias = (double)macroRandom;

    for (count = 0; (count < ULONG_MAX) && ((err = Cost(w0, w1, bias)) > eps); count++)
    {
        ew0 = (Cost(w0 + eps, w1, bias) - err) / eps;
        ew1 = (Cost(w0, w1 + eps, bias) - err) / eps;
        eb  = (Cost(w0, w1, bias + eps) - err) / eps;
        w0 -= (ew0 * eps);
        w1 -= (ew1 * eps);
        bias -= (eb * eps);
    }
    PrintFormat("%I64u > w0: %.4f %.4f || w1: %.4f %.4f || b: %.4f %.4f || %.4f", count, w0, ew0, w1, ew1, bias, eb, err);
    Print("w0 = ", w0, " || w1 = ", w1, " || Bias = ", bias);
    Print("Error Weight 0: ", ew0);
    Print("Error Weight 1: ", ew1);
    Print("Error Bias: ", eb);
    Print("Error: ", err);

    Print("Testing the neuron...");
    for (uchar p0 = 0; p0 < 2; p0++)
        for (uchar p1 = 0; p1 < 2; p1++)
            PrintFormat("%d OR %d IS %f", p0, p1, macroSigmoid((p0 * w0) + (p1 * w1) + bias));
}
//+------------------------------------------------------------------+

この更新されたコードを実行すると、下の画像のようなメッセージが端末に表示されます。


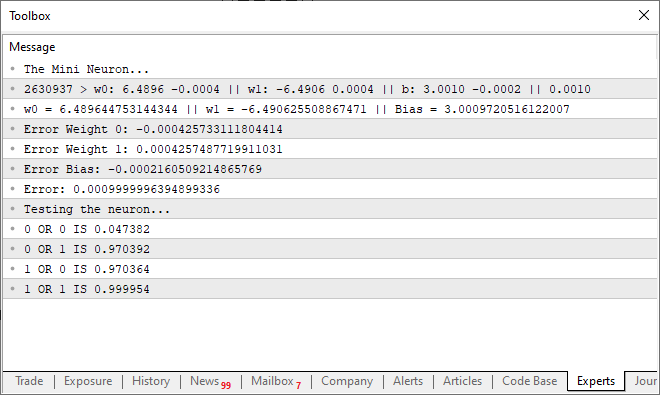
言い換えれば、私たちはこの単純なニューロンを訓練し、ORゲートの動作を理解させることに成功したというわけです。この瞬間から、私たちはもはや後戻りのできない領域に足を踏み入れました。この単一のニューロンは、もはや単に2つの値の相関を検出するだけではなく、より複雑な関係性をも学習できるようになったのです。


最終的な考察

この記事では、実際に動作しているのを見ると多くの人が驚くようなものを構築しました。MQL5のほんの数行のコードで、完全に機能する人工ニューロンを作成したのです。これを実現するには膨大なリソースが必要だと思っている人も多いかもしれませんが、親愛なる読者の皆さん、物事はこうして一歩ずつ進んでいくということを、今回で感じていただけたのではないでしょうか。わずか数本の記事の中で、私は多くの科学者たちが何年もかけて築き上げてきた研究を要約して紹介しました。このニューロン自体はシンプルなものですが、その仕組みの背後にあるロジックを設計するには長い年月が必要でした。今日においても、これらの計算をより効率的かつ高速にするための研究は続けられています。ここで使用したのは、2つの入力、5つのパラメータ、そして1つの出力を持つ単一のニューロンだけです。それでも、正しい方程式を見つけるにはある程度の時間がかかることがわかります。

もちろん、OpenCLを使ってGPUでの計算を高速化することも可能です。しかし、私の見解では、そのような最適化を導入するのはまだ時期尚早です。GPUの力を本当に必要とする前に、まだ学べることがたくさんあります。それでも、もし本格的にニューラルネットワークの世界に足を踏み入れたいと考えているなら、GPUへの投資は非常に価値があります。訓練において一部の処理が格段に速くなるからです。

この記事の最後に、完成したコードを添付しています。ぜひ自由に使って、実験して、楽しんでみてください。このニューロンがさまざまな状況にどのように対応するのか観察し、その限界を見つけてみてください。限界は確かに存在します。だからこそ、さらに学ぶべきことがたくさんあるのです。

MetaQuotes Ltdによりポルトガル語から翻訳されました。
元の記事: https://www.mql5.com/pt/articles/13745

添付されたファイル |
ZIPをダウンロード
Anexo.mq5 (2.22 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
取引におけるニューラルネットワーク：統合軌道生成モデル（UniTraj） 取引におけるニューラルネットワーク：統合軌道生成モデル（UniTraj）
エージェントの行動を理解することはさまざまな分野で重要ですが、ほとんどの手法は特定のタスク（理解、ノイズ除去、予測）に焦点を当てており、そのため実際のシナリオでは効果的に活用できないことが多いです。この記事では、さまざまな問題を解決するために適応可能なモデルについて説明します。
初級から中級へ：IF ELSE 初級から中級へ：IF ELSE
この記事では、IF演算子と、それに対応するELSEの使い方について解説します。この文は、あらゆるプログラミング言語において、最も重要かつ意義深いものです。しかし、その使いやすさにもかかわらず、使用経験や関連概念に対する理解がないと、時に混乱を招くことがあります。ここで提示されるコンテンツは、教育目的のみを目的としています。いかなる状況においても、提示された概念を学習し習得する以外の目的でアプリケーションを閲覧することは避けてください。
初級から中級へ：WHILE文とDO WHILE文 初級から中級へ：WHILE文とDO WHILE文
この記事では、最初のループ文を実際的かつ視覚的に見ていきます。多くの初心者はループを作成するという作業に直面すると不安を感じますが、正しく安全におこなう方法を知るには経験と練習が必要です。しかし、コード内でループを使用する際の主な問題と注意事項を示すことで、皆さんの悩みや苦しみを軽減できるかもしれません。
リプレイシステムの開発（第62回）：サービスの再生(III) リプレイシステムの開発（第62回）：サービスの再生(III)
この記事では、実際のデータを使用する際にアプリケーションのパフォーマンスに影響を及ぼす可能性のある「ティック過剰」の問題について取り上げます。このティック過剰は、1分足を適切なタイミングで構築するうえで支障となることがよくあります。