MQL5の分類タスクを強化するアンサンブル法

MetaTrader 5 — 統計と分析 | 23 4月 2025, 12:22

はじめに

以前の記事では、数値予測におけるモデルの組み合わせ手法について検討しました。本稿では、その延長として、分類タスクに特化したアンサンブル手法に焦点を当てて解説を進めます。その過程で、順序尺度に基づくクラス順位を出力する分類器の活用戦略についても考察します。分類タスクにおいても、出力が数値であれば数値的な組み合わせ手法が適用可能な場合がありますが、多くの分類器はより厳格なアプローチを採用しており、離散的なクラス判定のみを出力することが一般的です。また、数値出力に基づく分類器は、しばしば予測が不安定になりやすく、専用の組み合わせ手法の必要性が浮き彫りになります。

本記事で取り上げるアンサンブル分類器は、その構成要素である分類モデルについて、以下のような前提条件のもとで設計されています。まず、これらのモデルは相互に排他的かつ網羅的なクラスラベルを持つデータで学習されており、各インスタンスは必ず一つのクラスに所属することが前提です。「上記のいずれでもない」といった選択肢が必要な場合、それは独立したクラスとして扱うか、所定の閾値を用いた数値的手法で対応する必要があります。さらに、予測変数の入力ベクトルが与えられると、各モデルはN個の出力を生成することが期待されます（Nはクラス数を意味します）。これらの出力は、各クラスへの所属確率や信頼スコアであることもあれば、1つの出力のみが1.0（真）で、他は0.0（偽）となるような単純な二分決定である場合もあります。また、1〜Nの整数による順位付けで相対的な所属可能性を表すような出力もあり得ます。

本稿で紹介するいくつかのアンサンブル手法は、順位付けされた出力を生成する分類器から大きな恩恵を受けます。クラス所属の確率を正確に推定できるモデルは非常に有用ですが、出力が実際には確率を表していないにもかかわらず、それを確率として扱うことには大きなリスクがあります。出力の意味が曖昧な場合、順位に変換することで有効に活用できる場合があります。順位情報の有用性はクラス数が増えるほど高まります。2クラスの分類問題ではランクは追加情報を提供しませんし、3クラスの問題においてもその恩恵は限定的です。しかし、多数のクラスが関与する場合、予測に不確実性があるときでも次点のクラス選択を解釈できることは大きな意味を持ちます。たとえば、サポートベクターマシン(SVM)を拡張して、単なる二項分類だけでなく、各クラスに対する決定境界までの距離を出力させることで、予測信頼度に関するより深い洞察を得ることが可能です。

また、順位情報はアンサンブルにおけるもう一つの重要課題、つまり異なる分類モデルの出力の正規化にも対応します。たとえば、市場の動きを分析する2つのモデルがあるとします。1つは流動性の高い市場での短期的な価格変動に特化したモデルで、もう1つは数週間〜数か月単位の長期トレンドを重視するモデルです。後者のような広範な視点を持つモデルは、短期予測においてノイズを導入する可能性があります。こうした状況でも、出力を順位に変換することで、短期的な洞察が長期的なシグナルに埋もれてしまうのを防ぎ、よりバランスの取れた効果的な予測が可能になります。

分類器の組み合わせにおける代替的な目的

アンサンブル分類器の主な目的は、通常、分類精度の向上にあります。しかし、これは常に唯一の目的である必要はありません。分類タスクによっては、この特定の目標を超えた視点からアプローチすることで、より多くの利点を得られる場合があります。基本的な分類精度に加え、初期判断が誤っている可能性を考慮した、より洗練された評価指標を導入することが可能です。これを踏まえると、分類タスクは次の2つの異なるが補完的な目的からアプローチできます。これらはいずれも、クラスの組み合わせ戦略における性能評価指標として活用できます。

クラス集合の削減：この手法は、真のクラスを含む可能性が高い最小限のクラス集合（サブセット）を特定することを目的とします。ここでは、サブセット内の順位付けは二の次であり、集合がコンパクトで、かつ正しいクラスを含む可能性が高いことが重視されます。
クラスの順位付け：この方法では、各クラスへの所属確率の高低に基づいて順位付けをおこない、真のクラスをできるだけ上位に配置することを目指します。固定された順位しきい値を用いる代わりに、真のクラスが最上位に位置するまでの平均的な距離によって性能を評価します。

特定の用途においては、これらのうちいずれかの目的を優先することで、大きな効果が得られることがあります。明示的に指定されていない場合であっても、タスクに最も適した目的を選択し、それに対応する誤差指標を導入することで、単なる分類精度に頼るよりも、より信頼性の高い性能評価が可能になります。また、これら2つの目的は相互排他的である必要はありません。むしろ、ハイブリッドアプローチが非常に有効な場合があります。まず、クラス集合の削減に焦点を当てた組み合わせ手法を適用し、真のクラスが含まれる可能性が高い小規模なサブセットを特定します。次に、その絞り込まれた集合内で、別の方法を用いてクラスを順位付けします。この2段階のプロセスにより、最終的な予測はサブセット内で最も高くランク付けされたクラスとなり、セット削減による効率性と、順序付けによる精度の両立が可能となります。このような二重目的に基づく戦略は、特に分類の確信度が大きくばらつくような複雑な状況において、従来の単一クラス予測よりもより堅牢で柔軟な分類フレームワークを提供する可能性があります。それでは、こうした観点を踏まえて、アンサンブル分類器の検討を始めましょう。

多数決に基づくアンサンブル

多数決ルールは、投票というよく知られた概念に基づいた、アンサンブル分類におけるシンプルかつ直感的なアプローチです。この手法では、コンポーネントモデルの中で最も多くの票を得たクラスを最終的な予測結果として選択します。この単純な方法は、モデルが離散的なクラス選択しか出力できないようなシナリオにおいて特に有効であり、高度な機能を持たないモデルで構成されたシステムにおいても優れた選択肢となります。多数決ルールの形式的な数学表現は、以下の式によって表されます。

多数決方程式

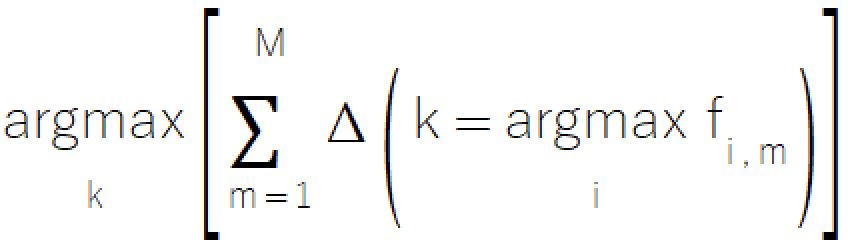
多数決ルールの実装はensemble.mqhファイルにあり、CMajorityクラスはclassify()メソッドを介してそのコア機能を管理します。

//+------------------------------------------------------------------+
//| Compute the winner via simple majority                           |
//+------------------------------------------------------------------+
class CMajority
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
   matrix            m_out;
public:
                     CMajority(void);
                    ~CMajority(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
  };

このメソッドは、予測子ベクトルと、IClassifyポインタとして渡されるコンポーネントモデルの配列を入力として受け取ります。IClassifyインターフェイスは、前の記事で説明したIModelインターフェイスとほぼ同じ方法でモデル操作を標準化します。

//+------------------------------------------------------------------+
//| IClassify interface defining methods for manipulation of         |
//|classification  algorithms                                        |
//+------------------------------------------------------------------+
interface IClassify
  {
//train a model
   bool train(matrix &predictors,matrix&targets);
//make a prediction with a trained model
   vector classify(vector &predictors);
//get number of inputs for a model
   ulong getNumInputs(void);
//get number of class outputs for a model
   ulong getNumOutputs(void);
  };

classify()関数は、選択されたクラスを表す整数値を返します。この値は0から（クラスの総数−1）までの範囲を取ります。返されるクラスは、コンポーネントモデルから最も多くの「票」を獲得したクラスに対応します。多数決ルールの実装は一見すると単純に思えるかもしれませんが、実運用には重大な課題があります。たとえば、複数のクラスが同数の票を獲得した場合はどうなるでしょうか。民主的な場面であれば、こうした状況では再投票がおこなわれるのが一般的ですが、ここではそのような対応は機能しません。この問題を公平に解決するために、本手法では比較の過程で各クラスの得票数に対して小さなランダムな変動を加えます。この工夫により、同点となったクラスにも均等な選択確率が与えられ、アルゴリズムの整合性を保ちつつ、選択の偏りを回避することができます。

//+------------------------------------------------------------------+
//|   ensemble classification                                        |
//+------------------------------------------------------------------+
ulong CMajority::classify(vector &inputs,IClassify *&models[])
  {
   double best, sum, temp;
   ulong ibest;
   best =0;
   ibest = 0;
   
   CHighQualityRandStateShell state;
   CHighQualityRand::HQRndRandomize(state.GetInnerObj());
   
   m_output = vector::Zeros(models[0].getNumOutputs());

   for(uint i  = 0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      m_output[classification.ArgMax()] += 1.0;
     }

   sum = 0.0;
   for(ulong i=0 ; i<m_output.Size() ; i++)
     {
      temp = m_output[i] + 0.999 * CAlglib::HQRndUniformR(state);
      if((i == 0)  || (temp > best))
        {
         best = temp ;
         ibest = i ;
        }
      sum += m_output[i] ;
     }

   if(sum>0.0)
      m_output/=sum;

   return ibest;
  }

多数決ルールは有用ではあるものの、注意すべきいくつかの制約が存在します。

この手法では、各モデルの最上位の選択肢のみが考慮され、下位ランクに含まれる有益な情報が無視されてしまう可能性があります。クラス出力の単純な算術平均を用いることでこの問題を回避できそうにも思えますが、実際にはノイズやスケーリングの問題を引き起こす可能性があります。
複数のクラスが関与するシナリオでは、単純な投票メカニズムでは各クラス間に存在する微妙な関係性を捉えることが困難になることがあります。
このアプローチでは、各コンポーネントモデルを一律に扱ってしまい、それぞれの性能特性や文脈における信頼性の違いを考慮できません。

次に紹介するのは、これらの課題の一部をより洗練された方法によって克服しようとする、もう一つの「投票」ベースの手法です。

ボルダ得点法

ボルダ得点法では、すべてのモデルにおいて、各クラスの上位にランク付けされたクラスの数を集計することで、各クラスのスコアを算出します。この手法は、下位の選択肢の情報を活用しつつ、その影響を適度に抑えるという点でバランスが取れており、単純な投票方式よりも洗練された代替手段として機能します。「m」個のモデルと「k」個のクラスからなるシステムにおいては、スコアの範囲が明確に定義されています。すべてのモデルで最下位に順位付けされたクラスのボルダ得点は0となり、逆にすべてのモデルで最上位に順位付けされたクラスは、最大スコアであるm(k−1)を獲得します。

この手法は、単純な投票方式に比べて大きな進歩を示しており、計算効率を維持しつつ、モデル予測の全体的な傾向をより的確に捉え、活用する能力が強化されています。ボルダ得点法は、各モデル内での同点を効果的に処理できますが、最終的なスコアにおける同点については、注意深い対応が求められます。なお、二項分類の場合、この手法は実質的に多数決ルールと同等に機能します。そのため、ボルダ得点法の明確なメリットが発揮されるのは、3クラス以上を扱うマルチクラス分類のケースにおいてです。この手法の高い効率性は、並び替えに基づく処理アプローチによって支えられており、インデックスの正確な対応関係を保ちながら、クラス出力の高速かつスムーズな処理を可能にします。

実装面では、多数決ルールと構造的に似ていますが、ボルダ得点法は追加の計算効率を取り入れている点で異なります。この処理は、ensemble.mqh内に定義されたCBordaクラスを通じて管理され、事前の訓練フェーズを必要とせずに動作します。

//+------------------------------------------------------------------+
//|  Compute the winner via Borda count                              |
//+------------------------------------------------------------------+
class CBorda
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
   matrix            m_out;
   long              m_indices[];
public:
                     CBorda(void);
                    ~CBorda(void);
   ulong             classify(vector& inputs, IClassify* &models[]);
  };

分類手順は、まず累積ボルダ得点を格納するための出力ベクトルの初期化から始まります。その後、入力ベクトルを用いてすべてのコンポーネントモデルが評価されます。次に、クラス間の関係性を追跡するためのインデックス配列が作成され、各モデルからの分類出力が昇順にソートされます。そして最後に、ソートされた順位情報に基づき、各クラスのボルダ得点法が体系的に加算されていきます。

//+------------------------------------------------------------------+
//| ensemble classification                                          |
//+------------------------------------------------------------------+
ulong CBorda::classify(vector &inputs,IClassify *&models[])
  {
   double best=0, sum, temp;
   ulong ibest=0;
   
   CHighQualityRandStateShell state;
   CHighQualityRand::HQRndRandomize(state.GetInnerObj());
   
   if(m_indices.Size())
      ArrayFree(m_indices);

   m_output = vector::Zeros(models[0].getNumOutputs());

   if(ArrayResize(m_indices, int(m_output.Size()))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return ULONG_MAX;
     }

   for(uint i = 0; i<models.Size(); i++)
     {
      vector classification  = models[i].classify(inputs);
      for(long j = 0; j<long(classification.Size()); j++)
         m_indices[j] = j;
      if(!classification.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortdsi(0,classification.Size()-1,classification,m_indices);
      for(ulong k =0; k<classification.Size(); k++)
         m_output[m_indices[k]] += double(k);
     }

   sum = 0.0;
   for(ulong i=0 ; i<m_output.Size() ; i++)
     {
      temp = m_output[i] + 0.999 * CAlglib::HQRndUniformR(state);
      if((i == 0)  || (temp > best))
        {
         best = temp ;
         ibest = i ;
        }
      sum += m_output[i] ;
     }

   if(sum>0.0)
      m_output/=sum;

   return ibest;

  }

次のセクションでは、最終的なクラス決定をおこなう際に、コンポーネントモデルによって生成された情報の大部分、あるいはほぼすべてを活用するアンサンブル手法について考察します。

コンポーネントモデル出力の平均化

コンポーネントモデルが、モデル間で意味のある、比較可能な相対的な数値出力を生成する場合、これらの数値情報を取り入れることで、アンサンブルの性能は大きく向上します。多数決法やボルダ得点法では、利用可能な情報の多くが無視されがちですが、出力の平均化をおこなうことで、より包括的にデータを活用するアプローチが実現します。この手法では、すべてのコンポーネントモデルにわたって、各クラスの出力を平均化します。モデルの数が一定であることから、この平均化は数学的には単純な出力の合計と等価です。この方法では、各分類モデルを数値予測子として扱い、それらを単純な平均により統合します。最終的な分類は、集計された出力値が最も高いクラスを選ぶことで決定されます。

平均方程式

数値予測タスクにおける平均化と分類タスクにおける平均化には、大きな違いがあります。数値予測では、通常、コンポーネントモデルは共通の訓練目標を共有しており、その結果、出力の一貫性が保たれます。しかし、分類タスクでは、個々のモデルにおいて出力のランキングだけが重要であり、このためにモデルが生成する出力は、しばしば比較できない場合があります。場合によっては、この不整合により、出力が暗黙の加重平均となり、実際の算術平均にならないことがあります。あるいは、個々のモデルが最終的な合計に不均等な影響を与え、アンサンブルの有効性を損なうこともあります。したがって、メタモデルの整合性を保つためには、すべてのコンポーネントモデルにおける出力の一貫性を検証することが重要です。

コンポーネントモデルの出力が確率であるという仮定のもとで、平均化に似た代替的な組み合わせ方法が開発されました。その一つが積ルールであり、これはモデル出力の加算を乗算に置き換えます。ただし、この方法には大きな問題があります。それは、確率に対する仮定にわずかな違反があるだけでも、極めて敏感に反応することです。たとえば、単一のモデルがクラスの確率を大幅に過小評価した場合、ゼロに近い値で乗算されるため、他の要因にかかわらずそのクラスには回復不可能なペナルティが与えられることになります。このような感度の高さが原因で、積ルールは理論的には優れていますが、実際のアプリケーションでは実用的ではないことがわかります。この方法は、数学的に正しいアプローチが実際の実装で問題を引き起こすことがあるという警告として、主に利用されます。

平均ルールの実装はCAvgClassクラスに含まれており、その構造はCMajorityクラスフレームワークと似ています。

//+------------------------------------------------------------------+
//| full resolution' version of majority rule.                       |
//+------------------------------------------------------------------+
class  CAvgClass
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
public:
                     CAvgClass(void);
                    ~CAvgClass(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
  };

分類中、classify()メソッドはすべてのコンポーネントモデルから予測を収集し、それぞれの出力を累積します。最終クラスは、最高累積スコアに基づいて決定されます。

//+------------------------------------------------------------------+
//| make classification with consensus model                         |
//+------------------------------------------------------------------+
ulong CAvgClass::classify(vector &inputs, IClassify* &models[])
  {
   m_output=vector::Zeros(models[0].getNumOutputs());
   vector model_classification;
   for(uint i =0 ; i<models.Size(); i++)
     {
      model_classification = models[i].classify(inputs);
      m_output+=model_classification;
     }

   double sum = m_output.Sum();
   ulong min = m_output.ArgMax();
   m_output/=sum;

   return min;
  }

中央値

平均を用いた集約は包括的なデータ利用という利点を持つ一方で、外れ値に対する感度が高いため、アンサンブルのパフォーマンスを損なう可能性があります。中央値は、情報の利用度がわずかに低下するものの、極端な値に対する耐性を維持しつつ、信頼性の高い中心傾向の測定を提供する堅牢な代替手段です。ensemble.mqhのCMedianクラスを通じて実装される中央値アンサンブル法は、アンサンブル分類に対して簡単で効果的なアプローチを提供します。この方法は、外れ値予測を管理し、クラス間で意味のある相対的な順序を維持するという課題に対応しています。具体的には、順位ベースの変換を実装することにより外れ値を処理します。具体的な手順として、各コンポーネントモデルからの出力を個別に順位付けし、その後、各クラスの順位の平均を計算します。このアプローチにより、極端な予測の影響を効果的に低減しながら、クラス予測間の本質的な階層関係を保つことができます。

中央値アプローチは、極端な予測が時折発生する場合でも安定性を高めます。特に非対称または歪んだ予測分布を扱う場合に有効であり、完全な情報利用と外れ値の管理との間でバランスの取れた妥協点を提供します。実務において中央値ルールを適用する場合、実際のユースケースにおける要件を評価することが重要です。特に、極端な予測が発生する可能性があるシナリオや、予測の安定性が最も重要な場合において、中央値法は信頼性とパフォーマンスの最適なバランスを提供することが多いです。

//+------------------------------------------------------------------+
//|  median of predications                                          |
//+------------------------------------------------------------------+
class CMedian
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
   matrix            m_out;
public:
                     CMedian(void);
                    ~CMedian(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
  };
//+------------------------------------------------------------------+
//| constructor                                                      |
//+------------------------------------------------------------------+
CMedian::CMedian(void)
  {

  }
//+------------------------------------------------------------------+
//| destructor                                                       |
//+------------------------------------------------------------------+
CMedian::~CMedian(void)
  {

  }
//+------------------------------------------------------------------+
//| consensus classification                                         |
//+------------------------------------------------------------------+
ulong CMedian::classify(vector &inputs,IClassify *&models[])
  {
   m_out = matrix::Zeros(models[0].getNumOutputs(),models.Size());
   vector model_classification;
   for(uint i = 0; i<models.Size(); i++)
     {
      model_classification = models[i].classify(inputs);
      if(!m_out.Col(model_classification,i))
        {
         Print(__FUNCTION__, "   ", __LINE__, " failed row insertion ", GetLastError());
         return ULONG_MAX;
        }
     }

   m_output = vector::Zeros(models[0].getNumOutputs());
   for(ulong i = 0; i<m_output.Size(); i++)
     {
      vector row = m_out.Row(i);
      if(!row.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortd(0,row.Size()-1,row);
      m_output[i] = row.Median();
     }

   double sum = m_output.Sum();
   ulong mx = m_output.ArgMax(); 
   
   if(sum>0.0)
      m_output/=sum;

   return mx;
  }

MaxMaxとMaxMinのアンサンブル分類器

場合によっては、コンポーネントモデルのアンサンブル内で、個々のモデルがクラスセットの特定のサブセットに関する専門知識を持つように設計されていることがあります。こうしたモデルは、自らの専門領域においては高い信頼度の出力を生成しますが、専門外のクラスに対しては中程度で意味の薄い値を出力する傾向があります。MaxMaxルールは、このような状況に対応するために、すべてのモデルの出力のうち、各クラスに対する最大値を用いて評価をおこないます。この手法は、高信頼の予測を重視し、情報量の少ない中間的な出力は無視するという特徴を持ちます。ただし、クラスに対する二次的な出力に分析上の価値があるようなケースには、この手法は適していないことに留意すべきです。

MaxMax式

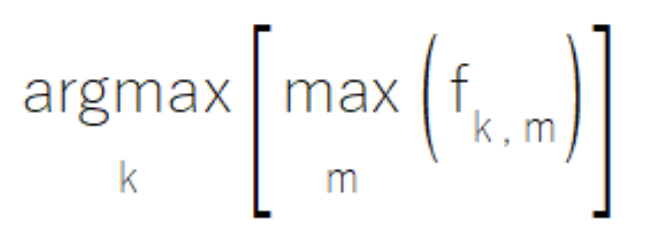
MaxMaxルールの実装は、ensemble.mqh内のCMaxmaxクラスにあり、モデルの特殊化パターンを活用するための構造化されたフレームワークを提供します。

//+------------------------------------------------------------------+
//|Compute the maximum of the predictions                            |
//+------------------------------------------------------------------+
class CMaxMax
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
   matrix            m_out;
public:
                     CMaxMax(void);
                    ~CMaxMax(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
  };
//+------------------------------------------------------------------+
//|    constructor                                                   |
//+------------------------------------------------------------------+
CMaxMax::CMaxMax(void)
  {
  }
//+------------------------------------------------------------------+
//|    destructor                                                    |
//+------------------------------------------------------------------+
CMaxMax::~CMaxMax(void)
  {
  }
//+------------------------------------------------------------------+
//|   ensemble classification                                        |
//+------------------------------------------------------------------+
ulong CMaxMax::classify(vector &inputs,IClassify *&models[])
  {
   double sum;
   ulong ibest;
   m_output = vector::Zeros(models[0].getNumOutputs());
   for(uint i  = 0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      for(ulong j = 0; j<classification.Size(); j++)
         {
            if(classification[j] > m_output[j])
               m_output[j] = classification[j];
         }
     }

   ibest  = m_output.ArgMax();
   sum  = m_output.Sum();

   if(sum>0.0)
      m_output/=sum;

   return ibest;
  }

逆に、一部のアンサンブルシステムでは、特定のクラスを識別するのではなく除外することに優れたモデルが採用されています。このような場合、インスタンスが特定のクラスに属しているとき、アンサンブル内の少なくとも1つのモデルが不正なクラスごとに明らかに低い出力を生成し、それらのクラスを考慮から事実上除外します。

MaxMin式

MaxMinルールは、各クラスに対するすべてのモデルの最小出力に基づいてクラス所属を評価することで、この特性を活用します。
このアプローチは、ensemble.mqh内のCMaxminクラスに実装されており、特定のモデルが持つ排除能力を活かすためのメカニズムを提供します。

//+------------------------------------------------------------------+
//| Compute the minimum of the predictions                           |
//+------------------------------------------------------------------+
class CMaxMin
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
   matrix            m_out;
public:
                     CMaxMin(void);
                    ~CMaxMin(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
  };
//+------------------------------------------------------------------+
//|  constructor                                                     |
//+------------------------------------------------------------------+
CMaxMin::CMaxMin(void)
  {

  }
//+------------------------------------------------------------------+
//|   destructor                                                     |
//+------------------------------------------------------------------+
CMaxMin::~CMaxMin(void)
  {
  }
//+------------------------------------------------------------------+
//|   ensemble classification                                        |
//+------------------------------------------------------------------+
ulong CMaxMin::classify(vector &inputs,IClassify *&models[])
  {
   double  sum;
   ulong ibest;

   for(uint i  = 0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      if(i == 0)
         m_output = classification;
      else
        {
         for(ulong j = 0; j<classification.Size(); j++)
            if(classification[j] < m_output[j])
               m_output[j] = classification[j];
        }
     }

   ibest  = m_output.ArgMax();
   sum  = m_output.Sum();

   if(sum>0.0)
      m_output/=sum;

   return ibest;
  }

MaxMaxまたはMaxMinアプローチを実装する際には、モデルアンサンブルの特性を慎重に評価する必要があります。MaxMaxアプローチの場合、各モデルが明確な専門性（特殊化）パターンを示していることの確認が不可欠です。特に、中程度の出力が有用な二次情報ではなくノイズを表していることを確認することが重要です。加えて、アンサンブル全体が関連するすべてのクラスを網羅的にカバーしていることも確認する必要があります。一方、MaxMinアプローチを適用する場合には、アンサンブル全体であらゆる潜在的な誤分類シナリオに対応できていることを確認し、除外が不十分なクラスが存在しないか注意を払う必要があります。

インターセクション法

インターセクション法は、分類器の組み合わせに対する特殊なアプローチであり、汎用的な分類を目的とするのではなく、主にクラス集合の削減を目的として設計されています。その直接的な応用範囲は限定的であるものの、本手法はより堅牢な手法、特にユニオン法の基盤となる先駆的な手法として、本記事に含まれています。このアプローチでは、各コンポーネントモデルが、入力ごとに最も可能性が高いクラスから最も低いクラスまで、全クラスに対する完全なランキングを生成する必要があります。この要件は多くの分類器で満たすことが可能であり、実数出力を順位付けするプロセスは、貴重な情報を保持しつつノイズを効果的に除去することで、性能向上に寄与することが多くあります。本手法の学習フェーズでは、訓練セット全体において真のクラスが一貫して含まれるよう、各コンポーネントモデルが保持すべき上位ランク出力の最小数を特定します。新たな入力に対しては、すべてのコンポーネントモデルから得られる最小サブセットの交差をとることで、真のクラスを含む最小限のクラス集合を導出し、それを最終的な決定とします。

交差点のベン図

複数のクラスと4つのモデルを含む実際の例を考えてみましょう。訓練セット内の5つのサンプルを調べると、真のクラスの順位パターンがモデルごとに異なることがわかります。

サンプル	モデル1	モデル2	モデル3	モデル4
1	3	21	4	5
2	8	4	8	9
3	1	17	12	3
4	7	16	2	8
5	7	8	6	1
最大	8	21	12	9

表は、2番目のサンプルにおける真のクラスが、最初のモデルでは8位、2番目のモデルでは4位、4番目のモデルでは9位にランク付けされたことを示しています。表の最終行には、列ごとの最大順位が示されており、それぞれ8、21、12、9となっています。未知のケースを評価する際には、アンサンブルはこれらの閾値に従って、各モデルから上位のクラスを選択し、それらを交差させることで、すべてのモデルに共通するクラスの最終的なサブセットを生成します。

CIntersectionクラスは、fit()関数を通じて独自の訓練手順を持ち、インターセクション法の実装を管理します。この関数は訓練データを分析し、各モデルにおける最悪ケースのランクを決定します。さらに、正解クラスが常に含まれるようにするために、保持すべき上位ランクのクラス数（最小値）を追跡します。

//+------------------------------------------------------------------+
//| Use intersection rule to compute minimal class set               |
//+------------------------------------------------------------------+
class CIntersection
  {
private:
   ulong             m_nout;
   long              m_indices[];
   vector            m_ranks;
   vector            m_output;
public:
                     CIntersection(void);
                    ~CIntersection(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
   bool              fit(matrix &inputs, matrix &targets, IClassify* &models[]);
   vector            proba(void) { return m_output;}
  };

CIntersectionクラスのclassify()メソッドを呼び出すと、入力データに対してすべてのコンポーネントモデルが順に評価されます。各モデルの出力ベクトルはソートされ、そのソート済みベクトルのインデックスを用いて、各モデルにおける上位ランクのサブセットに属するクラスの交差が計算されます。

//+------------------------------------------------------------------+
//|   fit an ensemble model                                          |
//+------------------------------------------------------------------+
bool CIntersection::fit(matrix &inputs,matrix &targets,IClassify *&models[])
  {
   m_nout = targets.Cols();

   m_output = vector::Ones(m_nout);
   m_ranks = vector::Zeros(models.Size());
   double best = 0.0;
   ulong nbad;
   if(ArrayResize(m_indices,int(m_nout))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return false;
     }

   ulong k;
   for(ulong i = 0; i<inputs.Rows(); i++)
     {
      vector trow = targets.Row(i);
      vector inrow = inputs.Row(i);
      k = trow.ArgMax();
      best = trow[k];

      for(uint j = 0; j<models.Size(); j++)
        {
         vector classification = models[j].classify(inrow);
         best = classification[k];
         nbad = 1;
         for(ulong ii = 0; ii<m_nout; ii++)
           {
            if(ii == k)
               continue;
            if(classification[ii] >= best)
               ++nbad;
           }
         if(nbad > ulong(m_ranks[j]))
            m_ranks[j] = double(nbad);
        }
     }

   return true;

  }
//+------------------------------------------------------------------+
//|  ensemble classification                                         |
//+------------------------------------------------------------------+
ulong CIntersection::classify(vector &inputs,IClassify *&models[])
  {
   
   for(long j =0; j<long(m_nout); j++)
         m_indices[j] = j;
         
   for(uint i =0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      ArraySort(m_indices);
      qsortdsi(0,classification.Size()-1,classification,m_indices);
      for(ulong j = 0; j<m_nout-ulong(m_ranks[i]); j++)
        {
         m_output[m_indices[j]] = 0.0;
        }
     }

   ulong n=0;
   double cut = 0.5;
   for(ulong i = 0; i<m_nout; i++)
     {
      if(m_output[i] > cut)
         ++n;
     }

   return n;
  }

理論的には洗練された手法である一方で、インターセクション法にはいくつかの重要な制約があります。訓練セット内の真のクラスが常に含まれるという保証がある一方で、その利点は手法の本質的な制約によって相殺されることがあります。特に、モデル間で上位にランク付けされたクラスに共通点がない場合、訓練セット外のケースでは空のクラスサブセットが生成されてしまう可能性があります。さらに深刻なのは、この手法が最悪ケースのパフォーマンスに依存している点であり、その結果としてクラスサブセットが不必要に大きくなり、手法の効果と効率の両方が損なわれます。

インターセクション法は、すべてのコンポーネントモデルがクラスセット全体にわたって一貫したパフォーマンスを示すような特定の状況では有用となり得ます。しかしながら、特定のクラスサブセットに特化したモデルを活用するような応用領域では、専門外の領域におけるモデル性能の低下に敏感であるため、実用性が限定されることが少なくありません。結局のところ、この手法の最大の価値は、多くの分類タスクへの直接的な適用ではなく、ユニオン法など、より堅牢なアプローチの概念的基盤としての貢献にあります。

ユニオンルール

ユニオンルールは、インターセクション法を戦略的に強化した手法であり、最悪ケースのパフォーマンスに過度に依存するというその主な制約を克服することを目的としています。特に、異なる専門領域を持つスペシャリストモデルを組み合わせる場合に効果を発揮し、評価の焦点を「最悪」から「最良」のパフォーマンスシナリオへと移行させます。初期の処理はインターセクション法と同様で、訓練セットに含まれる各ケースについて、コンポーネントモデルごとの真のクラスのランキングを分析します。ただしユニオンルールでは、最悪のパフォーマンスを監視するのではなく、各ケースにおいて最も優れた性能を示したモデルを特定し、そのパフォーマンスを記録していきます。そして、訓練データ全体における最良パフォーマンス中の最も悪いものを評価します。未知のケースを分類する際には、各コンポーネントモデルが提供する最適なサブセットを集約・統合することで、最終的なクラスのサブセットが構築されます。前述のデータセット例を振り返りましょう。今回は、「Perf」という接頭辞を持つパフォーマンス追跡用の列が追加されています。

サンプル	モデル1	モデル2	モデル3	モデル4	パフォーマンスモデル1	パフォーマンスモデル2	パフォーマンスモデル3	パフォーマンスモデル4
1	3	21	4	5	3	0	0	0
2	8	4	8	9	0	4	0	0
3	1	17	12	3	1	0	0	0
4	7	16	2	8	0	0	2	0
5	7	8	6	1	0	0	0	1
最大					3	4	2	1

追加の列は、各モデルが優れたパフォーマンスを示したインスタンスを記録しており、最下行にはこれらの最良ケースにおける最大値が示されています。

ユニオンルールは、インターセクション法と比較していくつかの明確な利点を備えています。特定のケースにおいて少なくとも1つのモデルが常に最良のパフォーマンスを発揮するため、空のクラスサブセットが生成される可能性が排除されます。またこの手法は、学習時に専門領域外での低パフォーマンスを無視することにより、スペシャリストモデルを効果的に活用でき、適切なモデルがその専門性を発揮できる環境を整えます。さらに、追跡行列上でゼロの列として現れるような、一貫して性能が低いモデルを自然に特定し、必要に応じて除外する仕組みを備えている点も重要です。

ユニオン法の実装は、パフォーマンス追跡列からの最大値を監視するためにm_ranksコンテナを活用する点で、インターセクション法と構造的に類似しています。

//+------------------------------------------------------------------+
//| Use union rule to compute minimal class set                      |
//+------------------------------------------------------------------+
class CUnion
  {
private:
   ulong             m_nout;
   long              m_indices[];
   vector            m_ranks;
   vector            m_output;
public:
                     CUnion(void);
                    ~CUnion(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
   bool              fit(matrix &inputs, matrix &targets, IClassify* &models[]);
   vector            proba(void) { return m_output;}
  };

ただし、クラス順位とフラグの初期化の処理において重要な相違点が現れます。訓練中、システムは各ケースに対してモデル間で最小順位を追跡し、必要に応じてm_ranksの最大値を更新します。

//+------------------------------------------------------------------+
//|  fit an ensemble model                                           |
//+------------------------------------------------------------------+
bool CUnion::fit(matrix &inputs,matrix &targets,IClassify *&models[])
  {
   m_nout = targets.Cols();

   m_output = vector::Zeros(m_nout);
   m_ranks = vector::Zeros(models.Size());
   double best = 0.0;
   ulong nbad;
   if(ArrayResize(m_indices,int(m_nout))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return false;
     }

   ulong k, ibestrank=0, bestrank=0;
   for(ulong i = 0; i<inputs.Rows(); i++)
     {
      vector trow = targets.Row(i);
      vector inrow = inputs.Row(i);
      k = trow.ArgMax();

      for(uint j = 0; j<models.Size(); j++)
        {
         vector classification = models[j].classify(inrow);
         best = classification[k];
         nbad = 1;
         for(ulong ii = 0; ii<m_nout; ii++)
           {
            if(ii == k)
               continue;
            if(classification[ii] >= best)
               ++nbad;
           }
         if(j == 0 || nbad < bestrank)
           {
            bestrank = nbad;
            ibestrank = j;
           }
        }
      if(bestrank > ulong(m_ranks[ibestrank]))
         m_ranks[ibestrank] =  double(bestrank);
     }

   return true;
  }

分類フェーズでは、特定のパフォーマンス基準を満たすクラスが順次追加されます。

//+------------------------------------------------------------------+
//| ensemble classification                                          |
//+------------------------------------------------------------------+
ulong CUnion::classify(vector &inputs,IClassify *&models[])
  {
   for(long j =0; j<long(m_nout); j++)
         m_indices[j] = j;
         
   for(uint i =0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      ArraySort(m_indices);
      qsortdsi(0,classification.Size()-1,classification,m_indices);
      for(ulong j =(m_nout-ulong(m_ranks[i])); j<m_nout; j++)
        {
         m_output[m_indices[j]] = 1.0;
        }
     }

   ulong n=0;
   double cut = 0.5;
   for(ulong i = 0; i<m_nout; i++)
     {
      if(m_output[i] > cut)
         ++n;
     }

   return n;
  }

ユニオンルールは、インターセクション法の多くの制限に効果的に対処できますが、すべてのコンポーネントモデルが低いランキングを生成するような外れ値的なケースには依然として脆弱です。このようなシナリオは確かに厄介ですが、適切に設計されたアプリケーションにおいてはまれであり、システム設計やモデル選定を工夫することで多くの場合回避が可能です。この手法の有効性は、各コンポーネントが特定の領域で優れた性能を発揮し、他の領域ではやや劣るといった専門性のあるモデルが用いられる環境で特に際立ちます。この特性により、多様な専門知識が求められる複雑な分類タスクにおいて、ユニオンルールは非常に有用です。

ロジスティック回帰に基づく分類器の組み合わせ

これまでに紹介したアンサンブル分類器の中で、ボルダ得点法は、同等の性能を持つ分類器を組み合わせるための、汎用的かつ効果的な手法として機能します。この手法は、すべてのモデルが同程度の予測能力を持っているという前提に基づいています。しかし、モデルごとに性能に大きな差がある場合には、個々のモデルの性能に応じた重み付けをおこなうことが望ましくなります。ロジスティック回帰は、こうした重み付きの組み合わせを実現するための、洗練されたフレームワークを提供します。

分類器の組み合わせにおけるロジスティック回帰の実装は、基本的には線形回帰の原理に基づいていますが、分類問題に特有の課題に対応しています。ロジスティック回帰では、連続値を直接予測するのではなく、各クラスに属する確率を算出することで、より洗練された分類アプローチを実現します。このプロセスは、元の訓練データを回帰に適した形式に変換するところから始まります。たとえば、3つのクラスと4つのモデルがあり、それぞれのモデルが次のような出力を生成するシステムを考えてみましょう。

	モデル1	モデル2	モデル3	モデル4
1	0.7	0.1	0.8	0.4
2	0.8	0.3	0.9	0.3
3	0.2	0.2	0.7	0.2

このデータは、元の各ケースに対して3つの新しい回帰用訓練データを生成します。正解クラスに対しては目標変数を1.0に、誤ったクラスに対しては0.0に設定します。予測子には、生の出力値ではなく比例ランキングを使用することで、数値的な安定性が向上します。

ensemble.mqhに定義されたCLogitRegクラスは、分類器アンサンブルにおける重み付き結合アプローチの実装を管理します。

//+------------------------------------------------------------------+
//|  Use logistic regression to find best class                      |
//|           This uses one common weight vector for all classes.    |
//+------------------------------------------------------------------+
class ClogitReg
  {
private:
   ulong             m_nout;
   long              m_indices[];
   matrix            m_ranks;
   vector            m_output;
   vector            m_targs;
   matrix            m_input;
   logistic::Clogit  *m_logit;
public:
                     ClogitReg(void);
                    ~ClogitReg(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
   bool              fit(matrix &inputs, matrix &targets, IClassify* &models[]);
   vector            proba(void) { return m_output;}
  };

fit()メソッドは、各ケースを体系的に処理することで回帰用の訓練セットを構築します。まず、各訓練サンプルの真のクラスメンバーシップが判定されます。次に、各コンポーネントモデルの評価結果が行列m_ranksに整理されます。この行列は、回帰問題の従属変数および独立変数を生成するために処理され、その後、m_logitオブジェクトを用いて回帰が実行されます。

//+------------------------------------------------------------------+
//| fit an ensemble model                                            |
//+------------------------------------------------------------------+
bool ClogitReg::fit(matrix &inputs,matrix &targets,IClassify *&models[])
  {
   m_nout = targets.Cols();
   m_input = matrix::Zeros(inputs.Rows(),models.Size());
   m_targs = vector::Zeros(inputs.Rows());
   m_output = vector::Zeros(m_nout);
   m_ranks = matrix::Zeros(models.Size(),m_nout);

   double best = 0.0;
   ulong nbelow;
   if(ArrayResize(m_indices,int(m_nout))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return false;
     }

   ulong k;
   if(CheckPointer(m_logit) == POINTER_DYNAMIC)
      delete m_logit;

   m_logit = new logistic::Clogit();

   for(ulong i = 0; i<inputs.Rows(); i++)
     {
      vector trow = targets.Row(i);
      vector inrow = inputs.Row(i);
      k = trow.ArgMax();
      best = trow[k];

      for(uint j = 0; j<models.Size(); j++)
        {
         vector classification = models[j].classify(inrow);
         if(!m_ranks.Row(classification,j))
           {
            Print(__FUNCTION__, "   ", __LINE__, " failed row insertion ", GetLastError());
            return false;
           }
        }
      for(ulong j = 0; j<m_nout; j++)
        {
         for(uint jj =0; jj<models.Size(); jj++)
           {
            nbelow = 0;
            best = m_ranks[jj][j];
            for(ulong ii =0; ii<m_nout; ii++)
              {
               if(m_ranks[jj][ii]<best)
                  ++nbelow;
              }
            m_input[i][jj] = double(nbelow)/double(m_nout);
           }
         m_targs[i] = (j == k)? 1.0:0.0;
        }
     }

   return m_logit.fit(m_input,m_targs);
  }

この実装は、分類器の組み合わせに対する洗練されたアプローチを提供するものであり、コンポーネントモデルが異なる分類タスクにおいて異なるレベルの有効性を示すようなシナリオにおいて、特に有用です。

加重分類プロセスは、ボルダ得点法に基づきつつ、モデル固有の重みを統合することで構築されています。アルゴリズムは、累積用ベクトルの初期化から始まり、各コンポーネントモデルを通じて未知のケースを順に処理します。m_logitオブジェクトによって計算された最適な重みは、コンポーネント分類器からの出力の寄与を調整するために適用されます。最終的なクラスは、m_output内の最大値に対応するインデックスとして決定されます。

//+------------------------------------------------------------------+
//| classify with ensemble model                                     |
//+------------------------------------------------------------------+
ulong ClogitReg::classify(vector &inputs,IClassify *&models[])
  {

   double temp;
   for(uint i =0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      for(long j =0; j<long(classification.Size()); j++)
         m_indices[j] = j;
      if(!classification.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortdsi(0,classification.Size()-1,classification,m_indices);
      temp = m_logit.coeffAt(i);
      for(ulong j = 0 ; j<m_nout; j++)
        {
         m_output[m_indices[j]] += j * temp;
        }
     }
   double sum = m_output.Sum();
   ulong ibest = m_output.ArgMax();
   double best = m_output[ibest];

   if(sum>0.0)
      m_output/=sum;

   return ibest;
  }

実装では、より高い安定性と過学習のリスクが低いことから、共通の重みが重視されています。ただし、十分な訓練データがあるアプリケーションでは、クラス固有の重みも有効な選択肢となります。クラス固有の重みを用いる手法については、後のセクションで詳しく説明します。ここでは、最適な重みがどのように導出されるか、特にロジスティック回帰モデルに注目して説明を進めます。

ロジスティック回帰の中心となるのは、以下に示すロジスティック変換（ロジット変換）です。

ロジット変換

この関数は、無限の範囲を[0, 1]の区間にマッピングします。上記の式において、xが極端に負の値を取ると、関数の出力は0に近づきます。反対に、xが大きくなるほど、関数の値は1に近づきます。x=0のとき、関数は0と1のちょうど中間である0.5を返します。回帰モデルにおいてxを予測変数とすると、x=0の場合、そのサンプルが特定のクラスに属する確率は50%になります。xの値が0より大きくなるにつれて、そのクラスに属する確率も上昇します。一方で、xの値が0より小さくなると、確率は減少します。

確率を表現する別の方法として「オッズ」があります。これは正式には「オッズ比」と呼ばれ、ある事象が起こる確率を、それが起こらない確率で割ったものです。ロジット変換において、e^xをf(x)を使って表すと、次の式が導かれます。

再配置されたロジット変換

この式の両辺に対数を適用し、xを回帰問題における予測変数とすることで、指数を取り除くことができ、次のような式が導かれます。

ロジスティック回帰

分類器アンサンブルの文脈において、この表現は、訓練データ内の各サンプルに対して、コンポーネント分類器から得られる予測値の線形結合によって、対応するクラスラベルのオッズの対数が得られることを意味しています。最適な重みwは、最大尤度推定や目的関数の最小化によって求めることができます。詳細な手法については、本記事の範囲を超えています。

MQL5におけるロジスティック回帰の包括的な実装を見つけるのは、当初は困難でした。AlglibライブラリのMQL5向けポートには、ロジスティック回帰用の専用ツールが含まれていますが、筆者はそれらを正常にコンパイルできたことがありません。また、Alglibツールのデモプログラムにも、それらを利用した例は見当たりませんでした。とはいえ、logistic.mqhファイルで定義されたClogitクラスの実装においては、Alglibライブラリが有用でした。このファイルには、CNDimensional_Gradインターフェイスを実装するCFgクラスの定義も含まれています。

//+------------------------------------------------------------------+
//|  function and gradient calculation object                        |
//+------------------------------------------------------------------+
class CFg:public CNDimensional_Grad
  {
private:
   matrix            m_preds;
   vector            m_targs;
   ulong             m_nclasses,m_samples,m_features;
   double            loss_gradient(matrix &coef,double &gradients[]);
   void              weight_intercept_raw(matrix &coef,matrix &x, matrix &wghts,vector &intcept,matrix &rpreds);
   void              weight_intercept(matrix &coef,matrix &wghts,vector &intcept);
   double            l2_penalty(matrix &wghts,double strenth);
   void              sum_exp_minus_max(ulong index,matrix &rp,vector &pr);
   void              closs_grad_halfbinmial(double y_true,double raw, double &inout_1,double &intout_2);
public:
   //--- constructor, destructor
                     CFg(matrix &predictors,vector &targets, ulong num_classes)
     {
      m_preds = predictors;
      vector classes = np::unique(targets);
      np::sort(classes);
      vector checkclasses = np::arange(classes.Size());
      if(checkclasses.Compare(classes,1.e-1))
        {
         double classv[];
         np::vecAsArray(classes,classv);
         m_targs = targets;
         for(ulong i = 0; i<targets.Size(); i++)
            m_targs[i] = double(ArrayBsearch(classv,m_targs[i]));
        }
      else
         m_targs = targets;

      m_nclasses = num_classes;
      m_features = m_preds.Cols();
      m_samples = m_preds.Rows();
     }
                    ~CFg(void) {}

   virtual void      Grad(double &x[],double &func,double &grad[],CObject &obj);
   virtual void      Grad(CRowDouble &x,double &func,CRowDouble &grad,CObject &obj);
  };
//+------------------------------------------------------------------+
//| this function is not used                                        |
//+------------------------------------------------------------------+
void CFg::Grad(double &x[],double &func,double &grad[],CObject &obj)
  {
   matrix coefficients;
   arrayToMatrix(x,coefficients,m_nclasses>2?m_nclasses:m_nclasses-1,m_features+1);
   func=loss_gradient(coefficients,grad);
   return;
  }
//+------------------------------------------------------------------+
//| get function value and gradients                                 |
//+------------------------------------------------------------------+
void CFg::Grad(CRowDouble &x,double &func,CRowDouble &grad,CObject &obj)
  {
   double xarray[],garray[];
   x.ToArray(xarray);
   Grad(xarray,func,garray,obj);
   grad = garray;
   return;
  }
//+------------------------------------------------------------------+
//| loss gradient                                                    |
//+------------------------------------------------------------------+
double CFg::loss_gradient(matrix &coef,double &gradients[])
  {
   matrix weights;
   vector intercept;
   vector losses;
   matrix gradpointwise;
   matrix rawpredictions;
   matrix gradient;
   double loss;
   double l2reg;

//calculate weights intercept and raw predictions
   weight_intercept_raw(coef,m_preds,weights,intercept,rawpredictions);
   gradpointwise = matrix::Zeros(m_samples,rawpredictions.Cols());
   losses = vector::Zeros(m_samples);
   double sw_sum = double(m_samples);
//loss gradient calculations
   if(m_nclasses>2)
     {
      double max_value, sum_exps;
      vector p(rawpredictions.Cols()+2);
      //---
      for(ulong i = 0; i< m_samples; i++)
        {
         sum_exp_minus_max(i,rawpredictions,p);
         max_value = p[rawpredictions.Cols()];
         sum_exps = p[rawpredictions.Cols()+1];
         losses[i] = log(sum_exps) + max_value;
         //---
         for(ulong k  = 0; k<rawpredictions.Cols(); k++)
           {
            if(ulong(m_targs[i]) == k)
               losses[i] -= rawpredictions[i][k];
            p[k]/=sum_exps;
            gradpointwise[i][k] = p[k] - double(int(ulong(m_targs[i])==k));
           }
        }
     }
   else
     {
      for(ulong i = 0; i<m_samples; i++)
        {
         closs_grad_halfbinmial(m_targs[i],rawpredictions[i][0],losses[i],gradpointwise[i][0]);
        }
     }
//---
   loss = losses.Sum()/sw_sum;
   l2reg = 1.0 / (1.0 * sw_sum);
   loss += l2_penalty(weights,l2reg);
   gradpointwise/=sw_sum;
//---
   if(m_nclasses>2)
     {
      gradient = gradpointwise.Transpose().MatMul(m_preds) + l2reg*weights;
      gradient.Resize(gradient.Rows(),gradient.Cols()+1);
      vector gpsum = gradpointwise.Sum(0);
      gradient.Col(gpsum,m_features);
     }
   else
     {
      gradient = m_preds.Transpose().MatMul(gradpointwise) + l2reg*weights.Transpose();
      gradient.Resize(gradient.Rows()+1,gradient.Cols());
      vector gpsum = gradpointwise.Sum(0);
      gradient.Row(gpsum,m_features);
     }
//---
   matrixToArray(gradient,gradients);
//---
   return loss;
  }
//+------------------------------------------------------------------+
//|  weight intercept raw preds                                      |
//+------------------------------------------------------------------+
void CFg::weight_intercept_raw(matrix &coef,matrix &x,matrix &wghts,vector &intcept,matrix &rpreds)
  {
   weight_intercept(coef,wghts,intcept);
   matrix intceptmat = np::vectorAsRowMatrix(intcept,x.Rows());
   rpreds = (x.MatMul(wghts.Transpose()))+intceptmat;
  }
//+------------------------------------------------------------------+
//| weight intercept                                                 |
//+------------------------------------------------------------------+
void CFg::weight_intercept(matrix &coef,matrix &wghts,vector &intcept)
  {
   intcept = coef.Col(m_features);
   wghts = np::sliceMatrixCols(coef,0,m_features);
  }
//+------------------------------------------------------------------+
//|  sum exp minus max                                               |
//+------------------------------------------------------------------+
void CFg::sum_exp_minus_max(ulong index,matrix &rp,vector &pr)
  {
   double mv = rp[index][0];
   double s_exps = 0.0;

   for(ulong k = 1; k<rp.Cols(); k++)
     {
      if(mv<rp[index][k])
         mv=rp[index][k];
     }

   for(ulong k = 0; k<rp.Cols(); k++)
     {
      pr[k] = exp(rp[index][k] - mv);
      s_exps += pr[k];
     }

   pr[rp.Cols()] = mv;
   pr[rp.Cols()+1] = s_exps;
  }
//+------------------------------------------------------------------+
//|  l2 penalty                                                      |
//+------------------------------------------------------------------+
double CFg::l2_penalty(matrix &wghts,double strenth)
  {
   double norm2_v;
   if(wghts.Rows()==1)
     {
      matrix nmat = (wghts).MatMul(wghts.Transpose());
      norm2_v = nmat[0][0];
     }
   else
      norm2_v = wghts.Norm(MATRIX_NORM_FROBENIUS);

   return 0.5*strenth*norm2_v;
  }
//+------------------------------------------------------------------+
//|   closs_grad_half_binomial                                       |
//+------------------------------------------------------------------+
void CFg::closs_grad_halfbinmial(double y_true,double raw, double &inout_1,double &inout_2)
  {
   if(raw <= -37.0)
     {
      inout_2 = exp(raw);
      inout_1 = inout_2 - y_true * raw;
      inout_2 -= y_true;
     }
   else
      if(raw <= -2.0)
        {
         inout_2 = exp(raw);
         inout_1 = log1p(inout_2) - y_true * raw;
         inout_2 = ((1.0 - y_true) * inout_2 - y_true) / (1.0 + inout_2);
        }
      else
         if(raw <= 18.0)
           {
            inout_2 = exp(-raw);
            // log1p(exp(x)) = log(1 + exp(x)) = x + log1p(exp(-x))
            inout_1 = log1p(inout_2) + (1.0 - y_true) * raw;
            inout_2 = ((1.0 - y_true) - y_true * inout_2) / (1.0 + inout_2);
           }
         else
           {
            inout_2 = exp(-raw);
            inout_1 = inout_2 + (1.0 - y_true) * raw;
            inout_2 = ((1.0 - y_true) - y_true * inout_2) / (1.0 + inout_2);
           }
  }

これは、LBFGS関数の最小化手順で必要です。Clogitには、訓練と推論のためのより一般的なメソッドがあります。

//+------------------------------------------------------------------+
//| logistic regression implementation                               |
//+------------------------------------------------------------------+
class Clogit
  {
public:
                     Clogit(void);
                    ~Clogit(void);
   bool              fit(matrix &predictors, vector &targets);
   double            predict(vector &preds);
   vector            proba(vector &preds);
   matrix            probas(matrix &preds);
   double            coeffAt(ulong index);
private:
   ulong             m_nsamples;
   ulong             m_nfeatures;
   bool              m_trained;
   matrix            m_train_preds;
   vector            m_train_targs;
   matrix            m_coefs;
   vector            m_bias;
   vector            m_classes;
   double            m_xin[];
   CFg               *m_gradfunc;
   CObject           m_dummy;
   vector            predictProba(double &in);
  };
//+------------------------------------------------------------------+
//| constructor                                                      |
//+------------------------------------------------------------------+
Clogit::Clogit(void)
  {
  }
//+------------------------------------------------------------------+
//| destructor                                                       |
//+------------------------------------------------------------------+
Clogit::~Clogit(void)
  {
   if(CheckPointer(m_gradfunc) == POINTER_DYNAMIC)
      delete m_gradfunc;
  }
//+------------------------------------------------------------------+
//| fit a model to a dataset                                         |
//+------------------------------------------------------------------+
bool Clogit::fit(matrix &predictors, vector &targets)
  {
   m_trained = false;
   m_classes = np::unique(targets);
   np::sort(m_classes);

   if(predictors.Rows()!=targets.Size() || m_classes.Size()<2)
     {
      Print(__FUNCTION__," ",__LINE__," invalid inputs ");
      return m_trained;
     }

   m_train_preds = predictors;
   m_train_targs = targets;

   m_nfeatures = m_train_preds.Cols();
   m_nsamples = m_train_preds.Rows();

   m_coefs = matrix::Zeros(m_classes.Size()>2?m_classes.Size():m_classes.Size()-1,m_nfeatures+1);

   matrixToArray(m_coefs,m_xin);

   m_gradfunc = new CFg(m_train_preds,m_train_targs,m_classes.Size());
//---
   CMinLBFGSStateShell state;
   CMinLBFGSReportShell rep;
   CNDimensional_Rep   frep;
//---
   CAlglib::MinLBFGSCreate(m_xin.Size(),m_xin.Size()>=5?5:m_xin.Size(),m_xin,state);
//---
   CAlglib::MinLBFGSOptimize(state,m_gradfunc,frep,true,m_dummy);
//---
   CAlglib::MinLBFGSResults(state,m_xin,rep);
//---
   if(rep.GetTerminationType()>0)
     {
      m_trained = true;
      arrayToMatrix(m_xin,m_coefs,m_classes.Size()>2?m_classes.Size():m_classes.Size()-1,m_nfeatures+1);
      m_bias = m_coefs.Col(m_nfeatures);
      m_coefs = np::sliceMatrixCols(m_coefs,0,m_nfeatures);
     }
   else
      Print(__FUNCTION__," ", __LINE__, " failed to train the model ", rep.GetTerminationType());

   delete m_gradfunc;


   return m_trained;
  }

//+------------------------------------------------------------------+
//| get probability for single sample                                |
//+------------------------------------------------------------------+
vector Clogit::proba(vector &preds)
  {
   vector predicted;

   if(!m_trained)
     {
      Print(__FUNCTION__," ", __LINE__," no trained model available ");
      predicted.Fill(EMPTY_VALUE);
      return predicted;
     }

   predicted = ((preds.MatMul(m_coefs.Transpose())));
   predicted += m_bias;

   if(predicted.Size()>1)
     {
      if(!predicted.Activation(predicted,AF_SOFTMAX))
        {
         Print(__FUNCTION__," ", __LINE__," errror ", GetLastError());
         predicted.Fill(EMPTY_VALUE);
         return predicted;
        }
     }
   else
     {
      predicted = predictProba(predicted[0]);
     }

   return predicted;
  }
//+------------------------------------------------------------------+
//|  get probability for binary classification                       |
//+------------------------------------------------------------------+
vector Clogit::predictProba(double &in)
  {
   vector out(2);

   double n = 1.0/(1.0+exp(-1.0*in));

   out[0] = 1.0 - n;
   out[1] = n;

   return out;
  }
//+------------------------------------------------------------------+
//| get probabilities for multiple samples                           |
//+------------------------------------------------------------------+
matrix Clogit::probas(matrix &preds)
  {
   matrix output(preds.Rows(),m_classes.Size());
   vector rowin,rowout;
   for(ulong i = 0; i<preds.Rows(); i++)
     {
      rowin = preds.Row(i);
      rowout = proba(rowin);
      if(rowout.Max() == EMPTY_VALUE || !output.Row(rowout,i))
        {
         Print(__LINE__," probas error ", GetLastError());
         output.Fill(EMPTY_VALUE);
         break;
        }
     }

   return output;
  }
//+------------------------------------------------------------------+
//| get probability for single sample                                |
//+------------------------------------------------------------------+
double Clogit::predict(vector &preds)
  {
   vector prob = proba(preds);
   if(prob.Max() == EMPTY_VALUE)
     {
      Print(__LINE__," predict error ");
      return EMPTY_VALUE;
     }

   return m_classes[prob.ArgMax()];
  }
//+------------------------------------------------------------------+
//|  get model coefficient at specific index                         |
//+------------------------------------------------------------------+
double Clogit::coeffAt(ulong index)
  {
   if(index<(m_coefs.Rows()))
     {
      return (m_coefs.Row(index)).Sum();
     }
   else
     {
      return 0.0;
     }
  }
}
//+------------------------------------------------------------------+

クラス固有の重みを用いたロジスティック回帰ベースのアンサンブル手法

前のセクションで紹介した単一の重みセットによるアプローチは、安定性と効果性の面で優れていますが、モデルの特殊化を十分に活かせないという制約があります。もし、個々のモデルが特定のクラスに対して他よりも高い性能を示す場合（設計によるものでも、自然な学習の結果でも）、各クラスごとに個別の重みセットを実装することで、それぞれのモデルの特化能力をより効果的に活用することが可能になります。しかし、クラス固有の重みセットに移行すると、最適化プロセスが大幅に複雑化します。単一の重みセットを最適化する代わりに、アンサンブルでは各クラスに対して1セット、合計でKセット（クラス数分）を扱う必要があり、それぞれがM個のパラメータを持つため、総計でKxMのパラメータを最適化することになります。このようなパラメータ数の増加は、データ要件や実装上のリスクを慎重に評価する必要性を伴います。

このような手法を堅牢に適用するためには、統計的な妥当性を確保できるだけの十分な訓練データが不可欠です。一般的な指針としては、各クラスにつき、使用するモデルの10倍以上の訓練ケースが必要とされます。たとえ十分なデータがあったとしても、このアプローチは慎重に適用すべきであり、クラス間で明確にモデルの性能差が確認できる場合に限り有効です。

CLogitRegSepクラスは、各クラスに個別のClogitオブジェクトを割り当てることで、CLogitRegクラスとは異なる方法でクラス固有の重みセットの実装を管理します。学習時には、すべてのデータをひとつのセットに統合するのではなく、各クラスごとの専用データセットに分割して処理します。

//+------------------------------------------------------------------+
//| Use logistic regression to find best class.                      |
//|              This uses separate weight vectors for each class.   |
//+------------------------------------------------------------------+
class ClogitRegSep
  {
private:
   ulong             m_nout;
   long              m_indices[];
   matrix            m_ranks;
   vector            m_output;
   vector            m_targs[];
   matrix            m_input[];
   logistic::Clogit  *m_logit[];
public:
                     ClogitRegSep(void);
                    ~ClogitRegSep(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
   bool              fit(matrix &inputs, matrix &targets, IClassify* &models[]);
   vector            proba(void) { return m_output;}
  };

未知のケースの分類プロセスは、単一重みアプローチとほぼ同様に進行しますが、ひとつ重要な違いがあります。それは、ボルダ得点の計算時にクラス固有の重みが適用されるという点です。このような特殊化により、システムは各クラスに特化したモデルの専門性を、より効果的に活用できるようになります。

//+------------------------------------------------------------------+
//| classify with ensemble model                                     |
//+------------------------------------------------------------------+
ulong ClogitRegSep::classify(vector &inputs,IClassify *&models[])
  {

   double temp;
   for(uint i =0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      for(long j =0; j<long(classification.Size()); j++)
         m_indices[j] = j;
      if(!classification.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortdsi(0,classification.Size()-1,classification,m_indices);

      for(ulong j = 0 ; j<m_nout; j++)
        {
         temp = m_logit[j].coeffAt(i);
         m_output[m_indices[j]] += j * temp;
        }
     }
   double sum = m_output.Sum();
   ulong ibest = m_output.ArgMax();
   double best = m_output[ibest];

   if(sum>0.0)
      m_output/=sum;

   return ibest;
  }

個別の重みセットを実装するには、厳格な検証手順が不可欠です。実務者は、説明のつかない極端な値が現れていないかを含め、重みの分布を継続的に監視し、その差異が既知のモデル特性と整合していることを確認する必要があります。また、回帰プロセスの不安定化を防ぐための安全策も講じるべきです。これらの対策は、包括的なテストプロトコルを維持することによって効果的に実施できます。

クラス固有の重みセットを効果的に導入するためには、いくつかの重要な要素に注意を払う必要があります。具体的には、各クラスに十分な訓練データが確保されていること、モデルの特殊化パターンが個別の重みを正当化するものであること、重みの安定性が保たれていること、そして単一重みアプローチよりも分類精度が向上していることを確認する必要があります。このようなロジスティック回帰の高度な実装により、より優れた分類性能が得られる一方で、複雑性の増加や潜在的リスクへの対応には、慎重な管理が求められます。

局所精度を活用したアンサンブル

個々のモデルの強みをさらに活用するために、予測変数空間における局所精度に着目することができます。多くの場合、コンポーネント分類器は予測空間の特定領域において、他よりも優れたパフォーマンスを発揮します。こうした特殊化は、特定の予測変数の条件下でモデルの性能が際立つ場合に現れます。たとえば、あるモデルは変数値が低い領域で最適に機能し、別のモデルは高い値の領域で優れているといったケースです。これらのパターンは、意図的に設計されたものであれ自然に形成されたものであれ、適切に活用することで分類精度を大幅に向上させることが可能です。

この実装は、シンプルながら効果的な手法に基づいています。未知のケースを評価する際、システムはすべてのコンポーネントモデルから分類結果を収集し、そのケースに対して最も信頼できるモデルを選択します。アンサンブルは、Woods、Kegelmeyer、Bowyerの論文「Combination of multiple classifiers using local accuracy estimates」で提案された手法を用いて、各モデルの信頼性を評価します。このアプローチは以下のステップで構成されています。

未知のケースとすべての訓練データとの間のユークリッド距離を計算する。
あらかじめ定められた数の最も近い訓練ケースを特定する。
各モデルについて、未知のケースと同じクラスに分類した近傍ケースに対して、その局所的な性能を評価する。
モデルが未知ケースとその近傍に対して同じクラスを予測した件数のうち、正しく分類された割合をパフォーマンス指標として算出する。

たとえば、最も近い10件の近傍を分析対象とした場合を考えてみましょう。ユークリッド距離により近傍を特定し、あるモデルが未知のケースをクラス3に分類したとします。その後、システムはそのモデルが10件の近傍に対してどのように分類したかを評価します。もし6件をクラス3に分類し、そのうち4件が正解だった場合、このモデルのパフォーマンス指標は0.67（4/6）となります。この評価をすべてのモデルに対して実行し、最も高スコアのモデルが最終的な分類を決定します。これにより、ケースごとに最も信頼できるモデルを選んで判断が下される仕組みになります。

同点が発生した場合には、「出力の最大値と出力合計の比率」によって算出された確信度を用いて、より信頼性の高いモデルを選択します。局所サブセットのサイズ（近傍数）は非常に重要な要素です。サブセットが小さいほど局所的な変化に敏感になり、分類に対してきめ細やかな判断が可能になります。一方で、サイズが大きいほどノイズに強くなり頑健になりますが、「局所性」が薄れる可能性があります。交差検証により、この最適なサイズを決定することが推奨されます。同点処理の観点からは、小さいサブセットの方が計算効率に優れるため優先されることもあります。このアプローチを適用することで、アンサンブルは各モデルの専門性を局所的に活用しつつ、計算効率も維持することが可能となります。この方法により、アンサンブルは予測変数空間の異なる領域に動的に適応でき、信頼性の指標を活用してモデル選択のための透明な指標を提供することができます。

ensemble.mqhのClocalAccクラスは、局所精度に基づいて分類器のアンサンブルから最も可能性の高いクラスを決定するように設計されています。

//+------------------------------------------------------------------+
//|  Use local accuracy to choose the best model                     |
//+------------------------------------------------------------------+
class ClocalAcc
  {
private:
   ulong             m_knn;
   ulong             m_nout;
   long              m_indices[];
   matrix            m_ranks;
   vector            m_output;
   vector            m_targs;
   matrix            m_input;
   vector            m_dist;
   matrix            m_trnx;
   matrix            m_trncls;
   vector            m_trntrue;
   ulong             m_classprep;
   bool              m_crossvalidate;
public:
                     ClocalAcc(void);
                    ~ClocalAcc(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
   bool              fit(matrix &inputs, matrix &targets, IClassify* &models[], bool crossvalidate = false);
   vector            proba(void) { return m_output;}
  };

fit()メソッドはClocalAccオブジェクトを訓練します。このメソッドは、入力データ(inputs)、目標値(targets)、分類器モデルの配列(models)、およびオプションの交差検証フラグ(crossvalidate)を受け取ります。訓練中、fit()は各入力データポイントと他のすべてのデータポイント間の距離を計算します。次に、各ポイントのk個の最も近い近傍を決定します。ここで、crossvalidateがtrueに設定されている場合、kは交差検証によって決定されます。このメソッドでは、各近傍について、アンサンブル内の各分類器のパフォーマンスを評価します。

//+------------------------------------------------------------------+
//|  fit an ensemble model                                           |
//+------------------------------------------------------------------+
bool ClocalAcc::fit(matrix &inputs,matrix &targets,IClassify *&models[], bool crossvalidate = false)
  {
   m_crossvalidate = crossvalidate;
   m_nout = targets.Cols();
   m_input = matrix::Zeros(inputs.Rows(),models.Size());
   m_targs = vector::Zeros(inputs.Rows());
   m_output = vector::Zeros(m_nout);
   m_ranks = matrix::Zeros(models.Size(),m_nout);
   m_dist = vector::Zeros(inputs.Rows());
   m_trnx = matrix::Zeros(inputs.Rows(),inputs.Cols());
   m_trncls = matrix::Zeros(inputs.Rows(),models.Size());
   m_trntrue = vector::Zeros(inputs.Rows());

   double best = 0.0;
   if(ArrayResize(m_indices,int(inputs.Rows()))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return false;
     }

   ulong k, knn_min,knn_max,knn_best=0,true_class, ibest=0;

   for(ulong i = 0; i<inputs.Rows(); i++)
     {
      np::matrixCopyRows(m_trnx,inputs,i,i+1,1);
      vector trow = targets.Row(i);
      vector inrow = inputs.Row(i);
      k = trow.ArgMax();
      best = trow[k];
      m_trntrue[i] = double(k);
      for(uint j=0; j<models.Size(); j++)
        {
         vector classification = models[j].classify(inrow);
         ibest = classification.ArgMax();
         best = classification[ibest];
         m_trncls[i][j] = double(ibest);
        }
     }
   m_classprep = 1;
   if(!m_crossvalidate)
     {
      m_knn=3;
      return true;
     }
   else
     {
      ulong ncases = inputs.Rows();
      if(inputs.Rows()<20)
        {
         m_knn=3;
         return true;
        }
      knn_min = 3;
      knn_max = 10;

      vector testcase(inputs.Cols()) ;
      vector clswork(m_nout) ;
      vector knn_counts(knn_max - knn_min + 1) ;

      for(ulong i = knn_min; i<=knn_max; i++)
         knn_counts[i-knn_min] = 0;
      --ncases;
      for(ulong i = 0; i<=ncases; i++)
        {
         testcase = m_trnx.Row(i);
         true_class = ulong(m_trntrue[i]);
         if(i<ncases)
           {
            if(!m_trnx.SwapRows(ncases,i))
              {
               Print(__FUNCTION__, "   ", __LINE__, " failed row swap ", GetLastError());
               return false;
              }
            m_trntrue[i] = m_trntrue[ncases];
            double temp;
            for(uint j = 0; j<models.Size(); j++)
              {
               temp = m_trncls[i][j];
               m_trncls[i][j] = m_trncls[ncases][j];
               m_trncls[ncases][j] = temp;
              }
           }

         m_classprep = 1;
         for(ulong knn = knn_min; knn<knn_max; knn++)
           {
            ulong iclass = classify(testcase,models);
            if(iclass == true_class)
              {
               ++knn_counts[knn-knn_min];
              }
            m_classprep=0;
           }
         if(i<ncases)
           {
            if(!m_trnx.SwapRows(i,ncases) || !m_trnx.Row(testcase,i))
              {
               Print(__FUNCTION__, "   ", __LINE__, " error ", GetLastError());
               return false;
              }
            m_trntrue[ncases] = m_trntrue[i];
            m_trntrue[i] = double(true_class);
            double temp;
            for(uint j = 0; j<models.Size(); j++)
              {
               temp = m_trncls[i][j];
               m_trncls[i][j] = m_trncls[ncases][j];
               m_trncls[ncases][j] = temp;
              }
           }
        }
      ++ncases;
      for(ulong knn = knn_min; knn<=knn_max; knn++)
        {
         if((knn==knn_min) || (ulong(knn_counts[knn-knn_min])>ibest))
           {
            ibest = ulong(knn_counts[knn-knn_min]);
            knn_best = knn;
           }
        }
      m_knn = knn_best;
      m_classprep = 1;
     }

   return true;
  }

classify()メソッドは、与えられた入力ベクトルに対するクラスラベルを予測します。このメソッドは、入力ベクトルとすべての訓練データポイントとの距離を計算し、k個の最寄りの近傍を特定します。アンサンブル内の各分類器について、これらの近傍に対する分類器の精度を評価します。最も高い精度を示した分類器が選択され、その予測されたクラスラベルが返されます.

//+------------------------------------------------------------------+
//|  classify with an ensemble model                                 |
//+------------------------------------------------------------------+
ulong ClocalAcc::classify(vector &inputs,IClassify *&models[])
  {
   double dist=0, diff=0, best=0, crit=0, bestcrit=0, conf=0, bestconf=0, sum ;
   ulong k, ibest, numer, denom, bestmodel=0, bestchoice=0 ;

   if(m_classprep)
     {
      for(ulong i = 0; i<m_input.Rows(); i++)
        {
         m_indices[i] = long(i);
         dist = 0.0;
         for(ulong j = 0; j<m_trnx.Cols(); j++)
           {
            diff = inputs[j] - m_trnx[i][j];
            dist+= diff*diff;
           }
         m_dist[i] = dist;
        }
      if(!m_dist.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortdsi(0, m_dist.Size()-1, m_dist,m_indices);
     }

   for(uint i = 0; i<models.Size(); i++)
     {
      vector vec = models[i].classify(inputs);
      sum = vec.Sum();
      ibest = vec.ArgMax();
      best = vec[ibest];
      conf = best/sum;
      denom = numer = 0;
      for(ulong ii = 0; ii<m_knn; ii++)
        {
         k = m_indices[ii];
         if(ulong(m_trncls[k][i]) == ibest)
           {
            ++denom;
            if(ibest == ulong(m_trntrue[k]))
               ++numer;
           }
        }
      if(denom > 0)
         crit = double(numer)/double(denom);
      else
         crit = 0.0;
      if((i == 0) || (crit > bestcrit))
        {
         bestcrit = crit;
         bestmodel = ulong(i);
         bestchoice = ibest;
         bestconf = conf;
         m_output = vec;
        }
      else
         if(fabs(crit-bestcrit)<1.e-10)
           {
            if(conf > bestconf)
              {
               bestcrit= crit;
               bestmodel = ulong(i);
               bestchoice = ibest;
               bestconf = conf;
               m_output = vec;
              }
           }
     }

   sum = m_output.Sum();
   if(sum>0)
      m_output/=sum;

   return bestchoice;
  }

ファジィ積分を用いたアンサンブルの組み合わせ

ファジィ論理は、真偽値ではなく、真実の度合いを扱う数学的なフレームワークです。分類器の組み合わせにおいては、各モデルの信頼性を考慮しながら、ファジィ論理を使用して複数のモデルの出力を統合することができます。ファジィ積分は、もともと菅野道夫によって1977年に提案されたもので、ユニバースのサブセットに値を割り当てるファジィ測度を使用します。この測度は、境界条件、単調性、連続性などの特定の特性を満たします。菅野はこの概念をλファジィ測度で拡張し、分離した集合の測度を組み合わせるための追加の要素を組み込みました。

ファジィ積分自体は、メンバーシップ関数とファジィ測度を用いて特定の式を使って計算されます。総当たりでの計算は可能ですが、有限集合の場合には再帰計算を用いたより効率的な方法が存在します。λの値は、最終的な測度が1になるように決定されます。分類器の組み合わせにおいては、各分類器をユニバースの要素として扱い、その信頼性をメンバーシップ値として考慮します。その後、各クラスについてファジィ積分を計算し、最も高い積分値を持つクラスを選択します。この方法は、個々の信頼性を考慮しつつ、複数の分類器の出力を効果的に組み合わせることができます。

CFuzzyIntクラスは、分類器を組み合わせるためのファジー積分法を実装します。

//+------------------------------------------------------------------+
//|  Use fuzzy integral to combine decisions                         |
//+------------------------------------------------------------------+
class CFuzzyInt
  {
private:
   ulong             m_nout;
   vector            m_output;
   long              m_indices[];
   matrix            m_sort;
   vector            m_g;
   double            m_lambda;
   double            recurse(double x);
public:
                     CFuzzyInt(void);
                    ~CFuzzyInt(void);
   bool              fit(matrix &predictors, matrix &targets, IClassify* &models[]);
   ulong             classify(vector &inputs, IClassify* &models[]);
   vector            proba(void) { return m_output;}
  };

このメソッドの中核は、の核心は、ファジィ測度を反復的に計算するrecurse()関数にあります。重要なパラメータλは、すべてのモデルのファジー測定が1に収束することを保証する値を見つけることによって決定されます。最初の値から始め、ファジィ測度がすべてのモデルで1に収束するまで徐々に調整をおこないます。通常、λの正しい値を範囲で絞り込み、その後、二分法を用いて探索を精密化します。

//+------------------------------------------------------------------+
//|  recurse                                                         |
//+------------------------------------------------------------------+
double CFuzzyInt::recurse(double x)
  {
   double val ;

   val = m_g[0] ;
   for(ulong i=1 ; i<m_g.Size() ; i++)
      val += m_g[i] + x * m_g[i] * val ;

   return val - 1.0 ;
  }

各モデルの信頼性を推定するために、まず訓練セットでの精度を評価します。その後、この精度からランダムな予測の期待精度を引き、その結果を0と1の間の値に再スケーリングして調整します。モデルの信頼性を推定するためのより高度な方法もありますが、このアプローチはそのシンプルさゆえに好まれます。

//+------------------------------------------------------------------+
//|  fit ensemble model                                              |
//+------------------------------------------------------------------+
bool CFuzzyInt::fit(matrix &predictors,matrix &targets,IClassify *&models[])
  {
   m_nout = targets.Cols();
   m_output = vector::Zeros(m_nout);
   m_sort = matrix::Zeros(models.Size(), m_nout);
   m_g = vector::Zeros(models.Size());

   if(ArrayResize(m_indices,int(models.Size()))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return false;
     }

   ulong  k=0, iclass =0 ;
   double  best=0, xlo=0, xhi=0, y=0, ylo=0, yhi=0, step=0 ;

   for(ulong i = 0; i<predictors.Rows(); i++)
     {
      vector trow = targets.Row(i);
      vector inrow = predictors.Row(i);
      k = trow.ArgMax();
      best = trow[k];
      for(uint ii = 0; ii< models.Size(); ii++)
        {
         vector vec = models[ii].classify(inrow);
         iclass = vec.ArgMax();
         best = vec[iclass];
         if(iclass == k)
            m_g[ii] += 1.0;
        }
     }

   for(uint i = 0; i<models.Size(); i++)
     {
      m_g[i] /= double(predictors.Rows()) ;
      m_g[i] = (m_g[i] - 1.0 / m_nout) / (1.0 - 1.0 / m_nout) ;
      if(m_g[i] > 1.0)
         m_g[i] = 1.0 ;
      if(m_g[i] < 0.0)
         m_g[i] = 0.0 ;
     }

   xlo = m_lambda = -1.0 ;
   ylo = recurse(xlo) ;
   if(ylo >= 0.0)    // Theoretically should never exceed zero
      return true;       // But allow for pathological numerical problems

   step = 1.0 ;

   for(;;)
     {
      xhi = xlo + step ;
      yhi = recurse(xhi) ;
      if(yhi >= 0.0)    // If we have just bracketed the root
         break ;        // We can quit the search
      if(xhi > 1.e5)    // In the unlikely case of extremely poor models
        {
         m_lambda = xhi ; // Fudge a value
         return true ;       // And quit
        }
      step *= 2.0 ;     // Keep increasing the step size to avoid many tries
      xlo = xhi ;       // Move onward
      ylo = yhi ;
     }

   for(;;)
     {
      m_lambda = 0.5 * (xlo + xhi) ;
      y = recurse(m_lambda) ;                     // Evaluate the function here
      if(fabs(y) < 1.e-8)                       // Primary convergence criterion
         break ;
      if(xhi - xlo < 1.e-10 * (m_lambda + 1.1))   // Backup criterion
         break ;
      if(y > 0.0)
        {
         xhi = m_lambda ;
         yhi = y ;
        }
      else
        {
         xlo = m_lambda ;
         ylo = y ;
        }
     }

   return true;

  }

分類時には、最も高いファジー積分を持つクラスが選択されます。各クラスのファジー積分は、モデルの出力と再帰的に計算されたファジー測度を繰り返し比較し、各ステップで最小値を選ぶことによって計算されます。クラスの最終的なファジー積分は、そのクラスにおけるモデルの総合的な信頼度を表します。

//+------------------------------------------------------------------+
//|   classify with ensemble                                         |
//+------------------------------------------------------------------+
ulong CFuzzyInt::classify(vector &inputs,IClassify *&models[])
  {
   ulong k, iclass;
   double sum, gsum, minval, maxmin, best ;

   for(uint i = 0; i<models.Size(); i++)
     {
      vector vec = models[i].classify(inputs);
      sum = vec.Sum();
      vec/=sum;
      if(!m_sort.Row(vec,i))
        {
         Print(__FUNCTION__, "   ", __LINE__, " row insertion error ", GetLastError());
         return false;
        }
     }

   for(ulong i = 0; i<m_nout; i++)
     {
      for(uint ii =0; ii<models.Size(); ii++)
         m_indices[ii] = long(ii);
      vector vec = m_sort.Col(i);
      if(!vec.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortdsi(0,long(vec.Size()-1), vec, m_indices);
      maxmin = gsum = 0.0;
      for(int j = int(models.Size()-1); j>=0; j--)
        {
         k = m_indices[j];
         if(k>=vec.Size())
           {
            Print(__FUNCTION__," ",__LINE__, " out of range ", k);
           }
         gsum += m_g[k] + m_lambda * m_g[k] * gsum;
         if(gsum<vec[k])
            minval = gsum;
         else
            minval = vec[k];
         if(minval > maxmin)
            maxmin = minval;
        }

      m_output[i] = maxmin;
     }

   iclass = m_output.ArgMax();
   best = m_output[iclass];

   return iclass;
  }

ペアワイズカップリング

ペアワイズカップリングは、特殊な二項分類器の力を活用する多クラス分類の独自のアプローチです。これは、K(K−1)/2個の二項分類器（Kはクラスの数）のセットを組み合わせており、各分類器は特定のクラスのペアを区別するように設計されています。たとえば、ターゲットが3クラスから成るデータセットがあるとしましょう。これらを比較するために、3つ(=3*(3-1)/2)のモデルセットを作成します。各モデルは、2つのクラスのみを区別するように設計されています。クラスがA、B、Cと指定されている場合、3つのモデルは次のように構成されます。

モデル1：クラスAとクラスBのどちらかを選択します。
モデル2：クラスAとクラスCのどちらかを選択します。
モデル3：クラスBとクラスCのどちらかを選択します。

訓練データは、各モデルの分類タスクに関連するサンプルが含まれるように分割する必要があります。これらのモデルを評価すると、確率のセットが得られ、それをKxKの行列として整理することができます。以下は、そのような行列の仮の例です。

	A	B	C
A	----	0.2	0.7
B	0.8	----	0.4
C	0.3	0.6	----

この行列では、クラスAとクラスBを区別するモデルにより、サンプルがクラスAに属する確率が0.2に割り当てられます。マトリックスは対称であるため、行列の右上の対角要素は、ペアで比較するクラスを決定するために計算された確率の完全なセットを示します。モデル出力が与えられた場合、サンプル外のケースが特定のクラスに属する確率を推定することが目標です。つまり、観測されたペアワイズ確率の分布に一致する、または少なくともできるだけ一致する確率のセットを見つける必要があります。関数最小化手法を使用せずに、これらの初期確率推定値を改善するために反復的なアプローチが採用されています。

この反復プロセスにより、初期のクラス確率推定値は徐々に改良され、個々の分類器からのペアワイズ予測とより一致するようになります。本質的には、現実世界を正確に反映する地図を作成する過程に似ています。最初は大まかなスケッチを作成し、新しい情報を基に小さな調整を加え、最終的に非常に精度の高い地図を完成させます。この反復的なアプローチは効率的で、通常は迅速に解決策に収束します。

CPairWiseクラスは、ペアワイズカップリングアルゴリズムを実装します。

//+------------------------------------------------------------------+
//|  Use pairwise coupling to combine decisions                      |
//+------------------------------------------------------------------+
class CPairWise
  {
private:
   ulong             m_nout;
   ulong             m_npairs;
   vector            m_output;
   vector            m_rij;
   vector            m_uij;
public:
                     CPairWise(void);
                    ~CPairWise(void);
   ulong             classify(ulong numclasses,vector &inputs,IClassify *&models[],ulong &samplesPerModel[]);
   vector            proba(void) { return m_output;}
  };

中核的な計算はclassify()メソッド内でおこなわれ、ペアワイズ分類器の出力からクラス確率を計算するための構造化されたプロセスに従います。このメソッドは、特定のテストケースに対してすべてのペアワイズモデルを評価することから始まります。各モデルは特定のクラスのペアに対応しており、テストケースがそのペア内の2つのクラスのいずれかに属する可能性を示す出力を生成します。

//+------------------------------------------------------------------+
//|  classify using ensemble model                                   |
//+------------------------------------------------------------------+
ulong CPairWise::classify(ulong numclasses,vector &inputs,IClassify *&models[],ulong &samplesPerModel[])
  {
   m_nout=numclasses;
   m_npairs = m_nout*(m_nout-1)/2;
   m_output = vector::Zeros(m_nout);
   m_rij = vector::Zeros(m_npairs);
   m_uij = vector::Zeros(m_npairs);

   long  k;
   ulong iclass=0 ;
   double rr, best=0, numer, denom, sum, delta, oldval ;

   for(ulong i = 0; i<m_npairs; i++)
     {
      vector vec = models[i].classify(inputs);
      rr = vec[0];
      if(vec[0]> 0.999999)
         vec[0] = 0.999999 ;
      if(vec[0] < 0.000001)
         vec[0] = 0.000001 ;
      m_rij[i] = vec[0] ;
     }

   k = 0 ;
   for(ulong i=0 ; i<m_nout-1 ; i++)
     {
      for(ulong j=i+1 ; j<m_nout ; j++)
        {
         rr = m_rij[k++] ;
         m_output[i] += rr ;
         m_output[j] += 1.0 - rr ;
        }
     }

   for(ulong i=0 ; i<m_nout ; i++)
      m_output[i] /= double(m_npairs) ;

   k = 0 ;
   for(ulong i=0 ; i<m_nout-1 ; i++)
     {
      for(ulong j=i+1 ; j<m_nout ; j++)
         m_uij[k++] = m_output[i] / (m_output[i] + m_output[j]) ;
     }

   for(int iter=0 ; iter<10000 ; iter++)
     {

      delta = 0.0 ;
      for(ulong i=0 ; i<m_nout ; i++)
        {

         numer = denom = 0.0 ;
         for(ulong j=0 ; j<m_nout ; j++)
           {
            if(i < j)
              {
               k = (long(i) * (2 * long(m_nout) - long(i) - 3) - 2) / 2 + long(j) ;
               numer += samplesPerModel[k] * m_rij[k] ;
               denom += samplesPerModel[k] * m_uij[k] ;
              }
            else
               if(i > j)
                 {
                  k = (long(j) * (2 * long(m_nout) - long(j) - 3) - 2) / 2 + long(i) ;
                  //Print(__FUNCTION__," ",__LINE__," k ", k);
                  numer += samplesPerModel[k] * (1.0 - m_rij[k]) ;
                  denom += samplesPerModel[k] * (1.0 - m_uij[k]) ;
                 }
           }

         oldval = m_output[i] ;
         m_output[i] *= numer / denom ;
         sum = 0.0 ;
         for(ulong j=0 ; j<m_nout ; j++)
            sum += m_output[j] ;
         for(ulong j=0 ; j<m_nout ; j++)
            m_output[j] /= sum ;

         if(fabs(m_output[i]-oldval) > delta)
            delta = fabs(m_output[i]-oldval) ;


         k = 0 ;
         for(ulong i=0 ; i<m_nout-1 ; i++)
           {
            for(ulong j=i+1 ; j<m_nout ; j++)
               m_uij[k++] = m_output[i] / (m_output[i] + m_output[j]) ;
           }

        }

      if(delta < 1.e-6)
         break ;

     }

   return m_output.ArgMax() ;

  }

初期出力（確率）が取得されると、それらはクラス確率の初期推定値として使用されます。その後、このメソッドではこれらの推定値を繰り返し調整して精度を向上させます。クラス確率を精緻化した後、最後のステップは最も高い確率を持つクラスを特定することです。最も高い確率を持つクラスは、指定されたテストケースに最も可能性が高いクラスと見なされ、そのインデックスがclassify()メソッドの出力として返されます。

結論：組み合わせ方法の比較

ClassificationEnsemble_Demo.mq5スクリプトは、この記事で説明したアンサンブルアルゴリズムのパフォーマンスをさまざまなシナリオにわたって比較するために設計されています。このスクリプトは、複数のモンテカルロレプリケーションを実行することで、さまざまな条件下での各アンサンブル手法のパフォーマンスを評価できます。ユーザーは、各実行で使用する訓練サンプルの数を指定することができ、これにより、小規模から大規模までさまざまなサイズのデータセットにわたってテストが可能になります。問題の複雑さが増すにつれて、クラスの数を調整して、アンサンブル法のスケーラビリティをテストすることができます。また、アンサンブル内で使用される基本分類器（モデル）の数を変更することで、さまざまなレベルの複雑さでアルゴリズムがどのように機能するかを評価できます。

ユーザーは、各シナリオのモンテカルロレプリケーションの数を指定して、アンサンブルアルゴリズムの安定性と一貫性を評価できます。サンプル外での誤分類確率がパフォーマンスメトリックとして使用され、モデルが目に見えないデータで評価され、現実世界の分類タスクがシミュレートされることが保証されます。4つ以上のモデルが使用されている場合、1つのモデルは意図的に無効にされます（たとえば、ランダムな予測をおこなうか、一定の出力を生成するなど）。これにより、アンサンブルアルゴリズムの堅牢性がテストされ、無関係なモデルや情報のないモデルの組み込みをどの程度うまく処理できるかが評価されます。

5つ以上のモデルが使用される場合、5番目のモデルは、モデルが不安定になったりノイズが多くなる可能性がある現実世界のシナリオをシミュレートするために、時々極端または不規則な予測を生成するように設定されます。この機能は、アンサンブル手法が信頼性の低いモデルをどのように処理するか、問題のあるモデルを適切に重み付けまたは重み付け解除することで優れた分類パフォーマンスを維持できるかを評価します。分類難易度係数はクラス間の広がりを定義し、コンポーネントモデルの問題の難易度を制御します。スプレッドが大きいほどクラスの区別が容易になり、スプレッドが小さいほど難易度が増します。これにより、さまざまな難易度レベルでのアンサンブル手法のパフォーマンスをテストし、困難なシナリオでも精度を維持する能力を評価することができます。

//+------------------------------------------------------------------+
//|                                  ClassificationEnsemble_Demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<ensemble.mqh>
#include<multilayerperceptron.mqh>
//--- input parameters
input int      NumSamples=10;
input int      NumClasses=3;
input int      NumModels=3;
input int      NumReplications=1000;
input double   ClassificationDifficultyFactor=0.0;

//+------------------------------------------------------------------+
//|  normal(rngstate)                                                |
//+------------------------------------------------------------------+
double normal(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndNormal(state);
  }
//+------------------------------------------------------------------+
//|   unifrand(rngstate)                                             |
//+------------------------------------------------------------------+
double unifrand(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndUniformR(state);
  }
//+------------------------------------------------------------------+
//|Multilayer perceptron                                             |
//+------------------------------------------------------------------+
class CMLPC:public ensemble::IClassify
  {
private:
   CMlp              *m_mlfn;
   double             m_learningrate;
   double             m_tolerance;
   double             m_alfa;
   double             m_beyta;
   uint               m_epochs;
   ulong              m_in,m_out;
   ulong              m_hl1,m_hl2;

public:
                     CMLPC(ulong ins, ulong outs,ulong numhl1,ulong numhl2);
                    ~CMLPC(void);
   void              setParams(double alpha_, double beta_,double learning_rate, double tolerance, uint num_epochs);
   bool              train(matrix &predictors,matrix&targets);
   vector            classify(vector &predictors);
   ulong             getNumInputs(void) { return m_in;}
   ulong             getNumOutputs(void) { return m_out;}
  };
//+------------------------------------------------------------------+
//| constructor                                                      |
//+------------------------------------------------------------------+
CMLPC::CMLPC(ulong ins, ulong outs,ulong numhl1,ulong numhl2)
  {
   m_in = ins;
   m_out = outs;
   m_alfa = 0.3;
   m_beyta = 0.01;
   m_learningrate=0.001;
   m_tolerance=1.e-8;
   m_epochs= 1000;
   m_hl1 = numhl1;
   m_hl2 = numhl2;
   m_mlfn = new CMlp();
  }
//+------------------------------------------------------------------+
//| destructor                                                       |
//+------------------------------------------------------------------+
CMLPC::~CMLPC(void)
  {
   if(CheckPointer(m_mlfn) == POINTER_DYNAMIC)
      delete m_mlfn;
  }
//+------------------------------------------------------------------+
//| set other hyperparameters of the i_model                           |
//+------------------------------------------------------------------+
void CMLPC::setParams(double alpha_, double beta_,double learning_rate, double tolerance, uint num_epochs)
  {
   m_alfa = alpha_;
   m_beyta = beta_;
   m_learningrate=learning_rate;
   m_tolerance=tolerance;
   m_epochs= num_epochs;
  }
//+------------------------------------------------------------------+
//| fit a i_model to the data                                          |
//+------------------------------------------------------------------+
bool CMLPC::train(matrix &predictors,matrix &targets)
  {
   if(m_in != predictors.Cols() || m_out != targets.Cols())
     {
      Print(__FUNCTION__, " failed training due to invalid training data");
      return false;
     }

   return m_mlfn.fit(predictors,targets,m_alfa,m_beyta,m_hl1,m_hl2,m_epochs,m_learningrate,m_tolerance);
  }
//+------------------------------------------------------------------+
//| make a prediction with the trained i_model                         |
//+------------------------------------------------------------------+
vector CMLPC::classify(vector &predictors)
  {
   return m_mlfn.predict(predictors);
  }
//+------------------------------------------------------------------+
//| clean up dynamic array pointers                                  |
//+------------------------------------------------------------------+
void cleanup(ensemble::IClassify* &array[])
  {
   for(uint i = 0; i<array.Size(); i++)
      if(CheckPointer(array[i])==POINTER_DYNAMIC)
         delete array[i];
  }
//+------------------------------------------------------------------+
//| global variables                                                 |
//+------------------------------------------------------------------+
int nreplications, nsamps,nmodels, divisor, nreps_done ;
int n_classes, nnn, n_pairs, nh_g ;
ulong ntrain_pair[];
matrix xdata, xbad_data, xtainted_data, test[],x_targ,xbad_targ,xwild_targ;
vector inputdata;
double cd_factor, err_score, err_score_1, err_score_2, err_score_3 ;
vector classification_err_raw, output_vector;
double classification_err_average ;
double classification_err_median ;
double classification_err_maxmax ;
double classification_err_maxmin ;
double classification_err_intersection_1 ;
double classification_err_intersection_2 ;
double classification_err_intersection_3 ;
double classification_err_union_1 ;
double classification_err_union_2 ;
double classification_err_union_3 ;
double classification_err_majority ;
double classification_err_borda ;
double classification_err_logit ;
double classification_err_logitsep ;
double classification_err_localacc ;
double classification_err_fuzzyint ;
double classification_err_pairwise ;
//+------------------------------------------------------------------+
//| ensemble i_model objects                                         |
//+------------------------------------------------------------------+
ensemble::CAvgClass average_ensemble ;
ensemble::CMedian median_ensemble ;
ensemble::CMaxMax maxmax_ensemble ;
ensemble::CMaxMin maxmin_ensemble ;
ensemble::CIntersection intersection_ensemble ;
ensemble::CUnion union_rule ;
ensemble::CMajority majority_ensemble ;
ensemble::CBorda borda_ensemble ;
ensemble::ClogitReg logit_ensemble ;
ensemble::ClogitRegSep logitsep_ensemble ;
ensemble::ClocalAcc localacc_ensemble ;
ensemble::CFuzzyInt fuzzyint_ensemble ;
ensemble::CPairWise pairwise_ensemble ;

int n_hid = 4 ;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndRandomize(rngstate.GetInnerObj());
//---
   nsamps = NumSamples ;
   n_classes = NumClasses ;
   nmodels = NumModels ;
   nreplications = NumReplications ;
   cd_factor = ClassificationDifficultyFactor ;

   if((nsamps <= 3)  || (n_classes <= 1)  || (nmodels <= 0)  || (nreplications <= 0) || (cd_factor < 0.0))
     {
      Alert(" Invalid inputs ");
      return;
     }

   divisor = 1 ;
   ensemble::IClassify* models[];
   ensemble::IClassify* model_pairs[];
   /*
      Allocate memory and initialize
   */
   n_pairs = n_classes * (n_classes-1) / 2 ;
   if(ArrayResize(models,nmodels)<0 || ArrayResize(model_pairs,n_pairs)<0 || ArrayResize(test,10)<0 ||
      ArrayResize(ntrain_pair,n_pairs)<0)
     {
      Print(" Array resize errors ", GetLastError());
      cleanup(models);
      cleanup(model_pairs);
      return;
     }

   ArrayInitialize(ntrain_pair,0);

   for(int i=0 ; i<nmodels ; i++)
      models[i] = new CMLPC(2,ulong(n_classes),4,0) ;

   xdata = matrix::Zeros(nsamps,(2+n_classes));
   xbad_data = matrix::Zeros(nsamps,(2+n_classes));
   xtainted_data = matrix::Zeros(nsamps,(2+n_classes));
   inputdata = vector::Zeros(3);

   for(uint i = 0; i<test.Size(); i++)
      test[i] = matrix::Zeros(nsamps,(2+n_classes));

   classification_err_raw = vector::Zeros(nmodels);
   classification_err_average = 0.0 ;
   classification_err_median = 0.0 ;
   classification_err_maxmax = 0.0 ;
   classification_err_maxmin = 0.0 ;
   classification_err_intersection_1 = 0.0 ;
   classification_err_intersection_2 = 0.0 ;
   classification_err_intersection_3 = 0.0 ;
   classification_err_union_1 = 0.0 ;
   classification_err_union_2 = 0.0 ;
   classification_err_union_3 = 0.0 ;
   classification_err_majority = 0.0 ;
   classification_err_borda = 0.0 ;
   classification_err_logit = 0.0 ;
   classification_err_logitsep = 0.0 ;
   classification_err_localacc = 0.0 ;
   classification_err_fuzzyint = 0.0 ;
   classification_err_pairwise = 0.0 ;

   for(int i_rep=0 ; i_rep<nreplications ; i_rep++)
     {
      nreps_done = i_rep + 1 ;

      if(i_rep>0)
         xdata.Fill(0.0);
      //---
      for(int i=0, z=0; i<nsamps ; i++)
        {
         xdata[i][0] = normal(rngstate) ;
         xdata[i][1] = normal(rngstate) ;
         if(i < n_classes)
            z = i ;
         else
            z = (int)(unifrand(rngstate) * n_classes) ;
         if(z >= n_classes)
            z = n_classes - 1 ;
         xdata[i][2+z] = 1.0 ;
         xdata[i][0] += double(z) * cd_factor ;
         xdata[i][1] -= double(z) * cd_factor ;
        }

      if(nmodels >= 4)
        {
         xbad_data = xdata;
         matrix arm = np::sliceMatrixCols(xbad_data,2);
         for(int i = 0; i<nsamps; i++)
            for(int z = 0; z<n_classes; z++)
               arm[i][z] = (unifrand(rngstate)<(1.0/double(n_classes)))?1.0:0.0;

         np::matrixCopy(xbad_data,arm,0,xbad_data.Rows(),1,2);
        }

      if(nmodels >= 5)
        {
         xtainted_data = xdata;
         matrix arm = np::sliceMatrixCols(xtainted_data,2);
         for(int i = 0; i<nsamps; i++)
            for(int z = 0; z<n_classes; z++)
               if(unifrand(rngstate)<0.1)
                  arm[i][z] = xdata[i][2+z] * 1000.0 - 500.0 ;

         np::matrixCopy(xtainted_data,arm,0,xtainted_data.Rows(),1,2);
        }

      for(int i=0 ; i<10 ; i++)         // Build a test dataset
        {
         if(i_rep>0)
            test[i].Fill(0.0);
         for(int j=0,z=0; j<nsamps; j++)
           {
            test[i][j][0] = normal(rngstate) ;
            test[i][j][1] = normal(rngstate) ;
            z = (int)(unifrand(rngstate) * n_classes) ;
            if(z >= n_classes)
               z = n_classes - 1 ;
            test[i][j][2+z] = 1.0 ;
            test[i][j][0] += double(z) * cd_factor ;
            test[i][j][1] -= double(z) * cd_factor ;
           }
        }

      for(int i_model=0 ; i_model<nmodels ; i_model++)
        {
         matrix preds,targs;
         if(i_model == 3)
           {
            targs = np::sliceMatrixCols(xbad_data,2);
            preds = np::sliceMatrixCols(xbad_data,0,2);
           }
         else
            if(i_model == 4)
              {
               targs = np::sliceMatrixCols(xtainted_data,2);
               preds = np::sliceMatrixCols(xtainted_data,0,2);
              }
            else
              {
               targs = np::sliceMatrixCols(xdata,2);
               preds = np::sliceMatrixCols(xdata,0,2);
              }

         if(!models[i_model].train(preds,targs))
           {
            Print(" failed to train i_model at shift ", i_model);
            cleanup(model_pairs);
            cleanup(models);
            return;
           }

         err_score = 0.0 ;
         for(int i=0 ; i<10 ; i++)
           {
            vector testvec,testin,testtarg;
            for(int j=0; j<nsamps; j++)
              {
               testvec = test[i].Row(j);
               testtarg = np::sliceVector(testvec,2);
               testin = np::sliceVector(testvec,0,2);
               output_vector = models[i_model].classify(testin) ;
               if(output_vector.ArgMax() != testtarg.ArgMax())
                  err_score += 1.0 ;
              }
           }
         classification_err_raw[i_model] += err_score / (10 * nsamps) ;
        }

      int i_model = 0;
      for(int i=0 ; i<n_classes-1 ; i++)
        {
         for(int j=i+1 ; j<n_classes ; j++)
           {

            ntrain_pair[i_model] = 0 ;
            for(int z=0 ; z<nsamps ; z++)
              {
               if((xdata[z][2+i]> 0.5)
                  || (xdata[z][2+j] > 0.5))
                  ++ntrain_pair[i_model] ;
              }
            nh_g = (n_hid < int(ntrain_pair[i_model]) - 1) ? n_hid : int(ntrain_pair[i_model]) - 1;
            model_pairs[i_model] = new CMLPC(2, 1, ulong(nh_g+1),0) ;
            matrix training;
            matrix preds,targs;
            ulong msize=0;
            for(int z=0 ; z<nsamps ; z++)
              {
               inputdata[0] = xdata[z][0] ;
               inputdata[1] = xdata[z][1] ;
               if(xdata[z][2+i]> 0.5)
                  inputdata[2] = 1.0 ;
               else
                  if(xdata[z][2+j] > 0.5)
                     inputdata[2] = 0.0 ;
                  else
                     continue ;
               training.Resize(msize+1,inputdata.Size());
               training.Row(inputdata,msize++);
              }
            preds = np::sliceMatrixCols(training,0,2);
            targs = np::sliceMatrixCols(training,2);
            model_pairs[i_model].train(preds,targs);
            ++i_model ;
           }
        }

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(average_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_average += err_score / (10 * nsamps) ;

      /*
      median_ensemble
      */

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(median_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_median += err_score / (10 * nsamps) ;

      /*
      maxmax_ensemble
      */

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(maxmax_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_maxmax += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(maxmin_ensemble.classify(rowtest,models) != rowtarg.ArgMax())   // If predicted class not true class
               err_score += 1.0 ;      // Count this misclassification
           }
        }
      classification_err_maxmin += err_score / (10 * nsamps) ;

      matrix preds,targs;
      err_score_1 = err_score_2 = err_score_3 = 0.0 ;
      preds = np::sliceMatrixCols(xdata,0,2);
      targs = np::sliceMatrixCols(xdata,2);

      intersection_ensemble.fit(preds,targs,models);
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            ulong class_ = intersection_ensemble.classify(rowtest,models) ;
            output_vector = intersection_ensemble.proba();

            if(output_vector[rowtarg.ArgMax()] < 0.5)
              {
               err_score_1 += 1.0 ;
               err_score_2 += 1.0 ;
               err_score_3 += 1.0 ;
              }
            else
              {
               if(class_ > 3)
                  err_score_3 += 1.0 ;
               if(class_ > 2)
                  err_score_2 += 1.0 ;
               if(class_ > 1)
                  err_score_1 += 1.0 ;
              }
           }
        }
      classification_err_intersection_1 += err_score_1 / (10 * nsamps) ;
      classification_err_intersection_2 += err_score_2 / (10 * nsamps) ;
      classification_err_intersection_3 += err_score_3 / (10 * nsamps) ;

      union_rule.fit(preds,targs,models);
      err_score_1 = err_score_2 = err_score_3 = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            ulong clss = union_rule.classify(rowtest,models) ;
            output_vector = union_rule.proba();

            if(output_vector[rowtarg.ArgMax()] < 0.5)
              {
               err_score_1 += 1.0 ;
               err_score_2 += 1.0 ;
               err_score_3 += 1.0 ;
              }
            else
              {
               if(clss > 3)
                  err_score_3 += 1.0 ;
               if(clss > 2)
                  err_score_2 += 1.0 ;
               if(clss > 1)
                  err_score_1 += 1.0 ;
              }
           }
        }

      classification_err_union_1 += err_score_1 / (10 * nsamps) ;
      classification_err_union_2 += err_score_2 / (10 * nsamps) ;
      classification_err_union_3 += err_score_3 / (10 * nsamps) ;

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(majority_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_majority += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(borda_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_borda += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      logit_ensemble.fit(preds,targs,models);
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(logit_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_logit += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      logitsep_ensemble.fit(preds,targs,models);
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(logitsep_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_logitsep += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      localacc_ensemble.fit(preds,targs,models);
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(localacc_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_localacc += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      fuzzyint_ensemble.fit(preds,targs,models);
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(fuzzyint_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_fuzzyint += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(pairwise_ensemble.classify(ulong(n_classes),rowtest,model_pairs,ntrain_pair)  != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_pairwise += err_score / (10 * nsamps) ;
      cleanup(model_pairs);
     }
   err_score = 0.0 ;
   PrintFormat("Test Config: Classification Difficulty - %8.8lf\nNumber of classes - %5d\nNumber of component models - %5d\n Sample Size - %5d", ClassificationDifficultyFactor,NumClasses,NumModels,NumSamples);
   PrintFormat("%5d    Replications:", nreps_done) ;
   for(int i_model=0 ; i_model<nmodels ; i_model++)
     {
      PrintFormat("  %.8lf", classification_err_raw[i_model] / nreps_done) ;
      err_score += classification_err_raw[i_model] / nreps_done ;
     }
   PrintFormat("       Mean raw error = %8.8lf", err_score / nmodels) ;
   PrintFormat("        average_ensemble error = %8.8lf", classification_err_average / nreps_done) ;
   PrintFormat("         median_ensemble error = %8.8lf", classification_err_median / nreps_done) ;
   PrintFormat("         maxmax_ensemble error = %8.8lf", classification_err_maxmax / nreps_done) ;
   PrintFormat("         maxmin_ensemble error = %8.8lf", classification_err_maxmin / nreps_done) ;
   PrintFormat("       majority_ensemble error = %8.8lf", classification_err_majority / nreps_done) ;
   PrintFormat("          borda_ensemble error = %8.8lf", classification_err_borda / nreps_done) ;
   PrintFormat("          logit_ensemble error = %8.8lf", classification_err_logit / nreps_done) ;
   PrintFormat("       logitsep_ensemble error = %8.8lf", classification_err_logitsep / nreps_done) ;
   PrintFormat("       localacc_ensemble error = %8.8lf", classification_err_localacc / nreps_done) ;
   PrintFormat("       fuzzyint_ensemble error = %8.8lf", classification_err_fuzzyint / nreps_done) ;
   PrintFormat("       pairwise_ensemble error = %8.8lf", classification_err_pairwise / nreps_done) ;
   PrintFormat(" intersection_ensemble error 1 = %8.8lf", classification_err_intersection_1 / nreps_done) ;
   PrintFormat(" intersection_ensemble error 2 = %8.8lf", classification_err_intersection_2 / nreps_done) ;
   PrintFormat(" intersection_ensemble error 3 = %8.8lf", classification_err_intersection_3 / nreps_done) ;
   PrintFormat("        Union error 1 = %8.8lf", classification_err_union_1 / nreps_done) ;
   PrintFormat("        Union error 2 = %8.8lf", classification_err_union_2 / nreps_done) ;
   PrintFormat("        Union error 3 = %8.8lf", classification_err_union_3 / nreps_done) ;
   cleanup(models);
  }

//+------------------------------------------------------------------+

スクリプトを実行して得られた結果の例を以下に示します。これらは、分類タスクを最高の難易度に設定した場合の結果です。

ClassificationDifficultyFactor=0.0

DM      0       05:40:06.441    ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 0.00000000
RP      0       05:40:06.441    ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes -     3
QI      0       05:40:06.441    ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models -     3
EK      0       05:40:06.441    ClassificationEnsemble_Demo (BTCUSD,D1)  Sample Size -    10
MN      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)  1000    Replications:
CF      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)   0.66554000
HI      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)   0.66706000
DP      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)   0.66849000
II      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        Mean raw error = 0.66703000
JS      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)         average_ensemble error = 0.66612000
HR      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)          median_ensemble error = 0.66837000
QF      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmax_ensemble error = 0.66704000
MD      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmin_ensemble error = 0.66586000
GI      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        majority_ensemble error = 0.66772000
HR      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)           borda_ensemble error = 0.66747000
MO      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)           logit_ensemble error = 0.66556000
MP      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        logitsep_ensemble error = 0.66570000
JD      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        localacc_ensemble error = 0.66578000
OJ      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        fuzzyint_ensemble error = 0.66503000
KO      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        pairwise_ensemble error = 0.66799000
GS      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 1 = 0.96686000
DP      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 2 = 0.95847000
QE      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 3 = 0.95447000
OI      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 1 = 0.99852000
DM      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 2 = 0.97931000
JR      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 3 = 0.01186000

次は分類難易度が中程度のテストの結果です。

LF      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 1.00000000
IG      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes -     3
JP      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models -     3
FQ      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)  Sample Size -    10
KH      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)  1000    Replications:
NO      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)   0.46236000
QF      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)   0.45818000
II      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)   0.45779000
FR      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        Mean raw error = 0.45944333
DI      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)         average_ensemble error = 0.44881000
PH      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)          median_ensemble error = 0.45564000
JO      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmax_ensemble error = 0.46763000
GS      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmin_ensemble error = 0.44935000
GP      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        majority_ensemble error = 0.45573000
PI      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)           borda_ensemble error = 0.45593000
DF      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)           logit_ensemble error = 0.46353000
FO      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        logitsep_ensemble error = 0.46726000
ER      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        localacc_ensemble error = 0.46096000
KP      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        fuzzyint_ensemble error = 0.45098000
OD      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        pairwise_ensemble error = 0.66485000
IJ      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 1 = 0.93533000
RO      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 2 = 0.92527000
OL      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 3 = 0.92527000
OR      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 1 = 0.99674000
KG      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 2 = 0.97231000
NK      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 3 = 0.00877000

最後の結果セットは、分類の難易度が比較的簡単に設定されて実行されたテストの結果を示しています。

PL      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 10.00000000
CN      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes -     3
PK      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models -     3
LH      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)  Sample Size -    10
EQ      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)  1000    Replications:
MD      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)   0.02905000
LO      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)   0.02861000
CF      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)   0.02879000
IK      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        Mean raw error = 0.02881667
RN      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)         average_ensemble error = 0.02263000
PQ      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)          median_ensemble error = 0.02956000
QD      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmax_ensemble error = 0.03426000
KJ      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmin_ensemble error = 0.02263000
IO      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        majority_ensemble error = 0.02956000
HP      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)           borda_ensemble error = 0.02956000
KM      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)           logit_ensemble error = 0.03171000
OE      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        logitsep_ensemble error = 0.04840000
GK      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        localacc_ensemble error = 0.03398000
FO      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        fuzzyint_ensemble error = 0.02263000
QM      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        pairwise_ensemble error = 0.65277000
CQ      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 1 = 0.96303000
DF      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 2 = 0.96167000
IK      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 3 = 0.96167000
IK      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 1 = 0.98620000
CP      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 2 = 0.95624000
LD      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 3 = 0.00000000

テキストで紹介されているすべてのコードは記事に添付されています。各ソースファイルの説明は以下の表に記載されています。

ファイル名	ファイルの説明
MQL5/include/np.mqh	ベクトルと行列を操作するためのユーティリティ関数のコレクション
MQL5/include/nom2ord.mqh	カテゴリデータをエンコードするためのクラス
MQL5/include/multilayerperceptron.mqh	フィードフォワードニューラルネットワークを表すCMlpクラスの定義
MQL5/include/logistic.mqh	ロジスティック回帰を実装するClogitクラスの定義
MQL5/include/ensemble.mqh	メタモデルのさまざまな実装の定義
MQL5/scripts/ClassificationEnsemble_Demo.mq5	ensemble.mqhで定義されたアンサンブル分類器のパフォーマンスを比較するスクリプト
MQL5/scripts/PairWise_Ensemble_Demo.mq5	CPairWiseクラスをペアワイズカップリングに適用する方法を示すデモスクリプト

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/16838

添付されたファイル |

ZIPをダウンロード

ensemble.mqh (146.05 KB)

logistic.mqh (15.51 KB)

multilayerperceptron.mqh (6.64 KB)

nom2ord.mqh (21.89 KB)

np.mqh (80.58 KB)

ClassificationEnsemble_Demo.mq5 (24.11 KB)

PairWise_Ensemble_Demo.mq5 (9.3 KB)

Mql5.zip (39.67 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

MQL5で自己最適化エキスパートアドバイザーを構築する（第3回）：ダイナミックトレンドフォローと平均回帰戦略

金融市場は一般的に、「レンジ相場」または「トレンド相場」のいずれかに分類されます。このような静的な市場の見方は、短期的な取引においては判断を容易にしてくれるかもしれません。しかし、実際の市場の動きとはかけ離れている側面もあります。この記事では、金融市場がこれら2つのモードをどのように移行するのかを探り、その理解を活かしてアルゴリズム取引戦略への自信をどのように高められるのかを考察します。

知っておくべきMQL5ウィザードのテクニック（第51回）：SACによる強化学習

Soft Actor Criticは、Actorネットワーク1つとCriticネットワーク2つ、合計3つのニューラルネットワークを用いる強化学習アルゴリズムです。これらのモデルは、CriticがActorネットワークの予測精度を高めるように設計された、いわばマスタースレーブの関係で連携します。本連載では、ONNXの導入も兼ねて、こうした概念を、ウィザード形式で構築されたエキスパートアドバイザー(EA)内のカスタムシグナルとしてどのように実装・活用できるかを探っていきます。

知っておくべきMQL5ウィザードのテクニック（第52回）：ACオシレーター

ACオシレーター（アクセラレーターオシレーター、Accelerator Oscillator）は、価格のモメンタムの「速度」だけでなく、その「加速」を追跡する、ビル・ウィリアムズによって開発されたインジケーターの一つです。最近の記事で取り上げたオーサムオシレーター(AO)と非常によく似ていますが、単なるスピードではなく加速に重点を置くことで、遅延の影響を回避しようとしています。本記事では、毎回のようにこのオシレーターからどのようなパターンが得られるかを分析し、ウィザード形式で構築されたエキスパートアドバイザー(EA)を通じて、それらが実際の取引においてどのような意味を持ち得るかを検証します。

DiscordとMetaTrader 5の統合：リアルタイム通知機能を備えたトレーディングボットの構築

この記事では、MetaTrader 5とDiscordサーバーを統合し、どこからでもリアルタイムで取引通知を受信する方法について解説します。Discordへのアラート配信を有効にするための、MetaTrader 5側およびDiscord側の設定方法を詳しく説明します。また、このような通知ソリューションでWebRequestやWebhookを利用する際に生じるセキュリティ上の注意点についても取り上げます。