
ニューラルネットワークが簡単に(第31部):進化的アルゴリズム
内容
はじめに
モデルを最適化するための非勾配法の研究を続けています。これらの最適化方法の主な利点は、勾配法を使用して最適化できないモデルを最適化できることです。これらは、モデル関数の導関数を決定できない場合、またはその計算がいくつかの要因によって複雑になる場合のタスクです。前回の記事で、遺伝的最適化アルゴリズムについて知りました。このアルゴリズムの理想は、自然科学から借りてきたものです。各モデルの重みは、モデルのゲノム内の個別の遺伝子によって表されます。最適化プロセスは、ランダムに初期化されたモデルの特定の母集団を評価します。母集団には有限の「寿命」があります。エポックの終わりに、アルゴリズムは母集団の「最良の」代表者を選択します。これにより、次のエポックの「子孫」が得られます。各個体(新しい母集団のモデル)の「親」のペアがランダムに選択されます。「両親の遺伝子」もランダムに受け継がれます。
1.アルゴリズム構築の基本原則
ご覧のとおり、以前に検討した遺伝的最適化アルゴリズムには多くのランダム性があります。母集団のほとんどを除外しながら、各母集団から最適な代表者を意図的に選択します。そのため、各エポックで母集団全体を完全に反復する間、多くの「無駄な」作業を実行することにいなります。さらに、必要な方向へのエポックからエポックへのモデルの母集団の開発は、偶然の要因に大きく依存します。目標に向けた方向性のある動きを保証するものは何もありません。
勾配降下法に戻ると、その時は各反復で意図的に逆勾配に向かって移動しました。このようにして、モデルエラーを最小限に抑えました。そして、モデルは必要な方向に動いていました。もちろん、勾配降下法を適用するには、各反復で関数の導関数を分析的に決定する必要があります。
そのような機会がなかったらどうするでしょうか。この2つの方法を何らかの方法で組み合わせることができるでしょうか。
まず、関数の導関数の幾何学的な意味を思い出してみましょう。関数の導関数は、特定の点における関数値の変化率を特徴付けます。これは、引数の変化が0に近づくときの関数値の変化とその引数の変化の比率の限界として定義されます。そのような制限が存在する場合。
これは、分析的な導関数に加えて、その近似を実験的に見つけることができることを意味します。引数xに関する関数の導関数を実験的に決定するには、他の条件が等しい場合にxパラメータの値をわずかに変更し、関数の値を計算する必要があります。関数値の変化と引数の変化の比率から、導関数の近似値が得られます。
ここでのモデルは非線形であるため、導関数のより良い定義を実験的に得るために、各引数に対して次の2つの操作を実行することをお勧めします。最初のケースでは何らかの値を加算し、2番目のケースでは同じ値を減算します。2つの操作の平均値は、特定の点で分析された引数に関して、関数導関数値のより正確な近似値を生成します。
この方法は、派生モデルの出力の正確性を評価するときによく使用されます。進化的アルゴリズムもこの特性を利用します。進化的最適化戦略の主なアイデアは、実験的に得られた勾配を使用して、モデルパラメータの最適化の方向を決定することです。
しかし、実験的な勾配を使用する際の主な問題は、多数の操作を実行する必要があるということです。たとえば、モデルの結果に対する1つのパラメータの影響を判断するには、同じソースデータを使用してモデルに対して3つのフィードフォワードパスを取得する必要があります。したがって、すべてのモデルパラメータには、反復回数の3倍の増加が伴います。
これはよくないので、何とかしなければなりません。
たとえば、1つのパラメータではなく2つのパラメータを変更できますが、この場合、それらのそれぞれの影響をどのように判断し、選択したパラメータをどのように変更するのでしょうか(同期的かどうか)。選択したパラメータが結果に与える影響が同じではなく、異なる強度で変更する必要がある場合はどうなるでしょうか。
モデル内で発生するプロセスは、私たちにとって重要ではなかったと言えます。要件を満たすモデルが必要です。最適ではない可能性があります。とにかく、最適性の概念は、提示されたすべての要件を最大限に満たすことです。
この場合、モデルとそのパラメータのセットを1つの全体として見ることができます。何らかのアルゴリズムを使用して、モデルのすべてのパラメータを一度に変更できます。パラメータを変更するためのアルゴリズムは、ランダムな分布など、任意のアルゴリズムにすることができます。
訓練サンプルでモデルをテストするという唯一の利用可能な方法で、変更の影響を評価します。新しいパラメータセットによって以前の結果が改善された場合は、それを受け入れます。結果が悪化した場合は、それを拒否して、以前のパラメータのセットに戻ります。新しいパラメータのループを何度も繰り返します。
これは、遺伝的アルゴリズムのように見えないでしょうか。でも、上記の実験的勾配の推定値はどこにあるのでしょうか。
遺伝的アルゴリズムに近づきましょう。再びモデルの母集団全体を使用し、その有効性を有限の訓練セットでテストします。ただし、この場合、各モデルがランダムに作成された一種の個体である遺伝的アルゴリズムとは対照的に、値が近いパラメータをすべての値に使用します。実際、1つのモデルを使用して、そのパラメータにランダムノイズを追加します。ランダムノイズを使用すると、単一の同一モデルが存在しない母集団が生成されます。少量のノイズにより、同じサブスペース内のすべてのモデルの結果をわずかな偏差で取得できます。これは、モデルの結果が同等であることを意味します。
![]()
ここで、w'は母集団のモデルのパラメータです。
wはソースモデルのパラメータです。
ɛはランダムノイズです。
母集団から各モデルの効率を評価するには、損失関数または報酬システムを使用できます。選択は、解決しようとしている問題に大きく依存します。また、最適化ポリシーも考慮します。損失関数を最小化し、総報酬を最大化します。この記事の実践的な部分では、強化学習の問題を解くときに実装したプロセスと同様に、総報酬を最大化します。
訓練サンプルで新しい母集団のパフォーマンスをテストした後、元のモデルのパラメータを最適化する方法を決定する必要があります。数学を適用すると、各パラメータが結果に与える影響をどうにかして判断することができます。ここでは、いくつかの仮定を使用します。しかし、モデルを全体として考えることにはすでに同意しました。つまり、個々の母集団モデルに追加されたノイズのセット全体が、訓練セットでのモデルの有効性をテストする際に得られる総報酬によって推定できるということです。したがって、元のモデルのパラメータに、母集団のすべてのモデルからの対応するパラメータノイズの加重平均を追加します。ノイズは総報酬によって重み付けされます。そしてもちろん、結果の加重平均にはモデルの学習係数が掛けられます。パラメータの更新式を以下に示します。ご覧のとおり、この式は、勾配降下法を使用するときに重みを更新する式と非常によく似ています。
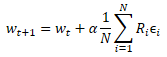
この進化的最適化アルゴリズムは、2017年9月にOpenAIチームによって記事「Evolution Strategies as a Scalable Alternative to Reinforcement Learning」で提案されました。この記事では、提案されたアルゴリズムは、以前に研究されたQ学習および方策勾配法に代わるものと見なされます。提案されたアルゴリズムは、優れた実行可能性と生産性を示しています。また、行動の頻度と報酬の遅延に対する耐性も示します。さらに、著者らが提案するアルゴリズムのスケーリング方法は、追加の計算リソースを利用することにより、ほぼ線形の依存関係で問題解決速度を向上させることができます。たとえば、1,000台以上の並列コンピューターを使用して、わずか10分で3次元のヒューマノイド歩行問題を解くことができました。ただし、この記事ではスケーリングの問題については考慮しません。
2.MQL5を使用した実装
アルゴリズムの理論的側面を検討したので、MQL5を使用して提案されたアルゴリズムの実装を検討する実用的な部分に移りましょう。実装しようとしているアルゴリズムは100%オリジナルではないことに注意してください。アルゴリズムの全体的な考え方は保持されますが、いくつかの変更があります。特に、著者はアクションを選択するために貪欲なアルゴリズムを使用することを提案しました。ただし、アクションを選択する際には確率的アルゴリズムを使用します。さらに、遺伝的アルゴリズムと同様に、突然変異パラメータを追加しました。元のアルゴリズムは突然変異を使用しませんでした。
アルゴリズムを実装するために、新しいニューラルネットワーククラスCNetEvolutionを作成しましょう—遺伝的アルゴリズムモデルから継承します。継承はprivateになります。したがって、使用するすべてのメソッドをオーバーライドする必要があります。一見すると、public継承では、一部のメソッドを再定義する必要がなく、親クラスのメソッドにリダイレクトするだけです.。ただし、publicでない継承は、未使用のメソッドへのアクセスをブロックします。これは、メソッドをオーバーロードするときに最も役立ちます。親クラスのオーバーロードされたメソッドがユーザーに表示されないため、不必要な混乱を避けることができます。
class CNetEvolution : protected CNetGenetic { protected: virtual bool GetWeights(uint layer) override; public: CNetEvolution() {}; ~CNetEvolution() {}; //--- virtual bool Create(CArrayObj *Description, uint population_size) override; virtual bool SetPopulationSize(uint size) override; virtual bool feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true) override; virtual bool Rewards(CArrayFloat *rewards) override; virtual bool NextGeneration(float mutation, float &average, float &mamximum); virtual bool Load(string file_name, uint population_size, bool common = true) override; virtual bool Save(string file_name, bool common = true); //--- virtual bool GetLayerOutput(uint layer, CBufferFloat *&result) override; virtual void getResults(CBufferFloat *&resultVals); };
新しいクラス本体でクラスの新しいインスタンスを宣言しません。さらに、内部変数を宣言しません。親クラスのオブジェクトと変数のみを使用します。したがって、クラスのコンストラクタとデストラクタは両方とも空のままです。
ノイズを追加する前に、元のモデルの重みを格納するオブジェクトを作成しないことに注意してください。これも元のアルゴリズムからの逸脱です。しかし、アルゴリズムを実装する際に、この問題に戻ります。
次は、モデルの母集団を作成するCreateメソッドです。このメソッドは、親クラスのメソッドと同様に、1つのモデルの説明と母集団サイズを含む動的配列をパラメータで受け取ります。主な機能は、親クラスのメソッドを使用して実装されます。ここでは、クラスを呼び出して、取得したパラメータを渡すだけです。
CNetGenetic::Create遺伝的アルゴリズムクラスメソッドで、1つのアーキテクチャとランダムな重みを持つモデルの集団を作成しました。次に、同様の母集団を作成する必要がありますが、モデルのパラメータは近くなければなりません。近くするには、少し後で検討するNextGenerationメソッドを呼び出します。
操作実行結果の確認も忘れてはいけません。メソッドの最後に、演算の論理結果を返します。
bool CNetEvolution::Create(CArrayObj *Description, uint population_size) { if(!CNetGenetic::Create(Description, population_size)) return false; float average, maximum; return NextGeneration(0,average, maximum); }
NextGenerationメソッドについては以前に触れました。そのアルゴリズムを見てみましょう。このメソッドの機能は、同じ名前を持つ親クラスメソッドの機能に似ていますが、アルゴリズム要件に関連する特定の仕様があります。
パラメータでは、メソッドは突然変異の確率と2つの変数を受け取ります。変数には、平均報酬と最大報酬が書き込まれます。
メソッド本体で、必要な報酬値を保存し、ミューテーションの最大値を制限します。訓練済みのモデルを取得する必要があるため、ミューテーションの上限を制限しています。突然変異値が高い場合、得られた結果に関係なく、反復ごとにランダムなモデルパラメータを生成します。結果として、母集団は常にランダムな訓練されていないモデルで構成されます。
bool CNetEvolution::NextGeneration(float mutation, float &average, float &maximum) { maximum = v_Rewards.Max(); average = v_Rewards.Mean(); mutation = MathMin(mutation, MaxMutation);
次に、モデルの重みを更新するためのベースを準備しましょう。この記事の理論的な部分で説明したように、パラメータを更新するときにノイズサイズを重み付けするための尺度は、訓練セットの個々のモデルの総報酬です。ただし、使用される報酬ポリシーに応じて、総報酬は正または負のいずれかになります。高い確率で、母集団のすべてのメンバーの総報酬が同じ符号を持つ状況が得られます。つまり、それらはすべて正または負のいずれかになります。
モデルパラメータへのすべてのノイズの追加がプラスまたはマイナスの影響を与えるわけではありません。この場合、一部のコンポーネントのプラスの影響は、他のコンポーネントのマイナスの影響によってカバーされます。せいぜい、正しい方向への進歩を遅らせるだけです。最悪の場合、モデルの訓練が逆方向に進む可能性があります。この効果の影響を最小限に抑えるために、特定のモデルの総報酬と母集団全体の平均総報酬の差を確率のv_Probabilityベクトルに書き込みましょう。
このステップは、追加するノイズが正規分布に属しているという仮定に関連しています。これは、元のモデルの総報酬が母集団の総報酬の総分布のほぼ中央にあることを意味します。差が計算されると、合計報酬が平均レベルを下回るモデルは、負の確率を受け取ります。モデルの総報酬が小さいほど、その確率は負になります。同様に、合計報酬が最も高いモデルは、最も高い正の確率も受け取ります。それの実際的な利点は何でしょうか。追加されたノイズが正の効果を持つ場合、それを正の確率に乗算することにより、重みを同じ方向にシフトします。したがって、必要な方向へのモデルの訓練をお勧めします。追加されたノイズが負の効果を持っていた場合、それを負の確率に乗算することにより、重みシフトの方向を負から正に変更します。これはまた、モデルの訓練を総報酬の最大化に向けます。
次に、独自のアルゴリズムに従って、ノイズの加重平均を使用してモデルパラメータを修正します。したがって、すべてのベクトル要素の絶対値の合計が1になるように、得られた確率のベクトルも正規化します。
v_Probability = v_Rewards - v_Rewards.Mean(); float Sum = MathAbs(v_Probability).Sum(); if(Sum == 0) v_Probability[0] = 1; else v_Probability = v_Probability / Sum;
ベクトルv_Probabilityに記述したモデル更新係数を決定した後、モデル層を反復するループに進みます。新しい母集団モデルのパラメータは、このループの本体で形成されます。
ループ本体では、まず現在の層オブジェクトの動的配列へのポインタを取得します。受信したポインタの有効性を即座に確認します。また、動的配列のサイズを確認してください。指定された母集団サイズと一致する必要があります。母集団のサイズが不十分な場合は、CreatePopulationメソッドを呼び出して追加のモデルを作成します。ここでは、親クラスのメソッドを変更せずに使用します。
for(int l = 1; l < layers.Total(); l++) { CLayer *layer = layers.At(l); if(!layer) return false; if(layer.Total() < (int)i_PopulationSize) if(!CreatePopulation()) return false;
その後、GetWeightsメソッドを呼び出します。これにより、モデルの現在の層の更新されたパラメータが作成されます。パラメータは、m_Weightsおよびm_WeightsConv行列で作成されます。メソッドのアルゴリズムについては後で考えます。
if(!GetWeights(l)) return false;
モデルパラメータを更新したら、母集団の入力を開始できます。これをおこなうには、反復回数が母集団のサイズに等しい入れ子ループを作成しましょう。
ループの本体で、分析中のニューラル層の現在のニューロンのオブジェクトへのポインタを取得します。取得したポインタの有効性をすぐに確認します。ここでは、重み行列オブジェクトへのポインタも取得します。
for(uint i = 0; i < i_PopulationSize; i++) { CNeuronBaseOCL* neuron = layer.At(i); if(!neuron) return false; CBufferFloat* weights = neuron.getWeights();
受信した重み行列ポインタが有効な場合は、この行列の操作を開始します。ここでは、重み行列の要素を反復処理する別のネストされたループを作成します。
ループ本体では、最初にミューテーションを使用する確率をチェックし、必要に応じて乱数を生成します。生成された乱数が突然変異確率よりも小さい場合、ランダムな重み係数を行列の現在の要素に書き込みます。その後、ループの次の反復に進みます。遺伝的アルゴリズムでも同様の方法が使用されました。
if(!!weights) { for(int w = 0; w < weights.Total(); w++) { if(mutation > 0) { int err_code; float random = (float)Math::MathRandomNormal(0.5, 0.5, err_code); if(mutation > random) { if(!weights.Update(w, GenerateWeight((uint)m_Weights.Cols()))) { Print("Error updating the weights"); return false; } continue; } }
現在の重みを更新する場合は、まず現在の値を確認します。必要に応じて、無効な数値をランダムな重みに置き換える必要があります。
if(!MathIsValidNumber(m_Weights[0, w])) { if(!weights.Update(w, GenerateWeight((uint)m_Weights.Cols()))) { Print("Error updating the weights"); return false; } continue; }
ネストされたループ反復の最後に、現在の重みにノイズを追加します。
if(!weights.Update(w, m_Weights[0, w] + GenerateWeight((uint)m_Weights.Cols()))) { Print("Error updating the weights"); return false; } } weights.BufferWrite(); }
母集団の現在の要素の重み行列のすべての要素にノイズを追加した後、更新されたパラメータをOpenCLコンテキストメモリに転送します。
必要に応じて、畳み込み層の重み行列について上記の反復を繰り返します。
if(neuron.Type() != defNeuronConvOCL) continue; CNeuronConvOCL* temp = neuron; weights = temp.GetWeightsConv(); for(int w = 0; w < weights.Total(); w++) { if(mutation > 0) { int err_code; float random = (float)Math::MathRandomNormal(0.5, 0.5, err_code); if(mutation > random) { if(!weights.Update(w, GenerateWeight((uint)m_WeightsConv.Cols()))) { Print("Error updating the weights"); return false; } continue; } } if(!MathIsValidNumber(m_WeightsConv[0, w])) { if(!weights.Update(w, GenerateWeight((uint)m_WeightsConv.Cols()))) { Print("Error updating the weights"); return false; } continue; } if(!weights.Update(w, m_WeightsConv[0, w] + GenerateWeight((uint)m_WeightsConv.Cols()))) { Print("Error updating the weights"); return false; } } weights.BufferWrite(); } }
反復は、シーケンスのすべての要素に対して繰り返されます。
メソッドの最後で、総報酬累積ベクトルをリセットしてメソッドを終了します。
v_Rewards.Fill(0); //--- return true; }
メソッドのシーケンスに従って、前のメソッドから呼び出されたGetWeightsメソッドを考えてみましょう。その目的は、最適化されるモデルのパラメータを更新することです。親の遺伝的アルゴリズムクラスCNetGeneticには、すべての母集団モデルの1つのニューラル層のパラメータをダウンロードするために使用される同じ名前のメソッドがありました。得られた行列を使用して、新しい母集団を作成しました。今回も同じロジックを使用しますが、使用する最適化アルゴリズムに従ってコンテンツがわずかに変化するだけです。
メソッドは、パラメータの行列を作成する必要があるニューラル層のインデックスをパラメータで受け取ります。メソッド本体で、モデルパラメータを更新するときに母集団の代表を使用する確率で、形成されたベクトルの可用性を確認します。同じ名前の親クラスメソッドを呼び出します。操作の実行を制御することを忘れないでください。
bool CNetEvolution::GetWeights(uint layer) { if(v_Probability.Sum() == 0) return false; if(!CNetGenetic::GetWeights(layer)) return false;
親クラスメソッドの操作が完了すると、m_Weightsおよびm_WeightsConv行列には、すべての母集団モデルの分析されたニューラル層の重みが含まれることが期待されます。
行列には重みが含まれていることに注意してください。ただし、モデルパラメータを更新するには、追加されたノイズの値と元のモデルのパラメータが必要です。
報酬の調整も同様に進めます。ノイズには正規分布があることがわかっています。母集団モデルの各パラメータは、元のモデルの対応するパラメータとノイズの合計です。元のモデルのパラメータは、母集団モデルの対応するパラメータの分布の中央にあると仮定します。したがって、対応する母集団パラメータの平均値のベクトルを使用できます。
if(m_Weights.Cols() > 0) { vectorf mean = m_Weights.Mean(0);
母集団モデルのパラメータの行列から平均値のベクトルを減算することにより、追加されたノイズの必要な行列を見つけることができます。
matrixf temp = matrixf::Zeros(1, m_Weights.Cols()); if(!temp.Row(mean, 0)) return false; temp = (matrixf::Ones(m_Weights.Rows(), 1)).MatMul(temp); m_Weights = m_Weights - temp;
同じ方法を使用して、追加されたノイズと、モデルの重みを更新する際のその使用の確率を決定すると、同等の値が得られます。次に、上記の式を使用してモデルパラメータを更新できます。その後、取得した値を適切な行列に転送するだけです。
mean = mean + m_Weights.Transpose().MatMul(v_Probability) * lr; if(!m_Weights.Resize(1, m_Weights.Cols())) return false; if(!m_Weights.Row(mean, 0)) return false; }
必要に応じて、2番目の行列に対して操作を繰り返します。
if(m_WeightsConv.Cols() > 0) { vectorf mean = m_WeightsConv.Mean(0); matrixf temp = matrixf::Zeros(1, m_WeightsConv.Cols()); if(!temp.Row(mean, 0)) return false; temp = (matrixf::Ones(m_WeightsConv.Rows(), 1)).MatMul(temp); m_WeightsConv = m_WeightsConv - temp; mean = mean + m_WeightsConv.Transpose().MatMul(v_Probability) * lr; if(!m_WeightsConv.Resize(1, m_WeightsConv.Cols())) return false; if(!m_WeightsConv.Row(mean, 0)) return false; } //--- return true; }
すべてのメソッドとクラスの完全なコードは、以下の添付ファイルにあります。
進化的アルゴリズムを実装するために変更されたメソッドのアルゴリズムを検討しました。クラスの機能を完成させるには、メソッドをオーバーライドして、スレッドを親クラスの対応するメソッドにリダイレクトする必要があります。これは、publicでない継承に必要な措置であることに注意してください。
bool CNetEvolution::SetPopulationSize(uint size) { return CNetGenetic::SetPopulationSize(size); } bool CNetEvolution::feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true) { return CNetGenetic::feedForward(inputVals, window, tem); } bool CNetEvolution::Rewards(CArrayFloat *rewards) { if(!CNetGenetic::Rewards(rewards)) return false; //--- v_Probability = v_Rewards - v_Rewards.Mean(); v_Probability = v_Probability / MathAbs(v_Probability).Sum(); //--- return true; } bool CNetEvolution::GetLayerOutput(uint layer, CBufferFloat *&result) { return CNet::GetLayerOutput(layer, result); } void CNetEvolution::getResults(CBufferFloat *&resultVals) { CNetGenetic::getResults(resultVals); }
クラスを完成するには、ファイルを操作するメソッドをオーバーライドする必要があります。まず、モデルの保存方法を決める必要があります。お気付きかもしれませんが、更新されたパラメータでモデルを個別に保存していません。パラメータを更新して、新しい母集団を構築しただけです。ただし、訓練済みのモデルを保存するには、1つだけ選択する必要があります。論理的には、最良の結果が得られたモデルを保存する必要があります。親クラスのメソッドの中に関連するメソッドが既にあります。操作の流れをそれにリダイレクトします。
bool CNetEvolution::Save(string file_name, bool common = true) { return CNetGenetic::SaveModel(file_name, -1, common); }
モデルの保存方法を決定しました。事前訓練済みモデルの読み込みメソッドに移りましょう。状況は似ていますが、わずかな違いがあります。訓練プロセスでは、母集団全体を保存するのではなく、最良の結果が得られた1つのモデルのみを保存します。したがって、そのようなモデルを読み込んだ後、特定のサイズの母集団を作成する必要があります。この可能性は、親クラスの読み込みメソッドで実装されます。しかし、その方法では、完全にランダムなパラメータを持つモデルの母集団が作成されます。ただし、ノイズを追加して、1つのモデルの周囲に母集団を作成する必要があります。したがって、最初に親クラスモデルのデータ読み込みメソッドを呼び出します。これにより、必要なサイズの機能と母集団が作成されます。次に、合計報酬のベクトルをリセットし、以前に検討したメソッドNextGenerationを呼び出します。必要な特性を持つ新しい母集団が作成されます。
bool CNetEvolution::Load(string file_name, uint population_size, bool common = true) { if(!CNetGenetic::Load(file_name, population_size, common)) return false; v_Rewards.Fill(0); float average, maximum; if(!NextGeneration(0, average, maximum)) return false; //--- return true; }
解明されていない点に注意してください。この新しい母集団生成方法は、読み込まれたモデルをランダムな重みで満たされたモデルからどのように分離するのでしょうか。この解決策はかなり簡単です。親クラスのメソッドでは、読み込まれたモデルはインデックス「0」で母集団に配置されます。ランダムパラメータを持つモデルが追加されます。追加されたノイズを使用する確率を決定するために、モデルの総報酬のベクトルを使用します。このメソッドは、新しい集団作成メソッドを呼び出す前に、以前にリセットされています。したがって、NextGenerationメソッド本体では、確率を決定するときにゼロ値のベクトルも取得します。ベクトル値の合計は0です。この場合、インデックス0(ファイルから読み込まれた)を持つモデルのみを使用して、新しい母集団モデルのパラメータベースを形成する100%の確率を決定します。ランダムモデルのパラメータを使用する確率は0です。したがって、新しい母集団は、ファイルからアップロードされたモデルを中心に構築されます。
bool CNetEvolution::NextGeneration(float mutation, float &average, float &maximum) { ............. ............. ............. v_Probability = v_Rewards - v_Rewards.Mean(); float Sum = MathAbs(v_Probability).Sum(); if(Sum == 0) v_Probability[0] = 1; else v_Probability = v_Probability / Sum; ............. ............. ............. }
新しいCNetEvolutionクラスのすべてのメソッドのアルゴリズムを検討しました。これで、モデルの訓練に進むことができます。この記事の次のセクションでおこないます。
3.テスト
モデルを訓練するために、前回の記事で使用したものに基づいてEvolution.mq5 EAを作成しました。EAのパラメータと設定は変更されていません。実際、遺伝的アルゴリズムモデル訓練EAでオブジェクトクラスを変更するだけで、進化的アルゴリズムを使用して新しいモデルを訓練できます。
新しいモデルがどのように作成されるかについて少し説明します。第7部と第8部で転移学習ソリューションを作成した後、EAコードでモデルアーキテクチャを指定しないことにしたことを思い出してください。これにより、EAコードを変更することなく、さまざまなモデルでの実験が可能になります。
新しいモデルを作成するには、以前に作成したNetCreatorを実行します。完全に新しいモデルを作成しているため、ツールの左側は使用せず、事前訓練済みのモデルは読み込まれません。
訓練プロセスでは、ローソク足ごとに12個の説明パラメータをモデルに入力します。また、20ローソク足の深い履歴データを分析する予定です。したがって、初期データ層のサイズは240ニューロン(12 * 20)になります。入力データ層として、活性化関数を使用せずに完全に接続されたニューラル層を使用します。ツール中央部で1層目のパラメータを指定し、[ADD LAYER]ボタンを押します。この操作の結果、最初のニューラル層の記述がツールの右側のブロックに表示されます。
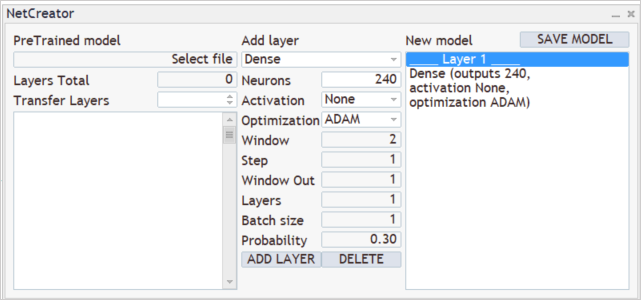
次に、モデルアーキテクチャの作成プロセスが続きます。たとえば、モデルで3つの隣接するローソク足のパターンを分析するとします。これをおこなうには、分析ウィンドウサイズが36ニューロン(12 * 3)の畳み込み層を追加します。分析されたウィンドウシフトステップを12ニューロンに設定します。これは、1つのローソク足を表す要素の数に対応します。モデルに行動の自由を与えるために、パターン分析用に12個のフィルターを作成します。活性化関数として、強気パターンと弱気パターンの論理的な分離を可能にする双曲線正接を使用しました。ニューラル層の出力は、活性化関数の範囲内で正規化されます。
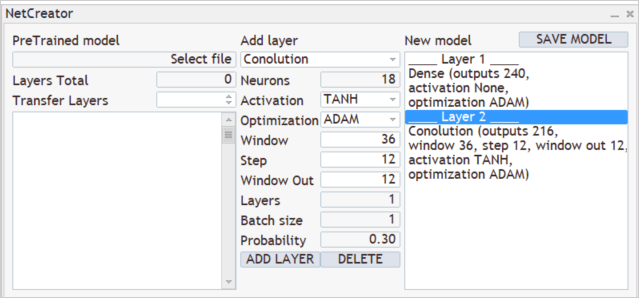
作成された畳み込み層は、最初に1つのフィルターのすべての要素のシーケンスを返し、次に別のフィルターのシーケンスを返します。これは、各行が個別のフィルターに対応し、行要素がソースデータシーケンス全体に対するフィルター操作の結果を表す行列と比較できます。
次に、以前に作成した畳み込み層のフィルターの結果を分析する必要があります。3つの畳み込み層のカスケードを構築し、それぞれが前の畳み込み層の結果を分析します。3つの層はすべて同じ特性を持ちます。隣接する2つのニューロンを1ニューロン単位で分析します。各層の2つのフィルターが分析に使用されます。
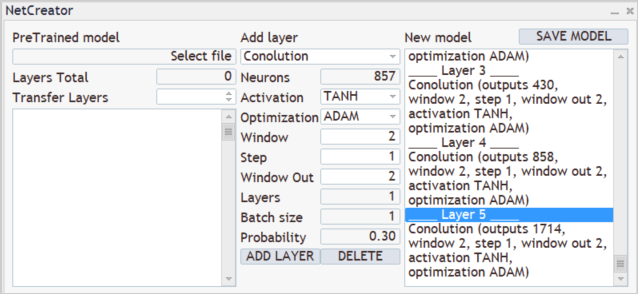
ご覧のとおり、小さな分析データウィンドウステップといくつかのフィルターを使用することにより、結果ベクトルのサイズが層ごとに大きくなります。通常、サブサンプリング層は次元削減に使用されます。フィルターの出力値を平均するか、最高値を取ります。できるだけ多くの有用な情報を保存しようとして、それらを使用しませんでした。
畳み込み層は、ある種の初期データ準備を実行し、いくつかのパターンを定義します。畳み込み層が多いほど、モデルはより複雑なパターンを見つけることができます。ただし、学習プロセスが複雑になるため、非常に深いモデルの作成は避けてください。非勾配モデルの最適化手法が勾配の爆発と減衰の問題を回避することは事実です。しかし、問題を解決するために深いネットワークが本当に必要なのでしょうか。さまざまなオプションを試して、モデルの増加が最終結果にどのように影響するかを判断してください。ある時点で、新しい層を追加しても結果が変わらないことに気付くでしょう。ただし、モデルを最適化するには追加のリソースが必要になります。
畳み込みニューラル層の結果は、それぞれ500個のニューロンを持つ3つの層の完全に接続されたパーセプトロンで処理されます。ここでは、活性化関数として双曲線正接も使用しました。さまざまな活性化関数がどのように機能するかを試して、結果を比較することをお勧めします。
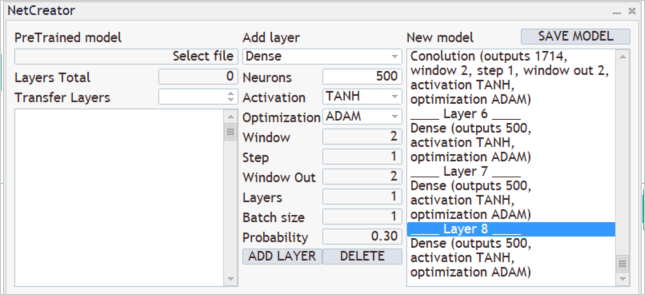
モデルの出力では、3つの行動(購入、販売、待機)の確率分布を取得したいと考えています。これをおこなうには、3つのニューロンの完全に接続された層をもう1つ作成します。今回は活性化関数を使用しません。
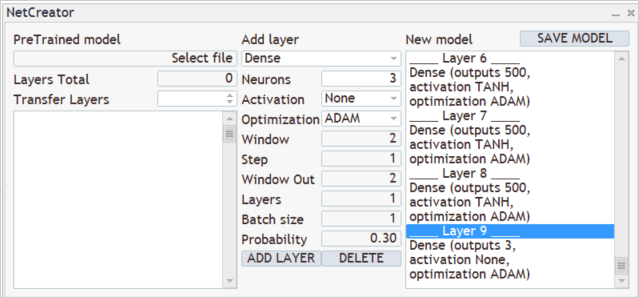
SoftMax層を使用して、結果を確率の領域に変換します。
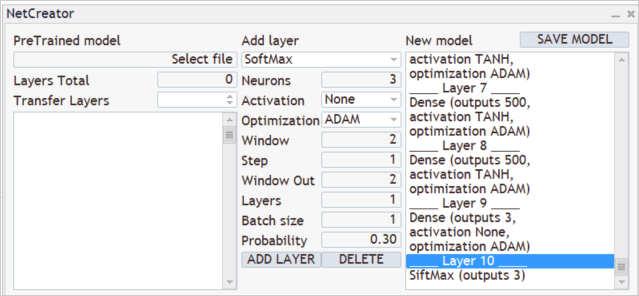
これで、新しいモデルの作成が完了しました。EAが使用するファイルに保存しましょう。[SAVE MODEL]をクリックすると、モデル保存機能が起動します。
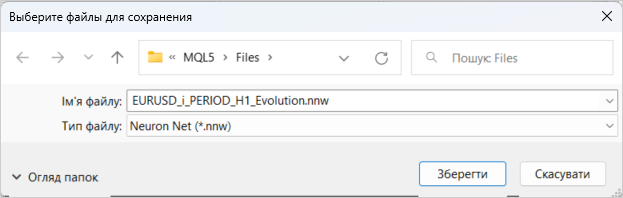
パーセプトロンは、過去2年間の履歴データを使用して訓練されました。モデルの訓練プロセスは、以前の記事で既に説明されています。ここではそれらについては詳しく説明しません。
不思議なことに、モデルの最適化中に、総エラーダイナミクスグラフは急激なダイナミクスを示しました。
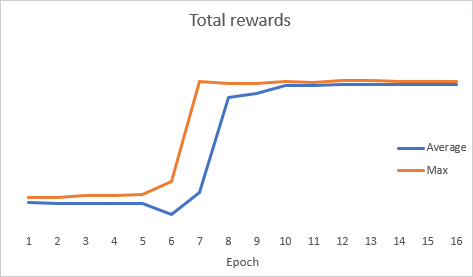
最適化後、モデルはストラテジーテスターでテストされました。モデルをテストするために、いくつかの以前の記事からのEAの正確なコピーであるEvolution-test.mq5EAを使用しました。変更は、読み込まれたモデルのファイル名のみに影響を与えました。完全なEAコードは添付ファイルにあります。
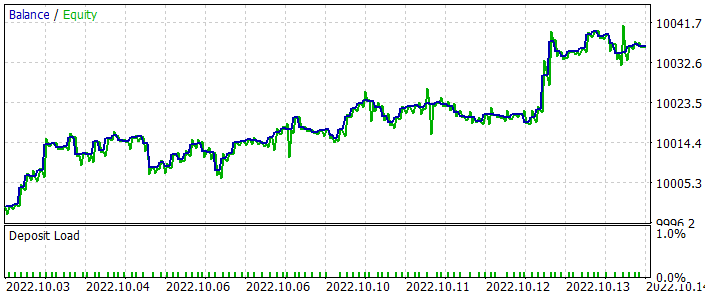
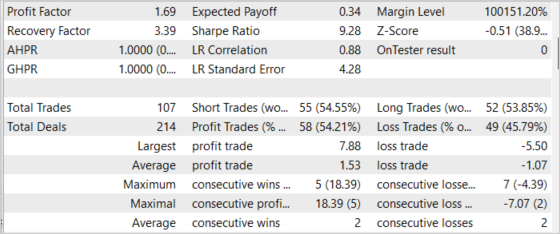
EAは過去2週間の期間テストされましたが、訓練サンプルには含まれていません。これは、EAが実際の条件に近い状態でテストされたことを意味します。テスト結果は、提案された方法の実行可能性を示しました。下のチャートでは、残高が増加するダイナミクスを確認できます。通常、テスト期間中に107回の取引が実行されました。これらのうち、ほぼ55%が利益を上げていました。勝てる取引と負ける取引の比率はほぼ1:1ですが、平均的な勝ち取引は平均的な負け取引よりも43%高くなっています。したがって、結果のプロフィットファクターは1.69です。リカバリーファクターは3.39に達しました。
結論
この記事では、別の非勾配最適化手法である進化的アルゴリズムについて知りました。このアルゴリズムを実装するためのクラスを作成しました。考慮されたアルゴリズムの有効性は、モデルの最適化とストラテジーテスターでの最適化結果のテストによって確認されます。テスト結果は、EAが利益を生み出すことができることを示しています。ただし、テストは短い時間間隔で実行されたことに注意してください。したがって、EAが長期的に利益を生み出すことができると確信することはできません。
この記事のモデルとEAは、テクノロジを実証することのみを目的としています。実際の口座で使用する前に、追加の設定と最適化が必要です。
参照文献
- ニューラルネットワークが簡単に(第26部):強化学習
- ニューラルネットワークが簡単に(第27部):ディープQラーニング(DQN)
- ニューラルネットワークが簡単に(第28部):方策勾配アルゴリズム
- ニューラルネットワークが簡単に(第29部):Advantage actor-criticアルゴリズム
- 自然進化戦略
- 強化学習のスケーラブルな代替手段としての進化戦略
- ニューラルネットワークが簡単に(第23部):転移学習用ツールの構築
- ニューラルネットワークが簡単に(第24部):転移学習用ツールの改善
記事で使用されているプログラム
| # | ファイル名 | タイプ | 詳細 |
|---|---|---|---|
| 1 | Evolution.mq5 | EA | モデルを最適化するためのEA |
| 2 | NetEvolution.mqh | クラスライブラリ | 進化的アルゴリズムを整理するためのライブラリ |
| 3 | Evolution-test.mq5 | EA | ストラテジーテスターでモデルをテストするためのEA |
| 4 | NeuroNet.mqh | クラスライブラリ | ニューラルネットワークモデルを作成するためのライブラリ |
| 5 | NeuroNet.cl | コードベース | ニューラルネットワークモデルを作成するためのOpenCLプログラムコードライブラリ |
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/11619
 フラクタルによる取引システムの設計方法を学ぶ
フラクタルによる取引システムの設計方法を学ぶ
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索