
ニューラルネットワークが簡単に(第27部):DQN (Deep Q-Learning)
内容
はじめに
前回は、強化学習の手法を模索し始め、初めて交差エントロピーの訓練可能なモデルを構築しました。今回は、引き続き強化学習法について学びます。Deep Q-Learningの手法に進みます。2013年、DeepMindチームはDeep Q-Learningを用いることで、7つのアタリ社のコンピュータゲームをうまくプレイできるモデルの作成に成功しました。注目すべきなのは、7つのゲームすべてにおいて、アーキテクチャやハイパーパラメータを変えずに、同じモデルが訓練されたことです。訓練結果によると、分析したゲームのうち6ゲームにおいて、モデルが以前に達成した結果を改善することができました。また、3つのゲームでは、モデルが人間を上回りました。この達成が発表されることにより、強化学習法の発展に新たな段階が始まりました。この手法を勉強して、取引に関する問題を解決するために使ってみましょう。
1.Q関数の概念
まず、前回学習した素材に戻りましょう。強化学習では、エージェントとその環境との相互作用のプロセスを構築します。エージェントは、現在の環境の状態を分析し、環境の状態を変化させる行動をとります。その行動に対して、環境はエージェントに報酬を返します。エージェントは報酬がどのように形成されるかを知りません。エージェントの目標は、分析下のセッションで可能な限り最大の総報酬を受け取ることです。
エージェントは行動に対する報酬は受け取りません。報酬を受け取るのは、ある状態から別の状態に遷移するときです。同時に、同じような状況である行動をとったとしても、同じ状態への遷移が保証されるわけではありません。行動をとると、期待される状態へ遷移する確率がある程度高くなるだけです。状態、行動、遷移の確率と依存関係はエージェントには未知です。エージェントは、環境との相互作用の過程からそれらを学習する必要があります。
実は、強化学習は、現在の状態、とった行動、報酬の間に何らかの関係があることを前提にしています。数学的な言い方をすれば、関数Qが存在し、この関数は、状態sと行動aに依存して、報酬rを返します。これはQ(s|a)と表記されます。この関数は行動効用関数と呼ばれます。
エージェントはこの関数を知りません。ただし、それが存在するならば、環境との相互作用の過程で、行動を無限に繰り返すことで、この関数を近似的に実現することができるのです。
実際の環境では、状態や行動を無限に繰り返すことは不可能ですが、十分に繰り返せば、許容できる誤差で関数を近似することができます。Q関数の表現形式は異なることができます。前回は、各行動の効用を決定しながら、状態、行動、平均報酬の依存関係の表を作りました。Q関数の表現方法は他にもあり、全く問題ない、あるいはさらに良い結果を得ることができます。これらは決定木、ニューラルネットワークなどです。
なお、エージェントが近似したQ関数は報酬を予測するものではなく、エージェントが過去に環境と相互作用した経験に基づいて、期待されるリターンを返すだけです。
2.Deep Q-learning
Deep Q-learningがニューラルネットワークを使ってQ関数を近似するものであることは、もうお分かりだと思います。そのような方法のメリットは何でしょうか。前回の交差エントロピーの表形式法の実装を思い出してください。表形式での実装は、可能な状態や行動の数が有限であることを前提としていることを強調しました。そこで、初期データをクラスタリングすることで、可能な状態の数を限定しました。でも、そんなにいいのでしょうか。クラスタリングは常に良い結果を生むのでしょうか。ニューラルネットワークを使用することで、可能な状態の数が制限されることはありません。これは、取引関連の問題を解決する上で、大きなメリットになると思います。
一番最初のわかりやすい方法は、前回の表をニューラルネットワークに置き換えることですが、残念ながら、そう簡単にはいきません。実際には、この方法はあまり良いものではないことが判明しました。この方法を実現するために、いくつかのヒューリスティックを追加する必要があります。
まず、エージェント訓練の目標を見てみましょう。一般的に、その目標は総報酬を最大化することです。下の図をご覧ください。エージェントは、startセルからFinishセルまで移動しなければなりません。エージェントは、Finishセルに到達したときに一度だけ報酬を受け取ることになります。それ以外の状態では、報酬はゼロです。
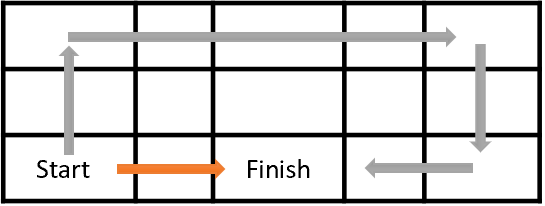
図には2つのパスが示されています。私たちにとって、橙色の道の方が短く、好ましいことは明らかですが、報酬の最大化という点では、両者は等価です。
同様に、取引においても、今資金を投入して遠い将来に収入を得るよりも、すぐに収入を得る方が望ましいです。これは、お金の価値、つまり金利、インフレ、その他多くの変数を考慮しています。ここでも同じことをします。この問題を解決するために、割引率ɣを導入し、将来の報酬の価値を低下させます。
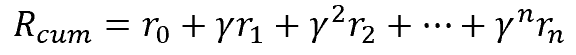
割引率ɣは0から1の範囲とすることができます。割引率が1であれば、割引は発生しません。また、割引率0では、将来の報酬は無視されることになります。実際には、割引率は1に近い値に設定されます。
ただし、ここでもう1つ問題があります。理論的には良くても実際にはうまくいかないことがあります。遷移と報酬のマップが完成していれば、将来の報酬を簡単に計算することができます。その中で、最終的に報酬が最大となる最適な道を選ぶことができます。しかし、現実的な問題を解く場合、ある行動をとった後に次の状態がどうなるかはわかりません。報酬もわかりません。これらはすべて、すでにすぐ次のステップについて言えます。セッション終了までの全経路について言えば、さらに深刻です。私たちは未来を見通すことはできません。次の報酬を受け取るために、エージェントは行動をとる必要があります。新しい状態に遷移した後で初めて環境から報酬が返ってきます。しかも、引き返すことはできません。後で最適な行動を選択するために、前の状態に戻って別の行動をとることはできません。
そこで、動的計画法を適用することにします。具体的にはベルマン最適化法です。これは、最適な戦略を選択するためには、各ステップで最適な行動を選択することが必要であると言うものです。つまり、各ステップで報酬が最大となる行動を選択することで、セッションの累積報酬が最大となるのです。行動効用関数を更新するための数式は以下の通りです。
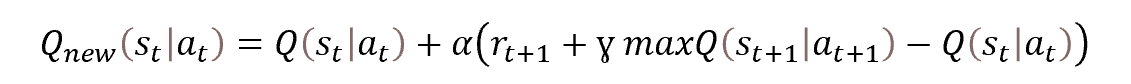
計算式をご覧ください。確率的勾配降下の重み更新式を連想させないでしょうか。実際、行動効用関数の値を更新するためには、関数の前回値に学習係数を掛けた偏差が必要です。
また、この関数では、ある時点tにおける関数の値を決定するためには次の時点t+1における行動効用関数の値が必要であることもわかります。つまり、状態stにいるときに行動atをとり、状態st+1に遷移した後に報酬rt+1を得るのです。行動効用関数の値を更新するには、次のステップで行動効用関数の最大値を報酬に加算する必要があります。つまり、次のステップで得られる最大の期待報酬を加算します。もちろん、エージェントは、未来を見て将来の報酬を決定することはできませんが、その近似関数を使うことができます。状態st+1にあるとき、与えられた状態から可能なすべての行動に対して関数の値を計算し、得られた値のうち最も高い値を取ることができるのです。訓練の過程で、その値は最初は真実から遠く離れたものになります。でも、何もしないよりはましです。エージェントが学習するにつれて、予測誤差は減少します。
2.1.経験再生
確率的勾配降下法が優れているのは、母集団からの小さな標本の値に基づいて関数値を更新することができる点です。実際に、ここでのエージェントは、セッションの各ステップで行動効用関数の値を更新することができます。ただし、教師あり訓練では、状態が互いに独立した訓練標本を使っていたので、この性質を強化するために、新しい訓練データセットを選択する前に、毎回母集団をシャッフルすることにした。
しか今し、教師あり学習では、エージェントは環境中を時間的に移動し、行動をとり、毎回、前の状態と密接に関連する新しい状態に入ります。ご自分の周りをご覧ください。歩いていても、座っていても、何か行動をとっても、周囲の環境は劇的に変化しません。あなたの行動は、この行動が向けられる、そのほんの一部を変えるだけなのです。同様に、エージェントが行動をとっても、対象となる環境の状態はあまり変化しません。つまり、連続した状態が大きく相互に関連することになるのです。ここでのエージェントは、そのような状態の自己相関を観測します。
その難しさは、小さな訓練係数を用いても、エージェントが行動効用関数を現在の状態に合わせ、過去の経験の記憶を犠牲にしてしまうことを防げないことに関連しています。
教師あり学習では、多数の反復の後に独立した状態を用いることで、モデルの重み値を平均化することが可能となります。強化学習の場合、連結して実質的に変化していない状態を使ってモデルを訓練すると、現在の状態に合わせてモデルが再訓練されます。
どのような時系列でもそうですが、状態間の関係は時間が長くなるにつれて減少していきます。そこで、この問題を解決するために、エージェントモデルの訓練時に、時間軸に沿って散在する状態を利用する必要があります。これは、履歴データがあれば簡単にできます。しかし、環境に沿って移動する場合、ここでのエージェントはそのような記憶を持っていません。現在の状態しか見ず、ある状態から別の状態にジャンプすることはできません。
そこで、エージェントのためにメモリを整理してはどうでしょうか。行動効用関数の値を更新するためには、次のようなデータセットが必要です。
状態→行動→報酬→状態
環境に沿って移動しながら、エージェントが必要なデータセットをバッファに保存するようにしましょう。バッファサイズはハイパーパラメータであり、モデルアーキテクチャによって決定されます。バッファが一杯になると、新しく到着したデータは古いものを追い出します。モデルの訓練には、現在の状態を使わず、エージェントの記憶からランダムに選んだデータを使用します。こうすることで、個々の状態間の関係を最小化し、モデルの解析データの一般化能力を高めます。
2.2.Target Netの使用
また、行動効用関数を学習する際に注意すべき点は、次のステップでこの関数の最大値maxQ(st+1|at+1)です。これは「未来からの値」であることにご注意ください。近似した行動効用関数に基づく予測値をとります。ただし、時間tにいるため、時間t+1の値を変更することはできません。関数値を更新するたびに、モデルの重みを更新し、それによって次の予測値を変化させます。
さらに、最大の報酬を得るためにエージェントを訓練します。モデル更新の各反復において、期待値を最大化します。予測値の使用は、再帰的に更新値を最大化します。このようにして、行動効用関数の値をプログレッションで最大化するのです。そのため、関数値が過大評価され、行動効用を予測する際の誤差が大きくなります。これはあまり良くないです。したがって、将来の行動の有用性を評価するための定常的なメカニズムが必要です。
この問題に対しては、将来の行動の有用性を予測するモデルを追加で作成することで対応できるでしょうが、この方法では、2つ目のモデルを訓練するための追加コストが必要になります。これは避けたいところです。一方、この機能を実行するモデルはすでに訓練しています。ただし、重みが変更された後、モデルは更新前と同じ関数の値を返すはずです。この物議を醸す問題は、モデルをコピーすることで解決できます。同じ行動効用関数モデルのインスタンスを2つ作るだけです。一方のインスタンスはK訓練され、もう一方のインスタンスは将来の行動の効用を予測するために使用されます。
行動効用関数のモデルが固定化されると、学習過程ではすぐに無関係になります。そのため、さらなる訓練が非効率になる可能性があります。この影響を排除するためには、学習過程で予測値のモデルを更新する必要があります。2番目のインスタンスは並列に訓練されません。その代わり、行動効用関数モデルの訓練済みインスタンスの重みを、ある周期性をもって2番目のインスタンスにコピーすることにします。このように、1つのモデルを訓練するだけで、行動効用関数モデルのかなり最新の2つのインスタンスが得られ、予測値の再帰的過大評価を回避することができます。
以上を整理してみます。
- エージェントを訓練するために、ニューラルネットワークを使用します。
- ニューラルネットワークは、行動効用Q関数の期待値を予測するように訓練されます。
- 隣接する状態間の相関を最小にするため、学習過程ではメモリバッファを使用し、そこからランダムに状態を抽出します。
- Q関数の将来の値を予測するために、訓練済みモデルの「凍結」コピーである第2のTarget Netモデルがあります。
- Target Netは、訓練済みモデルから重み行列を定期的にコピーすることで実現されます。
次に、MQL5を使用して説明した方法の実装を調べてみましょう。
3.MQL5を使用した実装
MQL5を用いたDeep Q-Learningアルゴリズムの実装には、「Q-learning.mq5」というEAファイルを使用します。EAの完全なコードは、添付ファイルに記載されています。ここでは、Deep Q-Learning法の実装にのみ焦点を当てます。
実装を進める前に、初期データと報酬体系をどうするか決めておきましょう。初期データは、以前の実験で使用したものと同じです。では、報酬制度はどうでしょうか。先に考えたフラクタル予測問題は、どちらかというと人工的なものです。もちろん、フラクタルの最大可能数を決定するモデルを作ることも可能ですが、私たちの主な目的は、取引業務から最大限の利益を得ることです。
この文脈では、次のローソク足の大きさを報酬の大きさとして使用することが完全に理にかなっています。もちろん、報酬の符号は、おこなった操作に対応したものでなければなりません。単純化したモデルでは、「買い」と「売り」の2つの取引操作があります。また、ポジションを持たないこともあります。
ここでは、モデルを複雑にし無いように、ポジションボリューム、ポジション増加、部分決済を決定します。エージェントが固定ロットのポジションを持つことができると仮定しましょう。また、エージェントはすべてのポジションを決済し、市場に入らないことができます。
また、報酬の方針に関しては、適切に準備された報酬体系によって訓練の結果が大きく左右されることを理解する必要があります。強化学習の実践では、報酬方針の選択を誤ると、予想外の結果になる例が数多くあります。モデルは学習して間違った結論を出すことがあります。また、最大限の報酬を得ようとするあまり、望ましい結果が得られず、行き詰ってしまうこともあります。例えば、ポジションを開いたり決済したりすることで、モデルに報酬を与えることができます。ただし、この報酬が取引から蓄積された利益に対する報酬を上回る場合、モデルは単にポジションを開いたり決済したりすることを学習できます。つまり、モデルが報酬を最大化し、私たちが損失を最大化することになるのです。
一方、操作の手数料のように、ポジションの開始と決済にペナルティを課せば、モデルは単純に市場に参加しないことを学習することができます。利益はありませんが、損失もありません。
以上のことを考え、3つの行動を想定したモデルを作ることにしました。買う、売る、市場外です。
エージェントは、新しいローソク足ごとに予想される動きの方向を予測し、以前のものを考慮せずに行動を選択することになります。そこで、モデルを単純化するために、エージェントにポジションの有無やポジションの方向に関する情報を入力しないことにします。従って、エージェントはポジションの開閉を追跡しません。ポジションの開閉による報酬はありません。
「市場外」の時間を最小限にするため、ポジションを持たないことにペナルティを課すことにしています。ただし、このペナルティは、負けたときのペナルティよりも低くします。
次が、エージェントの報酬方針です。
- 利益確定したポジションは、ローソク足実体の大きさと同じ報酬を受け取ります(各ローソク足での体系状態を分析します、ローソク足が開いてから閉じるまでポジションを保持します)。
- 「市場外」状態では、ローソク足実体の大きさ(ローソク足実体の大きさにマイナス記号を付けて利益喪失を示す)にペナルティが課されます。
- 負けポジションには、ローソク実体の大きさの2倍(損失額+損失利益額)のペナルティが課されます。
報酬体系を定義したところで、そのままメソッドの実装に移ることができます。
前述したように、今回のモデルでは2つのニューラルネットワークを使用します。そのために、ニューラルネットワークを扱うための2つのオブジェクトを作成する必要があります。StudyNetを訓練する一方、ターゲットネットはQ関数の未来の値を予測するために使用されます。
CNet StudyNet; CNet TargetNet;
Deep Q-Learning法の作業を整理するために、モデルの構築と訓練のためのハイパーパラメータを決定する新しい外部変数も必要です。
- Batch - 重量更新バッチサイズ
- UpdateTarget - 将来のQ関数を予測する「凍結」モデルにコピーする前に訓練済みモデルの重み行列を更新する回数
- terations - 訓練中のモデル更新の総反復回数
- DiscountFactor - 将来報酬割引率
input int Batch = 100; input int UpdateTarget = 20; input int Iterations = 1000; input double DiscountFactor = 0.9;
ニューラルネットワークモデルの作成は、このEA以外で実施する予定です。それを作成するために、転移学習に関連する記事からツールを使用します。この方法により、EAを修正することなく、様々なアーキテクチャを用いた実験が可能になります。そのため、EA初期化メソッドでは、以前に作成したモデルの読み込みのみを実装します。
//--- float temp1, temp2; if(!StudyNet.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false) || !TargetNet.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false)) return INIT_FAILED;
同じモデルの2つのインスタンスを使用しているため、両方のモデルが同じファイルから読み込まれることに注意してください。
異なるアーキテクチャの解決策を使用する可能性は、隠れ層の異なるアーキテクチャとそのサイズの使用だけでなく、分析された履歴の深さを調整する可能性も示唆します。従来はEAコードでモデルを作成し、履歴の深さは外部パラメータで決定していましたが、ソースデータ層の大きさによって、解析された履歴の深さを決定することができるようになりました。EAでは、ソースデータ層の大きさを元に解析的に判断します。変更されないのは分析履歴のローソク足1本あたりのニューロン数と結果層のサイズのみです。なぜなら、これらのパラメータは、使用する指標と予測可能な行動の数に構造的に関係しているからです。
if(!StudyNet.GetLayerOutput(0, TempData)) return INIT_FAILED; HistoryBars = TempData.Total() / 12; StudyNet.getResults(TempData); if(TempData.Total() != Actions) return INIT_PARAMETERS_INCORRECT;
これまで、Deep Q-Learningモデルにおけるオリジナル層の大きさについては触れてきませんでした。前述したように、Q関数は、状態ととった行動に応じて期待される報酬を返します。最も有用な行動を決定するためには、現在の状態において可能なすべての行動に対する関数値を計算する必要があります。ニューラルネットワークを使用することで、ニューロンの数がすべての可能な行動の数に等しい結果層を作成することができます。この場合、結果層の各ニューロンは、特定の行動の効用を予測する役割を担うことになります。これにより、ニューラルネットワークの1パスですべての行動の効用値が得られます。あとは、最大値を選べばいいだけです。
EA初期化関数の残りはそのままです。コード全体は添付ファイルに記載されています。
モデルの訓練処理は Train関数に作成されます。関数本体の冒頭で、訓練セッションのサイズを決定し、履歴データを読み込みます。これは、先に述べた教師あり・教師なし学習アルゴリズムで考えられている手順と同様です。
void Train(void) { //--- MqlDateTime start_time; TimeCurrent(start_time); start_time.year -= StudyPeriod; if(start_time.year <= 0) start_time.year = 1900; datetime st_time = StructToTime(start_time); //--- int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates); if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars)) { ExpertRemove(); return; } if(!ArraySetAsSeries(Rates, true)) { ExpertRemove(); return; } //--- RSI.Refresh(); CCI.Refresh(); ATR.Refresh(); MACD.Refresh();
履歴データを使ってモデルを訓練するので、メモリバッファを作成する必要はありません。単純に全ての履歴データを1つのメモリバッファとして利用すればいいのです。ただし、リアルタイムでモデルを訓練する場合は、メモリバッファを追加して管理する必要があります。
次に、補助変数を用意します。
- total - 訓練標本のサイズ
- use_target - 将来の報酬を予測するためのTarget Net使用フラグ
int total = bars - (int)HistoryBars - 240; bool use_target = false;
use_targetフラグを使うのは、Target Netモデルの最初の更新まで、将来の報酬予測を無効にする必要があるためです。実際はかなり微妙なポイントです。最初のステップでは、モデルはランダムな重みで初期化されます。したがって、予測される値はすべてランダムとなります。ほとんどの場合、真の値とはかけ離れたものになるでしょう。このようなランダムな値の使用は、モデルの学習プロセスを歪めてしまう可能性があります。この場合、モデルは報酬の真の値ではなく、モデル自体に埋め込まれたランダムな値を近似することになります。したがって、Target Netモデル更新の最初の反復の前に、このノイズを除去する必要があります。
次に、エージェントの訓練ループの体系を実装します。外側のループは、エージェントの重み行列を更新するための反復の合計数をカウントします。
for(int iter = 0; (iter < Iterations && !IsStopped()); iter += UpdateTarget) { int i = 0;
ネストされたループの中で、重み更新のバッチサイズとTarget Netの実現までの更新回数をカウントしていきます。ここで注意すべきなのは、このモデルの重みがバックプロパゲーションパスの各反復で更新されることです。したがって、更新バッチの使用は全く正しく見えません。モデルでは常に1に設定されているからです。ただし、Target Netの実機化で処理される状態の数のバランスを取るため、その頻度はパッケージサイズと実機化間の更新回数の積に等しくなります。
ループ本体では、現在のモデル訓練反復のためのシステムの状態をランダムに決定します。また、後続の2つの状態を書き込むために、バッファをクリアします。最初の状態は、学習済みモデルのフィードフォワードパスに使用されます。2つ目は、Target NetのQ関数値の予測に使用されます。
for(int batch = 0; batch < Batch * UpdateTarget; batch++) { i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (total)); State1.Clear(); State2.Clear(); int r = i + (int)HistoryBars; if(r > bars) continue;
そして、ネストされたループで、準備されたバッファに履歴データを入力します。不必要な操作を避けるため、2番目の状態バッファを満たす前に、Target Netフラグの使用を確認します。バッファは必要なときだけ満たされます。
for(int b = 0; b < (int)HistoryBars; b++) { int bar_t = r - b; float open = (float)Rates[bar_t].open; TimeToStruct(Rates[bar_t].time, sTime); float rsi = (float)RSI.Main(bar_t); float cci = (float)CCI.Main(bar_t); float atr = (float)ATR.Main(bar_t); float macd = (float)MACD.Main(bar_t); float sign = (float)MACD.Signal(bar_t); if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE) continue; //--- if(!State1.Add((float)Rates[bar_t].close - open) || !State1.Add((float)Rates[bar_t].high - open) || !State1.Add((float)Rates[bar_t].low - open) || !State1.Add((float)Rates[bar_t].tick_volume / 1000.0f) || !State1.Add(sTime.hour) || !State1.Add(sTime.day_of_week) || !State1.Add(sTime.mon) || !State1.Add(rsi) || !State1.Add(cci) || !State1.Add(atr) || !State1.Add(macd) || !State1.Add(sign)) break; if(!use_target) continue; //--- bar_t --; open = (float)Rates[bar_t].open; TimeToStruct(Rates[bar_t].time, sTime); rsi = (float)RSI.Main(bar_t); cci = (float)CCI.Main(bar_t); atr = (float)ATR.Main(bar_t); macd = (float)MACD.Main(bar_t); sign = (float)MACD.Signal(bar_t); if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE) continue; //--- if(!State2.Add((float)Rates[bar_t].close - open) || !State2.Add((float)Rates[bar_t].high - open) || !State2.Add((float)Rates[bar_t].low - open) || !State2.Add((float)Rates[bar_t].tick_volume / 1000.0f) || !State2.Add(sTime.hour) || !State2.Add(sTime.day_of_week) || !State2.Add(sTime.mon) || !State2.Add(rsi) || !State2.Add(cci) || !State2.Add(atr) || !State2.Add(macd) || !State2.Add(sign)) break; }
履歴データでバッファを正常に満たした後、そのサイズをチェックし、両方のモデルのフィードフォワードパスを実行します。操作実行結果の確認も忘れてはいけません。
if(IsStopped()) { ExpertRemove(); return; } if(State1.Total() < (int)HistoryBars * 12 || (use_target && State2.Total() < (int)HistoryBars * 12)) continue; if(!StudyNet.feedForward(GetPointer(State1), 12, true)) return; if(use_target) { if(!TargetNet.feedForward(GetPointer(State2), 12, true)) return; TargetNet.getResults(TempData); }
フィードフォワードパスが成功した後、環境から報酬を受け取り、上で定義した報酬方針に従ってバックプロパゲーションパスのためのターゲットのバッファを準備します。
次の2つの瞬間に注意してください。まず、Target Netフラグの使用状況を確認します。陽性の場合のみ予測値を追加します。flusをfalseに設定した場合、Q関数の予測値は0に設定する必要があります。
2つ目は、ベルマン方程式からの脱線です。ベルマン方程式では、将来の報酬の最大値を用いることはご記憶の通りです。こうすることで、最大限の利益を得られるようにモデルを訓練することができます。もちろん、この方法が最大の収益につながります。しかし、取引の場合、価格チャートが多くのノイズで埋め尽くされると、取引回数の増加につながります。さらに、ノイズは予測の質を低下させます。これは、新しいローソク足の一本一本を予測しようとすることに例えることができます。このため、トレンドを判断し、トレンド方向にポジションを建てるのではなく、ほぼすべての新しいローソク足でポジションを建てて閉じることになる可能性があります。
上記の要因の影響を排除するために、ベルマン方程式から脱線することにしました。Q関数モデルを更新するために、単方向の値を使うことにします。最大値は、「市場外」行動にのみ使用されます。
Rewards.Clear(); double reward = Rates[i - 1 + 240].close - Rates[i - 1 + 240].open; if(reward >= 0) { if(!Rewards.Add((float)(reward + (use_target ? DiscountFactor * TempData.At(0) : 0))) || !Rewards.Add((float)(-2 * (use_target ? reward + DiscountFactor * TempData.At(1) : 0))) || !Rewards.Add((float)(-reward + (use_target ? DiscountFactor * TempData.At(TempData.Maximum(0, 3)) : 0)))) return; } else if(!Rewards.Add((float)(2 * reward + (use_target ? DiscountFactor * TempData.At(0) : 0))) || !Rewards.Add((float)(-reward + (use_target ? DiscountFactor * TempData.At(1) : 0))) || !Rewards.Add((float)(reward + (use_target ? DiscountFactor * TempData.At(TempData.Maximum(0, 3)) : 0)))) return;
報酬バッファを準備した後、学習済みモデルでバックプロパゲーションパスを実行します。再度、操作実行結果を確認します。
if(!StudyNet.backProp(GetPointer(Rewards))) return; }
これでエージェント訓練の反復回数をカウントするネストされたループの操作は完了です。完成後、Target Netモデルを更新します。ここのモデルでは、重み交換方式は採用していません。新しい発明はしないことにしたのです。その代わり、モデルの保存と読み込みには、既存の仕組みを利用します。この場合、すべての内容を含むモデルの正確なコピーを得ることができます。
そこで、訓練したモデルをファイルに保存し、ファイルから保存したモデルをTargetNetに読み込みます。操作結果の確認も忘れてはいけません。
if(!StudyNet.Save(FileName + ".nnw", StudyNet.getRecentAverageError(), 0, 0, Rates[i].time, false)) return; float temp1, temp2; if(!TargetNet.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false)) return; use_target = true; PrintFormat("Iteration %d, loss %.5f", iter, StudyNet.getRecentAverageError()); }
TargetNetモデルが正常に更新されたら、useフラグを変更し、ログに情報メッセージを出力し、次のアウターループの反復処理に移ります。
訓練が完了したら、コメントを消去し、モデル訓練EAの終了を開始します。
Comment(""); //--- ExpertRemove(); }
EAの完全なコードは、添付ファイルに記載されています。
4.テスト
この手法は、過去2年間のH1時間枠のEURUSDデータでテストされました。これまでの実験と同じデータを使用し、指標はデフォルトのパラメータで使用しました。
テスト用に、以下のようなアーキテクチャの畳み込みモデルを作成しました。
- 初期データ層、240要素(ローソク足:20、1本のローソク足の記述のニューロン:12)
- 畳み込み層、入力データウィンドウ:24(ローソク足:2)、ステップ:12(ローソク足:1)、フィルタ出力:6
- 畳み込み層、入力データウィンドウ:2、ステップ:1、フィルタ:2
- 畳み込み層、入力データウィンドウ:3、ステップ:1、フィルタ:2
- 畳み込み層、入力データウィンドウ:3、ステップ:1、フィルタ:2
- 1000要素の完全連結ニューラル層
- 1000要素の完全連結ニューラル層
- 3要素からなる完全連結層(3行動の結果層)。
2層から7層まではシグモイドで活性化させました。結果層には、活性化関数として双曲線正接を使用しました。
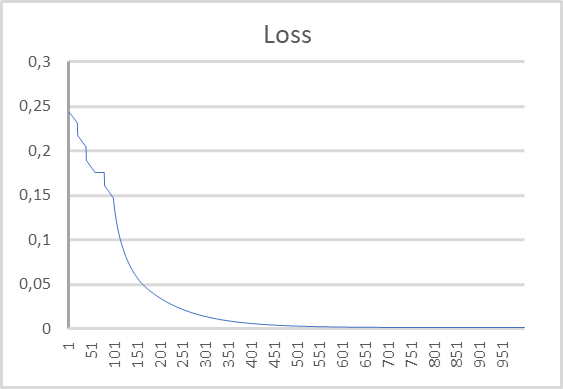
下図は、エラーダイナミクスのグラフです。グラフからわかるように、学習過程では、期待報酬の予測誤差がどんどん小さくなっていることがわかります。500回の繰り返しで0に近くなりました。1000回の繰り返しによるモデル訓練は、0.00105の誤差で終了しました。
結論
今回は、強化学習法の勉強を続けました。2013年にDeepMindチームが発表したDeep Q-Learning手法に注目しました。この達成が発表されることにより、強化学習法の発展に新たな段階が始まりました。この手法は、戦略構築のための訓練モデルの可能性を示すものでした。さらに、1つのモデルを使用することで、そのアーキテクチャやハイパーパラメータを構造的に変更することなく、様々な問題を解決するための訓練をおこなうことができます。これらは、学習済みアルゴリズムがEA結果を上回った最初の実験でした。
MQL5を使ったメソッドの実装を見てきました。モデルテストの結果、この手法を用いて実用的な取引モデルを構築する可能性があることが示されました。
参考文献リスト
記事で使用されているプログラム
| # | 名前 | タイプ | 詳細 |
|---|---|---|---|
| 1 | Q-learning.mq5 | EA | モデルを訓練するEA |
| 2 | NeuroNet.mqh | クラスライブラリ | ニューラルネットワークモデルを作成するためのライブラリ |
| 3 | NeuroNet.cl | コードベース | ニューラルネットワークモデルを作成するためのOpenCLプログラムコードライブラリ |
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/11369
 母集団最適化アルゴリズム
母集団最適化アルゴリズム
 一からの取引エキスパートアドバイザーの開発(第29部):おしゃべりプラットフォーム
一からの取引エキスパートアドバイザーの開発(第29部):おしゃべりプラットフォーム
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
