[Matematica pura, fisica, chimica, ecc.: problemi di allenamento del cervello non legati in alcun modo al commercio - pagina 614

Nuovo commento
 
Mathemat:

Dima, perché vuoi sapere la probabilità che differisce dall'uno per millesimi di percentuale? Se volete delle garanzie, non ce ne sono. Premi Nobel (LTCM) e lo stesso Niederhoffer si sono nascosti dietro le probabilità fino a un certo grado meno uno - e hanno comunque "colpito".

Per millesimi di percentuale - non è necessario. Ma 120 transazioni sono tante, dovrebbe essere possibile calcolare per un piccolo numero di transazioni, per esempio - per 20, 30, 40. E il 30% non è sufficiente per 120.

E le probabilità molto piccole (molto grandi) sono utilizzate per calcolare la durata approssimativa della vita del sistema. È importante sapere quanto durerà - un anno o 10 anni.
C'è qualcosa su cui contare? La matematica è il modo migliore di procedere.
 
Beh, almeno leggi un po' di terw di base, ti tornerà utile comunque.
 
GaryKa, Mathemat

Giusto?



 
DmitriyN: Giusto?

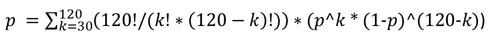
Questo è tutto!

Ma gli errori di arrotondamento possono mangiare tutta la precisione. È meglio contare la somma da 0 a 30. Sarà uguale all'aggiunta alla probabilità che volete conoscere.

 
Se le palle vengono restituite, allora sempre p=q, quindi possiamo semplificare la formula nella parte destra (* p^120)
 
Mislaid: Risolviamo il problema in modo cardinale: nessuna uguaglianza. Determinare che gli insiemi di numeri sulle facce del cubo non devono sovrapporsi.

Ci sono casi, ci sono casi in cui la somma delle facce è uguale a 17.

Per esempio, (333332) > (662111), con una probabilità di vincita di 23/36 ~ 0,64. È vero, non è semplice: (662111) non vince con un margine apprezzabile.

Sembra che finora la somma delle facce di 18 sia la più fertile.

 
GaryKa:
Se restituiamo le palle, allora è sempre p=q, quindi possiamo semplificare la formula nella parte destra (* p^120)

Non importa se torniamo o no. Estraiamo troppo poco per fare la differenza. Ma può essere semplificato decentemente. E nelle parentesi con le potenze rimarrà il moltiplicatore (1/2)^120.

Hehe.

2 Dima: Non preoccupatevi di queste combinazioni. Prendete in mano la distribuzione normale e fate un integrale definito da zero al limite inferiore corrispondente al vostro 30. Farete un grosso errore con le combinazioni in questa formula, a meno che non troviate una formula analitica per la somma semplice delle combinazioni.

Oppure provate la somma delle combinazioni da 0 a 30, i voti p non vi daranno fastidio. Potresti essere fortunato.

P.S. In breve, è semplice. Guarda qui.

Devi calcolare k1, k2 e poi l'integrale.

Prendiamo k1=0, k2=30, questo è più preciso. n=120, p=q=1/2. Allora

(k2-np)/sqrt(npq) = (30-60)/sqrt(120*1/2*1/2) ~ -5.477

(k1-np)/sqrt(npq) = (0-60)/sqrt(120*1/2*1/2) ~ -10,954.

Anche 1/sqrt(2*pi) ~ 0,39894 è utile.

Sostituiamo i primi due numeri nei limiti di integrazione, e sostituiamo 0,39894*exp(-x^2/2) nella funzione integranda, e otteniamo (ecco un servizio sulla presa di certi integrali):

2.163*10^(-8).

Quindi la vostra probabilità è 1-2,163*10^(-8) ~ 0,99999998.

Non provate nemmeno a prendere l'iniziale della funzione sotto l'integrale: è non intero.

 
Mathemat: ... Risolvere la distribuzione normale ... a meno che non si possa trovare una formula analitica per una semplice somma di combinazioni ...
Queste tue parole mi hanno dato un'idea interessante per cercare di trovare una formula analitica per calcolare una combinazione attraverso una distribuzione normale ))
 
Mathemat:
Cercherò di capirlo. Buoni collegamenti.
 
GaryKa: Queste tue parole mi hanno dato un'idea interessante - provare a trovare una formula analitica per calcolare la combinazione attraverso una distribuzione normale ))
Bene, questo è il teorema locale di Moab-Laplace.
1...607608609610611612613614615616617618619620621...628
Nuovo commento