Yatırımcının İstatistiksel Yemek Kitabı: Hipotezler

Giriş

Kendi alım satım sistemini oluşturmak isteyen her yatırımcı er ya da geç bir analist olacaktır. Onlar sürekli olarak piyasa trendleri bulmaya ve alım satım fikirlerini test etmeye çalışmaktadırlar. Bir fikri test etmek, Strateji Test Cihazının optimizasyon modundaki olağan en iyi parametre değerleri aramasından bilimsel (bazen sözde bilimsel) piyasa araştırmasına kadar farklı yaklaşımlara dayanabilir.

Bu makalede, araştırma ve çıkarım doğrulaması için kullanılan, istatistiksel analiz enstrümanı olarak kabul edilen istatistiksel hipotezi ele almayı öneriyorum. Hadi çeşitli hipotezleri Statistica paketi ve taşınan ALGLIB MQL5 sayısal analiz kitaplığı ile örnekler kullanarak test edelim.

1. Hipotez Kavramı

"İstatistiksel hipotez" kavramının birkaç tanımı vardır. Bazıları, incelenen nesnenin veya olgunun istatistiksel özellikleri hakkında bir varsayım içermektedir.

İstatistiksel bir hipotez, söz konusu olgunun bağlı olduğu olasılık yasaları hakkında bir varsayımdır.

Diğer tanımlar istatistiksel özelliklerin, bazı rastgele değişkenlerin dağılımı veya bu dağılımın parametreleri ile bağlantılı olması gerektiğine işaret etmektedir.

İstatistiksel hipotez, istatistik dağılım parametrelerine veya rastgele değişken dağılım prensibine ilişkin bir varsayımdır.

Matematiksel istatistik literatüründe "hipotez" kavramı ikinci şekilde yorumlanmaktadır. O halde ikisini ayırt edebiliriz:

1. Parametrik hipotez (dağılım parametrelerinin değerleri veya iki dağılımın parametrelerinin karşılaştırmalı değerleri hakkında hipotez);
2. Parametrik olmayan hipotez (rastgele bir değer dağılımının türü hakkında hipotez).

Bir sonraki bölümde, hipotez doğrulama yöntemini tartışacağız.

2. Hipotezlerin Test Edilmesi. Teori

Test edilecek hipoteze boş hipotez (Н0) denir. Bunun alternatifi rakip bir hipotezdir (Н1). Bu Н0'ın madalyonunun diğer tarafındadır, yani mantıksal olarak sıfır hipotezini reddeder.

Bazı alım satım sistemlerinin Zarar Durdurma verisinin popülasyonu olduğunu hayal edin. Test için temel oluşturan iki hipotez belirteceğiz.

H0 – ortalama Zarar Durdurma değeri 30 puana eşittir;

H1 – ortalama Zarar Durdurma değeri 30 puana eşit değildir.

Hipotezlerin kabul edilme ve reddedilme çeşitleri:

1. Н0 doğru ve kabul edilir;
2. Н0 yanlış ve Н1 lehine reddedilir;
3. Н0 doğru ancak Н1 lehine reddedilir;
4. Н0 yanlış ama kabul edilir.

Son iki değişken hatalarla bağlantılıdır.

Şimdi önem seviyesi değeri belirtilecektir. Gerçek hipotez boş (üçüncü değişken) iken, alternatif hipotezin kabul edilme olasılığıdır. Bu olasılığın minimize edilmesi tercih edilir.

Bizim durumumuzda böyle bir hata gerçekte öyle olmasına rağmen, Zarar Durdur'un ortalamada 30 puana eşit olmadığını varsayarsak ortaya çıkacaktır.

Genellikle önem seviyesi (α) 0,05'e eşittir. Bu, boş hipotezin test istatistik değerinin kritik bölgeyi 100'den fazla 5 durumda dolduramayacağı anlamına gelir.

Bizim durumumuzda test istatistik değeri klasik bir grafik üzerinde değerlendirilecektir (Şekil 1).

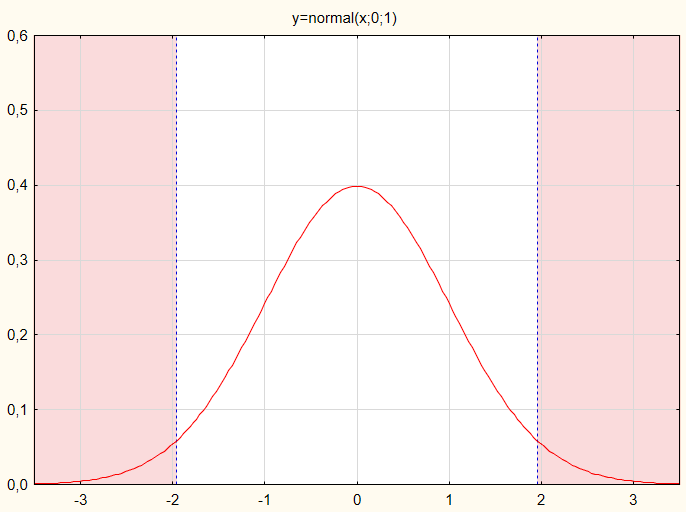
Şek.1. Normal olasılık yasasına göre test istatistik değer dağılımı

Boş hipotezin kabul edilmesi için test istatistik değerlerinin kırmızı bölgelere ulaşması gerekmemektedir. Örneğin amacı doğrultusunda, test istatistik değerlerinin normal olarak dağıldığını varsayalım.

Her test, kendi test istatistik değerini hesaplama formülüne sahiptir.

Varyant 4, ikinci türde (β) bir hata olduğunu işaret eder. Bizim durumumuzda, Zarar Durdur'un ortalamada 30 puana eşit olduğunu ve bu puan sayısına eşit olmadığını varsayarsak, böyle bir hata ortaya çıkacaktır.

3. İstatistiksel Hipotez Testi Örnekleri

Örnekler için kullanılan kaynak veriler Data.xls dosyasında saklanır.

3.1. Bağımlı Örnek Testi

Aşağıdaki durumu hayal edin. Bir yatırım popülasyonu oluşturan alım satım sistemi olduğunu varsayalım. 100 birim hacimli karlı yatırımlardan bir örnek alalım. Kaynak veriler "Karlar" sayfasındadır.

Dış durumları sildikten sonra Kar örneğinin tanımlayıcı istatistikleri Tablo 1'de sunulmaktadır:

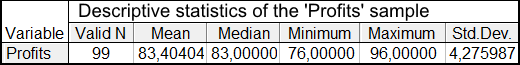
Tablo 1. Kar Örneği İstatistikleri

Örnek histogram aşağıdaki gibidir (Şekil 2).

Şek.2. Kar örneği histogramı

Ortalama değeri 83.4 puan ve medyan 83 puandır.

Piyasaya giriş noktası birkaç puan değişirse ne olur? Örneğin, bir alım satım sinyali göründükten sonra giriş fiyatını iyileştiren bir limit talimatı verilebilir.

Bu sonuçları nasıl etkileyecek? Bu soruya istatistiksel hipotezlerle cevap verilebilir.

Örneklerin bir popülasyondan alınmadığını Statistica paketinde resmi olarak kontrol ederiz:

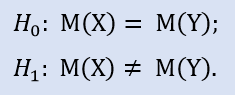
Giriş fiyatını 15 puan değiştirirsek, NewProfits örneğini almak zorundayız. İdeal olarak sonuç resmi aşağıdaki gibi olmalıdır (Şekil 3).

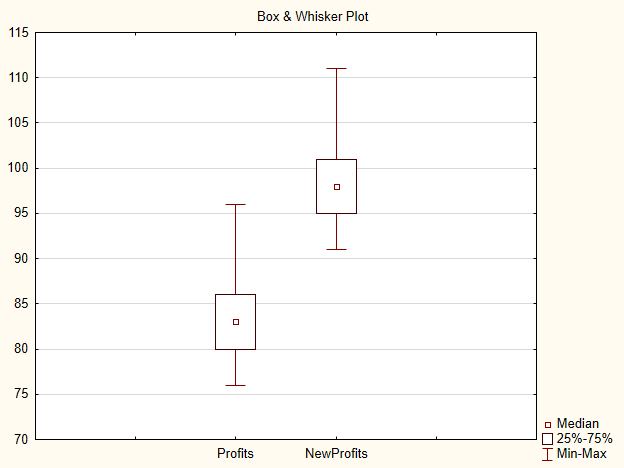
Şek.3. Kar ve Yeni Kar örnekleri için Grafik

Örneklerin medyanları farklı olduğu için alternatif hipotezin kabul edilme olasılığı yüksektir.

Bununla birlikte, piyasada daha iyi fiyatlar olmayabileceğinden bu resmi elde etmek zor olacaktır. Benim durumumda, ikinci örnek giriş fiyatı değiştirildikten sonra 84 tane yatırımı kapsıyordu. Basitçe diğer 15 yatırım gerçekleştirilmedi. Bu düzeltilmiş örnek NewProfitsReal olarak adlandırılacaktır.

"Kutu-ve-çizgi" türü çizimdeki iki örnek arasında çok fazla fark yoktur.

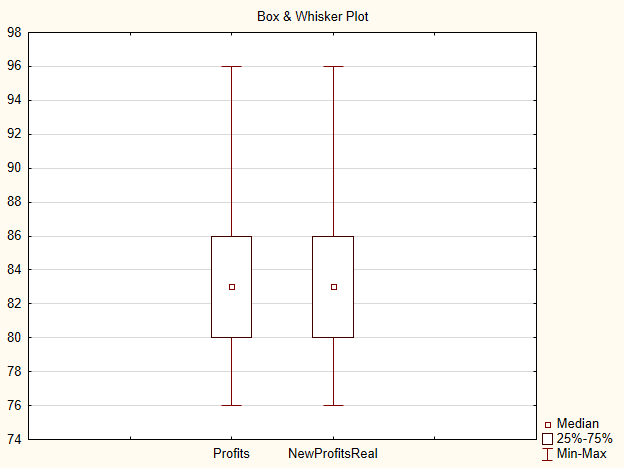
Şek.4. Profits ve NewProfitsReal örnekleri için Çizim

Bağlı örnek için parametrik olmayan bir Wilcoxon işaretli sıra testi yapalım.

Sonuçlar Tablo 2'dedir:

Tablo 2. Profits ve NewProfitsReal örnekleri için Wilcoxon test sonuçları

Önem seviyesi çok yüksektir, ki bu da boş hipotezi destekler.

Bu şekilde giriş noktası değişikliğinin sistem verimini etkilemediğini söyleyebiliriz. Ama bu görecelidir. Mutlak anlamda sistem, kaçırılan giriş noktaları nedeniyle daha az karlı çıkmıştır.

Wilcoxon testi MQL5'te programlı olarak gerçekleştirilebilir. Dağılım medyanını belirtilen m değeri ile karşılaştırsa da bu fark önemli değildir.

Şimdi kontrol edeceğiz:

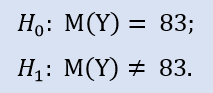
ALGLIB kitaplığı aşağıdaki prosedürü içerir: CAlglib::WilcoxonSignedRankTest(). Üç test türü için sonuç verir: iki taraflı, sol taraflı ve sağ taraflı.

test_profits.mq5 script dosyası bu hesaplamanın bir örneğini sağlar. "Experts" günlüğü, NewProfitsReal örneği için aşağıdaki sonuçlara sahiptir:

OO      0       12:04:08.814    test_profits (EURUSD.e,H1)      p-value for the two-sided test: 0.7472
HD      0       12:04:08.814    test_profits (EURUSD.e,H1)      p-value for the left-sided test: 0.6285
CM      0       12:04:08.814    test_profits (EURUSD.e,H1)      p-value for the right-sided test: 0.3736

Sol taraflı test şu şekildedir:

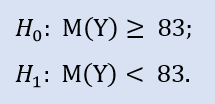
Burada, NewProfitsReal örneğinin medyanının 83'e eşit veya daha büyük olabileceği alternatifi kontrol ederiz. H0'ı reddetmede hata olasılığı 0.63'tür. Bu nedenle H0 kabul edilir.

Sağ taraflı test şöyle gözükür:

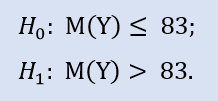
Bu testte, NewProfitsReal örneğinin medyanının 83'e eşit veya daha küçük olabileceği alternatifi kontrol ederiz. H0'ı reddetmede hata olasılığı 0,37'ye eşittir. Bu nedenle H0 kabul edilir.

3.2. Bağımsız Örnekleri Test Etme

Farklı aracıların alım satım talimatlarını ne kadar hızlı işlediğini ve alım satım talimatlarını yürütme süresi ile ilgili aracılar arasında bir fark olup olmadığını kontrol etmemiz gerektiğini varsayalım.

Bu yüzden, analiz için iki tane kaynak veri örneği vardır. Her örnek başlangıçta 50 gözlem içeriyordu. Dış durumları sildikten sonra, ilk örnekte (aracı А) 48 gözlem ve ikinci örnekte (aracı B) 49 gözlem kalmıştır. Veriler "ExecutionTime" sayfasında bulunabilir.

Şimdi kontrol edeceğiz:

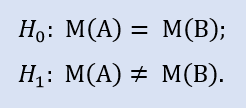
Örnek endeksleri bir resim üzerinde gösterelim (Şekil 5). Çizime göre medyan değerleri, önemli ölçüde olmasa da farklılık göstermektedir.

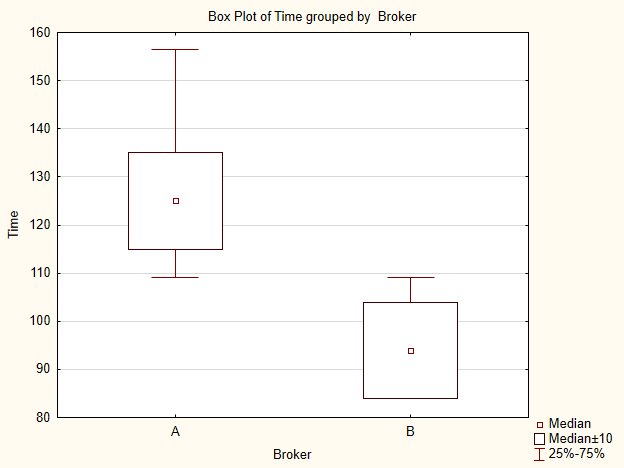
Şek.5. A ve B aracılarının veri örneği çizimi

Her örneğin hangi dağılıma ait olduğunu bilmediğimiz için karşılaştırmada parametrik olmayan testlere başvuracağız.

Örneğin Mann — Whitney U-testi yapalım (Tablo 3). Bunun en bilgilendirici test olduğuna inanılmaktadır.

Tablo 3. A ve B aracılarının veri örnekleri için Mann — Whitney U testi sonuçları

Sonuç: test sonuçları farklıdır ve bu nedenle örneklerin eşitliği ile ilgili boş hipotezler Н1 lehine reddedilir.

Mann — Whitney U-testi, MQL5'te programlı olarak gerçekleştirilebilir. ALGLIB kitaplığında CAlglib:: vardır MannWhitneyUTest() prosedürü. Üç test türü için sonuç verir: iki taraflı, sol taraflı ve sağ taraflı.

test_time_execution.mq5 script dosyası bir hesaplama örneği sağlar. "Expert" günlüğü, örnekleri karşılaştırmak için kullanılabilecek aşağıdaki sonuca sahiptir:

MR      0       12:55:08.577    test_time_execution (EURUSD.e,H1)       p-value for the two sided test: 0.0001
QF      0       12:55:08.577    test_time_execution (EURUSD.e,H1)       p-value for the left-sided test: 1.0000
PF      0       12:55:08.577    test_time_execution (EURUSD.e,H1)       p-value for the right-sided test: 0.0001

Sol taraflı test şu şekildedir:

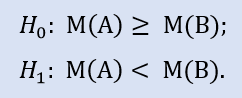
Boş hipotez, aracı A veri örneği medyanının, aracı B veri örneği medyanından daha büyük veya ona eşit olabileceğidir. Alternatif bunun reddidir. H0'ı reddetmede hata olasılığı 1.0'dır. Bu nedenle H0 kabul edilir.

Sağ taraflı test şöyle gözükür:

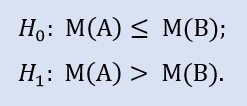
Boş hipotez, aracı A veri örneği medyanının, aracı B veri örneği medyanından daha az veya ona eşit olabileceğidir. Alternatif bunun reddidir.

H0'ı reddetmede hata olasılığı 0.0'dır. Bu nedenle H0, Н1 lehine reddedilir.

3.3. Korelasyon Testi

Bir strateji portföyü hayal edin. Amaç, portföydeki strateji sayısını azaltmaktır.

Seçim kriteri şu şekilde olacaktır: Zarar Durdur serilerinin karşılaştırılmasında iki strateji aynıysa, stratejilerden biri portföyden çıkarılacaktır. İki farklı sistemin iki Zarar durdur veri örneğini ele alalım. Varsayım: Sistemler piyasa girişinde aynı şekilde tepkiyi verir, piyasadan çıkarken farklı tepki verir.

Spearman Sıralar Arası Fark Korelasyon testini kullanacağız. Veri dosyasının "Korelasyon" sayfasında üç örnek vardır.

Korelasyon katsayısının sıfıra eşit olup olmadığını kontrol edin:

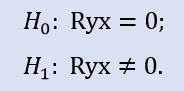
Stops1-Stops2 örnek çiftinin karşılaştırılması aşağıdaki sonucu verecektir (Tablo 4).

Tablo 4. Stops1 ve Stops2 örnekleri için Spearman Sıralar Arası Fark Korelasyon testi

Bu durumda, örnek öğeleri arasında bağlantı bulunmadığına ilişkin sıfır hipotezi, alternatifin lehi için reddedilemez. Bu nedenle kabul edilir.

Şekil 6'daki grafik, verilerin fark edilir bir yapılandırma oluşturmadığını göstermektedir. Veriler çizim düzleminde dağılmıştır.

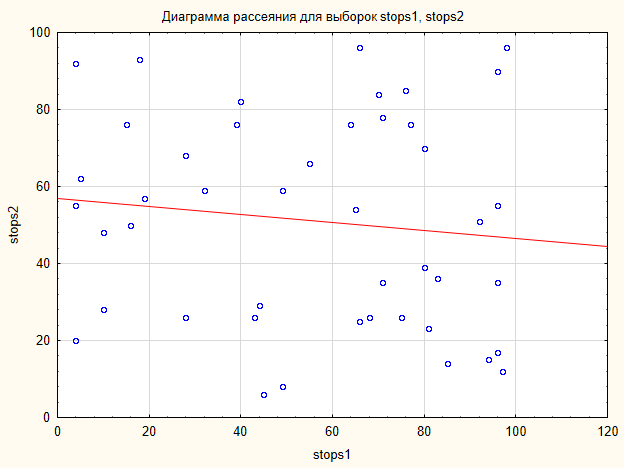
Şek.6. Stops1 ve Stops2 örnekleri için dağılım grafiği

Stops1-Stops3 örnekleri arasındaki ilişki kontrolünün sonuçları Tablo 5'te gösterilmektedir:

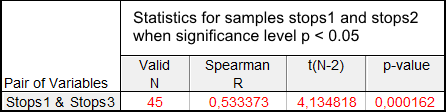
Tablo 5. Stops1 ve Stops3 örnekleri için Spearman Sıralar Arası Fark Korelasyon testi sonuçları

Bu durumda, hata olasılığı çok düşük olduğu için boş hipotez reddedilebilir.

Dolayısıyla mevcut ilişki hakkında alternatif kabul edilir. İlişki şuna benzer (Şekil 7).

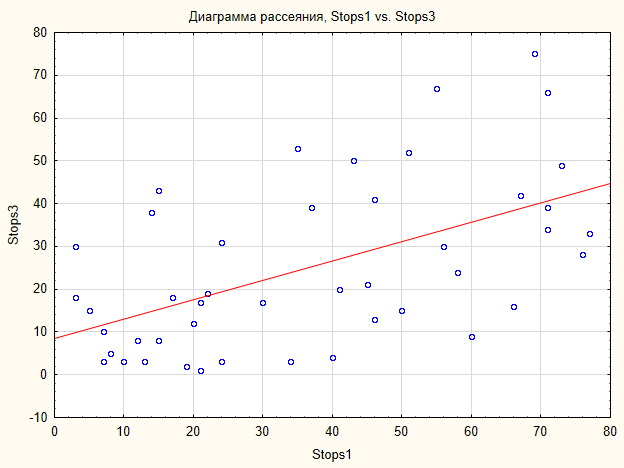
Şek.7. Stops1 ve Stops3 örnekleri için dağılım grafiği

Sonucu MQL5'teki kodla onaylayın. test_correlation.mq5 bir hesaplama örneği içerir.

ALGLIB kitaplığı, Spearman Sıralar Arası Fark Korelasyon katsayısının anlamlılık testi uygulanan CAlglib::SpearmanRankCorrelationSignificance() prosedürünü içerir.

Günlük aşağıdaki kayıtları içerir:

OO      0       12:57:43.545    test_correlation (EURUSD.e,H1)  ---===Samples Stops1 and Stops2===---
GO      0       12:57:43.545    test_correlation (EURUSD.e,H1)  p-value for the two-sided test: 0.9840
KK      0       12:57:43.545    test_correlation (EURUSD.e,H1)  p-value for the left-sided test: 0.4920
JJ      0       12:57:43.545    test_correlation (EURUSD.e,H1)  p-value for the right-sided test: 0.5080
DM      0       12:57:43.545    test_correlation (EURUSD.e,H1)  
HJ      0       12:57:43.545    test_correlation (EURUSD.e,H1)  ---===Samples Stops1 and Stops3===---
NS      0       12:57:43.545    test_correlation (EURUSD.e,H1)  p-value for the two-sided test: 0.0002
RO      0       12:57:43.545    test_correlation (EURUSD.e,H1)  p-value for the left-sided test: 0.9999
FG      0       12:57:43.545    test_correlation (EURUSD.e,H1)  p-value for the right-sided test: 0.0001

Sol taraflı test şu şekildedir:

Bu testte, değişkenler arasında negatif olmayan bir korelasyon olduğuna dair boş hipotez (yani korelasyon ya sıfırdır ya da negatiftir) doğrulanır.

Sol taraflı test, Stops1-Stops2 örnek çifti için sıfır hipotezinin kabul edildiğini gösterir. Sol taraflı test, Stops1-Stops3 örnek çifti için boş hipotezin de kabul edildiğini gösterir. Sorulacak mantıklı soru "Neden Stops1-Stops2 örnekleri arasında bağlantı yoktur ve Stops1-Stops3 arasında bir bağlantı vardır?" olacaktır. Bunun nedeni, kontroldeki ifadenin "sıfıra eşit veya büyük" olmasıdır. İlk durumda "sıfıra eşit" H0 için önemlidir ve ikinci durumda "sıfırdan büyüktür".

Sağ taraflı test şöyle gözükür:

Burada, negatif bir korelasyonun ne olduğuna dair sıfır hipotezi kontrol edilir.

Stops1-Stops2 örnek çifti için olan sağ taraflı test, boş hipotezin kabul edildiğini gösterir. Stops1-Stops3 örnek çifti için olan sağ taraflı test, boş hipotezin reddedildiğini gösterir.

Son bir yorum. Test, Stops1-Stops3 örnekleri arasında pozitif olasılıksal bir bağlantı olduğunu ortaya çıkardı. Bu bağlantının gücü ortalamadır. Bu nedenle strateji 1 veya 3'ü reddetme kararı yatırımcıya kalmıştır.

Sonuç

Bu yazıda nicel değişkenlerin matematiksel istatistikler kullanılarak değerlendirilebileceğini örnekler üzerinde göstermeye çalıştım. Acemi geliştiricilerin bu makaleyi gelecektekialım satım sistemleri için yararlı bulacağını umuyorum. Matematiksel istatistik yöntemlerinin kullanımıyla ilgili makale serilerinin de devam etmesini temenni ediyorum.

ALGLIB kitaplığı dosyalarının ayrıca indirilmesi gereklidir.