Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Vous ne le croiriez pas, mais même le hasard a un modèle. C'est ce qu'on appelle la loi des grands nombres.
noooo.... ceci est ancien, le "plus récent" est le "principe d'équivalence informatique".
J'ai l'impression que le forum se détériore rapidement.
D'un côté, c'est une bonne chose - avoir de la viande dans le commerce est essentiel. D'un autre côté, il n'y aura bientôt plus personne à qui parler.
J'ai l'impression que le forum se détériore rapidement.
D'un côté, c'est une bonne chose - avoir de la viande dans le commerce est essentiel. D'un autre côté, il n'y aura bientôt plus personne avec qui discuter.
Le forum se dégrade rapidement car tous les sujets ont été abordés depuis de nombreuses années.
... tous les sujets ont été abordés au fil des ans.
C'est absurde), une telle opinion peut être une indication que vous faites aussi partie de la foule de la dégradation.
denis.eremin:Je vais l'expliquer pour la dernière fois - une marche aléatoire est une série de nombres qui, par définition, n'a PAS de lois. Pas du tout.
Par conséquent, vous ne pouvez gagner de l'argent que par hasard.
CHINGIZ MUSTAFAEV:
Vous ne le croirez pas, mais même le hasard a un modèle. On l'appelle la loi des grands nombres.
En effet, il y en a, et les gens disent qu'il n'y a pas de modèle.
"La loi des grands nombres.
La loi des grands nombres au sens large
désigne le principe général selon lequel, lorsque
un grand nombre de variables aléatoires, leurrésultatmoyen
cesse d'être aléatoire et peut être
prédit avec un degré élevé de certitude."
Ou comme ceci
"La loi des grands nombres.
L'effet cumulatif d'un grand nombre de facteurs aléatoires entraîne,
"sous certaines conditions générales, un résultat qui est presque indépendant du hasard,
c'est-à-dire de nature systémique."
En effet, il y en a, et les gens disent qu'il n'y a pas de modèle.
"La loi des grands nombres
La loi des grands nombres au sens large
désigne le principe général selon lequel, lorsque
un grand nombre de variables aléatoires, leurrésultatmoyen
cesse d'être aléatoire et peut être
prédit avec un degré élevé de certitude."
Ou comme ceci
"L'effet cumulatif d'un grand nombre de facteurs aléatoires entraîne,
"sous certaines conditions générales, un résultat qui est presque indépendant du hasard,
c'est-à-dire de nature systémique."
noooo.... c'est ancien, le "nouveau" est "le principe d'équivalence informatique".
hmm, intéressant, je vais devoir lire ça).
Mise en œuvre spécifique.
Une fois de plus, vous avez la pièce parfaite et vous pensez qu'en pariant sur l'aigle, vous ferez un bénéfice car c'est votre stratégie commerciale de génie.
Tu retournes une centaine de fois, 60/40 et tu gagnes de l'argent.
Une autre centaine de fois, 51/49, et vous êtes dans l'argent.
Encore une fois, 72/18, et vous faites des bénéfices.
Vous arrivez au formulaire, vous jetez les résultats et vous écrivez : " mais qu'en est-il de ces trois histogrammes dont le bénéfice est le plus évident " ?
En voici une pour ceux qui sont complètement dans la TANQUE MARRON,
Parier non pas sur le fait qu'une pièce de monnaie tombe pile ou face, c'est inutile et vraiment impossible à gagner, mais que dans une SÉRIE de cent tirs, environ 40-45% seront pile, et 50-100 de ces SÉRIES, SÉRIES dont 40-45 tirs seront pile tend à 90-95%.
Pourquoi pensez-vous que les filets fonctionnent, ce sont les mêmes lancers, et le nombre de filets est une SÉRIE de nombreux lancers =D
En voici un pour ceux qui sont totalement BORROWN TANK,
Ne pas parier sur le fait que vous avez une pièce de monnaie tomber pile ou face, il est inutile et vraiment ne peut pas gagner, mais que dans une SÉRIE de 100 coups, environ 40-45% seront pile, et sur 50-100 de ces SÉRIES, SÉRIES qui 40-45 coups seront pile tend à 90-95%.
Pourquoi pensez-vous que les filets fonctionnent, ce sont les mêmes lancers, et le nombre de filets est une SÉRIE de nombreux lancers =D
Encore une fois - bravo !!! Non, même - bravissimo !!! C'est la série dont je parle, qui ne peut être comprise (par pure inculture) par un certain Docteur.
La réponse est revenue.
a décidé de revérifier les 3000 trajectoires...Franchement, un résultat inattendu pour moi, mais je suis enclin à pécher que je fais quelque chose de mal. Je vais devoir tout revérifier en prenant les livres intelligents :)))
Passons maintenant aux résultats :
Nous commençons par évaluer la distribution des victoires et des défaites pour vérifier la normalité, en regardant visuellement
quelque chose qui ressemble à la normale.
Tests :
Test de normalité de Shapiro-Wilk
W = 0,99894, valeur p = 0,06206
Test de normalité d'Anderson-Darling
A = 0,78803, valeur p = 0,04098
au niveau de signification de 5 %... bienoh-presque normal
à 1 % - rejet de l'hypothèse nulle de normalité
Plus intéressant)
Test t à un échantillon pour que la moyenne de l'échantillon soit égale à zéro :
Test t à un échantillon
t = 5.5464, df = 2999, p-value = 3.17e-08
hypothèse alternative : la vraie moyenne n'est pas égale à 0
Intervalle de confiance de 95 % :
10.74520 22.49687
estimations de l'échantillon :
moyenne de x
16.62104
Ainsi, l'hypothèse selon laquelle le bénéfice moyen est égal à zéro peut être facilement rejetée, même avec un niveau de confiance de 1 %.
Maintenant la même chose après avoir supprimé les valeurs aberrantes des résultats.
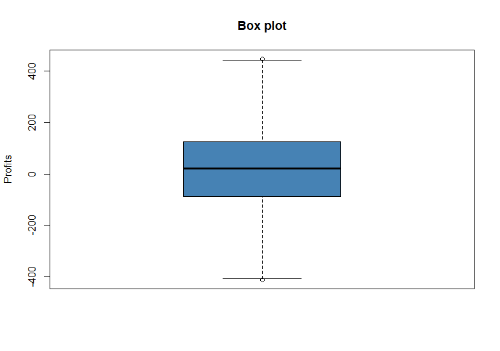
Test de normalité de Shapiro-Wilk
W = 0,99781, valeur p = 0,0003555
Test de normalité d'Anderson-Darling
A = 0,70627, valeur p = 0,06521
Test t à un échantillon
t = 6.1144, df = 2972, valeur p = 1.096e-09
hypothèse alternative : la vraie moyenne n'est pas égale à 0
Intervalle de confiance de 95 % :
12.08241 23.48974
estimations de l'échantillon :
moyenne de x
17.78607
Comme on peut le voir, tout est encore ambigu en ce qui concerne la normalité de la distribution, mais les données sur la moyenne sont encore plus convaincantes.
Quelle est la conclusion ? Je dois revérifier et réfléchir sérieusement)))