Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Je ne sais pas, j'ai écrit la formule et toutes les variables sont définies. Permettez-moi également de préciser qu'il s'agit du montant du profit pris chaque mois (et non du profit total pour les m mois).
Il reste à dériver la formule de la somme des séries, vous avez écrit que vous le faites facilement - faites-le. Puis on prend la dérivée, on l'égalise à zéro...
Dans mes termes, votre formule pour le retrait du mois en cours ressemble à ceci :
Par conséquent, la décomposition de la dérivée bête de cette fonction est aussi difficile que celle de la fonction ci-dessus.
Je pense que vous pouvez essayer de pré-prologarithmiser f et ensuite chercher son maximum... Peut-être que ce sera plus facile comme ça.
avtomat:
Puis, dans un deuxième temps, ouvrez la valve qui divise le flux en deux parties. Cela modifiera le flux d'entrée.
Vous ne voyez pas encore la solution ?
Non, je ne sais pas à quoi tu penses. Dites-moi.
Pour certains, même le théorème de Pythagore, tel qu'ils l'interprètent, ne peut être compris.
OFFTOP :
A l'école, ils ont donné la preuve la plus succincte du théorème de Pythagore.
Notez que l'idée de base la plus simple (non standard) est p.2. Aucune connaissance des propriétés des triangles semblables n'est utilisée, et aucune connaissance de la trigonométrie n'est non plus nécessaire pour comprendre l'existence de la fonction f. C'est-à-dire qu'une telle preuve peut être donnée dans les écoles primaires après avoir bien (et non comme d'habitude) expliqué aux enfants ce qu'est l'aire.
OFFTOP :
Ils ont donné la preuve la plus succincte du théorème de Pythagore à l'école.
Dans quelle classe ?
La formule S = c^2 * f(alpha) n'est pas évidente pour un élève de 7ème année. C'est prendre pour acquis que ça l'est en quelque sorte.
Par conséquent, il est tout aussi difficile de briser la dérivée bestiale de cette fonction que la précédente.
L'ensemble du processus est-il bloqué par le dérivé ?
Cette fonction est-elle x0*k*(1-(1+q-k)^2)/(k-q) ?
Si c'est le cas, ce n'est pas un problème, je les ai résolus facilement, il faut juste se rappeler un peu. La variable q ?
dans quelle classe ?
La formule S = c^2 * f(alpha) n'est pas évidente pour un élève de 7ème année. C'est prendre pour acquis que ça l'est en quelque sorte.
Presque tout enfant qui a été initié au concept de l'aire d'une figure suffisamment bien pour le ressentir n'aura guère de difficultés à comprendre la preuve ci-dessus.
Si un enfant comprend vraiment ce qu'est l'aire, il en comprend la mesure et comprend également que l'aire de toute figure peut être exprimée par ses caractéristiques (dans ce cas l'hypoténuse et l'angle) qui définissent uniquement la figure.
Aucune connaissance des propriétés des triangles semblables et de la trigonométrie n'est nécessaire.
Lors d'une visite récente, j'ai vu deux pyramides de pierre (semblables aux pyramides égyptiennes). Je les ai pris dans mes mains et les ai mis à leur base (ils sont de taille légèrement différente) :
Et a trouvé une autre preuve du théorème de Pythagore (clair dans la construction).
Integer:
Весь процесс уперся в производную?
Вот эта функция - x0*k*(1-(1+q-k)^2)/(k-q)?
Если это так, то это как бы не проблема, я их легко решал, только вспомнить надо немного. Переменная q?
Non, le problème est la dérivée de k de :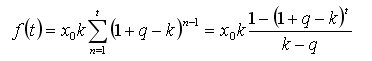
Il doit être mis en équation avec zéro et résolu par rapport à k.
Je ne peux pas le faire de manière intelligente, alors je vais faire simple :
Disons qu'il y a 10 000 sur le dépôt au début de la période. Chaque période, nous ajoutons 5% au dépôt et les réinvestissons dans le dépôt. Chaque période, nous sommes autorisés à retirer seulement 3%.
Si on retire tous les 3% de son argent à chaque période, on obtient plus de 4k$ (et on se fout du dépôt), sinon on obtient seulement 0.5k$ (mais avec beaucoup sur le dépôt).
Presque tout enfant qui a été initié au concept de l'aire d'une figure suffisamment bien pour le ressentir n'aura guère de difficultés à comprendre la preuve ci-dessus.
Si un enfant comprend vraiment ce qu'est l'aire, il en comprend la mesure et comprend également que l'aire de toute figure peut être exprimée par ses caractéristiques (dans ce cas, l'hypoténuse et l'angle), qui définissent de manière unique la figure.
Mais ce n'est pas une preuve rigoureuse.
Je ne peux pas le faire de manière intelligente, alors je vais faire simple :
C'est pourquoi nous avons besoin d'une solution analytique générale, non pas pour dessiner de tels tableaux, mais pour substituer deux valeurs d'entrée dans une formule simple et obtenir la réponse.
C'est le but, tout ce qui précède est "on a l'impression que c'est comme ça que ça va être". Que "cela peut d'une certaine manière être exprimé par quelque chose".
Mais ce n'est pas une preuve rigoureuse.
Quel genre de preuve solide est-ce là ? ! C'est évident :