Locataire - page 7
Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Je suis arrivé au point où j'ai besoin d'une formule pour la somme d'une série de puissance :(
Ai-je besoin de cette solution générale, si la réponse est un chiffre unique qui ne dépend d'aucune condition ? Écrivez un programme et laissez la machine de fer faire le travail.
Je suis arrivé au point où j'ai besoin d'une formule pour la somme d'une série de puissance :(
Eh bien, c'est une sorte de non-question ! Dessinez une vue générale d'une série de puissance.
La formule du bénéfice retirable pour chaque mois :
fp = (d * (1 + pp) ^ (m - 1)) * ps
d est le dépôt initial.
Le taux bancaire (ratio) est de pp+ps. pp - on le garde, ps - on le retire. Dans un premier temps, nous effectuons le dépôt (pp+ps), puis nous en retirons une partie (ps) et gardons l'autre partie (pp). Peut-être serait-il préférable d'entrer le coefficient de retrait de l'accumulé, puis dans la formule sera l'intérêt bancaire et le coefficient de retrait de l'accumulé).
m est le numéro du mois.
Sergei,
Je vous suggère de compléter le problème par le taux d'inflation, c'est-à-dire de retirer le maximum possible de k = q - inflation. (c'est-à-dire que le dépôt ne reste pas inférieur au montant initial en termes réels / naturellement, pour simplifier, nous considérons l'inflation comme une valeur constante/).
Je me demande dans quelle mesure la solution va changer.
Alexei, quelle différence cela fait-il ?
Soit un taux d'inflation mensuel de I pour cent. Ensuite, pour l'équation du montant du retrait pour la période t , nous pouvons écrire :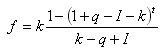
Pour la dérivée de k: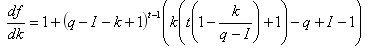
c'est-à-dire qu'en remplaçant les variables q-I par Q, nous arrivons automatiquement aux mêmes expressions que ci-dessus et donc nous ne nous faciliterons pas la vie en termes d'obtention d'une solution analytique pour df/dk=0.
Qu'est-ce que tu voulais dire par là ? Il suffit d'ajouter un terme supplémentaire responsable de l'inflation à l'expression ? C'est certainement intéressant, mais ce n'est pas la meilleure façon de compliquer le modèle sans avoir la solution pour le scénario le plus simple.
La formule de retrait des bénéfices pour chaque mois :
fp = (d * (1 + pp) ^ (m - 1)) * ps
d est le dépôt initial.
Le taux bancaire (ratio) est de pp+ps. pp - on le garde, ps - on le retire. Dans un premier temps, nous effectuons le dépôt (pp+ps), puis nous en retirons une partie (ps) et gardons l'autre partie (pp). Peut-être serait-il préférable d'entrer le coefficient de retrait de l'accumulé, puis dans la formule sera l'intérêt bancaire et le coefficient de retrait de l'accumulé).
m - numéro d'ordre du mois.
Tout d'abord, regardons le remplissage de la première cuve uniquement -- la deuxième cuve est éteinte, la valve est fermée -- il n'y a pas de retrait du dépôt.
.
.
et rappelez-vous que pour la version discrète utilisée le facteur de croissance = 0.2
Eh bien, ce sont des subtilités...
.
.
dans un deuxième temps, ouvrons la valve ;)
.
zy.
ici nous n'introduirons pas de décalage - afin de ne pas compliquer les choses
Je pense qu'il est utile de se souvenir de la formule d'annuité et de la façon dont elle est dérivée...
;)
Je pense qu'il est utile de se souvenir de la formule d'annuité et de la façon dont elle est dérivée...
;)
Eh bien, les banquiers ne sont pas en règle !
cette rente explique donc comment ouvrir la vanne ?
:)))