
Aplicación de OpenCL para simular patrones de velas
Introducción
Cuando un usuario comienza a dominar OpenCL, termina por preguntarse dónde utilizarlo. En la práctica, ejemplos tan ilustrativos como la multiplicación de matrices o la clasificación de volúmenes de datos, no encuentran implementación masiva en la construcción de indicadores o sistemas comerciales automáticos. Otro mode de aplicación, las redes neuronales, exige ciertos conocimeitnos en esta esfera, y adquirirlos para un programador no iniciado resultará un trabajo bastante arduo y absorbente, sin garantías, además, de que vaya a tener resultados positivos en el trading. Todo esto se convierte en un factor disuasorio para aquellos que querrían sentir todo el potencial de OpenCL en los ejemplos de resolución de tareas elementales.
En este artículo, analizaremos la aplicación OpenCL para resolver la tarea más simple del trading algorítmico: la búsqueda de patrones de velas y su simulación en la historia. Desarrollaremos un algortimo de simulación de pasada única y la optimización de dos parámetros en el modo comercial "OHLC en M1". A continuación, compararemos el rendimiento del simulador de estrategias incorporado con el de un simulador escrito en OpenCL, y descubriremos cuál de los dos es más rápido, y cuánto más.
Se supone que el lector ya está familiarizado con las bases de OpenCL. Si no es así, le recomendamos leer los artículos "OpenCL: El puente hacia mundos paralelos" y "OpenCL: De una programación simple a una más intuitiva". Asimismo, no le vendrá mal tener a mano las especificaciones de "The OpenCL Specification Version 1.2". En el artículo prestaremos atención especialmente al algoritmo de construcción del simulador, sin concentrarnos en las bases programáticas de OpenCL.
- Introducción
- 1. Implementación en MQL5
- 2. Implementando en OpenCL
- 2.1 Cargando los datos de precio
- 2.2 Simulación única
- 2.2.1. Buscando patrones en OpenCL
- 2.2.2. Trasladando las órdenes al marco temporal M1
- 2.2.3. Obteniendo los resultados de las transacciones
- 2.3. Iniciando la simulación
- 2.4. Optimización
- 2.4.1. Preparando las órdenes
- 2.4.2. Obteniendo los resultados de las transacciones
- 2.4.3. Buscando patrones y formando los resultados de la simulación
- 2.5. Iniciando la optimización
- 3. Comparando el rendimiento
- 3.1. Optimizando con la pareja EURUSD
- 3.2. Optimizando con la pareja GBPUSD
- 3.3. Optimizando con la pareja USDJPY
- 3.4. Recuadro resumido del rendimiento
- Conclusión
1. Implementación en MQL5
Para asegurarnos de que la implementación del simulador en OpenCL funciona correctamente, debemos apoyarnos en algo. Por eso, para comenzar, vamos a escribir un experto en MQL5, y después compararemos los resultados de su simulación y optimización con el simulador estándar con los resultados correspondientes del simulador implementado en OpenCL.
- Barra pin bajista
- Barra pin alcista
- Envolvente bajista
- Envolvente alcista
La estrategia será sencilla:
- Barra pin bajista o envolvente bajista — venta
- Barra pin alcista o envolvente alcista — compra
- Número de posiciones abiertas simultáneamente — no está limitado
- Tiempo máximo de mantenimiento de una posición abierta — limitado, el usuario lo establece
- Los niveles de Take Profit y Stop Loss son fijos, el usuario los establece
La presencia de un patrón se comprueba con las barras completamente cerradas. En otras palabras, en el momento de aparición de una nueva barra, buscaremos el patrón en la tres anteriores.
Los niveles de detección de patrones son los siguientes:
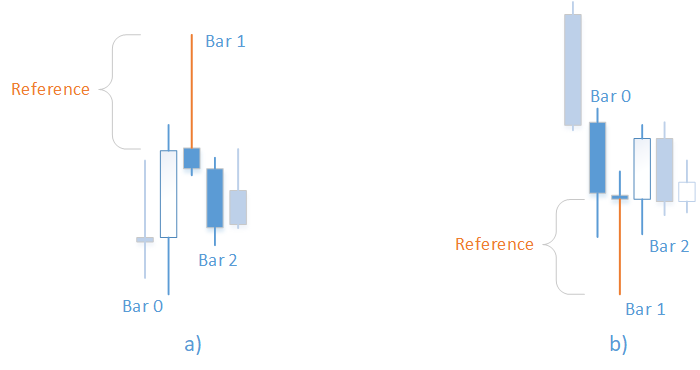
Fig.1. Patrones "Barra pin bajista" (a) y "Barra pin alcista" (b)
Para la barra pin bajista (Fig. 1, a):
- La sombra superior ("cola") de la primera barra es superior a la magnitud de apoyo establecida: tail>=Reference
- La barra cero es alcista: Close[0]>Open[0]
- La segunda barra es bajista: Open[2]>Close[2]
- El precio High de la primera barra es un máximo local: High[1]>MathMax(High[0],High[2])
- El cuerpo de la primera barra es menor que su sombra superior: MathAbs(Open[1]-Close[1])<tail
- "Cola" tail = High[1]-max(Open[1],Close[1])
Para la barra pin (Fig. 1, b):
- La sombra inferior ("cola") de la primera barra es superior a la magnitud de apoyo establecida: tail>=Reference
- La barra cero es bajista: Open[0]>Close[0]
- La segunda barra es alcista: Close[2]>Open[2]
- El precio Low de la primera barra es un mínimo local: Low[1]<MathMin(Low[0],Low[2])
- El cuerpo de la primera barra es inferior a la sombra inferior: MathAbs(Open[1]-Close[1])<tail
"Cola" tail = min(Open[1],Close[1])-Low[1]

Fig. 2. Patrones "Envolvente bajista" (a) y "Envolvente alcista" (b)
Para la envolvente bajista (Fig. 2, a):
- La primera barra es alcista, su cuerpo es superior a la magnitud de apoyo establecida: (Close[1]-Open[1])>=Reference
- El precio High de la barra cero es inferior al precio de cierre de la primera barra: High[0]<Close[1]
- El precio de apertura de la segunda barra es superior al precio de cierre de la primera barra: Open[2]>CLose[1]
- El precio de cierre de la segunda barra es inferior al precio de apertura de la primera barra: Close[2]<Open[1]
Para la envolvente alcista (Fig. 2, b):
- La primera barra es bajista, su cuerpo es superior a la magnitud de apoyo establecida: (Open[1]-Close[1])>=Reference
- El precio Low de la barra cero es superior al precio de cierre de la primera barra: Low[0]>Close[1]
- El precio de apertura de la segunda barra es inferior al precio de cierre de la primera barra: Open[2]<Close[1]
- El precio de cierre de la segunda barra es superior al precio de apertura de la primera barra: Close[2]>Open[1]
1.1 Buscando patrones
ENUM_PATTERN Check(MqlRates &r[],uint flags,double ref) { //--- barra pin bajista if((flags&PAT_PINBAR_BEARISH)!=0) {// double tail=H(1)-MathMax(O(1),C(1)); if(tail>=ref && C(0)>O(0) && O(2)>C(2) && H(1)>MathMax(H(0),H(2)) && MathAbs(O(1)-C(1))<tail) return PAT_PINBAR_BEARISH; } //--- barra pin alcista if((flags&PAT_PINBAR_BULLISH)!=0) {// double tail=MathMin(O(1),C(1))-L(1); if(tail>=ref && O(0)>C(0) && C(2)>O(2) && L(1)<MathMin(L(0),L(2)) && MathAbs(O(1)-C(1))<tail) return PAT_PINBAR_BULLISH; } //--- envolvente bajista if((flags&PAT_ENGULFING_BEARISH)!=0) {// if((C(1)-O(1))>=ref && H(0)<C(1) && O(2)>C(1) && C(2)<O(1)) return PAT_ENGULFING_BEARISH; } //--- envolvente alcista if((flags&PAT_ENGULFING_BULLISH)!=0) {// if((O(1)-C(1))>=ref && L(0)>C(1) && O(2)<C(1) && C(2)>O(1)) return PAT_ENGULFING_BULLISH; } //--- no se ha encontrado nada return PAT_NONE; }
Aquí debemos prestar atención al enumerador ENUM_PATTERN, cuyos valores son banderas que se pueden combinar y transmitir como argumento, usando un O bit a bit:
enum ENUM_PATTERN { PAT_NONE=0, PAT_PINBAR_BEARISH = (1<<0), PAT_PINBAR_BULLISH = (1<<1), PAT_ENGULFING_BEARISH = (1<<2), PAT_ENGULFING_BULLISH = (1<<3) };
Asimismo, para que el registro de las condiciones sea más compacto, se han introducido los macros:
#define O(i) (r[i].open) #define H(i) (r[i].high) #define L(i) (r[i].low) #define C(i) (r[i].close)
La función Check() se llamará desde la función IsPattern(), que ha sido diseñada para comprobar la presencia de los patrones indicados en el momento de apertura de una nueva barra:
ENUM_PATTERN IsPattern(uint flags,uint ref) { MqlRates r[]; if(CopyRates(_Symbol,_Period,1,PBARS,r)<PBARS) return 0; ArraySetAsSeries(r,false); return Check(r,flags,double(ref)*_Point); }
1.2 Montando el experto
Para comenzar, vamos a aclarar los parámetros de entrada. En primer lugar, en las condiciones de determinación de los patrones, tenemos la magnitud de apoyo. Se trata de la longitud de "cola" para la barra pin o la zona de cruce de los cuerpos para la envolvente. La indicaremos en puntos:
input int inp_ref=50;
En segundo lugar, se trata del conjunto de patrones con el que trabajamos. Para mayor comodidad, no usaremos en los parámetros de entrada el registro de banderas, sino que lo escribiremos en cuatro parámetros de tipo bool:
input bool inp_bullish_pin_bar = true; input bool inp_bearish_pin_bar = true; input bool inp_bullish_engulfing = true; input bool inp_bearish_engulfing = true;
Que combinaremos en una variable no asignada en la función de inicialización:
p_flags = 0; if(inp_bullish_pin_bar==true) p_flags|=PAT_PINBAR_BULLISH; if(inp_bearish_pin_bar==true) p_flags|=PAT_PINBAR_BEARISH; if(inp_bullish_engulfing==true) p_flags|=PAT_ENGULFING_BULLISH; if(inp_bearish_engulfing==true) p_flags|=PAT_ENGULFING_BEARISH;
A continuación, se indica el tiempo permisible de mantenimiento de posición expresado en horas, los niveles de Take Profit y Stop Loss, y el volumen del lote:
input int inp_timeout=5; input bool inp_bullish_pin_bar = true; input bool inp_bearish_pin_bar = true; input bool inp_bullish_engulfing = true; input bool inp_bearish_engulfing = true; input double inp_lot_size=1;Para comerciar, usaremos la clase CTrade de la biblioteca estándar. Para medir la velocidad del simulador, usaremos la clase CDuration, que permite medir los intervalos temporales entre puntos de control de ejecución del programa en microsegundos y mostrarlos en un aspecto cómodo. En este caso, mediremos el tiempo entre las funciones OnInit() y OnDeinit(). El código completo de la clase se encuentra en el archivo Duration.mqh en los anexos.
CDuration time; int OnInit() { time.Start(); // ... return(INIT_SUCCEEDED); } void OnDeinit(const int reason) { time.Stop(); Print("La simulación ha durado "+time.ToStr()); }
El funcionamiento del experto es muy sencillo y consiste en lo siguiente.
En la función OnTick(), en primer lugar se encuentra el procesamiento de las posiciones abiertas. Consiste en cerrar la posición forzosamente, si su tiempo de mantenimiento ha superado el valor indicado en los parámetros de entrada. Después le sigue la comprobación de la apertura de una nueva barra. Si la comprobación ha tenido éxito, comprobamos la presencia del patrón con la ayuda de la función IsPattern(). Al encontrar algún patrón, abrimos una posición de compra o venta de acuerdo con la estrategia. El código completo de la función OnTick() se muestra más abajo:
void OnTick() { //--- procesando las posiciones abiertas int total= PositionsTotal(); for(int i=0;i<total;i++) { PositionSelect(_Symbol); datetime t0=datetime(PositionGetInteger(POSITION_TIME)); if(TimeCurrent()>=(t0+(inp_timeout*3600))) { trade.PositionClose(PositionGetInteger(POSITION_TICKET)); } else break; } if(IsNewBar()==false) return; //--- comprobando la presencia del patrón ENUM_PATTERN pat=IsPattern(p_flags,inp_ref); if(pat==PAT_NONE) return; //--- abriendo posiciones double ask=SymbolInfoDouble(_Symbol,SYMBOL_ASK); double bid=SymbolInfoDouble(_Symbol,SYMBOL_BID); if((pat&(PAT_ENGULFING_BULLISH|PAT_PINBAR_BULLISH))!=0)//покупка trade.Buy(inp_lot_size,_Symbol,ask,NormalizeDouble(ask-inp_sl*_Point,_Digits),NormalizeDouble(ask+inp_tp*_Point,_Digits),DoubleToString(ask,_Digits)); else//venta trade.Sell(inp_lot_size,_Symbol,bid,NormalizeDouble(bid+inp_sl*_Point,_Digits),NormalizeDouble(bid-inp_tp*_Point,_Digits),DoubleToString(bid,_Digits)); }
1.3 Simulación
Para comenzar, vamos a inicializar la optimización, para tener una idea de los valores de los parámetros de entrada con los que este experto puede comerciar de forma rentable, o aunque sea abrir alguna posición. Vamos a optimizar dos parámetros: la magnitud de apoyo para los patrones y el nivel de Stop Loss en puntos. Establecemos un nivel de Take Profit de 50 puntos, eligiendo además todos los patrones de simulación.
Realizaremos la optimización con la pareja M5. Intervalo temporal: 01.01.2018 — 01.10.2018. Optimización rápida (algoritmo temporal), modo comercial "OHLC en M1".
Eligiremos los valores de los parámetros optimizables en un intervalo amplio con un amplio número de gradaciones:
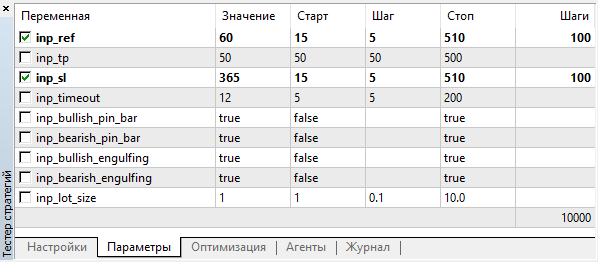
Fig. 3. Parámetros de optimización
Después de finalizar la optimización, clasificamos los resultados según el tamaño del beneficio:
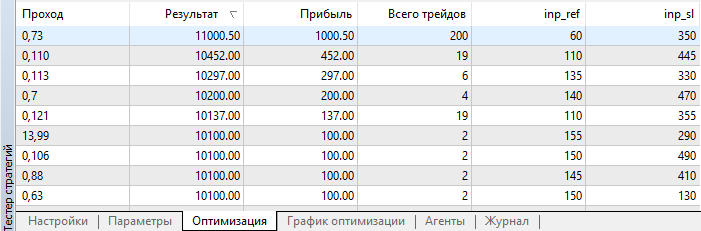
Fig. 4. Resultados de optimización
Como podemos ver, el mejor resultado, con un beneficio de 1000.50, se ha obtenido con una magnitud de apoyo de 60 puntos y un nivel de Stop Loss de 350 puntos. Vamos a iniciar la simulación con estos parámetros, prestando atención a su tiempo de ejeución.
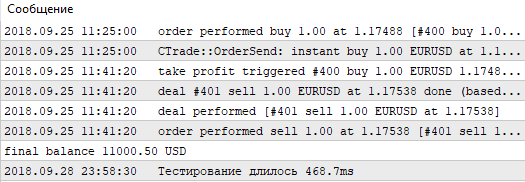
Fig. 5. Tiempo de simulación de una pasada única con el simulador estándar
Recordamos estos valores y pasamos a la simulación con esta estrategia, pero sin usar el simulador estándar. Vamos a escribir el nuestro, usando las posibilidades de OpenCL.
2. Implementando en OpenCL
Para trabajar con OpenCL, usaremos la clase COpenCL de la biblioteca estándar con algunas mejoras. El objetivo de las mejoras es obtener el máximo de información sobre los errores, pero sin saturar el código con la consola y las condiciones. Para ello, crearemos la clase COpenCLx, cuyo código completo se encuentra en el archivo adjunto OpenCLx.mqh:
class COpenCLx : public COpenCL { private: COpenCL *ocl; public: COpenCLx(); ~COpenCLx(); STR_ERROR m_last_error; // estructura del último error COCLStat m_stat; // estadísticas de OpenCL //--- trabajando con los búferes bool BufferCreate(const ENUM_BUFFERS buffer_index,const uint size_in_bytes,const uint flags,const string function,const int line); template<typename T> bool BufferFromArray(const ENUM_BUFFERS buffer_index,T &data[],const uint data_array_offset,const uint data_array_count,const uint flags,const string function,const int line); template<typename T> bool BufferRead(const ENUM_BUFFERS buffer_index,T &data[],const uint cl_buffer_offset,const uint data_array_offset,const uint data_array_count,const string function,const int line); template<typename T> bool BufferWrite(const ENUM_BUFFERS buffer_index,T &data[],const uint cl_buffer_offset,const uint data_array_offset,const uint data_array_count,const string function,const int line); //--- estableciendo los parámetros template<typename T> bool SetArgument(const ENUM_KERNELS kernel_index,const int arg_index,T value,const string function,const int line); bool SetArgumentBuffer(const ENUM_KERNELS kernel_index,const int arg_index,const ENUM_BUFFERS buffer_index,const string function,const int line); //--- trabajando con el kernel bool KernelCreate(const ENUM_KERNELS kernel_index,const string kernel_name,const string function,const int line); bool Execute(const ENUM_KERNELS kernel_index,const int work_dim,const uint &work_offset[],const uint &work_size[],const string function,const int line); //--- bool Init(ENUM_INIT_MODE mode); void Deinit(void); };
Como vemos, la clase contiene un puntero al objeto COpenCL, así como varios métodos que sirven de envoltorio para los métodos homónimos de la clase COpenCL. Cada uno de estos métodos tiene entre los argumentos el nombre de la función y la línea desde la que es llamada. Además, en lugar de los índices de los kernels y búferes, se han aplicado enumeradores. Esto se ha hecho para que en el mensaje sobre el error se pueda usar EnumToString(), lo cual es mucho más informativo que simplemente un índice.
Vamos a analizar uno de estos métodos con más detalle.
bool COpenCLx::KernelCreate(const ENUM_KERNELS kernel_index,const string kernel_name,const string function,const int line) { if(ocl==NULL) { SET_UERRx(UERR_NO_OCL,"El objeto OpenCL no existe",function,line); return false; } //--- Iniciando ejecución del kernel ::ResetLastError(); if(!ocl.KernelCreate(kernel_index,kernel_name)) { string comment="Error al crear el kernel "+EnumToString(kernel_index)+", nombre \""+kernel_name+"\""; SET_ERRx(comment,function,line); if(!m_last_error.code) SET_UERRx(UERR_KERNEL_CREATE,comment,function,line); return(false); } //--- return true; }
Aquí se hacen dos comprobaciones: si existe un objeto de la clase COpenCL y si se ha ejecutado con éxito el método de creación del kernel. Pero, en lugar de mostrar el texto con la función Print(), los mensajes se transmiten a los macros junto con el código de error, el nombre de la función y la llamada de la línea. Estos macros guardan información sobre el error en el miembro de la clase m_last_error, cuya estructura mostramos más abajo:
struct STR_ERROR { int code; // código string comment; // comentario string function; // función en la que ha sucedido el error int line; // línea en la que ha sucedido el error };
Solo hay cuatro macros así. Los vamos a ver por orden.
El macros SET_ERR registra el último error de ejecución, la función y la línea desde la que ha sido llamado, y el comentario que se transmite como parámetro:
#define SET_ERR(c) do {m_last_error.function = __FUNCTION__; \ m_last_error.line =__LINE__; \ m_last_error.code=::GetLastError(); m_last_error.comment=c;} while(0)
El macros SET_ERRx es análogo al macros SET_ERR:
#define SET_ERRx(c,f,l) do {m_last_error.function = f; m_last_error.line = l; \ m_last_error.code=::GetLastError(); m_last_error.comment=c;} while(0)
Se distingue en que el nombre de la función y la línea se transmiten como parámetros. ¿Para qué se hace esto? Imagínese que en el método KernelCreate() ha sucedido un error. En caso de usar el macros SET_ERR, veremos el nombre del método KernelCreate(), pero resultará mucho más cómodo saber desde dónde se ha llamado el método. Para ello, transmitimos la función y la línea de llamada de este método como argumentos, y sustituimos estos argumentos en el macros.
A continuación, el macros SET_UERR. Está diseñado para registrar los errores personalizados:
#define SET_UERR(err,c) do {m_last_error.function = __FUNCTION__; \ m_last_error.line =__LINE__; \ m_last_error.code=ERR_USER_ERROR_FIRST+err; m_last_error.comment=c;} while(0)
En él, en lugar de llamar GetLastError(), transmitimos el código de error como parámetro. En el resto, es análogo al macros SET_ERR.
El macros SET_UERRx ha sido pensado para registrar los errores personalizados con la transmisión del nombre de la función y la línea de llamada como parámetros:
#define SET_UERRx(err,c,f,l) do {m_last_error.function = f; m_last_error.line = l; \ m_last_error.code=ERR_USER_ERROR_FIRST+err; m_last_error.comment=c;} while(0)
De esta forma, en caso de que aparezca un error, tendremos en nuestras manos toda la información necesaria. Y la diferencia más importante respecto a los errores mostrados en la consola de la clase COpenCL, es la concretización: sobre qué kernel concretamente se está hablando y desde dónde precisamente se llama su método de creación. Basta con comparar la muestra de la clase COpenCL (línea superior) y la muestra ampliada de la clase COpenCLx (las dos líneas inferiores):

Fig. 6. Error al crear el kernel
Vamos a analizar otro ejemplo más del método-envoltorio. Nos referimos precisamente al método de creación del búfer:
bool COpenCLx::BufferCreate(const ENUM_BUFFERS buffer_index,const uint size_in_bytes,const uint flags,const string function,const int line) { if(ocl==NULL) { SET_UERRx(UERR_NO_OCL,"El objeto OpenCL no existe",function,line); return false; } //--- calculando y comprobando la memoria libre if((m_stat.gpu_mem_usage+=size_in_bytes)==false) { CMemsize cmem=m_stat.gpu_mem_usage.Comp(size_in_bytes); SET_UERRx(UERR_NO_ENOUGH_MEM,"No hay memoria libre de GPU. No es suficiente "+cmem.ToStr(),function,line); return false; } //--- creando búfer ::ResetLastError(); if(ocl.BufferCreate(buffer_index,size_in_bytes,flags)==false) { string comment="Error al crear el búfer "+EnumToString(buffer_index); SET_ERRx(comment,function,line); if(!m_last_error.code) SET_UERRx(UERR_BUFFER_CREATE,comment,function,line); return(false); } //--- return(true); }
En él, aparte de comprobar la existencia del objeto de clase COpenCL y el resultado de la ejecución de la operación, existe también la función de cálculo y la comprobación de la memoria libre. Puesto que no vamos a tener trato con volúmenes de memoria relativamente grandes (cientos de megabytes), debemos controlar su proceso de gasto. De esto se ocupa la clase СMemsize, cuyo código completo se encuentra en Memsize.mqh.
Aquí nos encontramos con un detalle desagradable. Aunque la depuración sea cómoda, el código se hace gigantesco. Por ejemplo, el código de creación del búfer tendrá el aspecto siguiente:
if(BufferCreate(buf_ORDER_M1,len*sizeof(int),CL_MEM_READ_WRITE,__FUNCTION__,__LINE__)==false) return false;
Aquí hay demasiada información sobrante, que molesta a la hora de concentrarse en el algoritmo. De nuevo acuden los macros en nuestra ayuda. Cada uno de los métodos-envoltorios es duplicado mediante un macros que hace su llamada más compacta. Para el método BufferCreate(), se trata del macros _BufferCreate:
#define _BufferCreate(buffer_index,size_in_bytes,flags) \ if(BufferCreate(buffer_index,size_in_bytes,flags,__FUNCTION__,__LINE__)==false) return false
Gracias a él, la llamada del método de creación del búfer adopta el aspecto:
_BufferCreate(buf_ORDER_M1,len*sizeof(int),CL_MEM_READ_WRITE);
Y la creación de kernels, adquiere el aspecto:
_KernelCreate(k_FIND_PATTERNS,"find_patterns");
Aquí debemos prestar atención a que la mayoría de macros semejantes termina en "return false", excepto _KernelCreate, que termina en "break". Esto lo debemos tener en cuenta al construir el código. Todos los macros han sido definidos en el archivo OCLDefines.mqh.
En la clase también se contienen los métodos de inicialización y desinicialización. El primero, aparte de la creación del objeto de clase COpenCL, también se ocupa de comprobar el soporte de double, de crear kernels y de obtener el tamaño de la memoria disponible:
bool COpenCLx::Init(ENUM_INIT_MODE mode) { if(ocl) Deinit(); //--- creando el objeto de la clase COpenCL ocl=new COpenCL; while(!IsStopped()) { //--- inicializando OpenCL ::ResetLastError(); if(!ocl.Initialize(cl_tester,true)) { SET_ERR("Error al inicializar OpenCL"); break; } //--- comprobando el soporte del trabajo con double if(!ocl.SupportDouble()) { SET_UERR(UERR_DOUBLE_NOT_SUPP,"El trabajo con double (cl_khr_fp64) no es soportado por el dispositivo"); break; } //--- estableciendo el número de kernels if(!ocl.SetKernelsCount(OCL_KERNELS_COUNT)) break; //--- creando kernels if(mode==i_MODE_TESTER) { _KernelCreate(k_FIND_PATTERNS,"find_patterns"); _KernelCreate(k_ARRAY_FILL,"array_fill"); _KernelCreate(k_ORDER_TO_M1,"order_to_M1"); _KernelCreate(k_TESTER_STEP,"tester_step"); }else if(mode==i_MODE_OPTIMIZER){ _KernelCreate(k_ARRAY_FILL,"array_fill"); _KernelCreate(k_TESTER_OPT_PREPARE,"tester_opt_prepare"); _KernelCreate(k_TESTER_OPT_STEP,"tester_opt_step"); _KernelCreate(k_FIND_PATTERNS_OPT,"find_patterns_opt"); } else break; //--- creando búferes if(!ocl.SetBuffersCount(OCL_BUFFERS_COUNT)) { SET_UERR(UERR_SET_BUF_COUNT,"Error al crear los búferes"); break; } //--- obteniendo el tamaño de la memoria operativa long gpu_mem_size; if(ocl.GetGlobalMemorySize(gpu_mem_size)==false) { SET_UERR(UERR_GET_MEMORY_SIZE,"Error al obtener el tamaño de la memoria operativa"); break; } m_stat.gpu_mem_size.Set(gpu_mem_size); m_stat.gpu_mem_usage.Max(gpu_mem_size); return true; } Deinit(); return false; }
El argumento mode crea el modo de inicialización. Puede tratarse de la optimización o de la simulación única. Dependiendo de ello, se crean diferentes kernels.
Los enumeradores de los kernels y búferes se declaran en el archivo OCLInc.mqh. Allí mismo se encuentran los códigos de los kernels, adjuntos en forma de recurso, como línea cl_tester.
El método Deinit() elimina los programas OpenCL y los objetos:
void COpenCLx::Deinit() { if(ocl!=NULL) { //--- remove OpenCL objects ocl.Shutdown(); delete ocl; ocl=NULL; } }
Ahora que hemos creado todas las comodidades, podemos proceder a características más creativas. Teniendo, en este caso, un código bastante compacto, al tiempo que información exhaustiva sobre los errores.
Pero para comenzar, debemos cargar los datos con los que vamos a trabajar. Y esto no es tan sencillo como puede parecer a primera vista.
2.1 Cargando los datos de precio
La clase CBuffering se ocupa de la carga de datos.
class CBuffering { private: string m_symbol; ENUM_TIMEFRAMES m_period; int m_maxbars; uint m_memory_usage; //cuánto tiempo ocupa bool m_spread_ena; //cargar el búfer de spread datetime m_from; datetime m_to; uint m_timeout; //error de límite de tiempo ulong m_ts_abort; //bandera de tiempo en microsegundos, cuando se debe interrumpir la operación //--- carga forzosa bool ForceUploading(datetime from,datetime to); public: CBuffering(); ~CBuffering(); //--- número de datos en los búferes int Depth; //--- búferes double Open[]; double High[]; double Low[]; double Close[]; double Spread[]; datetime Time[]; //--- obteniendo los límites reales de tiempo de los datos cargados datetime TimeFrom(void){return m_from;} datetime TimeTo(void){return m_to;} //--- int Copy(string symbol,ENUM_TIMEFRAMES period,datetime from,datetime to,double point=0); uint GetMemoryUsage(void){return m_memory_usage;} bool SpreadBufEnable(void){return m_spread_ena;} void SpreadBufEnable(bool ena){m_spread_ena=ena;} void SetTimeout(uint timeout){m_timeout=timeout;} };
No vamos a profundizar en su funcionamiento, ya que la carga de datos no tiene relación directa con el tema del artículo. Solo vamos a analizar brevemente su uso.
La clase contiene los búferes Open[], High[], Low[], Close[], Time[] y Spread[]. Podemos trabajar con ellos después de procesar con éxito el método Copy(). Preste atención a que el búfer Spread[] tiene el tipo double, y se descarga no en puntos, sino en diferencia de precio. Además, el copiado del búfer Spread[] está inicialmente activado, y en caso necesario, se puede activar usando el método SpreadBufEnable();
Para la carga se usa el método Copy(). El argumento point presentado se usa solo para recalcular el spread de puntos a diferencia de precio. Si el copiado del spread está activado, este argumento no se usa.
Los motivos principales por los que se ha debido crear una clase aparte para la carga de datos son:
- La imposibilidad de cargar los datos en una cantidad que supere TERMINAL_MAXBARS, con la ayuda de la función CopyTime() y sus similares.
- Ausencia de garantías de que el terminal tenga estos datos de forma local.
La clase CBuffering sabe copiar grandes volúmenes de datos que superen TERMINAL_MAXBARS. Asimismo, sabe iniciar la carga de los datos ausentes con el servidor y esperar a que finalice. Debido a dicha espera, merece la pena prestar atención al método SetTimeout(), que está diseñado para establecer el tiempo máximo de carga de los datos (incluyendo la espera) en milisegundos. Por defecto, en el constructor de la clase se ha indicado un valor de 5000, es decir, 5 segundos. Si establecemos el tiempo límite como cero, esto desactivará su uso. Se trata de algo muy poco recomendable, pero en ciertas ocasiones puede resultar útil.
En este caso, además, algunas limitaciones permanecen vigentes: los datos del periodo M1 no se terminan en un periodo superior a un año, lo cual actúa en cierta medida como intervalo de trabajo de nuestro simulador.
2.2 Simulación única
El proceso de simulación única constará de los siguientes puntos:
- Carga de los búferes de las series temporales
- Inicialización de OpenCL
- Copiado de los búferes de las series temporales en los búferes de OpenCL
- Inicio del kernel que encuentra los patrones en el gráfico actual y coloca los resultados en el búfer de órdenes como puntos de entrada en el mercado
- Inicio del kernel que traslada las órdenes al gráfico M1
- Inicio del kernel que calcula los resultados de las transacciones por órdenes en el gráfico M1 y las coloca en el búfer
- Procesamiento del búfer de resultados y cálculo de los resultados de simulación
- Desinicialización de OpenCL
- Eliminación de los búferes de las series temporales
La clase CBuffering se ocupa de la carga de las series temporales. A continuación, estos datos se deben copiar en los búferes de OpenCL, para que los kernels puedan trabajar con ellos. Con este propósito se ha pensado el método LoadTimeseriesOCL(), cuyo código se muestra más abajo:
bool CTestPatterns::LoadTimeseriesOCL() { //--- búfer Open: _BufferFromArray(buf_OPEN,m_sbuf.Open,0,m_sbuf.Depth,CL_MEM_READ_ONLY); //--- búfer High: _BufferFromArray(buf_HIGH,m_sbuf.High,0,m_sbuf.Depth,CL_MEM_READ_ONLY); //--- búfer Low: _BufferFromArray(buf_LOW,m_sbuf.Low,0,m_sbuf.Depth,CL_MEM_READ_ONLY); //--- búfer Close: _BufferFromArray(buf_CLOSE,m_sbuf.Close,0,m_sbuf.Depth,CL_MEM_READ_ONLY); //--- búfer Time: _BufferFromArray(buf_TIME,m_sbuf.Time,0,m_sbuf.Depth,CL_MEM_READ_ONLY); //--- búfer Open (M1): _BufferFromArray(buf_OPEN_M1,m_tbuf.Open,0,m_tbuf.Depth,CL_MEM_READ_ONLY); //--- búfer High (M1): _BufferFromArray(buf_HIGH_M1,m_tbuf.High,0,m_tbuf.Depth,CL_MEM_READ_ONLY); //--- búfer Low (M1): _BufferFromArray(buf_LOW_M1,m_tbuf.Low,0,m_tbuf.Depth,CL_MEM_READ_ONLY); //--- búfer Close (M1): _BufferFromArray(buf_CLOSE_M1,m_tbuf.Close,0,m_tbuf.Depth,CL_MEM_READ_ONLY); //--- búfer Spread (M1): _BufferFromArray(buf_SPREAD_M1,m_tbuf.Spread,0,m_tbuf.Depth,CL_MEM_READ_ONLY); //--- búfer Time (M1): _BufferFromArray(buf_TIME_M1,m_tbuf.Time,0,m_tbuf.Depth,CL_MEM_READ_ONLY); //--- el copiado se ha ejecutado con éxito return true; }
Bien, los datos ya están cargados. Y ya hemos llegado a la implementación del algoritmo propiamente dicho.
2.2.1 Buscando patrones en OpenCL
El código de definición del patrón en OpenCL apenas se distingue del código de MQL5:
//--- patrones #define PAT_NONE 0 #define PAT_PINBAR_BEARISH (1<<0) #define PAT_PINBAR_BULLISH (1<<1) #define PAT_ENGULFING_BEARISH (1<<2) #define PAT_ENGULFING_BULLISH (1<<3) //--- precios #define O(i) Open[i] #define H(i) High[i] #define L(i) Low[i] #define C(i) Close[i] //+------------------------------------------------------------------+ //| Comprobando la presencia de patrones | //+------------------------------------------------------------------+ uint Check(__global double *Open,__global double *High,__global double *Low,__global double *Close,double ref,uint flags) { //--- barra pin bajista if((flags&PAT_PINBAR_BEARISH)!=0) {// double tail=H(1)-fmax(O(1),C(1)); if(tail>=ref && C(0)>O(0) && O(2)>C(2) && H(1)>fmax(H(0),H(2)) && fabs(O(1)-C(1))<tail) return PAT_PINBAR_BEARISH; } //--- barra pin alcista if((flags&PAT_PINBAR_BULLISH)!=0) {// double tail=fmin(O(1),C(1))-L(1); if(tail>=ref && O(0)>C(0) && C(2)>O(2) && L(1)<fmin(L(0),L(2)) && fabs(O(1)-C(1))<tail) return PAT_PINBAR_BULLISH; } //--- envolvente bajista if((flags&PAT_ENGULFING_BEARISH)!=0) {// if((C(1)-O(1))>=ref && H(0)<C(1) && O(2)>C(1) && C(2)<O(1)) return PAT_ENGULFING_BEARISH; } //--- envolvente alcista if((flags&PAT_ENGULFING_BULLISH)!=0) {// if((O(1)-C(1))>=ref && L(0)>C(1) && O(2)<C(1) && C(2)>O(1)) return PAT_ENGULFING_BULLISH; } //--- no se ha encontrado nada return PAT_NONE; }
Entre las pequeñas diferencias, encontramos la transmisión de búferes según el puntero, y no según el enlace. Además de ello, también tenemos la presencia del modificador __global, que indica que los búferes de las series temporales se encuentran en la memoria global. Todos los búferes OpenCL que vamos a crear se encuentran en la memoria global.
La función Check() es llamada por el kernel find_patterns():
__kernel void find_patterns(__global double *Open,__global double *High,__global double *Low,__global double *Close, __global int *Order, // búfer de órdenes __global int *Count, // número de órdenes en el búfer const double ref, // parámetro del patrón const uint flags) // qué patrones buscar { //--- trabaja en una dimensión //--- índice de la barra size_t x=get_global_id(0); //--- tamaño del espacio de la búsqueda de patrones size_t depth=get_global_size(0)-PBARS; if(x>=depth) return; //--- comprobando la presencia de patrones uint res=Check(&Open[x],&High[x],&Low[x],&Close[x],ref,flags); if(res==PAT_NONE) return; //--- colocando órdenes if(res==PAT_PINBAR_BEARISH || res==PAT_ENGULFING_BEARISH) {//sell int i=atomic_inc(&Count[0]); Order[i*2]=x+PBARS; Order[(i*2)+1]=OP_SELL; } else if(res==PAT_PINBAR_BULLISH || res==PAT_ENGULFING_BULLISH) {//buy int i=atomic_inc(&Count[0]); Order[i*2]=x+PBARS; Order[(i*2)+1]=OP_BUY; } }
Precisamente este vamos a utilizar para la búsqueda de patrones y la colocación de órdenes en un búfer reservado especialmente para ello.
El kernel find_patterns() trabaja en un tamaño unidimensional de tareas. Al iniciarlo, se creará el número work-items que nosotros indiquemos en el tamaño del espacio de tareas para la dimensión 0. En este caso, se trata del número de barras en el periodo actual. Para comprender qué barra se está procesando, debemos obtener el índice de la tarea:
size_t x=get_global_id(0);Donde cero es el índice de la dimensión.
Order[i*2]=x+PBARS; Order[(i*2)+1]=OP_SELL;
Para obtener este número ordinal de la orden, usamos la función atómica atomic_inc(). El asunto es que, en el momento de ejecución de esta tarea, no tenemos ni idea de qué tareas y con qué barras han sido ejecutadas. Se trata de cálculos paralelos, y aquí no existe ninguna secuencialidad en absoluto. Y el número de la tarea no está relacionado en absoluto con el número de tareas ya ejecutadas. Por consiguiente, no sabemos cuántas órdenes han sido ya ubicadas en el búfer. Si intentamos leer su número, que se ubica en la celda 0 del búfer Count[], en este mismo momento otra tarea puede escribir algo en el mismo sitio. Para evitar situaciones semejantes, se usan las funciones atómicas.
En nuestro caso, la función atomic_inc() pide para comenzar acceso a las otras tareas a la celda Count[0], y acto seguido incrementa su valor en una unidad, mientras que devuelve el anterior como resultado.
int i=atomic_inc(&Count[0]);
Está claro que esto ralentiza el funcionamiento, por eso, mientras el acceso a Count[0] permanece bloqueado, las otras tareas simplemente quedan a la espera. Pero en algunos casos, como en el nuestro, no hay otra salida.
Después de que se ejecuten todas las tareas, obtenemos un búfer formado por órdenes Order[], y su número en la celda Count[0].
2.2.2 Trasladando las órdenes al marco temporal M1
Bien, ya hemos encontrado los patrones en el marco temporal actual, pero la simulación se debe realizar en el marco temporal M1. Esto significa que para todos los puntos de entrada encontrados en el periodo actual, es necesario encontrar las barras correspondientes en el periodo M1. Aprovechando que el comercio con patrones presupone un número de puntos de entrada relativamente pequeño incluso en los marcos temporales menores, elegiremos un enfoque general, aunque totalmente conveniente en este caso.
Se trata precisamente de la iteración. Vamos a comparar la hora de cada orden encontrarda con la hora de cada barra del periodo M1. Para ello, crearemos el kernel order_to_M1():
__kernel void order_to_M1(__global ulong *Time,__global ulong *TimeM1, __global int *Order,__global int *OrderM1, __global int *Count, const ulong shift) // desplazamiento temporal en segundos { //--- trabajando en las dos dimensiones size_t x=get_global_id(0); //índice del índice Time en Order if(OrderM1[x*2]>=0) return; size_t y=get_global_id(1); //índice en TimeM1 if((Time[Order[x*2]]+shift)==TimeM1[y]) { atomic_inc(&Count[1]); //--- según los índices pares, colocamos los índices en el búfer TimeM1 OrderM1[x*2]=y; //--- colocamos las operaciones según los índices impares (OP_BUY/OP_SELL) OrderM1[(x*2)+1]=Order[(x*2)+1]; } }
Aquí ya nos encontranmos con un espacio bidimensional de tareas. La dimensión del espacio 0 es igual al número de órdenes colocadas, y la dimensión del espacio 1 es igual al número de barras del periodo M1. Si coinciden la hora de apertura de la barra de la orden y la barra M1, en el búfer OrderM1[] se copia la operación de la orden actual y se establece el índice de la barra en las series temporales del periodo M1.
Pero aquí hay dos cosas que no debería haber a primera vista.
- La primera es la función atómica atomic_inc(), que calcula por algún motivo los puntos de entrada encontrados en el periodo M1. En la dimensión 0, cada orden funciona con su propio índice, y en la dimensión 1 no puede haber más de una coincidencia. Significa que el intento de acceso está por completo excluido. ¿Para qué necesitamos este cálculo entonces?
- La segunda es el argumento shift, que se añade a la hora de la barra del periodo actual.
Existen motivos especiales para ello. En el mundo nada es ideal. Y la presencia de una barra en M5 con una hora de apertura 01:00:00 no significa en absoluto que haya una barra en el gráfico M1 con la misma hora de apertura.
La barra correspondiente en el gráfico М1 puede tener un tiempo de apertura tanto de 01:01:00, como de 01:04:00. Es decir, el número de variaciones será igual a la proporción de la duración de los marcos temporales. Precisamente para ello se ha introducido la función de cálculo del número de puntos de entrada encontrados para el periodo M1:
atomic_inc(&Count[1]);
Si después de finalizar el trabajo del kernel, el número de órdenes М1 encontradas es igual al número de órdenes encontradas en el marco temporal actual, significa que la tarea se ha ejecutado totalmente. En caso contrario, necesitaremos iniciar de nuevo con otro valor del argumento shift. Estos inicios pueden darse en una cantidad igual a los periodos М1 que quepan en el periodo actual.
Al iniciar de nuevo el argumento shift con un valor cero, los puntos de entrada encontrados no han sido reescritos con otros valores; se ha introducido la comprobación siguiente:
if(OrderM1[x*2]>=0) return;
Pero para que funcione, antes del inicio del kernel, es necesario rellenar el búfer OrderM1[] con el valor -1. Para ello, crearemos el kernel de rellenado del búfer array_fill():
__kernel void array_fill(__global int *Buf,const int value) { //--- trabaja en una dimensión size_t x=get_global_id(0); Buf[x]=value; }
2.2.3 Obteniendo los resultados de las transacciones
Después de encontrar los puntos de entrada en М1, podemos proceder a obtener los resultados de las transacciones. Para ello, necesitaremos un kernel que acompañe las posiciones abiertas. En otras palabras, esperar a que se cierren según uno de los siguientes cuatro motivos. A saber:
- Alcanzar el nivel de Take Profit
- Alcanzar el nivel de Stop Loss
- Expiración del tiempo máximo de mantenimiento de una posición abierta
- Finalización del periodo de simulación
El espacio de tareas para el kernel será unidimensional, y su tamaño será igual al número de órdenes. El kernel iterará por la barras, comenzando por la barra de apertura de posición, y comprobará las condiciones descritas más arriba. Dentro de la barra se modelarán en el modo "1 minute OHLC", que se describe en la documentación, en el apartado "Simulación de estrategias comerciales".
Lo importante es que una posición se cierre prácticamente justo después de la apertura, otra más tarde, y otra más por límite de tiempo o finalización de la simulación. Esto significa que el tiempo de ejecución de las tareas para diferentes puntos de entrada se diferenciará manifiestamente.
La práctica ha demostrado que el acompañamiento de posición hasta el cierre en una pasada no es efectivo. Podemos obtener resultados sustancialmente mejores en cuanto a rapidez si dividimos el espacio de la simulación (es decir, el número de barras hasta el cierre forzoso por límite de tiempo del mantenimiento de posición) en varias partes, y ejecutamos el procesamiento en varias pasadas.
Aquellas tareas que no han finalizado en la pasada actual, se posponen a la siguiente. De esta forma, con cada pasada, el tamaño del espacio de tareas disminuirá. Pero, para implementar esto, es imprescindible implicar un búfer más para guardar los índices de tareas. Cada tarea es un índice del punto de entrada en el búfer de órdenes. En el momento del primer inicio, el contenido del búfer de tareas se corresponderá por entero con el búfer de órdenes. En los siguientes inicios, en ellos se encontrarán los índices de aquells órdenes cuyas posiciones aún no se han abierto. Para tener posibilidad de trabajar con el búfer de tareas y al mismo tiempo colocar allí tareas para el siguiente inicio, debe tener dos bancos: con un banco trabajaremos en el siguiente inicio, y en el otro, formaremos las tareas para el siguiente.
En el trabajo, esto tendrá el aspecto siguiente. Supongamos que tenemos 1000 puntos de entrada según los cuales debemos obtener los resultados de las transacciones. El tiempo de mantenimiento de la posición abierta es equivalente a 800 barras. Hemos decidido dividir la simulación en 4 pasadas. Gráficamente, esto tendrá el mismo aspecto que se muestra en la figura 7.
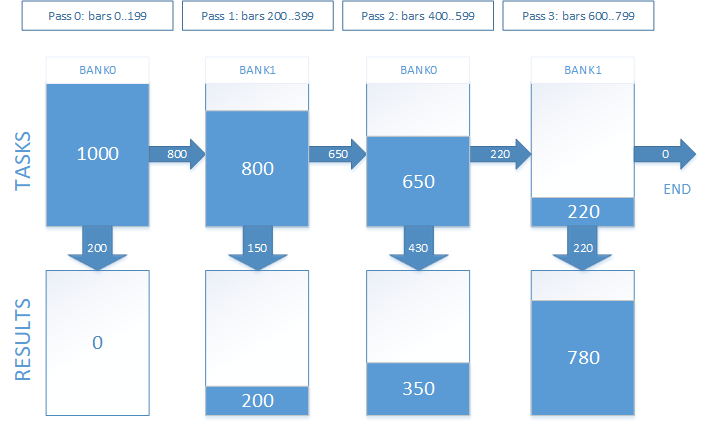
Fig. 7. Ejecución del acompañamiento de posiciones abiertas en varias pasadas
Por experiencia hemos establecido que el número de pasadas es igual a 8, para el límite de tiempo del mantenimiento de una posición abierta es igual a 12 horas (o 720 barras de minuto). Precisamente este valor se ha establecido por defecto. Variará para diferentes valores de límite de tiempo y diferentes dispositivos de OpenCL. Y se recomienda en cuanto a la selección para obtener el máximo rendimiento.
Bien, ya se ha añadido a los argumentos del kernel, aparte de las series temporales, el búfer de tareas Tasks[] y el número del banco de tareas con el que estamos trabajando. Además, añadimos el búfer Res[] para guardar los resultados.
El número de datos actuales en el búfer de tareas se retorna a través del búfer Left[], que tiene el tamaño de dos elementos, que indican el tamaño de los bancos, respectivamente.
Puesto que la simulación se ejecuta por partes, entre los argumentos del kernel debemos transmitir desde qué barra y hasta qué barra se realizará el acompañamiento. Se trata de una magnitud relativa, que se suma con el índice de la barra de apertura de posición, para obtener el índice absoluto de la barra actual en las series temporales. Asimismo, es necesario transmitir al kernel el índice máximo permitido de la barra en las series temporales, para no salir de los límites de los búferes.
Como resultado, el conjunto de argumentos del kernel tester_step(), que precisamente va a ocuparse del acompañamiento de las posiciones abiertas, tiene el aspecto siguiente:
__kernel void tester_step(__global double *OpenM1,__global double *HighM1,__global double *LowM1,__global double *CloseM1, __global double *SpreadM1, // se expresa como la diferencia de precios, y no en puntos __global ulong *TimeM1, __global int *OrderM1, // búfer de órdenes, donde [0] es el índice en OHLC(M1), [1] es la operación (Buy/Sell) __global int *Tasks, // búfer de tareas (posiciones abiertas), en él se encuentran los índices a las órdenes en el búfer OrderM1 __global int *Left, // número de tareas restantes, dos elementos: [0] - para bank0, [1] - para bank1 __global double *Res, // búfer de resultados const uint bank, // banco actual const uint orders, // número de órdenes en OrderM1 const uint start_bar, // el número de serie de la barra se está procesando (como el desplazamiento con respecto al índice indicado en OrderM1) const uint stop_bar, // hasta qué barra se procesa (inclusive) const uint maxbar, // índice máximo permitido de la barra (última barra de la matriz) const double tp_dP, // TP en diferencia de precios const double sl_dP, // SL en diferencia de precios const ulong timeout) // qué tiempo debe transcurrir tras la apertura para cerrar la transacción forzosamente (en segundos)
El kernel tester_step() funciona en una dimensión. La dimensión de las tareas de esta dimensión cambiarácon cada llamada, comenzando desde el número de órdenes, y disminuyendo con cada pasada.
Al propio inicio del código del kernel, obtenemos el identificador de tareas:
size_t id=get_global_id(0);A continuación, partiendo desde el índice del banco actual, que se transmite a través del argumento bank, leemos el índice del siguiente:
uint bank_next=(bank)?0:1;
Calculamos el índice de la orden con la que vamos a trabajar. En el primer inicio (con start_bar igual a cero), el búfer de tareas se corresponde con el búfer de órdenes, por eso, el índice de la orden es igual al índice de la tarea. En los siguientes inicios, obtendremos el índice de la orden del búfer de tareas, teniendo en cuenta el banco actual y el índice de la tarea:
if(!start_bar) idx=id; else idx=Tasks[(orders*bank)+id];
Conociendo el índice de la orden, obtenemos el índice de la barra en las series temporales y el código de la operación:
//--- índice de la barra en el búfer M1 en el que se ha abierto la posición uint iO=OrderM1[idx*2]; //--- operación (OP_BUY/OP_SELL) uint op=OrderM1[(idx*2)+1];
Usando como base el valor del argumento timeout, calculamos la hora de cierre forzoso de la posición:
ulong tclose=TimeM1[iO]+timeout;A continuación, viene el procesamiento de la posición. Vamos a analizarlo usando el ejemplo de la operación BUY (para la operación SELL será análogo).
if(op==OP_BUY) { //--- precio de apertura de la posición double open=OpenM1[iO]+SpreadM1[iO]; double tp = open+tp_dP; double sl = open-sl_dP; double p=0; for(uint j=iO+start_bar; j<=(iO+stop_bar); j++) { for(uint k=0;k<4;k++) { if(k==0) { p=OpenM1[j]; if(j>=maxbar || TimeM1[j]>=tclose) { //--- cierre forzoso según el tiempo Res[idx]=p-open; return; } } else if(k==1) p=HighM1[j]; else if(k==2) p=LowM1[j]; else p=CloseM1[j]; //--- comprobando si el TP o SL se han activado if(p<=sl) { Res[idx]=sl-open; return; } else if(p>=tp) { Res[idx]=tp-open; return; } } } }
Si no se ha activado ni una de las condiciones para la salida del kernel, la tarea se pospone a la siguiente pasada:
uint i=atomic_inc(&Left[bank_next]);
Tasks[(orders*bank_next)+i]=idx;
Después de procesar todas las pasadas, en el búfer Res[] se encontrarán los resultados de todas las transacciones. Para obtener el resultado de la simulación, debemos sumarlos.
Ahora que entendemos el algoritmo y tenemos preparados los kernels, podemos proceder a su inicio.
2.3 Iniciando la simulación
En este punto, nos ayudará la clase CTestPatterns:
class CTestPatterns : private COpenCLx { private: CBuffering *m_sbuf; // Series temporales del periodo actual CBuffering *m_tbuf; // Series temporales del periodo M1 int m_prepare_passes; uint m_tester_passes; bool LoadTimeseries(datetime from,datetime to); bool LoadTimeseriesOCL(void); bool test(STR_TEST_STAT &stat,datetime from,datetime to,STR_TEST_PARS &par); bool optimize(STR_TEST_STAT &stat,datetime from,datetime to,STR_OPT_PARS &par); void buffers_free(void); public: CTestPatterns(); ~CTestPatterns(); //--- iniciando simulación única bool Test(STR_TEST_STAT &stat,datetime from,datetime to,STR_TEST_PARS &par); //--- iniciando optimización bool Optimize(STR_TEST_STAT &stat,datetime from,datetime to,STR_OPT_PARS &par); //--- obteniendo el puntero a las estadísticas de ejecución del programa COCLStat *GetStat(void){return &m_stat;} //--- obteniendo el código del último error int GetLastError(void){return m_last_error.code;} //--- obteniendo la estructura del último error STR_ERROR GetLastErrorExt(void){return m_last_error;} //--- reseteando el último error void ResetLastError(void); //--- en cuántas pasadas dividimos el inicio del kernel de simulación void SetTesterPasses(uint tp){m_tester_passes=tp;} //--- en cuántas pasadas dividimos el inicio del kernel de preparación de órdenes void SetPrepPasses(int p){m_prepare_passes=p;} };
Vamos a ver con más detalle el método Test():
bool CTestPatterns::Test(STR_TEST_RESULT &result,datetime from,datetime to,STR_TEST_PARS &par) { ResetLastError(); m_stat.Reset(); m_stat.time_total.Start(); //--- cargando los datos de las series temporales m_stat.time_buffering.Start(); if(LoadTimeseries(from,to)==false) return false; m_stat.time_buffering.Stop(); //--- inicializando OpenCL m_stat.time_ocl_init.Start(); if(Init(i_MODE_TESTER)==false) return false; m_stat.time_ocl_init.Stop(); //--- iniciando la simulación bool result=test(stat,from,to,par); Deinit(); buffers_free(); m_stat.time_total.Stop(); return result; }
En la entrada tiene un intervalo de fechas en el que es necesario simular la estrategia, además de los enlaces a las estructuras de los parámetros y los resultados de la simulación.
En el caso de funcionar con éxito, el kernel retornará "true" y registrará los resultados en el argumento result. Si durante la ejecución ha surgido un error, el método retornará "false"; para obtener los detalles sobre el error, deberemos llamar GetLastErrorExt().
Primero cargamos los datos de las series temporales. Después, realizamos la inicialización de OpenCL. Aquí se incluye la creación de objetos y kernels. Si todo ha funcionado con éxito, llamamos el método test(), en el que se ha implementado todo el algoritmo de simulación. En esencia, el método Test() sirve de envoltorio para test(). Esto se ha hecho para que en cualquier salida del método test siempre se realice una desinicialización y liberación de los búferes de las series temporales.
En el método test() todo comienza con la carga de los búferes de las series temporales OpenCL:if(LoadTimeseriesOCL()==false) return false;
Esto se hace con la ayuda del método LoadTimeseriesOCL(), que ya hemos visto más arriba.
En primer lugar, se inicia el kernel find_patterns(), al que le corresponde el enumerador k_FIND_PATTERNS. Pero, antes de iniciarlo, es necesario crear los búferes de las órdenes y los resultados:
_BufferCreate(buf_ORDER,m_sbuf.Depth*2*sizeof(int),CL_MEM_READ_WRITE); int count[2]={0,0}; _BufferFromArray(buf_COUNT,count,0,2,CL_MEM_READ_WRITE);
El búfer de órdenes tiene un tamaño dos veces superior al número de barras en el marco temporal actual. Puesto que no sabemos cuántos patrones se encontrarán, podemos suponer que el patrón se encontrará en cada barra. Esta medida de precaución puede parecer absurda a primera vista, teniendo en cuenta los patrones con los que trabajamos en el momento actual. Pero, en lo sucesivo, al añadir otros patrones, esto puede evitarnos muchos problemas.
A continuación, establecemos los argumentos:
_SetArgumentBuffer(k_FIND_PATTERNS,0,buf_OPEN); _SetArgumentBuffer(k_FIND_PATTERNS,1,buf_HIGH); _SetArgumentBuffer(k_FIND_PATTERNS,2,buf_LOW); _SetArgumentBuffer(k_FIND_PATTERNS,3,buf_CLOSE); _SetArgumentBuffer(k_FIND_PATTERNS,4,buf_ORDER); _SetArgumentBuffer(k_FIND_PATTERNS,5,buf_COUNT); _SetArgument(k_FIND_PATTERNS,6,double(par.ref)*_Point); _SetArgument(k_FIND_PATTERNS,7,par.flags);
Para el kernel find_patterns(), indicamos un espacio unidimensional de tareas con un desplazamiento inicial igual a cero:
uint global_size[1]; global_size[0]=m_sbuf.Depth; uint work_offset[1]={0};
Iniciamos la ejecución del kernel find_patterns():
_Execute(k_FIND_PATTERNS,1,work_offset,global_size);Merece la pena notar que la salida del método Execute() no significa que el programa haya sido ejecutado. El programa puede aún ejecutarse o esperar en la cola de ejecución. Para conocer su estado en el momento actual, debemos usar la función CLExecutionStatus(). Si debemos esperar la finalización de la ejecución del programa, podemos preguntar periódicamente su estado. O ejeuctar la lectura del búfer en el que el programa coloca los resultados. En el segundo caso, la espera de la finalización del programa tendrá lugar en el método de lectura del búfer BufferRead().
_BufferRead(buf_COUNT,count,0,0,2);
Ahora, en el búfer count[] con el índice 0, se ubica el número de patrones o el número de órdenes ubicadas en el búfer correspondiente. El siguiente paso es encontrar los puntos de entrada correspondientes en el marco temporal M1. El kernel order_to_M1() acumulará el número encontrado en el mismo búfer count[], pero según el índice 1. Se considerará una finalización exitosa la activación de la condición (count[0]==count[1]).
Pero, para comenzar, debemos crear un búfer de órdenes para M1 y llenarlo con el valor -1. Puesto que ya conocemos el número de órdenes, indicaremos el tamaño exacto del búfer sin margen:
int len=count[0]*2; _BufferCreate(buf_ORDER_M1,len*sizeof(int),CL_MEM_READ_WRITE);
Indicamos los argumentos para el kernel array_fill():
_SetArgumentBuffer(k_ARRAY_FILL,0,buf_ORDER_M1); _SetArgument(k_ARRAY_FILL,1,int(-1));
Establecemos el espacio unidimensional de tareas con un desplazamiento inicial igual a cero, y un tamaño igual al búfer. Iniciamos la ejecución:
uint opt_init_work_size[1]; opt_init_work_size[0]=len; uint opt_init_work_offset[1]={0}; _Execute(k_ARRAY_FILL,1,opt_init_work_offset,opt_init_work_size);
El paso siguiente es la preparación para el inicio de la ejecución del kernel order_to_M1():
//--- estableciendo el argumento _SetArgumentBuffer(k_ORDER_TO_M1,0,buf_TIME); _SetArgumentBuffer(k_ORDER_TO_M1,1,buf_TIME_M1); _SetArgumentBuffer(k_ORDER_TO_M1,2,buf_ORDER); _SetArgumentBuffer(k_ORDER_TO_M1,3,buf_ORDER_M1); _SetArgumentBuffer(k_ORDER_TO_M1,4,buf_COUNT); //--- el espacio de tareas para el kernel k_ORDER_TO_M1 es bidimensional uint global_work_size[2]; //--- la 1-era dimensión son las órdenes dejadas por el kernel k_FIND_PATTERNS global_work_size[0]=count[0]; //--- la 2-nda dimensión son todas las barras del gráfico M1 global_work_size[1]=m_tbuf.Depth; //--- el desplazamiento inicial en el espacio de tareas para ambas dimensiones es igual a cero uint global_work_offset[2]={0,0};
El argumento bajo el índice 5 no ha sido establecido, porque su valor será distinto, y su establecimiento se realizará directamente antes del inicio de la ejecución del kernel. Debido al motivo mencionado anteriormente, la ejecución del kernel order_to_M1() puede hacerse necesaria varias veces con un valor diferente de desplazamiento en segundos. El número máximo de inicios estará limitado por la relación entre la duración de los periodos del gráfico actual y el gráfico M1:
int maxshift=PeriodSeconds()/PeriodSeconds(PERIOD_M1);
El ciclo completo tendrá el aspecto siguiente:
for(int s=0;s<maxshift;s++) { //--- estableciendo el desplazamiento de la pasada actual _SetArgument(k_ORDER_TO_M1,5,ulong(s*60)); //--- ejecutando el kernel _Execute(k_ORDER_TO_M1,2,global_work_offset,global_work_size); //--- leyendo los resultados _BufferRead(buf_COUNT,count,0,0,2); //--- según el índice 0 se encuentra el número de órdenes en el gráfico actual //--- según el índice 1 se encuentra el número de barras que le corresponden en el gráfico М1 //--- ambos valores coinciden, salimos del ciclo if(count[0]==count[1]) break; //--- en el caso contrario, vamos a la siguiente iteración e iniciamos el kernel con otro desplazamiento } //--- en el caso de que salgamos del ciclo, pero no por break, comprobamos de nuevo que el número de órdenes se corresponda if(count[0]!=count[1]) { SET_UERRt(UERR_ORDERS_PREPARE,"Error al preparar las órdenes M1"); return false; }
Ha llegado el momento de iniciar el kernel tester_step(), que calcula los resultados de las transacciones abiertas según los puntos de entrada localizados. Para comenzar, vamos a crear los búferes que faltan y establecer los argumentos:
//--- creamos el búfer Tasks, en el que se formará el número de tareas para la siguiente pasada _BufferCreate(buf_TASKS,m_sbuf.Depth*2*sizeof(int),CL_MEM_READ_WRITE); //--- creamos el búfer Result, en el que se encontrarán los resultados de las transacciones _BufferCreate(buf_RESULT,m_sbuf.Depth*sizeof(double),CL_MEM_READ_WRITE); //--- establecemos los argumentos para el kernel de la simulación única _SetArgumentBuffer(k_TESTER_STEP,0,buf_OPEN_M1); _SetArgumentBuffer(k_TESTER_STEP,1,buf_HIGH_M1); _SetArgumentBuffer(k_TESTER_STEP,2,buf_LOW_M1); _SetArgumentBuffer(k_TESTER_STEP,3,buf_CLOSE_M1); _SetArgumentBuffer(k_TESTER_STEP,4,buf_SPREAD_M1); _SetArgumentBuffer(k_TESTER_STEP,5,buf_TIME_M1); _SetArgumentBuffer(k_TESTER_STEP,6,buf_ORDER_M1); _SetArgumentBuffer(k_TESTER_STEP,7,buf_TASKS); _SetArgumentBuffer(k_TESTER_STEP,8,buf_COUNT); _SetArgumentBuffer(k_TESTER_STEP,9,buf_RESULT); uint orders_count=count[0]; _SetArgument(k_TESTER_STEP,11,uint(orders_count)); _SetArgument(k_TESTER_STEP,14,uint(m_tbuf.Depth-1)); _SetArgument(k_TESTER_STEP,15, double(par.tp)*_Point); _SetArgument(k_TESTER_STEP,16, double(par.sl)*_Point); _SetArgument(k_TESTER_STEP,17,ulong(par.timeout));
A continuación, recalculamos el tiempo máximo de mantenimiento de la posición en barras en el gráfico M1:
uint maxdepth=(par.timeout/PeriodSeconds(PERIOD_M1))+1;
Después comprobamos que sea correcto el número establecido de pasadas de ejecución del kernel. Por defecto, su valor es igual a 8, pero para seleccionar el rendimiento óptimo para los diferentes dispositivos OpenCL, se permite establecer otros valores con la ayuda del método SetTesterPasses().
if(m_tester_passes<1) m_tester_passes=1; if(m_tester_passes>maxdepth) m_tester_passes=maxdepth; uint step_size=maxdepth/m_tester_passes;
Establecemos el tamaño del espacio de tareas para la única dimensión e iniciamos el ciclo de cálculo de los resultados de las transacciones:
global_size[0]=orders_count; m_stat.time_ocl_test.Start(); for(uint i=0;i<m_tester_passes;i++) { //--- estableciendo el índice del banco actual _SetArgument(k_TESTER_STEP,10,uint(i&0x01)); uint start_bar=i*step_size; //--- estableciendo el índice de la barra desde la que comienza la simulación en la pasada actual _SetArgument(k_TESTER_STEP,12,start_bar); //--- estableciendo el índice de la barra en la que finaliza la simulación en la pasada actual (inclusive) uint stop_bar=(i==(m_tester_passes-1))?(m_tbuf.Depth-1):(start_bar+step_size-1); _SetArgument(k_TESTER_STEP,13,stop_bar); //--- reseteando el número de tareas en el banco siguiente //--- en él se formará ahora el número de órdenes que han quedado para la siguiente pasada count[(~i)&0x01]=0; _BufferWrite(buf_COUNT,count,0,0,2); //--- iniciando la ejecución del kernel de simulación _Execute(k_TESTER_STEP,1,work_offset,global_size); //--- leyendo el número de órdenes que han quedado para la siguiente pasada _BufferRead(buf_COUNT,count,0,0,2); //--- establecemos un nuevo número de tareas que es igual al número de estas órdenes global_size[0]=count[(~i)&0x01]; //--- si no quedan tareas, salimos del ciclo if(!global_size[0]) break; } m_stat.time_ocl_test.Stop();
Creamos un búfer para leer los resultados de las transacciones:
double Result[]; ArrayResize(Result,orders_count); _BufferRead(buf_RESULT,Result,0,0,orders_count);
Para obtener resultados que se puedan comparar con los resultados del simulador estándar, los valores leídos se deberán dividir por _Point. El código del cálculo del resultado y las estadísticas de simulación se muestra más abajo:
m_stat.time_proc.Start(); result.trades_total=0; result.gross_loss=0; result.gross_profit=0; result.net_profit=0; result.loss_trades=0; result.profit_trades=0; for(uint i=0;i<orders_count;i++) { double r=Result[i]/_Point; if(r>=0) { result.gross_profit+=r; result.profit_trades++; }else{ result.gross_loss+=r; result.loss_trades++; } } result.trades_total=result.loss_trades+result.profit_trades; result.net_profit=result.gross_profit+result.gross_loss; m_stat.time_proc.Stop();
Vamos a escribir un breve script que nos permita iniciar el simulador.
#include <OCL_Patterns\TestPatternsOCL.mqh> CTestPatterns tpat; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { datetime from=D'2018.01.01 00:00'; datetime to=D'2018.10.01 00:00'; //--- estableciendo los parámetros de simulación STR_TEST_PARS pars; pars.ref= 60; pars.sl = 350; pars.tp = 50; pars.flags=15; // todos los patrones pars.timeout=12*3600; //--- estructura de los resultados STR_TEST_RESULT res; //--- iniciando la simulación tpat.Test(res,from,to,pars); STR_ERROR oclerr=tpat.GetLastErrorExt(); if(oclerr.code) { Print(oclerr.comment); Print("code = ",oclerr.code,", function = ",oclerr.function,", line = ",oclerr.line); return; } //--- resultados de la simulación Print("Net Profit: ", res.net_profit); Print("Gross Profit: ", res.gross_profit); Print("Gross Loss: ", res.gross_loss); Print("Trades Total: ", res.trades_total); Print("Profit Trades: ",res.profit_trades); Print("Loss Trades: ", res.loss_trades); //--- estadísticas de la ejecución COCLStat ocl_stat=tpat.GetStat(); Print("GPU memory size: ", ocl_stat.gpu_mem_size.ToStr()); Print("GPU memory usage: ", ocl_stat.gpu_mem_usage.ToStr()); Print("Buffering: ", ocl_stat.time_buffering.ToStr()); Print("OpenCL init: ", ocl_stat.time_ocl_init.ToStr()); Print("OpenCL buffering: ", ocl_stat.time_ocl_buf.ToStr()); Print("OpenCL prepare orders: ", ocl_stat.time_ocl_orders.ToStr()); Print("OpenCL test: ", ocl_stat.time_ocl_test.ToStr()); Print("OpenCL total execution: ",ocl_stat.time_ocl_exec.ToStr()); Print("Post-processing: ", ocl_stat.time_proc.ToStr()); Print("Total: ", ocl_stat.time_total.ToStr()); }
Hemos elegido el intervalo de tiempo de simulación, así como el símbolo y el periodo en los que hemos iniciado la simulación del experto implementado en MQL5. Hemos establecido los valores de la magnitud de apoyo y el nivel de Stop Loss que han sido encontrados en el proceso de optimización. Solo queda iniciar el script y comparar el resultado obtenido con el resultado del simulador estándar.
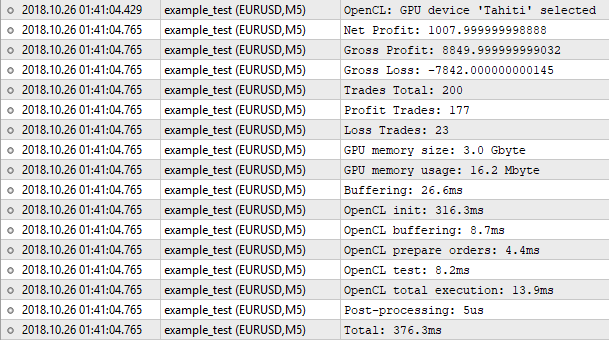
Fig.8. Resultados del simulador implementado en OpenCL
Bien, el número de transacciones coincide. Pero el valor del beneficio neto, no. El simulador estándar muestra el número 1000.50, y el nuestro, 1007.99. El motivo es el siguiente. Para lograr estos resultados, debemos tener en cuenta, como el mínimo, el swap. Pero su implementación en el simulador no estará justificada. Para la valoración en bruto, donde se aplica la simulación en el modo OHLC en M1, podemos despreciar estas minucias. Lo importante es que el resultado es muy próximo, y eso significa que nuestro algoritmo funciona correctamente.
Ahora vamos a prestar atención a las estadísticas de ejecución del programa. No hemos ocupado mucha memoria, solo 16 megabytes. Lo que más tiempo ha llevado ha sido la inicialización de OpenCL. El proceso completo de simulación, en este caso, ha ocupado 376 milisegundos, lo cual es comparable casi al milímetro con el simulador estándar. No merece la pena esperar un crecimiento del rendimiento aquí. Con un número de 200 transacciones, la mayoría del tiempo se empleará en operaciones preparatorias: inicialización, copiado de búferes, etc. Para sentir la diferencia, necesitamos cientos de veces más órdenes para la simulación. Ya es hora de pasar a la optimización.
2.4. Optimización
El algoritmo de optimización se parecerá al algoritmo de simulación única, pero al mismo tiempo tendrá una diferencia sustancial. En el simulador nosotros buscábamos primero los patrones, y después leíamos los resultados de las transacciones, mientras que aquí todo será al revés. Primero leemos los resultados de las transacciones, y ya después pasamos a buscar los patrones. Existe un motivo para esto.
Tenemos dos parámetros optimizables. El primero es la magnitud de apoyo para la localización de patrones. El segundo es el nivel de Stop Loss, que participa en el proceso de cálculo del resultado de la transacción. Es decir, uno de ellos influye en el número de puntos de entrada, y el segundo, en los resultados de las transacciones y la duración del acompañamiento de la posición abierta. Si conservamos la misma secuencialidad de acciones que en el algoritmo de simulación única, no podremos evitar la simulación repetida de los mismos puntos de entrada, y esto supone una pérdida de tiempo enorme. Porque una barra pin con una "cola" de 300 puntos será encontrada con cualquier valor de magnitud de apoyo igual o menor al valor dado.
Por eso, en nuestro caso, será mucho más económico calcular los resultados de las transacciones con los puntos de entrada en cada barra (incluyendo tanto la compra, como la venta), y ya después operar con estos datos en el proceso de búsqueda de los patrones. De esta forma, la secuencialidad de las acciones al optimizar será la siguiente:
- Carga de los búferes de las series temporales
- Inicialización de OpenCL
- Copiado de los búferes de las series temporales en los búferes de OpenCL
- Inicio del kernel de preparación de órdenes (en cada barra del marco temporal hay dos órdenes, la compra y la venta)
- Inicio del kernel que traslada las órdenes al gráfico M1
- Inicio del kernel que calcula los resultados de las transacciones por órdenes
- Inicio del kernel que encuentra los patrones y forma los resultados de simulación para cada combinación de parámetros optimizados a partir de los resultados preparados de las operaciones
- Procesamiento del búfer de resultados y localización de los parámetros optimizados que se corresponden con el mejor resultado
- Desinicialización de OpenCL
- Eliminación de los búferes de las series temporales
Además, el número de tareas para la búsqueda de patrones se multiplicará por el número de valores de la magnitud de apoyo, mientras que el número de tareas para el cálculo de los resultados de las transacciones se multiplicará por el número de valores del nivel de Stop Loss.
2.4.1 Preparando las órdenes
Estamos suponiendo que los patrones buscados pueden ser encontrados en cualquier barra. Esto significa que en cada barra debemos colocar una orden de compra o venta. En este caso, además, el tamaño del búfer de órdenes se puede expresar a través de la fórmula:
N = Depth*4*SL_count;
donde Depth es el tamaño de los búferes de las series temporales, y SL_count es el número de valores de Stop Loss.
Además, los índices de las barras deberán ser de la serie temporal M1. El kernel tester_opt_prepare() buscará en las series temporales M1 barras con la misma hora de apertura, que se corresponda con la hora de apertura de las barras del periodo actual, e irá colocándolas en el formato indicado más arriba. En general, su funcionamiento será muy parecido al funcionamiento del kernel order_to_M1():
__kernel void tester_opt_prepare(__global ulong *Time,__global ulong *TimeM1, __global int *OrderM1,// búfer de órdenes __global int *Count, const int SL_count, // número de valores de SL const ulong shift) // desplazamiento temporal en segundos { //--- trabajando en las dos dimensiones size_t x=get_global_id(0); //índice en Time if(OrderM1[x*SL_count*4]>=0) return; size_t y=get_global_id(1); //índice en TimeM1 if((Time[x]+shift)==TimeM1[y]) { //--- encontrando de paso el índice máximo de la barra para el periodo М1 atomic_max(&Count[1],y); uint offset=x*SL_count*4; for(int i=0;i<SL_count;i++) { uint idx=offset+i*4; //--- para cada barra, añadiremos dos órdenes: de compra y de venta OrderM1[idx++]=y; OrderM1[idx++]=OP_BUY |(i<<2); OrderM1[idx++]=y; OrderM1[idx] =OP_SELL|(i<<2); } atomic_inc(&Count[0]); } }
Pero tendrá una diferencia importante, la localización del índice máximo de la serie temporal M1. Ahora explicaremos para qué se hace esto.
En el caso de la simulación con una pasada única, hemos topado con relativamente pocas órdenes. Y el número de tareas, que es igual al número de órdenes multiplicado por el tamaño de los búferes de las series temporales M1, no era tan grande. Si tomamos en cuenta los datos en los que hemos realizado la simulación, se trata de 200 órdenes multiplicadas por 279039 barras М1, lo que finalmente da 55,8 millones de tareas.
En la situación actual, el número de tareas será relativamente grande. Por ejemplo, tenemos 279039 barras M1, multiplicadas por 55843 barras del periodo actual (M5), lo que es igual a 15,6 mil millones de tareas. También debemos tener en cuenta que deberemos iniciar este kernel de nuevo con otro valor de desplazamiento de tiempo. Aquí el método de iteración será demasiado costoso.
Para solucionar esta cuestión, dejaremos a pesar de todo la iteración, pero dividiremos el intervalo de procesamiento de las barras del periodo actual en varias partes. Asimismo, limitaremos también el intervalo de las barras de minuto que les corresponden. Pero, dado que los valores de cálculo del índice del límite superior del intervalo de barras de minuto será en la mayoría de los casos superior al real, retornaremos con la ayuda de Count[1] el índice máximo de la barra de minuto, para que la siguiente pasada comience desde este lugar.
2.4.2 Obteniendo los resultados de las transacciones
Después de preparar las órdenes, podemos pasar a la obtención de los resultados de las transacciones.
El kernel tester_opt_step() se parecerá mucho a tester_step(). Por eso, no vamos a mostrar el código al completo, solo analizaremos las diferencias. En primer lugar, han cambiado los parámetros de entrada
__kernel void tester_opt_step(__global double *OpenM1,__global double *HighM1,__global double *LowM1,__global double *CloseM1, __global double *SpreadM1,// se expresa como la diferencia de precios, y no en puntos __global ulong *TimeM1, __global int *OrderM1, // búfer de órdenes, donde [0] es el índice en OHLC(M1), [1] es la operación (Buy/Sell) __global int *Tasks, // búfer de tareas (posiciones abiertas), en él se encuentran los índices a las órdenes en el búfer OrderM1 __global int *Left, // número de tareas restantes, dos elementos: [0] - para bank0, [1] - para bank1 __global double *Res, // búfer de resultados, se colocan por orden de llegada, const uint bank, // banco actual const uint orders, // número de órdenes en OrderM1 const uint start_bar, // número de serie de la barra que se está procesando (como el desplazamiento con respecto al índice indicado en OrderM1) - en esencia, "i" del ciclo que inicia el kernel const uint stop_bar, // hasta qué barra se procesa (inclusive) - para la mayoría de los casos, será igual al valor bar const uint maxbar, // índice máximo permitido de la barra (última barra de la matriz) const double tp_dP, // TP en diferencia de precios const uint sl_start, // SL en puntos - valor inicial const uint sl_step, // SL en puntos - salto const ulong timeout, // qué tiempo debe transcurrir tras la apertura para cerrar la transacción forzosamente (en segundos) const double point) // _Point
En lugar del argumento sl_dP, a través del cual se transmitía el valor del nivel de SL, expresado como diferencia de precios, se han añadido dos argumentos: sl_start y sl_step, así como el argumento point. Ahora, para calcular el valor del nivel de SL, debemos aplicar la fórmula:
SL = (sl_start+sl_step*sli)*point;
donde sli es el índice del valor de Stop Loss contenido en la orden.
La segunda diferencia es el código de obtención del índice sli del búfer de órdenes:
//--- operación (bytes 1:0) e índice de SL (bytes 9:2) uint opsl=OrderM1[(idx*2)+1]; //--- obteniendo el índice de SL uint sli=opsl>>2;
En el resto, el código es idéntico al kernel tester_step().
Después de ejecutar, obtenemos en el búfer Res[] los resultados de la compra y la venta para cada barra y cada uno de los resultados de Stop Loss.
2.4.3 Buscando patrones y formando los resultados de la simulación
A diferencia de la simulación, aquí sumaremos los resultados de las transacciones directamente en el kernel, y no en el código MQL. En todo esto existe una desventaja desagradable: deberemos convertir los resultados al tipo entero, lo que provocará con toda seguridad una pérdida de precisión. Precisamente por esto motivo debemos transmitir al argumento point el valor _Point dividido por 100.
La conversión forzosa de los resultados al tipo int viene condicionada por el hecho de que las funciones atómicas no funcionen con el tipo double. Para sumar los resultados, usaremos atomic_add().
El kernel find_patterns_opt() funcionará en un espacio de tareas tridimensional:
- Dimensión 0: índice de la barra en el marco temporal actual
- Dimensión 1: índice del valor de la magnitud de apoyo para los patrones
- Dimensión 2: índice del valor del nivel de Stop Loss
Durante el trabajo, se formará el búfer de resultados, que contendrá las estadísticas de simulación para cada combinación del nivel de Stop Loss y la magnitud de apoyo. Entendemos por estadísticas de simulación la estructura que contiene las siguientes magnitudes:
- Beneficio total
- Pérdidas totales
- Número de transacciones rentables
- Número de transacciones con pérdidas
Todas ellas tienen el tipo int. Partiendo de ellas, podemos también calcular el beneficio neto y el número total de transacciones. El código del kernel se muestra más abajo:
__kernel void find_patterns_opt(__global double *Open,__global double *High,__global double *Low,__global double *Close, __global double *Test, // búfer de resultados de simulación para cada barra, tamaño 2*x*z ([0]-buy, [1]-sell ... ) __global int *Results, // búfer de resultados, tamaño 4*y*z const double ref_start, // parámetro del patrón const double ref_step, // const uint flags, // qué patrones buscar const double point) // _Point/100 { //--- trabajando en tres dimensiones //--- índice de la barra size_t x=get_global_id(0); //--- índice del valor ref size_t y=get_global_id(1); //--- índice del valor de SL size_t z=get_global_id(2); //--- número de barras size_t x_sz=get_global_size(0); //--- número de valores ref size_t y_sz=get_global_size(1); //--- número de valores de sl size_t z_sz=get_global_size(2); //--- tamaño del espacio de la búsqueda de patrones size_t depth=x_sz-PBARS; if(x>=depth)//no abrimos junto al final del búfer return; // uint res=Check(&Open[x],&High[x],&Low[x],&Close[x],ref_start+ref_step*y,flags); if(res==PAT_NONE) return; //--- calculando el índice del resultado de la transacción en el búfer Test[] int ri; if(res==PAT_PINBAR_BEARISH || res==PAT_ENGULFING_BEARISH) //sell ri = (x+PBARS)*z_sz*2+z*2+1; else //buy ri=(x+PBARS)*z_sz*2+z*2; //--- obteniendo el resultado del índice calculado, convertimos en centavos int r=Test[ri]/point; //--- calculando el índice de los resultados de simulación en el búfer Results[] int idx=z*y_sz*4+y*4; //--- añadiendo el resultado de la transacción según el patrón actual if(r>=0) {//--- profit //--- sumando el beneficio total en centavos atomic_add(&Results[idx],r); //--- aumentando el número de transacciones rentables atomic_inc(&Results[idx+2]); } else {//--- loss //--- sumando las pérdidas totales en centavos atomic_add(&Results[idx+1],r); //--- aumentando el número de transacciones con pérdidas atomic_inc(&Results[idx+3]); } }
El búfer Test[] en los argumentos representa los resultados obtenidos después de ejecutar el kernel tester_opt_step().
2.5 Iniciando la optimización
El código de inicio de la ejecución de los kernels de MQL5 durante la optimización se ha construido de forma análoga al proceso de simulación. El método público Optimize() es el envoltorio del método optimize(), en el que se ha implementado el orden de preparación y el inicio de la ejecución de los kernels.
bool CTestPatterns::Optimize(STR_TEST_RESULT &result,datetime from,datetime to,STR_OPT_PARS &par) { ResetLastError(); if(par.sl.step<=0 || par.sl.stop<par.sl.start || par.ref.step<=0 || par.ref.stop<par.ref.start) { SET_UERR(UERR_OPT_PARS,"Los parámetros de optimización se han establecido correctamente"); return false; } m_stat.Reset(); m_stat.time_total.Start(); //--- cargando los datos de las series temporales m_stat.time_buffering.Start(); if(LoadTimeseries(from,to)==false) return false; m_stat.time_buffering.Stop(); //--- inicializando OpenCL m_stat.time_ocl_init.Start(); if(Init(i_MODE_OPTIMIZER)==false) return false; m_stat.time_ocl_init.Stop(); //--- iniciando optimización bool res=optimize(result,from,to,par); Deinit(); buffers_free(); m_stat.time_total.Stop(); return res; }
No vamos a analizar con detalle cada línea, aclararemos solo aquellos lugares que se distinguen en algo. En concreto, el inicio del kernel tester_opt_prepare().
Para comenzar, crearemos un búfer para controlar el número de barras procesadas y retornar el índice máximo de la barra М1:
int count[2]={0,0}; _BufferFromArray(buf_COUNT,count,0,2,CL_MEM_READ_WRITE);
A continuación, estableceremos los argumentos y el tamaño del espacio de tareas.
_SetArgumentBuffer(k_TESTER_OPT_PREPARE,0,buf_TIME); _SetArgumentBuffer(k_TESTER_OPT_PREPARE,1,buf_TIME_M1); _SetArgumentBuffer(k_TESTER_OPT_PREPARE,2,buf_ORDER_M1); _SetArgumentBuffer(k_TESTER_OPT_PREPARE,3,buf_COUNT); _SetArgument(k_TESTER_OPT_PREPARE,4,int(slc)); // número de valores de SL //--- el kernel k_TESTER_OPT_PREPARE tendrá un espacio de tareas bidimensional uint global_work_size[2]; //--- la dimensión 0 tiene las órdenes en el periodo actual global_work_size[0]=m_sbuf.Depth; //--- la dimensión 1, todas las barras М1 global_work_size[1]=m_tbuf.Depth; //--- para el primer inicio, estableceremos un desplazamiento en el espacio de tareas igual a cero para ambas dimensiones uint global_work_offset[2]={0,0};
Aumentaremos el desplazamiento en el espacio de tareas de la 1-era dimensión después de procesar parte de las barras. Su valor será igual al valor máximo de la barra М1 retornado por el kernel, aumentado en 1.
int maxshift=PeriodSeconds()/PeriodSeconds(PERIOD_M1); int prep_step=m_sbuf.Depth/m_prepare_passes; for(int p=0;p<m_prepare_passes;p++) { //compensación para el espacio de tareas del periodo actual global_work_offset[0]=p*prep_step; //compensación para el espacio de tareas del periodo M1 global_work_offset[1]=count[1]; //dimesnión de tareas para el periodo actual global_work_size[0]=(p<(m_prepare_passes-1))?prep_step:(m_sbuf.Depth-global_work_offset[0]); //dimensión de tareas para el periodo M1 uint sz=maxshift*global_work_size[0]; uint sz_max=m_tbuf.Depth-global_work_offset[1]; global_work_size[1]=(sz>sz_max)?sz_max:sz; // count[0]=0; _BufferWrite(buf_COUNT,count,0,0,2); for(int s=0;s<maxshift;s++) { _SetArgument(k_TESTER_OPT_PREPARE,5,ulong(s*60)); //--- execute kernel _Execute(k_TESTER_OPT_PREPARE,2,global_work_offset,global_work_size); //--- leyendo el resultado (el número deberá coincidir con m_sbuf.Depth) _BufferRead(buf_COUNT,count,0,0,2); if(count[0]==global_work_size[0]) break; } count[1]++; } if(count[0]!=global_work_size[0]) { SET_UERRt(UERR_ORDERS_PREPARE,"Error al preparar las órdenes M1"); return false; }
El parámetro m_prepare_passes indica el número de pasadas en el que se debe dividir el proceso de preparación de órdenes. Por defecto, su valor es igual a 64. Es posible cambiarlo con la ayuda del método SetPrepPasses().
Después de leer los resultados de simulación en el búfer OptResults[], se ejecuta la búsqueda de la combinación de parámetros optimizados con la que se ha obtenido el beneficio neto máximo.
int max_profit=-2147483648; uint idx_ref_best= 0; uint idx_sl_best = 0; for(uint i=0;i<refc;i++) for(uint j=0;j<slc;j++) { uint idx=j*refc*4+i*4; int profit=OptResults[idx]+OptResults[idx+1]; //sum+=profit; if(max_profit<profit) { max_profit=profit; idx_ref_best= i; idx_sl_best = j; } }
Después de ello, recalculamos los resultados en double y establecemos los valores buscados de los parámetros utilizados en la estructura correspondiente.
uint idx=idx_sl_best*refc*4+idx_ref_best*4; result.gross_profit=double(OptResults[idx])/100; result.gross_loss=double(OptResults[idx+1])/100; result.profit_trades=OptResults[idx+2]; result.loss_trades=OptResults[idx+3]; result.trades_total=result.loss_trades+result.profit_trades; result.net_profit=result.gross_profit+result.gross_loss; //--- par.ref.value= int(par.ref.start+idx_ref_best*par.ref.step); par.sl.value = int(par.sl.start+idx_sl_best*par.sl.step);
Debemos tener en cuenta que la conversión de int a double y viceversa influirá necesariamente en los valores de los resultados, y que estos se distinguirán ligeramente de los obtenidos en la simulación única.
Vamos a escribir un pequeño script para iniciar la optimización:
#include <OCL_Patterns\TestPatternsOCL.mqh> CTestPatterns tpat; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { datetime from=D'2018.01.01 00:00'; datetime to=D'2018.10.01 00:00'; //--- estableciendo los parámetros de optimización STR_OPT_PARS optpar; optpar.ref.start = 15; optpar.ref.step = 5; optpar.ref.stop = 510; optpar.sl.start = 15; optpar.sl.step = 5; optpar.sl.stop = 510; optpar.flags=15; optpar.tp=50; optpar.timeout=12*3600; //--- estructura de los resultados STR_TEST_RESULT res; //--- iniciando optimización tpat.Optimize(res,from,to,optpar); STR_ERROR oclerr=tpat.GetLastErrorExt(); if(oclerr.code) { Print(oclerr.comment); Print("code = ",oclerr.code,", function = ",oclerr.function,", line = ",oclerr.line); return; } //--- valores de los parámetros optimizados Print("Ref: ",optpar.ref.value,", SL: ",optpar.sl.value); //--- resultados de la simulación Print("Net Profit: ", res.net_profit); Print("Gross Profit: ", res.gross_profit); Print("Gross Loss: ", res.gross_loss); Print("Trades Total: ", res.trades_total); Print("Profit Trades: ",res.profit_trades); Print("Loss Trades: ", res.loss_trades); //--- estadísticas de la ejecución COCLStat ocl_stat=tpat.GetStat(); Print("GPU memory size: ", ocl_stat.gpu_mem_size.ToStr()); Print("GPU memory usage: ", ocl_stat.gpu_mem_usage.ToStr()); Print("Buffering: ", ocl_stat.time_buffering.ToStr()); Print("OpenCL init: ", ocl_stat.time_ocl_init.ToStr()); Print("OpenCL buffering: ", ocl_stat.time_ocl_buf.ToStr()); Print("OpenCL prepare orders: ", ocl_stat.time_ocl_orders.ToStr()); Print("OpenCL test: ", ocl_stat.time_ocl_test.ToStr()); Print("OpenCL total execution: ",ocl_stat.time_ocl_exec.ToStr()); Print("Post-processing: ", ocl_stat.time_proc.ToStr()); Print("Total: ", ocl_stat.time_total.ToStr()); }
Hemos puesto los mismos parámetros de entrada que hemos usado al optimizar en el simulador estándar. Iniciamos:
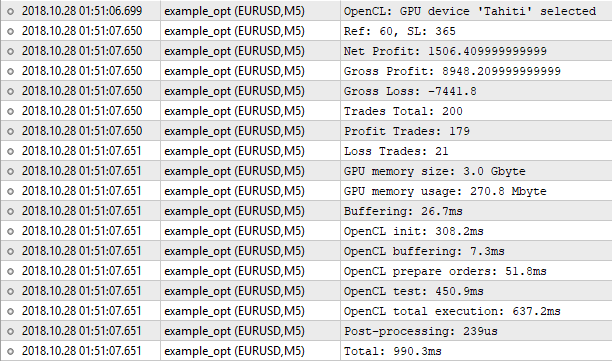
Fig. 9. Optimización en el simulador OpenCL
Podemos ver que los resultados no coinciden en absoluto con los encontrados por el simulador estándar. ¿Por qué ha sucedido eso? ¿Acaso es posible que la pérdida de precisión al convertir de double a int y viceversa haya jugado un papel decisivo? En teoría, si los resultados se diferenciasen en fracciones tras la coma, esto podría suceder. Pero los resultados se han diferenciado sustancialmente.
El simulador estándar ha encontrado los valores Ref = 60 y SL = 350 con un beneficio neto de 1000.50. Nuestro OpenCL ha encontrado los valores Ref = 60 y SL = 365 con un beneficio neto de 1506.40. Intentemos iniciar el simulador estándar con los valores que ha encontrado el simulador OpenCL:

Fig. 10. Comprobación de los resultados de optimización encontrados por el simulador OpenCL
El resultado es muy semejante al nuestro. Entonces, no se trata de una pérdida de precisión. Es el algoritmo genético el que ha omitido esta combinación de parámetros optimizados. Iniciamos el simulador incorporado en el modo de optimización lenta, con la iteración de parámetros completa.
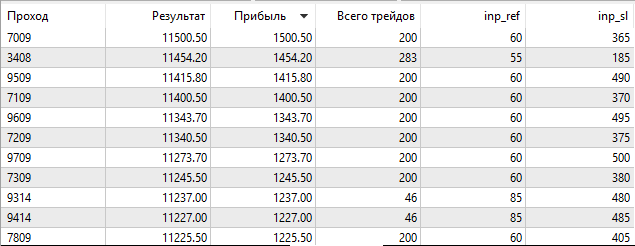
Fig. 11. Inicio del simulador de estrategias incorporado en el modo de optimización lenta
Podemos ver que en el modo de iteración de parámetros completa, el simulador incorporado ha encontrado los mismos valores buscados Ref = 60 y SL = 365 que nuestro simulador OpenCL. Esto significa que el algoritmo de optimización implementado por nosotros funciona correctamente.
3. Comparando el rendimiento
Ha llegado el momento de comparar el rendimiento del simulador estándar y el simulador implementado con el uso de OpenCL.
Compararemos el gasto de tiempo en la optimización de los parámetros de la estrategia descrita más arriba. Iniciaremos el simulador incorporado en dos modos: optimización rápida (algoritmo genético) y lenta (iteración de parámetros completa). El inicio se realizará en un PC con las siguientes características:
| Sistema operativo | Windows 10 (build 17134) x64 |
| Procesador | AMD FX-8300 Eight-Core Processor, 3600MHz |
| RAM | 24574 Mb |
| Tipo de media en la que está instalado MetaTrader | HDD |
Para los agentes de simulación se han reservado 6 núcleos de 8.
El simulador OpenCL se iniciará en una tarjeta de vídeo AMD Radeon HD 7950 con una capacidad de memoria de 3Gb y una frecuencia de GPU 800Mhz.
Realizaremos la optimización con tres parejas de divisas: EURUSD, GBPUSD y USDJPY. En esta caso, además, la ejecutaremos en cada pareja con cuatro intervalos temporales para cada uno de los modos de optimización. Usaremos las siguientes abreviaturas para ellos:
| Modo de optimización | Descripción |
|---|---|
| Tester Fast | Simulador de estrategias incorporado, algorítmo genético |
| Tester Slow | Simulador de estrategias incorporado, iteración de parámetros completa |
| Tester OpenCL | Simulador implementado con la ayuda de OpenCL |
Designación de los intervalos de simulación:
| Periodo | Intervalo de fechas |
|---|---|
| 1 mes | 2018.09.01 - 2018.10.01 |
| 3 meses | 2018.07.01 - 2018.10.01 |
| 6 meses | 2018.04.01 - 2018.10.01 |
| 9 meses | 2018.01.01 - 2018.10.01 |
De los resultados obtenidos, para nosotros serán importantes los valores de los parámetros buscados, la magnitud del beneficio neto, el número de transacciones y el tiempo invertido en la optimización.
3.1. Optimizando con la pareja EURUSD
Periodo H1, 1 mes:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 15 | 15 | 15 |
| Stop Loss | 330 | 510 | 500 |
| Beneficio neto | 942.5 | 954.8 | 909.59 |
| Número de transacciones | 48 | 48 | 47 |
| Duración de la optimización | 10 seg | 6 min 2 seg | 405.8 ms |
Periodo H1, 3 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 50 | 65 | 70 |
| Stop Loss | 250 | 235 | 235 |
| Beneficio neto | 1233.8 | 1503.8 | 1428.35 |
| Número de transacciones | 110 | 89 | 76 |
| Duración de la optimización | 9 seg | 8 min 8 seg | 457.9 ms |
Periodo H1, 6 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 15 | 20 | 20 |
| Stop Loss | 455 | 435 | 435 |
| Beneficio neto | 1641.9 | 1981.9 | 1977.42 |
| Número de transacciones | 325 | 318 | 317 |
| Duración de la optimización | 15 seg | 11 min 13 seg | 405.5 ms |
Periodo H1, 9 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 15 | 15 | 15 |
| Stop Loss | 440 | 435 | 435 |
| Beneficio neto | 1162.0 | 1313.7 | 1715.77 |
| Número de transacciones | 521 | 521 | 520 |
| Duración de la optimización | 20 seg | 16 min 44 seg | 438.4 ms |
Periodo M5, 1 mes:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 135 | 45 | 45 |
| Stop Loss | 270 | 205 | 205 |
| Beneficio neto | 47 | 417 | 419.67 |
| Número de transacciones | 1 | 39 | 39 |
| Duración de la optimización | 7 seg | 9 min 27 seg | 418 ms |
Periodo M5, 3 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 120 | 70 | 70 |
| Stop Loss | 440 | 405 | 405 |
| Beneficio neto | 147 | 342 | 344.85 |
| Número de transacciones | 3 | 16 | 16 |
| Duración de la optimización | 11 seg | 8 min 25 seg | 585.9 ms |
Periodo M5, 6 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 85 | 70 | 70 |
| Stop Loss | 440 | 470 | 470 |
| Beneficio neto | 607 | 787 | 739.6 |
| Número de transacciones | 22 | 47 | 46 |
| Duración de la optimización | 21 seg | 12 min 03 seg | 796.3 ms |
Periodo M5, 9 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 60 | 60 | 60 |
| Stop Loss | 495 | 365 | 365 |
| Beneficio neto | 1343.7 | 1500.5 | 1506.4 |
| Número de transacciones | 200 | 200 | 200 |
| Duración de la optimización | 20 seg | 16 min 44 seg | 438.4 ms |
3.2. Optimizando con la pareja GBPUSD
Periodo H1, 1 mes:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 175 | 90 | 90 |
| Stop Loss | 435 | 185 | 185 |
| Beneficio neto | 143.40 | 173.4 | 179.91 |
| Número de transacciones | 3 | 13 | 13 |
| Duración de la optimización | 10 seg | 4 min 33 seg | 385.1 ms |
Periodo H1, 3 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 175 | 145 | 145 |
| Stop Loss | 225 | 335 | 335 |
| Beneficio neto | 93.40 | 427 | 435.84 |
| Número de transacciones | 13 | 19 | 19 |
| Duración de la optimización | 12 seg | 7 min 37 seg | 364.5 ms |
Periodo H1, 6 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 165 | 170 | 165 |
| Stop Loss | 230 | 335 | 335 |
| Beneficio neto | 797.40 | 841.2 | 904.72 |
| Número de transacciones | 31 | 31 | 32 |
| Duración de la optimización | 18 seg | 11 min 3 seg | 403.6 ms |
Periodo H1, 9 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 165 | 165 | 165 |
| Stop Loss | 380 | 245 | 245 |
| Beneficio neto | 1303.8 | 1441.6 | 1503.33 |
| Número de transacciones | 74 | 74 | 75 |
| Duración de la optimización | 24 seg | 19 min 23 seg | 428.5 ms |
Periodo M5, 1 mes:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 335 | 45 | 45 |
| Stop Loss | 450 | 485 | 485 |
| Beneficio neto | 50 | 484.6 | 538.15 |
| Número de transacciones | 1 | 104 | 105 |
| Duración de la optimización | 12 seg | 9 min 42 seg | 412.8 ms |
Periodo M5, 3 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 450 | 105 | 105 |
| Stop Loss | 440 | 240 | 240 |
| Beneficio neto | 0 | 220 | 219.88 |
| Número de transacciones | 0 | 16 | 16 |
| Duración de la optimización | 15 seg | 8 min 17 seg | 552.6 ms |
Periodo M5, 6 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 510 | 105 | 105 |
| Stop Loss | 420 | 260 | 260 |
| Beneficio neto | 0 | 220 | 219.82 |
| Número de transacciones | 0 | 23 | 23 |
| Duración de la optimización | 24 seg | 14 min 58 seg | 796.5 ms |
Periodo M5, 9 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 185 | 195 | 185 |
| Stop Loss | 205 | 160 | 160 |
| Beneficio neto | 195 | 240 | 239.92 |
| Número de transacciones | 9 | 9 | 9 |
| Duración de la optimización | 25 seg | 20 min 58 seg | 4.4 ms |
3.3. Optimizando con la pareja USDJPY
Periodo H1, 1 mes:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 60 | 50 | 50 |
| Stop Loss | 425 | 510 | 315 |
| Beneficio neto | 658.19 | 700.14 | 833.81 |
| Número de transacciones | 18 | 24 | 24 |
| Duración de la optimización | 6 seg | 4 min 33 seg | 387.2 ms |
Periodo H1, 3 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 75 | 55 | 55 |
| Stop Loss | 510 | 510 | 460 |
| Beneficio neto | 970.99 | 1433.95 | 1642.38 |
| Número de transacciones | 50 | 82 | 82 |
| Duración de la optimización | 10 seg | 6 min 32 seg | 369 ms |
Periodo H1, 6 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 150 | 150 | 150 |
| Stop Loss | 345 | 330 | 330 |
| Beneficio neto | 273.35 | 287.14 | 319.88 |
| Número de transacciones | 14 | 14 | 14 |
| Duración de la optimización | 17 seg | 11 min 25 seg | 409.2 ms |
Periodo H1, 9 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 190 | 190 | 190 |
| Stop Loss | 425 | 510 | 485 |
| Beneficio neto | 244.51 | 693.86 | 755.84 |
| Número de transacciones | 16 | 16 | 16 |
| Duración de la optimización | 24 seg | 17 min 47 seg | 445.3 ms |
Periodo M5, 1 mes:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 30 | 35 | 35 |
| Stop Loss | 225 | 100 | 100 |
| Beneficio neto | 373.60 | 623.73 | 699.79 |
| Número de transacciones | 53 | 35 | 35 |
| Duración de la optimización | 7 seg | 4 min 34 seg | 415.4 ms |
Periodo M5, 3 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 45 | 40 | 40 |
| Stop Loss | 335 | 250 | 250 |
| Beneficio neto | 1199.34 | 1960.96 | 2181.21 |
| Número de transacciones | 71 | 99 | 99 |
| Duración de la optimización | 12 seg | 8 min | 607.2 ms |
Periodo M5, 6 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 130 | 40 | 40 |
| Stop Loss | 400 | 130 | 130 |
| Beneficio neto | 181.12 | 1733.9 | 1908.77 |
| Número de transacciones | 4 | 229 | 229 |
| Duración de la optimización | 19 seg | 12 min 31 seg | 844 ms |
Periodo M5, 9 meses:
| Resultado | Tester Fast | Tester Slow | Tester OpenCL |
|---|---|---|---|
| Reference | 35 | 30 | 30 |
| Stop Loss | 460 | 500 | 500 |
| Beneficio neto | 3701.30 | 5612.16 | 6094.31 |
| Número de transacciones | 681 | 1091 | 1091 |
| Duración de la optimización | 34 seg | 18 min 56 seg | 1 seg |
3.4. Recuadro resumido del rendimiento
Partiendo de los resultados obtenidos, se puede ver que el simulador estándar en el modo de optimización rápida (algoritmo genético) omite con frecuencia los mejores resultados. Por eso, sería más justo comparar el rendimiento con respecto al simulador OpenCL en el modo de iteración de parámetros completa. Para que resulte más visual, crearemos un recuadro que resuma el gasto de tiempo en la optimización.
| Condiciones de optimización | Tester Slow | Tester OpenCL | Ratio |
|---|---|---|---|
| EURUSD, H1, 1 mes | 6 min 2 seg | 405.8 ms | 891 |
| EURUSD, H1, 3 meses | 8 min 8 seg | 457.9 ms | 1065 |
| EURUSD, H1, 6 meses | 11 min 13 seg | 405.5 ms | 1657 |
| EURUSD, H1, meses | 16 min 44 seg | 438.4 ms | 2292 |
| EURUSD, M5, 1 mes | 9 min 27 seg | 418 ms | 1356 |
| EURUSD, M5, 3 meses | 8 min 25 seg | 585.9 ms | 861 |
| EURUSD, M5, 6 meses | 12 min 3 seg | 796.3 ms | 908 |
| EURUSD, M5, 9 meses | 17 min 39 seg | 1 seg | 1059 |
| GBPUSD, H1, 1 mes | 4 min 33 seg | 385.1 ms | 708 |
| GBPUSD, H1, 3 meses | 7 min 37 seg | 364.5 ms | 1253 |
| GBPUSD, H1, 6 meses | 11 min 3 seg | 403.6 ms | 1642 |
| GBPUSD, H1, 9 meses | 19 min 23 seg | 428.5 ms | 2714 |
| GBPUSD, M5, 1 mes | 9 min 42 seg | 412.8 ms | 1409 |
| GBPUSD, M5, 3 meses | 8 min 17 seg | 552.6 ms | 899 |
| GBPUSD, M5, 6 meses | 14 min 58 seg | 796.4 ms | 1127 |
| GBPUSD, M5, 9 meses | 20 min 58 seg | 970.4 ms | 1296 |
| USDJPY, H1, 1 mes | 4 min 33 seg | 387.2 ms | 705 |
| USDJPY, H1, 3 meses | 6 min 32 seg | 369 ms | 1062 |
| USDJPY, H1, 6 meses | 11 min 25 seg | 409.2 ms | 1673 |
| USDJPY, H1, 9 meses | 17 min 47 seg | 455.3 ms | 2396 |
| USDJPY, M5, 1 mes | 4 min 34 seg | 415.4 ms | 659 |
| USDJPY, M5, 3 meses | 8 min | 607.2 ms | 790 |
| USDJPY, M5, 6 meses | 12 min 31 seg | 844 ms | 889 |
| USDJPY, M5, 9 meses | 18 min 56 seg | 1 seg | 1136 |
Conclusión
En este artículo hemos implementado el algoritmo de construcción de un simulador con una estrategia comercial sencilla que usa OpenCL. No hay duda de que esta implementación es solo una de las posibles soluciones, y tiene multitud de defectos. Entre ellos:
- El trabajo en el modo OHLC en M1, que solo sirve para una valoración en bruto
- No se tienen en cuenta swaps y comisiones
- Trabajo incorrecto con los cursos cruzados
- No hay trailing stop
- No se tiene en cuenta el número de posiciones abiertas simultáneamente
- Entre los parámetros retornados no existe el valor de reducción
No obstante, este algoritmo puede ayudar considerablemente en los casos en los que hay que valorar de forma rápida y general la capacidad de trabajo de los patrones sencillos, porque permite hacer esto miles de veces más rápido que el simulador incorporado iniciado en el modo de iteración de parámetros completa, y decenas de veces más rápido que el simulador que usa el algoritmo genético.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/4236
 Reversión: creando un punto de entrada y escribiendo un algoritmo de comercio manual
Reversión: creando un punto de entrada y escribiendo un algoritmo de comercio manual
 WebRequest multiflujo asincrónico en MQL5
WebRequest multiflujo asincrónico en MQL5
 Las 100 mejores pasadas de optimización (Parte 1). Creando un analizador de optimizaciones
Las 100 mejores pasadas de optimización (Parte 1). Creando un analizador de optimizaciones
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso