Métodos de ordenamiento y su visualización a través de MQL5

Contenido

• Introducción
• Aplicación de la librería Graphics\Graphic.mqh
• Funciones de intercambio, comparación y límites
• Métodos del ordenamiento
•   Ordenamiento por selección
•   Ordenamiento por inserción
•   Ordenamiento de burbuja
•   Ordenamientos rápidos
•   Ordenamiento por mezcla
•   Ordenamiento piramidal
•   Ordenamientos por el tiempo lineal MSD y LSD
•   Otros tipos de ordenamientos
• Tabla sumaria de la velocidad de los métodos
• Todos los métodos en una pantalla
• Testeamos multihilo
• Observaciones de los redactores del artículo
  

Introducción

En la Red se puede encontrar una serie de videos con demostración de diferentes tipos de ordenamientos. Por ejemplo, aquí tiene la visualización de 24 algoritmos de ordenación. He cogido este video como base, junto con la lista de los algoritmos de ordenación.

Para trabajar con los gráficos, en MQL5 ha sido desarrollada una librería especial— Graphic.mqh. Ya ha sido descrita en los artículos: en particular, aquí se cuenta detalladamente sobre las posibilidades de la librería. Mi tarea consiste en describir sus puntos de aplicación práctica, así como contar detalladamente sobre los mismos ordenamientos. Existe por lo menos un artículo separado para cada tipo de ordenamiento, y para algunos de ellos ya has sido publicadas las investigaciones completas, por eso describiré sólo la idea general.

Aplicación de la librería Graphics\Graphic.mqh

El trabajo con la librería empieza con su conexión.

#include <Graphics\Graphic.mqh>

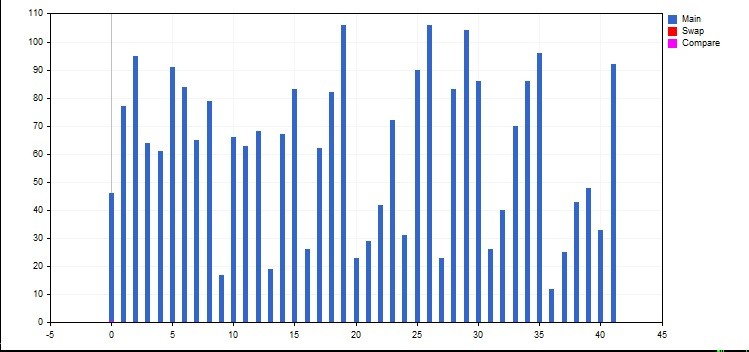
Nosotros vamos a ordenar las columnas del histograma, para eso usaremos la función de intercambio Gswap() y de comparación GBool(). Los elementos con los que van a realizarse las operaciones (comparación, sustitución, etc) se resaltan con color. Para eso, a cada color se le asignará un objeto separado tipo CCurve (curva). Con el fin de no redistribuir estos objetos por las funciones Gswap (int i, int j, CGraphic &G, CCurve &A, CCurve &B, CCurve &C), hagamos que sean globales. La clase CCurve no tiene constructor por defecto, por eso no se podrá declararla como global. Por lo tanto, declararemos los punteros tipo CCurve *CMain como globales.

Hay tres maneras diferentes para establecer el color. El más ilustrativo de ellas es C'0x00,0x00,0xFF', o C'Blue, Green, Red'. La curva se crea a través del método de la clase CGraphic CurveAdd(), que tiene varias implementaciones. Para la mayor parte de los elementos conviene elegir CurveAdd(arr, CURVE_HISTOGRAM, "Main") con un solo array de valores; para los elementos auxiliares, conviene CurveAdd(X, Y, CURVE_HISTOGRAM, "Swap") con el array de argumentos X y array de valores, ya que habrá sólo dos elementos. Los arrays para las líneas auxiliares conviene hacerlos globales.

#include <Graphics\Graphic.mqh> 
                               
#property script_show_inputs
input int N  =42;

CGraphic Graphic;
CCurve *CMain;
CCurve *CGreen;
CCurve *CBlue;
CCurve *CRed;
CCurve *CViolet;

double X[2],Y[2],XZ[2],YZ[2];

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   //arrays------------------------------  
   double arr[];
   FillArr(arr,N);
   X[0]=0;X[1]=0;
   Y[0] =0;Y[1]=0;
   //-------------------------------------
   Graphic.Create(0,"G",0,30,30,780,380);

   CMain =Graphic.CurveAdd(arr,CURVE_HISTOGRAM,"Main"); //index 0
   CMain.HistogramWidth(4*50/N);

   CBlue  =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Pivot"); //index 1
   CBlue.Color(C'0xFF,0x00,0x00');
   CBlue.HistogramWidth(4*50/N);

   CRed  =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Swap"); //index 2
   CRed.Color(C'0x00,0x00,0xFF');
   CRed.HistogramWidth(4*50/N);

   CGreen  =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Borders"); //index 3
   CGreen.Color(C'0x00,0xFF,0x00');
   CGreen.HistogramWidth(4*50/N);

   CViolet  =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Compare"); //index 4
   CViolet.Color(C'0xFF,0x00,0xFF');
   CViolet.HistogramWidth(4*50/N);

   Graphic.XAxis().Min(-0.5);

   Graphic.CurvePlot(4);
   Graphic.CurvePlot(2);
   Graphic.CurvePlot(0);
  //Graphic.CurvePlotAll(); simplemente mostrar todas las curvas existentes
   Graphic.Update();

   Sleep(5000);
   int f =ObjectsDeleteAll(0);
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void FillArr(double &arr[],int num)
  {
   int x =ArrayResize(arr,num);
   for(int i=0;i<num;i++)
     arr[i]=rand()/328+10; 
  }

Graphic.XAxis().Min(-5) establece los márgenes desde el eje de ordenadas para que el elemento cero no se converja con él. Histogramwidth() es el ancho de la columna.

La función FillArr() rellena los arrays con números aleatorios de 10 (para no convergerse con el eje de abscisas) a 110. El array arr está hecho como local para que las funciones del intercambio tengan una apariencia estándar swap(arr, i, j). El último comando ObjectDeleteAll borra los que hemos dibujado. De los contrario, tendremos que eliminar el objeto a través del menú «Lista de objetos», Ctrl+B.  

Nuestra plantilla está terminada, se puede pasar al ordenamiento.

Funciones de intercambio, comparación y límites

Vamos a escribir las funciones para visualizar el intercambio, comparación y selección de los límites para los ordenamientos por división. La primera función de intercambio void Gswap() es estándar, pero con adición de la curva CRed para seleccionar los elementos a comparar.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void Gswap(double &arr[],int i, int j)
  {
   X[0]=i;X[1]=j;
   Y[0] =arr[i];Y[1] =arr[j];
   CRed.Update(X,Y);
   Graphic.Redraw();
   Graphic.Update();
   Sleep(TmS);

   double sw = arr[i];
   arr[i]=arr[j];
   arr[j]=sw;

   //-------------------------
   Y[0] =0;
   Y[1] =0;
   CRed.Update(X,Y);
   CMain.Update(arr);
   Graphic.Redraw();
   Graphic.Update();
  //-------------------------
  }

Primero, seleccionamos las columnas, luego, pasado un tiempo Sleep(TmS) que determina la velocidad de la demostración, devolvemos el estado inicial. De la misma manera, escribimos las funciones de comparación para "<" y "<=" en forma de bool GBool(double arr, int i, int j) y GBoolEq(double arr, int i, int j). Ahí añadimos las columnas de otro color CViole.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool GBool(double &arr[], int i, int j)
  {
   X[0]=i;X[1]=j;
   Y[0] =arr[i];Y[1] =arr[j];
   CViolet.Update(X,Y);
   Graphic.Redraw();
   Graphic.Update();
   Sleep(TmC);
   Y[0]=0;
   Y[1]=0;
   CViolet.Update(X,Y);
   Graphic.Redraw();
   Graphic.Update();
   return arr[i]<arr[j];
  }

Es la función para seleccionar los límites cuyas columnas no hace falta borrar.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void GBorders(double &a[],int i,int j)
  {
   XZ[0]=i;XZ[1]=j;
   YZ[0]=a[i];YZ[1]=a[j];
   CGreen.Update(XZ,YZ);
   Graphic.Redraw();
   Graphic.Update();
  }

Ahora pasaremos directamente a los propios ordenamientos.

Métodos del ordenamiento 

Antes de empezar a analizar los métodos, le recomendaría iniciar el programa VisualSort que se encuentra en el archivo adjunto VisualSort.ex5. Permitirá observar visualmente cómo funciona cada ordenamiento por separado. El código completo de los ordenamientos se encuentra en el archivo adjunto GSort.mqh. Ha salido bastante extenso, por eso aquí he descrito solamente las ideas principales.

• El primer ordenamiento con el que habitualmente comienza el estudio es el ordenamiento por selección (Selection sort). Buscamos el valor mínimo en la lista actual y lo intercambiamos con el valor de la primera posición no ordenada. 

template <typename T>
void Select(T &arr[])
  {
   int n = ArraySize(arr);
   for(int j=0;j<n;j++)
     {
      int mid=j;
      for(int i=j+1;i<n;i++)
        {   
         if(arr[i]<arr[mid])
          {
           mid=i;
          }   
        }
      if(arr[j]>arr[mid]){swap(arr,j,mid);}
     }
  }

Aquí en adelante, la función de intercambio se representa por las funciones Gswap() que hemos escrito antes, y la comparación de los elementos del array luego se sustituye por GBool(). Por ejemplo, if(arr[i]<arr[mid]) => if(GBool(arr,i,mid).

• El siguiente ordenamiento (que por cierto, se utiliza a menudo durante el juego a los naipes) es el ordenamiento por inserción. En este método, los elementos de la sucesión de entrada se revisan uno por uno, y cada nuevo elemento entrante se coloca en el lugar óptimo entre los ordenados anteriormente. Método básico:

template<typename T>
void Insert(T &arr[])
  {
   int n= ArraySize(arr);
   for(int i=1;i<n;i++)
     {
      int j=i;
      while(j>0)
        {
         if(arr[j]<arr[j-1])
           {
            swap(arr,j,j-1);
            j--;
           }
         else j=0;   
        }
      }
  }

Los derivados de este ordenamiento es el ordenamiento de Shell (Shell Sort) y el ordenamiento por inserción binaria (Binary Insertion Sort). La idea del método Shell consiste en la comparación de los elementos que se encuentran no simplemente uno al lado del otro, sino a una determinada distancia. En otras palabras, se trata del ordenamiento por inserción con unos recorridos preliminares «ordinarios». Binary Insertion utiliza la búsqueda binaria para buscar los lugares de inserción. En la demostración arriba mencionada (VisualSort.ex5), se ve perfectamente como Shell «va peinando» poco a poco el array usando el peine más pequeño. En este sentido, parece al método Comb descrito más abajo.

• El ordenamiento por burbuja y sus derivados — el ordenamiento por el método de sacudida (Shake Sort), ordenamiento Gnome (Gnom), ordenamiento Peine (Comb) y Odd-Even Sort. La idea del ordenamiento de burbuja es simple: recorremos el array del principio al final y comparamos dos elementos cercanos. Si no están ordenados, los alteramos. Al final de cada iteración, el elemento mayor va a encontrarse al final del array. Luego, el proceso se repite, y al final obtenemos un array completamente ordenado. Es el algoritmo básico del ordenamiento de burbuja:

template<typename T>
void BubbleSort(T &a[])
  {
   int n =ArraySize(a);  
   for (int i = 0; i < n - 1; i++)
     {
      bool swapped = false;
      for (int j = 0; j < n - i - 1; j++)
        {
         if (a[j] > a[j + 1])
          {
           swap(a,j,j+1);
           swapped = true;                                        
          }
        }
     if (!swapped)
       break;
    }
 }

En caso del ordenamiento por sacudida, los recorridos se realizan en ambas direcciones, por eso «emergen» no sólo los elementos grandes, sino también «se asientan» los pequeños. El ordenamiento Gnome es interesante por el hecho de que está implementada sólo por un ciclo. Éste es su código:

void GGnomeSort(double &a[])
  {
   int n =ArraySize(a);
   int i=0;
   while(i<n)
     {
      if(i==0||GBoolEq(a,i-1,i))
        i++; //if(i==0||a[i-1]<a[i])
      else
        {
         Gswap(a,i,i-1); //Intercambio a[i] y a[i-1]
         i--;
        }      
     }
   }

Si marcamos el lugar de los elementos ya ordenados, obtendremos el ordenamiento por inserción. Comb utiliza la misma idea que Shell: recorre el array con el peine con diferentes pasos. Incluso ha sido calculado el coeficiente óptimo de reducción para él = 1,247  ≈ ( 1 / ( 1-е^(-φ) ) ), donde е el exponente; φ es el número «de oro». En cuanto a la velocidad, Comb y Shell no ceden ante los ordenamientos rápidos en los arrays no muy grandes. Odd-Even Sort recorre alternativamente los elementos pares e impares. Puesto que ha sido ideado como ordenamiento para la implementación multihilo, en nuestro caso es absolutamente inútil. 

• Los métodos más complejos se basan en la técnica «divide y vencerás». Los ejemplos clásicos son los siguientes: ordenamiento Hoare u ordenamiento rápido

La idea general del algoritmo consiste en los siguiente: elegimos un elemento del array, al que llamaremos pivote (pivot). Puede ser cualquier elemento del array. Comparamos todos los demás elementos con el pivote y los resituamos de manera que a un lado queden todos los menores que el pivote, y al otro los mayores, separando así el array en dos segmentos continuos. Repetimos esta secuencia de operaciones de forma recursiva para cada segmento mientras éstos contengan más de un elemento. La idea principal consiste en el pseudocódigo:

 algorithm quicksort(A, lo, hi) is
 if (lo < hi)
   { 
    p = partition(A, lo, hi);
    quicksort(A, lo, p – 1);
    quicksort(A, p, hi);
   }

La diferencia de los variantes del ordenamiento en este caso se reduce a diferentes maneras de separación del array. En la versión original, los punteros van de lados opuestos al encuentro. El puntero izquierdo encuentra el elemento mayor que el pivote, y el puntero derecho, el menor, y ellos se intercambian. En otra versión, ambos punteros corren de izquierda a derecha. Cuando el primero encuentra el menor elemento, lo resitúa en la posición del segundo puntero. Para los casos, cuando en el array hay muchos elementos iguales, la división asigna sitio para los elementos iguales al pivote. Este esquema se aplica cuando es necesario ordenar por ejemplo a los empleados según sólo dos criterios, «H» y «M». El esquema de la división se muestra a continuación:

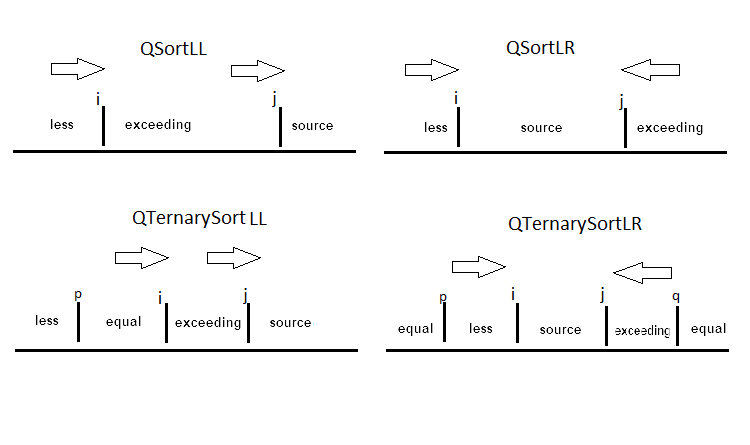
Como ejemplo, mostraré sólo QSortLR con la variante de la división Hoare:

//----------------------QsortLR----------------------------------------+
void GQsortLR(double &arr[],int l,int r)
  {
   if(l<r)
     {
      GBorders(arr,l,r);
      int mid =PartitionLR(arr,l,r);
      GQsortLR(arr,l,mid-1);
      GQsortLR(arr,mid+1,r);   
     }
  }

int PartitionLR(double &arr[],int l,int r)
  {
   int i =l-1;
   int j =r;
   for(;;)
     {
      while(GBool(arr,++i,r));
      j--; 
      while(GBool(arr,r,j)){if(j==l) break;j--;}
      if(i>=j) 
        break;
      Gswap(arr,i,j);
     }
//---------------------------------------------
 Gswap(arr,i,r);
 YZ[0]=0;YZ[1]=0;
 CGreen.Update(XZ,YZ);
 Graphic.Redraw();    
 Graphic.Update();
  
 return i;
}

En vez de dos partes, se puede dividir el array en 3, 4, 5, etc. con varios pivotes. Como opción se utiliza el ordenamiento DualPivot, con dos pivotes. 

• Otros métodos basados en la técnica «divide y vencerás» utilizan la mezcla de las partes ya ordenadas del array. Dividen el array hasta que alcance la longitud de 1, es decir, quede ordenado, luego se utiliza la función de la mezcla que también ordena los elementos. Principio general:

void GMergesort (double &a[], int l, int r)
  {
   int m = (r+l)/2;
   GMergesort(a, l, m); 
   GMergesort(a, m+1, r) ; 
   Merge(a, l, m, r);
  }

El ordenamiento BitonicSort() hace una mitad del array ascendiente, la otra, descendiente, luego las reúne.

• Ordenamiento con árbol (ordenamiento piramidal)

El principio general es el siguiente. Primero, formamos un «montón» a partir del array, usando el método de «tamización». Luego, eliminamos el elemento mayor que se encuentra en la cima del montón. Lo colocamos al final del array original como el mayor de todos, y situamos en su lugar el último elemento de la parte no ordenada. Construimos nuevo montón de tamaño n-1, etc. Los «montones» pueden construirse de acuerdo con los principios diferentes. Por ejemplo, el ordenamiento Smooth() utiliza los montones cuyo número de elementos es igual a los números de Leonardo L(x+2) = L(x+1) +L(x) +1.

• Ordenamientos por el tiempo lineal MSD y LSD Ordenamiento por cuentas y ordenamientos MSD y LSD

El ordenamiento por cuentas (Counting sort) es un algoritmo de ordenación en el que se utiliza el diapasón de los números del array a ordenar (lista) para calcular los elementos que coinciden. La aplicación del ordenamiento por cuentas resulta conveniente sólo cuando los números a enumerar tienen el intervalo de los valores posibles que es bastante pequeño en comparación con la cantidad a enumerar, por ejemplo, un millón de números naturales inferiores a 1000. Su principio se aplica en los ordenamientos por Radix. Aquí tiene su algoritmo:

void CountSort(double &a[])
  { 
   int count[];
   double aux[];
   int k =int(a[int(ArrayMaximum(a))]+1);
   int n =ArraySize(a);
   ArrayResize(count,k);
   ArrayResize(aux,n);  
   for (int i=0;i<k;i++) count[i] = 0; 
   for (int i=0;i<n;i++) count[int(a[i])]++;             // número de elementos iguales a i 
   for (int i=1;i<k;i++) count[i] = count[i]+count[i-1]; // número de elementos que no supera i
   for(int j=n-1;j>=0;j--) aux[--count[int(a[j])]]=a[j]; // llenamos el array intermedio 
   for(int i=0;i<n;i++)a[i]=aux[i];
  }

La idea del ordenamiento por cuentas se aplica en los ordenamientos MSD y LSD en el tiempo lineal. Se tiene en cuenta el tiempo N*R, donde N es la cantidad de los elementos, y R es la cantidad de los dígitos en la representación del número en el sistema numérico seleccionado.  MSD (most significant digit) ordena según el dígito más significativo, LSD (least significant digit), según el dígito menos significativo. Por ejemplo, en el sistema binario LSD contará cuántos números se terminan en 0, cuántos en 1, y luego en la primera mitad colocará los números pares (0), y en la segunda, los impares (1). MSD, al revés, empieza con el dígito más significativo. Si se coge el sistema decimal, primero colocará los números < 100, y luego >100. Luego, el array será ordenado en los segmentos 0-19, 10-19,..., 100-109, etc. Según este método, se ordenan los números enteros. Pero la cotización 1,12307 se puede hacerla entera, 1.12307*100 000.

Combinando el ordenamiento rápido y el ordenamiento Radix, obtenemos el ordenamiento rápido binario QuicksortB(). Aquí se aplica la división del ordenamiento QSortLR, la selección no se realiza por el povote (pivot) del array, sino por el dígito mayor. Para eso, aquí tanto en LSD como en MSD se usa la función de la búsqueda de la cifra del dígito n.

int digit(double x,int rdx,int pos) // Aquí x es el número, rdx es el sistema numérico
  {				    // en nuestro caso es 2, pos es el número del dígito 
   int mid =int(x/pow(rdx,pos));
   return mid%rdx;
  }

Primero, ocurre la división según el dígito mayor int d =int(log(a[ArrayMaximum(a)])/log(2)), luego recursivamente se ordenan las partes según los dígitos menores. Aparenta a QuickSortLR.

• Algunos ordenamientos específicos

El ordenamiento cíclico (Cycle Sort) está destinado para los sistemas donde la reescritura de datos provoca el desgaste de los recursos. Por consiguiente, el objetivo es encontrar un ordenamiento con el número menor posible de los intercambios (Gswap). Para eso, se usan los traslados cíclicos. Sumariamente, 1 se traslada en 3, 3 en 2, 2 en 1. Cada elemento se traslada 0 o 1 vez. Todo eso requiere bastante tiempo, O(n^2). Para más información, por favor, siga este enlace.

Ordenamiento vagante (Stooge sort). Es otro ejemplo de un ordenamiento artificial y muy lento. El algoritmo consiste en lo siguiente. Si el valor del elemento al final de la lista es menos que el valor del elemento al principio, hay que alternarlos. Si hay 3 o más elementos en el subconjunto de la lista, entonce: llamaremos recursivamente a Stoodge() para los primeros 2/3 de la lista, llamaremos recursivamente a Stoodge() par los últimos 2/3, volveremos a llamar recursivamente a Stoodge() para los primeros 2/3, etc.

Tabla sumaria de la velocidad de los métodos

Métodos del ordenamiento	Tiempo medio
Ordenamiento por selección (Selection sort)	O(n^2)
Ordenamiento por inserción (Insertion sort)	O(n^2)
Ordenamiento por inserción binaria (Binary Selection Sort)	O(n^2)
Ordenamiento Shell (Shell sort)	O(n*log(n))
Ordenamiento de burbuja (Bubble sort)	O(n^2)
Ordenamiento por sacudida (Shaker/Cocktail sort)	O(n^2)
Ordenamiento de Gnome (Gnom Sort)	O(n^2)
Ordenamiento por peine (Comb Sort)	O(n*log(n))
Ordenamiento por mezcla (Merge Sort)	O(n*log(n))
Ordenamiento bitónico (Bitonic sort)	O(n*log(n))
Ordenamiento piramidal (Heap sort)	O(n*log(n))
Ordenamiento suave (Smooth sort)	O(n*log(n))
Ordenamiento rápido(LR) (Quick sort LR)	O(n*log(n))
Ordenamiento rápido(LL) (Quick sort LL)	O(n*log(n))
Quick Sort (ternary, LR ptrs)	O(n*log(n))
Quick Sort (ternary, LL ptrs)	O(n*log(n))
Quick Sort (dual pivot)	O(n*log(n))
Ordenamiento por cuentas (Counting sort)	O(n+k)
Ordenamiento LSD (Radix LSD)	O(n*k)
Ordenamiento MSD (Radix MSD)	O(n*k)
Ordenamiento rápido binario (Quick Binary sort)	O(n*log(n))
Ordenamiento cíclico (Cycle sort)	O(n^2)
Stoodge sort	O(n^2.7)

Todos los métodos en una pantalla

Vamos a mostrar simultáneamente todos los ordenamientos descritos en la misma pantalla. En el video original, los ordenamientos analizados fueron iniciados uno por uno, luego todo eso fue montado en el editor de video. Pero el terminal de trading no cuenta con las capacidades de un estudio de video. Se puede solucionar este problema de varias maneras.

Variante №1.

Imitar multihilo. Hagamos la ejecución del ordenamiento en paralelo, para que después de cada comparación e intercambio se pueda salir de la función y pasar el turno a otra comparación, y luego volver a entrar en el mismo lugar. Considerando que no hay operador GOTO, la tarea se complica. Pues, por ejemplo, así será el ordenamiento sencillo por selección que hemos mostrado al principio:

void CSelect(double &arr[])
  {
   static bool ch;
   static int i,j,mid;
   int n =ArraySize(arr);

   switch(mark)
     {
      case 0:
        j=0;
        mid=j;
        i=j+1;
        ch =arr[i]<arr[mid];     
        if(ch)
          mid =i;
        mark =1; 
        return;     
        break;
  
      case 1:
        for(i++;i<n;i++)
          {   
          ch =arr[i]<arr[mid];
          mark =1;
          if(ch)
            mid=i;
          return;     
         }
       ch =arr[j]>arr[mid];
       mark=2;
       return;
       break;
          
     case 2:
       if(ch)
         {
          swap(arr,j,mid);
          mark=3;
          return;
         }
       for(j++;j<n;j++)
         { 
          mid=j;
          for(i=j;i<n;i++)
            {   
             ch =arr[i]<arr[mid];     
             if(ch)
               mid=i;
             mark =1;
             return;     
            }
         ch =arr[j]>arr[mid];
         mark =2;
         return;                               
        }
       break;
  
   case 3:
     for(j++;j<n;j++)
       { 
        mid=j;
        for(i=j;i<n;i++)
          {   
           ch =arr[i]<arr[mid];     
           if(ch)
             mid=i;
             mark =1;
           return;     
          }
        ch =arr[j]>arr[mid];
        mark=2;
        return;
       }
     break;   
    } 
   mark=10;
 }

Esta versión es bastante funcional. En este caso, el array será ordenado:

while(mark !=10)
  {
   CSelectSort(arr);
   count++;
  }

La variable count mostrará el número general de comparaciones y traslados. En este caso, el código ha crecido en 3-4 veces, y eso es un ordenamiento más simple. Hay otros ordenamientos compuestos de varias funciones, son recursivos...

Variante №2

Existe una opción más simple. En el terminal MQL5 se soporta el concepto multihilo. Para implementarlo, es necesario llamar el indicador personalizado desde el Asesor Experto para cada ordenamiento. Pero el indicador debe ser con un par de divisas diferente para cada hilo. En la ventana Observación de Mercado (Market Watch) debe haber suficientes instrumentos para cada ordenamiento.

n = iCustom(SymbolName(n,0),0,"IndcatorSort",...,SymbolName(n,0),Sort1,N);

Aquí SymbolName (n,0) es un instrumento separado para cada hilo y los parámetros que se traspasan en el indicador. Para fijar el nombre del objeto gráfico conviene usar SymbolName (n,0). En un gráfico puede haber sólo un objeto de la clase CGraphic con este nombre. El tipo del ordenamiento y el número de los elementos en el array, así como los tamaños del lienzo CGraphic no se muestran aquí.

En el indicador se realiza la selección de la función del ordenamiento y otras acciones adicionales relacionadas con el diseño (por ejemplo, firma de los ejes con el nombre del ordenamiento).

switch(SortName)
  {
   case 0:
     Graphic.XAxis().Name("Selection");   
     CMain.Name("Selection");Select(arr); break;
   case 1:
     Graphic.XAxis().Name("Insertion");
     CMain.Name("Insertion");Insert(arr);break;
   etc.............................................
  }

La creación de los objetos gráficos requiere un determinado tiempo. Por eso, para que los ordenamientos empiecen a trabajar simultáneamente, han sido añadidas las variables globales. NAME es una variable global con el nombre del instrumento que al principio tenía el valor 0. Después de la creación de todos los objetos necesarios, ella obtiene el valor 1, y después de la finalización del ordenamiento, obtiene el valor 2. Así, se puede seguir el momento del comienzo y de conclusión de ordenamientos. Para eso en el EA se arranca el temporizador:

void OnTimer()
  {
   double x =1.0;
   double y=0.0;
   static int start =0;
   for(int i=0;i<4;i++)
     {
      string str;
      str = SymbolName(i,0);
      x =x*GlobalVariableGet(str);
      y=y+GlobalVariableGet(str);
     }
  if(x&&start==0)
    {
     start=1;
     GlobalVariableSet("ALL",1);
     PlaySound("Sort.wav");
    }
  if(y==8) {PlaySound("success.wav"); EventKillTimer();}   
 }

Aquí la variable х capta el inicio, y la variable у , el final del proceso.

Al principio de la acción, se reproduce el sonido cogido del video original. Para trabajar con las fuentes, debe encontrarse en la carpeta MetaTrader/Sound junto con los demás sonidos de sistema en el formato *.wav o si se encuentra en otro lugar, hay que indicar la ruta a partir de la carpeta MQL5. Para terminar, se usa el archivo success.wav.

Pues bien, creamos el EA y el indicador. Asesor Experto:

enum SortMethod
  {
   Selection,
   Insertion,
   ..........Métodos de ordenamiento.........
  };

input int Xscale =475;          //Escala de la gráfica
input int N=64;                 //Número de elementos
input SortMethod Sort1;         //Método
..........Diferentes parámetros de entrada.................

int OnInit()
  {
   //--- Establecemos las variables globales, iniciamos el temporizador, etc.
   for(int i=0;i<4;i++)
     {
      SymbolSelect(SymbolName(i,0),1);
      GlobalVariableSet(SymbolName(i,0),0);}
      ChartSetInteger(0,CHART_SHOW,0);
      EventSetTimer(1);  
      GlobalVariableSet("ALL",0);
//.......................Abrimos un indicador hilo separado para cada ordenamiento.........
   x=0*Xscale-Xscale*2*(0/2);//serie con longitud 2
   y=(0/2)*Yscale+1;
   SymbolSelect(SymbolName(0,0),1); // Sin ella, en algunos símbolos puede surgir el  error    
   S1 = iCustom(SymbolName(0,0),0,"Sort1",0,0,x,y,x+Xscale,y+Yscale,SymbolName(0,0),Sort1,N);

   return(0);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ChartSetInteger(0,CHART_SHOW,1);
   EventKillTimer();
   int i =ObjectsDeleteAll(0);
   PlaySound("ok.wav");
   GlobalVariableSet("ALL",0);
   IndicatorRelease(Sort1);
   .......Todo lo que hay que eliminar......
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
   ...Vacío... 
  }
//+------------------------------------------------------------------+
void OnTimer()
  {
   ....Descripción arriba.... 
   }

Y su indicador:

#include <GSort.mqh>  //Activamos todos los ordenamientos escritos previamente
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+

..........Bloque de parámetros de entrada.....................................
input int SortName;         //method
int N=30;                   //number
......................................................................
int OnInit()
  {
   double arr[];
   FillArr(arr,N);                 //llenamos el array con números aleatorios  
   GlobalVariableSet(NAME,0);      //establecemos las variables globales  
  
   Graphic.Create(0,NAME,0,XX1,YY1,XX2,YY2);      //NAME — par de divisas
   Graphic.IndentLeft(-30);
   Graphic.HistoryNameWidth(0);
   CMain =Graphic.CurveAdd(arr,CURVE_HISTOGRAM,"Main"); //index 0
   CMain.HistogramWidth(2);

   CRed  =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Swap"); //index 1
   CRed.Color(C'0x00,0x00,0xFF');
   CRed.HistogramWidth(width);
   ......Diferentes parámetros gráficos..........................
   Graphic.CurvePlotAll();
   Graphic.Update();
   GlobalVariableSet(NAME,1);

   while(!GlobalVariableGet("ALL")); //Esperando a que todos los objetos gráficos se creen

   switch(SortName)
     {
      case 0:
        Graphic.XAxis().Name("Selection");   
        CMain.Name("Selection");GSelect(arr); break;
      .....Lista de ordenamientos..............................................
     }

   GlobalVariableSet(NAME,2);
   return INIT_SUCCEEDED;
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(...)
  {
   ..............Vacío........................
  }
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   Graphic.Destroy();
   delete CMain;
   delete CRed;
   delete CViolet;
   delete CGreen;
   ObjectDelete(0,NAME);
  }

Testeamos multihilo

Light.ex5 y Sort24.ex5 están listos para el trabajo del programa. Están compilados a través de los recursos y no requieren nada más. A la hora de trabajar con las fuentes, deben estar instalados en las carpetas correspondientes de los indicadores y sonidos.

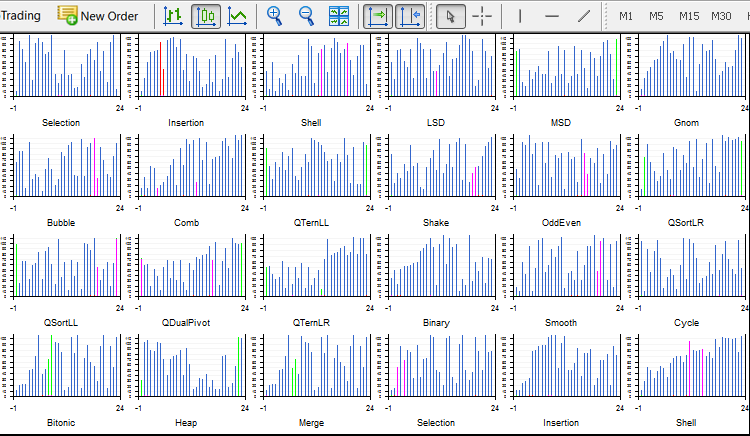
La versión Sort24.ex5 con 24 ordenamientos es inestable, termina el trabajo una de dos veces en mi ordenador de un solo núcleo. Hay que cerrar todo los que sobra y no tocar nada. En cada ordenamiento hay cinco objetos gráficos: cuatro curvas y un lienzo. Todos ellos se redibujan de forma incorrecta. 24 hilos crean 120 (!) objetos gráficos separados que van cambiando constantemente en 24 hilos. Lo he hecho como una presentación para demostrar que en principio es posible, y no he vuelto a trabajar con ella.

La versión Light.ex5 es funcional y bastante estable, muestra 4 ordenamientos al mismo tiempo. Aquí han sido añadidas las posibilidades de elegir el número de los elementos y los métodos de ordenamiento en cada ventana. Aparte de eso, existe la posibilidad de elegir el modo de barajar el array: aleatorio, ascendiente (es decir, ya ordenado), descendiente (ordenado en orden inverso) y el array que contiene muchos elementos iguales (step array). Por ejemplo, el ordenamiento rápido decae hasta O(n^2) en el array ordenado en orden inverso, mientras que el ordenamiento piramidal siempre ordenará en n*log(n). Lamentablemente, la función Sleep() no se soporta en los indicadores, así que la velocidad depende sólo del sistema. Además, la cantidad de recursos asignados a cada hilo también es aleatoria. Si iniciamos el mismo ordenamiento en cada ventana, no llegarán al final al mismo tiempo.

Resumiendo:

• VisualSort de un hilo es funcional a 100%
• Light de cuatro hilos es estable
• Sort24 de 24 hilos es inestable

Se podría seguir la primera opción, imitando el concepto de multihilo. Entonces, controlaríamos el proceso a 100%. Trabajarían las funciones Sleep(), cada ordenamiento tardaría el mismo tiempo, etc. Pero se perdería el propio concepto de la programación multihilo en MQL5.

La versión definitiva:

....................................................................................................................................................................

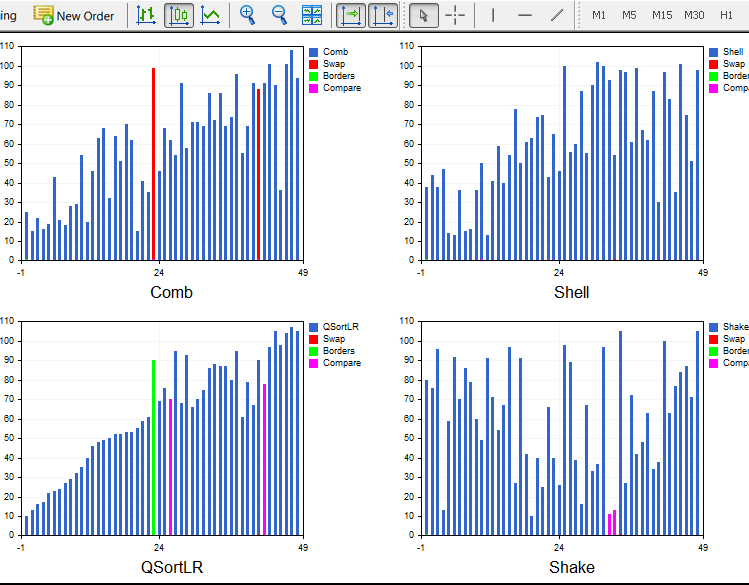
Lista de archivos adjuntos

• VisaulSort.ex5 - cada ordenamiento por separado
• Programs(Sort24.ex5, Light.ex5)  - programas hechos
• Archivos de sonido
• Codes. Códigos fuentes de los programas - ordenamientos, indicadores, archivos incluidos, Asesores Expertos.

Observaciones de los redactores del artículo

El autor del artículo ha implementado una versión interesante del ordenamiento multihilo usando el arranque simultáneo de varios indicadores. Esta arquitectura consume muchos recursos del ordenador, por eso hemos mejorado un poco los códigos fuente del autor, a saber:

• en el archivo auxiliary.mq hemos prohibido la llamada al redibujado del gráfico desde cada indicador
  

  //+------------------------------------------------------------------+
  //|                                                                  |
  //+------------------------------------------------------------------+
  void GBorders(double &a[],int i,int j)
    {
     XZ[0]=i;XZ[1]=j;
     YZ[0]=a[i]+2;YZ[1]=a[j]+5;
     CGreen.Update(XZ,YZ);
     Graphic.Redraw(false);
     Graphic.Update(false);
    }
  

• hemos añadido la función randomize() que prepara los mismos datos aleatorios en el array para todos los indicadores
• al archivo IndSort2.mq5 han sido añadidos los parámetros externos que establecen el tamaño del array con datos aleatorios (el autor la tiene estrictamente igual a 24) y el número inicializador sid para la generación de datos
  

  input uint sid=0;             //initialization of randomizer  
  int   N=64;                   //number of bars on histogramm
  

• al archivo Sort24.mq5 ha sido añadido el temporizador para el dibujado del gráfico usando ChartRedraw()
  

  //+------------------------------------------------------------------+
  //| Timer function                                                   |
  //+------------------------------------------------------------------+
  void OnTimer()
    {
     double x=1.0;
     double y=0.0;
     static int start=0;
  //--- comprobamos en el ciclo la bandera de inicialización de cada indicador
     for(int i=0;i<methods;i++)
       {
        string str;
        str=SymbolName(i,0);
        x=x*GlobalVariableGet(str);
        y=y+GlobalVariableGet(str);
       }
  //--- todos los indicadores se han inicializado con éxito
     if(x && start==0)
       {
        start=1;
        GlobalVariableSet("ALL",1);
        PlaySound("Sort.wav");
       }
  //--- todos los ordenamientos han terminado
     if(y==methods*2)
       {
        PlaySound("success.wav");
        EventKillTimer();
       }
  //--- actualizar los gráficos de ordenamientos
     ChartRedraw();
    }
  

• los archivos de sonido han sido trasladados a la carpeta <>\MQL5\Sounds para poder activarlos como recurso
  

  #resource "\\Sounds\\Sort.wav";
  #resource "\\Sounds\\success.wav";
  #resource "\\Indicators\\Sort\\IndSort2.ex5"
  

La estructura lista para la compilación se adjunta en el archivo moderators_edition.zip que sólo hay que descomprimir y copiar a su terminal. Si su ordenador no es muy potente, recomendamos establecer methods=6 o methods=12 en los parámetros de entrada.