
您应当知道的 MQL5 向导技术(第 14 部分):以 STF 进行多意向时间序列预测
概述
这篇关于时空融合(STF)的论文激起了我对这个主题的兴趣,这要归功于它的双边预测方式。作为复习者,该论文的灵感来自于解决一个基于概率的预测问题,譬如 Uber 和 Didi 等打车平台的供需双边如何协调。协调供需关系在各种双边市场中很常见,例如 Amazon、Airbnb 和 eBay,本质上,公司不仅为传统的“客户”或购买者服务,还要迎合客户的供应商。
故此,在供应侧部分依赖于需求的情况下,双边预测对这些公司来说可能很重要。诚然需求和供应的双重预测,某种意义上突破了预测时间序列或数据集特定值的传统方式。该论文还引入了所谓的因果论框架,其中供需之间的因果“协调”关系由矩阵 G 捕获,所有预测都是通过变换器网络进行的,其结果值得注意。
从中汲取灵感,我们看看通过使用看跌和看涨作为这两个度量的代理,来预测交易证券的供求关系。严格来说,尽管典型的智能信号类将这两个数值作为 0-100 范围内的整数计算,这正如从 MQL5 函数库文件、或迄今为止在本系列中我们的编码文件中所见。新内容将是,在我们进行预测时添加的空间矩阵和时间参数(我们从论文中引用的 2 个额外输入)。
交易证券的空间量化是主观的,而时间度量的选择亦如此。使用证券的最高价和最低价序列作为供需的锚点,我们将这些缓冲区之间的自相关值当作空间矩阵的坐标,并使用星期索引作为时间指标。这种可以定制和改进的基本方式,符合我们在本文中的目的。
该论文使用了变换器网络,我们不会用到它,因为它对于我们的目的来说效率低下,不过所有预报都将通过自定义的手动编码多层感知器进行。由于该主题有如此多的函数库和代码示例,尝试编写自己的多层感知器看似是浪费时间。然而,所用的网络类长度不到 300 行,且在自定义层数、和每层的规模方面具有合理的可扩展性,而这在大多数可用的样板库中仍然缺乏。
故此,通过使用单一神经网络,而非转换器,该论文的 causaltrans 框架无法在此实现。然而,我们仍有很多可以使用的东西,因为我们仍然会对需求和供应进行双重预测,且在此过程中还会用到空间矩阵和时间。如常,任何交易系统都存在固有的风险,因此欢迎读者在进一步使用此处分享的任何素材之前自行尽责调查。
STF 概述
STF 主要用于遥感和以视觉为中心的活动,于其中,空间和时间度量值可有机地结合。
如果您不太热衷于探索交易之外的 STF 潜力,那么您可以跳过本节,并继续 MQL5 实现。
举例,如果我们看看遥感,由卫星拍摄的图像捕捉到了受检数据和区域的空间分量,而时间则指图像拍摄时间。这些信息不仅可以形成时间序列,而且对于预测所研究地区的天气、植被、甚至动物栖息地的变化也很重要,这一切都归功于 STF。
我们一项项研究 STF 如何有助于解决森林砍伐和植被相关问题。第一步与机器学习的惯常问题一样,是数据收集。遥感卫星应在一段时间内捕获研究区域的多光谱图像。鉴于卫星是多光谱的,可以捕获肉眼不可见、但内含植被或水体等相关的波段内的反射和吸收波长信息。所有这些都增加了把数据建模成系列类型的丰富性(和复杂性),因为这些图像是在一段时间内捕获的。
空间数据集成后续如何,因为每张图像都自带时间戳,可用相应的 GPS 坐标系来映射每张图像,确保所有图像与其捕获时间点的空间信息一致性。
接下来将我们的“数据”常规化,确保其格式与植被和森林砍伐相关。达成这一目标的途径之一是按索引记录每张图像在不同时间点的光谱特征,如此这般数据不仅更容易经训练模型处理,而且还可以专注于手头的主题。
这种常规化还涉及对所捕获图像随时间的变化进行检测,以便可以提取或定义重要的植被特征,这些可能包括增长率、季节性变化、分布形态、等等。这些特征中的每一个都可以形成数据的一个维度。
模型训练之后会遵循这些,模型的选择可能会有变数,但人们会期望神经网络成为主要候选者。相当一部分图像(现在是已常规化的数据)将用于此目的,并保留较小的数据集用于测试,这种情况很典型。
故此,模型的预测将依据成功的训练和测试结果上进行,要记住的关键是解释,因为已经完成了很多常规化,有因于此必须小心模型输出的逆行。
在我们引用的最近由 ACM 收录的论文中,未来需求和供应的方程表述如下:
x v (t+δt) = f x (x v (t), G v (t), δt),
y v (t+δt) = f y (x v (t), y v (t), G v (t), δt),
其中:
- x v 是关于时间的需求函数,
- y v 是相对于时间的供应函数,
- G v 也是空间信息的向量或矩阵,
- δt 是进行预测的时间增量,
- t 是时间。
故此,在我们的例子中,函数 f x 和 f y 将是神经网络,其参数向量或矩阵持有馈送到各自输入层的数据。
利用 MQL5 实现 STF
为了利用 MQL5 实现 STF,我们将按照上面分享的方程来设定我们如何结构化输入数据以便建模。从这两个方程中可以清晰地看出,每个方程的输入数据通常采用向量或矩阵格式,当然这会带来无数的可能性、和挑战。两个方程中每个 f-函数的潜在输入都是相似的缓冲区,两个方程之间的唯一区别是供应方程不仅取决于其先前的值,还取决于需求值。这遵循了该论文作者的论点,即供应取决于需求,而不是相反。
故此,考虑到两个方程之间的重叠,缓冲区的总数为 4。这些都存在于供应方程中,它们如下列出:先前的需求、先前的供应、空间值、和时间增量。
在本文中,需求缓冲区被解释为“看涨”价格点的时间序列缓冲区。可以说,更简略的缓冲区可能是多头合约的真实交易量,但经纪商很少分享此类信息,即使他们分享了,鉴于外汇市场交易量信息的躁动性质,它也不能准确表示交易量。故此,选择最高价减去开盘价,作为真实多头交易量合约的替代缓冲。其它可以填补这一角色的可能缓冲区可能是特定货币的度量值,如利率、通货膨胀,甚至是央行货币供应指数。选择最高价减去开盘价作为缓冲,是为了衡量上行波动性,由于这可以理解为与多头交易量合约呈正相关,故它被用作下一个最佳代理。这些值只能为正数或零,零读数示意上吊线或横盘价格柱线。
供应缓冲区与上面的前身一样,也是按开盘价减去最低价来近似计算。这也可以被视为下行波动率的读数,它与看跌成交量合约呈正相关。同样,与上面一样,该缓冲区的值仅为正值,零值表示墓碑十字星或横盘柱线。供给方程与需求方程的不同之处在于它需要更多的输入,这意味着它的模型也会与需求相似、但亦有区别。故此,预测模型将有两个实例,一个针对需求,一个针对供应。由于我们的最终结果是获得单一信号,因此这将通过从需求预测中减去供应预测来判定。回想一下,综上所述,需求和供应模型的所有输入都是正数或零,故此,输出也理应如此,有因于此,通过从需求输出中减去供给模型输出,我们得到一个双精度数字,其正值表示看涨,其负值表示看跌。
时间缓冲区的选择很简单,就是星期几的索引。下一节中涵盖的测试将在日线时间帧内进行,如此星期几索引很容易与此相关。不过,如果要研究替代时间帧,例如低于日线时间帧,则可以考虑跨度在日内甚至周内的索引。举例,在 8-小时时间帧内,一个交易周内有 15 根 8-小时柱线,其提供了 15 个可能的周内时间索引。您可以选择日内时间或日内交易时段等等。此处的选择很多,也许更好的方式就是进行初步测试,从而选择最适合您的交易系统运转的方法。返回星期几索引的简单函数,如下:
//+------------------------------------------------------------------+ //| Temporal (Time) Indexing function | //+------------------------------------------------------------------+ int CSignalNetwork::T(datetime Time) { MqlDateTime _dt; if(TimeToStruct(Time,_dt)) { if(_dt.day_of_week==TUESDAY) { return(1); } else if(_dt.day_of_week==WEDNESDAY) { return(2); } else if(_dt.day_of_week==THURSDAY) { return(3); } else if(_dt.day_of_week==FRIDAY||_dt.day_of_week==SATURDAY) { return(4); } } return(0); }
G 矩阵捕获了我们模型的空间数据,这在定义时可能很棘手。我们如何定义证券交易环境中的空间?举例,如果我们研究参考论文,供需之间的元数据交叉表格经由论文所说的图形关注度转换器(GAT)来“常规化”。它们在两层进行操作:第一层捕获复杂的节点关系,第二层聚合相邻信息,以便进行最终节点预测。然后,GAT 读数成为通过相应神经网络馈送内容的一部分,用于预测需求或供应。在我们的例子中,我们的看涨和看跌价格缓冲区的元数据,将取自这些缓冲区分享的相关性读数。这些相关性的捕获方式如下面的代码所示:
//+------------------------------------------------------------------+ //| Spatial (Space) Indexing function. Returns Matrix Determinant | //| This however can be customised to return all matrix values as | //| a vector, depending on the detail required. | //+------------------------------------------------------------------+ double CSignalNetwork::G(vector &X,vector &Y) { matrix _m; if(X.Size()!=2*m_train_set||Y.Size()!=2*m_train_set) { return(0.0); } _m.Init(2,2); vector _x1,_x2,_y1,_y2; _x1.Init(m_train_set);_x1.Fill(0.0); _x2.Init(m_train_set);_x2.Fill(0.0); _y1.Init(m_train_set);_y1.Fill(0.0); _y2.Init(m_train_set);_y2.Fill(0.0); for(int i=0;i<m_train_set;i++) { _x1[i] = X[i]; _x2[i] = X[i+m_train_set]; _y1[i] = Y[i]; _y2[i] = Y[i+m_train_set]; } _m[0][0] = _x1.CorrCoef(_x2); _m[0][1] = _x1.CorrCoef(_y2); _m[1][0] = _y1.CorrCoef(_x2); _m[1][1] = _y1.CorrCoef(_y2); return(_m.Det()); }
注意,我们返回一个值,该值表述矩阵,而非其行列式的单个读数。也可以交替使用单个读数,因为相关值始终从 -1.0 到 +1.0 常规化,这可能会导致模型的整体结果更准确。尽管出于我们的目的,但我们坚持使用行列式,因为效率更重要,对于初步测试更是如此。
所有提到的 4 个数据缓冲区,或许这有助于谈论我们的基本模型,这是一个简单的神经网络,无需使用任何函数库即可编码。我们将网络分解为非常基本的组成部分:输入、权重、偏差、隐藏输出、输出和目标;并仅在进行前向验算和反向验算时才用到这些内容。我们的网络接口如下:
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ class Cnetwork { protected: matrix weights[]; vector biases[]; vector inputs; vector hidden_outputs[]; vector target; int hidden_layers; double Softplus(double X); double SoftplusDerivative(double X); public: vector output; void Get(vector &Target) { target.Copy(Target); } void Set(vector &Inputs) { inputs.Copy(Inputs); } bool Get(string File, double &Criteria, datetime &Version); bool Set(string File, double Criteria); void Forward(); void Backward(double LearningRate); void Cnetwork(int &Settings[],double InitialWeight,double InitialBias) { ... ... }; void ~Cnetwork(void) { }; };
除了用于设置和获取输入和目标的常用函数外,还包括一些训练之后导出权重和偏差的函数。前馈算法是普通的,在每一层都使用软加进行激活,而反向传播函数也是旧派,依赖于链式规则、和梯度下降方法来调整网络权重和偏差。初始化网络需要一些输入,这些输入在类实例可以安全使用之前需要经过“验证”。用来创建网络的输入是设置数组、初始权重值(整个网络)、以及初始偏差值。设置数组按其自身大小判定网络将具有的隐藏层数,其索引处的每个整数设置相应层的大小。
void Cnetwork(int &Settings[],double InitialWeight,double InitialBias) { int _size = ArraySize(Settings); if(_size >= 2 && _size <= USHORT_MAX && Settings[ArrayMinimum(Settings)] > 0 && Settings[ArrayMaximum(Settings)] < USHORT_MAX) { ArrayResize(weights, _size - 1); ArrayResize(biases, _size - 1); ArrayResize(hidden_outputs, _size - 2); hidden_layers = _size - 2; for(int i = 0; i < _size - 1; i++) { weights[i].Init(Settings[i + 1], Settings[i]); weights[i].Fill(InitialWeight); biases[i].Init(Settings[i + 1]); biases[i].Fill(InitialBias); if(i < _size - 2) { hidden_outputs[i].Init(Settings[i + 1]); hidden_outputs[i].Fill(0.0); } } output.Init(Settings[_size - 1]); target.Init(Settings[_size - 1]); } else { printf(__FUNCSIG__ + " invalid network settings. "); //~Cnetwork(void); } };
由于我们同时预测需求和供应,故我们需要两个单独的网络实例,每个任务由其一处理。我们的获取输出函数充当“检查开立多头”和“检查开立空头”函数的饲喂源,它据上面已提到的数据缓冲区来填充每个网络的相应输入层。对于需求,由于需求仅取决于其先验值,加上空间和时间参数,其输入层的大小为 3;然而,供应除了取决于其先验值之外,还会受到先前需求的影响,如此这般,如果您考虑类似的空间和时间输入,其输入层的大小为 4。这些层的填充在每个新柱线的获取输出函数中处理,如下所示:
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CSignalNetwork::GetOutput() { ... ... for(int i = 0; i < m_train_set; i++) { for(int ii = 0; ii < __LONGS_INPUTS; ii++) { if(ii==0)//time { m_model_longs.x[i][ii] = T(m_time.GetData(i)); } else if(ii==1)//spatial matrix { vector _x,_y; _x.CopyRates(m_symbol.Name(),m_period,2,StartIndex() + ii + i,2*m_train_set); _y.CopyRates(m_symbol.Name(),m_period,4,StartIndex() + ii + i,2*m_train_set); m_model_longs.x[i][ii] = G(_x,_y); } else if(ii==2)//demand { m_model_longs.x[i][ii] = (m_high.GetData(StartIndex() + ii + i) - m_open.GetData(StartIndex() + ii + i)); } } if(i > 0) //assign classifier { m_model_longs.y[i - 1] = (m_high.GetData(StartIndex() + i - 1) - m_open.GetData(StartIndex() + i - 1)); } } for(int i = 0; i < m_train_set; i++) { for(int ii = 0; ii < __SHORTS_INPUTS; ii++) { if(ii==0)//time { m_model_shorts.x[i][ii] = T(m_time.GetData(i)); } else if(ii==1)//spatial matrix { vector _x,_y; _x.CopyRates(m_symbol.Name(),m_period,4,StartIndex() + ii + i,2*m_train_set); _y.CopyRates(m_symbol.Name(),m_period,2,StartIndex() + ii + i,2*m_train_set); m_model_shorts.x[i][ii] = G(_x,_y); } else if(ii==2)//demand { m_model_shorts.x[i][ii] = (m_high.GetData(StartIndex() + ii + i) - m_open.GetData(StartIndex() + ii + i)); } else if(ii==3)//supply { m_model_shorts.x[i][ii] = (m_open.GetData(StartIndex() + ii + i) - m_low.GetData(StartIndex() + ii + i)); } } if(i > 0) //assign classifier { m_model_shorts.y[i - 1] = (m_open.GetData(StartIndex() + i - 1) - m_low.GetData(StartIndex() + i - 1)); } } ... ... }
在这之后,我们依据训练循环中从模型结构体中提取的信息来为两个网络分配输入值和目标值,其中每次循环遍历网络的一组数量的局次。从初步测试中发现,理想的局次数量约为 10000,每次训练循环的学习率为 0.5。这当然是计算密集型的,这就是为什么下一节中介绍的测试结果采用了非常保守的数值,大约 250 个局次。
设置输出函数允许我们记录每次验算的网络权重和偏差,前提是验算结果超过初始化时所用的权重设定的准则。初始化时,可以选择读取权重,这些权重设定的准则将用作当前测试运行的基准。
测试运行
我们依据 2023 年的日线时间帧,针对 EURUSD 进行了测试运行,网络设置非常简单。需求预测网络总共有 3 层,其中一个是隐藏的,它们的大小分别为 3、5 和 1。供应预测网络也有 3 层,但如上所述,输入层的大小不同,因此它们的大小为 4、5 和 1。两个网络末尾的 1 层存储每个网络的输出。
如常,将本文末尾附带的代码组装为智能交易系统,是通过 MQL5 向导实现的,因此,如果您是新手或不熟悉,请参考此处和此处的指导。
这两个设置非常基本,可以说是您能遇到的最简单的,因为引用的网络类最多可以生成 UCHAR_MAX 层,每个层的大小也是 UCHAR_MAX(如果初始化设置定义了这一点)。随着用到的层数越来越多,甚至更大的层大小,计算资源会不断提升,但值得指出的是,即使设置了少量层,典型情况下认为层大小在 100-个单位范围内就足够了。
我们一如既往地执行运行,没有离场价格目标,持仓直到信号逆转,因为这种方式更倾向于长线,并能更好地评估主要价格趋势。按照一些理想设置的真实即刻报价验算为我们提供了以下报告:
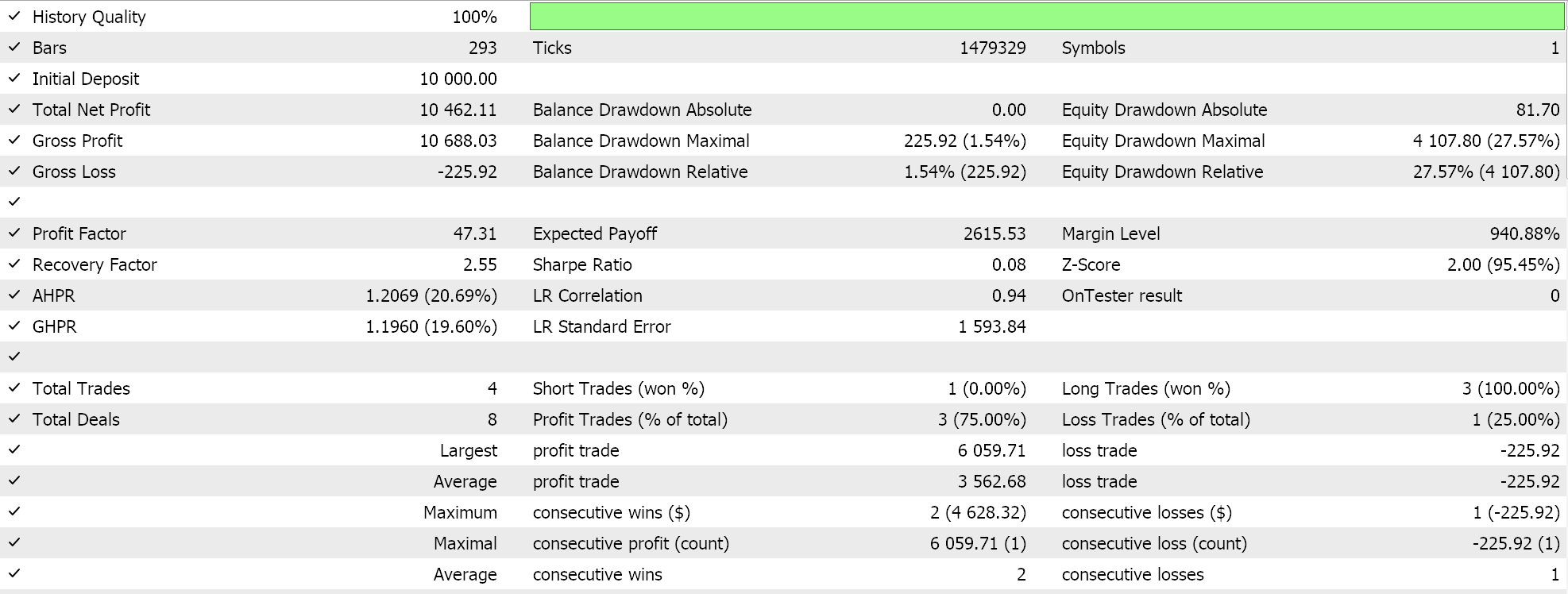
净值曲线如下所示:
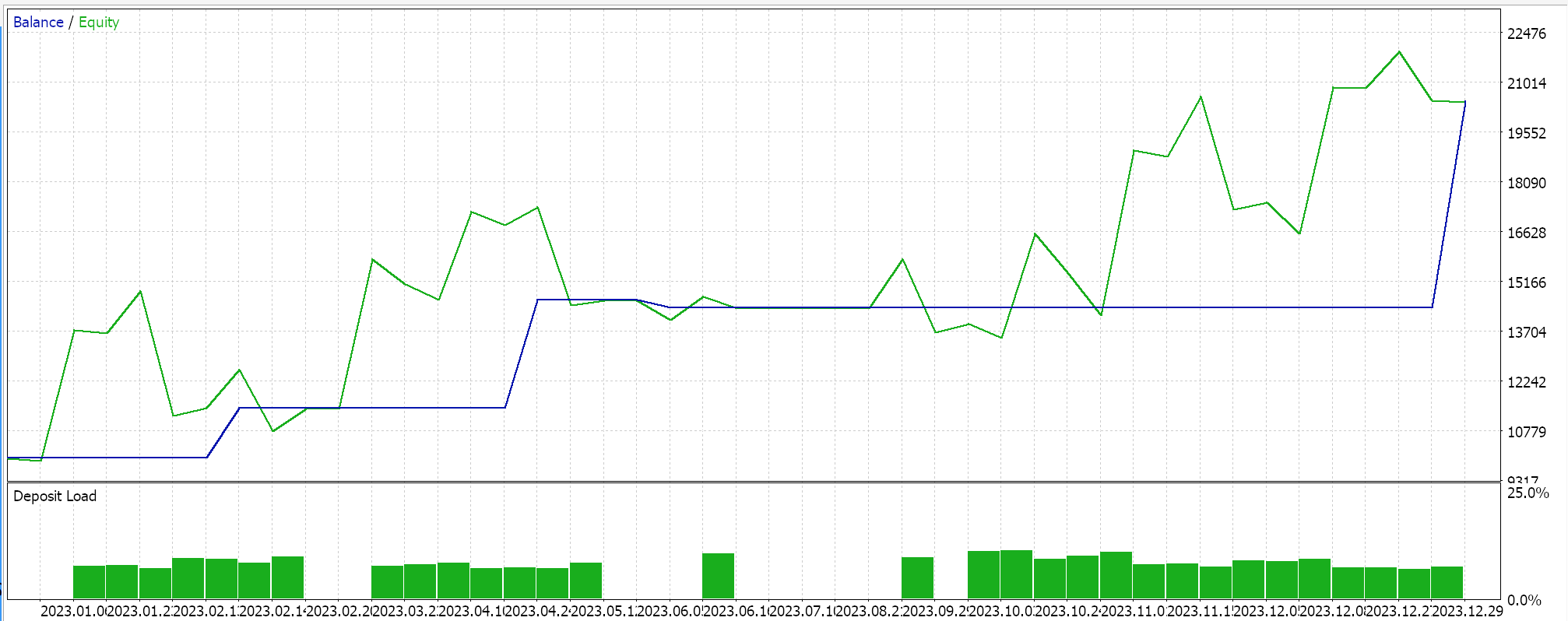
如果我们深入研究这份报告,很明显全年的交易太少了,这首先不是一件坏事,因为它们的品质很稳定,看得出它们被长时间持有,直到触发信号逆转,并且在这个测试周期内,它们遭遇的回撤最小。不过,问题在于,在横盘或震荡行情中往往要谨慎,尤其是在涉及杠杆的情况下,对价格的微观波动更加敏感。在我们测试的系统中,我们采用日线时间帧,这没关系,因其倾向于专注大局;但若令它更实用一点,我们就不得不考虑较小的时间帧,大概是 4-小时、甚至 1-小时。当我们这样做时,仅为测试的计算资源就会可观地增加,事实上,说这种关系呈指数级并不夸张。记住,这是一个由 3 层组成的非常基本的网络,隐藏层有 5 个点,空间矩阵简化为行列式。所有这些因素都很重要,因为若开始处理较小的时间帧时,筛选噪音的需求变得更加重要,而做到这一点的最好方法之一就是有点吹毛求疵。
此外,在引用的网络类中,有一些函数可帮助在每次验算的开头和结束时导入和导出网络的权重和偏移设置。我没有将它们用于这些测试运行,因为这也会略微减慢过程,但在覆盖扩展区间测试时需要用到它们(我们在该测试时只考虑了一年)。当采用它们时,需要仔细权衡测试运行的准则,因为默认情况下,在网络类中,越大越好。故此,例如,如果人们更关心回撤,则需要相应地修改网络类中附加的代码以便在每次验算时反映这一点,仅当来自运行的准则值小于前值时,才会更新写入文件的权重。这也意味着每次运行时的开始或默认值应是 DBL_MAX,或足够高的值,从而避免不必要的错误。
结束语
STF 处理双重预测的能力无疑是一种有趣的方法,这并不常见,但无疑具有优调和改进的潜力。例如,我们测试中使用的空间信息的 G 矩阵,可以通过将输入数据向量拆分为更小的部分来扩展到 n x n,甚至它的每个值都可以是网络的输入数据点,以及许多其它调整,这些变化是以牺牲计算资源为代价的。
事实上,一般来说,通过神经网络实现 STF 本质上是一项计算密集型工作,需要覆盖相当大量的数据进行测试,以便获得可靠的交叉验证。这就体现出它的主要局限性,上面所引用论文中的实现,其中用到了网络变换器,这一点更加明显。
然而,随着我们看到英伟达在这一领域中变得越来越重要,这项工艺的一个方面正在慢慢被业界接受。可以探索其它更高效的替代模型,如随机森林,前提是它们的相关设置也不会过于复杂,但随着计算成本开始降低,这样做的成本效益也许会受到质疑。
尽然,MQL5 向导仍是一个快速原型和测试思路的工具,这篇有关时空融合的文章就此展示了另一种勾绘。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/14552
 开发交易机器人:Python与MQL5结合(第二部分):模型选择、创建与训练,以及Python自定义测试器
开发交易机器人:Python与MQL5结合(第二部分):模型选择、创建与训练,以及Python自定义测试器
 神经网络变得简单(第 81 部分):上下文引导运动分析(CCMR)
神经网络变得简单(第 81 部分):上下文引导运动分析(CCMR)
 构建K线趋势约束模型(第5部分):通知系统(第一部分)
构建K线趋势约束模型(第5部分):通知系统(第一部分)
