Red neuronal en la práctica: Función de recta

Introducción

Hola a todos, y bienvenidos a un nuevo artículo sobre redes neuronales.

En el artículo anterior "Red neuronal en la práctica: Mínimos cuadrados", vimos cómo podríamos, en casos muy simples, encontrar la ecuación que mejor describe el conjunto de datos que tenemos para usar. La ecuación generada en ese sistema era muy sencilla, con solo una variable utilizada. A pesar de haber mostrado cómo podríamos realizar el cálculo, aquí seremos un poco más directos. Esto se debe a que la matemática empleada para crear la ecuación basada en los valores presentes en una base de datos requiere un conocimiento considerable de matemáticas analíticas y cálculo algebraico. Además, claro está, de conocer qué tipo de datos existen en la base que estamos utilizando.

Dado que este es un artículo cuyo objetivo es ser lo más didáctico posible, no quiero complicar la vida de ninguno de ustedes, queridos lectores. Si realmente te sientes interesado en profundizar en los cálculos, te sugiero leer artículos o libros sobre el tema. Básicamente, tendrás que estudiar matemáticas analíticas y cálculo algebraico. Para hacer el proceso menos teórico y tedioso, te propongo comenzar estudiando teoría de juegos. Allí tendrás contacto con los cálculos y análisis de una forma más divertida, sin la monotonía de ver interminables cuentas.

Existe una gran cantidad de material muy bien explicado y de fácil comprensión en Internet sobre este tema. Pero si tu objetivo es solo ver el código, siéntete bienvenido, ya que en este artículo no profundizaré en la parte matemática. La cuestión matemática es bastante densa y requiere comprender cada uno de los detalles, lo que tomaría mucho tiempo para explicarlo todo, y muchos quizás no estén interesados en estos aspectos.

Así que en este artículo, pasaremos rápidamente por algunos métodos para obtener la función que podría representar nuestros datos en la base. No me adentraré en detalles sobre cómo usar estadísticas y estudios de probabilidad para interpretar los resultados. Dejo esto como tarea para aquellos que realmente deseen profundizar en la parte matemática del asunto. De todas formas, estudiar estos temas será crucial para que puedas comprender todo lo que involucra los estudios de redes neuronales. Aquí seré bastante suave con el tema.

Creando la ecuación de forma genérica

Vamos a empezar haciendo algunos cálculos. (Ay, Dios mío, ¡aquí viene otra vez!). Tranquilo, querido lector, no necesitas ponerte nervioso ni preocuparte por lo que vamos hacer. Esta vez prometo ser más amable. Vamos a hacerlo de forma diferente a lo que hicimos en el artículo anterior. Aquí nuestro objetivo será crear un sistema que sea capaz de generar una ecuación de recta mucho más genérica. Y para no dejarte completamente abrumado con el desarrollo de las fórmulas que vamos a usar. No vamos a profundizar en el desarrollo matemático detrás de las ecuaciones utilizadas. Esto no es realmente necesario, ya que en el artículo anterior hicimos una demostración básica de cómo sería el desarrollo de una ecuación matemática, basada en algunas ideas y principios fundamentales. Aquí simplemente intentaremos entender lo que estas ecuaciones realmente significan. Por supuesto, intentaré, en la medida de lo posible, hacer las cosas más accesibles. Aunque al principio puedan parecer confusas. Evitaré que te sientas así. Lee el artículo con calma y sin prisas. Observa cómo se va desenvolviendo todo, ya que aquí estaré resumiendo varias investigaciones en el área de matemáticas para mostrarte cómo podemos hacer que una red neuronal asimile un conocimiento basado en la información contenida en una base de datos.

Pero antes de comenzar, quiero dejar claro algo: lo que veremos aquí se refiere a una red neuronal, que no recibirá ninguna información nueva en su base de datos. Es decir, la base de datos ya está completamente construida Y solo queremos que genere una ecuación que mejor represente lo que ya se encuentra en la base de datos. Solo después, usando otros mecanismos, podremos filtrar las probabilidades de que una nueva información esté o no relacionada con lo que ya se encuentra en la base de datos. Estos mecanismos normalmente se adentran en el tema de la inteligencia artificial. Pero eso será para otro momento.

Bien, volviendo a nuestro código de ejemplo. En él tenemos dos conjuntos de datos, que pueden ser trazados en un plano 2D. Usando solo coordenadas X e Y. Analizando las cosas con calma, podemos notar que la ecuación que buscamos será relativamente simple de construir. Ya que nuestros datos pueden expresarse con una cierta proximidad a una línea recta probable. Hay casos en los que esto no ocurre, donde la ecuación puede ser una curva o una función trigonométrica. Pero vamos paso a paso. Primero debemos entender estos casos más simples. Así que comencemos entendiendo lo siguiente: la ecuación que queremos obtener tiene el siguiente formato que se muestra en la imagen a continuación.

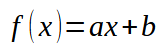
Aquí el valor de la constante < a > representa el coeficiente angular. Por su parte, la constante < b > es el punto de intersección. Cuando < b > es igual a cero, la raíz de la función también es cero. En el artículo anterior, vimos cómo calcular este coeficiente cuando < b > es cero. Además, al final de ese mismo artículo, vimos cómo ajustar ambos valores para intentar aproximar las constantes de la ecuación, construyendo así la función de recta mostrada anteriormente. Recordemos una vez más que si cambias el valor de la constante < b >, también cambiarás la raíz de la función. Entender esto es importante para poder resolver el sistema mediante polinomios. Sin embargo, aquí utilizaremos un método adaptado de lo que ya fue explicado en el artículo anterior.

Creo que ha quedado claro que intentar encontrar estos valores mediante bucles de prueba y error —lo que en programación se conoce como fuerza bruta, donde se prueban todos los valores posibles— no es, ni de lejos, el mejor camino. Aunque se puede hacer, el tiempo de procesamiento sería enorme en la mayoría de los casos. En casos como el nuestro, sería simplemente bastante largo y tedioso, pero factible. Sin embargo, cuando el número de variables aumenta significativamente, el proceso se vuelve impracticable, ya sea manualmente o mediante fuerza bruta.

Dicho esto, incluso si decidieras usar fuerza bruta, en el artículo anterior demostré una forma de calcular el coeficiente angular cuando la constante < b > es igual a cero. Este método hacía que encontrar el coeficiente fuera una tarea relativamente simple y rápida. independientemente de la cantidad de datos presentes en la base. La única restricción era que la ecuación generada tenía que ser una línea recta. Sin embargo, si la constante < b > no es cero, ese mismo cálculo ya no serviría. Solo nos daría una estimación aproximada de la dirección a seguir, algo que exploraremos más adelante. Por ahora, nos basaremos en funciones conocidas, como la que vimos al principio de este tema.

Muy bien, pensemos entonces en un caso genérico de solución. Recordemos que es esencial conocer el tipo de polinomio que se utilizará. Si no lo sabemos, la búsqueda de la ecuación que mejor represente los datos puede volverse muy lenta, incluso en los casos más simples. Así que ten esto en mente: todo lo que veremos a partir de ahora se basa en esto: conocimiento previo.

Ok, vamos a generalizar el método de mínimos cuadrados para cualquier caso. Para hacer esto, es crucial conocer el tipo de polinomio que se usará. Empecemos con uno simple que genere una línea recta. Este polinomio puede generalizarse utilizando la expresión que se muestra a continuación.

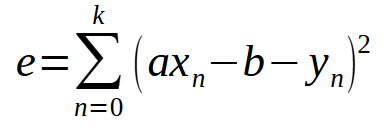
Espera un momento, ¿no es esta la misma fórmula que vimos en el artículo anterior? ¡Sí! Es básicamente la misma. Pero ahora tenemos la variable < b > incluida en la fórmula, ya que ahora no asumimos que es igual a cero. Si desarrollas esta suma, llegarás a algo similar a lo que hicimos en el artículo anterior. Sin embargo, para que lo entiendas mejor, al generalizar este cálculo debemos considerar la derivada tanto con respecto a la variable < a > como con respecto a < b >. Así obtenemos la definición que se muestra a continuación.

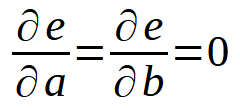
Es decir, lo mismo que hicimos en el artículo anterior. Sin embargo, este principio no se limita solo a una ecuación de línea recta. Podemos utilizar el mismo enfoque para cualquier caso. Por ejemplo, supongamos que el conjunto de datos se pueda expresar o representar mejor como una parábola. En este caso, deberíamos pensar en cómo buscar una ecuación cuadrática utilizando los datos que tenemos en nuestra base. Las dos últimas definiciones se transformarían en lo que se muestra a continuación.

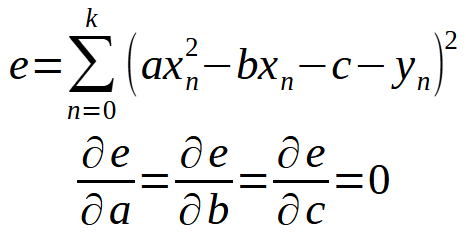
De esta manera, solo tendrías que desarrollar este nuevo sumatorio para encontrar cómo crear la ecuación, que en este caso sería una ecuación cuadrática. Es decir, encontrar las constantes necesarias para que dicha ecuación cuadrática represente todo lo que está en la base de datos. Pero volviendo a nuestro caso, donde usamos una ecuación de línea recta, si desarrollamos el cálculo ahora considerando < b > diferente de cero, obtendremos primero la siguiente ecuación que se muestra a continuación.

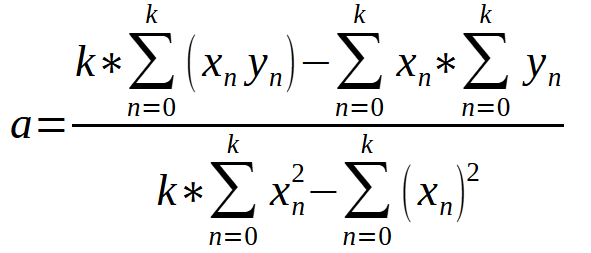
Esta ecuación nos permite calcular el valor de < a > basándonos en la información contenida en nuestra base de datos.

Una vez que hemos obtenido el valor de la constante < a >, podemos usar la ecuación que se muestra a continuación para buscar la constante < b >.

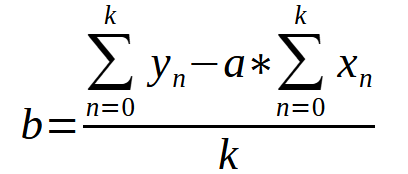
En ambos casos, el valor de < k > es el número de puntos en el gráfico. Tal vez, al mirar solo las ecuaciones, puedas sentirte confundido y pienses que esto es algo complicado de entender, o no sepas cómo convertir estas expresiones en un código utilizando cualquier lenguaje de programación. Así podrías obtener los valores de las constantes sin tener que hacerlo manualmente. No obstante, al igual que hicimos en el artículo anterior, aquí vamos a traducir este formato matemático a un formato en lenguaje de programación, en este caso MQL5. Pero podrías utilizar cualquier otro lenguaje, y los resultados serían los mismos. A continuación, verás cómo quedarían estas ecuaciones en nuestro código MQL5. Esto se puede observar en el fragmento que está justo abajo.

28. //+------------------------------------------------------------------+
29. void Func_01(void)
30. {
31.     int A[]={
32.                   -100, -150,
33.                    -80,  -50,
34.                     30,   80,
35.                    100,  120
36.             };
37. 
38.     int vx, vy;
39.     uint k;
40.     double ly, err, dx, dy, dxy, dx2, a, b;
41.     string s0 = "";
42. 
43.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
44.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
45. 
46.     err = dx = dy = dxy = dx2 = 0;
47.     k = 0;    
48.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++, k++)
49.     {
50.         vx = A[c1++];
51.         vy = A[c1++];
52.         dx += vx;
53.         dy += vy;
54.         dxy += (vx * vy);
55.         dx2 += MathPow(vx, 2);
56.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
57.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle))) - global.Const_B;
58.         s0 += StringFormat("%.4f || ", MathAbs(ly));
59.         canvas.LineVertical(global.x + vx, global.y - vy, global.y + (int)(ly - vy), ColorToARGB(clrPurple));
60.         err += MathPow(ly, 2);
61.     }
62.     a = ((k * dxy) - (dx * dy)) / ((k * dx2) - MathPow(dx, 2));
63.     b = (dy - (a * dx)) / k;
64.     PlotText(3, StringFormat("Error: %.8f", err));
65.     PlotText(4, s0);
66.     PlotText(5, StringFormat("f(x) = %.4fx %c %.4f", a, (b < 0 ? '-' : '+'), MathAbs(b)));
67. }
68. //+------------------------------------------------------------------+

Muy bien, vamos a entender lo que está ocurriendo en este fragmento. En las líneas 46 y 47, estamos inicializando todas las variables con el valor cero. Esto es porque queremos mostrar explícitamente que están comenzando en cero, aunque podríamos omitir esta declaración, ya que normalmente el compilador inicializa las variables en cero de manera implícita. En la línea 52, estamos calculando la suma de todos los valores de X, y en la línea 53, la suma de los valores de Y. En la línea 54, calculamos la suma del producto entre los valores de X e Y. Finalmente, en la línea 55, calculamos la suma de los cuadrados de los valores de X.

Todos estos cálculos mencionados se utilizan en las fórmulas que vimos anteriormente. Es decir, hacer los cálculos es mucho más sencillo de lo que parece. Todos los cálculos mencionados se utilizan en las fórmulas que vimos anteriormente. Por eso, hacer los cálculos es mucho más sencillo de lo que parece.

Ahora, efectivamente, vamos a calcular los valores de las constantes que se utilizan en la ecuación de la recta. Para hacerlo, usamos la línea 62, donde calculamos el valor del coeficiente de inclinación, y en la línea 63, calculamos el valor de la intersección. ¿Te has dado cuenta de lo fácil que es transformar una fórmula matemática en un cálculo que pueda ejecutar nuestro programa? Hay personas que dicen entender la matemática, pero no pueden escribirla en términos de programación. A mi parecer, estas personas se engañan a sí mismas. Ya que escribir una fórmula matemática en términos de programación es tan sencillo como leer la fórmula. Claro, si no entiendes la fórmula, tampoco podrás explicarle al computador, que no es más que una calculadora gigante, cómo realizar el cálculo.

De todas formas, no trazamos la recta en el gráfico; solo mostramos la ecuación generada. Esto se hace en la línea 66, para que puedas visualizar manualmente si los valores calculados son los más adecuados para ese conjunto de datos específico. En la animación a continuación, muestro el resultado de la ejecución de nuestro programa con los valores indicados en la matriz A, presente en la línea 31.

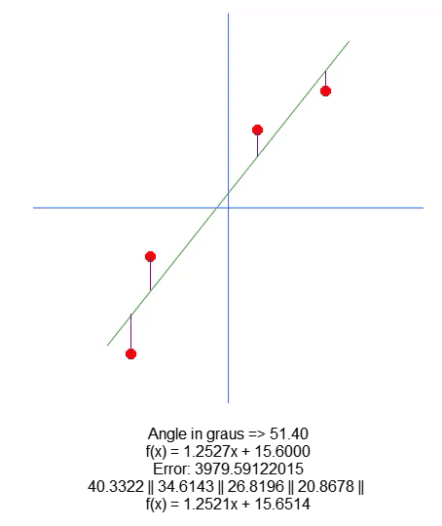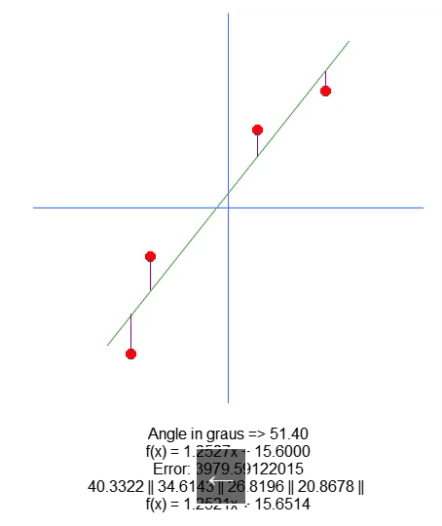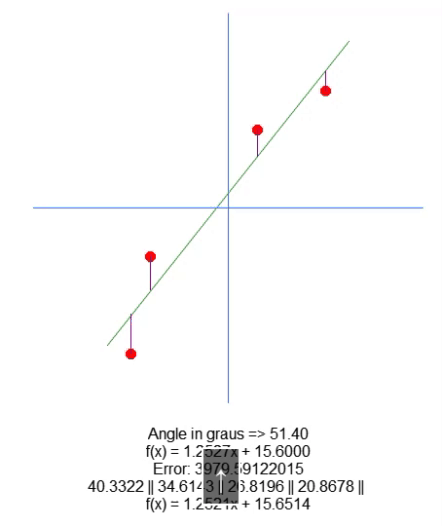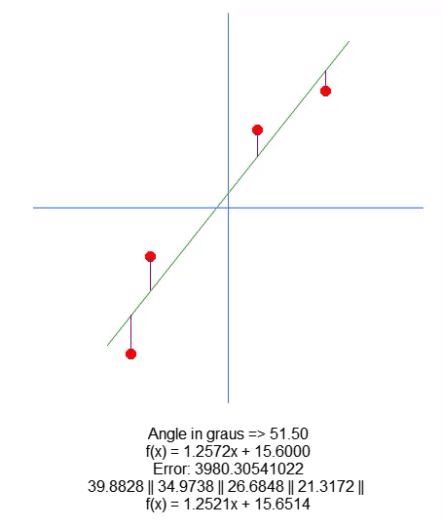
Observa cómo los valores de error cambian mientras intentamos encontrar el punto perfecto. Compara la ecuación de la recta ideal con la ecuación de la recta que estamos intentando construir utilizando las flechas de dirección. Debido a la falta de un ajuste perfecto, obtenemos un valor cercano a los ideales. Entender esto es importante, ya que pronto exploraremos esta misma propiedad, pero de una manera diferente.

Ahora, quizás te preguntes: ¿Hay una forma de acercarnos aún más al valor calculado? Sí, querido lector. Para lograrlo, solo necesitas cambiar un valor en el programa. Este valor se muestra en el código a continuación.

void NewAngle(const char direct, const char updow, const double step = 0.1)

El valor a modificar es el argumento step. Aquí estamos utilizando un paso de 0.1, como puedes ver claramente en el código, pero puedes usar un valor menor o mayor. Si utilizas un valor menor, el programa necesitará más tiempo para alcanzar los valores calculados, pero la precisión del error será mayor debido a la menor variación. Ten en cuenta que una cosa compensa a la otra: no existe una solución 100% perfecta, sino un punto de equilibrio ideal.

Una vez que tenemos este código capaz de calcular la ecuación de la recta, podemos modificar libremente los valores presentes en la matriz A, creando cualquier tipo de condición o base de conocimiento. Quizás solo sea necesario ajustar el tipo de variables que estás utilizando. Aquí estamos usando enteros, pero si deseas usar tipos de datos flotantes, como double o float, solo tienes que cambiar el tipo. El cálculo no cambiará. Esto para obtener la ecuación de la recta. Sin embargo, si los datos de la base se representan mejor con una ecuación cuadrática, por ejemplo, deberás cambiar el cálculo para encontrar el mejor sistema de constantes que represente tu base de datos. Como se mencionó antes. Todo depende del contexto; no hay una solución 100% efectiva para todos los casos posibles e imaginables.

Muy bien, pero quizás estés pensando que solo existe esta forma de calcular la ecuación de la recta. Si has pensado esto, significa que aún no conoces lo suficiente. Para mostrar una forma diferente de obtener los mismos valores que hemos visto en este tema, vamos a explorar un nuevo apartado, separando adecuadamente los conceptos. Sin embargo, este próximo apartado será solo una introducción a lo que veremos en el siguiente artículo.

Pseudo-Inversa

Hasta ahora, las cosas pueden haber parecido muy complejas y difíciles de implementar en código. Esto se debe a que cada cambio necesario debe ser implementado de manera correspondiente en el código generado. Sin embargo, existe una forma más agradable de codificar situaciones en las que las variables cambian constantemente. Al menos, eso pienso yo, aunque no sé qué opinas tú, querido lector. Cuando se trata de codificar algo donde la cantidad de variables cambia frecuentemente, prefiero dejar de lado los cálculos escalares y pasar a los cálculos matriciales. Trabajar con matrices nos permite factorizar cualquier cosa sin tener que crear múltiples variables temporales. Sé que muchos de ustedes pueden pensar que crear un código para factorizar matrices es la cúspide de la complejidad, y a menudo usan bibliotecas que realizan estas factorizaciones sin entender cómo funcionan. Esto puede hacer que te vuelvas dependiente de estas bibliotecas, precisamente porque no entiendes cómo se realizan estos cálculos.

Hace algún tiempo, escribí dos artículos cuyo objetivo era presentar la factorización de matrices. Allí, mostré los elementos más básicos que necesitas aprender para poder crear un código que realice operaciones de factorización utilizando matrices. Muchos problemas se vuelven más simples y rápidos de resolver cuando se emplean matrices para realizar los cálculos.

Los artículos son: "Factorización de matrices: lo básico" y "Factorización de matrizes: un modelado más práctico". Si te interesa aprender más sobre el tema, te recomiendo leer y practicar lo que se expone en esos artículos. Por supuesto, solo cubren lo básico, pero si entiendes el contenido allí presente, podrás comprender lo que haremos en este apartado.

Aquí utilizaremos matrices para encontrar los valores que obtuvimos en el tema anterior. Para entender lo que vamos a hacer, es necesario saber cómo factorizan las matrices. No me refiero a la parte de la programación, ya que programar estos cálculos es la parte fácil. Me refiero a que debes tener, querido lector, al menos un conocimiento básico sobre cómo realizar cálculos utilizando matrices. No voy a entrar en detalles sobre cómo hacer estos cálculos, puesto que asumiré que tienes un mínimo de conocimiento sobre el tema. No necesitas ser un experto. Solo saber lo esencial será suficiente para lo que vamos a hacer.

Muy bien, volvamos al tema de cómo encontrar la ecuación de la recta. Considerando que tenemos una base de datos cuyo contenido queremos preservar en forma de ecuación matemática. A primera vista, esto parece extremadamente complejo. Como si solo un genio pudiera lograr tal hazaña. Pero no, haremos lo mismo que en el tema anterior. Solo que de una manera ligeramente diferente.

Comencemos nuevamente con lo básico. La ecuación de error se muestra en la imagen a continuación.

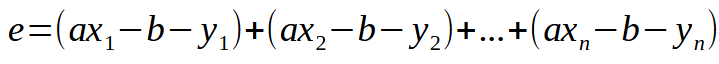
Esta es la forma escalar de escribir la ecuación. Sin embargo, podemos escribir la misma ecuación en forma matricial. Como se muestra a continuación.

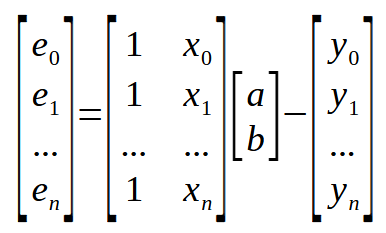
Esta representación matricial que se ve arriba. Es exactamente lo que se muestra en la imagen anterior. Sin agregar ni quitar absolutamente nada. Pero podemos simplificar aún más esta representación matricial. De la siguiente manera.

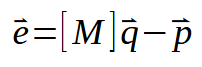
Sé que esta representación puede parecer extremadamente complicada. Pero seguimos representando exactamente lo que el cálculo escalar estaría realizando. Sin embargo, esta forma más compacta de factorización matricial nos permitirá entender mejor cómo se llevarán a cabo los cálculos. Ya que tendremos que escribir menos elementos en la fórmula. Aquí estamos diciendo que el vector < e > es igual a la matriz < M >, que contiene los valores de x. Multiplicado por el vector < q >, que contiene las constantes que estamos buscando. Estas son: el coeficiente angular y el punto de intersección. Luego, restamos el vector < p >, que representa los valores de la matriz que contiene los valores de y.

Ahora quiero recordarte lo siguiente, querido lector: estamos buscando la derivada de las constantes < a > y < b > con respecto al error, que podemos calcular fácilmente. Ya que tenemos la ubicación de los puntos a usar en el cálculo. Así, cuando lo representamos en forma matricial, podemos ver las cosas como se muestran a continuación.

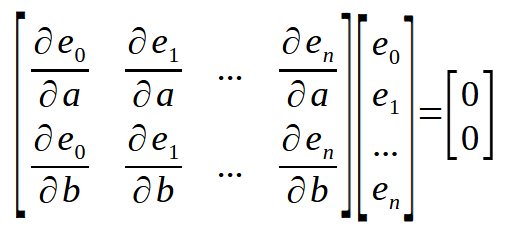
Aquí hay un pequeño detalle que se puede observar inmediatamente a continuación.

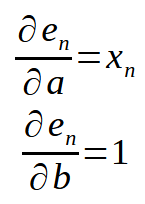
Recordando que < n > representa el índice en el array dentro de nuestro código. La ecuación anterior puede reescribirse como se muestra a continuación.

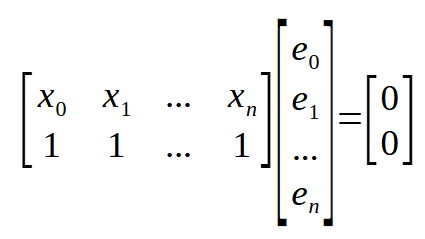
Perfecto. Ahora tenemos algo realmente interesante en nuestras manos. Si observas las matrices anteriores, notarás que este mismo resultado que mostramos aquí. También aparece en otro lugar. Solo que esta matriz está transpuesta, como se le denomina, lo que compacta aún más la fórmula. Esto se verá en la imagen a continuación.

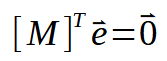
El siguiente paso es hacer algunas sustituciones con los datos que ya tenemos. De esta manera, obtenemos la siguiente formulación, vista a continuación.

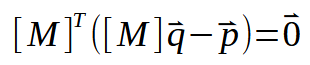
Ahora, desarrollemos este cálculo o fórmula, como prefieras llamarlo, mostrado arriba. Esto nos lleva a lo siguiente:

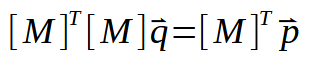
Si la matriz transpuesta puede invertirse, obtendremos algo como lo que se muestra a continuación.

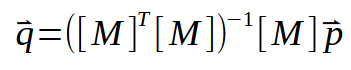
Este resultado de ahora, es de hecho una factorización muy bonita e interesante de ver. Tanto es así que la persona que la creó realmente mereció el Premio Nobel de Matemáticas en 2020. Esta formulación es conocida como Pseudo Inversa, o Inversa de Moore-Penrose, en honor a sus creadores. Ya que nos proporciona exactamente lo que buscamos, es decir, los valores del coeficiente angular y de la intersección. Y estos estarán dentro del vector < q >. Este tipo de cálculo puede implementarse en varios programas diferentes, muchos de ellos dedicados exclusivamente a trabajar con cálculos. Por ejemplo, usando SCILab, puedes utilizar el programa que se muestra a continuación. Este calculará los valores del coeficiente angular y el punto de intersección.

clc;
clear;
clf;

x=[-100; -80; 30; 100];
y=[-150; -50; 80; 120];

A = [ones(x), x];

plot(x, y, 'ro');
zoom_rect([-150, -180, 180, 180]);
xgrid;

x = pinv(A) * y;
b = x(1);
a = x(2);

x =[-120:1:120];
y = a * x + b;

plot(x, y, 'b-');

El resultado de la ejecución puede verse justo a continuación:

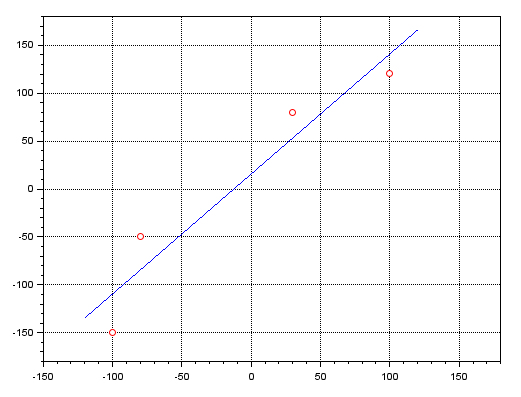
Los puntos en rojo muestran la ubicación de los mismos puntos que se ven en el programa en MQL5. La línea azul, por su parte, muestra el resultado de la ecuación de la recta obtenida mediante la pseudo inversa. Lo mismo se puede lograr usando MATLAB, además de otros programas como Excel. Esto se debe a la gran utilidad de esta pseudo inversa en diversas áreas del conocimiento.

Para que te hagas una idea, estimado lector, de lo interesante que es esta pseudo inversa, basta con modificar ligeramente los vectores utilizados, así como las matrices de la ecuación. Podemos resolver cualquier tipo de polinomio, y de una manera bastante eficiente.

Consideraciones finales

Dado que la pseudo inversa es una factorización que debe hacerse esencialmente utilizando matrices, no mostraré en este artículo cómo sería el programa para encontrar las constantes < a > y < b >. Esto se debe a la explicación necesaria para que realmente entiendas lo que está ocurriendo. No se trata solo de mostrar el código en sí. Trabajar con matrices requiere un nivel de atención mucho mayor, debido a la forma en que se manejan. Cuando lo hacemos manualmente, las operaciones realizadas son relativamente simples. Sin embargo, hacerlo en forma de código es algo completamente diferente. Incluso en los artículos en los que menciono cómo utilizar factorizaciones en matrices, las cosas que se hacen allí no son genéricas. Son muy específicas. Y para nuestro objetivo, necesitamos un código más genérico. De lo contrario, la pseudo inversa no podrá ser calculada correctamente en cualquier caso en que intentemos hacerlo.