神经网络实践：直线函数

概述

我很高兴欢迎大家，并邀请您阅读一篇关于神经网络的新文章。

在上一篇文章"神经网络实践 ：最小二乘法"中，我们研究了在非常简单的情况下，如何找到最能描述数据集的方程。在这个系统中生成的方程非常简单，它只使用了一个变量。我们已经演示了如何进行计算，所以这里就直奔主题。这是因为，根据数据库中的现有数值创建方程所使用的数学知识需要大量的分析数学和代数计算知识。除此之外，当然，有必要知道我们正在使用的数据库中是什么类型的数据。

由于这篇文章是为了宽泛的教学，我不想给我的读者带来困难。如果你真的有兴趣深入研究计算，我建议你研究一下这方面的资料。如前所述，你将主要学习分析数学和代数微积分。为了使这个过程不那么理论化和乏味，我建议你从学习博弈论开始。在那里，您可以以更有趣的形式熟悉计算和分析，而无需对无休止的计算进行单调的复习。

网络上有很多关于这个主题的材料，这些材料都解释得很好，很容易理解。但是，如果你的目标只是查看代码，那么欢迎你，因为我不会在本文中讨论数学部分。这个数学问题相当深奥，需要理解每一个细节和大量时间。大多数读者可能对这些方面不感兴趣。

因此，在本文中，我们将简要介绍一些方法，以获得一个可以表示数据库中数据的函数。我不会详细介绍如何使用统计和概率研究来解释结果。让我们把它留给那些真正想深入研究数学方面的人。探索这些问题对于理解研究神经网络所涉及的内容至关重要。在这里，我们将非常冷静地探讨这个问题。

创建一般形式的方程式

首先，我们来计算一下。(又来？）冷静下来，亲爱的读者，你不必担心我们会做什么。这一次，我保证会更加仁慈。今天，我们将采取不同的行动。我们的目标是创建一个能够生成更一般直线方程的系统。为了不让你们对我们将要使用的公式的发展感到完全震惊，我们不会进入方程背后的数学发展。这不是必要的，因为在上一篇文章中，我们展示了基于一些基本思想和原理开发数学方程的示例。在这里，我们将尝试理解这些方程的实际含义。当然，我们会尽量让一切尽可能方便。虽然一开始它们可能看起来很混乱，但我不会让你感到困惑。读这篇文章不要着急，看看整个事情是如何展开的，因为在这里，我将综合各种数学研究，向你展示我们如何让神经网络根据数据库中包含的信息学习知识。

但在我们开始之前，我想明确一件事：我们在这里看到的是一个神经网络，它不会在数据库中接收任何新信息。也就是说，数据库已经完全创建，我们只是希望它生成一个最能代表数据库中已有内容的方程。只有在之后，我们才能利用其他机制过滤出新信息与数据库中已有信息相关或无关的可能性。这种机制通常属于人工智能领域，但这是另一个要讨论的问题。

现在让我们回到代码示例。在这个例子中，我们已经有了两个可以在二维平面上绘制的数据集。也就是说，只使用 X 和 Y 坐标。在冷静地分析了情况后，我们可以看到，所需的方程相对容易构建，因为我们的数据可以用一条可能的直线的近似值来表示。有时情况并非如此，因为方程可能是曲线或三角函数。但让我们一步一个脚印吧。首先，我们需要处理比较简单的情况。让我们先来了解一下：我们想要得到的方程格式如下。

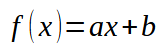
这里常数 < a > 的值代表斜率。常数 < b > 是交点。当 < b > 为零时，函数的根也为零。在上一篇文章中，我们探讨了如何计算 < b > 为零时的系数。此外，在那篇文章的末尾，我们还看到了如何调整这两个值来尝试逼近等式中的常数，从而构建上图所示的线性函数。让我们再次回想，如果我们改变常数 < b > 的值，函数的根也会发生变化。理解这一点对于使用多项式求解系统非常重要。然而，在这里我们将使用一种改编自上一篇文章的方法。

我认为很明显，试图通过试错法找到这些值在编程中被称为蛮力，即尝试所有可能的值（这远非最佳方式）。虽然这是可以做到的，但在大多数情况下，处理时间会很长。在像我们这样的情况下，这只需要花费大量的时间和精力，但这是完全可行的。然而，随着变量数量的显著增加，无论是手动还是蛮力，这个过程都变得不切实际。

不过，即使我们决定使用蛮力，在上一篇文章中，我也演示了当常数 < b > 为零时计算斜率的方法。这种方法使得无论数据库中的数据量如何，都可以相对简单快速地找到角系数。唯一的限制是，得到的方程必须是一条直线。但是，如果常数 < b > 不等于零，那么这种计算就不再有效。这只能让我们大致确定前进的方向。我们稍后再看这个。现在，我们将尝试根据已知函数来做事情，比如本主题开头提到的函数。

现在让我们考虑一下解决方案的一般情况。记住，你需要知道你使用的多项式的类型。如果没有这些知识，即使在最简单的情况下，找到最能代表数据的方程也可能非常耗时。所以请记住：我们接下来看到的一切都基于这些先验知识。

让我们把最小二乘法推广到任何情况。要做到这一点，你需要知道所使用的多项式的类型。我们将从一个生成直线的简单方法开始。这个多项式可以用下面的表达式来概括。

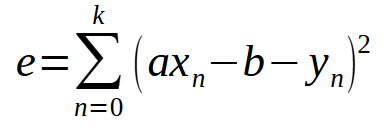
等等，这不就是我们在上一篇文章中看到的公式吗？就是它！它基本上是一样的，但现在公式中包含了变量 < b >，因为我们不再假设它为零。如果我们扩大这个总和，就会得出与上一篇文章类似的结果。不过，为了更好地理解，在推广这种计算方法时，我们必须同时考虑变量 < a > 和 < b > 的导数。这样我们就可以得到下图所示的定义。

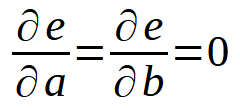
换句话说，一切都与我们在上一篇文章中所做的相同。然而，该原理不限于直线方程。在任何一种情况下，我们都可以使用相同的方法。例如，假设一个数据集可以最好地表示为抛物线。在这种情况下，我们需要考虑如何使用数据库中的数据找到一个二次方程。最后的两个定义转换为以下内容。

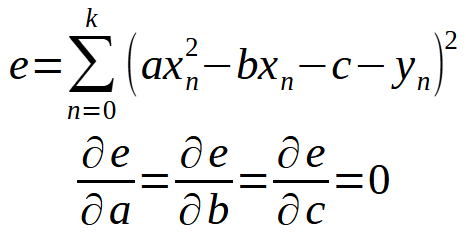
因此，我们需要开发一个新的术语，找到生成方程的方法，这里的方程就是一元二次方程。也就是说，我们需要找到常量，这样一元二次方程才能显示数据库中的所有内容。但是，回到我们使用直线方程的情况，如果我们现在假设 < b > 不为零，继续计算，我们首先会得到下面的方程。

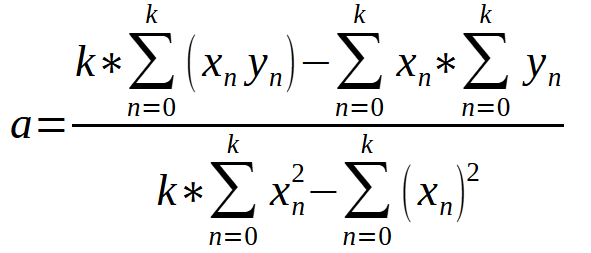
通过这个等式，我们可以根据数据库中的数据计算出 < a > 的值。

得出常数 < a > 的值后，我们就可以利用下面的方程求出常数 < b >。

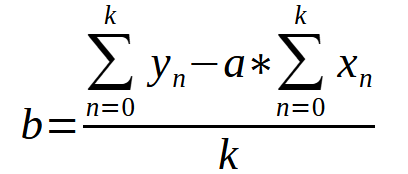
在这两种情况下，< k > 的值都是图形上的点的数量。也许，单看方程式，你可能会感到困惑，认为这是一件复杂的事情。或者，您可能不知道如何使用某种编程语言将这些表达式转换成代码。这样就无需手动操作就能获取常量的值。这就是我们在上一篇文章中所做的。我们将把这种数学格式转换成编程语言格式，这里指的是 MQL5，但您也可以使用任何其他语言，结果都是一样的。下面你可以看到这些方程式在我们的 MQL5 代码中的样子。

28. //+------------------------------------------------------------------+
29. void Func_01(void)
30. {
31.     int A[]={
32.                   -100, -150,
33.                    -80,  -50,
34.                     30,   80,
35.                    100,  120
36.             };
37. 
38.     int vx, vy;
39.     uint k;
40.     double ly, err, dx, dy, dxy, dx2, a, b;
41.     string s0 = "";
42. 
43.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
44.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
45. 
46.     err = dx = dy = dxy = dx2 = 0;
47.     k = 0;    
48.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++, k++)
49.     {
50.         vx = A[c1++];
51.         vy = A[c1++];
52.         dx += vx;
53.         dy += vy;
54.         dxy += (vx * vy);
55.         dx2 += MathPow(vx, 2);
56.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
57.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle))) - global.Const_B;
58.         s0 += StringFormat("%.4f || ", MathAbs(ly));
59.         canvas.LineVertical(global.x + vx, global.y - vy, global.y + (int)(ly - vy), ColorToARGB(clrPurple));
60.         err += MathPow(ly, 2);
61.     }
62.     a = ((k * dxy) - (dx * dy)) / ((k * dx2) - MathPow(dx, 2));
63.     b = (dy - (a * dx)) / k;
64.     PlotText(3, StringFormat("Error: %.8f", err));
65.     PlotText(4, s0);
66.     PlotText(5, StringFormat("f(x) = %.4fx %c %.4f", a, (b < 0 ? '-' : '+'), MathAbs(b)));
67. }
68. //+------------------------------------------------------------------+

让我们弄清楚这个片段中发生了什么。在第 46 和 47 行，我们将所有变量初始化为零。这是因为我们要明确显示变量的起始值为零，尽管我们可以跳过这个声明，因为编译器通常会隐式地将变量初始化为零。在第 52 行，我们计算所有 X 值的总和，在第 53 行，我们计算 Y 值的总和。在第 54 行，我们计算 X 值和 Y 值的乘积之和。最后，在第 55 行，我们计算 X 值的平方和。

所有这些计算都用于我们之前已经看过的公式中。换句话说，计算比看起来容易得多。上述所有计算都用于我们之前探讨的公式中。所以这次就简单多了。

现在我们需要计算直线方程中使用的常数的值。为此，我们使用第 62 行计算斜率值，使用第 63 行找出截距值。您是否注意到，将数学公式转化为我们的程序可以执行的计算是多么容易？有些人声称理解数学，但无法将其转化为编程术语。在我看来，这些人在自欺欺人，因为用代码编写数学公式和阅读一样容易。当然，如果我们不理解这个公式，我们就无法向计算机解释如何进行计算，因为计算机只是一个巨大的计算器。

现在，我们绘制出结果方程。这在第 66 行完成的。这样，我们就可以手动直观地查看计算值是否最适合给定的数据集。在下面的 GIF 中，您可以看到在第 31 行矩阵 A 中指定的值下运行程序的结果。

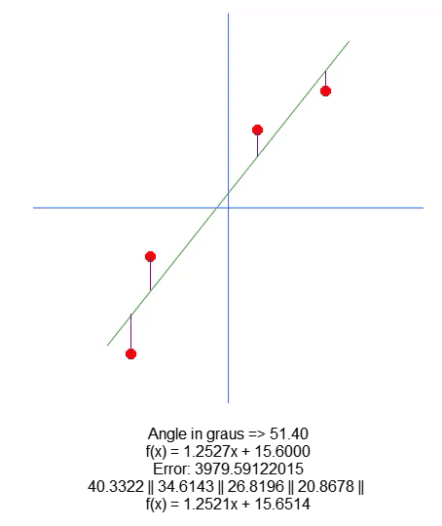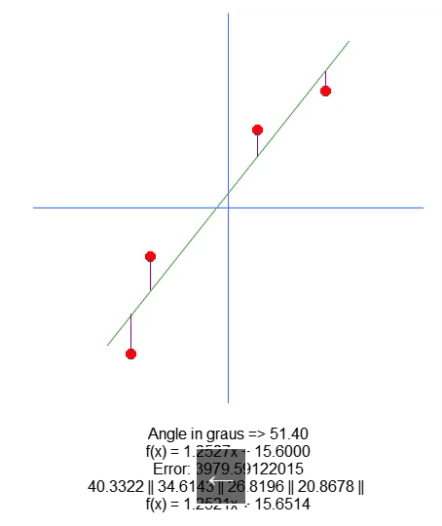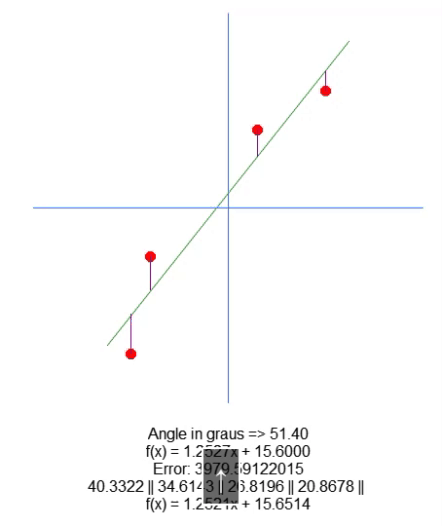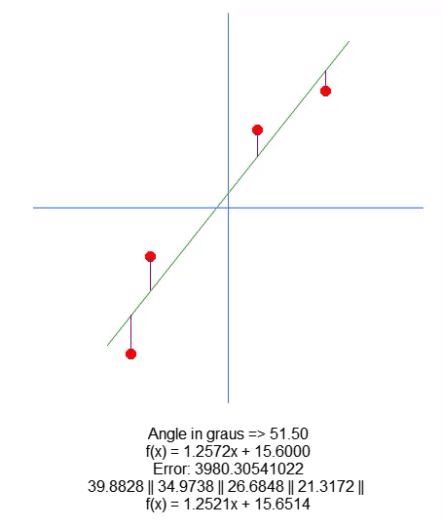
当我们试图找到理想点时，看看误差值是如何变化的。将理想直线方程与我们试图用箭头绘制的直线方程进行比较。我们没有得到一个非常精确的设置，但我们的值非常接近理想值。理解这一点很重要，因为我们很快就会以不同的方式研究这个属性。

现在你可能想知道：有没有一种方法可以更接近计算值？是的，亲爱的读者，有的。为此，您只需更改程序中的值，如下面的代码所示。

void NewAngle(const char direct, const char updow, const double step = 0.1)

要更改的值是 step 参数。如代码所示，这里我们使用的 step 为 0.1，但您也可以使用更小或更大的值。如果使用较小的值，程序达到计算值所需的时间会更长，但由于方差较小，误差精度会更高。请记住，两者缺一不可：没有百分之百完美的解决方案，但有一个理想的平衡点。

一旦我们有了可以计算直线方程的代码，我们就可以自由地改变矩阵 A 中的值，以创建任何条件或知识库。您可能只需要更改所使用的变量类型。这里我们使用的是整数，但如果你想使用浮点数据类型，如 double 或 float，只需更改类型，计算结果不会改变。为了得到直线方程，这是必要的。然而，如果数据库中的数据最好用二次方程来表示，我们将不得不修改计算，以找到表示我们数据库的最佳常数系统，如上所述。这一切都取决于背景；对于所有可能和可想象的情况，没有 100% 有效的解决方案。

但你可能会认为这是计算直线方程的唯一方法。如果你正是这样想的，那么你的知识还不够。为了展示另一种获得我们在本主题中一直在研究的相同值的方法，我们将研究一个新的部分，对概念进行相应的划分。本节将介绍我们将在下一篇文章中看到的内容。

伪逆

到目前为止，一切似乎都很复杂，很难在代码中实现。这是因为每个必需的修改都必须在生成的代码中正确实现。然而，对于变量不断变化的情况，有一种更好的方法来编写代码。至少我是这么认为的。当涉及到编写变量数量频繁变化的代码时，我更喜欢从标量计算转向矩阵计算。矩阵运算允许我们考虑任何因素，而无需创建大量时间变量。我知道你们中的很多人都认为编写矩阵分解代码非常困难，并且经常在不了解其工作原理的情况下使用执行这种因式分解的库。这会让你依赖这些库，因为你不了解计算是如何完成的。

前段时间，我写了两篇介绍矩阵分解的文章。在这些文章中，我们探讨了创建执行矩阵分解操作的代码所应了解的最基本要素。如果使用矩阵进行计算，很多问题都能更容易、更快速地解决。

文章："矩阵分解：基础知识" 和 "矩阵分解：更实用的建模"。如果您想进一步了解这一主题，我建议您阅读这些文章，并在实践中进行测试。当然，它们只涉及基础知识，但如果你了解了它们的内容，就能理解我们在本节中要做的事情。

在这里，我们将使用矩阵来查找上一主题中获得的值。为了理解我们要做什么，我们需要知道矩阵是如何加起来的。我不是说编程，因为编程这些计算是容易的部分。我的意思是，你至少应该掌握如何使用矩阵进行计算的基本知识。我不会详细介绍如何进行这些计算，因为我假定您在这方面有一定的知识。您不需要成为专家，了解基本知识对于我们要做的事情来说就足够了。

现在，让我们回到如何求直线方程的问题上来，因为我们有一个数据库，而且我们想把数据库内容保存为数学方程。乍一看，这似乎很难，好像只有天才才能做到这一点。但是，不，我们将做与上一个主题相同的事情。只是有点不同，

让我们从基础开始。误差方程如下图所示。

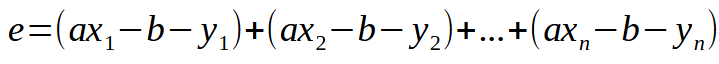
这就是方程的标量形式。不过，我们可以用矩阵形式写出相同的方程，如下所示。

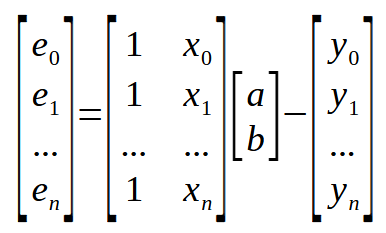
该矩阵表示法与上一幅图中的表示法完全相同，没有任何添加的内容。但我们还可以进一步简化这种矩阵表示法。我们的做法如下：

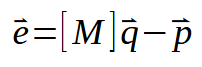
我知道这种表述方式可能看起来非常复杂。然而，这正是标量计算所要做的。不过，这种更紧凑的矩阵因式分解形式可以让我们更好地理解计算的执行方式，因为我们需要在公式中写入的元素更少。这里我们指出，向量 < e > 等于包含 x 值的矩阵 < M > 乘以包含我们正在寻找的常数的向量 < q >。这些包括角系数和交点。然后减去向量 < p >，该向量表示包含 y 值的矩阵的值。

现在我想提醒大家：我们正在寻找常数 <a> 和 <b> 相对于误差的导数，而我们可以很容易地计算出来。现在我们有了计算中要用到的点的位置。因此，如果我们用矩阵的形式来表示，就可以得到以下结果。

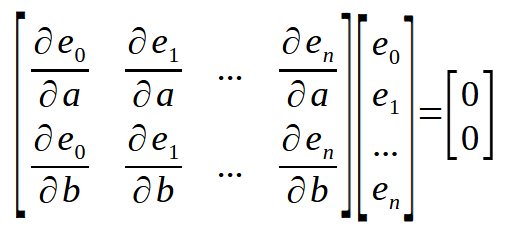
这里有一个小细节：

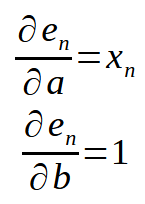
如果我们记住 < n > 代表代码中的数组索引，上面的等式就可以重写如下。

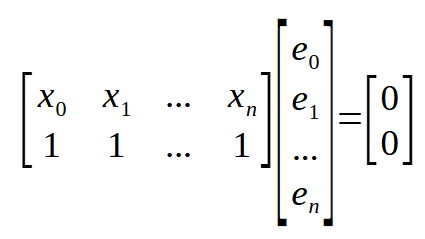
好了，现在我们有了一些非常有趣的东西。如果你看看上面的矩阵，你可以看到我们在这里显示了相同的结果。它也出现在其他地方，只有这个矩阵被转置，这使得公式更加紧凑。请看下图。

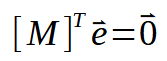
下一步是在我们已有的数据中进行一些替换。这样，我们得到以下公式。

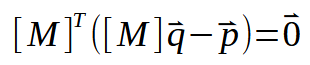
现在让我们开发上面显示的这个计算或公式（你可以随心所欲地称呼它）。这就给我们带来了以下结果：

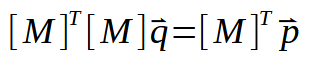
现在，如果我们将转置矩阵反转，就会得到类似的结果：

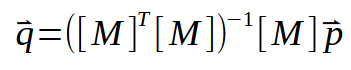
这个结果实际上是一个非常好和有趣的分解，以至于创造它的人实际上应该获得 2020 年的诺贝尔数学奖（好吧，诺贝尔奖里没有数学这一项）。这一公式被称为摩尔-彭罗斯伪逆，以其创造者的名字命名。它准确地给了我们想要的东西，即角系数和截距值。而这两个向量都将位于向量 < q > 的内部。这种类型的计算可以在各种不同的程序中实现，其中许多程序是专门为计算而设计的。例如，使用SCILab，您可以使用下面显示的程序。它将计算斜率和交点的值。

clc;
clear;
clf;

x=[-100; -80; 30; 100];
y=[-150; -50; 80; 120];

A = [ones(x), x];

plot(x, y, 'ro');
zoom_rect([-150, -180, 180, 180]);
xgrid;

x = pinv(A) * y;
b = x(1);
a = x(2);

x =[-120:1:120];
y = a * x + b;

plot(x, y, 'b-');

执行结果如下：

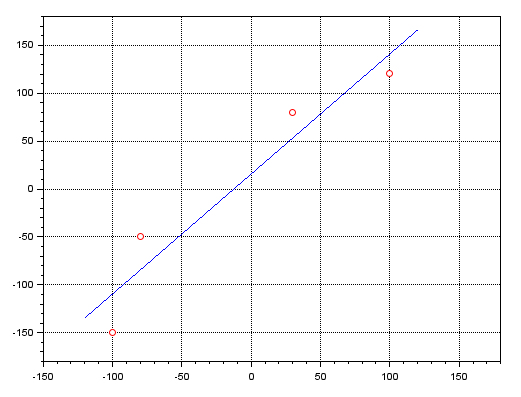
红点表示 MQL5 程序中相同点的位置。蓝线显示了使用伪逆得到的直线方程的结果。使用 MATLAB 以及 Excel 等其他程序也可以完成相同的操作。这是因为这种伪逆在各个领域都非常有用。

为了让你了解这种伪逆有多有趣，我们可以稍微修改一下所用的向量以及方程的矩阵。您可以求解任何类型的多项式，而且相当有效。

最后的探讨

由于伪逆是一种必须使用矩阵才能完成的分解，因此我不会在本文中展示查找常数 < a > 和 < b > 的程序。这是因为我们需要考虑某些解释，以便您真正理解发生了什么。这不仅仅是介绍代码本身，矩阵运算由于其处理过程的特殊性，需要更多的关注。手动操作时，操作相对简单。然而，在代码中实现这一点则完全不同。即使在我们讨论如何在矩阵中使用分解的那些文章中，它们所做的也不是一般性的，而是非常具体的。但为了我们的目的，我们需要一个更通用的代码。否则，将无法正确计算伪逆。