Teoría de Categorías en MQL5 (Parte 23): Otra mirada a la media móvil exponencial doble

Introducción

La implementación operativa de las teoría de categorías en MQL5 parece una tarea difícil. Existen pocos materiales disponibles para el estudio. Claro que hay muchos libros disponibles, pero suelen estar dirigidos a estudiantes universitarios o de posgrado. Tratar de simplificar este tema no es tarea fácil, sobre todo porque el objetivo no es presentar argumentos ni teorías académicas, sino interpretar y aplicar sus principios a los tráders. Para ello, ampliaremos nuestro tema y echaremos un nuevo vistazo a sencillos indicadores de uso cotidiano.

El objetivo de este artículo será destacar el concepto de composición horizontal en las transformaciones naturales. Ya consideramos su antónimo en el anterior artículo, donde vimos cómo podemos derivar tres funtores entre dos categorías, lo que implica dos transformaciones naturales en composición vertical cuando las categorías son conjuntos de datos simples, como series temporales de precios y series temporales de medias móviles de los mismos precios. En este artículo, ampliaremos horizontalmente las series temporales de medias móviles añadiendo una tercera categoría de medias móviles, más conocidas como media móvil exponencial doble. Nuestra variante de este conocido indicador no utilizará esta fórmula literalmente, sino que suavizará la media móvil constituyendo la media móvil de la media móvil. Las relaciones entre funtores serán similares a las que teníamos en el último artículo, pero solo tendremos dos funtores entre categorías en lugar de los tres que teníamos en el artículo anterior. Sin embargo, como en el último trabajo, cada funtor entre dos categorías cualesquiera tendrá su propio periodo de media móvil, por lo que una transformación natural entre cada par de funtores podrá ayudarnos a formar un búfer de series temporales para el análisis.

La importancia de la previsión de la volatilidad en la negociación quizá no sea tan decisiva como la determinación del tipo de posición (larga o corta). No obstante, nos ofrece la oportunidad de explorar cualquier opción potencial para utilizar y mejorar otras estrategias de señales de entrada existentes o incluso crear otras nuevas que utilicen sus ideas. Hemos usado este enfoque muchas veces en artículos anteriores. Intentaremos combinar nuestras previsiones de volatilidad, que se procesarán en el ejemplar de la clase de seguimiento del asesor, con la clase de señal del oscilador Awesome incorporada. Como siempre, los lectores podrán probar esta clase con otras señales o con sus propias estrategias para averiguar qué les funciona mejor. En este artículo analizaremos el oscilador Awesome.

Información general

En artículos anteriores, entre otros, repasamos brevemente conceptos clave de la teoría de categorías: los órdenes como categorías, los funtores, los morfismos como funtores en situaciones especiales y, por último, el cuadrado de la naturalidad, que demuestra la existencia de transformaciones naturales.

Entender qué suponemos por composición "horizontal" de las transformaciones naturales en este artículo es crucial, ya que no nos referimos simplemente a una representación esquemática de las transformaciones naturales en dos dimensiones. Veamos el siguiente esquema:

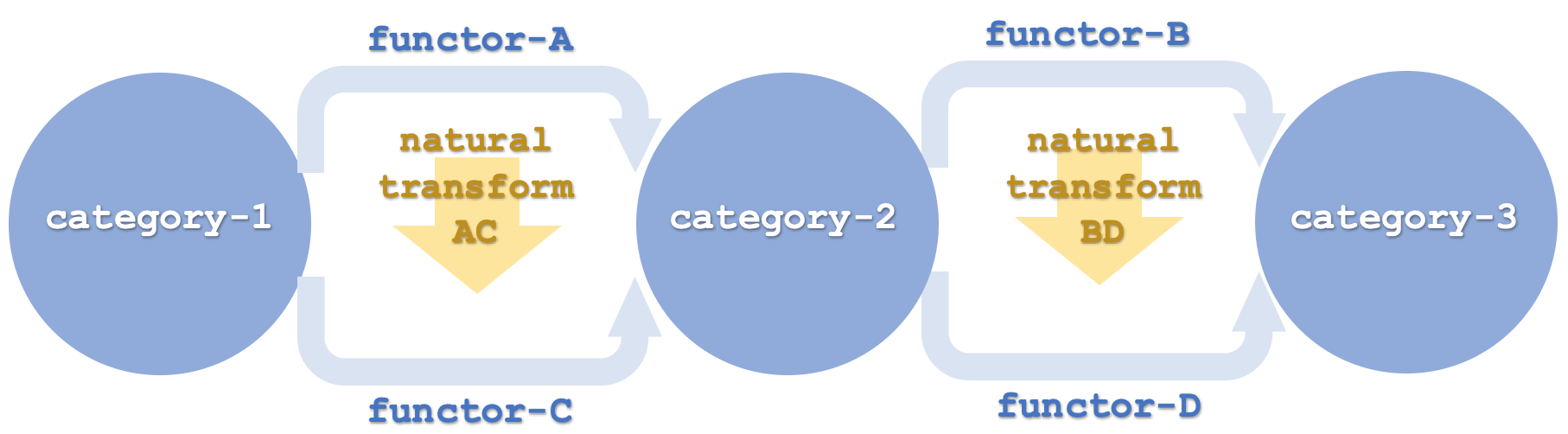
La horizontalidad se utiliza aquí para referirse a los funtores dispuestos en una cadena de tal forma que diferentes pares (o conjuntos) se asocien con diferentes categorías de dominios y codominios, como se muestra arriba, donde los dos primeros funtores A y C vinculan la categoría-1 y la categoría-2, mientras que los funtores B y D vinculan la categoría-2 y la categoría-3. Esto contrasta con el artículo anterior, en el que todos los funtores vinculaban el mismo par de categorías. Incluso si las dos categorías del último artículo se dibujaran verticalmente, lo cual significaría que las transformaciones naturales tendrían lugar horizontalmente, seguiría siendo una composición vertical. Del mismo modo, aunque las categorías se dibujen en una secuencia vertical, lo cual significaría que las transformaciones naturales parecen producirse en un orden "vertical", seguiría considerándose una composición horizontal.

Así pues, nuestras categorías serán series temporales de precios, series temporales de medias móviles y series temporales de medias móviles exponenciales dobles. El uso de series temporales exponenciales dobles puede crear cierta confusión al comparar esta categoría con la de las series temporales de precios. De hecho, la ^3ª categoría supone una media móvil exponencial doble de la categoría-1. Si tomáramos simplemente los funtores B y D como una media móvil exponencial doble para los objetos de categoría 2, el resultado no nos resultaría muy útil. Después de todo, ¿qué es una DEMA de una media móvil? Así, estos funtores parecen representar la categoría 1, es decir, la serie de precios de origen. La estructura deberá considerarse como un mapa de medias móviles de la categoría 2. El lector puede ejecutar sus propias pruebas de la forma correspondiente, ya que el código fuente completo se adjunta al final de este artículo, pero resulta importante tener en cuenta esta distinción.

Categorías y funtores

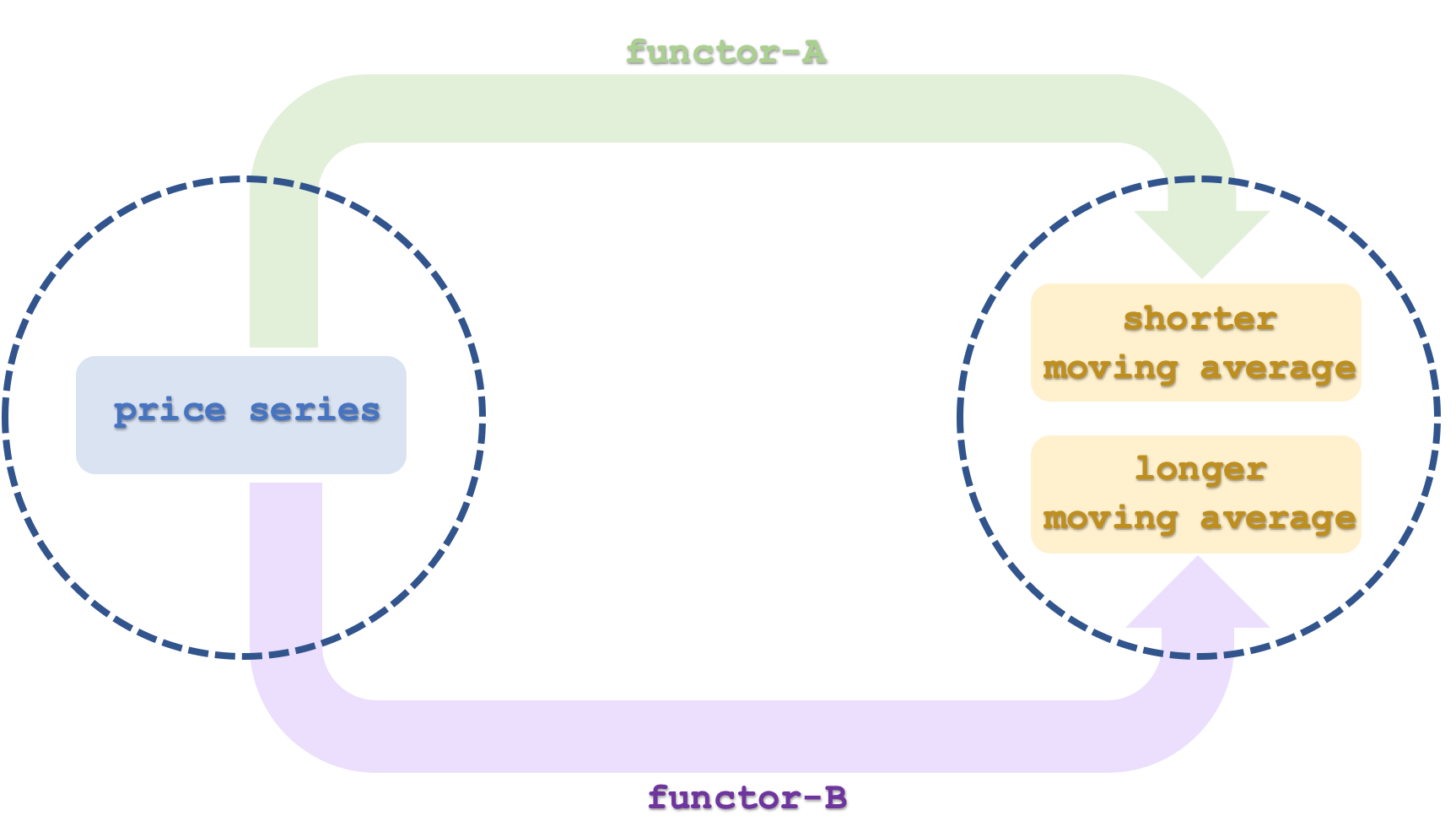
Bien, nuestra primera categoría, la categoría-1, tiene una serie temporal de precios. En un artículo anterior ya vimos cómo el orden puede ser integrado como categoría. Nuestra serie temporal aquí será muy similar al orden lineal, como se indica aquí. Los objetos de esta categoría serán los valores de precio y la hora de cada intervalo, lo cual significa que cada objeto tendrá al menos dos elementos: un precio y un valor de fecha y hora. Los morfismos de una categoría vendrán determinados por el intervalo temporal de la serie. Simplemente vincularán los valores de los precios en orden ascendente a lo largo del tiempo. El instrumento cuyas series temporales analizaremos en este artículo será el EURUSD.

Las medias móviles del precio serán nuestra categoría-2. Al igual que la primera categoría, se trata de una serie temporal, que también puede considerarse un orden lineal y, por consiguiente, una categoría. Constará principalmente de dos objetos, cada uno de los cuales representará una serie temporal. El primero será mapeado por el funtor A y supondrá una media móvil de la serie de precios durante el periodo definido por el funtor A. Este modelo tendrá esencialmente dos periodos de media móvil, y el utilizado por el funtor A será el más corto de los dos. El segundo funtor, denominado C, también representará la serie temporal de precios en la categoría-2 y tendrá un periodo de media móvil más largo que el funtor A. Cada uno de nuestros objetos de la categoría-2 supondrá una serie temporal.

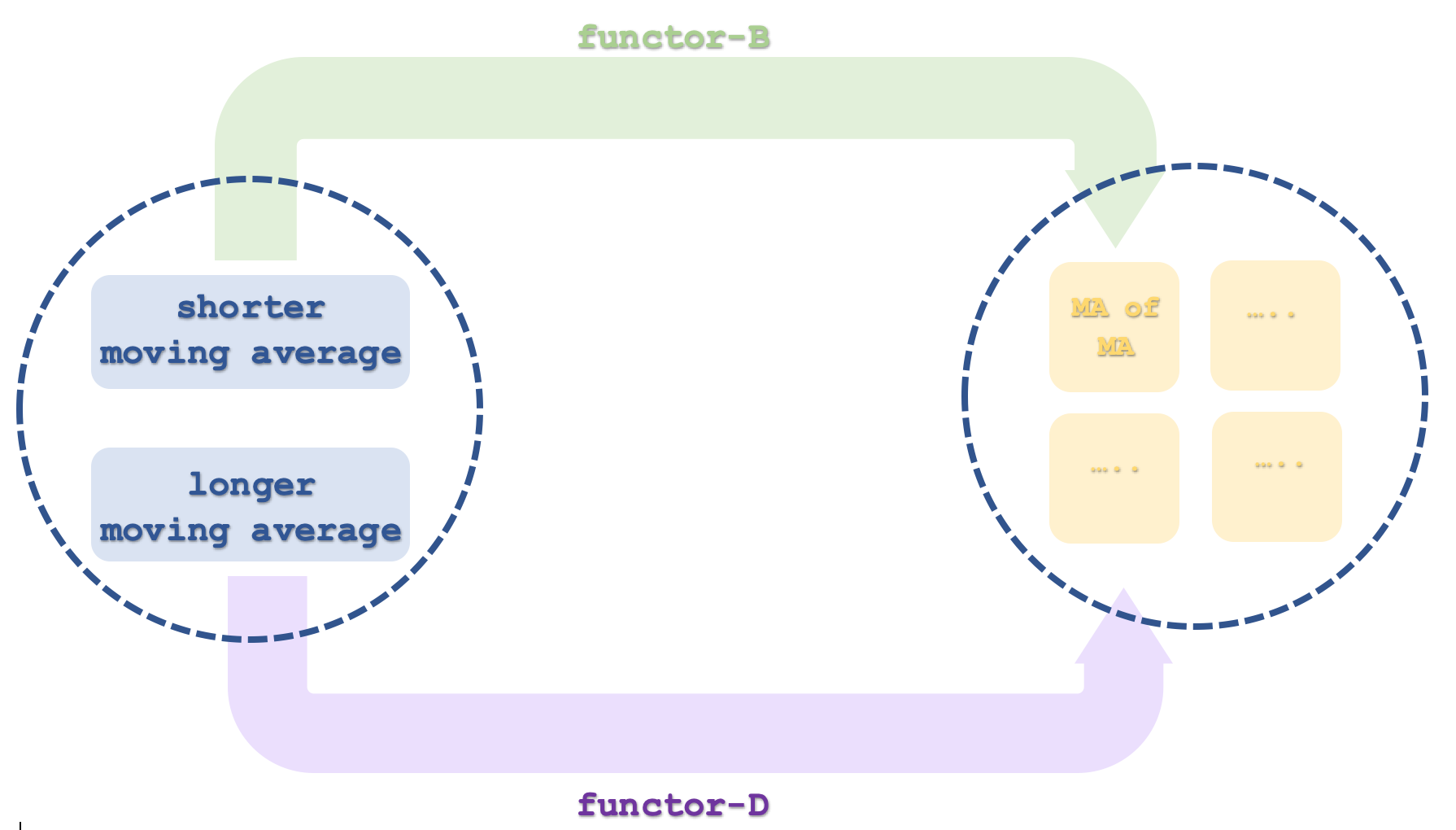
La tercera y última categoría, la categoría-3, incluirá cuatro objetos que supondrán series temporales, aunque solo consideraremos 2. Cada par de objetos (4 objetos son 2 pares) se emparejará con un funtor que calculará la media móvil de la media móvil para obtener la media móvil exponencial doble (DEMA). Como hemos explicado antes, la DEMA desde el código muestra la serie de precios de la categoría-1, pero esto será solo para facilitar los cálculos y no requerirá la creación de un indicador especial. Como se trata de la media móvil de una media móvil, podrá considerarse una representación de la categoría-2. Ahora la categoría-2 tendrá dos series temporales de medias móviles que podrán tomarse como una media móvil rápida y lenta. Sin embargo, esto significa que nuestra categoría-3 tendrá 4 objetos porque cada uno de los dos funtores de la categoría-2 se mapeará con dos objetos, vinculándose así a un objeto o serie temporal específicos.

Funtores y transformaciones naturales

Podrían darse un total de 6 transformaciones naturales a partir de estos dos pares de funtores, pero como solo vamos a utilizar 2 de los 4 objetos de categoría-3, ese número será 2. Recordemos que una transformación natural es la diferencia entre dos objetos de un codominio de funtores. Seguiremos fácilmente esta definición restando los dos objetos de media móvil. Como hicimos en el último artículo, cada transformación natural será capturada como un búfer de series temporales, y la correlación de estos búferes nos ayudará a tomar decisiones sobre el establecimiento de trailing stop(s) en posiciones abiertas. En el último artículo, esta correlación entre los búferes de transformación natural servía de filtro contra el ruido blanco. En el presente artículo, como solo nos interesa el ajuste del trailing stop, servirá de nuevo como filtro si debemos aplicar un ajuste del stop loss respecto a las tendencias de las medias móviles. Así, una tendencia negativa con una correlación positiva entre estos búferes supondría una señal para reducir el stop loss en una posición corta. Del mismo modo, una tendencia positiva con una correlación suficiente (nuestro umbral es superior a cero) indicaría un movimiento de stop loss hacia las posiciones largas, si las hubiera. Por lo tanto, en muchos casos no tendremos señal por correlaciones negativas o porque el tipo de posición que se abra sea incompatible con la señal generada, ya que nuestras decisiones de stop loss serán específicas para cada posición. Como vimos en el último artículo, este modelo puede recrearse como un ejemplar de la clase de señal del asesores e incorporarse al asesor mediante el Wizard, donde nuestras señales pueden probarse más a fondo para evaluar el rendimiento y los resultados.

Previsión de la volatilidad

Por lo tanto, la previsión de la volatilidad es lo que hará nuestro ejemplar de la clase de trailing del asesor, como ha sido el caso en varios artículos de esta serie. Esto se conseguirá mediante un filtro. Las tendencias medias móviles deberán confirmarse mediante una correlación significativa entre los búferes de transformación natural. Otro enfoque de la volatilidad que podríamos adoptar es tener una categoría-1 en forma de rangos de precio (máximos menos mínimos). Entonces las medias de esta serie serán la categoría-2, mientras que la categoría-3 será su DEMA, como hacemos con los precios de cierre en el código adjunto. El proceso resulta muy similar, pero este enfoque puede producir resultados más adaptados y sensibles a la volatilidad.

Aplicación práctica en MQL5

La configuración del entorno MQL5 para este modelo será muy semejante a la que hemos considerado en esta serie. Como ya hemos mencionado, el ejemplar de la clase de trailing del asesor se construye como parte del asesor en el Wizard MQL5. Para que funcione o se pueda poner a prueba, primero tendremos que seleccionar un ejemplar de la clase de señal del asesor en el Wizard. Este artículo utilizará la clase de señal de Awesome Oscillator incorporada. "Incorporada" aquí significa que la clase ya existe en la biblioteca de señales de IDE.

Aquí no deberemos escribir código para los funtores, ya que podemos utilizar ejemplares incorporados de las clases de media móvil. Las clases CiMA y CiDEMA pueden satisfacer fácilmente las necesidades de media móvil y la media móvil exponencial doble. Sin embargo, declararemos y utilizaremos los ejemplares de la clase CObjects para gestionar estos valores medios. Su declaración será la siguiente:

...

   CObjects<double>        m_o_average_a;
   CObjects<double>        m_o_average_b;
   CObjects<double>        m_o_average_c;
   CObjects<double>        m_o_average_d;
...

Al igual que en el artículo anterior, necesitaremos inicializar los búferes de transformación natural, ya que la capacidad de leer señales resulta importante desde el principio. Su tamaño, como antes, será el parámetro de entrada m_transformations, como lo fue en el último artículo, por lo que este importante paso se gestionará de forma casi idéntica a lo que implementamos en el último artículo, con la principal diferencia de que tendremos cuatro ejemplares de media móvil para usar en los búferes. La actualización de estos valores, que también será un poco como la inicialización, se realizará así:

//+------------------------------------------------------------------+
//| Refresh function from Natural Transformations.                   |
//+------------------------------------------------------------------+
void CTrailingCT::Refresh(void)
   {
      if(!m_init)
      {
         Init();
      }
      else
      {
         m_close.Refresh(-1);
         
         int _x=StartIndex();
         
         for(int i=m_functor_ab+m_functor_ab-1;i>0;i--)
         {
            m_e_price.Let();m_e_price.Cardinality(1);m_o_prices.Get(i,m_e_price);m_o_prices.Set(i-1,m_e_price);
         }
         
         double _p=m_close.GetData(_x);
         m_e_price.Let();m_e_price.Cardinality(1);m_e_price.Set(0,_p);m_o_prices.Set(0,m_e_price);
         
         for(int i=0;i<m_transformations+1;i++)
         {
            double _a=0.0;
            for(int ii=i;ii<m_functor_ab+i;ii++)
            {
               _a+=m_close.GetData(_x+ii);
            }
            _a/=m_functor_ab;
            m_e_price.Let();m_e_price.Cardinality(1);m_e_price.Set(0,_a);m_o_average_a.Set(i,m_e_price);
            //
            double _b=0.0;
            for(int ii=i;ii<m_functor_cd+i;ii++)
            {
               m_e_price.Let();m_e_price.Cardinality(1);m_o_average_a.Get(i,m_e_price);
               double _b_i=0.0;m_e_price.Set(0,_b_i);
               _b+=_b_i;
            }
            _b/=m_functor_cd;
            m_e_price.Let();m_e_price.Cardinality(1);m_e_price.Set(0,_b);m_o_average_b.Set(i,m_e_price);
            //
            double _c=0.0;
            for(int ii=i;ii<m_functor_ab+i;ii++)
            {
               _c+=m_close.GetData(_x+ii);
            }
            _c/=m_functor_ab;
            m_e_price.Let();m_e_price.Cardinality(1);m_e_price.Set(0,_c);m_o_average_c.Set(i,m_e_price);
            //
            double _d=0.0;
            for(int ii=i;ii<m_functor_cd+i;ii++)
            {
               m_e_price.Let();m_e_price.Cardinality(1);m_o_average_c.Get(i,m_e_price);
               double _d_i=0.0;m_e_price.Set(0,_d_i);
               _d+=_d_i;
            }
            _d/=m_functor_cd;
            m_e_price.Let();m_e_price.Cardinality(1);m_e_price.Set(0,_d);m_o_average_d.Set(i,m_e_price);
         }
         
         
         for(int i=m_transformations-1;i>0;i--)
         {
            m_natural_transformations_ac[i]=m_natural_transformations_ac[i-1];
            m_natural_transformations_bd[i]=m_natural_transformations_bd[i-1];
         }
         //
         double _a=0.0;
         m_e_price.Let();m_e_price.Cardinality(1);m_o_average_a.Get(0,m_e_price);m_e_price.Get(0,_a);
         double _b=0.0;
         m_e_price.Let();m_e_price.Cardinality(1);m_o_average_b.Get(0,m_e_price);m_e_price.Get(0,_b);
         double _c=0.0;
         m_e_price.Let();m_e_price.Cardinality(1);m_o_average_c.Get(0,m_e_price);m_e_price.Get(0,_c);
         double _d=0.0;
         m_e_price.Let();m_e_price.Cardinality(1);m_o_average_d.Get(0,m_e_price);m_e_price.Get(0,_d);
         
         m_natural_transformations_ac[0]=_a-_c;
         m_natural_transformations_bd[0]=_b-_d;
      }
   }

La función de actualización puede parecer un tanto complicada. Comenzaremos actualizando el puntero del precio de cierre, ya que será la base de la categoría-1. Antes de asignar el último valor a un único objeto de esta categoría, deberemos desplazar todos los elementos existentes dentro de ese objeto. A continuación, haremos casi lo mismo con los dos objetos de la categoría-2. La diferencia aquí reside en que primero deberemos calcular la media móvil para cada periodo respectivo, y una vez hecho esto, asignaremos los valores después de desplazar los valores en ambos objetos como hicimos en la categoría-1. Después, tendremos que ocuparnos de los objetos de la categoría-3. Son cuatro, pero, como ya hemos dicho, solo usaremos dos de ellos para nuestras predicciones. Obtendremos los valores de estos objetos a partir de los dos objetos que acabamos de rellenar, y modificando ligeramente la fórmula de DEMA, que resta la media móvil de la media móvil a la media móvil doble, calcularemos el valor requerido, la media móvil de la media móvil.

La integración de nuestro modelo con los datos de precios diarios de EURUSD para las ejecuciones de prueba se realizará después de construir nuestro ejemplar de clase de trailing del asesor utilizando el Wizard MQL5. Como siempre, hay una guía para esto. Como hemos mencionado antes, construiremos este asesor con el oscilador Awesome como un ejemplar de la clase de señal del asesor.

Las pruebas históricas y el análisis de los datos históricos del EURUSD se realizarán desde el 01.01.2020 hasta el 01.01.2023. A continuación le mostramos nuestro informe de pruebas con los mejores resultados de optimización:

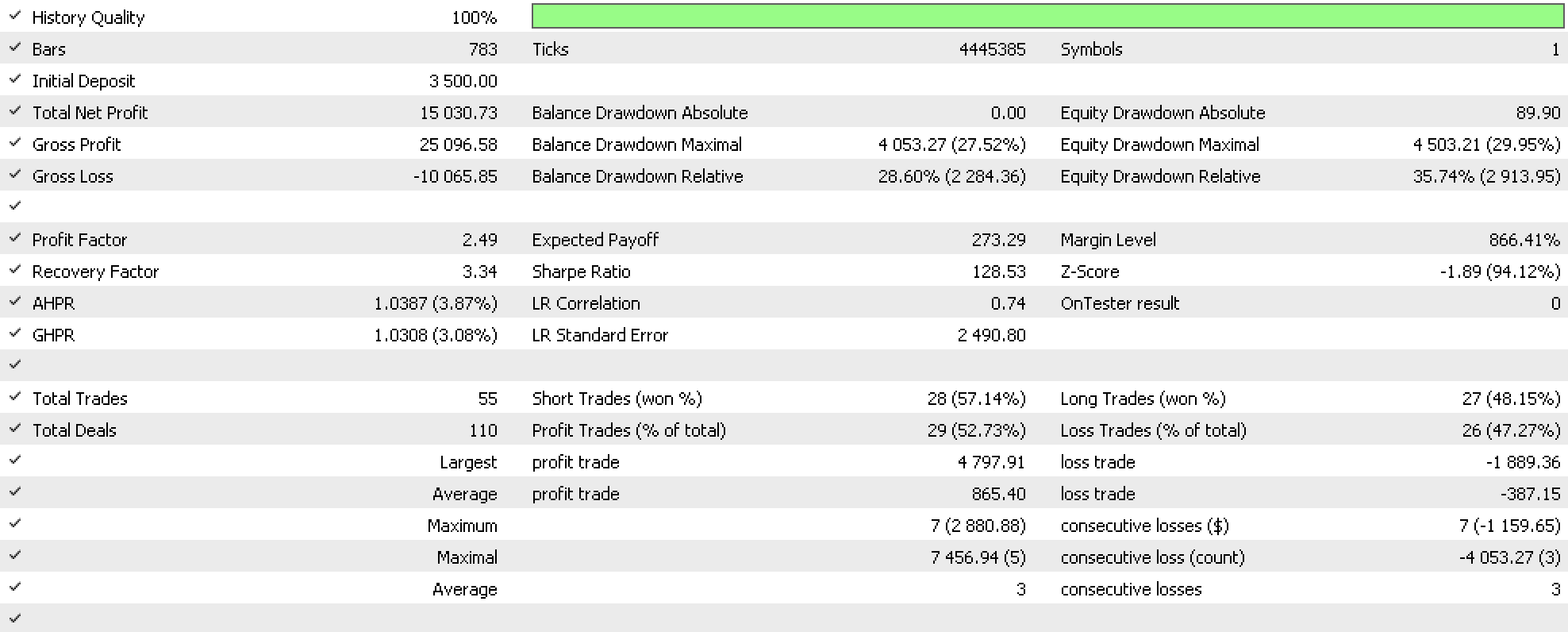
Los aspectos más importantes del informe que merece la pena destacar suelen ser la correlación de beneficio MAE y el periodo de tenencia y correlación de beneficios. Estos dos indicadores suelen presentarse en forma de gráficos en la parte inferior del informe completo. Lo anteriormente mencionado supondrá un resumen de los indicadores más comunes a los que hay que prestar atención.

Pruebas forward

Si realizamos la prueba forward desde el 2023.01.01.01 hasta el 2023.08.01 con la mejor configuración de nuestro backtest, obtendremos los siguientes resultados:

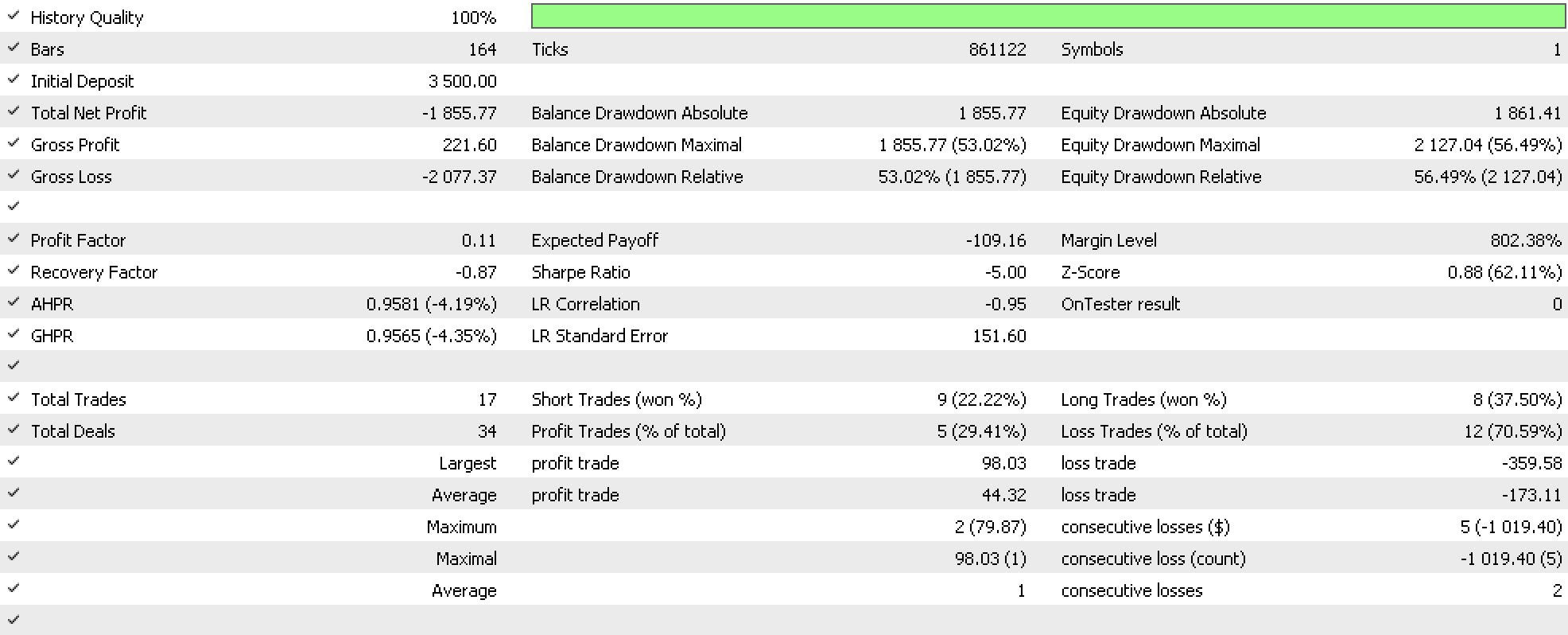
No hemos obtenido los resultados que queríamos, lo cual suele significar una de dos cosas. La tesis de nuestro modelo (uso de la clase trailing) es aleatoria y no se podrá confiar en ella en los sistemas comerciales, o bien hemos implementado la idea con errores que afectan al orden de control en el código de nuestra clase final. No obstante, aunque obtuviéramos un resultado positivo, seguiríamos necesitando realizar pruebas más exhaustivas durante un periodo de tiempo mucho más largo. En el caso de Fórex, esto podría significar hasta dos décadas, y estas pruebas deberían incluir ejecuciones en ticks reales. Las "señales" únicas de ajuste del trailing stop generadas por nuestro asesor no ocurren muy a menudo, porque la tendencia de la media móvil debe estar en la dirección de la posición abierta. Por este motivo, la eficacia de la clase de trailing no se ha verificado lo suficiente en periodos de prueba cortos, uno de los cuales es un periodo de tres años. Además, estos resultados se basan en la combinación de nuestra clase de trailing con el oscilador Awesome, pero ¿cómo sería el rendimiento si se combinara con otras señales de entrada? Todas estas y otras cuestiones deberán considerarse a la hora de realizar una evaluación.

La prueba con datos reales es otro paso necesario antes de desplegar este asesor o una variante del mismo que incorpore lo que hemos tratado aquí. El primer paso en este proceso será crear una cuenta demo con nuestro posible bróker; en condiciones ideales, con el mismo tipo de cuenta que utilizaremos en tiempo real. A continuación, adjuntaremos el asesor al gráfico del símbolo o los símbolos comerciados. También será una buena idea utilizar el servicio MetaQuote VPS, ya que supone un menor quebradero de cabeza a la hora de configurar todo y tiene un precio competitivo; pero cualquiera que sea la elección, la necesidad de supervisar el diario de registro del asesor seguirá siendo clave, ya que esto nos permitirá alcanzar el rendimiento esperado y los resultados comerciales requeridos. Tanto MetaQuote VPS como un servidor VPS normal nos permitirán hacer esto fácilmente. Además, la cuenta demo en el modo de tiempo real deberá comenzar con la cantidad de capital que se utilizará si la prueba resulta positiva. Por último, un diario personal de negociación sería otra buena idea, especialmente si las ideas aquí presentadas pasan a formar parte de otro sistema comercial que dependa de las noticias de una forma u otra. Tenga en cuenta que el Simulador de Estrategias MQL5 aún no permite realizar pruebas cuando se leen los eventos del calendario económico, por lo que podría resultar útil registrarlos por uno mismo, para que al visualizarlos podamos evaluar fácilmente la importancia relativa de cada noticia a largo plazo.

Interpretar los resultados y decidir qué hacer a continuación es algo muy subjetivo, pero como punto de referencia podemos argumentar que en un sistema lo suficientemente rentable como para cumplir los requisitos de los objetivos, la correlación entre el beneficio y el MAE debería ser positiva, y tanto el periodo de mantenimiento como el beneficio de cada operación deberían tener una correlación positiva. La última métrica suele denominarse esperanza, pero por desgracia este valor no se calcula en los informes de los simuladores de estrategias.

Conclusión

Hoy hemos visto cómo la composición horizontal de las transformaciones naturales puede resultar útil en la previsión. Las previsiones que hemos analizado en este artículo se refieren a los rangos de barras de precio que pueden considerarse una medida de la volatilidad. Estas previsiones se han usado (como se ha hecho varias veces en esta serie de artículos) ajustando el trailing stop de las posiciones abiertas. Aunque los resultados del entrenamiento dentro de la muestra han sido positivos, los resultados fuera de la misma han resultado peores. No obstante lo dicho, este fallo no quita la necesidad de realizar pruebas más exhaustivas durante un periodo de tiempo más largo antes de poder emitir un veredicto sobre la eficacia del sistema.

Las implicaciones de estos resultados para el desarrollo del sistema comercial suponen que estos pueden combinarse con diferentes clases de señales de entrada para producir mejores resultados, o incluso podemos modificar nuestros conjuntos de datos de entrada para representar diferentes escenarios de prueba.

Como siempre, invito al lector a explorar estas y otras formas de introducir cambios y probar el código adjunto.

Enlaces

Los enlaces, como siempre, son en su mayoría a artículos de la Wikipedia Pero esta vez hay algunos de la Investopedia

Encontrará más información sobre la creación y el uso del código incluido en el asesor aquí y aquí.