Teoría de categorías en MQL5 (Parte 8): Monoides

Introducción

En un artículo anterior sobre teoría de categorías, descubrimos los conceptos clave de los conjuntos múltiples, relativos e indexados y analizamos sus implicaciones para el comercio algorítmico. Continuando con el tema, hoy presentamos el concepto de monoide. Los monoides ocupan un lugar importante en las matemáticas y la informática, pues ofrecen un enfoque estructurado de la modelación de operaciones en conjuntos de elementos.

Por definición, los monoides son un conjunto de tres elementos, concretamente, de conjuntos; una operación binaria que toma dos elementos cualquiera de este conjunto y siempre genera un elemento que también es miembro del mismo, y un elemento de identidad (identity element) que pertenece al conjunto, de forma que cuando se conjuga con cualquier otro miembro de este conjunto en la operación binaria anterior, siempre obtenemos un elemento que es diferente de aquel con el que se conjuga el actual elemento de identidad. Esta operación binaria también es asociativa. En otras palabras, un monoide es una forma de combinar elementos en un conjunto según unas reglas predefinidas. Los monoides ofrecen un enfoque sistemático y flexible para la adición y el procesamiento de datos.

Formalmente, un monoide M con elementos-miembros a, b y c; un elemento de identidad e; una operación binaria *; puede ser definido como:

M * M - - > M;                      1

e * a - - > a;                        2

a * e - - > a;                        3

a * (b * c) - - > (a * b) * c     4

En la ecuación 1 se enfatiza que la unión de dos elementos cualesquiera de un conjunto en un par da un elemento del conjunto. En las ecuaciones 2 y 3 se enfatiza la importancia del elemento de identidad en el sentido de que siempre terminamos con un elemento de operación binaria que no supone una identidad. Finalmente, en la ecuación 4 se enfatiza la asociatividad de la operación binaria *.

Ilustración y métodos

Para ilustrar el uso potencial de los monoides por parte de los tráders, consideraremos cinco cuestiones que algunos o la mayoría de los tráders pueden enfrentar antes de realizar transacciones:

1. La duración del periodo retrospectivo.
2. El marco temporal del gráfico que se utilizará.
3. El precio aplicado.
4. El parámetro aplicado.
5. Y si merece la pena, dada esta información, operar en un rango o tendencia.

Para cada una de estas soluciones, pensaremos:

• un conjunto de valores posibles entre los que elegir;
•  una operación binaria que nos ayude a elegir entre dos elementos cualesquiera. Esta operación puede ser un método MQL5 que sea llamado por otro método de forma iterativa sobre todos los elementos de los conjuntos hasta que se realice una selección.
• Y también el índice del elemento de identidad de este conjunto. Precisamente el índice, ya que este elemento está incluido en el conjunto que es un array.
• La elección de una operación binaria ideal que simplemente elija entre dos elementos supone una elección entre:
• La operación de selección del menor de dos elementos.
•  La operación para elegir el mayor de dos elementos a evaluar
•  La operación que elige de un conjunto el elemento más próximo a la media de los dos elementos de la operación binaria.
•  Y por último, la operación que elige de un conjunto el elemento que está más alejado de la media de los dos elementos de la operación binaria.

Vamos a analizar cinco puntos de decisión: el periodo retrospectivo, el marco temporal, el precio aplicado, el indicador y la interpretación de la señal. Otros tráders pueden tener otros criterios en cuanto a la decisión clave. Por lo tanto, no estamos ante una guía paso a paso definitiva, sino ante criterios seleccionados en el marco del artículo.

Al utilizar monoides de teoría de categorías para clasificar datos, debemos tomar algunas precauciones para garantizar resultados precisos y significativos. Los parámetros más importantes son:

1) Una estructura monoide bien definida:

Debemos asegurarnos de que los datos con los que estamos trabajando formen la estructura monoide correcta tal como se define. Esto implica comprobar que cumplan con los axiomas de un monoide, como la presencia de un elemento de identidad y asociatividad bajo una operación binaria. Aquí tenemos tres ejemplos de trampas que pueden llevarnos a una estructura monoide mal definida:

Ausencia de cierre:

Si una operación binaria utilizada en un monoide no da como resultado elementos que pertenezcan al mismo conjunto o dominio, el cierre se romperá. Por ejemplo, si intentamos definir un monoide de números naturales usando la operación de resta, encontraremos elementos que no son números naturales (por ejemplo, si restamos 5 a 3 tendremos -2, que no es un número natural). La operación, estrictamente hablando, no supone ni una suma, ni una resta, ni una multiplicación, es solo un método bien definido que toma dos elementos cualesquiera de un conjunto y retorna un elemento que es miembro de ese conjunto.

No asociatividad:

Otra dificultad surge cuando la operación binaria no cumple la propiedad de asociatividad. Si los elementos de nuestro monoide no se combinan de manera asociativa, esto puede conducir a resultados ambiguos e inconsistentes. Por ejemplo, consideremos un monoide en el que la operación es la multiplicación y los elementos son matrices. Si tenemos tres matrices a, b y c, entonces esta operación no será asociativa, es decir, (a * b) * c ≠ a * (b * c), por lo que la estructura monoide se romperá.

La ausencia de un elemento de identidad:

Todo monoide debe tener un elemento de identidad que actúe como elemento neutro en una operación binaria. Si en un monoide no hay un elemento de identidad, realizar operaciones con ciertos elementos se volverá algo problemático. Por ejemplo, si definimos un monoide de números reales usando el operador de división, entonces no habrá elemento de identidad, ya que la división por cero no está definida.

A continuación le mostramos tres ejemplos de estructuras monoides regulares:

Suma de números enteros:

El conjunto de números enteros con la operación binaria de suma (+) forma un monoide. El elemento de identidad es 0, mientras que la suma es asociativa y cerrada sobre el conjunto de los enteros.

Multiplicación de números racionales distintos de cero:

El conjunto de números racionales distintos de cero (fracciones) con la operación de multiplicación binaria (×) forma un monoide. El elemento de identidad es 1, mientras que la multiplicación es asociativa y cerrada para números racionales distintos de cero.

Concatenación de líneas:

Un conjunto de líneas con una operación de concatenación binaria forma un monoide. El elemento de identidad es la línea vacía (""), mientras que la concatenación es asociativa y cerrada para líneas.

Estos ejemplos demuestran estructuras monoides bien definidas que cumplen las propiedades requeridas y se pueden usar de forma efectiva con fines clasificatorios.

2) Semántica e interpretabilidad:

Debemos comprender la semántica de una operación monoide y cómo se relaciona con sus datos. Consideremos si las clasificaciones resultantes corresponden a las interpretaciones previstas y si tienen sentido en el contexto de su área temática. A continuación le presentamos cinco ejemplos ilustrativos:

Clasificación de la frecuencia de palabras:

Supongamos que utilizamos monoides para clasificar las previsiones trimestrales de una empresa a partir de las transcripciones de las llamadas según la frecuencia de las palabras. Si bien una operación monoide puede implicar simplemente la suma del número de palabras, la interpretabilidad de las clasificaciones resultantes debe considerarse con especial cuidado, ya que dependerá de la semántica asignada a los diferentes rangos de frecuencia. Por ejemplo, podemos interpretar los documentos con una alta frecuencia de palabras como más centrados en un tema en particular, mientras que una baja frecuencia de palabras puede indicar un contenido más amplio o variado. No debe centrarse solo en el número total de palabras y utilizarlo como base para sus operaciones monoide clave.

Análisis de sentimiento:

Digamos que estamos usando un monoide para clasificar el sentimiento de un texto. La operación monoide podría funcionar mejor si añade las puntuaciones de sentimiento de palabras u oraciones individuales. Consideremos el siguiente ejemplo. Supongamos que tenemos muchas reseñas de clientes sobre un producto y deseamos organizarlas en tres categorías de sentimiento: positivo, neutro y negativo. Entonces decidimos utilizar un enfoque monoide donde la operación monoide implica añadir las puntuaciones de opinión de las oraciones individuales en cada revisión. En este ejemplo, asignamos un estado de ánimo en el rango de -1 a 1, donde -1 representa un estado de ánimo muy negativo, 0 es un estado de ánimo neutro y 1 es un estado de ánimo muy positivo. La operación monoide luego realizará una suma simple de las puntuaciones de sentimiento. Echemos un vistazo a los comentarios de los clientes:

Comentario: "El producto es bueno, pero el servicio al cliente deja mucho que desear."

La forma correcta de categorizar este comentario es dividirlo en oraciones individuales y asignar puntajes de opinión a cada oración:

Oración 1: "El producto es bueno". - Valoración del sentimiento: 0,8 (positivo)

Oración 2: "Pero el servicio al cliente deja mucho que desear". - Valoración del sentimiento: -0,7 (negativo)

Luego, para tener una valoración del sentimiento general para el comentario, aplicaremos una operación monoide, que en este caso será la sumatoria:

Valoración general del sentimiento = 0,8 + (-0,7) = 0,1

En función de la semántica asignada a los rangos de puntuación del sentimiento, interpretaremos una puntuación de sentimiento general de 0,1 como ligeramente positiva. Por lo tanto, clasificaremos este comentario como "neutral" o "ligeramente positivo" según la clasificación monoide. Si ambas oraciones se consideraran en su conjunto, entonces la valoración sería positiva debido a la presencia de la palabra "bueno", cosa que, por supuesto, no es cierta. Como ve, hay detalles a tener en cuenta.

Clasificación de imágenes:

Un monoide para clasificar imágenes según características visuales como el color, la textura o la forma implicará la unión de estas características, y la interpretabilidad de estas características combinadas que dan como resultado una clasificación dependerá de cómo las asignemos a sus categorías previstas o significativas. La semántica asignada a diferentes combinaciones de características puede influir en gran medida en la forma en que comprendemos los resultados de la clasificación.

Vamos a considerar el siguiente ejemplo para mostrar la importancia de la semántica y la interpretabilidad en la clasificación de imágenes usando monoides. Supongamos que estamos utilizando un enfoque monoide para clasificar las imágenes en dos categorías: "Perro" y "Gato", en función de las características visuales. Para los tráders, la clasificación de imágenes puede ser reemplazada por, digamos, patrones de cabeza y hombros alcistas y bajistas, pero el principio sigue siendo el mismo. La operación monoide implicará combinar las características de color y textura leídas de las imágenes. En el marco de nuestra tarea, digamos que tenemos dos características visuales clave: "Color del pelaje" y "Complejidad de la textura". El color del pelaje se puede clasificar como "claro" u "oscuro", mientras que la complejidad de la textura se puede clasificar como "simple" o "compleja". Ahora veamos dos imágenes.

Supongamos que la imagen 1 tiene un gato blanco con una textura de piel simple, lo cual implicará:

• Color del pelaje: Claro
• Complejidad de la textura: Simple
• Supongamos que en la imagen 2 hay un perro negro con una textura de pelaje compleja, esto implicará:
• Color del pelaje: Oscuro
• Complejidad de la textura: Compleja

Para clasificar estas imágenes usando un enfoque monoide, combinaremos las características visuales según una operación monoide (como concatenación, suma, etc.):

Para la imagen 1: "Claro" + "Simple" = "ClaroSimple"

Para la imagen 2: "Oscuro" + "Compleja" = "OscuroCompleja"

Ahora viene el momento más importante: la semántica y la interpretabilidad. Debemos asignar un valor a las características combinadas para asignarlas de nuevo a categorías significativas. En nuestro caso, ya que estamos usando un ejemplo muy simple:

"ClaroSimple" puede interpretarse como la categoría "Gatos" porque el color del pelaje claro y la textura simple son rasgos comunes de los gatos.

"OscuroCompleja" se puede interpretar como la categoría "Perros", ya que el color oscuro del pelaje y la textura compleja a menudo se asocian con los perros.

Asignando la semántica y la interpretación correspondiente a las características combinadas, podremos clasificar correctamente la imagen 1 como "Gato" y la imagen 2 como "Perro".

Segmentación de clientes:

Supongamos que usa monoides para segmentar a los clientes en función de su comportamiento de compra. Una operación monoide puede incluir la adición de datos de transacciones o atributos de clientes. No obstante, la interpretabilidad de los segmentos resultantes dependerá de cómo interpretemos y etiquetemos esos segmentos. Por ejemplo, podemos asignar atributos como "clientes valiosos" o "clientes a punto de abandonar" según la semántica y el conocimiento del área objeto.

Clasificación de series temporales:

Vamos a considerar la posibilidad de usar monoides para clasificar los datos de las series temporales como tendencias del mercado de valores. Una transacción monoide puede incluir una combinación de diferentes características, como el precio, el volumen y la volatilidad. No obstante, la interpretabilidad de las clasificaciones dependerá de cómo definamos la semántica de las combinaciones resultantes en relación con las condiciones del mercado. Diferentes interpretaciones pueden llevarnos a diferentes conclusiones e implicaciones en la toma de decisiones.

En todos estos ejemplos, la semántica asignada a la operación monoide y las clasificaciones resultantes serán fundamentales para una interpretación significativa, así como en la toma de decisiones. La consideración cuidadosa de esta semántica nos asegurará que las clasificaciones resultantes se ajusten a las interpretaciones requeridas y permitan un análisis y una comprensión eficientes de los datos.

3) Preprocesamiento de datos:

Esto es importante en relación al control de calidad de los datos antes de clasificarlos con monoides. Es recomendable preprocesar los datos para garantizar la compatibilidad con la estructura monoide. Por ejemplo, todos los resultados de una función operativa deberán ser miembros definidos de un conjunto monoide, no datos flotantes con múltiples puntos decimales que puedan resultar ambiguos al redondearse. Esto se puede conseguir normalizando los datos (regularización) o convirtiéndolos a un formato adecuado para la operación monoide. Asimismo, también será necesario abordar el problema del manejo de los valores ausentes para que nuestro sistema comercial sea más consistente en general.

4) Homogeneidad de los datos:

Asegúrese de que los datos a clasificar tengan cierto grado de homogeneidad dentro de cada categoría. Por ejemplo, en la etapa de selección de parámetros, el monoide del conjunto que usaremos deberá tener ambos indicadores con valores o pesos consistentes y comparables. Como estamos utilizando el oscilador RSI y las bandas de Bollinger, claramente este no será el caso por defecto. No obstante, normalizaremos uno de ellos para asegurar su comparabilidad y homogeneidad. Los monoides funcionan mejor al aplicarse a datos que exhiben características similares en cada clase.

5) Número cardinal de categorías:

Vamos a analizar el número cardinal, o el número de categorías distintas que se pueden formar con un monoide. Si el número de categorías resultantes es demasiado grande o demasiado pequeño, la utilidad de la clasificación o la interpretabilidad de los resultados podrían verse afectadas.

Ahora ilustraremos la influencia del número cardinal de estas categorías con un ejemplo:

Supongamos que estamos trabajando en un problema de clasificación para predecir la dirección de una pareja de divisas según el sentimiento de los eventos de las noticias del calendario, y que tenemos un conjunto de datos con una variable de destino "Sentimiento" que puede tomar tres valores posibles: "por encima de lo esperado ", "se corresponde con las expectativas" y "por debajo de lo esperado".

Aquí tenemos un conjunto de datos de ejemplo:

Índice	Sentimiento
Producción manufacturera de la Fed m/m	por debajo
Índice de precios de GDT	se corresponde
Inventarios de las empresas m/m	por encima
Índice del mercado de la vivienda NAHB	por debajo

En este ejemplo, podemos notar que la variable "Sentimiento" tiene tres categorías: "Por encima", "Se corresponde" y "Por debajo". El número cardinal se refiere al número de categorías distintas en una variable.

El número cardinal de la variable "Sentimiento" en este conjunto de datos es 3 porque la variable tiene tres categorías únicas.

El número cardinal de estas categorías puede resultar importante para problemas de clasificación. Consideraremos dos escenarios:

Escenario 1:

Aquí tenemos un número cardinal desequilibrado que conduce a un conjunto de datos desequilibrado donde la categoría "Por encima" tiene significativamente más muestras en comparación con las categorías "Se corresponde" y "Por debajo". Por ejemplo, supongamos que el 80% de las muestras están etiquetadas como "Por encima", el 10% están etiquetadas como "Se corresponde" y el 10% están etiquetadas como "Por debajo".

En este escenario, un número cardinal desequilibrado podría introducir un error sistémico en el modelo de clasificación. El modelo puede predecir más a menudo la clase mayoritaria ("Por encima"), sin embargo, puede tener dificultades para predecir las clases minoritarias ("Se corresponde" y "Por debajo"). Esto puede provocar que se reduzcan la precisión y la recuperación para las clases minoritarias, lo cual influye en el rendimiento general y la interpretabilidad del modelo de clasificación.

Escenario 2:

En este caso, en lugar de asignar valores string a los elementos de nuestro conjunto monoide, como en el caso anterior, usaremos datos de coma flotante para ponderar y describir con mayor precisión cada elemento del conjunto monoide. Es decir, tendremos un número cardinal ilimitado, lo cual significa que no hay un número establecido de pesos/valores posibles para cada uno de los elementos del conjunto, a diferencia del escenario 1.

6) Escalabilidad:

La estimación de la escalabilidad de la clasificación monoide resulta especialmente necesaria al trabajar con grandes conjuntos de datos. Dependiendo de la complejidad computacional, es posible que sea necesario considerar métodos alternativos u optimizaciones para procesar de forma eficiente grandes cantidades de datos. Un enfoque interesante a la hora de trabajar con grandes conjuntos de datos consiste en realizar ingeniería de características. Los homomorfismos monoides se pueden utilizar en la ingeniería de características para varios problemas. Uno de ellos puede ser la valoración de una empresa pública:

los homomorfismos pueden transformar las características de entrada en un nuevo espacio de características con un poder predictivo más preciso para los modelos de puntuación. Tomemos un ejemplo con un conjunto de datos que contiene varios indicadores financieros, tales como ingresos, beneficio, activos y pasivos para un conjunto de empresas públicas.

Un enfoque común sería usar homomorfismos monoides para obtener y centrarse en ratios financieros clave ampliamente utilizados en los modelos de valoración. Por ejemplo, podemos definir un homomorfismo que asigne un conjunto de monoides de ingresos a un nuevo conjunto normalizado de monoides que representen la tasa de crecimiento de los ingresos. Esta transformación reducirá claramente los requisitos de nuestros datos al hacer que nuestros monoides resulten más escalables, porque muchas empresas que figuran de forma independiente en el conjunto de monoides de ingresos tendrán la misma tasa de crecimiento de ingresos en el codominio.

De manera similar, podemos usar un homomorfismo monoide para asignar un monoide de ganancias a un monoide que represente las ganancias por acción (earnings per share, EPS). Las EPS son una métrica de valoración ampliamente utilizada que mide las ganancias por acción de una empresa. Existen muchos otros coeficientes importantes. Todos ellos tienen el mismo objetivo: mantener la escalabilidad del modelo de clasificación monoide.

Por otro lado, debemos minimizar nuestra dependencia de los entornos informáticos distribuidos, como Apache Hadoop o Apache Spark, para procesar datos en paralelo en varios nodos de un clúster. Estos enfoques permiten distribuir la carga de trabajo y acelerar el tiempo de procesamiento, lo cual posibilita el procesamiento de grandes conjuntos de datos; sin embargo, esto requerirá costes significativos posteriores. Y decimos "posteriores", porque todos los problemas que estamos tratando de resolver podrían haberse resuelto de manera más elegante a nivel de diseño monoide.

7) Generalización:

La generalización de los resultados de clasificación debe evaluarse utilizando datos nuevos e invisibles. Los métodos de clasificación basados ​​en monoides deben posibilitar una categorización fiable y consistente en diferentes conjuntos de datos y contextos.

Supongamos que estamos desarrollando una clasificación basada en monoides para predecir la solvencia de prestatarios potenciales. Nuestro conjunto de datos contendrá datos crediticios históricos, como ingresos, rating crediticio, relación deuda-ingresos, historial de empleo, etc.

Para evaluar la generalización de los resultados de clasificación, deberemos valorar cómo de bien rinde el modelo con datos nuevos e invisibles. Por ejemplo, tras entrenar un modelo con un conjunto de datos de una región o periodo temporal en particular, deberemos probarlo con un conjunto de datos de una región o periodo temporal distinto. Si el modelo muestra una categorización consistente y sólida en este y otros conjuntos de datos diversos, esto indicará una buena generalización.

A la hora de lograr la generalización en los métodos de clasificación basados ​​en monoides, las posibles dificultades incluyen el sobreajuste, el desplazamiento de datos y el desplazamiento de selección de características. El sobreajuste ocurre cuando, por ejemplo, una función de operación monoide se vuelve demasiado específica para los datos de entrenamiento, lo cual provoca un rendimiento deficiente en los datos nuevos. Por el contrario, el desplazamiento de datos puede ocurrir si el conjunto de datos de entrenamiento no es representativo de un conjunto más amplio, lo cual da como resultado una clasificación sesgada. Si se da un desplazamiento en la selección de características, elegir características que no capten la información relevante para el contexto dado influirán en la generalización del modelo.

8) Métricas de evaluación:

Debemos determinar las métricas apropiadas para evaluar la calidad y eficiencia de la clasificación monoide. Dichas métricas deben ser relevantes para nuestro problema y los objetivos específicos, considerando factores como la precisión, la validez, el recuerdo o la puntuación F1.

9) Sobreajuste y subajuste:

Debemos evitar el sobreajuste y el subajuste del modelo de clasificación monoide. Utilizaremos técnicas como la validación cruzada, la regularización o la interrupción anticipada para evitar estos problemas y ayudar a modelar la generalización.

10) Interpretabilidad y explicabilidad:

Vamos a considerar la interpretabilidad y explicabilidad de las clasificaciones resultantes. Los monoides pueden ofrecernos poderosas posibilidades de clasificación, pero es importante comprender cómo se toman las decisiones de clasificación y poder explicarlas.

Implementación

Periodo de análisis retrospectivo:

Utilizaremos un dominio monoide de 8 números enteros del 1 al 8 para representar las opciones para los periodos retrospectivos disponibles. Una unidad de periodo será equivalente a cuatro, y nuestro marco temporal de prueba se fijará en una hora, aunque el marco temporal de nuestro análisis variará, como se describe en la siguiente sección. En cada nueva barra, tendremos que seleccionar un periodo. La unidad de medida de cada uno de ellos será el porcentaje relativo del movimiento de este periodo respecto al anterior de igual duración. Por ejemplo, si el cambio de precio en puntos para el periodo 1 (4 barras) fue A y el periodo anterior fue B, entonces el peso o valor del periodo 1 vendría dado por la siguiente fórmula:

= ABS(A)/(ABS(A) + ABS(B))

donde la función ABS() representa el valor absoluto. Esta fórmula se verifica en cuanto a la división por cero, garantizando así que el mínimo denominador sea comparable con el coste del valor en cuestión.

Nuestra operación monoide y el elemento de identidad serán elegidos de la optimización por los siguientes métodos ofrecidos al principio del artículo.

Marco temporal:

Un conjunto monoide para un marco temporal tendrá ocho marcos temporales, de la siguiente manera:

• PERIOD_H1
• PERIOD_H2
• PERIOD_H3,
• PERIOD_H4,
• PERIOD_H6,
• PERIOD_H8,
• PERIOD_H12,
• PERIOD_D1

La ponderación y la asignación del valor de cada uno de estos marcos temporales seguirán el mismo patrón que el anterior en el periodo retrospectivo, lo cual significará que compararemos los cambios porcentuales en el precio de cierre según los cambios anteriores de la barra de precios en el marco temporal correspondiente.

Precio aplicado:

El monoide de un conjunto de precios aplicados tendrá cuatro posibles precios aplicados para elegir:

• MODE_MEDIAN ((High + Low) / 2)
• MODE_TYPICAL ((High + Low + Close) / 3)
• MODE_OPEN
• MODE_CLOSE

La ponderación y asignación de valores aquí será diferente a la que indicamos anteriormente. En este caso, utilizaremos la desviación estándar de cada precio aplicado para el periodo seleccionado en el periodo retrospectivo para determinar el peso o valor de cada precio aplicado. El funcionamiento y la selección del índice de identidad será el mismo que hemos descrito anteriormente.

Indicador:

El conjunto de monoides para seleccionar un indicador tendrá solo dos opciones, a saber:

• Oscilador RSI
• Bandas de Bollinger

El oscilador RSI está normalizado en el rango de 0 a 100; las bandas de Bollinger no solo no están normalizadas, sino que también tienen varios flujos de búfer. Para normalizar las Bandas de Bollinger y hacerlas comparables con el oscilador RSI, tomaremos la diferencia entre el precio actual y la banda base C y la dividiremos por el tamaño de la brecha entre las bandas superior e inferior D. Entonces, nuestro valor para las bandas primero tendrá el aspecto siguiente:

= C/(ABS(C) + ABS(D))

Al igual que antes, este valor se comprobará en cuanto a la división por cero. Sin embargo, este valor puede ser negativo y tiende a un valor decimal de 1,0. Para normalizar estos dos aspectos y obtenerlos entre 0 y 100 como RSI, añadiremos 1,0 para asegurarnos de que siempre sea positivo y luego multiplicaremos la suma por 50,0 para asegurarnos de que esté en el rango de 0 a 100. Por consiguiente, nuestros valores, que ahora oscilarán entre 0 y 100 tanto para RSI como para las Bandas de Bollinger, representarán nuestro peso, y la función del operador y el índice del elemento se elegirán como se especifica en los métodos anteriores.

Solución:

Para este último monoide, nuestro conjunto también tendrá solo dos opciones.

• Comercio de tendencia
• Comercio en el rango

Para cuantificar estos dos elementos, consideraremos, durante el periodo retrospectivo seleccionado, la cantidad de puntos de precio que un valor retrocede frente a su tendencia probable al final del periodo como el porcentaje del rango de precios total de ese periodo. Deberá ser un valor decimal entre 0,0 y 1,0, y medirá directamente el peso del comercio de rango, lo cual significa que una operación de tendencia será igual a este valor restado de 1.0. El método de trabajo y la selección del índice serán como más arriba.

A continuación le mostramos la implementación de nuestras soluciones monoides como un ejemplar de la clase de trailing incorporada del asesor.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingCT::Operate_8(CMonoid<double> &M,EOperations &O,double &Values[],int &InputIndices[],int &OutputIndices[])
   {
      for(int i=0;i<8;i++)
      {
         m_element.Let();
         if(m_lookback.Get(i,m_element))
         {
            if(!m_element.Get(0,Values[InputIndices[i]]))
            {
               printf(__FUNCSIG__+" Failed to get double for 1 at: "+IntegerToString(i+1));
            }
         }
         else{ printf(__FUNCSIG__+" Failed to get element for 1 at: "+IntegerToString(i+1)); }
      }
      
      //
      
      if(O==OP_LEAST)
      {
         for(int i=0;i<8;i+=2)
         {
            if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[i/2]=i; }
            else if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[i/2]=i+1; }
            else { OutputIndices[i/2]=m_lookback.Identity(); }
         }
      }
      else if(O==OP_MOST)
      {
         for(int i=0;i<8;i+=2)
         {
            if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[i/2]=i; }
            else if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[i/2]=i+1; }
            else { OutputIndices[i/2]=m_lookback.Identity(); }
         }
      }
      else if(O==OP_CLOSEST)
      {
         for(int i=0;i<8;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=DBL_MAX;
            for(int ii=0;ii<8;ii++)
            {
               if(_gap>fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[i/2]=_index;
         }
      }
      else if(O==OP_FURTHEST)
      {
         for(int i=0;i<8;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=0.0;
            for(int ii=0;ii<8;ii++)
            {
               if(_gap<fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[i/2]=_index;
         }
      }
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingCT::Operate_4(CMonoid<double> &M,EOperations &O,double &Values[],int &InputIndices[],int &OutputIndices[])
   {
      for(int i=0;i<4;i++)
      {
         m_element.Let();
         if(m_lookback.Get(i,m_element))
         {
            /*printf(__FUNCSIG__+
               " values size: "+IntegerToString(ArraySize(Values))+
               " in indices size: "+IntegerToString(ArraySize(InputIndices))+
               " in indices index: "+IntegerToString(InputIndices[i])
               );*/
               
            if(!m_element.Get(0,Values[InputIndices[i]]))
            {
               printf(__FUNCSIG__+" Failed to get double for 1 at: "+IntegerToString(i+1));
            }
         }
         else{ printf(__FUNCSIG__+" Failed to get element for 1 at: "+IntegerToString(i+1)); }
      }
      
      //
      
      if(O==OP_LEAST)
      {
         for(int i=0;i<4;i+=2)
         {
            if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[i/2]=i; }
            else if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[i/2]=i+1; }
            else { OutputIndices[i/2]=m_lookback.Identity(); }
         }
      }
      else if(O==OP_MOST)
      {
         for(int i=0;i<4;i+=2)
         {
            if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[i/2]=i; }
            else if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[i/2]=i+1; }
            else { OutputIndices[i/2]=m_lookback.Identity(); }
         }
      }
      else if(O==OP_CLOSEST)
      {
         for(int i=0;i<4;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=DBL_MAX;
            for(int ii=0;ii<4;ii++)
            {
               if(_gap>fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[i/2]=_index;
         }
      }
      else if(O==OP_FURTHEST)
      {
         for(int i=0;i<4;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=0.0;
            for(int ii=0;ii<4;ii++)
            {
               if(_gap<fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[i/2]=_index;
         }
      }
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingCT::Operate_2(CMonoid<double> &M,EOperations &O,double &Values[],int &InputIndices[],int &OutputIndices[])
   {
      for(int i=0;i<2;i++)
      {
         m_element.Let();
         if(m_lookback.Get(i,m_element))
         {
            if(!m_element.Get(0,Values[InputIndices[i]]))
            {
               printf(__FUNCSIG__+" Failed to get double for 1 at: "+IntegerToString(i+1));
            }
         }
         else{ printf(__FUNCSIG__+" Failed to get element for 1 at: "+IntegerToString(i+1)); }
      }
      
      //
      
      if(m_lookback_operation==OP_LEAST)
      {
         for(int i=0;i<2;i+=2)
         {
            if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[0]=i; }
            else if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[0]=i+1; }
            else { OutputIndices[0]=m_lookback.Identity(); }
         }
      }
      else if(m_lookback_operation==OP_MOST)
      {
         for(int i=0;i<2;i+=2)
         {
            if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[0]=i; }
            else if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[0]=i+1; }
            else { OutputIndices[0]=m_lookback.Identity(); }
         }
      }
      else if(m_lookback_operation==OP_CLOSEST)
      {
         for(int i=0;i<2;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=DBL_MAX;
            for(int ii=0;ii<2;ii++)
            {
               if(_gap>fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[0]=_index;
         }
      }
      else if(m_lookback_operation==OP_FURTHEST)
      {
         for(int i=0;i<2;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=0.0;
            for(int ii=0;ii<2;ii++)
            {
               if(_gap<fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[0]=_index;
         }
      }
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int CTrailingCT::GetLookback()
   {
      m_close.Refresh(-1);
      
      int _x=StartIndex();
      
      for(int i=0;i<8;i++)
      {
         int _period=(__LOOKBACKS[i]*PeriodSeconds(PERIOD_H4))/PeriodSeconds(m_period);
         double _value=fabs(m_close.GetData(_x)-m_close.GetData(_x+_period))/(fabs(m_close.GetData(_x)-m_close.GetData(_x+_period))+fabs(m_close.GetData(_x+_period)-m_close.GetData(_x+_period+_period)));
         
         m_element.Let();
         m_element.Cardinality(1);
         if(m_element.Set(0,_value))
         {
            ResetLastError();
            if(!m_lookback.Set(i,m_element,true))
            {
               printf(__FUNCSIG__+" Failed to assign element at index: "+IntegerToString(i)+", for lookback. ERR: "+IntegerToString(GetLastError()));
            }
         }
      }
      
      //r of 8
      double _v1[8];ArrayInitialize(_v1,0.0);
      int _i1_in[8];for(int i=0;i<8;i++){ _i1_in[i]=i; }
      int _i1_out[4];ArrayInitialize(_i1_out,-1);
      Operate_8(m_lookback,m_lookback_operation,_v1,_i1_in,_i1_out);
      
      
      //r of 4
      double _v2[8];ArrayInitialize(_v2,0.0);
      int _i2_out[2];ArrayInitialize(_i2_out,-1);
      Operate_4(m_lookback,m_lookback_operation,_v2,_i1_out,_i2_out);
      
      
      //r of 2
      double _v3[8];ArrayInitialize(_v3,0.0);
      int _i3_out[1];ArrayInitialize(_i3_out,-1);
      Operate_2(m_lookback,m_lookback_operation,_v2,_i2_out,_i3_out);
      
      return(4*__LOOKBACKS[_i3_out[0]]);
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_TIMEFRAMES CTrailingCT::GetTimeframe(void)
   {
      for(int i=0;i<8;i++)
      {
         ResetLastError();
         double _value=0.0;
         double _buffer[];ArrayResize(_buffer,3);ArrayInitialize(_buffer,0.0);ArraySetAsSeries(_buffer,true);
         if(CopyClose(m_symbol.Name(),__TIMEFRAMES[i],0,3,_buffer)>=3)
         {
            _value=fabs(_buffer[0]-_buffer[1])/(fabs(_buffer[0]-_buffer[1])+fabs(_buffer[1]-_buffer[2]));
         }
         else{ printf(__FUNCSIG__+" Failed to copy: "+EnumToString(__TIMEFRAMES[i])+" close prices. err: "+IntegerToString(GetLastError())); }
         
         m_element.Let();
         m_element.Cardinality(1);
         if(m_element.Set(0,_value))
         {
            ResetLastError();
            if(!m_timeframe.Set(i,m_element,true))
            {
               printf(__FUNCSIG__+" Failed to assign element at index: "+IntegerToString(i)+", for lookback. ERR: "+IntegerToString(GetLastError()));
            }
         }
      }
      
      //r of 8
      double _v1[8];ArrayInitialize(_v1,0.0);
      int _i1_in[8];for(int i=0;i<8;i++){ _i1_in[i]=i; }
      int _i1_out[4];ArrayInitialize(_i1_out,-1);
      Operate_8(m_timeframe,m_timeframe_operation,_v1,_i1_in,_i1_out);
      
      
      //r of 4
      double _v2[8];ArrayInitialize(_v2,0.0);
      int _i2_out[2];ArrayInitialize(_i2_out,-1);
      Operate_4(m_timeframe,m_timeframe_operation,_v2,_i1_out,_i2_out);
      
      
      //r of 2
      double _v3[8];ArrayInitialize(_v3,0.0);
      int _i3_out[1];ArrayInitialize(_i3_out,-1);
      Operate_2(m_timeframe,m_timeframe_operation,_v2,_i2_out,_i3_out);
      
      return(__TIMEFRAMES[_i3_out[0]]);
   }

Entonces, la función Operate_8 concatena los ocho elementos en el conjunto de monoides y ofrece una opción de cuatro, uno de cada par. De forma similar, la función Operate_4 combina los cuatro elementos obtenidos de Operate_8 y ofrece una opción de dos, nuevamente uno de cada par, y finalmente la función Operate_2 combina estos dos elementos de Operate_4 para obtener un elemento rentable.

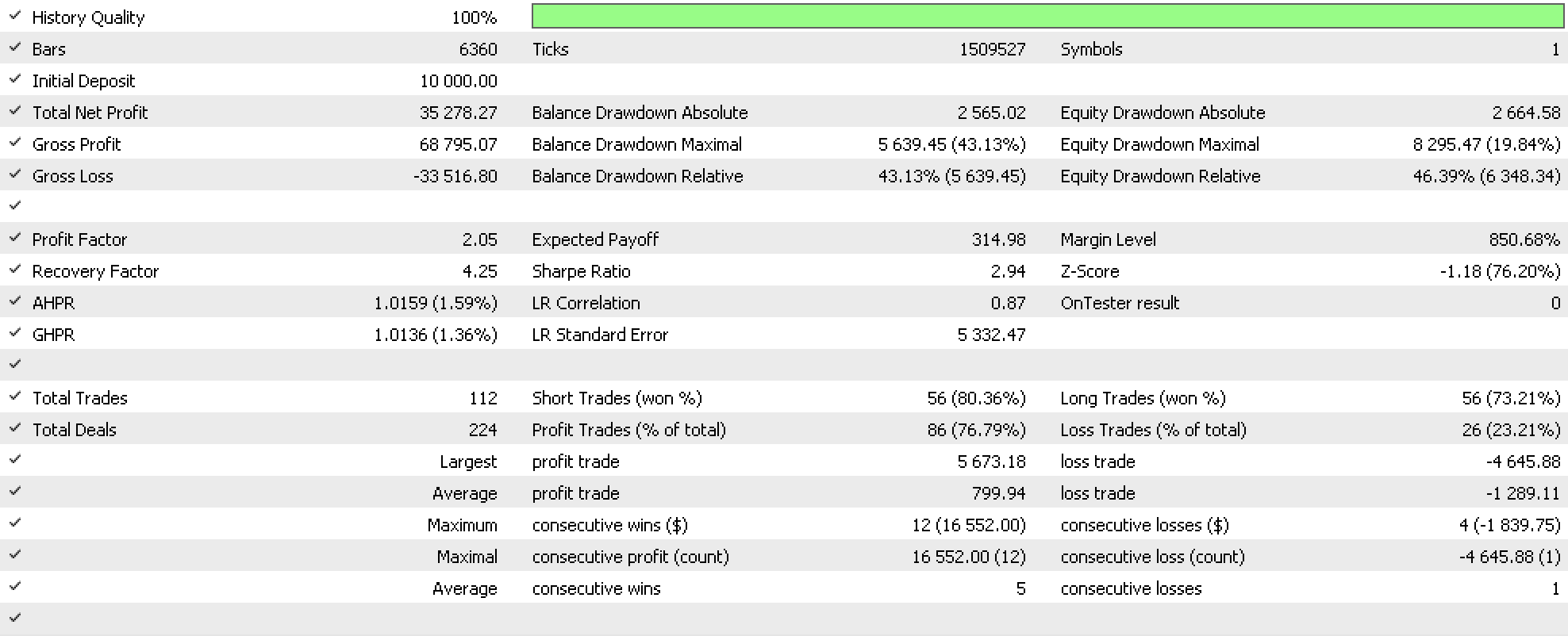
Si realizamos pruebas con este sistema para determinar el trailing stop ideal para las posiciones abiertas en un asesor que utilice la señal RSI integrada de la clase de asesor de las señales y la gestión de capital fija de la clase de fondos del asesor, obtendremos el siguiente informe.

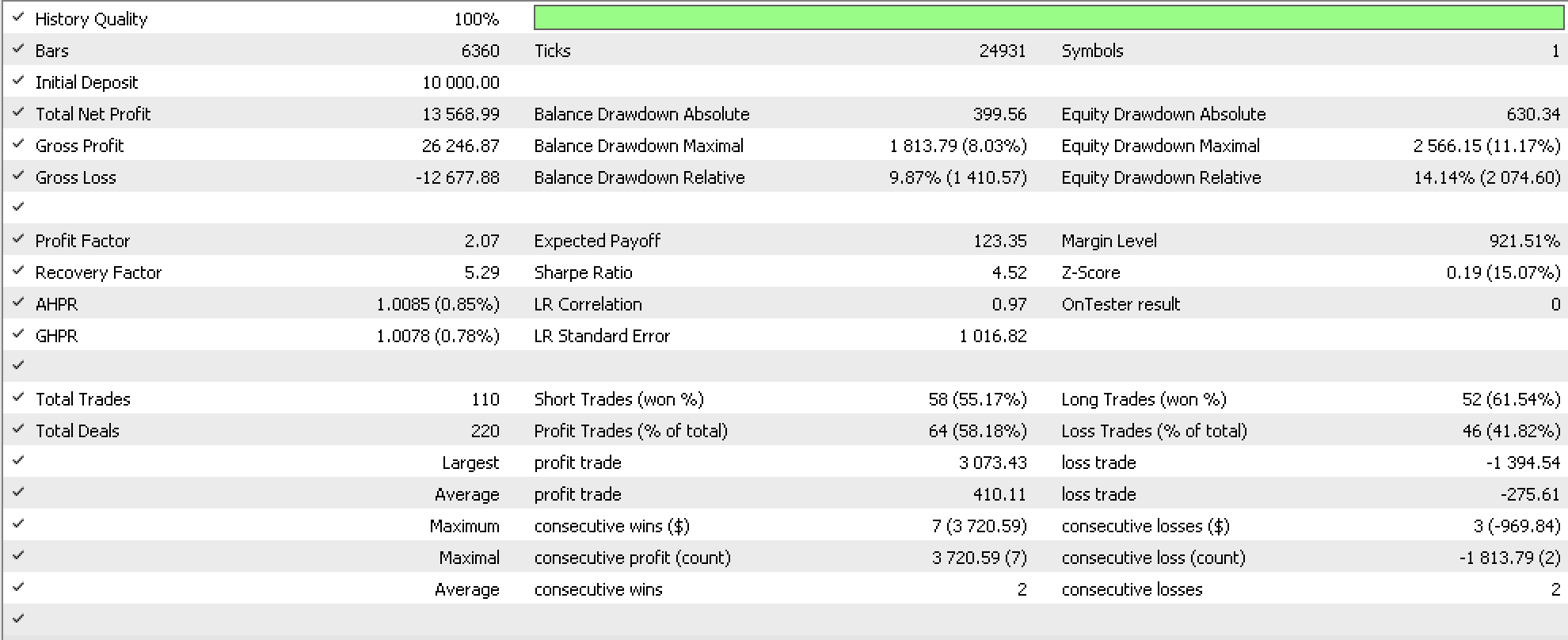
Una pasada similar en un asesor experto muy parecido, cuya única diferencia es el trailing stop incorporado basado en una media móvil, ofrecerá los siguientes resultados.

Conclusión

Hoy hemos analizado los monoides como un medio de clasificación de datos y, por lo tanto, como un conjunto de soluciones. Además, hemos enfatizado la importancia de los monoides generalizables bien formados sin sobreajuste, así como otras precauciones clave para implementar un sistema bien equilibrado. También hemos analizado una posible implementación de este sistema que ajusta las posiciones de stop loss funcionando como un ejemplar de la clase de trailing integrada del asesor.