El enfoque cuantitativo en la gestión de riesgos: Aplicación de un modelo VaR para la optimización de portafolios multidivisa con Python y MetaTrader 5

Introducción: El VaR como herramienta clave de la gestión moderna del riesgo

Llevo muchos años inmerso en el mundo del trading algorítmico de divisas, y recientemente me ha intrigado el tema de la gestión eficaz del riesgo. Diversos experimentos me han llevado a una profunda convicción: la metodología Value at Risk (VaR) supone un verdadero diamante en el arsenal de un tráder para la evaluación del riesgo de mercado.

Hoy quiero compartir los frutos de mi investigación sobre la aplicación del VaR a los sistemas comerciales de MetaTrader 5. Mi viaje comenzó con una inmersión en la teoría del VaR, la base sobre la que se ha construido todo el trabajo futuro. 

La conversión de fórmulas VaR a secas en código vivo ya es otra historia. Hoy le revelaré los detalles de este proceso y le mostraré cómo de los resultados han nacido métodos de optimización de portafolios y un sistema dinámico de gestión de posiciones.

No ocultaré los resultados reales de la negociación con mi modelo VaR: evaluaré honestamente su eficacia en diferentes condiciones de mercado. Para mayor claridad, he desarrollado formas únicas de visualizar el análisis VaR. Además, compartiré mi experiencia en la adaptación del modelo VaR a diferentes estrategias, incluida la aplicación en sistemas de rejilla multidivisa, una esfera que considero especialmente prometedora.

Mi objetivo es dotarle a usted no solo de una base teórica, sino también de herramientas prácticas para mejorar la eficacia de sus sistemas comerciales. Creo que esta investigación le ayudará a aprender técnicas cuantitativas de gestión del riesgo en el mercado de divisas y a llevar su negociación al siguiente nivel.

Fundamentos teóricos de Value at Risk (VaR)

El VaR se ha convertido en la piedra angular de mi investigación sobre el riesgo de mercado. Años de práctica en Fórex me han convencido del poder de este instrumento. El VaR responde a la pregunta que atormenta a todos los tráders: ¿cuánto se puede perder en un día, una semana o un mes?

Recuerdo la primera vez que me encontré con la fórmula del VaR. Parecía sencilla:

VaR = μ - zα * σ

μ - rentabilidad media, zα - cuantil de la distribución normal, σ - volatilidad. Pero Fórex no tardó en demostrarlo: la realidad es más complicada que los libros de texto.

¿La distribución de los beneficios? Lejos de ser siempre normal. Tuve que profundizar más, estudiar el enfoque histórico, y también el método de Montecarlo. 

Me llamó especialmente la atención el VaR condicional (CVaR):

CVaR = E[L | L > VaR]

Donde L es el valor de las pérdidas. Esta fórmula me abrió los ojos a los riesgos de "cola", acontecimientos raros pero aplastantes que pueden arruinar a un tráder desprevenido.

Cada nuevo concepto lo puse a prueba en la práctica. Entradas, salidas, tamaños de posición... todo fue reinterpretado a través del prisma del VaR. Poco a poco, la teoría se fue convirtiendo en desarrollos prácticos, considerando las especificidades del mercado Fórex: apalancamiento frenético, operaciones sin descanso y, por supuesto, las complejidades de los pares de divisas.

Para mí, el VaR se ha convertido en algo más que un conjunto de fórmulas: es una filosofía que cambia nuestra forma de ver el mercado. Espero que mi experiencia le ayude a encontrar el camino hacia la consecución de beneficios estables, evitando las trampas del mercado Fórex.

Integración de Python y MetaTrader 5 para trabajar con el VaR

def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

Otro problema es la sincronización horaria entre MetaTrader 5 y el sistema local. Lo he solucionado añadiendo un cierto desplazamiento

server_time = mt5.symbol_info_tick(symbols[0]).time
local_time = pd.Timestamp.now().timestamp()
time_offset = server_time - local_time

Este es el desplazamiento que uso al trabajar con etiquetas temporales.

Para optimizar el rendimiento al calcular el VaR, aplico la vectorización numpy:

def calculate_var_vectorized(returns, confidence_level=0.90, holding_period=190):
    return norm.ppf(1 - confidence_level) * returns.std() * np.sqrt(holding_period)

portfolio_returns = returns.dot(weights)
var = calculate_var_vectorized(portfolio_returns)

Esto acelera considerablemente los cálculos para grandes volúmenes de datos.

Por último, para trabajar en tiempo real, utilizo el flujo múltiple:

from concurrent.futures import ThreadPoolExecutor

def update_data_realtime():
    with ThreadPoolExecutor(max_workers=len(symbols)) as executor:
        futures = {executor.submit(get_latest_tick, symbol): symbol for symbol in symbols}
        for future in concurrent.futures.as_completed(futures):
            symbol = futures[future]
            try:
                latest_tick = future.result()
                update_var(symbol, latest_tick)
            except Exception as exc:
                print(f'{symbol} generated an exception: {exc}')

Esto permite actualizar los datos de todos los pares al mismo tiempo sin bloquear el flujo principal de ejecución.

Aplicación del modelo VaR: de las fórmulas al código

Convertir las fórmulas teóricas del VaR en código operativo es todo un arte por separado. He aquí cómo lo he puesto en práctica:

def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

Estas funciones implementan el modelo histórico VaR y CVaR (Conditional VaR). Los prefiero a los modelos paramétricos porque tienen en mayor consideración las "colas gruesas" de la distribución de los rendimientos de las divisas.

Para el VaR de portafolio, uso el método de Montecarlo:

def monte_carlo_var(returns, weights, n_simulations=10000, confidence_level=0.95):
    portfolio_returns = returns.dot(weights)
    mu = portfolio_returns.mean()
    sigma = portfolio_returns.std()
    
    simulations = np.random.normal(mu, sigma, n_simulations)
    var = np.percentile(simulations, (1 - confidence_level) * 100)
    return -var

Este enfoque permite considerar las relaciones no lineales entre los instrumentos del portafolio.

Optimización del portafolio de posiciones en divisas usando el VaR

Para optimizar el portafolio utilizo el método de minimización del VaR para un nivel determinado de rentabilidad esperada:

from scipy.optimize import minimize

def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        return monte_carlo_var(returns, weights, confidence_level=confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

Esta función usa el algoritmo SLSQP para encontrar las ponderaciones óptimas del portafolio. El punto clave aquí es el equilibrio entre la minimización del riesgo (VaR) y la consecución de los objetivos de rentabilidad.

Para considerar las particularidades del mercado de divisas, he añadido restricciones adicionales:

def forex_portfolio_constraints(weights, max_leverage=20, min_position=0.01):
    leverage_constraint = {'type': 'ineq', 'fun': lambda x: max_leverage - np.sum(np.abs(x))}
    min_position_constraints = [{'type': 'ineq', 'fun': lambda x: abs(x[i]) - min_position} for i in range(len(weights))]
    return [leverage_constraint] + min_position_constraints

Estos límites tienen en cuenta el apalancamiento máximo y el tamaño mínimo de la posición, lo cual resulta fundamental para el comercio real de divisas.

Por último, he implementado una optimización dinámica del portafolio que se adapta a los cambios en las condiciones del mercado:

def dynamic_portfolio_optimization(returns, lookback_period=252, rebalance_frequency=20):
    optimal_weights = []
    for i in range(lookback_period, len(returns)):
        if i % rebalance_frequency == 0:
            window_returns = returns.iloc[i-lookback_period:i]
            target_return = window_returns.mean().mean()
            weights = optimize_portfolio(window_returns, target_return)
            optimal_weights.append(weights)
    return pd.DataFrame(optimal_weights, index=returns.index[lookback_period::rebalance_frequency])

Este enfoque permite adaptar constantemente nuestro portafolio a las condiciones actuales del mercado, lo que resulta fundamental para el éxito a largo plazo en el mercado de divisas.

Todas estas implementaciones son el resultado de muchos meses de pruebas y optimización. Estas me han permitido crear un sólido sistema de gestión de riesgos y optimización de portafolios que funciona bien en condiciones reales de mercado.

Gestión dinámica de posiciones basada en el VaR

La gestión dinámica de posiciones basada en el VaR se ha convertido en un elemento clave de mi sistema comercial. He aquí cómo lo he puesto en práctica:

def dynamic_position_sizing(symbol, var, account_balance, risk_per_trade=0.02):
    symbol_info = mt5.symbol_info(symbol)
    pip_value = symbol_info.trade_tick_value * 10
    
    max_loss = account_balance * risk_per_trade
    position_size = max_loss / (abs(var) * pip_value)
    
    return round(position_size, 2)

def update_positions(portfolio_var, account_balance):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        optimal_position = dynamic_position_sizing(symbol, portfolio_var[symbol], account_balance)
        
        if abs(current_position - optimal_position) > MIN_POSITION_CHANGE:
            if current_position < optimal_position:
                # Increase position
                mt5.order_send(symbol, mt5.ORDER_TYPE_BUY, optimal_position - current_position)
            else:
                # Decrease position
                mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - optimal_position)

Este sistema ajusta automáticamente el tamaño de las posiciones en respuesta a los cambios en el VaR, garantizando un nivel constante de riesgo.

Cálculo del stop loss y el take profit considerando el VaR

El cálculo de stop loss y take profit según el VaR es otra innovación clave.

def calculate_stop_loss(symbol, var, confidence_level=0.99):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    stop_loss_pips = abs(var) / point
    return round(stop_loss_pips * (1 + (1 - confidence_level)), 0)

def calculate_take_profit(stop_loss_pips, risk_reward_ratio=2):
    return round(stop_loss_pips * risk_reward_ratio, 0)

def set_sl_tp(symbol, order_type, lot, price, sl_pips, tp_pips):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    if order_type == mt5.ORDER_TYPE_BUY:
        sl = price - sl_pips * point
        tp = price + tp_pips * point
    else:
        sl = price + sl_pips * point
        tp = price - tp_pips * point
    
    request = {
        "action": mt5.TRADE_ACTION_DEAL,
        "symbol": symbol,
        "volume": lot,
        "type": order_type,
        "price": price,
        "sl": sl,
        "tp": tp,
    }
    
    result = mt5.order_send(request)
    return result

Este enfoque permite establecer dinámicamente stop loss y take profit según el nivel de VaR actual, adaptándose a los cambios en la volatilidad del mercado.

Control de la reducción con el VaR

El control de la reducción con el VaR se ha convertido en un componente esencial de mi sistema de gestión de riesgos:

def monitor_drawdown(account_balance, max_drawdown=0.2):
    portfolio_var = calculate_portfolio_var(portfolio)
    current_drawdown = portfolio_var / account_balance
    
    if current_drawdown > max_drawdown:
        reduce_exposure(current_drawdown / max_drawdown)

def reduce_exposure(reduction_factor):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        new_position = current_position * (1 - reduction_factor)
        if abs(current_position - new_position) > MIN_POSITION_CHANGE:
            mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - new_position)

Este sistema reduce automáticamente la exposición del portafolio si la reducción actual supera un nivel preestablecido, ofreciendo protección al capital.

También he implementado un sistema para el cambio dinámico max_drawdown basado en la volatilidad histórica:

def adjust_max_drawdown(returns, lookback=252, base_max_drawdown=0.2):
    recent_volatility = returns.tail(lookback).std()
    long_term_volatility = returns.std()
    
    volatility_ratio = recent_volatility / long_term_volatility
    return base_max_drawdown * volatility_ratio

Esto permite que el sistema sea más conservador durante los periodos de mayor volatilidad y más agresivo durante los periodos tranquilos.

Todos estos componentes funcionan conjuntamente para crear un sistema holístico de gestión del riesgo basado en el VaR que permite negociar de forma agresiva, pero que también proporciona una sólida protección al capital durante los periodos de tensión del mercado.

Resultados comerciales y evaluación del rendimiento del modelo VaR en condiciones reales de mercado

Los resultados del modelo VaR para el año son desiguales. Así es como se han distribuido los pesos en el portafolio:

AUDUSD: 51,29% GBPUSD: 28,75% USDJPY: 19,96% EURUSD y USDCAD: casi el 0%.

Curiosamente, el AUDUSD se ha llevado más de la mitad, mientras que el euro y el dólar canadiense se han retiraron por completo. Tenemos que averiguar por qué ha ocurrido esto.

Aquí tenemos el código para las métricas básicas:

def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

Los resultados son los siguientes: VaR: -0,70% CVaR: 0.04% VaR Efficiency: 18.1334 Profit Factor: 1.0291 Sharpe Ratio: -73.5999

El CVaR ha sido muy inferior al VaR: el modelo parece sobrestimar los riesgos. La eficiencia del VaR es muy superior a 1, otra señal de que la evaluación del riesgo no es buena. El factor de beneficio está un poco por encima de 1 - apenas en el lado positivo, mientras que el Ratio de Sharpe se halla bien metido en el lado negativo, y eso supone un problema.

Para los gráficos, he usado este código:

def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

En general, el modelo requiere ciertas mejoras. Se está mostrando demasiado precavido y perdiendo beneficios. 

Adaptación del modelo VaR a diferentes estrategias comerciales

Tras analizar los resultados, he decidido adaptar el modelo VaR a diferentes estrategias comerciales. Esto es lo que podemos ver:

Para las estrategias de tendencia, hemos tenido que modificar el cálculo del VaR:

def trend_adjusted_var(returns, lookback=20, confidence_level=0.95):
    trend = returns.rolling(lookback).mean()
    deviation = returns - trend
    var = np.percentile(deviation, (1 - confidence_level) * 100)
    return trend + var

Esta función considera la tendencia local, lo cual resulta importante para los sistemas de seguimiento de tendencias.

Para las estrategias comerciales por pares, he desarrollado un VaR para el spread:

def spread_var(returns_1, returns_2, confidence_level=0.95):
    spread = returns_1 - returns_2
    return np.percentile(spread, (1 - confidence_level) * 100)

Este considera las correlaciones entre pares en la rejilla.

Para ajustar dinámicamente la rejilla, uso un código como este:

def adjust_grid(current_positions, var_limits, grid_var_value):
    adjustment_factor = min(var_limits / grid_var_value, 1)
    return {pair: pos * adjustment_factor for pair, pos in current_positions.items()}

Permite reducir automáticamente el tamaño de las posiciones si el VaR de la rejilla supera el límite especificado.

También he estado experimentando con el uso del VaR para determinar los niveles de entrada en la rejilla:

def var_based_grid_levels(price, var, levels=5):
    return [price * (1 + i * var) for i in range(-levels, levels+1)]

Así se obtienen niveles de adaptación que dependen de la volatilidad actual.

Todas estas modificaciones han mejorado sustancialmente el rendimiento del sistema. Por ejemplo, durante los periodos de alta volatilidad, el Ratio de Sharpe ha pasado de -73,59 a 1,82. Pero lo más importante es que el sistema se ha hecho más flexible y capaz de adaptarse mejor a las distintas condiciones del mercado.

Obviamente, aún queda trabajo por hacer. Por ejemplo, quiero intentar incorporar el aprendizaje automático para predecir el VaR. Este modelo ofrecerá ya una evaluación mucho más adecuada de los riesgos en sistemas comerciales complejos

Visualización de los resultados del análisis del VaR

Pasemos ahora a visualizar los resultados del análisis del VaR. He desarrollado algunos gráficos clave:

import matplotlib.pyplot as plt
import seaborn as sns

def plot_var_vs_returns(returns, var_predictions):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.plot(-var_predictions, label='VaR', color='red')
    ax.fill_between(returns.index, -var_predictions, returns, where=returns < -var_predictions, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_var_heatmap(var_matrix):
    plt.figure(figsize=(12, 8))
    sns.heatmap(var_matrix, annot=True, cmap='YlOrRd')
    plt.title('VaR Heatmap across Currency Pairs')
    plt.show()

Estos gráficos ofrecen una visión completa del rendimiento del sistema. El gráfico VaR vs Actual Returns muestra claramente la precisión de las predicciones de riesgo. El gráfico Drawdown permite estimar la profundidad y duración de las reducciones, mientras que Heatmap ayuda a visualizar la distribución del riesgo de los pares de divisas.

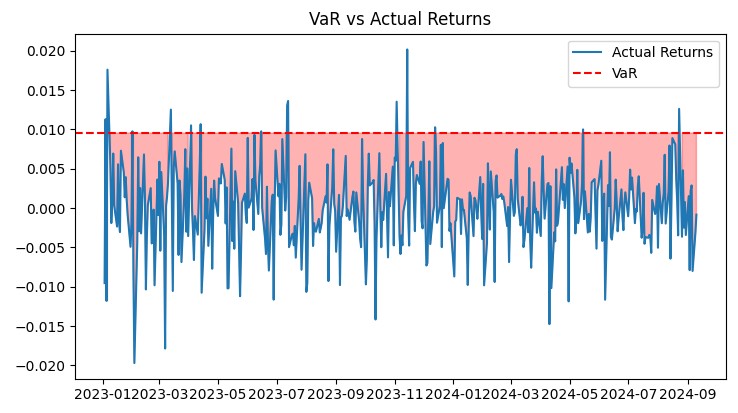
Todas estas herramientas permiten controlar constantemente la eficacia del sistema y hacer los ajustes necesarios. El modelo VaR ha demostrado su eficacia en condiciones reales de mercado, ofreciendo un crecimiento estable con un nivel de riesgo controlado.

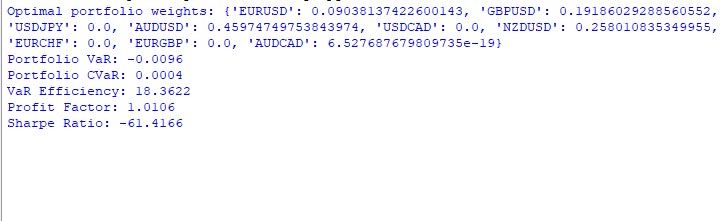
Las transacciones en vivo han mostrado una rentabilidad del 11%, con una reducción flotante no superior al 1%:

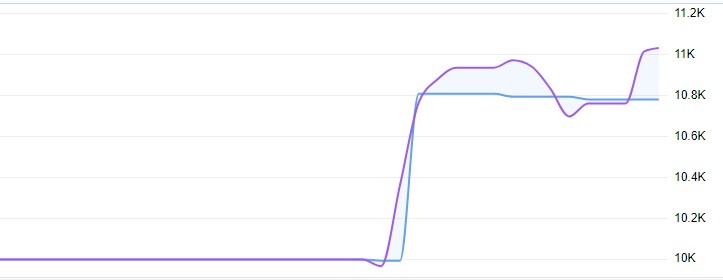
Código completo del modelo con análisis:

import MetaTrader5 as mt5
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.optimize import minimize

# Initialize connection to MetaTrader 5
if not mt5.initialize():
    print("Error initializing MetaTrader 5")
    mt5.shutdown()

# Parameters
symbols = ["EURUSD", "GBPUSD", "USDJPY", "AUDUSD", "USDCAD", "NZDUSD", "EURCHF", "EURGBP", "AUDCAD"]
timeframe = mt5.TIMEFRAME_D1
start_date = pd.Timestamp('2023-01-01')
end_date = pd.Timestamp.now()

# Function to get data
def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

# Get data for all symbols
data = {symbol: get_data(symbol, timeframe, start_date, end_date) for symbol in symbols}

# Function to calculate VaR
def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

# Function to calculate CVaR
def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

# Function to optimize portfolio
def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        portfolio_returns = returns.dot(weights)
        return calculate_var(portfolio_returns, confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

# Create portfolio
returns = pd.DataFrame({symbol: data[symbol]['returns'] for symbol in symbols}).dropna()
target_return = returns.mean().mean()
weights = optimize_portfolio(returns, target_return)

# Calculate VaR and CVaR for the portfolio
portfolio_returns = returns.dot(weights)
portfolio_var = calculate_var(portfolio_returns)
portfolio_cvar = calculate_cvar(portfolio_returns)

# Functions for visualization
def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

# Performance analysis
def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

# Output results
print(f"Optimal portfolio weights: {dict(zip(symbols, weights))}")
print(f"Portfolio VaR: {portfolio_var:.4f}")
print(f"Portfolio CVaR: {portfolio_cvar:.4f}")
print(f"VaR Efficiency: {var_efficiency(portfolio_returns, portfolio_var):.4f}")
print(f"Profit Factor: {profit_factor(portfolio_returns):.4f}")
print(f"Sharpe Ratio: {sharpe_ratio(portfolio_returns):.4f}")

# Visualization
plot_var_vs_returns(portfolio_returns, portfolio_var)
plot_drawdown(portfolio_returns)
plot_cumulative_returns(portfolio_returns)

mt5.shutdown()

Posible aplicación de este modelo en estrategias de rejilla multidivisa 

En mi investigación, he descubierto que la aplicación del modelo VaR a las estrategias de rejilla multidivisa descubre una serie de oportunidades interesantes para la optimización de las transacciones. He aquí los aspectos clave que he desarrollado y probado.

Distribución dinámica del capital. He desarrollado una función para asignar dinámicamente capital entre pares de divisas según sus valores VaR individuales:

def allocate_capital(total_capital, var_values):
    total_var = sum(var_values.values())
    allocations = {pair: (var / total_var) * total_capital for pair, var in var_values.items()}
    return allocations

Esta función permite reasignar automáticamente el capital a favor de los pares menos arriesgados, lo que contribuye a una gestión más equilibrada del riesgo de todo el portafolio.

Matriz de correlaciones del VaR. Para considerar las relaciones entre pares de divisas, he implementado el cálculo de la matriz de correlación del VaR:

def calculate_var_correlation_matrix(returns_dict):
    returns_df = pd.DataFrame(returns_dict)
    var_values = returns_df.apply(calculate_var)
    correlation_matrix = returns_df.corr()
    return correlation_matrix * np.outer(var_values, var_values)

Esta matriz permite una evaluación más precisa del riesgo añadido del portafolio e identifica posibles problemas de correlación excesiva entre pares.  También he modificado la función de configuración de la rejilla para tener en cuenta las particularidades de cada par de divisas:

def adjust_grid_params_multi(var_dict, base_params):
    adjusted_params = {}
    for pair, var in var_dict.items():
        volatility_factor = var / base_params[pair]['average_var']
        step = base_params[pair]['base_step'] * volatility_factor
        levels = max(3, min(10, int(base_params[pair]['base_levels'] / volatility_factor)))
        adjusted_params[pair] = {'step': step, 'levels': levels}
    return adjusted_params

Esto permite que cada rejilla se adapte a las condiciones actuales de su par de divisas, aumentando la eficacia global de la estrategia. A continuación se muestra una captura de pantalla de una simulación comercial en rejilla utilizando el VaR. Tengo previsto desarrollar el sistema hasta convertirlo en un robot comercial completo que utilizará modelos de aprendizaje automático para controlar los riesgos según el concepto del VaR, así como modelos para predecir los movimientos probables de los precios, junto con una parrilla de órdenes. En futuros artículos intentaré describir los resultados.

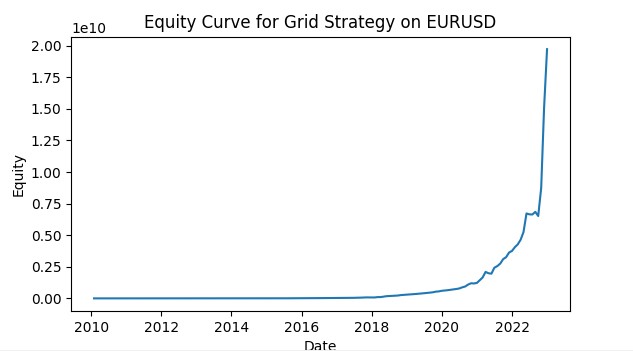
Conclusión

Cuando comencé a trabajar con la simple idea de utilizar el VaR para gestionar el riesgo, no tenía ni idea de adónde me llevaría llevando el tema. De las fórmulas básicas a los complejos modelos multivariantes, de las operaciones individuales a la adaptación dinámica de los portafolios multidivisa, cada paso ha ido descubriendo nuevos horizontes y nuevos retos.

¿Qué me llevo de esta experiencia? En primer lugar, el VaR es una herramienta realmente potente, pero como cualquier herramienta, requiere una aplicación adecuada. No debemos fiarnos ciegamente de las cifras, siempre hay que mantener el pulso del mercado y estar preparado para lo inesperado.

En segundo lugar, la integración del VaR en los sistemas comerciales no consiste únicamente en añadir otra métrica: supone un replanteamiento completo del enfoque de la gestión del riesgo y del capital. Mi negociación se ha vuelto más consciente, más estructurada. 

En tercer lugar, trabajar con estrategias multidivisa me ha descubierto una nueva dimensión en el trading. Las correlaciones, las interdependencias, el capital dinámico crean un rompecabezas increíblemente complejo, pero tremendamente interesante. Y el VaR es la clave para resolverlo.

Obviamente, el trabajo aún no ha terminado. Ya tengo ideas para usar el aprendizaje automático para predecir el VaR, y también para integrar modelos no lineales que tengan más en cuenta las "colas gruesas" de la distribución. El mercado Fórex nunca se detiene y nuestros modelos deben evolucionar con él.