Redes neuronales: así de sencillo (Parte 30): Algoritmos genéticos

Contenido

• Introducción
• 1. Métodos evolutivos de optimización
• 2. Aplicación usando MQL5
• 3. Simulación
• Conclusión
• Enlaces
• Programas usados en el artículo.

Introducción

Vamos a continuar analizando los algoritmos de aprendizaje no supervisado. Como el lector recordará, todos los métodos analizados anteriormente usaban un método analítico para determinar la dirección y la intensidad del cambio en los parámetros del modelo durante el proceso de aprendizaje. Por consiguiente, un requisito básico para todos los modelos entrenados era que la función del modelo resulte diferenciable en toda la gama de valores válidos. Debido a esta propiedad, usábamos el método de descenso de gradiente y determinábamos analíticamente el impacto de cada parámetro del modelo en el resultado global; asimismo, ajustábamos los coeficientes de peso para reducir el error.

No obstante, existen bastantes tareas en las que no resulta posible diferenciar la función original. Puede tratarse de funciones indiferenciadas o de un modelo propenso a experimentar problemas de gradiente explosivo o atenuado, y los métodos para afrontar dichas manifestaciones resultan ineficaces. En estos casos, podemos recurrir a métodos evolutivos de optimización.

1. Métodos evolutivos de optimización

Los métodos evolutivos de optimización pertenecen a los métodos sin gradiente y nos permiten optimizar modelos que no pueden optimizarse con los métodos anteriormente analizados, aunque no se limita a ellos. A veces incluso resulta interesante ver cómo se entrena un modelo con el método evolutivo y otro con el algoritmo de distribución del gradiente de error.

Por el nombre, ya podemos adivinar que las ideas principales del método se toman de las ciencias naturales, concretamente, de la teoría de la evolución de Darwin. Según esta teoría, cualquier población de organismos vivos es lo suficientemente fecunda como para producir descendencia y crecimiento de la población, pero los limitados recursos disponibles para vivir restringen el crecimiento de la población, y aquí es donde la selección natural desempeña un papel fundamental, según el cual sobreviven los más fuertes, o el más adaptado para sobrevivir en el entorno. Así, con cada generación, la población se desarrolla y se adapta cada vez más a su hábitat. En este caso, además, los miembros de la población desarrollan nuevos rasgos y habilidades que les ayudan a sobrevivir, mientras que olvidan todo aquello que ya no les resulta relevante.

Como podemos ver, en la breve descripción de la teoría que acabamos de presentar, no existe absolutamente nada matemático. Por supuesto, podemos calcular el tamaño máximo posible de la población basándonos en el número total de recursos disponibles y su consumo por un miembro de la población. Sin embargo, esto no influye en los principios generales de la teoría,

y, por extraño que parezca, esta teoría ha servido de prototipo a toda una familia de métodos evolutivos. En este artículo, ofrecemos al lector una introducción al algoritmo de optimización genética, que es uno de los algoritmos básicos de los métodos evolutivos. El algoritmo se basa en dos principios básicos de la teoría de la evolución de Darwin: la herencia y la selección natural.

La esencia del método consiste en observar cada generación de la población y seleccionar al mejor de sus miembros, pero lo primero es lo primero.

Como estamos observando la población en su conjunto, se cumplirá el requisito básico de la finitud de la vida de cada generación. Es decir, al igual que en los algoritmos de aprendizaje por refuerzo analizados anteriormente, se considerará el requisito de finitud del proceso. También en este caso usaremos los mismos planteamientos. En particular, la limitación a una sola sesión.

Como ya hemos dicho, observaremos a una población completa. Por consiguiente, a diferencia de los algoritmos comentados con anterioridad, no estaremos creando un único modelo, sino toda una población que "vivirá" en las mismas condiciones al mismo tiempo. El tamaño de la población constituirá un hiperparámetro y determinará la capacidad de la población para aprender sobre su entorno. Cada miembro de la población actuará según su política individual. Como consecuencia, cuanto mayor resulte la población observada, más estrategias diferentes observaremos, y mejor se estudiará el hábitat.

Este proceso puede compararse con una selección aleatoria y repetida de la acción de un agente en el mismo estado en el aprendizaje por refuerzo, solo que ahora utilizaremos varios agentes al mismo tiempo, cada uno de los cuales tomará su propia decisión.

El uso de miembros independientes de la población resulta conveniente al paralelizar el proceso de optimización. Con mucha frecuencia, para reducir el tiempo necesario para encontrar el modelo óptimo, el proceso de optimización se ejecuta en paralelo en varias máquinas, usando todos los recursos disponibles. Cada miembro de la población "vive" en su propio hilo del microprocesador, y el proceso de optimización al completo está controlado y gestionado por una máquina de nodo en la que se evalúan los resultados de cada agente y se genera una nueva población.

La selección natural se ejecuta después de finalizar la sesión de una generación. En este proceso, se seleccionarán los mejores individuos de toda la población para producir descendencia, es decir, una nueva generación de la población. El número de mejores representantes seleccionados será un hiperparámetro que indicaremos como una fracción del tamaño total de la población.

Los criterios de selección de los mejores representantes dependerán del arquitecto del proceso de optimización. Aquí pueden darse recompensas, como en el aprendizaje por refuerzo, o bien introducirse una función de pérdida, como en el aprendizaje supervisado. Como consecuencia, elegiremos los agentes con la máxima recompensa total o el mínimo valor de la función de pérdida.

Tenga en cuenta que no usaremos un gradiente de error. Por consiguiente, la función de selección de los mejores representantes podría no estar diferenciada.

Tras seleccionar a los padres de la futura descendencia, tendremos una nueva generación de la población a crear. Para ello, seleccionaremos al azar una pareja de modelos de entre los mejores representantes seleccionados, que serán los padres del nuevo modelo. El lector estará de acuerdo con que resulta simbólico elegir una pareja para crear un nuevo modelo.

En el proceso de creación de un nuevo modelo, todos sus parámetros se tratarán como un cromosoma, y cada coeficiente de peso individual será un gen independiente que se heredará de uno de los progenitores.

Los algoritmos de herencia pueden variar, pero todos se suelen basar en 2 reglas:

• ningún gen cambia de lugar;
• la aleatoriedad de la selección parental para cada gen.

En este caso, además, podemos seleccionar aleatoriamente un progenitor para cada miembro de la población de la nueva generación, o podemos crear directamente una pareja de agentes con herencia de genes especular.

El proceso es cíclico hasta que la nueva generación de la población se haya rellenado por completo. Los padres previamente seleccionados no forman parte de la nueva generación de la población y se eliminarán tras producir descendencia.

Para la nueva generación, iniciaremos una nueva sesión y repetiremos el proceso de optimización.

Nótese que decimos deliberadamente "optimización", no "entrenamiento". El proceso descrito se parece poco a un entrenamiento. Hablamos de simple selección natural en el proceso de la evolución, y, como ya sabrá, durante la evolución, aunque con poca frecuencia, se producen diversas mutaciones que forman parte integral del proceso evolutivo. Por consiguiente, también introduciremos cierto grado de incertidumbre en nuestro proceso de optimización.

Probablemente, esto le suene extraño. Durante la optimización, casi todo se basa en la selección aleatoria: primero generamos aleatoriamente la primera población, luego seleccionamos aleatoriamente los padres y, por último, copiamos aleatoriamente los parámetros de los modelos, pero no hay ninguna novedad tras toda esta aleatoriedad. Eso es lo que añadiremos gracias a la mutación.

En el proceso de optimización, introduciremos otro hiperparámetro responsable de la fracción de mutación. Dicho proceso indicará la probabilidad con la que añadiremos genes aleatorios a la descendencia creada en lugar de copiar estos. En otras palabras, cada nuevo miembro de la población recibirá un gen aleatorio con la probabilidad del parámetro de mutación, en lugar de heredarlo de los padres. De esta forma, en cada nueva generación se introducirá algo nuevo, además de la herencia de los padres. Por así decirlo, esta es la máxima similitud con nuestro desarrollo.

2. Aplicación usando MQL5

Tras examinar los aspectos teóricos de los algoritmos, vamos a pasar a la parte práctica de nuestro artículo. Asimismo, vamos a construir el algoritmo analizado usando MQL5, Por supuesto, no encontraremos prácticamente matemáticas en el algoritmo presentado, pero sí que habrá algo esencial: un algoritmo de acción claro. Precisamente esto será lo que implementaremos.

De entrada, diremos que el modelo que hemos construido antes no resulta adecuado para este tipo de tarea. Al construir nuestra clase para trabajar con redes neuronales CNet, se presuponía el uso únicamente de modelos lineales simples. Ahora deberemos aplicar varios modelos lineales en paralelo. Hay dos formas de hacerlo.

Tenemos una primera forma, que requiere menos tiempo del programador, pero que a la vez consume más recursos: simplemente deberemos crear un array dinámico de objetos en el que crearemos varios modelos idénticos, y luego extraeremos los modelos uno a uno del array y los procesaremos igualmente uno a uno. En esta versión, el funcionamiento completo de cada modelo individual se implementará dentro de la funcionalidad existente. Solo nos quedará aplicar los métodos necesarios para seleccionar a los padres y crear una nueva generación, así como el proceso de selección de agentes.

Este método, no obstante, también tiene ciertas desventajas: consume muchos recursos y crea muchos objetos redundantes. Así, para cada agente, crearemos un ejemplar independiente de la clase de contexto OpenCL, y con ello, se creará un contexto independiente, una copia del programa y los objetos de todos los kernels. Esto es aceptable cuando se usan varios dispositivos informáticos en paralelo. De lo contrario, la creación de objetos redundantes provocará un uso irracional de los recursos y limitará mucho el tamaño de la población, lo que repercutirá negativamente en los resultados del proceso de optimización.

Así que decidimos "arremangarnos" e introducir cambios en nuestra clase de modelado de redes neuronales. No obstante, para no romper el proceso de trabajo, hemos creado una nueva clase CNetGenetic con herencia pública de la clase CNet.

class CNetGenetic : public CNet
  {
protected:
   uint              i_PopulationSize;
   vector            v_Probability;
   vector            v_Rewards;
   matrixf           m_Weights;
   matrixf           m_WeightsConv;

   //---
   bool              CreatePopulation(void);
   int               GetAction(CBufferFloat * probability);
   bool              GetWeights(uint layer);
   float             NextGenerationWeight(matrixf &array, uint shift, vector &probability);
   float             GenerateWeight(uint total);

public:
                     CNetGenetic();
                    ~CNetGenetic();
   //---
   bool              Create(CArrayObj *Description, uint population_size);
   bool              SetPopulationSize(uint size);
   bool              feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true);
   bool              Rewards(CArrayFloat *targetVals);
   bool              NextGeneration(double quantile, double mutation, double &average, double &mamximum);
   bool              Load(string file_name, uint population_size, bool common = true);
   bool              SaveModel(string file_name, int model, bool common = true);
   //---
   bool              CopyModel(CArrayLayer *source, uint model);
   bool              Detach(void);
  };

Conoceremos el propósito de los métodos de la clase a medida que implementemos la funcionalidad. Bien, ahora echaremos un vistazo a las variables:

• i_PopulationSize — tamaño de la población;
• v_Probability — vector de probabilidades de selección de un modelo como "padre";
• v_Probability — vector de recompensas totales acumuladas por cada modelo individual;
• m_Weights — matriz para registrar los parámetros de todos los modelos;
• m_WeightsConv — matriz similar para registrar todos los parámetros de las capas neuronales convolucionales.

En el constructor de la clase, solo inicializaremos las variables anteriores. Aquí estableceremos el tamaño por defecto de la población y llamaremos al método para cambiar las variables correspondientes.

CNetGenetic::CNetGenetic() :  i_PopulationSize(100)
  {
   SetPopulationSize(i_PopulationSize);
  }

Esta clase no usa instancias de otros objetos, y por lo tanto, el destructor de la clase permanecerá vacío.

Antes hemos mencionado el método para indicar el tamaño de la población SetPopulationSize, cuyo algoritmo es bastante trivial y sencillo. El método obtiene en los parámetros el tamaño de la población. En el cuerpo del método, guardaremos el valor resultante en la variable correspondiente e inicializaremos con valores cero el vector de probabilidad y recompensa.

bool CNetGenetic::SetPopulationSize(uint size)
  {
   i_PopulationSize = size;
   v_Probability = vector::Zeros(i_PopulationSize);
   v_Rewards = vector::Zeros(i_PopulationSize);
//---
   return true;
  }

A continuación, le proponemos examinar el método de inicialización del objeto de clase Create. Por analogía al método similar de la clase padre, el método obtiene el puntero al único objeto de descripción de un agente en sus parámetros, y luego añadimos el tamaño de la población.

bool CNetGenetic::Create(CArrayObj *Description, uint population_size)
  {
   if(CheckPointer(Description) == POINTER_INVALID)
      return false;
//---
   if(!SetPopulationSize(population_size))
      return false;
   CNet::Create(Description);
   return CreatePopulation();
  }

En el cuerpo del método, primero comprobaremos la validez del puntero resultante a la descripción de la arquitectura de la capa neuronal. Solo después de que la prueba se haya superado con éxito, llamaremos al método que ya conocemos para especificar el tamaño de la población.

A continuación, llamaremos al método similar de la clase padre, en el que se creará un agente basado en la descripción obtenida y se inicializarán todos los objetos adicionales.

Por último, llamaremos al método para crear la población CreatePopulation, que rellenará la población copiando el modelo creado anteriormente. Veamos con más detalle el algoritmo de dicho método.

Al inicio del método, comprobaremos el número de capas neuronales del modelo creado. Deberemos ver al menos 2 de ellas.

bool CNetGenetic::CreatePopulation(void)
  {
   if(!layers || layers.Total() < 2)
      return false;

A continuación, guardaremos en la variable local el puntero a la capa neuronal de los datos de origen.

   CLayer *layer = layers.At(0);
   if(!layer || !layer.At(0))
      return false;
//---
   CNeuronBaseOCL *neuron_ocl = layer.At(0);
   int prev_count = neuron_ocl.Neurons();

Obsérvese que la primera capa neuronal solo se usa para registrar los datos de origen, y que todos los agentes de nuestra población trabajarán con los mismos datos de origen. Por ello, no tendrá sentido que copiemos la capa de datos de origen según el número de agentes de la población. Así, la duplicación de las capas neuronales se realizará partiendo de la siguiente capa neuronal, cuyo índice será "1".

Recordemos la estructura de nuestros objetos de almacenamiento de capas neuronales. La clase responsable de organizar el funcionamiento del modelo en el nivel superior será CNet. Esta contiene un ejemplar del objeto de array dinámico de capas neuronales CArrayLayer. En este array dinámico, almacenaremos en un array dinámico los punteros a los objetos de arrays dinámicos anidados directamente en la capa neuronal CLayer. Y ya en ella escribimos los punteros a los objetos de neurona CNeuronBaseOCL y otros.

CNet -> CArrayLayer -> CLayer -> CNeuronBaseOCL

No olvidemos que creamos originalmente esta estructura al organizar el proceso de los cálculos usando MQL5 en CPU. Por aquel entonces, cada neurona era una entidad independiente; más adelante, al transferir los cálculos a la GPU usando la tecnología OpenCL, nos vimos obligados a pasar al uso de búferes de datos, y, esencialmente, cada capa neuronal se expresaba en una sola neurona CNeuronBaseOCL que realizaba la función de la capa neuronal. Lo mismo ocurrirá con el uso de otros tipos de neuronas.

Así, cada objeto de capa neuronal CLayer ahora solo contendrá un objeto de neurona. Antes no cambiábamos la arquitectura de almacenamiento para mantener la compatibilidad con desarrollos anteriores, y ahora esto nos servirá de otra forma adicional. Simplemente añadiremos al array dinámico CLayer el número necesario de objetos para almacenar toda la población de nuestros agentes. Así obtendremos dentro de un único modelo los objetos paralelos de las capas neuronales de todos los agentes de nuestra población, y solo tendremos que organizar su funcionamiento según el índice de agente que corresponda.

Siguiendo esta lógica, organizaremos a continuación un ciclo de duplicación de capas neuronales. En él iteraremos secuencialmente por todas las capas neuronales de nuestro modelo y añadiremos el número necesario de neuronas similares a la primera neurona creada anteriormente en cada capa.

En el cuerpo del ciclo, primero comprobaremos la validez del puntero a la capa neuronal creada anteriormente.

   for(int i = 1; i < layers.Total(); i++)
     {
      layer = layers.At(i);
      if(!layer || !layer.At(0))
         return false;
      //---

Entonces obtendremos una descripción de la arquitectura de la neurona,

      neuron_ocl = layer.At(0);
      CLayerDescription *desc = neuron_ocl.GetLayerInfo();
      int outputs = neuron_ocl.getConnections();

y crearemos objetos similares, incrementando la capa neuronal hasta el tamaño de población requerido; para ello, creamos otro ciclo anidado.

      for(uint n = layer.Total(); n < i_PopulationSize; n++)
        {
         CNeuronConvOCL *neuron_conv_ocl = NULL;
         CNeuronProofOCL *neuron_proof_ocl = NULL;
         CNeuronAttentionOCL *neuron_attention_ocl = NULL;
         CNeuronMLMHAttentionOCL *neuron_mlattention_ocl = NULL;
         CNeuronDropoutOCL *dropout = NULL;
         CNeuronBatchNormOCL *batch = NULL;
         CVAE *vae = NULL;
         CNeuronLSTMOCL *lstm = NULL;
         switch(layer.At(0).Type())
           {

            case defNeuron:
            case defNeuronBaseOCL:
               neuron_ocl = new CNeuronBaseOCL();
               if(CheckPointer(neuron_ocl) == POINTER_INVALID)
                  return false;
               if(!neuron_ocl.Init(outputs, n, opencl, desc.count, desc.optimization, desc.batch))
                 {
                  delete neuron_ocl;
                  return false;
                 }
               neuron_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_ocl))
                 {
                  delete neuron_ocl;
                  return false;
                 }
               neuron_ocl = NULL;
               break;

            case defNeuronConvOCL:
               neuron_conv_ocl = new CNeuronConvOCL();
               if(CheckPointer(neuron_conv_ocl) == POINTER_INVALID)
                  return false;
               if(!neuron_conv_ocl.Init(outputs, n, opencl, desc.window, desc.step, desc.window_out,
                                                           desc.count, desc.optimization, desc.batch))
                 {
                  delete neuron_conv_ocl;
                  return false;
                 }
               neuron_conv_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_conv_ocl))
                 {
                  delete neuron_conv_ocl;
                  return false;
                 }
               neuron_conv_ocl = NULL;
               break;

            case defNeuronProofOCL:
               neuron_proof_ocl = new CNeuronProofOCL();
               if(!neuron_proof_ocl)
                  return false;
               if(!neuron_proof_ocl.Init(outputs, n, opencl, desc.window, desc.step, desc.count,
                                                                   desc.optimization, desc.batch))
                 {
                  delete neuron_proof_ocl;
                  return false;
                 }
               neuron_proof_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_proof_ocl))
                 {
                  delete neuron_proof_ocl;
                  return false;
                 }
               neuron_proof_ocl = NULL;
               break;

            case defNeuronAttentionOCL:
               neuron_attention_ocl = new CNeuronAttentionOCL();
               if(CheckPointer(neuron_attention_ocl) == POINTER_INVALID)
                  return false;
               if(!neuron_attention_ocl.Init(outputs, n, opencl, desc.window, desc.count, desc.optimization, desc.batch))
                 {
                  delete neuron_attention_ocl;
                  return false;
                 }
               neuron_attention_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_attention_ocl))
                 {
                  delete neuron_attention_ocl;
                  return false;
                 }
               neuron_attention_ocl = NULL;
               break;

            case defNeuronMHAttentionOCL:
               neuron_attention_ocl = new CNeuronMHAttentionOCL();
               if(CheckPointer(neuron_attention_ocl) == POINTER_INVALID)
                  return false;
               if(!neuron_attention_ocl.Init(outputs, n, opencl, desc.window, desc.count, desc.optimization, desc.batch))
                 {
                  delete neuron_attention_ocl;
                  return false;
                 }
               neuron_attention_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_attention_ocl))
                 {
                  delete neuron_attention_ocl;
                  return false;
                 }
               neuron_attention_ocl = NULL;
               break;

            case defNeuronMLMHAttentionOCL:
               neuron_mlattention_ocl = new CNeuronMLMHAttentionOCL();
               if(CheckPointer(neuron_mlattention_ocl) == POINTER_INVALID)
                  return false;
               if(!neuron_mlattention_ocl.Init(outputs, n, opencl, desc.window, desc.window_out,
                                               desc.step, desc.count, desc.layers, desc.optimization, desc.batch))
                 {
                  delete neuron_mlattention_ocl;
                  return false;
                 }
               neuron_mlattention_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_mlattention_ocl))
                 {
                  delete neuron_mlattention_ocl;
                  return false;
                 }
               neuron_mlattention_ocl = NULL;
               break;

El algoritmo para añadir objetos será igual al usado para crear un nuevo objeto en la clase padre.

Tras añadir todos los elementos de la población de una capa de neuronas, alinearemos el tamaño de la capa con el tamaño de la población, y luego eliminaremos el objeto de descripción de neuronas.

        }
      if(layer.Total() > (int)i_PopulationSize)
         layer.Resize(i_PopulationSize);
      delete desc;
     }
//---
   return true;
  }

Una vez completadas todas las iteraciones del sistema de ciclos, tendremos una población completa dentro de nuestro único ejemplar del modelo, y saldremos del método con un resultado positivo.

El código completo de este método, así como el código de toda la clase, se encuentra en el archivo adjunto al artículo.

Cuando hayamos terminado de trabajar con los métodos de inicialización del objeto de clase CNetGenetic, pasaremos a describir el método de pasada directa. Su nombre y sus parámetros serán los mismos que los de la clase padre. Aquí puede ver el puntero al objeto de array dinámico de los datos de origen, así como los parámetros para crear las marcas temporales de los datos de origen.

En el cuerpo del método, comprobaremos la validez del puntero resultante y de los objetos internos usados,

bool CNetGenetic::feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true)
  {
   if(CheckPointer(layers) == POINTER_INVALID || CheckPointer(inputVals) == POINTER_INVALID || layers.Total() <= 1)
      return false;

y también prepararemos las variables locales.

   CLayer *previous = NULL;
   CLayer *current = layers.At(0);
   int total = MathMin(current.Total(), inputVals.Total());
   CNeuronBase *neuron = NULL;
   if(CheckPointer(opencl) == POINTER_INVALID)
      return false;
   CNeuronBaseOCL *neuron_ocl = current.At(0);
   CBufferFloat *inputs = neuron_ocl.getOutput();
   int total_data = inputVals.Total();
   if(!inputs.Resize(total_data))
      return false;

Después transferiremos los datos de origen al búfer de capa neuronal de datos de origen y los registraremos en el contexto OpenCL. Al mismo tiempo, añadiremos marcas temporales, si fuera necesario.

   for(int d = 0; d < total_data; d++)
     {
      int pos = d;
      int dim = 0;
      if(window > 1)
        {
         dim = d % window;
         pos = (d - dim) / window;
        }
      float value = pos / pow(10000, (2 * dim + 1) / (float)(window + 1));
      value = (float)(tem ? (dim % 2 == 0 ? sin(value) : cos(value)) : 0);
      value += inputVals.At(d);
      if(!inputs.Update(d, value))
         return false;
     }
   if(!inputs.BufferWrite())
      return false;

A continuación, organizaremos un sistema de ciclos para aplicar directamente una pasada directa por todos los agentes de la población analizada. El ciclo externo recorrerá las capas neuronales en orden ascendente, mientras que el ciclo anidado iterará por los agentes.

Nótese que al indicar la neurona de la capa anterior, deberemos controlar claramente la correspondencia de los agentes. Cada agente trabajará en su propia vertical neuronal, que vendrá determinada por el número ordinal de la neurona en la capa, pero al mismo tiempo, no hemos duplicado la capa de datos de origen. Por consiguiente, al especificar el índice de la neurona correspondiente de la capa anterior, primero comprobaremos el número ordinal de la propia capa neuronal. Para la capa de datos de origen, el número ordinal de la neurona de la capa anterior será siempre "0", mientras que para todas las capas siguientes, se corresponderá con el número ordinal del agente.

Como todos los agentes son completamente independientes, podremos realizar transacciones para todos ellos al mismo tiempo.

   for(int l = 1; l < layers.Total(); l++)
     {
      previous = current;
      current = layers.At(l);
      if(CheckPointer(current) == POINTER_INVALID)
         return false;
      //---
      for(uint n = 0; n < i_PopulationSize; n++)
        {
         CNeuronBaseOCL *current_ocl = current.At(n);
         if(!current_ocl.FeedForward(previous.At(l == 1 ? 0 : n)))
            return false;
         continue;
        }
     }
//---
   return true;
  }

Obviamente, el uso de un ciclo no dota a los cálculos de un paralelismo total, pero al mismo tiempo, realizaremos secuencialmente iteraciones para todos los agentes, uno a uno. Esto nos permitirá explotar para todos los agentes los datos de origen generados una vez, reduciendo así el coste de preparación de los datos de origen para cada agente individual.

Obviamente, no nos olvidaremos de supervisar el proceso de las operaciones en cada paso, y cuando se completen las iteraciones del sistema de ciclos anidados, saldremos del método.

El algoritmo genético no ofrece una pasada inversa con una distribución del gradiente de error. No obstante, deberemos evaluar el rendimiento de los modelos. En este artículo, optimizaremos el agente del artículo anterior, que entrenamos con el algoritmo de gradiente de políticas. Para optimizar el rendimiento del modelo, maximizaremos la recompensa total del modelo por sesión. Como consecuencia, después de cada acción subsiguiente, deberemos retornar a cada agente su recompensa. Como recordará, la recompensa depende de la acción elegida, y cada agente realiza una acción distinta. Antes, solíamos obtener una distribución de probabilidad del agente respecto a la realización de acciones. Para ello, muestreábamos una acción de la distribución resultante y retornábamos la recompensa correspondiente al agente. Ahora tenemos muchos agentes de este tipo, y para evitar repetir estas iteraciones para cada agente individual en el programa externo, simplemente lo envolveremos todo en un método aparte Rewards, en cuyos parámetros un programa externo (entorno) transmitirá la recompensa para todas las acciones posibles. Este enfoque nos permitirá evaluar cada acción una sola vez, independientemente del número de agentes utilizados.

En el cuerpo del método, primero comprobaremos la validez de los punteros al vector de recompensa y al array dinámico de nuestras capas neuronales obtenidos en los parámetros.

bool CNetGenetic::Rewards(CArrayFloat *rewards)
  {
   if(!rewards || !layers || layers.Total() < 2)
      return false;

A continuación, extraeremos del array dinámico el puntero a la capa de resultados del funcionamiento del agente e inmediatamente comprobaremos la validez del puntero obtenido.

   CLayer *output = layers.At(layers.Total() - 1);
   if(!output)
      return false;

Después organizaremos un ciclo por todos los agentes de nuestra población iterados e interrogados. Para cada agente, muestrearemos una acción de la distribución correspondiente. Según la acción seleccionada, el agente recibirá su recompensa, que se sumará a las anteriormente obtenidas en el vector v_Rewards bajo el índice del agente.

   for(int i = 0; i < output.Total(); i++)
     {
      CNeuronBaseOCL *neuron = output.At(i);
      if(!neuron)
         return false;
      int action = GetAction(neuron.getOutput());
      if(action < 0)
         return false;
      v_Rewards[i] += rewards.At(action);
     }

A partir de los resultados de la evaluación de los agentes, podremos componer una distribución de probabilidad del acierto de los agentes respecto a los padres de la futura generación,

   v_Probability = v_Rewards - v_Rewards.Min();
   if(!v_Probability.Clip(0, v_Probability.Max()))
      return false;
   v_Probability = v_Probability / v_Probability.Sum();
//---
   return true;
  }

y luego saldremos del método con un resultado positivo. El lector podrá familiarizarse con el código completo de todos los métodos y clases utilizados en el archivo adjunto.

La funcionalidad creada basta para implementar cada sesión individual para la población analizada y evaluar las acciones de los agentes, pero una vez finalizada la sesión, deberemos seleccionar a los mejores representantes y crear una nueva generación de nuestra población. Esta funcionalidad la implementaremos en el método NextGeneration. En los parámetros de este método, transmitiremos 2 hiperparámetros: la proporción de individuos a eliminar y el parámetro de mutación. Además, los parámetros del método contendrán 2 variables en las que retornaremos la recompensa media y máxima de los agentes seleccionados.

En el cuerpo del método, primero podremos a cero las probabilidades de seleccionar los agentes que no se encuentren entre los elegidos, y también calcularemos directamente las recompensas máxima y media ponderada de los candidatos seleccionados.

bool CNetGenetic::NextGeneration(double quantile, double mutation, double &average, double &maximum)
  {
   maximum = v_Rewards.Max();
   v_Probability = v_Rewards - v_Rewards.Quantile(quantile);
   if(!v_Probability.Clip(0, v_Probability.Max()))
      return false;
   v_Probability = v_Probability / v_Probability.Sum();
   average = v_Rewards.Average(v_Probability);

Tenga en cuenta que aquí estamos usando las operaciones vectoriales recién añadidas. Esto nos permitía eliminar el uso de ciclos y acortar el código del programa. El método vector::Max() nos permite definir el valor máximo de un vector completo en una línea de código. El método vector::Quantile(...) retorna el valor del cuantil especificado para el vector. Usaremos este valor para descartar a los agentes débiles. Tras la operación vectorial de resta, sus probabilidades pasarán a ser negativas.

Usando las funciones vector::Clip(0, vector::Max()), resetearemos todos los valores negativos del vector.

Y con la misma maestría, en una sola línea, normalizaremos todos los valores del vector entre 0 y 1 con un valor total de todos los elementos igual a 1,

v_Probability = v_Probability / v_Probability.Sum();

mientras que la operación vector::Average(weights) se utilizará para determinar el valor medio ponderado del vector. El vector weights contiene los pesos de cada elemento del vector. Antes hemos reseteado las probabilidades de los agentes débiles, por lo que sus valores no se considerarán al calcular la media vectorial ponderada.

Así, el uso de operaciones vectoriales reducirá enormemente el código del programa y facilitará el trabajo del programador, cosa que agradecemos especialmente al equipo de MetaQuotes. Podrá estudiar con detalle las operaciones con vectores y matrices en el apartado correspondiente de la Documentación.

Pero volvamos a nuestro método. Ya hemos determinado los candidatos y sus probabilidades. Ahora añadiremos la proporción de mutaciones a la distribución y recalcularemos las probabilidades.

   if(!v_Probability.Resize(i_PopulationSize + 1))
      return false;
   v_Probability[i_PopulationSize] = mutation;
   v_Probability = (v_Probability / (1 + mutation)).CumSum();

En esta fase, tendremos la distribución de la probabilidad del uso de los agentes como padres de la siguiente generación, y podremos pasar directamente a la creación de una nueva población. Para ello, organizaremos un ciclo en el que generaremos cada capa neuronal de la nueva población. Debemos decir que generaremos matrices de pesos de todos los agentes a la vez en cada nivel de la capa neuronal, y así capa por capa.

Sin embargo, para evitar la creación de nuevos objetos, simplemente sobrescribiremos las matrices de pesos de los agentes existentes. Por consiguiente, antes de actualizar los pesos de la siguiente capa neuronal, primero llamaremos a la función GetWeights, que copiará los parámetros de la capa neuronal actual de todos los agentes en las matrices m_Weights y m_WeightsConv especialmente creadas. Aquí solo se enumerarán las matrices de pesos de las capas completamente conectadas y convolucionales, ya que son las únicas utilizadas en la arquitectura del modelo optimizado. Si utilizamos otras arquitecturas de capas neuronales, deberemos añadir las matrices adecuadas para almacenar temporalmente los parámetros.

   for(int l = 1; l < layers.Total(); l++)
     {
      if(!GetWeights(l))
        {
         PrintFormat("Error of load weights from layer %d", l);
         return false;
        }

Una vez que tengamos una copia de los parámetros del modelo, podremos empezar a editar los parámetros de los objetos sin problemas. Primero obtendremos el puntero al objeto de capa neuronal. y luego organizaremos un ciclo anidado de enumeración de todos nuestros agentes. En él, recuperaremos el puntero a la matriz de pesos del agente correspondiente,

      CLayer* layer = layers.At(l);
      for(uint i = 0; i < i_PopulationSize; i++)
        {
         CNeuronBaseOCL* neuron = layer.At(i);
         CBufferFloat* weights = neuron.getWeights();

y si el puntero obtenido es válido, organizaremos otro ciclo anidado en el que iteraremos por todos los elementos de la matriz de pesos y los sustituiremos por los parámetros padre correspondientes.

         if(!!weights)
           {
            for(int w = 0; w < weights.Total(); w++)
               if(!weights.Update(w, NextGenerationWeight(m_Weights, w, v_Probability)))
                 {
                  Print("Error of update weights");
                  return false;
                 }
            weights.BufferWrite();
           }

Aquí debemos decir que nos hemos desviado ligeramente del algoritmo básico. No hemos extraído una pareja de padres por casualidad. En su lugar, tomaremos a la vez y de forma aleatoria los pesos de todos los agentes seleccionados, según su distribución de probabilidad. El muestreo directo de los coeficientes de peso se realiza en el método NextGenerationWeight.

Después de generar los valores del siguiente búfer de datos, copiaremos sus valores en el contexto OpenCL.

Si fuera necesario, repetiremos las operaciones para la matriz de la capa convolucional.

         if(neuron.Type() != defNeuronConvOCL)
            continue;
         CNeuronConvOCL* temp = neuron;
         weights = temp.GetWeightsConv();
         for(int w = 0; w < weights.Total(); w++)
            if(!weights.Update(w, NextGenerationWeight(m_WeightsConv, w, v_Probability)))
              {
               Print("Error of update weights");
               return false;
              }
         weights.BufferWrite();
        }
     }

Tras actualizar los parámetros de todos los agentes, resetearemos el valor del vector de acumulación de recompensas para determinar correctamente el rendimiento de la nueva generación y saldremos del método con un resultado positivo.

   v_Rewards.Fill(0);
//---
   return true;
  }

Ya hemos analizado el algoritmo de los métodos de clase básicos que forman la base de la organización del algoritmo genético. Sin embargo, también existen algunos métodos auxiliares. Su algoritmo no es complicado, y podrá leer sobre él en el archivo adjunto. No obstante, también querríamos llamar su atención sobre el método de almacenamiento del modelo. La cuestión es que el método de almacenamiento de la clase padre guardará todos los agentes, y podrá utilizarse para proseguir con la optimización más adelante, pero no se puede usar para almacenar un agente individual, y el objetivo de la optimización es encontrar el agente óptimo. Por lo tanto, para almacenar el mejor agente, crearemos el método SaveModel. En los parámetros del método, transmitiremos el nombre del archivo para guardar el modelo, el número ordinal del agente y la bandera de escritura en el directorio Common.

En el cuerpo del método, primero comprobaremos el número ordinal del agente. Si no cumple con el número de agentes activos, lo sustituiremos por el número de agente con mayor probabilidad. Precisamente este será el agente con la máxima rentabilidad.

bool CNetGenetic::SaveModel(string file_name, int model, bool common = true)
  {
   if(model < 0 || model >= (int)i_PopulationSize)
      model = (int)v_Probability.ArgMax();

A continuación, crearemos un ejemplar del nuevo objeto modelo y copiaremos en este los parámetros del modelo necesario.

   CNetGenetic *new_model = new CNetGenetic();
   if(!new_model)
      return false;
   if(!new_model.CopyModel(layers, model))
     {
      new_model.Detach();
      delete new_model;
      return false;
     }

Ahora podremos simplemente llamar al método de almacenamiento de la clase padre para el nuevo modelo.

   bool result = new_model.Save(file_name, 0, 0, 0, 0, common);

Después de guardar el modelo, deberemos borrar el objeto recién creado antes de salir del método. No obstante, al copiar los datos, no crearemos nuevos objetos de capa neuronal, sino que simplemente utilizaremos los punteros a ellos. Por consiguiente, al borrar el objeto de modelo, también borraremos todos los objetos del agente almacenado en nuestro modelo global. Para evitar que esto ocurra, primero usaremos el método Detach, que separará los objetos de las capas neuronales del modelo almacenado. A continuación, podremos eliminar sin problemas el objeto de modelo creado en este método.

   new_model.Detach();
   delete new_model;
//---
   return result;
  }

Encontrará el código completo de todos los métodos de esta clase en el archivo adjunto. Ahora vamos a crear el asesor experto "Genetic.mq5", donde organizaremos el proceso de optimización del modelo. Crearemos el nuevo asesor usando como base el asesor "Actor_Critic.mq5" del artículo anterior.

En los parámetros externos del asesor, añadiremos los hiperparámetros para organizar el nuevo proceso.

input int                  PopulationSize =  50;
input int                  Generations = 1000;
input double               Quantile =  0.5;
input double               Mutation = 0.01;

También sustituiremos el objeto de trabajo del modelo.

CNetGenetic          Models;

La inicialización del modelo en el asesor se organizará de forma similar a la inicialización del modelo padre en los asesores anteriormente comentados.

int OnInit()
  {
//---
.............
.............
//---
   if(!Models.Load(MODEL + ".nnw", PopulationSize, false))
      return INIT_FAILED;
//---
   if(!Models.GetLayerOutput(0, TempData))
      return INIT_FAILED;
   HistoryBars = TempData.Total() / 12;
   Models.getResults(TempData);
   if(TempData.Total() != Actions)
      return INIT_PARAMETERS_INCORRECT;
//---
   bEventStudy = EventChartCustom(ChartID(), 1, 0, 0, "Init");
//---
   return(INIT_SUCCEEDED);
  }

El proceso de optimización propiamente dicho se organiza, como siempre, en la función Train. Al principio de la función, de forma similar a los asesores anteriormente comentados, definiremos el periodo de optimización (entrenamiento),

void Train(void)
  {
//---
   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year -= StudyPeriod;
   if(start_time.year <= 0)
      start_time.year = 1900;
   datetime st_time = StructToTime(start_time);

y cargaremos la muestra de entrenamiento.

   int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates);
   if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars))
     {
      ExpertRemove();
      return;
     }
   if(!ArraySetAsSeries(Rates, true))
     {
      ExpertRemove();
      return;
     }
//---
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();

Tras generar los datos de origen, prepararemos las variables locales. Al hacerlo, excluiremos el último mes de la muestra de entrenamiento para comprobar el rendimiento del modelo optimizado con los nuevos datos.

   CBufferFloat* State = new CBufferFloat();
   float loss = 0;
   uint count = 0;
   uint total = bars - HistoryBars - 1;
   ulong ticks = GetTickCount64();
   uint test_size=22*24;

A continuación, crearemos un sistema de ciclos anidados para organizar el proceso de optimización. El ciclo externo será el responsable de contar las generaciones de optimización. En el ciclo anidado, contaremos las iteraciones de la optimización. En este caso, hemos organizado la iteración completa de la muestra de entrenamiento por parte de todos los agentes. Sin embargo, puede usar el muestreo aleatorio para reducir el tiempo por sesión. Solo deberemos procurar que resulte suficiente para evaluar las principales tendencias de la muestra de entrenamiento. Obviamente, en tal caso, es posible que disminuya la precisión de la optimización, pero debemos encontrar el equilibrio importante entre la precisión de los resultados y el coste de optimización del modelo.

   for(int gen = 0; (gen < Generations && !IsStopped()); gen ++)
     {
      for(uint i = total; i > test_size; i--)
        {
         uint r = i + HistoryBars;
         if(r > (uint)bars)
            continue;

En el cuerpo del ciclo anidado, definiremos los límites del patrón actual y crearemos el búfer de datos inicial.

         State.Clear();
         for(uint b = 0; b < HistoryBars; b++)
           {
            uint bar_t = r - b;
            float open = (float)Rates[bar_t].open;
            TimeToStruct(Rates[bar_t].time, sTime);
            float rsi = (float)RSI.Main(bar_t);
            float cci = (float)CCI.Main(bar_t);
            float atr = (float)ATR.Main(bar_t);
            float macd = (float)MACD.Main(bar_t);
            float sign = (float)MACD.Signal(bar_t);
            if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE)
               continue;
            //---
            if(!State.Add((float)Rates[bar_t].close - open) || !State.Add((float)Rates[bar_t].high - open) ||
               !State.Add((float)Rates[bar_t].low - open) || !State.Add((float)Rates[bar_t].tick_volume / 1000.0f) ||
               !State.Add(sTime.hour) || !State.Add(sTime.day_of_week) || !State.Add(sTime.mon) ||
               !State.Add(rsi) || !State.Add(cci) || !State.Add(atr) || !State.Add(macd) || !State.Add(sign))
               break;
           }
         if(IsStopped())
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         if(State.Total() < (int)HistoryBars * 12)
            continue;

A continuación, llamaremos al método de pasada directa para nuestra población optimizada.

         if(!Models.feedForward(State, 12, true))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }

Como podemos ver, este proceso es prácticamente idéntico a las anteriores operaciones de formación de modelos. Al fin y al cabo, todas las diferencias en los procesos se organizan en las bibliotecas, mientras que la interfaz de funcionamiento de los métodos permanece inalterada, y ahora estamos llamando a la pasada directa para un modelo, pero en el cuerpo de la clase CNetGenetic hay una pasada directa para todos los agentes activos de la población.

A continuación, deberemos transmitir la recompensa actual a los agentes. Como ya hemos dicho, aquí no interpelaremos a todos los agentes. En su lugar, crearemos un búfer en el que indicaremos la recompensa por cada acción en un estado determinado, y transmitiremos este búfer en los parámetros del siguiente método. 

         double reward = Rates[i - 1].close - Rates[i - 1].open;
         TempData.Clear();
         if(!TempData.Add((float)(reward < 0 ? 20 * reward : reward)) ||
            !TempData.Add((float)(reward > 0 ? -reward * 20 : -reward)) ||
            !TempData.Add((float) - fabs(reward)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         if(!Models.Rewards(TempData))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }

Utilizaremos la política de recompensas en su forma original sin cambios. Esto nos permitirá evaluar de forma exacta el impacto del proceso de optimización en el resultado global.

Tras finalizar las iteraciones del ciclo de procesamiento de un estado del sistema, mostraremos en el gráfico la información sobre el paso del mismo para inspeccionar visualmente el proceso; luego pasaremos a la siguiente iteración del ciclo.

         if(GetTickCount64() - ticks > 250)
           {
            uint x = total - i;
            double perc = x * 100.0 / (total - test_size);
            Comment(StringFormat("%d from %d -> %.2f%% from %.2f%%", x, total - test_size, perc, 100));
            ticks = GetTickCount64();
           }
        }

Al finalizar la siguiente sesión, guardaremos los parámetros del mejor agente

      Models.SaveModel(MODEL+".nnw", -1, false);

y pasaremos a la siguiente generación. Todo lo que deberemos hacer es llamar a un método, CNetGenetic::NextGeneration. Recuerde controlar el proceso de ejecución de las operaciones.

      double average, maximum;
      if(!Models.NextGeneration(Quantile, Mutation, average, maximum))
        {
         PrintFormat("Error of create next generation: %d", GetLastError());
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }
      //---
      PrintFormat("Genegation %d, Average Cummulative reward %.5f, Max Reward %.5f", gen, average, maximum);
     }

Por último, mostraremos en el diario de registro la información sobre los resultados obtenidos y pasaremos a evaluar la nueva generación de la población analizada en una nueva iteración del ciclo.

Una vez terminado el proceso de optimización, borraremos los datos y finalizaremos el funcionamiento del asesor.

   delete State;
   Comment("");
//---
   ExpertRemove();
  }

Como podemos ver, esta organización de la clase ha facilitado al máximo el trabajo en el lado del programa principal. En la práctica, la organización del proceso de optimización consistirá en la realización de llamadas sucesivas a 3 métodos de la clase, lo cual resulta comparable al entrenamiento de modelos al utilizar métodos de gradiente. De esta forma, reduciremos significativamente el número total de transacciones por agente.

3. Simulación

Las pruebas del proceso de optimización se han realizado manteniendo todos los parámetros usados anteriormente. Hemos tomado la muestra de entrenamiento de la historia del instrumento EURUSD, con el marco temporal H1. Para la optimización, hemos tomado la historia de los últimos 2 años. Para el asesor, hemos tomado los parámetros externos por defecto. Como modelo para la prueba, hemos tomado la arquitectura del artículo anterior con la búsqueda de la distribución de probabilidad óptima de la toma de decisiones. Este enfoque nos permitirá sustituir el modelo optimizado en el asesor experto "REINFORCE-test.mq5" utilizado anteriormente. Como podemos ver, este es el tercer enfoque en el proceso de entrenamiento del modelo de arquitectura única. Hemos entrenado previamente un modelo similar con los algoritmos Policy Gradient y Actor-Crítico. Resulta más interesante observar los resultados de la optimización.

Como recordará, no hemos utilizado los datos del último mes para optimizar el modelo. Esto nos deja pocos datos para poner a prueba el modelo optimizado. Al ejecutar el modelo optimizado en el simulador de estrategias con los datos del último mes, hemos obtenido el siguiente resultado.

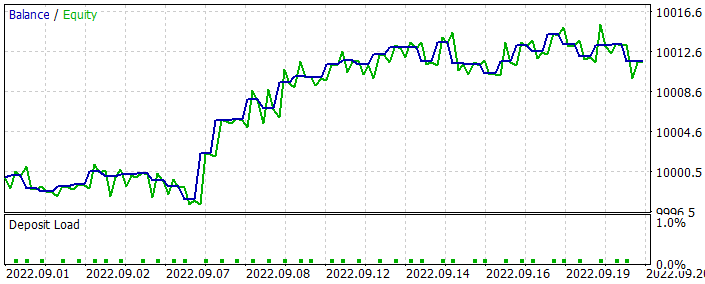
Como podemos ver en el gráfico, hemos obtenido un gráfico de balance creciente, pero su rendimiento es algo inferior al obtenido entrenando un modelo similar con el método Actor-Crítico. Al mismo tiempo, también se observa una disminución del número de transacciones. De hecho, el número de transacciones se ha reducido a la mitad.

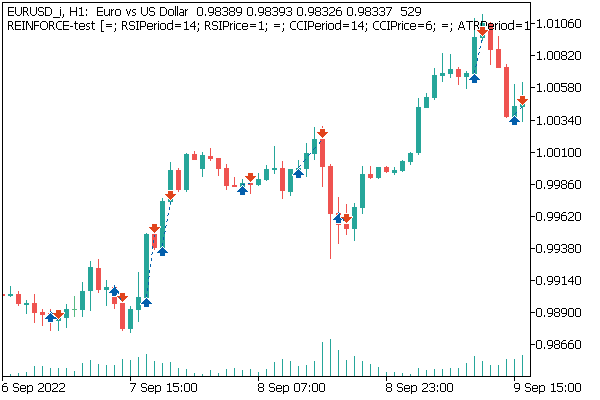
Si observamos el gráfico del instrumento con las operaciones realizadas, podremos ver un claro intento de comerciar siguiendo la tendencia. A nuestro juicio, parece un resultado interesante. Al entrenar un modelo similar utilizando métodos de gradiente, el modelo intentaba ejecutar una operación en la mayoría de los movimientos, y a menudo esto ofrecía un aspecto caótico. Aquí podemos ver una cierta lógica que concuerda con los principios bien conocidos del trading.

¿O solo me lo parece a mí, y todas mis conclusiones son "traídas por los pelos"? Recomendamos al lector realizar sus propios experimentos: le resultará interesante observar los resultados.

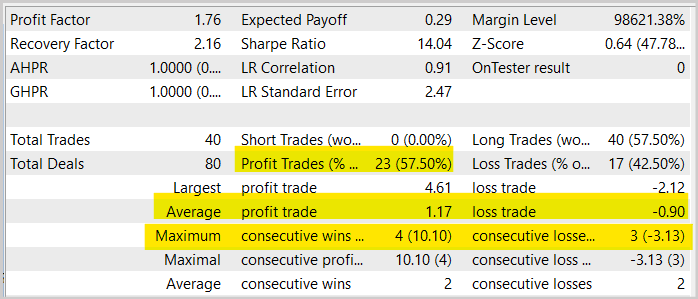
En general, podemos observar un aumento de la proporción de operaciones rentables de casi el 1,5% en comparación con la misma prueba del modelo entrenado con el método Actor-Crítico. Sin embargo, al mismo tiempo, el número de transacciones se ha multiplicado por dos. Además, también podemos observar una disminución de los beneficios y las pérdidas medios por transacción. Todo lo mencionado conlleva una disminución general del volumen de negocios y, por consiguiente de la rentabilidad total del periodo. No obstante, debemos señalar que las pruebas realizadas durante un mes no pueden considerarse representativas para el funcionamiento de un asesor con un horizonte temporal largo. Así que, una vez más, le animamos a probar sus modelos a fondo antes de utilizarlos en transacciones reales.

Conclusión

En este artículo, nos hemos familiarizado con el método genético de optimización de modelos, que podemos utilizar al optimizar cualquier modelo paramétrico. Una de las principales ventajas de este método es que se puede utilizar para optimizar modelos indiferenciados. Esto resulta completamente imposible al entrenar modelos utilizando métodos de gradiente, y, en concreto, con el método de descenso de gradiente en todas sus variantes.

En el artículo también ofrecemos una variante de implementación del algoritmo usando MQL5, e incluso hemos optimizado el modelo de prueba, comprobando sus resultados en el simulador de estrategias.

Según los resultados de las pruebas, podemos afirmar que el modelo ha funcionado bastante bien, y que el método puede utilizarse para optimizar modelos comerciales. No obstante, antes de poner un modelo a trabajar en una cuenta real, deberemos probarlo a fondo y de forma exhaustiva.

Enlaces

1. Redes neuronales: así de sencillo (Parte 26): Aprendizaje por refuerzo
2. Redes neuronales: así de sencillo (Parte 27): Aprendizaje Q profundo (DQN)
3. Redes neuronales: así de sencillo (Parte 28): Algoritmo de gradiente de políticas
4. Redes neuronales: así de sencillo (Parte 29): Algoritmo actor-crítico con ventaja (Advantage actor-critic)

Programas usados en el artículo.

#	Nombre	Tipo	Descripción
1	Genetic.mq5	Asesor	Asesor para la optimización de modelos
2	NetGenetic.mqh	Biblioteca de clases	Biblioteca para organizar un algoritmo genético
3	REINFORCE-test.mq5	Asesor	Asesor Experto para probar modelos en el Simulador de Estrategias
4	NeuroNet.mqh	Biblioteca de clases	Biblioteca para organizar modelos de redes neuronales
5	NeuroNet.cl	Biblioteca	Biblioteca de código OpenCL para organizar modelos de redes neuronales