Características del Wizard MQL5 que debe conocer (Parte 02): Mapas de Kohonen

 

1. Introducción    

1.1 Continuamos con la serie de artículos sobre el Wizard MQL5, hoy veremos los  Mapas de Kohonen. Según la Wikipedia, son un método para proyectar un espacio multidimensional en un espacio con una dimensionalidad más baja (la mayoría de las veces, bidimensional) manteniendo la estructura de datos topológicos. El método fue sugerido por Teuvo Kohonen en la década de 1980.

En términos simples, los mapas de Kohonen (también conocidos como mapas autoorganizados) superan la complejidad sumativa sin perder la claridad de lo que se suma. La suma sirve como forma de organización, de ahí el nombre de autoorganización. Con los datos o mapas reorganizados, tenemos dos conjuntos de datos relacionados: los datos de entrada originales de alta dimensionalidad y los datos de salida generalizados de menor dimensionalidad, que generalmente (aunque no siempre) se representan en dos dimensiones. Los datos de entrada son conocidos, y los de salida, desconocidos (en nuestro caso, "estudiados").  

Si, para los objetivos de este artículo, nos centramos únicamente en la serie de precios, los datos conocidos (iniciales) en cualquier momento serán los precios restantes del momento dado, mientras que los datos desconocidos (funtoriales) serán los que se ubican a la derecha. La forma en que clasificamos los datos conocidos y desconocidos afectará el número de dimensiones tanto para los datos originales como para los funtoriales. Aquí, deberemos prestar la máxima atención, ya que este dependerá en gran medida de las opiniones del tráder y su enfoque de la negociación.  

1.2 Un concepto erróneo común sobre los mapas de Kohonen es que los datos funtoriales deben ser una imagen 2D como la que se muestra a continuación.

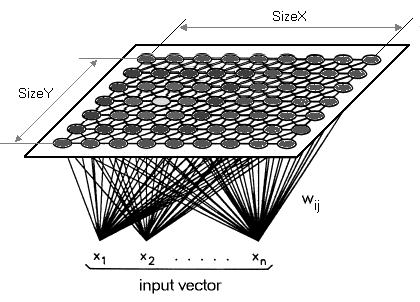
Esta interpretación tiene derecho a existir, pero cuando se aplica al trading, el functor puede (y, quizás, debería) tener una dimensión. Por lo tanto, en lugar de reducir nuestros datos multidimensionales a un mapa bidimensional, los trazaremos en una sola línea. Por definición, los mapas de Kohonen están diseñados para reducir la dimensionalidad. En el presente artículo, aprovecharemos esta función y la llevaremos al siguiente nivel. Los mapas de Kohonen se diferencian de las redes neuronales convencionales tanto en el número de capas como en el algoritmo subyacente. Se trata de un conjunto de una sola capa de neuronas, generalmente realizado en forma de cuadrícula bidimensional lineal. Todas las neuronas de esta capa, a la que llamamos funtor, se conectan a los datos originales,pero no entre sí.. Esto significa que las neuronas no dependerán del peso de las demás directamente y se actualizarán solo cuando cambien los datos de origen. La capa de datos del funtor es un "mapa"que se autoorganizará en cada iteración de entrenamiento según los datos de entrada. Por consiguiente, después del entrenamiento, cada neurona tendrá un tamaño ajustado al peso en la capa del funtor, y esto permitirá el cálculo de la distancia euclidiana entre dos de estas neuronas.

 

2. Creando la clase

2.1 Estructura de la clase

2.1.1 Primero definiremos la clase abstracta Dimension. Este código resultaría más ordenado si implementáramos la mayor parte en un archivo separado y simplemente hiciéramos referencia al mismo, pero este tema, junto con los temas del dinero y las clases de trailing, los abarcaremos en el próximo artículo, así que ahora, como en el artículo anterior, todo el código estará en el archivo de señal. Las dimensiones siempre son importantes en esta red porque influyen mucho en el resultado. Los datos de entrada serán multidimensionales, como suele ser el caso normalmente. Los datos funtoriales (de salida) tendrán una dimensión, a diferencia de los típicos x e y. Dada la multidimensionalidad tanto de los datos originales como de los funtoriales, el tipo de datos ideal sería un array double.

Sin embargo, siguiendo el orden establecido al estudiar la biblioteca MQL5, en su lugar usaremos una lista de arrays del tipo double. Al igual que en el artículo anterior, los datos de entrada serán los cambios en los mínimos menos los cambios en los máximos durante una barra. Como regla general, será mejor elegir los datos de entrada en función de nuestra propia comprensión del mercado. No le recomendamos usar los datos de otras personas en cuentas reales e incluso de prueba. Cada tráder debe modificar el código que se muestra aquí para adaptarlo a sus propios datos de entrada. Como ya hemos mencionado, los datos funtoriales serán unidimensionales. Como también es una lista, podremos configurarla para añadir dimensiones adicionales. No obstante, para nuestros propósitos, nos centraremos en el cambio entre la apertura y el cierre de la barra más reciente. El Wizard MQL5 nos permite especificar lo que se considera una barra eligiendo nuestro propio marco temporal. La clase «dimension» se heredará de la interfaz double de la lista en la biblioteca de código MQL5. A la clase se añadirán dos funciones: Get y Set. Como sus nombres sugieren, nos ayudarán a recuperar y establecer los valores en una lista después de proporcionar un índice.

#include                        <Generic\ArrayList.mqh>
#include                        <Generic\HashMap.mqh>

#define                         SCALE 5

#define                         IN_WIDTH 2*SCALE
#define                         OUT_LENGTH 1

#define                         IN_RADIUS 100.0
#define                         OUT_BUFFER 10000

//
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cdimension                :  public CArrayList<double>
  {
    public:
        
      Cdimension()              {};
      ~Cdimension()             {};
        
     virtual double             Get(const int Index)                                    
                                {       
                                  double _value=0.0; TryGetValue(Index,_value); return(_value); 
                                };
     virtual void               Set(const int Index,double Value)       
                                {  
                                  Insert(Index,Value);                                                                                                                   
                                };
  };

2.1.2La clase Feed heredará de la clase «dimension» recién creada. No se añadirán características especiales aquí. Solo el constructor especificará la capacidad de la lista (similar al tamaño de un array), y el tamaño por defecto de nuestra lista de entrada será 10.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cfeed             : public Cdimension
 {
   public:
                
     Cfeed()            { Clear(); Capacity(IN_WIDTH);  };
     ~Cfeed()           {                               };
 };

2.1.3La clase funtor es similar a la clase feed, salvo por el tamaño. Como ya hemos mencionado, analizaremos una (no dos) dimensiones para nuestros datos funtoriales, por lo que el tamaño del conjunto será 1.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cfunctor          : public Cdimension
 {
   public:
                
   Cfunctor()           { Clear(); Capacity(OUT_LENGTH); };
   ~Cfunctor()          {                                };
 };

2.1.4De mayor interés resulta la clase Neuron. La declararemos como una clase que hereda de una interfaz en la biblioteca MQL5, y que acepta dos tipos de datos personalizados: clave y valor. La interfaz de la plantilla analizada es HashMap.  Las dos clases declaradas anteriormente se utilizarán como datos de usuario: la clase Feed como nuestra clave y la clase Functor como nuestro valor. Tampoco tenemos funciones, solo punteros a las clases Feed, Functor y 'key-value' (clave-valor). Como sugiere su nombre, el propósito de esta clase es definir una neurona. La neurona será nuestra unidad de datos porque incluye tanto un tipo de datos de entrada como un tipo de datos de salida (funtoriales). Esta será la entrada de la neurona, que se comparará con las neuronas ya entrenadas para mostrar cuál podría ser el funtor. Además, las neuronas mostradas tienen sus propios datos funtoriales, que se actualizan cada vez que se entrena una nueva neurona.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cneuron           : public CHashMap<Cfeed*,Cfunctor*>
 {
   public:
                
    double              weight;
                        
    Cfeed               *fd;
    Cfunctor            *fr;
                        
    CKeyValuePair
    <
    Cfeed*,
    Cfunctor*
    >                   *ff;
                        
    Cneuron()           {
                          weight=0.0;
                          fd = new Cfeed();
                          fr = new Cfunctor();
                          ff = new CKeyValuePair<Cfeed*,Cfunctor*>(fd,fr);
                          Add(ff);
                        };
                                                                        
   ~Cneuron()           {
                          ZeroMemory(weight);
                          delete fd;
                          delete fr;
                          delete ff;
                        };
 };

2.1.5Luego viene la clase abstracta Layer. La clase hereda de la plantilla de lista de la clase de neurona y tiene un objeto, el puntero a la neurona. Al ser una clase abstracta, el cometido de este puntero de neurona será su uso por parte de las clases que heredan de esta clase. Hay dos clases de este tipo: la capa de entrada y la capa de salida. Estrictamente hablando, los mapas de Kohonen no deben clasificarse como redes neuronales, ya que no tienen conexiones directas con los pesos y el algoritmo de retropropagación. Con frecuencia, los mapas de Kohonen se denominan un tipo diferente de redes neuronales. 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Clayer            : public CArrayList<Cneuron*>
 {
   public:
                
    Cneuron             *n;
                
    Clayer()            { n = new Cneuron();     };
    ~Clayer()           { delete n;              };
 };

2.1.6La clase Input Layer se hereda de la clase abstracta layer. Aquí es donde se almacenarán los valores actuales y últimos del flujo de datos cuando la red está funcionando. En lugar de ser una capa típica con múltiples neuronas, contará con una única neurona que contendrá los datos funtoriales y originales más recientes, por lo tanto, su tamaño será 1.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cinput_layer      : public Clayer
 {
   public:
                
   static const int     size;
                        
    Cinput_layer()      {
                          Clear();
                          Capacity(Cinput_layer::size);
                          for(int s=0; s<size; s++)
                          {
                            n = new Cneuron();
                            Add(n);
                          }
                        }
    ~Cinput_layer()     {};
 };
 const int Cinput_layer::size=1;

2.1.7La clase Output Layer también heredará de la clase layer, pero servirá como nuestro mapa, ya que las neuronas "entrenadas" se almacenarán aquí. Los datos funtoriales de las neuronas en esta capa serán equivalentes a una imagen de un mapa autoorganizado típico. Su tamaño inicial es de 10 000 y se incrementará en el mismo valor a medida que se entrenen nuevas neuronas.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Coutput_layer      : public Clayer
 {
   public:
                
    int                  index;
    int                  size;
                        
    Coutput_layer()      {
                           index=0;
                           size=OUT_BUFFER;
                           Clear();
                           Capacity(size);
                           for(int s=0; s<size; s++)
                           {
                             n = new Cneuron();
                             Add(n);
                           }
                         };
                                                                        
    ~Coutput_layer()     {
                           ZeroMemory(index);
                           ZeroMemory(size);
                         };
 };

2.1.8La clase Network,como la clase neuron, también se hereda de la interfaz de la plantilla HashMap. Las clases input layer y output layer sirven como clave y valor. Tiene la mayoría de las funciones (9) no solo para obtener el tamaño de la lista, sino también para extraer y actualizar las neuronas en las capas correspondientes.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cnetwork           : public CHashMap<Cinput_layer*,Coutput_layer*>
 {
   public:
                
     Cinput_layer        *i;
     Coutput_layer       *o;
                        
     CKeyValuePair
     <
     Cinput_layer*,
     Coutput_layer*
     >                   *io;
                        
     Cneuron             *i_neuron;
     Cneuron             *o_neuron;
                        
     Cneuron             *best_neuron;
                        
     Cnetwork()          {
                           i = new Cinput_layer();
                           o = new Coutput_layer();
                           io = new CKeyValuePair<Cinput_layer*,Coutput_layer*>(i,o);
                           Add(io);
                                                                                
                           i_neuron = new Cneuron();
                           o_neuron = new Cneuron();
                                                                                
                           best_neuron = new Cneuron();
                         };
                                                                        
     ~Cnetwork()         {
                           delete i;
                           delete o;
                           delete io;
                           delete i_neuron;
                           delete o_neuron;
                           delete best_neuron;
                         };
                        
      virtual int        GetInputSize()
                         {
                           TryGetValue(i,o);
                           return(i.size);
                         };
                        
      virtual int        GetOutputIndex()
                         {
                           TryGetValue(i,o);
                           return(o.index);
                         };
                        
      virtual void       SetOutputIndex(const int Index)
                         {
                           TryGetValue(i,o);
                           o.index=Index;
                           TrySetValue(i,o);
                         };
                        
      virtual int        GetOutputSize()
                         {
                           TryGetValue(i,o);
                           return(o.size);
                         };
                        
      virtual void       SetOutputSize(const int Size)
                         {
                           TryGetValue(i,o);
                           o.size=Size;
                           o.Capacity(Size);
                           TrySetValue(i,o);
                         };
                        
      virtual void       GetInNeuron(const int NeuronIndex)
                         {
                           TryGetValue(i,o);
                           i.TryGetValue(NeuronIndex,i_neuron);
                         };
                        
      virtual void       GetOutNeuron(const int NeuronIndex)
                         {
                           TryGetValue(i,o);
                           o.TryGetValue(NeuronIndex,o_neuron);
                         };
                        
      virtual void       SetInNeuron(const int NeuronIndex)
                         {
                           i.TrySetValue(NeuronIndex,i_neuron);
                         };
                        
      virtual void       SetOutNeuron(const int NeuronIndex)
                         {
                           o.TrySetValue(NeuronIndex,o_neuron);
                         };
 };

2.1.9 La clase map es la última clase genérica. Llama a un ejemplar de la clase de red e incluye otras variables para entrenar las neuronas y obtener la neurona más adecuada para la red. 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cmap
  {
    public:
                        
      Cnetwork               *network;
                        
      static const double     radius;
      static double           time;
                        
      double                  QE;       //proxy for Quantization Error
      double                  TE;       //proxy for Topological Error
                        
      datetime                refreshed;
                        
      bool                    initialised;
                        
      Cmap()                  {
                                network = new Cnetwork();
                                                                                        
                                initialised=false;
                                                                                        
                                time=0.0;
                                                                                        
                                QE=0.50;
                                TE=5000.0;
                                                                                        
                                refreshed=D'1970.01.05';
                               };
                                                                                
      ~Cmap()                  {
                                 ZeroMemory(initialised);
                                                                                        
                                 ZeroMemory(time);
                                                                                        
                                 ZeroMemory(QE);
                                 ZeroMemory(TE);
                                                                                        
                                 ZeroMemory(refreshed);
                               };
 };
 const double Cmap::radius=IN_RADIUS;
 double Cmap::time=10000/fmax(1.0,log(IN_RADIUS));

 

2.2. Topología

2.2.1 El entrenamiento de neuronas es un aprendizaje competitivoque incluye el ajustes de los pesos de funtoriales de las neuronas existentes en la capa de salida y la adición de una nueva neurona de entrenamiento. La velocidad a la que se ajustan estos pesos y, lo que es más importante, el número de iteraciones necesarias para ajustar estos pesos, son parámetros muy sensibles para determinar el rendimiento de la red. Con cada iteración del ajuste de peso, se calcula un nuevo radio más pequeño. Yo llamo a este radio funtor-error. No debemos confundirlo con el error topológico del mapa autoorganizado (SOM Topological-error). Sin embargo, se le conoce más comúnmente como el radio de la vecindad, medido por la distancia euclidiana. Uso la palabra "error" porque este parámetro deberá minimizarse para obtener los mejores resultados de red. Cuantas más iteraciones realicemos, menor será el funtor-error. Además del número de iteraciones, la tasa de aprendizaje deberá reducirse gradualmente desde un número cercano a la unidad hasta cero.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalKM::NetworkTrain(Cmap &Map,Cneuron &TrainNeuron)
  {
    Map.TE=0.0;

    int _iteration=0;
    double _training_rate=m_training_rate;

    int _err=0;
    double _functor_error=0.0;

    while(_iteration<m_training_iterations)
    {
      double _current_radius=GetTrainingRadius(Map,_iteration);

      for(int i=0; i<=Map.network.GetOutputIndex(); i++)
      {
        Map.network.GetOutNeuron(i);
        double _error = EuclideanFunctor(TrainNeuron,Map.network.o_neuron);

        if(_error<_current_radius)
        {
          _functor_error+=(_error);
          _err++;

          double _remapped_radius = GetRemappedRadius(_error, _current_radius);

          SetWeights(TrainNeuron,Map.network.o_neuron,_remapped_radius,_training_rate);

          Map.network.SetOutNeuron(i);
        }
      }

      _iteration++;
      _training_rate=_training_rate*exp(-(double)_iteration/m_training_iterations);
    }

    int
    _size=Map.network.GetOutputSize(),
    _index=Map.network.GetOutputIndex();
    Map.network.SetOutputIndex(_index+1);
    if(_index+1>=_size)
    {
      Map.network.SetOutputSize(_size+OUT_BUFFER);
    }

    Map.network.GetOutNeuron(_index+1);
    for(int w=0; w<IN_WIDTH; w++)
    {
      Map.network.o_neuron.fd.Set(w,TrainNeuron.fd.Get(w));
    }
    
    for(int l=0; l<OUT_LENGTH; l++)
    {
      Map.network.o_neuron.fr.Set(l,TrainNeuron.fr.Get(l));
    }

    Map.network.SetOutNeuron(_index+1);

    if(_err>0)
    {
      _functor_error/=_err;
      Map.TE=_functor_error*IN_RADIUS;
    }
  }

2.2.2 El error topológico es un atributo clave de los mapas de Kohonen. Podemos pensar en ello como una medida de la proximidad de la capa de salida respecto al objetivo previsto a largo plazo. Con cada entrenamiento, las neuronas de la capa de salida se adaptan al resultado real o previsto, por lo que surge la necesidad de medir este progreso. Cuanto más preservemos la capa de salida, más cerca estaremos de nuestro objetivo. Para los objetivos de este artículo, usaremos el funtor-error como nuestro valor aproximado (proxy).

2.3. Cuantificación

2.3.1 El mapeo de neuronas consiste en la búsqueda de los pesos de los funtores más adecuados para una neurona para la que solo están presentes los datos iniciales. Esto se hace hallando la neurona en la capa de salida con la distancia euclidiana de datos de origen más corta respecto a la neurona para la que no se conocen datos funtoriales. Al igual que con el aprendizaje, llamo a esta distancia fuente-error. Nuevamente, cuanto menor sea este valor, más fiable deberá ser la red.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalKM::NetworkMapping(Cmap &Map,Cneuron *MapNeuron)
  {
    Map.QE=0.0;
    
    Map.network.best_neuron = new Cneuron();

    int _random_neuron=rand()%Map.network.GetOutputIndex();

    Map.network.GetInNeuron(0);
    Map.network.GetOutNeuron(_random_neuron);

    double _feed_error = EuclideanFeed(Map.network.i_neuron,Map.network.o_neuron);

    for(int i=0; i<Map.network.GetOutputIndex(); i++)
    {
      Map.network.GetOutNeuron(i);

      double _error = EuclideanFeed(Map.network.i_neuron,Map.network.o_neuron);

      if(_error < _feed_error)
      {
        for(int w=0; w<IN_WIDTH; w++)
        {
          Map.network.best_neuron.fd.Set(w,Map.network.o_neuron.fd.Get(w));
        }

        for(int l=0; l<OUT_LENGTH; l++)
        {
          Map.network.best_neuron.fr.Set(l,Map.network.o_neuron.fr.Get(l));
        }

        _feed_error = _error;
      }
    }

    Map.QE=_feed_error/IN_RADIUS;
}

2.3.2 El error de cuantificación es otro atributo importante de los mapas Kohonen, que, en mi opinión, no tiene una definición clara. Creo que se trata de un error de conversión de datos de alta dimensionalidad a datos de baja dimensionalidad. En nuestro caso, este será un error al convertir los datos originales a funtoriales. Para los objetivos de este artículo, usaremos como nuestra aproximación la fuente-error.

 

3. Ensamblaje con la ayuda del Wizard MQL5

3.1 El ensamblaje con el Wizard es bastante simple. Recomendamos al lector que realice pruebas con marcos temporales más altos, porque las 10 000 iteraciones de entrenamiento ideales por barra tomarán bastante tiempo con un entrenamiento largo. 

 

 

4. Pruebas en el simulador de estrategias

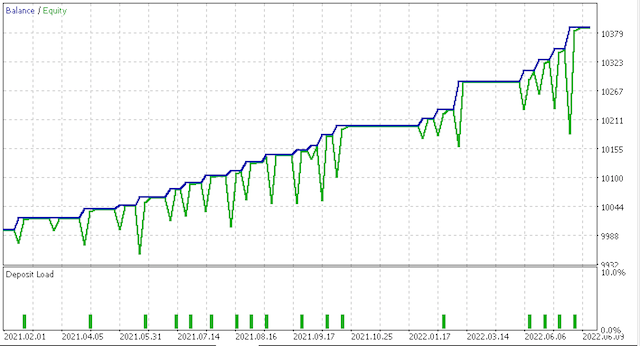
4.1 Para los propósitos de nuestra prueba, los datos de entrada predeterminados investigarán la sensibilidad de nuestro proxy de error de cuantificación (quantization error proxy, QE) y el proxy de error topológico (topological error proxy, TE). Vamos a considerar los dos escenarios. Para empezar, usaremos en las pruebas valores muy conservadores de QE y TE, iguales a 0,5 y 12,5. Luego probaremos estos datos de entrada para 0.75 y 25.0,respectivamente.

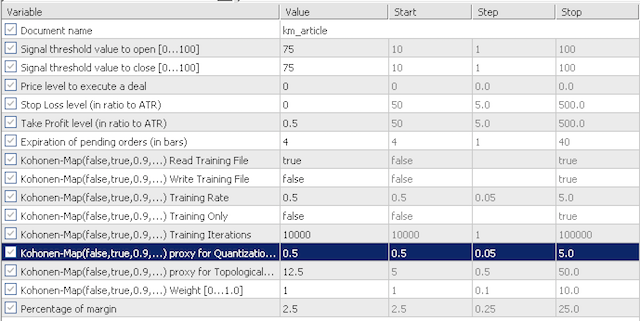
ajustes conservadores

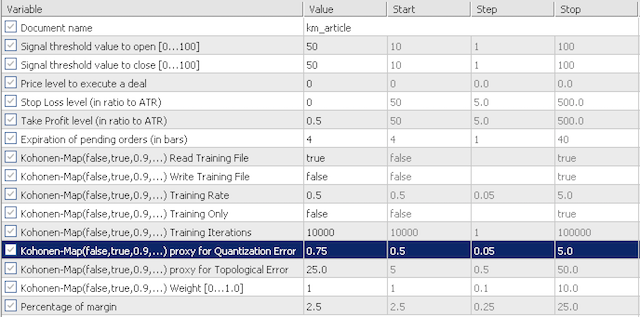
ajustes agresivos

 

 

No hay muchos parámetros de entrada. Tenemos una "lectura de entrenamiento" (training read) que determinará si debemos leer el archivo de entrenamiento antes de la inicialización. Si falta este archivo, el asesor no realizará la validación. También tendremos una "escritura de entrenamiento" (training write) que, como sugiere el nombre, determinará si el archivo de entrenamiento deberá escribirse después de que se desinicialice el asesor. El entrenamiento siempre tiene lugar después del inicio del asesor. El parámetro de entrada training only (solo entrenamiento) hace posible participar exclusivamente en el entrenamiento sin negociación. Otros dos parámetros importantes de los mapas de Kohonen son la tasa de entrenamiento (training rate) y las iteraciones de entrenamiento. En general, cuanto más altos sean estos dos valores (la tasa de entrenamiento limitada a 1,0), mejor resultará el rendimiento, pero esto tendrá un coste en cuanto al tiempo de ejecución y los recursos computacionales. 

El asesor experto ha realizado el entrenamiento en un periodo en forma de V del 01/10/2018 al 01/06/2021, y también ha pasado las pruebas forward desde la fecha de finalización del entrenamiento hasta el presente.

El uso de valores conservadores ha ofrecido los siguientes resultados:

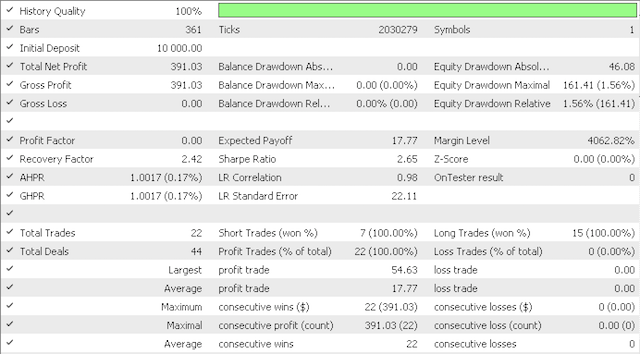
Curva de equidad:

La variante más agresiva ha ofrecido los siguientes resultados:

 

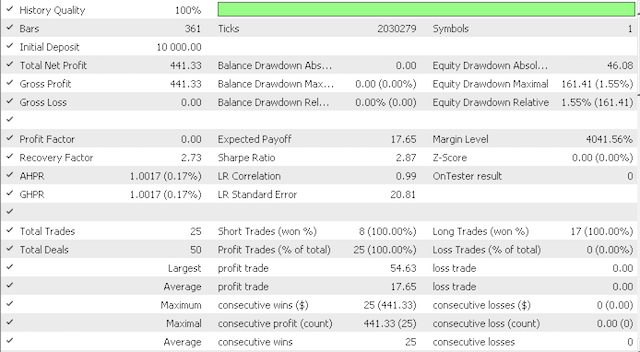
Curva de equidad:

 

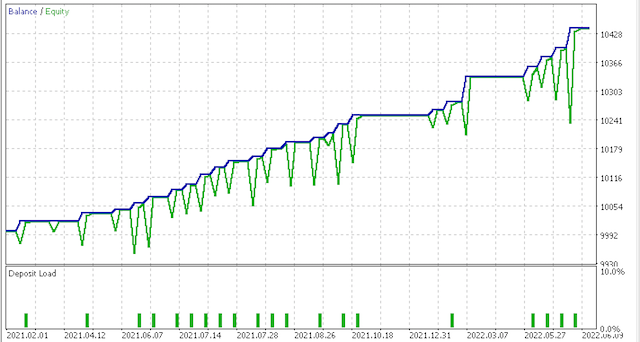
Obviamente, se requieren más pruebas y ajustes en cuanto al riesgo y el tamaño de la posición, pero para un sistema que aprende en tan poco tiempo, los resultados son prometedores. Sin embargo, al comparar los dos escenarios anteriores, vemos que la opción más conservadora funciona peor, dado que su índice de Sharpe de 0,43 es casi la mitad de su valor de 0,85 con un número mayor de operaciones. El uso de mapas de Kohonen requiere más estudio antes de su uso. Los datos sin procesar y funtoriales deben ajustarse para adaptarse a nuestro estilo comercial. La prueba previa siempre debe realizarse con los datos de ticks de su bróker durante periodos de tiempo significativos.

 

5. Conclusión

5.1 El Wizard MQL5 es una herramienta muy flexible para crear sistemas comerciales rápidamente. En este artículo, hemos analizado una variante de los mapas de Kohonen que transfieren los datos multidimensionales de origen de las series temporales de los precios a una dimensión que va de -1,0 a 1,0. Aunque no es una práctica común, este enfoque demuestra la esencia misma de los mapas de Kohonen, que consiste en reducir la complejidad y simplificar la toma de decisiones. También hemos mostrado el uso del código de la biblioteca MQL, en particular ArrayList y HashMap. Espero que haya disfrutado el artículo. ¡Gracias por su atención!