Возможности Мастера MQL5, которые вам нужно знать (Часть 02): Карты Кохонена

 

1. Введение    

1.1 Продолжая серию о Мастере MQL5, мы займемся  картами Кохонена. Согласно Википедии, они представляют собой метод проецирования многомерного пространства в пространство с более низкой размерностью (чаще всего, двухмерное) с сохранением топологической структуры данных. Метод был предложен Теуво Кохоненом в 1980-х годах. 

Карты Кохонена (также известные как самоорганизующиеся карты) преодолевают суммирующую сложность, не теряя четкости того, что суммируется. Суммирование служит формой организации (отсюда и определение "самоорагнизующиеся"). Таким образом, с реорганизованными данными, или картами, у нас есть два набора связанных данных: исходные входные многомерные данные и обобщенные выходные данные с более низкой размерностью, которые обычно (хотя и не всегда) представлены в двух измерениях. Входные данные являются известными, выходные – неизвестными (в нашем случае "изучаемыми").  

Если мы в целях этой статьи сосредоточимся только на ценовых рядах, известные (исходные) данные в любой момент времени – это цены, оставшиеся с данного времени, а  неизвестные (функторные) данные – те, что располагаются справа. То, как мы классифицируем известные и неизвестные данные, влияет на количество измерений как для исходных, так и для функторных данных. На этот момент необходимо обращать наиболее пристальное внимание, так как он во многом зависит от представлений трейдера и его подхода к торговле.  

1.2  Распространенное заблуждение относительно карт Кохонена заключается в том, что функторные данные обязательно должны представлять собой двухмерное изображение наподобие представленного ниже.

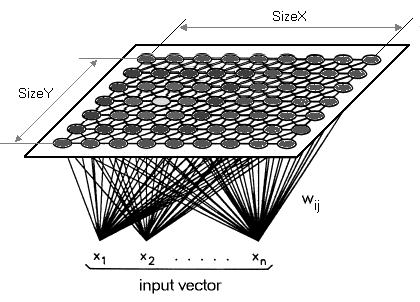
Такая интерпретация имеет право на существование, но в применении к трейдингу функтор может (а, возможно, и должен) иметь одно измерение. Таким образом, вместо того, чтобы сводить наши многомерные данные к двухмерной карте, мы нанесем их на одну линию. Карты Кохонена по определению предназначены для уменьшения размерности. В этой статье я хочу воспользоваться этой особенностью и поднять ее на новый уровень. Карты Кохонена отличаются от обычных нейронных сетей как количеством слоев, так и лежащим в их основе алгоритмом. Это однослойный набор нейронов, обычно выполненный в виде линейной двухмерной сетки. Все нейроны этого слоя, который мы называем функтором, подключаются к исходным данным, но не друг к другу. Это означает, что нейроны не зависят от веса друг друга напрямую и обновляются только при изменении исходных данных. Слой функторных данных представляет собой "карту", которая самоорганизуется на каждой итерации обучения в зависимости от исходных данных. Таким образом, после обучения каждый нейрон имеет размер с поправкой на вес в функторном слое, и это позволяет вычислить евклидово расстояние между любыми двумя такими нейронами.

 

2. Создание класса

2.1  Структура класса

2.1.1 Первым определим абстрактный класс Dimension. Этот код был бы более аккуратным, если бы я сделал большую его часть в отдельном файле и просто сослался бы на него, но эту тему, вместе с темами денег и трейлинг-классов, я хочу раскрыть в следующей статье, поэтому сейчас, как и в предыдущей статье, весь код будет находиться в сигнальном файле. Измерения всегда важны в этой сети, поскольку они сильно влияют на результат. Входные данные будут многомерными, как это обычно и бывает. Функторные (выходные) данные будут иметь одно измерение, в отличие от типичных x и y. Учитывая многомерность как исходных, так и функторных данных, идеальным типом данных будет двойной массив.

Однако, следуя порядку, установленному при изучении библиотеки MQL5, мы вместо этого будем использовать список массивов типа double. Как и в предыдущей статье, входные данные будут представлять собой изменения минимумов за вычетом изменений максимумов на протяжении одного бара. Как правило, входные данные лучше выбирать исходя из своего понимания рынка. Не стоит использовать чужие данные на реальном и даже на тестовом счетах. Каждому трейдеру необходимо изменить приведенный здесь код, чтобы адаптировать его под собственные входные данные. Как уже говорилось, функторные данные будут одномерными. Поскольку это также список, его можно настроить для добавления дополнительных измерений. Однако для наших целей мы сосредоточимся на изменении между открытием и закрытием самого последнего бара. Мастер MQL5 позволяет указать, что считать баром, путем выбора собственного таймфрейма. Класс dimension будет унаследован от double-интерфейса списка в библиотеке кода MQL5. К классу будут добавлены две функции – Get и Set. Как следует из их названий, они помогают извлекать и устанавливать значения в списке после предоставления индекса.

#include                        <Generic\ArrayList.mqh>
#include                        <Generic\HashMap.mqh>

#define                         SCALE 5

#define                         IN_WIDTH 2*SCALE
#define                         OUT_LENGTH 1

#define                         IN_RADIUS 100.0
#define                         OUT_BUFFER 10000

//
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cdimension                :  public CArrayList<double>
  {
    public:
        
      Cdimension()              {};
      ~Cdimension()             {};
        
     virtual double             Get(const int Index)                                    
                                {       
                                  double _value=0.0; TryGetValue(Index,_value); return(_value); 
                                };
     virtual void               Set(const int Index,double Value)       
                                {  
                                  Insert(Index,Value);                                                                                                                   
                                };
  };

2.1.2 Класс Feed будет наследоваться от только что созданного класса dimension. Никакие специальные функции здесь не добавляются. Только конструктор будет указывать емкость списка (аналогично размеру массива), а размер нашего списка входных данных по умолчанию будет равен 10.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cfeed             : public Cdimension
 {
   public:
                
     Cfeed()            { Clear(); Capacity(IN_WIDTH);  };
     ~Cfeed()           {                               };
 };

2.1.3 Класс Functor похож на класс feed за исключением размера. Как уже говорилось, мы будем рассматривать одно (а не два) измерения для наших функторных данных, поэтому размер множества будет равен 1.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cfunctor          : public Cdimension
 {
   public:
                
   Cfunctor()           { Clear(); Capacity(OUT_LENGTH); };
   ~Cfunctor()          {                                };
 };

2.1.4 Наибольший интерес представляет класс Neuron. Мы объявим его как класс, наследуемый от интерфейса в библиотеке MQL5, который принимает два пользовательских типа данных – ключ и значение. Рассматриваемый интерфейс шаблона – HashMap.  Два класса, объявленные выше, будут использованы в качестве пользовательских данных: класс Feed – в качестве нашего ключа и класс Functor – в качестве нашего значения. У нас также нет функций, а только указатели на классы Feed, Functor, а также на класс ‘key-value’ (ключ-значение). Как следует из названия, цель этого класса состоит в определении нейрона. Нейрон – это наша единица данных, поскольку он включает в себя как тип входных данных, так и тип выходных (функторных) данных. Это входные данные нейрона, которые сопоставляются с уже обученными нейронами, чтобы показать, каким может быть функтор. Кроме того, у отображаемых нейронов есть свои функторные данные, которые корректируются всякий раз, когда обучается новый нейрон.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cneuron           : public CHashMap<Cfeed*,Cfunctor*>
 {
   public:
                
    double              weight;
                        
    Cfeed               *fd;
    Cfunctor            *fr;
                        
    CKeyValuePair
    <
    Cfeed*,
    Cfunctor*
    >                   *ff;
                        
    Cneuron()           {
                          weight=0.0;
                          fd = new Cfeed();
                          fr = new Cfunctor();
                          ff = new CKeyValuePair<Cfeed*,Cfunctor*>(fd,fr);
                          Add(ff);
                        };
                                                                        
   ~Cneuron()           {
                          ZeroMemory(weight);
                          delete fd;
                          delete fr;
                          delete ff;
                        };
 };

2.1.5 Следующим идет абстрактный класс Layer. Он наследуется от шаблона списка класса нейрона и имеет один объект - указатель нейрона. Будучи абстрактным классом, этот указатель нейрона предназначен для использования классами, унаследованными от этого класса. Есть два таких класса, а именно входной слой и выходной слой. Строго говоря, карты Кохонена не следует классифицировать как нейронные сети, так как они не имеют прямых связей с весами и алгоритма обратного распространения. Часто карты Кохонена относят к иному типу нейронных сетей. 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Clayer            : public CArrayList<Cneuron*>
 {
   public:
                
    Cneuron             *n;
                
    Clayer()            { n = new Cneuron();     };
    ~Clayer()           { delete n;              };
 };

2.1.6 Класс Input Layer наследуется от абстрактного класса layer. Это место, где хранятся текущие и последние значения потока данных, когда сеть работает. Класс не является типичным слоем с несколькими нейронами. Вместо этого он содержит один нейрон с самыми последними исходными и функторными данными, поэтому его размер будет равен 1.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cinput_layer      : public Clayer
 {
   public:
                
   static const int     size;
                        
    Cinput_layer()      {
                          Clear();
                          Capacity(Cinput_layer::size);
                          for(int s=0; s<size; s++)
                          {
                            n = new Cneuron();
                            Add(n);
                          }
                        }
    ~Cinput_layer()     {};
 };
 const int Cinput_layer::size=1;

2.1.7 Класс Output Layer также наследуется от класса layer, но он служит нашей картой, так как здесь хранятся "обученные" нейроны. Функторные данные нейронов в данном слое эквивалентны изображению типичной самоорганизующейся карты. Ее начальный размер составляет 10 000 и будет увеличен на то же значение по мере тренировки новых нейронов.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Coutput_layer      : public Clayer
 {
   public:
                
    int                  index;
    int                  size;
                        
    Coutput_layer()      {
                           index=0;
                           size=OUT_BUFFER;
                           Clear();
                           Capacity(size);
                           for(int s=0; s<size; s++)
                           {
                             n = new Cneuron();
                             Add(n);
                           }
                         };
                                                                        
    ~Coutput_layer()     {
                           ZeroMemory(index);
                           ZeroMemory(size);
                         };
 };

2.1.8 Класс Network, как и класс neuron, также наследуется от интерфейса шаблона HashMap. Классы input layer и output layer служат его ключом и значением. Он имеет наибольшее количество функций (9) не только для получения размера списка, но также для извлечения и обновления нейронов на соответствующих слоях.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cnetwork           : public CHashMap<Cinput_layer*,Coutput_layer*>
 {
   public:
                
     Cinput_layer        *i;
     Coutput_layer       *o;
                        
     CKeyValuePair
     <
     Cinput_layer*,
     Coutput_layer*
     >                   *io;
                        
     Cneuron             *i_neuron;
     Cneuron             *o_neuron;
                        
     Cneuron             *best_neuron;
                        
     Cnetwork()          {
                           i = new Cinput_layer();
                           o = new Coutput_layer();
                           io = new CKeyValuePair<Cinput_layer*,Coutput_layer*>(i,o);
                           Add(io);
                                                                                
                           i_neuron = new Cneuron();
                           o_neuron = new Cneuron();
                                                                                
                           best_neuron = new Cneuron();
                         };
                                                                        
     ~Cnetwork()         {
                           delete i;
                           delete o;
                           delete io;
                           delete i_neuron;
                           delete o_neuron;
                           delete best_neuron;
                         };
                        
      virtual int        GetInputSize()
                         {
                           TryGetValue(i,o);
                           return(i.size);
                         };
                        
      virtual int        GetOutputIndex()
                         {
                           TryGetValue(i,o);
                           return(o.index);
                         };
                        
      virtual void       SetOutputIndex(const int Index)
                         {
                           TryGetValue(i,o);
                           o.index=Index;
                           TrySetValue(i,o);
                         };
                        
      virtual int        GetOutputSize()
                         {
                           TryGetValue(i,o);
                           return(o.size);
                         };
                        
      virtual void       SetOutputSize(const int Size)
                         {
                           TryGetValue(i,o);
                           o.size=Size;
                           o.Capacity(Size);
                           TrySetValue(i,o);
                         };
                        
      virtual void       GetInNeuron(const int NeuronIndex)
                         {
                           TryGetValue(i,o);
                           i.TryGetValue(NeuronIndex,i_neuron);
                         };
                        
      virtual void       GetOutNeuron(const int NeuronIndex)
                         {
                           TryGetValue(i,o);
                           o.TryGetValue(NeuronIndex,o_neuron);
                         };
                        
      virtual void       SetInNeuron(const int NeuronIndex)
                         {
                           i.TrySetValue(NeuronIndex,i_neuron);
                         };
                        
      virtual void       SetOutNeuron(const int NeuronIndex)
                         {
                           o.TrySetValue(NeuronIndex,o_neuron);
                         };
 };

2.1.9  Класс Map представляет собой последний обобщающий класс. Он вызывает экземпляр сетевого класса и включает другие переменные для обучения нейронов и получения наиболее подходящего нейрона для сети. 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cmap
  {
    public:
                        
      Cnetwork               *network;
                        
      static const double     radius;
      static double           time;
                        
      double                  QE;       //proxy for Quantization Error
      double                  TE;       //proxy for Topological Error
                        
      datetime                refreshed;
                        
      bool                    initialised;
                        
      Cmap()                  {
                                network = new Cnetwork();
                                                                                        
                                initialised=false;
                                                                                        
                                time=0.0;
                                                                                        
                                QE=0.50;
                                TE=5000.0;
                                                                                        
                                refreshed=D'1970.01.05';
                               };
                                                                                
      ~Cmap()                  {
                                 ZeroMemory(initialised);
                                                                                        
                                 ZeroMemory(time);
                                                                                        
                                 ZeroMemory(QE);
                                 ZeroMemory(TE);
                                                                                        
                                 ZeroMemory(refreshed);
                               };
 };
 const double Cmap::radius=IN_RADIUS;
 double Cmap::time=10000/fmax(1.0,log(IN_RADIUS));

 

2.2. Топология

2.2.1  Обучение нейронов – конкурентное обучение, включающее в себя настройку весов функторов существующих нейронов в выходном слое и добавление нового обучающего нейрона. Скорость, с которой корректируются эти веса, и, что наиболее важно, количество итераций, необходимых для корректировки этих весов, являются очень чувствительными параметрами при определении эффективности сети. На каждой итерации корректировки весов вычисляется новый меньший радиус. Я называю этот радиус функтором-ошибкой  (functor-error). Его не следует путать с топологической ошибкой самоорганизующейся карты (SOM Topological-error). Тем не менее, чаще всего его называют радиусом окрестности, измеренным евклидовым расстоянием. Я употребляю слово "ошибка", так как этот параметр необходимо минимизировать для получения лучших результатов сети. Чем больше итераций выполняется, тем меньше будет функтор-ошибка. Помимо количества итераций, скорость обучения необходимо постепенно снижать от числа, близкого к единице, до нуля.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalKM::NetworkTrain(Cmap &Map,Cneuron &TrainNeuron)
  {
    Map.TE=0.0;

    int _iteration=0;
    double _training_rate=m_training_rate;

    int _err=0;
    double _functor_error=0.0;

    while(_iteration<m_training_iterations)
    {
      double _current_radius=GetTrainingRadius(Map,_iteration);

      for(int i=0; i<=Map.network.GetOutputIndex(); i++)
      {
        Map.network.GetOutNeuron(i);
        double _error = EuclideanFunctor(TrainNeuron,Map.network.o_neuron);

        if(_error<_current_radius)
        {
          _functor_error+=(_error);
          _err++;

          double _remapped_radius = GetRemappedRadius(_error, _current_radius);

          SetWeights(TrainNeuron,Map.network.o_neuron,_remapped_radius,_training_rate);

          Map.network.SetOutNeuron(i);
        }
      }

      _iteration++;
      _training_rate=_training_rate*exp(-(double)_iteration/m_training_iterations);
    }

    int
    _size=Map.network.GetOutputSize(),
    _index=Map.network.GetOutputIndex();
    Map.network.SetOutputIndex(_index+1);
    if(_index+1>=_size)
    {
      Map.network.SetOutputSize(_size+OUT_BUFFER);
    }

    Map.network.GetOutNeuron(_index+1);
    for(int w=0; w<IN_WIDTH; w++)
    {
      Map.network.o_neuron.fd.Set(w,TrainNeuron.fd.Get(w));
    }
    
    for(int l=0; l<OUT_LENGTH; l++)
    {
      Map.network.o_neuron.fr.Set(l,TrainNeuron.fr.Get(l));
    }

    Map.network.SetOutNeuron(_index+1);

    if(_err>0)
    {
      _functor_error/=_err;
      Map.TE=_functor_error*IN_RADIUS;
    }
  }

2.2.2  Топологическая ошибка – ключевой атрибут карт Кохонена. Я воспринимаю его как меру того, насколько выходной слой близок к намеченной долгосрочной цели. С каждым обучением нейроны выходного слоя адаптируются к истинному или предполагаемому результату, поэтому возникает вопрос, как измерить этот прогресс. Чем больше мы сохраняем выходной слой, тем ближе мы к нашей цели. Для целей этой статьи функтор-ошибка будет использоваться в качестве нашего приближенного значения (proxy).

2.3. Квантование

2.3.1  Картирование нейронов – поиск весов функторов, наиболее подходящих для нейрона, для которого присутствуют только исходные данные. Это делается путем нахождения нейрона в выходном слое с кратчайшим евклидовым расстоянием исходных данных от нейрона, для которого не известны данные функтора. Как и в случае с обучением, я называю это расстояние исходник-ошибка (feed-error). Опять же, чем меньше значение, тем надежнее должна быть сеть.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalKM::NetworkMapping(Cmap &Map,Cneuron *MapNeuron)
  {
    Map.QE=0.0;
    
    Map.network.best_neuron = new Cneuron();

    int _random_neuron=rand()%Map.network.GetOutputIndex();

    Map.network.GetInNeuron(0);
    Map.network.GetOutNeuron(_random_neuron);

    double _feed_error = EuclideanFeed(Map.network.i_neuron,Map.network.o_neuron);

    for(int i=0; i<Map.network.GetOutputIndex(); i++)
    {
      Map.network.GetOutNeuron(i);

      double _error = EuclideanFeed(Map.network.i_neuron,Map.network.o_neuron);

      if(_error < _feed_error)
      {
        for(int w=0; w<IN_WIDTH; w++)
        {
          Map.network.best_neuron.fd.Set(w,Map.network.o_neuron.fd.Get(w));
        }

        for(int l=0; l<OUT_LENGTH; l++)
        {
          Map.network.best_neuron.fr.Set(l,Map.network.o_neuron.fr.Get(l));
        }

        _feed_error = _error;
      }
    }

    Map.QE=_feed_error/IN_RADIUS;
}

2.3.2 Ошибка квантования – еще один важный атрибут карт Кохонена, который, на мой взгляд, не имеет четкого определения. Я считаю, что это ошибка перевода многомерных данных в данные с низкой размерностью. В нашем случае это ошибка при конвертации исходных данных в функторные. Для целей этой статьи исходник-ошибка будет использоваться в качестве нашего приближенного значения.

 

3. Сборка с помощью Мастера MQL5

3.1 Сборка с помощью Мастера довольно проста. Я советую начинать тестирование с больших таймфреймов, поскольку идеальные 10 000 тренировочных итераций на бар потребуют некоторого времени при долгом обучении. 

 

 

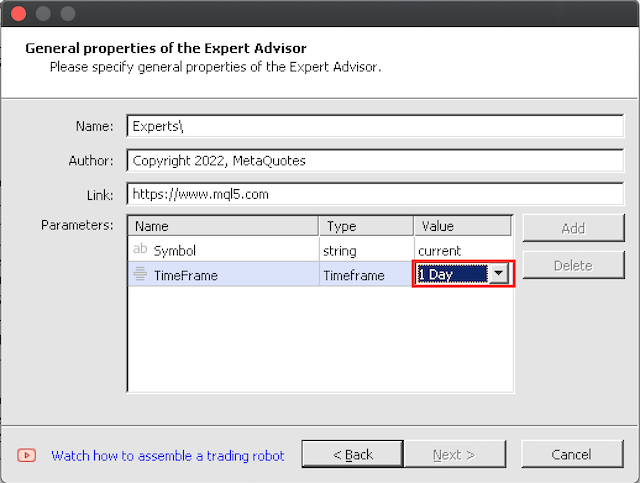
4. Тестирование в тестере стратегий

4.1   В целях нашего тестирования входные данные по умолчанию будут исследовать чувствительность нашей приближенной ошибки квантования (quantization error proxy, QE) и приближенной топологической ошибки (topological error proxy, TE). Рассмотрим два сценария. Для начала используем в тестировании очень консервативные значения QE и TE, равные 0,5 и 12,5. Затем проверим эти входные данные на 0,75 и 25,0 соответственно.

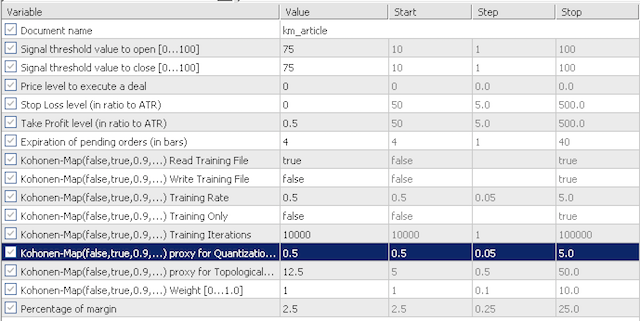
консервативные настройки

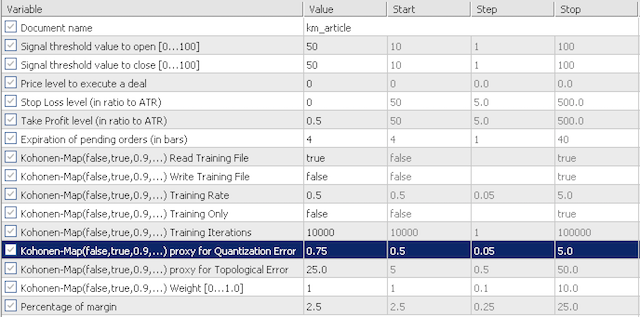
агрессивные настройки

 

 

Входных параметров не так много. У нас есть "обучающее чтение" (training read), которое определяет, должны ли мы читать обучающий файл перед инициализацией. Если этот файл отсутствует, советник не будет проводить валидацию. У нас также есть "обучающая запись" (training write), которая, как следует из названия, определяет, следует ли записывать обучающий файл после деинициализации советника. Обучение всегда происходит после запуска советника. Входной параметр training only (только обучение) дает возможность заниматься исключительно обучением без торговли. Двумя другими важными параметрами карт Кохонена являются training rate (скорость обучения) и итерации обучения. Как правило, чем выше эти два значения (скорость обучения ограничена 1,0), тем выше производительность, однако это отражается на времени работы и затрачиваемых вычислительных ресурсах. 

Советник прошел обучение на V-образном периоде с 01.10.2018 по 01.06.2021, а также прошел форвард-тестирование с даты окончания обучения до настоящего времени.

Использование консервативных значений дало следующие результаты:

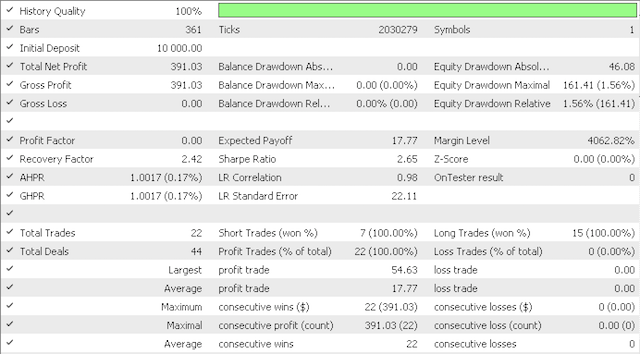
Кривая эквити:

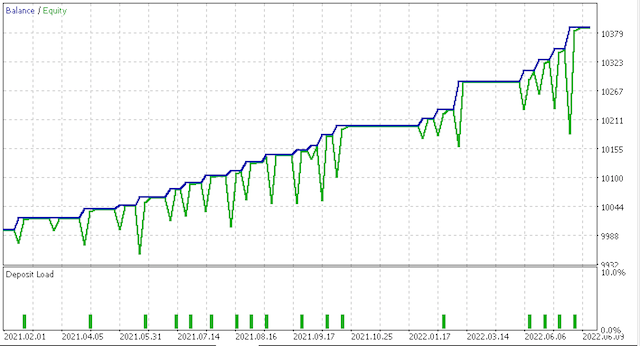
Более агрессивный вариант дал следующие результаты:

 

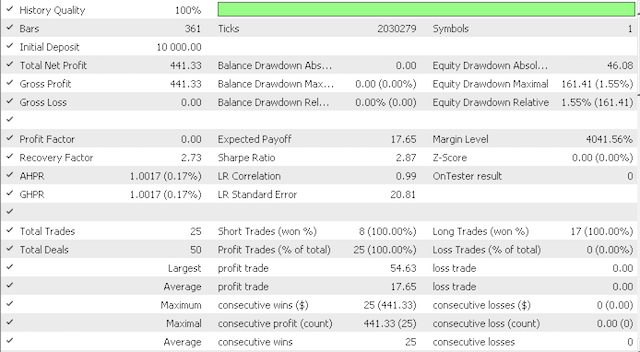
Кривая эквити:

 

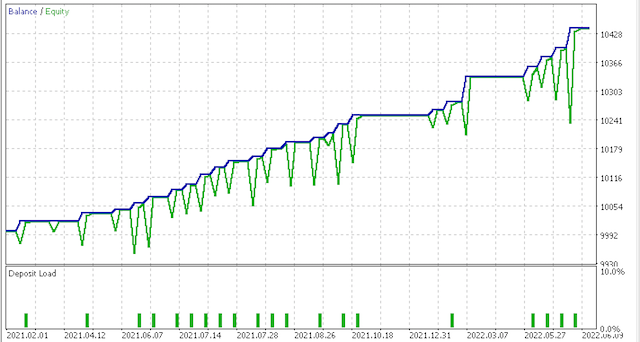
Конечно, требуются дополнительное тестирование и тонкая настройка риска и размера позиции, но для системы, которая обучается в течение такого короткого периода времени, результаты многообещающие. Тем не менее, сравнивая два приведенных выше сценария, мы видим, что более консервативный вариант показывает меньшую результативность, учитывая, что его значение коэффициента Шарпа 0,43 составляет почти половину значения 0,85 при большем количестве сделок. Использование карт Кохонена требует дополнительного изучения перед использованием. Исходные и функторные данные необходимо настроить в соответствии с вашем стилем торговли. Предварительное тестирование всегда должно проводиться на реальных тиковых данных вашего брокера в течение значительных периодов времени.

 

5. Заключение

5.1 Мастер MQL5 – очень гибкий инструмент для быстрого создания торговых систем. В этой статье мы рассмотрели вариант карт Кохонена, которые переносят многомерные исходные данные ценовых временных рядов в одно измерение в диапазоне от -1,0 до 1,0. Хотя этот подход и не является общепринятой практикой, он демонстрирует саму суть карт Кохонена, заключающуюся в уменьшении сложности и упрощении принятия решений. Также мы показали применение кода из библиотеки MQL, в частности ArrayList и HashMap. Надеюсь, вам понравилась статья. Спасибо за внимание!