Comparing different types of moving averages in trading

Contents

• Introduction
• Types of moving averages
• Moving Average technical indicator
• Exponential moving average (EMA)-based technical indicators
• Comparing various types of moving averages
• Trading strategy specification
• Developing the Expert Adviser
• Expert Adviser testing and performance
• Conclusion

Introduction

Moving Average (MA) is one of the most popular technical indicators in the Forex market. Our purpose is to consider various MAs as well as to compare them within trading under equal conditions of entering and exiting of the market.

Let us consider seven types of moving averages: Moving Average, Adaptive Moving Average, Double Exponential Moving Average, Fractal Adaptive Moving Average, Triple Exponential Moving Average, Variable Index Dynamic Average and Nick Rypock Moving Average.

Types of moving averages

This section contains a short description and formulae to calculate the moving averages.

Moving Average technical indicator

Moving Average is one of the most widespread technical indicators. It depicts the average value of symbol price for a given period of time. There are different variants of MA indicator:

• Simple Moving Average (SMA);
• Exponential Moving Average (EMA);
• Smoothed Moving Average (SMMA);
• Linear Weighted Moving Average (LWMA).

Below, we give calculating formulae for each variant of the Moving Average indicator:

Variant of Moving Average indicator	Calculating formula	Comment
Simple Moving Average (SMA)		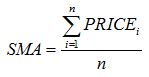n is a number of unit periods (for example, if n=6 at a chart with the timeframe of M15, the indicator will be calculated for the preceding 1.5 hours) PRICE is the current price value, the following variants may be selected in indicator settings: high, low, open, close, median price ((high+Low)/2), typical price ((high+Low+Close)/3), weighted close ((high+Low+Close+Close)/4) or data of the previous indicator
Exponential Moving Average (EMA)		EMA(i-1) is the previous value F is the smoothing factor (a share of price value use). F coefficient is selected randomly within the range from 0 to 1, for example, F=2/(n+1), where n is a number of unit periods PRICE  is the current price value
Smoothed Moving Average (SMMA)		SMMA(i-1) is the previous value n is a number of unit periods PRICE is the current price value
Linear Weighted Moving Average (LWMA)		PRICE is the current price value n is a number of unit periods

Let us consider displays of different variants of Moving Average indicator at a price chart. Figure 1 demonstrates variants of Moving Average indicator with the period of 12, as calculated by Close prices.

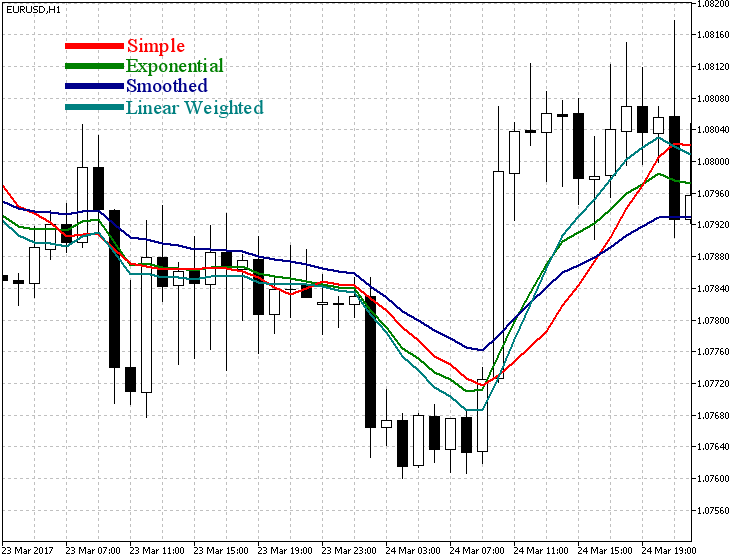
Fig. 1. Variants of Moving Average indicator

As the figure shows, Simple Moving Average in flat slightly fluctuates and this can yield false trade signals. Smoothed Moving Average, as it follows from its name, looks more smoothed. Exponential Moving Average and Linear Weighted Moving Average behave somewhat similarly in flat. Linear Weighted Moving Average during trend movement approaches prices closer than the rest of lines and, as opposed to SMMA and EMA, it does not depend on its previous value.

Exponential moving average (EMA) - based technical indicators

Exponential moving average (EMA) underlies a number of other technical indicators.

Indicator	Description	Calculating formula	Description of calculating formula
Adaptive Moving Average (AMA)	MA with low sensitivity to noises. If compared with the rest of moving averages this indicator has a minimal lag when determining trend reversals and change. At price spikes it does not give strong fluctuations and thus, it does not cause false trade signals.		AMA(i-1) is the previous value of indicator Price(i) is the current price value SSC(i) —  smoothing constant
Double Exponential Moving Average	It is used to smooth price or values of other indicators.  The main advantage is absence of false signals at the moments when the price moves in zigzag fashion. It sustains position maintenance during the period of a strong trend and reduces signal lag as compared to ordinary EMA.		EMA(Price, n, i) — EMA current value from Price price with n period. EMA2(Price, n, i) = EMA(EMA(Price, n, i), n, i) — double EMA from Price with n period.
Triple Exponential Moving Average	Synthesis of single, double and triple exponential MA. The total lag is much less than that for each of those MAs separately. The indicator is applied instead of traditional moving averages as well for smoothing a price chart and values of other indicators.		EMA(Price, n, i) — EMA current value from Price price with n period. EMA2(Price, n, i) = EMA(EMA(Price, n, i), n, i) — double EMA from Price with n period. EMA3(Price, n, i)=EMA(EMA2(Price, n, i), n, i) — triple EMA from Price price with n period.
Fractal Adaptive Moving Average	Here the smoothing factor is calculated on the basis of the current fractal dimension of price series. Indicator advantage is that it follows a strong trend and drastically slows down during consolidation periods.		Price(i) is the current price value A(i) — current exponential smoothing factor
Variable Index Dynamic Average	This is an EMA with its averaging period changing dynamically and depending on market volatility.  Market volatility is measured by Chande Momentum Oscillator (CMO). It measures a ratio between totals of positive and negative increments for a given period (CMO period). CMO value is a coefficient for EMA smoothing factor. Thus, two parameters are set with the indicator: CMO oscillator period and EMA smoothing period.		F=2/(n+1) is a smoothing factor, n is a number of unit periods ABS is a mathematical function which computes absolute value of the variable VIDYA(i-1) is the previous value of indicator CMO(i) is the value of CMO oscillator
Nick Rypock Moving Average	The indicator is not a part of a standard MetaTrader 5 distribution. Its main advantage is that there are almost no fluctuations in flat; it strictly follows the trend.		NRMA(i-1) is the previous value of indicator Price(i) is the current price value F=2/(n+1) is a smoothing factor, n is a number of unit periods NRratio is the ratio to smoothing factor

Differences of indicators from the ordinary EMA

Let us compare the above considered indicators with the ordinary EMA. Figure 2 demonstrates:

• Adaptive Moving Average (period - 12, fast EMA — 2, slow EMA — 30, shift — 0)
• Double Exponential Moving Average (period - 12, shift - 0)
• Fractal Adaptive Moving Average (period - 12, shift - 0)
• Exponential Moving Average (period - 12, shift - 0)
• Triple Exponential Moving Average (period - 12, shift - 0)
• Variable Index Dynamic Average (CMO period — 12, EMA period — 12, shift — 0)
• Nick Rypock Moving Average (method of averaging — SMA, depth of smoothing — 3, smoothing parameter — 15 (not used for SMA), Kf — 1, Fast — 12, Sharp — 2, vertical and horizontal shift — 0).

All the indicators are made on the basis of Close prices.

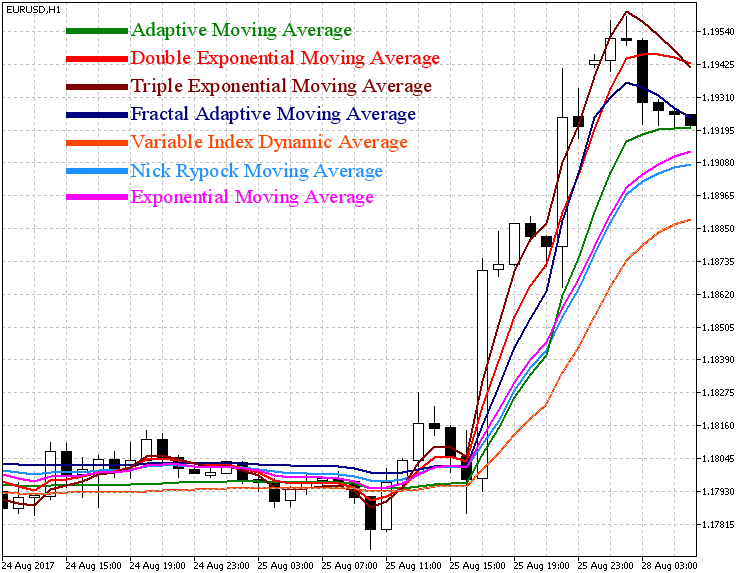
Fig. 2 Comparison of Exponential moving average (EMA) - based indicators

As figure 2 shows, DEMA and TEMA as compared to ordinary EMA, more accurately follow the price movement; however, their fluctuations in flat may give false trade signals. The rest of indicators (FRAMA, AMA, VIDYA, NRMA) in flat almost do not swing and do not respond to minor price changes. In trend, almost all the indicators behave equally. TEMA and FRAMA responded to a change in trend direction faster than others.

Comparing various types of moving averages

Let us compare the above considered technical indicators on the trading strategy with equal conditions of entering and exiting the market.

Trading strategy specification

To test the indicator, a simple strategy with obvious conditions of entering and exiting the market was chosen.

Market entry conditions. 

• Preliminary buy signal: indicator line crosses the body of bullish candlestick. Further, if the difference between the current and previous values of the indicator is more than the specified parameter Growth factor (indicator grows), we should open a buy trade.
• Preliminary sell signal: indicator line crosses the body of bearish candlestick. Further, if the difference between the previous and current values of the indicator is more than the specified parameter Growth factor (indicator falls), we should open a sell trade.

Market exit conditions:

• upon reaching TakeProfit or StopLoss levels;
• if a buy trade is opened and indicator line has crossed the body of bearish candlestick;
• if a buy trade is opened and indicator line has crossed the body of bullish candlestick.

Figures 3, 4 show examples of trading on such strategy.

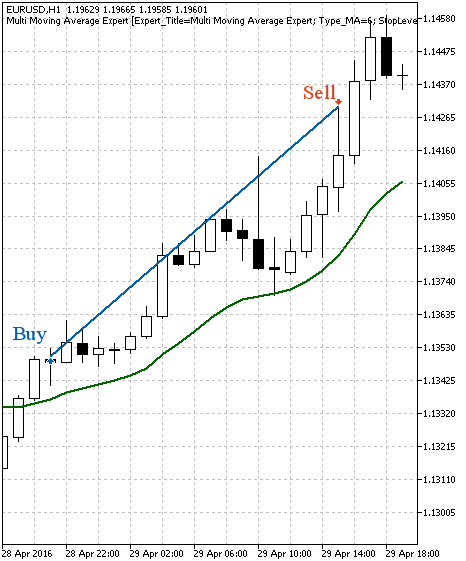
Fig. 3. Example of a buy trade

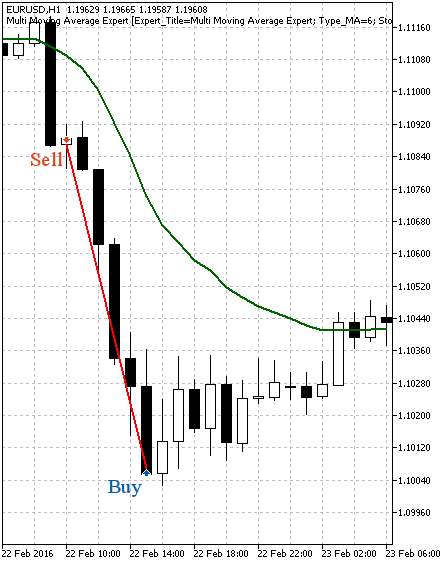
Fig. 4. Example of a sell trade

A similar trading strategy is realised in Moving Average Expert Adviser which can be found in MetaTrader 5 terminal navigator.

Creation of Expert Adviser

Let us write Expert Adviser for trading on the above specified strategy. A feature of choosing between one of the following technical indicators will be implemented in Expert Adviser: MA (with methods Simple, Exponential, Smoothed, Linear Weighted), DEMA, TEMA, FRAMA, AMA, VIDYA, NRMA. The selected indicator will be drawn on the chart. As well, we may specify indicator input parameters, set size of TakeProfit and StopLoss, size of a lot for trading, value of indicator growth coefficient (Growth factor).

We will check conditions of entering and exiting the market only at a new bar instead of each tick. At first, availability of an open position is checked (for this purpose, SelectPosition function is provided in the EA). If there are no such positions we check the entry condition (CheckForOpen function), if available - we check the exit one (CheckForClose function).

Full Expert Adviser code is attached to the article (file MultiMovingAverageExpert.mq5). Let us consider only realization of entry/exit conditions. Checkup of entry conditions is realized in CheckForOpen function as follows:

   if(rt[0].open>ma[0] && rt[0].close<ma[0])               ////checkup of crossing of the body of bearish candlestick
     {
      if(BuyCross)
         BuyCross=false;                                   //delete the buy precondition (if before that there was crossing of bullish candlestick by the line)
      SellCross=true;                                      //set Sell trade precondition
     }
   else
   if(rt[0].open<ma[0] && rt[0].close>ma[0])               //checkup of crossing of the body of bullish candlestick
     {
      if(SellCross)
         SellCross=false;                                 //delete Sell trade precondition (if prior to that there was crossing of bearish candlestick by indicator line)
      BuyCross=true;                                      //set Buy trade precondition
     }
   if(SellCross && ma[0]>ma[1] && ma[0]-ma[1]>GFactor)
     {
      signal=ORDER_TYPE_SELL;                             //if indicator falls, sell condition occurs
      SellCross=false;                                    //delete Sell trade precondition
     }
   else
   if(BuyCross && ma[1]>ma[0] && ma[1]-ma[0]>GFactor)
     {
      signal=ORDER_TYPE_BUY;                             // if indicator grows, buy condition occurs
      BuyCross=false;                                    //delete Buy trade precondition
     }

• Arrayrt[] keeps historical data on prices
• Array ma[] keeps indicator values
• rt[0].close, rt[0].open is the value of the previous close/open price
• ma[0] is the previous value of indicator
• ma[1] — current value of indicator
• GFactor is coefficient of indicator growth
• Variable signal is further used to form a buy or sell trade request.

Checkup of exit conditions is realized in CheckForClose function as follows:

   bool signal=false;
   long type=PositionGetInteger(POSITION_TYPE);

   if(type==(long)POSITION_TYPE_BUY && rt[0].open>ma[0] && rt[0].close<ma[0])       //if buying position is open and 
                                                                                    //indicator line crosses the body of bearish candlestick 
      signal=true;                                                                  //signal to deal closing
   if(type==(long)POSITION_TYPE_SELL && rt[0].open<ma[0] && rt[0].close>ma[0])      //if buy position is open and
                                                                                    //indicator line crosses the body of bullish candlestick  
      signal=true;                                                                  //signal to deal closing
   if(signal)
     {
      if(TerminalInfoInteger(TERMINAL_TRADE_ALLOWED) && Bars(_Symbol,_Period)>100)
         ExtTrade.PositionClose(_Symbol,3);                                         //close deal
     }

Expert Adviser testing and performance

We will test Expert Adviser on currency pairs EURUSD, GBPUSD, USDJPY, USDCAD, AUDUSD, timeframe H1. TakeProfit — 80 points, StopLoss — 50 points, volume of trade lot is 0.1, deposit - 10,000 USD, testing mode - all ticks, leverage 1:100, 5-digit quotes, server: MetaQuotes-Demo.

Testing performed for a period from 01.01.2016 to 09.09.2017.

For each indicator, there were optimised the period (variation range - 5 - 50, pace 1) and parameter Growth factor (variation range 0.0001 —  0.0001, pace 0.001).

For Variable Index Dynamic Average, there were optimized EMA period (as indicator calculation period) and CMO oscillator period (variation range - 5 — 50, pace 1).

For Nick Rypock Moving Average, the Fact parameter was optimized which determines the period of the indicator calculation.

The indicator values are calculated on the basis of Close price without horizontal and vertical shift. Some indicators have additional parameters:

Name of moving average	Parameter values
Adaptive Moving Average	Period of fast EMA - 2 Period of slow EMA - 30
Nick Rypock Moving Average	Method of averaging - SMA Depth of smoothing — 3 Smoothing parameter — 15 (not used with the method of averaging SMA) KF=1 Sharp=2

Testing results on currency pair EURUSD

Testing results on currency pair EURUSD (variants with the maximum total net profit) are presented in the below table:

Name of moving average	Parameters optimized and their values	Q-ty of trades	Total net profit	Profit factor	Recovery factor	Sharpe ratio	Balance drawdown maximal	Equity drawdown maximal
Moving Average (method of averaging Simple)	Period —15, Growth factor — 0.0002	383	1309.82	1.32	3.14	0.1	397.29 (3.81%)	417.26 (3.99%)
Moving Average (method of averaging Exponential)	Period —11, Growth factor — 0.0003	405	1109.72	1.22	3.02	0.08	346.35 (3.39%)	367.45 (3.6%)
Moving Average (method of averaging Smoothed)	Period —6, Growth factor — 0.0003	405	1109.72	1.22	3.02	0.08	346.35 (3.39%)	367.45 (3.6%)
Moving Average (method of averaging Weighted)	Period —22, Growth factor — 0.0002	351	1505.35	1.34	3.65	0.11	383.71 (3.41%)	412.88 (3.91%)
Adaptive Moving Average	Period —14, Growth factor — 0.0001	384	1024.19	1.19	1.63	0.07	600.06 (5.41%)	627.36 (5.64%)
Double Exponential Moving Average	Period —28, Growth factor — 0.0003	366	1676.43	1.39	3.49	0.12	460.33 (4.39%)	481.03 (4.58%)
Triple Exponential Moving Average	Period —44, Growth factor — 0.0002	482	1842.81	1.35	5.31	0.11	321.07 (3.14%)	347.27 (3.39%)
Fractal Adaptive Moving Average	Period —16, Growth factor — 0.0007	174	766.52	1.37	2.69	0.12	252.4 (2.5%)	285.08 (2.78%)
Variable Index Dynamic Average	Period EMA — 12, period CMO — 2, Growth factor — 0.0003	333	1237.31	1.26	2.86	0.09	385.44 (3.43%)	432.81 (3.84%)
Nick Rypock Moving Average	Period —15, Growth factor — 0.0001	295	1669.62	1.42	4.14	0.14	376.22 (3.5%)	403.52 (3.75%)

The following conclusions can be made based on testing results:

• The biggest indicator of Total net profit and Recovery factor - Triple Exponential Moving Average, however its other indices are not the highest ones, as well rather good results are shown by Double Exponential Moving Average and Nick Rypock Moving Average.
• The worst indices of Profit factor, Recovery factor, Sharpe ratio, as well as the biggest Equity and Balance drawdown are shown by Adaptive Moving Average.

For a more vivid comparison of testing results, let us normalize the indices of Total net profit, Profit factor, Sharpe ratio, Recovery factor, Balance and Equity drawdowns maximal by the following formula:

where:

• nValue — normalized parameter value within the interval from 0 to 1,
• Value — current parameter value,
• MaxValue — maximal parameter value,
• MinValue — minimal parameter value.

Outcomes are represented in the table (the best results are in yellow, the worst one is in red color):

Name of moving average	Total net profit	Profit factor	Recovery factor	Sharpe ratio	Balance drawdown maximal	Equity drawdown maximal	Sum of indicators exclusive of drawdowns	Sum of indicators inclusive of drawdowns
Moving Average (method of averaging Simple)	0.50479	0.56522	0.41033	0.42857	0.41676	0.38618	1.9089	1.10597
Moving Average (method of averaging Exponential)	0.31887	0.13043	0.37772	0.14286	0.27024	0.24065	0.96988	0.459
Moving Average (method of averaging Smoothed)	0.31887	0.13043	0.37772	0.14286	0.27024	0.24065	0.96988	0.459
Moving Average (method of averaging Weighted)	0.68646	0.65217	0.54891	0.57143	0.3777	0.37338	2.45898	1.7079
Adaptive Moving Average	0.23941	0	0	0	1	1	0.23941	-1.76059
Double Exponential Moving Average	0.84541	0.86957	0.50543	0.71429	0.59808	0.57248	2.9347	1.76413
Triple Exponential Moving Average	1	0.69565	1	0.57143	0.19572	0.18169	3.26708	2.88787
Fractal Adaptive Moving Average	0	0.78261	0.28804	0.71429	0	0	1.78494	1.78494
Variable Index Dynamic Average	0.43742	0.29631	0.33361	0.27656	0.38267	0.43161	1.34419	0.52992
Nick Rypock Moving Average	0.83909	1	0.68207	1	0.35615	0.34603	3.52115	2.81897

In the last column of the table, when summing up indicators, the values of Balance and Equity drawdowns maximal are taken with the negative sign (the less the drawdown, the best the strategy). Thus, the best results for the considered strategy are demonstrated by Triple Exponential Moving Average, Nick Rypock Moving Average и Double Exponential Moving Average (in the table shown in yellow). Testing results for TEMA, NRMA and DEMA are shown in fig. 5-10

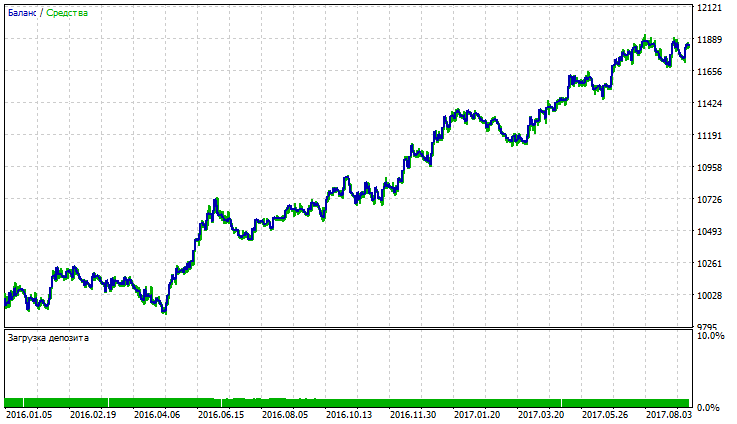
Fig. 5. Balance (equity) chart for Triple Exponential Moving Average

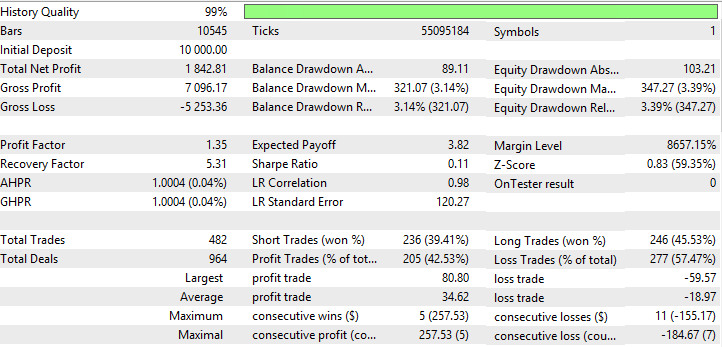
Fig. 6. Report for Triple Exponential Moving Average

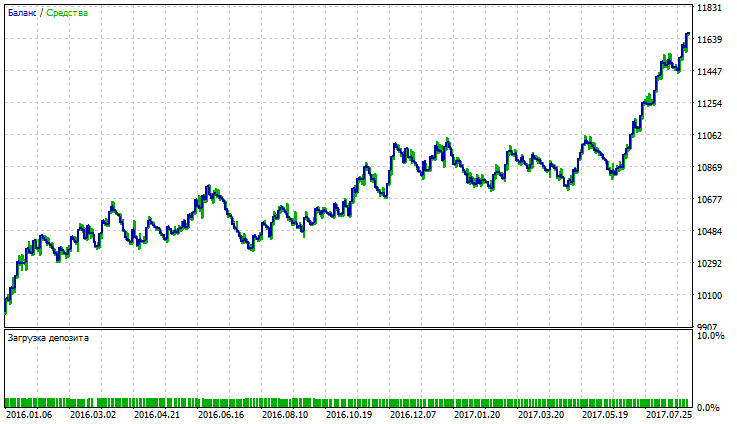
Fig. 7. Balance (equity) chart for Nick Rypock Moving Average

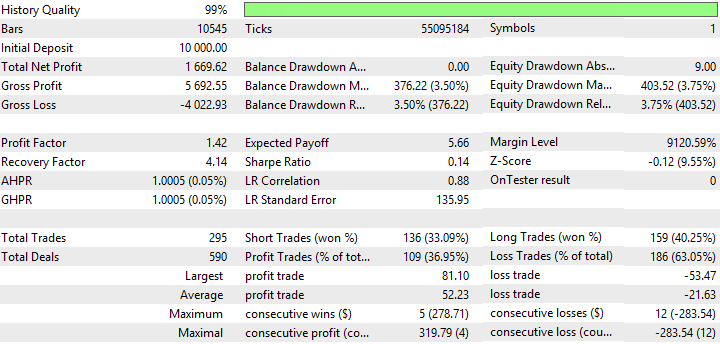
Fig. 8. Report for Nick Rypock Moving Average

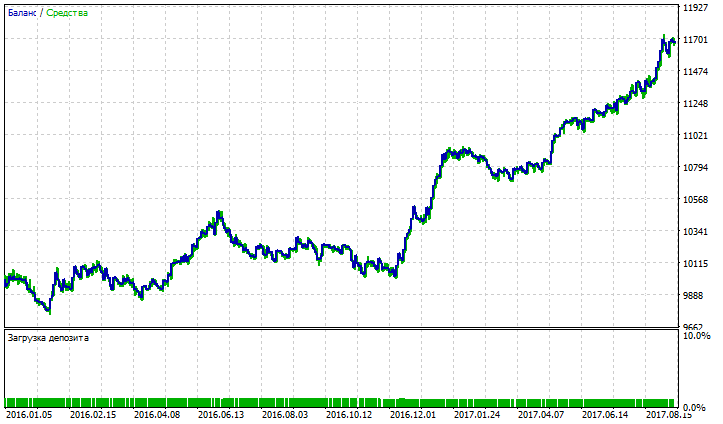
Fig. 9. Balance (equity) chart for  Double Exponential Moving Average 

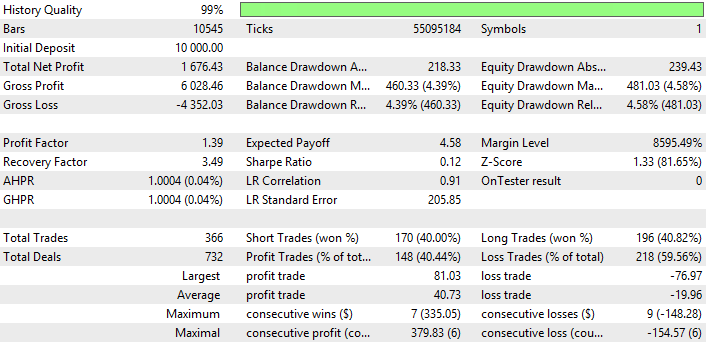
Fig. 10. Report for Double Exponential Moving Average 

Fig. 5, 7, 9 demonstrate that balance (equity) chart for TEMA looks more stable than NRMA and DEMA; although it has slight drawdowns. At the balance (equity) chart of NRMA, we observe a spike in profit for the last 3 months of trading, at DEMA chart profit growth (with a slight drawdown) starts from December 2016.

Testing results on currency pair   GBPUSD

Testing results on currency pair GBPUSD are provided in the table:

Name of moving average	Parameters optimised and their values	Q-ty of trades	Total net profit	Profit factor	Recovery factor	Sharpe ratio	Balance drawdown maximal	Equity   drawdown maximal
Moving Average (method of averaging Simple)	Period —38, Growth factor — 0.0005	52	1013.56	1.98	3.82	0.32	207.04 (2.7%)	265.06 (2.65%)
Moving Average (method of averaging Exponential)	Period —41, Growth factor — 0.0002	219	787.12	1.14	1.23	0.07	576.96 (5.21%)	639.44 (5.75%)
Moving Average (method of averaging Smoothed)	Period —42, Growth factor — 0.0003	48	817.42	1.71	3.85	0.26	151.32 (1.51%)	212.24 (2.04%)
Moving Average (method of averaging Weighted)	Period —50, Growth factor — 0.0001	328	1086.08	1.17	1.26	0.07	818.34 (7.45%)	861.04 (7.82%)
Adaptive Moving Average	Period —21, Growth factor — 0.001	100	1102.16	1.61	4.61	0.21	176.46 (1.71%)	239.12 (2.28%)
Double Exponential Moving Average	Period —23, Growth factor — 0.0007	263	1070.88	1.21	1.96	0.08	466.24 (4.42%)	547.58 (5.16%)
Triple Exponential Moving Average	Period —30, Growth factor — 0.0009	214	1443.90	1.39	4.11	0.14	322.76 (3.02%)	351.14 (3.28%)
Fractal Adaptive Moving Average	Period —38, Growth factor — 0.0001	819	651.54	1.05	0.85	0.02	747.98 (7.12%)	764.88 (7.28%)
Variable Index Dynamic Average	Period EMA — 35, period CMO — 7, Growth factor — 0.0004	73	1606.98	1.99	5.20	0.34	251.94 (2.52%)	309 (3.08%)
Nick Rypock Moving Average	Fact — 45, Growth factor — 0.0005	53	978.30	1.80	3.86	0.29	200.64 (1.99%)	253.58 (2.51%)

Normalized results are represented in the table (the best results are in yellow, the worst one is in red color):

Name of moving average	Total net profit	Profit factor	Recovery factor	Sharpe ratio	Balance drawdown maximal	Equity drawdown maximal	Sum of indicators exclusive of drawdowns	Sum of indicators inclusive of drawdowns
Moving Average (method of averaging Simple)	0.3789	0.98929	0.68343	0.91799	0.08354	0.08141	2.96961	2.80467
Moving Average (method of averaging Exponential)	0.1419	0.09351	0.08718	0.13465	0.63812	0.65845	0.45724	-0.8393
Moving Average (method of averaging Smoothed)	0.17416	0.70302	0.69032	0.74598	0	0	2.31347	2.31347
Moving Average (method of averaging Weighted)	0.45481	0.12036	0.09417	0.14629	1	1	0.81562	-1.1844
Adaptive Moving Average	0.47164	0.58999	0.86402	0.57613	0.03769	0.04143	2.50177	2.42265
Double Exponential Moving Average	0.4389	0.17142	0.25383	0.1936	0.47213	0.51686	1.05774	0.06875
Triple Exponential Moving Average	0.82931	0.36161	0.74969	0.36845	0.25702	0.21409	2.30906	1.83795
Fractal Adaptive Moving Average	0	0	0	0	0.89452	0.85179	0	-1.7463
Variable Index Dynamic Average	1	1	1	1	0.15085	0.14914	4	3.70001
Nick Rypock Moving Average	0.342	0.79826	0.69126	0.82047	0.07394	0.06372	2.65199	2.51433

As the tables suggest, Variable Index Dynamic Average has the best indicators, as well Nick Rypock Moving Average and Moving Average with Simple method of averaging turned out to be rather well. Testing results for VIDYA, NRMA and SMA are shown in fig. 11-16.

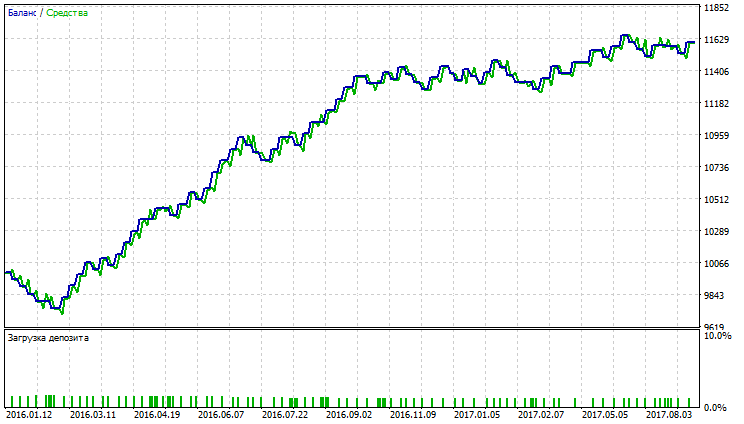
Fig. 11. Balance (equity) chart of Variable Index Dynamic Average

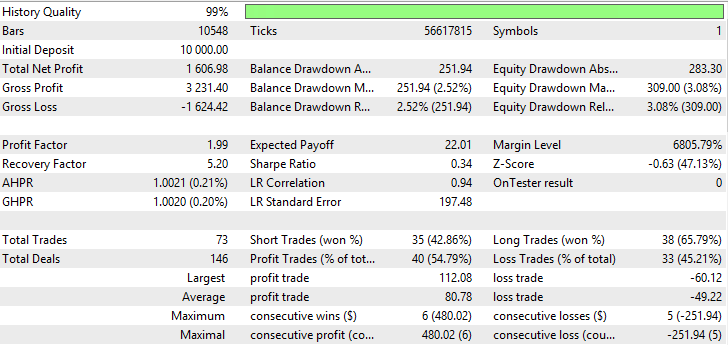
Fig. 12. Report for Variable Index Dynamic Average

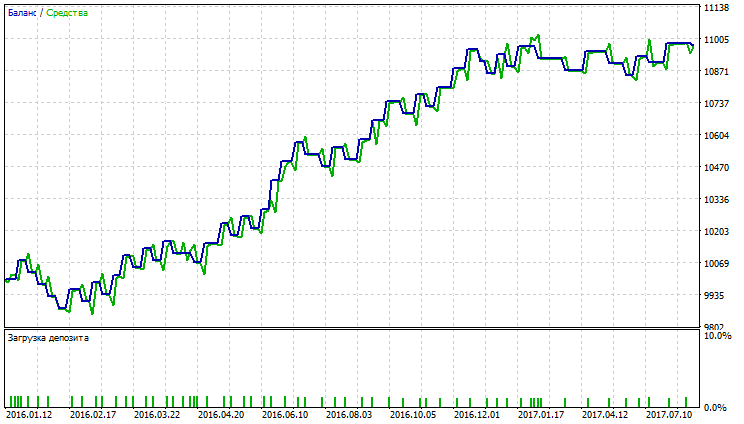
Fig. 13. Balance (equity) chart for  Nick Rypock Moving Average

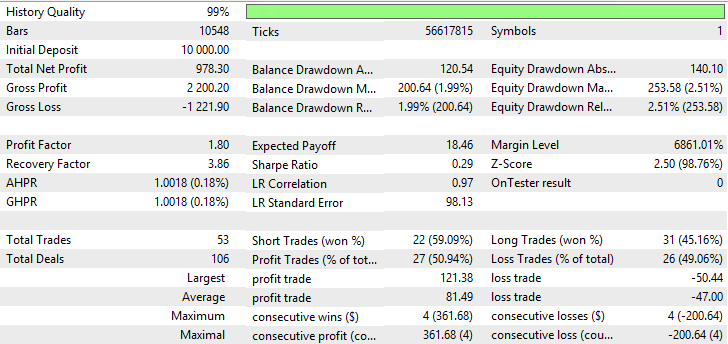
Fig. 14. Report for Variable Index Nick Rypock Moving Average

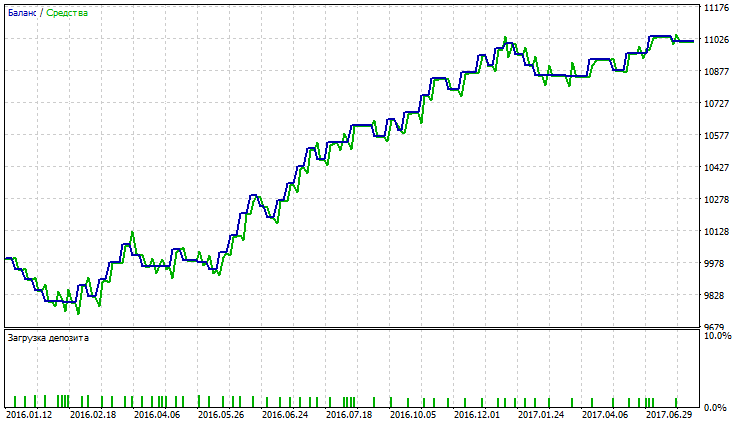
Fig. 15. Balance (equity) chart of Simple Moving Average 

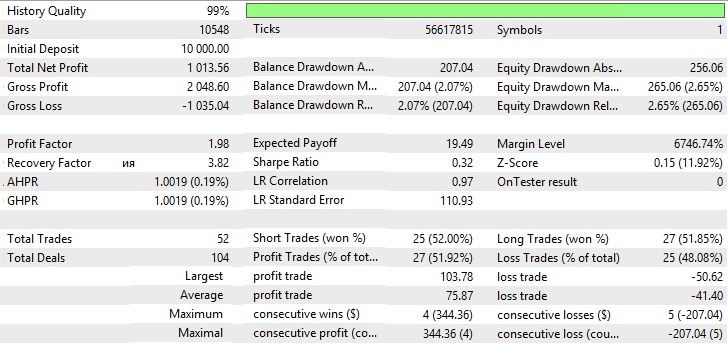
Fig. 16. Report for  Simple Moving Average 

Fig. 11-16 demonstrate that VIDYA, NRMA and SMA look somewhat the same, at trading commencement a slight drawdown is observed; further, charts grow, number of deals with VIDYA is greater than with NRMA and SMA. Percentage of profitable trades with VIDYA exceeds those with NRMA and SMA.

Testing results on currency pair  USDJPY

Testing results on currency pair  USDJPY are provided in the following table:

Name of moving average	Parameters optimized and their values	Q-ty of trades	Total net profit	Profit factor	Recovery factor	Sharpe ratio	Balance drawdown maximal	Equity   drawdown maximal
Moving Average (method of averaging Simple)	Period —34, Growth factor — 0.0004	451	1784.95	1.32	3.69	0.1	465.52 (4.17%)	483.34 (4.32%)
Moving Average (method of averaging Exponential)	Period —42, Growth factor — 0.0007	465	1135.23	1.20	2.21	0.07	461.52 (4.08%)	514.61 (4.53%)
Moving Average (method of averaging Smoothed)	Period —33, Growth factor — 0.0008	372	1702.94	1.36	5.15	0.12	296.57 (2.58%)	330.6 (2.87%)
Moving Average (method of averaging Weighted)	Period —50, Growth factor — 0.0005	477	1892.24	1.33	4.66	0.10	384.06 (3.68%)	406.1 (3.88%)
Adaptive Moving Average	Period —46, Growth factor — 0.0006	403	1460.51	1.26	2.56	0.09	527.75 (4.77%)	569.67 (5.13%)
Double Exponential Moving Average	Period —18, Growth factor — 0.001	1062	1459.18	1.15	3.55	0.05	366.24 (3.30%)	410.56 (3.69%)
Triple Exponential Moving Average	Period —50, Growth factor — 0.0003	657	1115.86	1.15	1.87	0.05	537.18 (4.68%)	597.71 (5.18%)
Fractal Adaptive Moving Average	Period —24, Growth factor — 0.0008	1030	615.92	1.06	0.8	0.02	734.03 (6.58%)	766.01 (6.85%)
Variable Index Dynamic Average	Period EMA — 18, period CMO — 42, Growth factor — 0.001	238	2338.68	1.64	5.14	0.21	417.66 (3.62%)	454.69 (3.93%)
Nick Rypock Moving Average	Fact —28, Growth factor — 0.0002	435	1465.32	1.27	3.00	0.09	456.65 (4.02%)	488.7 (4.29%)

Normalized results are represented in the table (the best results are in yellow, the worst one is in red color):

Name of moving average	Total net profit	Profit factor	Recovery factor	Sharpe ratio	Balance drawdown maximal	Equity drawdown maximal	Sum of indicators exclusive of drawdowns	Sum of indicators inclusive of drawdowns
Moving Average (method of averaging Simple)	0.67858	0.45316	0.66457	0.4324	0.38621	0.3508	2.22871	1.49171
Moving Average (method of averaging Exponential)	0.30144	0.25001	0.32251	0.25216	0.37706	0.42261	1.12612	0.32645
Moving Average (method of averaging Smoothed)	0.63098	0.51885	1	0.50010	0	0	2.64993	2.64993
Moving Average (method of averaging Weighted)	0.74086	0.46535	0.88693	0.42881	0.2	0.1734	2.52195	2.14855
Adaptive Moving Average	0.49025	0.34559	0.40481	0.36951	0.52846	0.54907	1.61017	0.53264
Double Exponential Moving Average	0.48948	0.15054	0.63263	0.14711	0.15926	0.18364	1.41976	1.07686
Triple Exponential Moving Average	0.2902	0.15141	0.2445	0.15928	0.55002	0.61347	0.84538	-0.3181
Fractal Adaptive Moving Average	0	0	0	0	1	1	0	-2
Variable Index Dynamic Average	1	1	0.99825	1	0.2768	0.285	3.99825	3.43645
Nick Rypock Moving Average	0.49305	0.36549	0.50479	0.37182	0.36593	0.36311	1.73515	1.00611

As the tables suggest, Variable Index Dynamic Average and Moving Average have the best indicators with Smoothed and Linear Weighted methods of averaging. Indicators of Total net profit, Profit factor, Sharpe ratio with VIDYA exceed those with SMMA and LWMA, but  SMMA and LWMA have the least balance and equity drawdown. Testing results for VIDYA,  SMMA and LWMA  are shown in fig. 17-22.

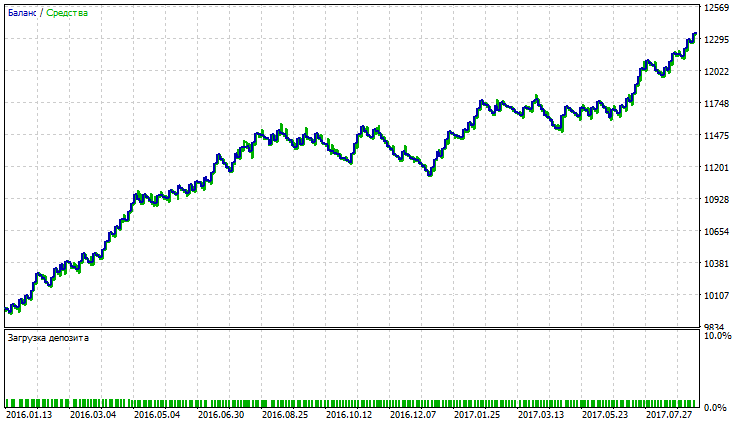
Fig. 17. Balance (equity) chart of Variable Index Dynamic Average

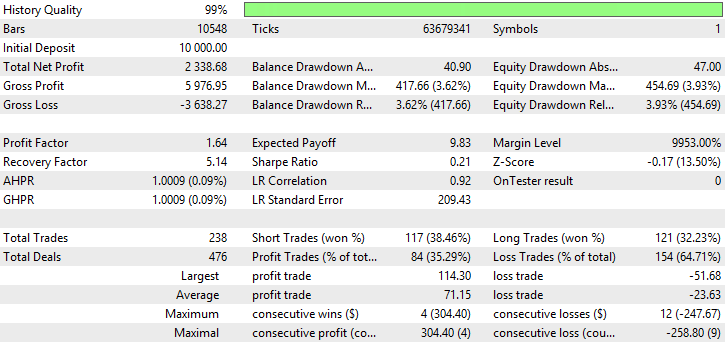
Fig. 18. Report for  Variable Index Dynamic Average

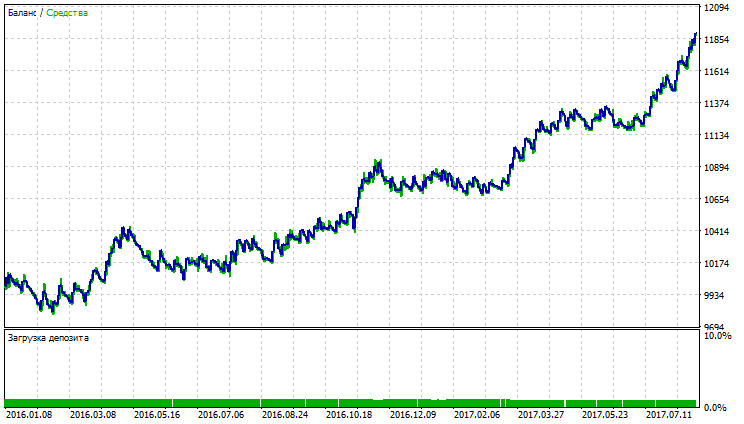
Fig. 19. Balance (equity) chart of  Linear Weighted Moving Average 

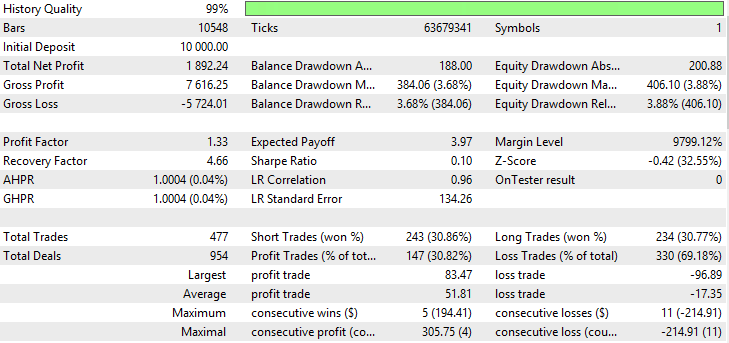
Fig. 20. Report for  Linear Weighted Moving Average 

Fig. 21. Balance (equity) chart of  Smoothed Moving Average 

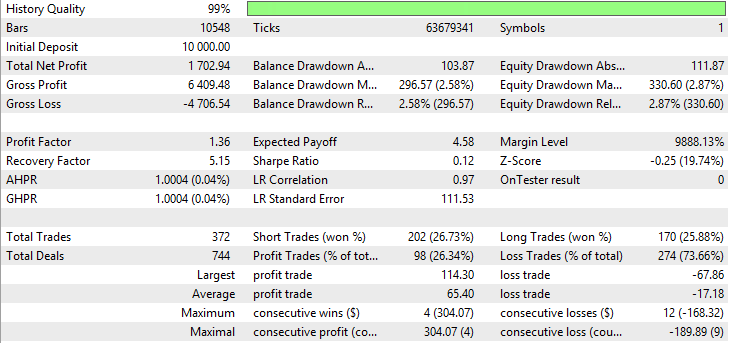
Fig. 22. Report for  Smoothed Moving Average

Fig. 17-22 show that notwithstanding low percentage of profitable trades, the indicators demonstrate high total net profit. This is connected with the fact that currency pair USDJPY has high volatility.

Testing results on currency pair  USDCAD

Testing results on currency pair  USDCAD are provided in the below table:

Name of moving average	Parameters optimized and their values	Q-ty of trades	Total net profit	Profit factor	Recovery factor	Sharpe ratio	Balance drawdown maximal	Equity   drawdown maximal
Moving Average (method of averaging Simple)	Period —39, Growth factor — 0,0004	59	1101.44	2.30	7.11	0.40	133.44 (1.25%)	154.92 (1.45%)
Moving Average (method of averaging Exponential)	Period —31, Growth factor — 0.0005	76	951.88	1.74	3.01	0.27	278.08 (2.56%)	316.57 (2.91%)
Moving Average (method of averaging Smoothed)	Period —50, Growth factor — 0.0001	121	1262.26	1.57	3.07	0.22	343.76 (3.19%)	411.32 (3.81%)
Moving Average (method of averaging Weighted)	Period —46, Growth factor — 0.0005	46	903.64	2.34	5.31	0.42	128.97 (1.22%)	170.05 (1.61%)
Adaptive Moving Average	Period —38, Growth factor — 0.0009	41	990.44	3.18	8.62	0.55	77.57 (0.73%)	114.96 (1.09%)
Double Exponential Moving Average	Period —44, Growth factor — 0.0007	73	941.93	2.07	5.33	0.32	137.28 (1.28%)	176.6 (1.64%)
Triple Exponential Moving Average	Period —49, Growth factor — 0.0009	76	559.18	1.62	3.28	0.20	122.21 (1.2%)	170.57 (1.66%)
Fractal Adaptive Moving Average	Period —15, Growth factor — 0.0009	185	504.26	1.27	2.44	0.09	197.12 (1.95%)	206.37 (2.04%)
Variable Index Dynamic Average	Period EMA — 34, period CMO — 9, Growth factor — 0.0002	111	1563.99	1.86	6.17	0.30	185.64 (1.70%)	253.36 (2.32%)
Nick Rypock Moving Average	Fact — 41, Growth factor —0.0004	81	594.91	1.39	1.74	0.16	309.02 (2.88%)	342.16 (3.18%)

Normalized results are represented in the table (the best results are in yellow, the worst one is in  red colour):

Name of moving average	Total net profit	Profit factor	Recovery factor	Sharpe ratio	Balance drawdown maximal	Equity drawdown maximal	Sum of indicators exclusive of drawdowns	Sum of indicators inclusive of drawdowns
Moving Average (method of averaging Simple)	0.56352	0.53776	0.78104	0.67198	0.20989	0.13484	2.5543	2.20957
Moving Average (method of averaging Exponential)	0.42239	0.24419	0.18441	0.37529	0.75326	0.68029	1.22628	-0.2073
Moving Average (method of averaging Smoothed)	0.71528	0.15751	0.19342	0.26924	1	1	1.33545	-0.6646
Moving Average (method of averaging Weighted)	0.37687	0.55859	0.5199	0.69827	0.1931	0.18589	2.15363	1.77465
Adaptive Moving Average	0.45878	1	1	1	0	0	3.45878	3.45878
Double Exponential Moving Average	0.413	0.42112	0.52277	0.48957	0.22431	0.20799	1.84645	1.41415
Triple Exponential Moving Average	0.05182	0.18256	0.22388	0.23681	0.1677	0.18764	0.69508	0.33974
Fractal Adaptive Moving Average	0	0	0.10249	0	0.44912	0.30844	0.10249	-0.6551
Variable Index Dynamic Average	1	0.30606	0.64482	0.43945	0.40599	0.467	2.39033	1.51734
Nick Rypock Moving Average	0.08554	0.06124	0	0.14059	0.86949	0.76664	0.28737	-1.3488

As the tables suggest, Adaptive Moving Average, Moving Average with Simple method of averaging and Variable Index Dynamic Average have the best indicators. Adaptive Moving Average demonstrates the best indicators of Profit factor, Recovery factor and Sharpe ratio, as well it has the least balance and equity drawdowns. Variable Index Dynamic Average has the biggest total net profit, however, other indicators are not the highest. Testing results for AMA, SMA and VIDYA  are shown in fig. 23-28.

Fig. 23. Balance (equity) chart of Adaptive Moving Average

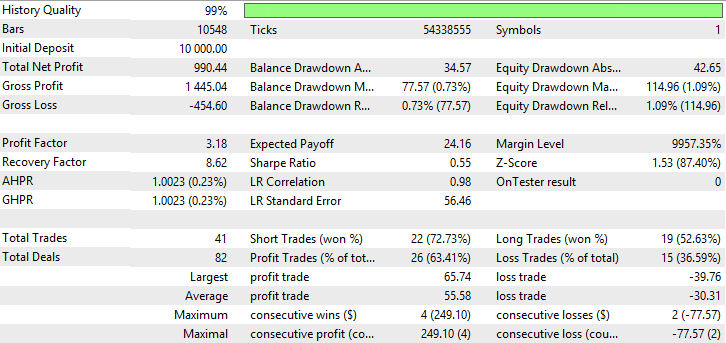
Fig. 24. Report for  Adaptive Moving Average

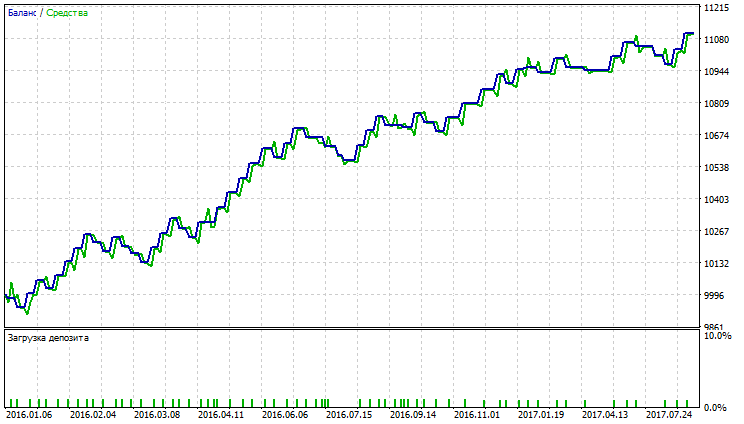
Fig. 25. Balance (equity) chart of Simple Moving Average

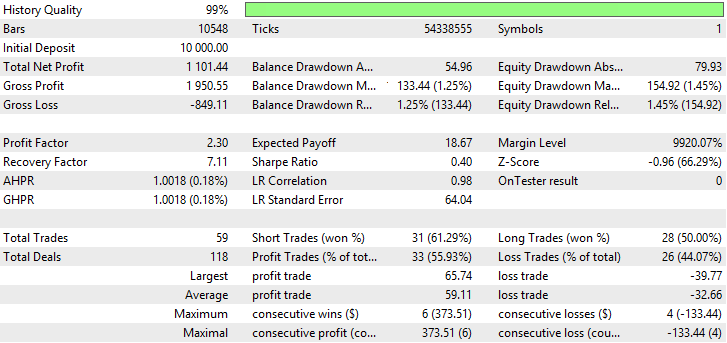
Fig. 26. Report for  Simple Moving Average

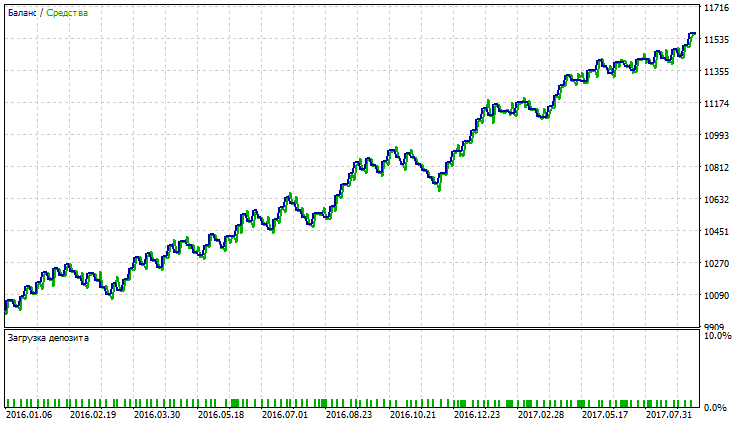
Fig. 27. Balance (equity) chart of Variable Index Dynamic Average

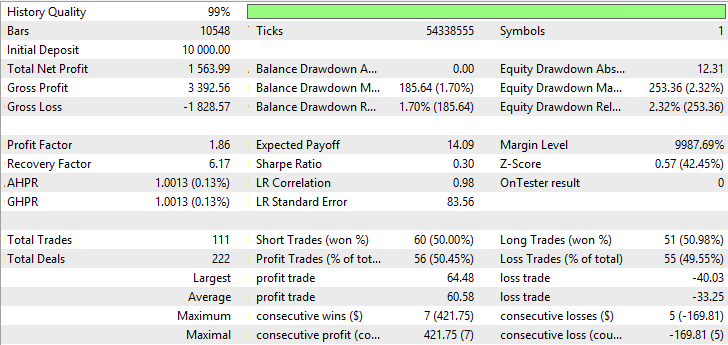
Fig. 28. Report for  Variable Index Dynamic Average

Fig. 23-28 demonstrates AMA has the lowest quantity of trades and the biggest percentage of profitable trades. SMA and VIDYA have the highest profit for the account of a bigger quantity of trades, whereas the number of profitable trades exceeds those loss. Big drawdowns in charts AMA, SMA and VIDYA are not observed.

Testing results on currency pair  AUDUSD

Testing results on currency pair  AUDUSD are provided in the below table:

Name of moving average	Parameters optimized and their values	Q-ty of trades	Total net profit	Profit factor	Recovery factor	Sharpe ratio	Balance drawdown maximal	Equity   drawdown maximal
Moving Average (method of averaging Simple)	Period —7, Growth factor — 0.0009	78	262.48	1.36	1.23	0.11	175.85 (1.74%)	214.18 (2.11%)
Moving Average (method of averaging Exponential)	Period —40, Growth factor — 0.0004	24	652.88	2.62	2.82	0.47	206.76 (1.93%)	231.76 (2.16%)
Moving Average (method of averaging Smoothed)	Period —21, Growth factor — 0.0004	24	651.18	2.61	2.81	0.47	206.76 (1.93%)	231.76 (2.16%)
Moving Average (method of averaging Weighted)	Period —32, Growth factor — 0.0005	24	383.64	1.97	2.25	0.30	116.38 (1.11%)	170.24 (1.62%)
Adaptive Moving Average	Period —21, Growth factor — 0.0007	58	252.39	1.30	0.54	0.11	392.15 (3.80%)	464.47 (4.48%)
Double Exponential Moving Average	Period —40, Growth factor — 0.0006	39	296.15	1.70	1.53	0.20	156.62 (1.51%)	193.02 (1.86%)
Triple Exponential Moving Average	Period —21, Growth factor — 0.001	69	273.12	1.35	1.05	0.11	228.5 (2.20%)	259.71 (2.50%)
Fractal Adaptive Moving Average	Period —38, Growth factor — 0.0007	83	109.01	1.11	0.55	0.04	142.85 (1.42%)	196.47 (1.94%)
Variable Index Dynamic Average	Period EMA — 26, period CMO — 5, Growth factor — 0.0006	23	697.59	2.99	2.96	0.53	151.35 (1.41%)	235.38 (2.19%)
Nick Rypock Moving Average	Period —22, Growth factor — 0.0006	34	509.27	1.90	2.55	0.28	94.58 (0.9%)	200 (1.89%)

Normalized results are represented in the table (the best results are in yellow, the worst one is in  red colour):

Name of moving average	Total net profit	Profit factor	Recovery factor	Sharpe ratio	Balance drawdown maximal	Equity drawdown maximal	Sum of indicators exclusive of drawdowns	Sum of indicators inclusive of drawdowns
Moving Average (method of averaging Simple)	0.26075	0.12921	0.28183	0.13463	0.27311	0.14934	0.80642	0.38397
Moving Average (method of averaging Exponential)	0.92404	0.80629	0.93942	0.86552	0.37699	0.20909	3.53527	2.94919
Moving Average (method of averaging Smoothed)	0.92115	0.8006	0.93639	0.86226	0.37699	0.20909	3.5204	2.93433
Moving Average (method of averaging Weighted)	0.4666	0.45691	0.70658	0.52861	0.07326	0	2.1587	2.08544
Adaptive Moving Average	0.2436	0.10105	0	0.13347	1	1	0.47812	-1.5219
Double Exponential Moving Average	0.31795	0.31405	0.40942	0.31848	0.20849	0.07742	1.3599	1.07399
Triple Exponential Moving Average	0.27882	0.12776	0.20999	0.14014	0.45005	0.30408	0.75672	0.00259
Fractal Adaptive Moving Average	0	0	0.00473	0	0.16221	0.08915	0.00473	-0.2466
Variable Index Dynamic Average	1	1	1	1	0.19078	0.22139	4	3.58783
Nick Rypock Moving Average	0.68004	0.42124	0.82757	0.48773	0	0.10115	2.41659	2.31545

As the tables suggest, Variable Index Dynamic Average and Moving Average have the best indicators with Exponential and Smoothed methods of averaging. VIDYA demonstrates the best indicators of Total net profit, Profit factor, Recovery factor and Sharpe ratio. EMA and SMMA have almost equal indicators and equal quantity of trades. Testing results for VIDYA, EMA and SMMA are shown in fig. 29-34.

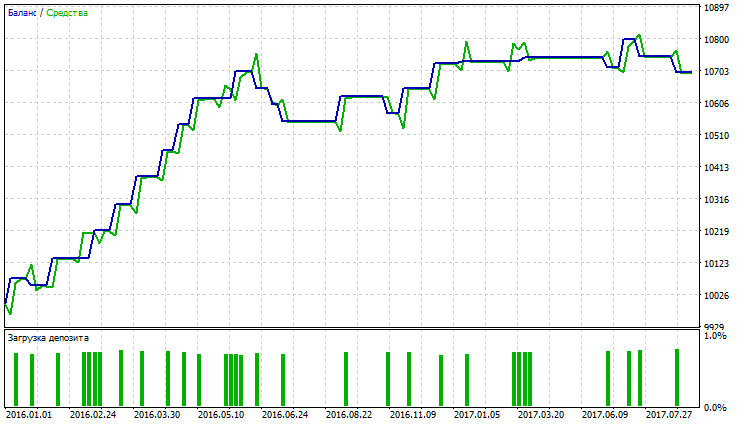
Fig. 29. Balance (equity) chart of Variable Index Dynamic Average

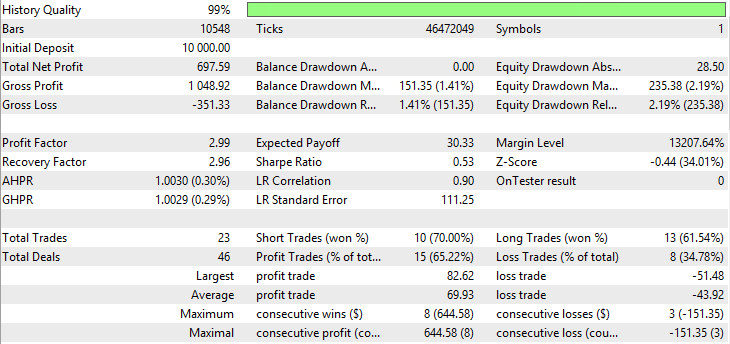
Fig. 30. Report for  Variable Index Dynamic Average

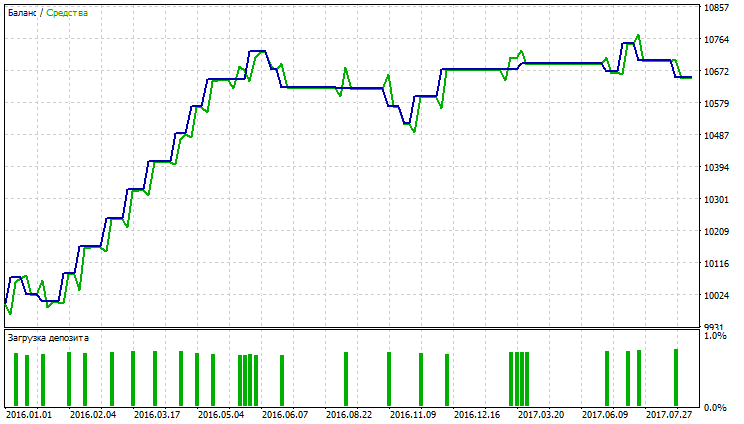
Fig. 31. Balance (equity) chart of  Exponential Moving Average

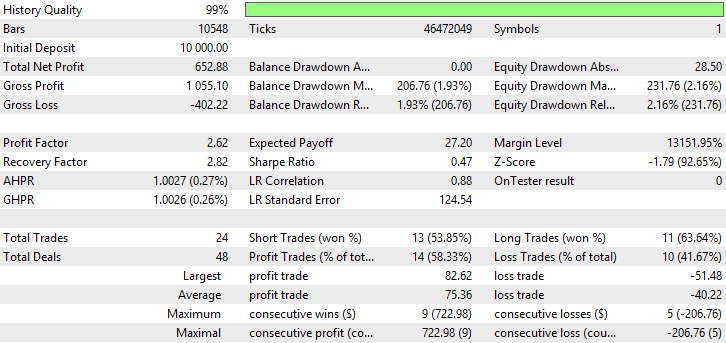
Fig. 32. Report for  Exponential Moving Average

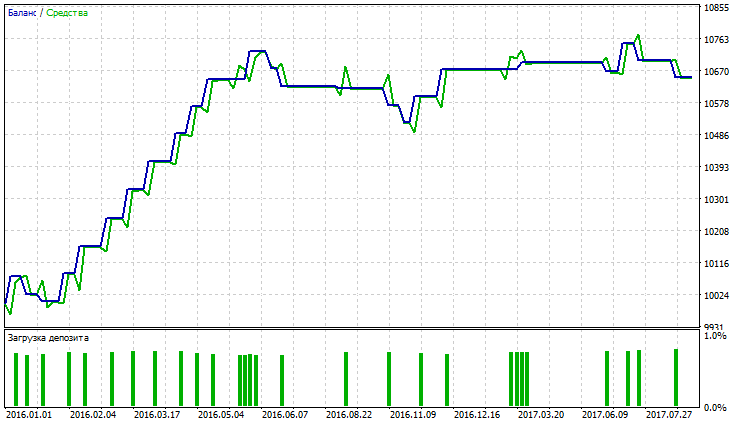
Fig. 33. Balance (equity) chart of Smoothed Moving Average

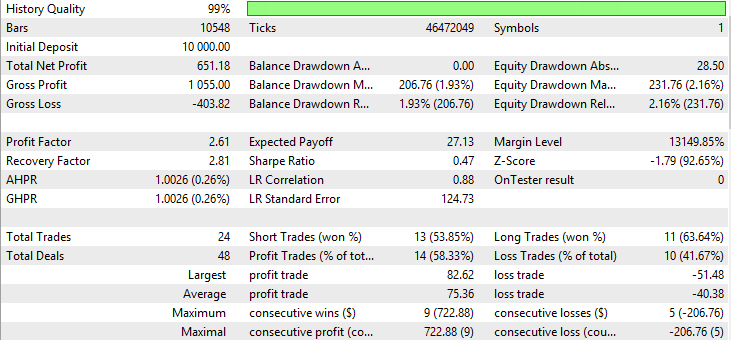
Fig. 34. Report for  Smoothed Moving Average

Fig. 29-34 show that balance (equity) charts for VIDYA, EMA and SMMA are approximately equal, VIDYA has a bigger number of profitable trades than EMA and SMMA. Currency pair AUDUSD has low volatility which explains the obtained results.

The following conclusions may be made on the basis of testing results on currency pairs EURUSD, GBPUSD, USDJPY, USDCAD, AUDUSD:

• the best results on currency pairs with high (GBPUSD, USDJPY) and low volatility (AUDUSD) were demonstrated by Variable Index Dynamic Average
• on USDCAD, the best indices were demonstrated by Adaptive Moving Average, however on currency pair EURUSD it demonstrates the worst results
• on EURUSD, the best indices were demonstrated by Triple Exponential Moving Average
• the worst results on currency pairs GBPUSD, USDJPY, USDCAD, AUDUSD were demonstrated by Fractal Adaptive Moving Average
• fair results were demonstrated by standard indicator Moving Average with various averaging periods.

Conclusion

We have considered different moving averages (MA (with methods Simple, Exponential, Smoothed, Linear Weighted), DEMA, TEMA, FRAMA, AMA, VIDYA, NRMA), for each MA a procedure of its calculation is described. Comparison and optimization of moving averages in trading under equal conditions of entering and exiting the market have been performed.

The following conclusions can be made based on obtained results:

• by optimizing parameters of any of the considered moving averages, a profitable strategy may be received;
• the majority of moving averages are variations of EMA indicator;
• the main advantage of EMA-based moving averages is a decrease in false signals in flat and a faster response to trend change;
• the best results were demonstrated by Variable Index Dynamic Average, it can be used both on currency pairs with high and low volatility, as well as on currency pairs with average volatility.

The article considers four technical indicators (AMA, FRAMA, VIDYA, NRMA), which differ from EMA by the method of calculation of smoothing factor. Possibly, for somebody this will serve as an incentive to make a new, more efficient variation of EMA indicator.