
Нейросети — это просто (Часть 38): Исследование с самоконтролем через несогласие (Self-Supervised Exploration via Disagreement)
Введение
Проблема исследования является главным препятствием в обучении с подкреплением, особенно в тех случаях, когда агент получает редкие и задержанные награды, что затрудняет выработку эффективной стратегии. Одно из возможных решений этой проблемы — генерация "внутренних" наград, основанных на модели окружающей среды. С подобным алгоритмом мы познакомились при изучении модуля внутреннего любопытства. Однако большинство созданных алгоритмов исследовались только в контексте компьютерных игр, а за пределами бесшумных моделируемых окружений обучение предсказательных моделей представляет собой сложную задачу из-за стохастической природы взаимодействия агента и окружающей среды. Одним из подходов для решения проблемы стохастичности окружающей среды является алгоритм, который предложил Дипак Патак (Deepak Pathak) в статье "Self-Supervised Exploration via Disagreement".
Данный алгоритм основывается на методе самообучения, где агент использует информацию, полученную в процессе взаимодействия с окружающей средой, для генерации "внутренних" наград и обновления своей стратегии. Алгоритм основан на использовании нескольких моделей агента, которые взаимодействуют со средой и генерируют различные предсказания. Если модели не согласны друг с другом, это считается "интересным" событием, и агент стимулируется исследовать эту область среды. Таким образом, алгоритм стимулирует агента на изучение новых областей окружающей среды и позволяет ему получать более точные предсказания о будущих наградах.
1. Алгоритм исследования через несогласие
Алгоритм исследования через несогласие (Disagreement-based Exploration) является одним из методов обучения с подкреплением, который позволяет агенту исследовать среду, не полагаясь на внешние вознаграждения, а находя новые, неизведанные области с помощью ансамбля моделей.
В статье "Self-Supervised Exploration via Disagreement" авторы описывают этот подход и предлагают простой метод, который заключается в тренировке ансамбля моделей прямой динамики и поощрении агента исследовать пространство действий, где есть максимальная несогласованность или дисперсия между предсказаниями моделей из ансамбля.
Таким образом вместо того, чтобы выбирать действия, которые дают наибольшее ожидаемое вознаграждение, агент выбирает действия, которые максимизируют несогласие между моделями в ансамбле. Это позволяет агенту исследовать области пространства состояний, где модели в ансамбле не согласны между собой и где, вероятнее всего, есть новые и неизведанные области среды.
При этом все модели в ансамбле сходятся к среднему значению, в итоге уменьшая разброс ансамбля и предоставляя агенту более точные предсказания о состояниях среды и возможных последствиях действий.
Кроме того, алгоритм исследования через несогласие позволяет агенту успешно справляться со стохастичностью взаимодействия с окружающей средой. Результаты экспериментов, проведенных авторами статьи, показали, что предложенный подход действительно улучшает исследование в стохастических средах и превосходит ранее существующие методы внутренней мотивации и моделирования неопределенности. Кроме того, они заметили, что их подход может быть расширен для обучения с учителем, где значение образца определяется не на основе истинной метки, а на основе состояния ансамбля моделей.
Таким образом, алгоритм исследования через несогласие представляет собой многообещающий подход к решению проблемы исследования в стохастических средах. Он позволяет агенту исследовать среду более эффективно и без необходимости полагаться на внешние вознаграждения, что может быть особенно полезным в реальных приложениях, где внешние вознаграждения могут быть ограничены или дорогостоящими.
Более того, данный алгоритм может применяться в различных контекстах, включая работу с высокомерными данными, такими как изображения, где измерение и максимизация модельной неопределенности может быть особенно сложной задачей.
Авторы статьи продемонстрировали эффективность предложенного алгоритма на нескольких задачах, включая контроль робота, игры на Atari и задачи навигации в лабиринтах. В результате их исследований они показали, что алгоритм исследования через несогласие значительно превосходит другие методы исследования в терминах скорости, сходимости и качества обучения.
Таким образом, данный подход к исследованию через несогласие представляет собой важный шаг в области обучения с подкреплением, который может помочь агентам лучше и более эффективно исследовать окружающую среду и достигать лучших результатов в различных задачах.
Рассмотрим предложенный алгоритм.
В процессе взаимодействия с окружающей средой агент оценивает текущее состояние Xt и, руководствуясь своей внутренней политикой, совершает некоторое действие At. В результате происходит изменение состояния среды до нового состояния Xt+1. Набор таких данных сохраняется в буфере воспроизведения опыта, который мы используем для обучения ансамбля динамических моделей, прогнозирующих будущее состояние среды.
Для сохранения независимости оценки будущего состояния среды на начальном этапе все весовые матрицы динамических моделей в ансамбле заполняются случайными значениями. В процессе обучения каждая модель получает свой случайный набор обучающих данных из буфера воспроизведения опыта.
Каждая модель в нашем ансамбле обучается предсказывать следующее состояние настоящей среды. Части пространства состояний, которые были хорошо исследованы агентом, собрали достаточно данных для обучения всех моделей, что приводит к согласованности между моделями. Поскольку модели обучены, эта особенность должна обобщаться на незнакомые, но похожие части пространства состояний. Однако области, которые являются новыми и неизведанными, все еще будут иметь высокую ошибку предсказания для всех моделей, поскольку ни одна из них еще не была обучена на таких примерах, что приводит к расхождению в предсказании следующего состояния. Поэтому мы используем это расхождение в качестве внутренней награды для направления политики. Конкретно, внутренняя награда Ri определяется как дисперсия по выходу различных моделей в ансамбле.
![]()
Обратите внимание, что в приведенной формуле отсутствует зависимость внутреннего вознаграждения от будущего состояния системы. Этим свойством мы воспользуемся позже при реализации данного метода.
В случае стохастического сценария, при наличии достаточного количества выборок динамическая модель прогнозирования должна научиться предсказывать среднее значение стохастических выборок. Таким образом, дисперсия выходов в ансамбле уменьшится, предотвращая застревание агента в стохастических локальных минимумах исследования. Обратите внимание, что это отличается от целей, основанных на ошибке предсказания, которые после достаточного количества выборок установятся на среднее значение. А среднее отличается от отдельных истинных случайных состояний, ошибка предсказания остается высокой, что заставляет агента навсегда интересоваться стохастическим поведением.
При использовании предложенного алгоритма каждый шаг взаимодействия агента со средой даёт информацию не только о награде, полученной от среды, но и об информации, необходимой для обновления внутренней модели агента о том, как изменяется состояние среды при совершении действий. Это позволяет агенту извлекать ценную информацию о среде, даже если ему не предоставляется явной внешней награды.
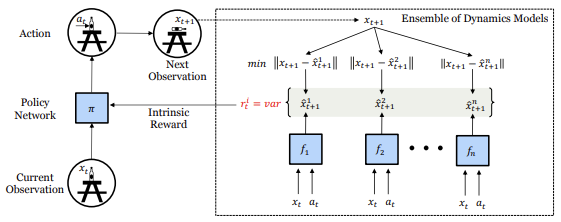
Для обучения политики агента используется внутренняя награда Ri, которая вычисляется как дисперсия выходов различных моделей в ансамбле. Чем больше расхождение между выходами моделей, тем выше значение внутренней награды. Это позволяет агенту исследовать новые области пространства состояний, где предсказание следующего состояния является неопределённым, и научиться принимать лучшие решения на основе этих данных.
Агент обучается в режиме онлайн на данных, собранных им самим в процессе взаимодействия со средой. Вместе с тем ансамбль моделей обновляется после каждого взаимодействия агента со средой, что позволяет агенту обновлять свою внутреннюю модель о среде на каждом шаге и получать более точные прогнозы состояний среды в будущем.
2. Реализация средствами MQL5
В своей реализации мы не будем полностью повторять предложенный алгоритм, а лишь возьмем его основные идеи и перенесем на наши задачи.
Первое, что мы сделаем, это попросим ансамбль динамических моделей прогнозировать сжатое (скрытое) состояние системы, по аналогии с модулем внутреннего любопытства. Это позволит нам "сжать" размер динамических моделей и ансамбля в целом.
Вторым моментом является тот факт, что для определения внутреннего вознаграждения нам не нужно знание истинного состояния системы, а достаточно прогнозных значений динамическими моделями ансамбля. Это позволяет нам использовать прогнозное вознаграждение не только для стимулирования последующего изучения, но и для принятия решения о совершении действия в режиме реального времени. Мы не будем искажать внешнее вознаграждение введением внутренней составляющей при обучении политики агента, а позволим ему сразу выстраивать политику максимизирования внешнего вознаграждения — это наша основная цель.
Однако для максимального изучения окружающей среды в процессе обучения, при выборе действия агента мы будем добавлять к прогнозному вознаграждению дисперсию расхождения прогнозов динамических моделей по каждому возможному действию агента.
Это приводит нас к еще одному моменту: для параллельного вычисления прогнозных состояний после каждого действия мы попросим наши динамические модели дать нам прогнозы по каждому возможному действию агента на основании текущего состояния, увеличив размер слоя результатов каждой модели в соответствии с количеством возможных действий.
После определения основных направлений нашей работы мы можем перейти к реализации алгоритма. Сразу встает вопрос реализации ансамбля динамических моделей. Все нами ранее созданные модели являются линейными. Организация параллельных вычислений осуществляется средствами OpenCL в рамках одного подпроцесса и одного нейронного слоя. Организация параллельных вычислений нескольких моделей на данный момент не представляется возможной. Создание последовательности вычислений нескольких моделей ведет к значительному увеличению времени на обучения модели.
Для решения этого вопроса я решил воспользоваться методом организации параллельных вычислений при организации многоголового внимания. Тогда мы объединили данные всех голов внимания в единые тензоры, а деление осуществляли на уровне пространства задач в OpenCL.
Мы не будем сейчас переделывать всю нашу библиотеку для решения подобных задач. На данном этапе нам не важна особая точность прогнозных значений будущего состояния системы. Достаточно лишь получить относительную синхронность работы ансамбля моделей. Поэтому в динамических моделях прогнозирования мы воспользуемся полносвязными слоями.
Вначале мы создадим кернелы OpenCL программы для организации данного функционала. Кернел прямого прохода FeedForwardMultiModels практически полностью повторил аналогичный кернел базового полносвязного слоя. Но есть небольшие отличия.
Параметры кернела остались без изменений. Здесь можно найти три буфера данных (тензоры матрицы весов, исходных данных и результатов), а также две константы: размер слоя исходных данных и функция активации. Но если в качестве размера слоя исходных данных ранее мы указывали полный размер предыдущего слоя, то теперь мы ожидаем получить количество элементов текущей модели.
__kernel void FeedForwardMultiModels(__global float *matrix_w, __global float *matrix_i, __global float *matrix_o, int inputs, int activation ) { int i = get_global_id(0); int outputs = get_global_size(0); int m = get_global_id(1); int models = get_global_size(1);
В теле кернела, мы сначала идентифицируем текущий поток. И тут можно заметить появление второй размерности пространства задач, которое идентифицирует текущую модель. Общая размерность задач укажет на размер ансамбля.
Далее мы объявляем необходимые локальные переменные и определим смещение в буферах данных с учетом вычисляемого нейрона и текущей модели в ансамбле.
float sum = 0; float4 inp, weight; int shift = (inputs + 1) * (i + outputs * m); int shift_in = inputs * m; int shift_out = outputs * m;
Непосредственно математическая часть вычисления состояния нейрона и функции активации осталась без изменений. Мы лишь добавили поправки на смещение в буферах данных.
for(int k = 0; k <= inputs; k = k + 4) { switch(inputs - k) { case 0: inp = (float4)(1, 0, 0, 0); weight = (float4)(matrix_w[shift + k], 0, 0, 0); break; case 1: inp = (float4)(matrix_i[shift_in + k], 1, 0, 0); weight = (float4)(matrix_w[shift + k], matrix_w[shift + k + 1], 0, 0); break; case 2: inp = (float4)(matrix_i[shift_in + k], matrix_i[shift_in + k + 1], 1, 0); weight = (float4)(matrix_w[shift + k], matrix_w[shift + k + 1], matrix_w[shift + k + 2], 0); break; case 3: inp = (float4)(matrix_i[shift_in + k], matrix_i[shift_in + k + 1], matrix_i[shift_in + k + 2], 1); weight = (float4)(matrix_w[shift + k], matrix_w[shift + k + 1], matrix_w[shift + k + 2], matrix_w[shift + k + 3]); break; default: inp = (float4)(matrix_i[shift_in + k], matrix_i[shift_in + k + 1], matrix_i[shift_in + k + 2], matrix_i[shift_in + k + 3]); weight = (float4)(matrix_w[shift + k], matrix_w[shift + k + 1], matrix_w[shift + k + 2], matrix_w[shift + k + 3]); break; } float d = dot(inp, weight); if(isnan(sum + d)) continue; sum += d; }
После вычисления значения указанной в параметрах функции активации полученный результат сохраняем в буфер данных matrix_o.
if(isnan(sum)) sum = 0; switch(activation) { case 0: sum = tanh(sum); break; case 1: sum = 1 / (1 + exp(-sum)); break; case 2: if(sum < 0) sum *= 0.01f; break; default: break; } matrix_o[shift_out + i] = sum; }
Подобное решение позволяет нам в одном кернеле параллельно вычислять значение одного слоя всех моделей в ансамбле. Конечно, здесь есть ограничение — архитектура всех моделей в ансамбле идентична, различия лишь в весовых коэффициентах.
Немного другая ситуация с обратным проходом. Алгоритмом предусмотрено обучение динамических моделей в ансамбле на различном наборе обучающих данных. Мы не будем отдельно формировать пакеты обучения для каждой модели. Вместо этого при каждом обратном проходе мы будем обучать только одну, случайно выбранную модель из ансамбля. Для других моделей мы передадим нулевой градиент на предыдущий слой. Именно такие изменения мы внесем в алгоритм кернела распределения градиента внутри слоя CalcHiddenGradientMultiModels.
Аналогичный кернел базового полносвязного нейронного слоя в параметрах получал указатели на четыре буфера данных и две переменные. Это тензор матрицы весов, тензор результатов предыдущего слоя для вычисления производной функции активации. Также есть 2 буфера градиентов: текущего и предыдущего нейронных слоев. Первый содержит полученные градиенты ошибок, а второй используется для записи результатов работы кернела и передачи градиента ошибки на предыдущий нейронный слой. В переменных указывается количество нейронов в текущем слое и функция активации предыдущего слоя. К указанным параметрам мы добавляем идентификатор обучаемой модели, который будем случайным образом выбирать на стороне основной программы.
__kernel void CalcHiddenGradientMultiModels(__global float *matrix_w, __global float *matrix_g, __global float *matrix_o, __global float *matrix_ig, int outputs, int activation, int model ) {
В теле кернела мы прежде всего идентифицируем поток. Как и в кернеле прямого прохода, мы используем двухмерное пространство задач. В первом измерении мы идентифицируем поток в рамках одной модели, а второе измерение указывает на модель в ансамбле. Для сбора градиентов ошибки мы запускаем кернел в разрезе нейронов предыдущего слоя. Каждый поток собирает градиенты ошибок со всех направлений на одном отдельно взятом нейроне.
int i = get_global_id(0); int inputs = get_global_size(0); int m = get_global_id(1); int models = get_global_size(1);
Обратите внимание, распределять градиент мы будем только по одной модели, а запускаем потоки для всего ансамбля. Это связано с необходимостью обнуления градиента ошибки других моделей. На следующем этапе мы проверяем необходимость обновления градиента для конкретной модели. И если нам достаточно лишь обнулить градиент, то мы выполняем только эту функцию и выходим из кернела без выполнения лишних операций.
//--- int shift_in = inputs * m; if(model >= 0 && model != m) { matrix_ig[shift_in + i] = 0; return; }
Здесь мы оставляем себе небольшую лазейку на возможное будущее применение. И если в качестве номера модели для обновления указать отрицательное число, то градиент будет рассчитан для всех моделей ансамбля.
Далее мы объявляем локальные переменные и определяем смещение в буферах данных.
//--- int shift_out = outputs * m; int shift_w = (inputs + 1) * outputs * m; float sum = 0; float out = matrix_o[shift_in + i]; float4 grad, weight;
После чего следует математическая часть распределения градиента ошибки, которая полностью повторяет аналогичный функционал базового полносвязного нейрона. Конечно, мы добавляем необходимое смещение в буферах данных. Результат операций сохраняем в буфер градиентов предыдущего слоя.
for(int k = 0; k < outputs; k += 4) { switch(outputs - k) { case 1: weight = (float4)(matrix_w[shift_w + k * (inputs + 1) + i], 0, 0, 0); grad = (float4)(matrix_g[shift_out + k], 0, 0, 0); break; case 2: grad = (float4)(matrix_g[shift_out + k], matrix_g[shift_out + k + 1], 0, 0); weight = (float4)(matrix_w[shift_w + k * (inputs + 1) + i], matrix_w[shift_w + (k + 1) * (inputs + 1) + i], 0, 0); break; case 3: grad = (float4)(matrix_g[shift_out + k], matrix_g[shift_out + k + 1], matrix_g[shift_out + k + 2], 0); weight = (float4)(matrix_w[shift_w + k * (inputs + 1) + i], matrix_w[shift_w + (k + 1) * (inputs + 1) + i], matrix_w[shift_w + (k + 2) * (inputs + 1) + i], 0); break; default: grad = (float4)(matrix_g[shift_out + k], matrix_g[shift_out + k + 1], matrix_g[shift_out + k + 2], matrix_g[shift_out + k + 3]); weight = (float4)(matrix_w[shift_w + k * (inputs + 1) + i], matrix_w[shift_w + (k + 1) * (inputs + 1) + i], matrix_w[shift_w + (k + 2) * (inputs + 1) + i], matrix_w[shift_w + (k + 3) * (inputs + 1) + i]); break; } sum += dot(grad, weight); } if(isnan(sum)) sum = 0; switch(activation) { case 0: out = clamp(out, -1.0f, 1.0f); sum = clamp(sum + out, -1.0f, 1.0f) - out; sum = sum * max(1 - pow(out, 2), 1.0e-4f); break; case 1: out = clamp(out, 0.0f, 1.0f); sum = clamp(sum + out, 0.0f, 1.0f) - out; sum = sum * max(out * (1 - out), 1.0e-4f); break; case 2: if(out < 0) sum *= 0.01f; break; default: break; } matrix_ig[shift_in + i] = sum; }
Далее нам предстоит модифицировать кернел обновления матрицы весов UpdateWeightsAdamMultiModels. Как и в кернеле распределения градиентов ошибки, к уже имеющимся параметрам кернела базового полносвязного слоя мы добавим идентификатор модели.
Надо сказать, что аналогичный кернел базового нейронного слоя уже запускается в двух-мерном пространстве задач. Но в то же время, нам нет необходимости выполнять какие-либо операции с необновляемыми моделями. Поэтому и вызывать кернел мы будем только для одной модели, а параметр идентификатора модели мы будем использовать для определения смещения в буферах данных. В остальном алгоритм кернела остался без изменений. Вы можете самостоятельно ознакомиться с ним во вложении.
На этом мы завершаем работу на стороне OpenCL программы и переходим к работе с кодом нашей MQL5 библиотеки. Здесь мы создадим новый класс CNeuronMultiModel наследником нашего базового класса CNeuronBaseOCL.
Набор методов класса довольно стандартный и включает методы инициализации класса, работы с файлами, прямого и обратного прохода. Также мы вводим две новые переменные, в которые будем записывать количество моделей в ансамбле и идентификатор модели к обучению. Последний будет меняться при каждом обратном проходе.
class CNeuronMultiModel : public CNeuronBaseOCL { protected: int iModels; int iUpdateModel; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronMultiModel(void){}; ~CNeuronMultiModel(void){}; virtual bool Init(uint numInputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, ENUM_OPTIMIZATION optimization_type, int models); virtual void SetActivationFunction(ENUM_ACTIVATION value) { activation = value; } //--- virtual bool calcHiddenGradients(CNeuronBaseOCL *NeuronOCL); //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual int Type(void) const { return defNeuronMultiModels; } };
В классе мы не создаем новых внутренних объектов, поэтому конструктор и деструктор класса остаются пустыми. А нашу работу по созданию методов мы начнем с метода инициализации класса Init. В параметрах метод получает:
- numInputs — количество нейронов в предыдущем слое для одной модели
- open_cl — указатель на объект OpenCL
- numNeurons — количество нейронов в слое одной модели
- models — количество моделей в ансамбле.
bool CNeuronMultiModel::Init(uint numInputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, ENUM_OPTIMIZATION optimization_type, int models) { if(CheckPointer(open_cl) == POINTER_INVALID || numNeurons <= 0 || models <= 0) return false;
В теле метода мы сразу проверяем актуальность указателя на объект OpenCL и корректность указания размерности слоя и ансамбля. После чего мы сохраняем необходимые константы во внутренние переменные.
OpenCL = open_cl;
optimization = ADAM;
iBatch = 1;
iModels = models;
Здесь стоит обратить внимание, что был создан кернел обновления матрицы весов только методом Adam. Поэтому мы укажем этот метод оптимизации модели вне зависимости от полученного в параметрах.
После этого мы создаем буфера для записи результатов работы нейронного слоя и градиентов ошибки. Обратите внимание, что размеры всех буферов увеличиваются пропорционально количеству моделей в ансамбле. На начальном этапе буфера инициализируются нулевыми значениями.
//--- if(CheckPointer(Output) == POINTER_INVALID) { Output = new CBufferFloat(); if(CheckPointer(Output) == POINTER_INVALID) return false; } if(!Output.BufferInit(numNeurons * models, 0.0)) return false; if(!Output.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(Gradient) == POINTER_INVALID) { Gradient = new CBufferFloat(); if(CheckPointer(Gradient) == POINTER_INVALID) return false; } if(!Gradient.BufferInit((numNeurons + 1)*models, 0.0)) return false; if(!Gradient.BufferCreate(OpenCL)) return false;
Далее мы инициализируем случайными значениями буфер матрицы весов. Размер буфера должен быть достаточным для хранения весовых коэффициентов всех моделей ансамбля в рамках текущего нейронного слоя.
//--- if(CheckPointer(Weights) == POINTER_INVALID) { Weights = new CBufferFloat(); if(CheckPointer(Weights) == POINTER_INVALID) return false; } int count = (int)((numInputs + 1) * numNeurons * models); if(!Weights.Reserve(count)) return false; float k = (float)(1 / sqrt(numInputs + 1)); for(int i = 0; i < count; i++) { if(!Weights.Add((2 * GenerateWeight()*k - k)*WeightsMultiplier)) return false; } if(!Weights.BufferCreate(OpenCL)) return false;
Реализация метода оптимизации Adam требует создание двух буферов данных для записи 1 и 2 моментов. Размер указанных буферов аналогичен размеру матрицы весов. На начальном этапе инициализируем данные буферы нулевыми значениями.
//--- if(CheckPointer(DeltaWeights) != POINTER_INVALID) delete DeltaWeights; //--- if(CheckPointer(FirstMomentum) == POINTER_INVALID) { FirstMomentum = new CBufferFloat(); if(CheckPointer(FirstMomentum) == POINTER_INVALID) return false; } if(!FirstMomentum.BufferInit(count, 0)) return false; if(!FirstMomentum.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(SecondMomentum) == POINTER_INVALID) { SecondMomentum = new CBufferFloat(); if(CheckPointer(SecondMomentum) == POINTER_INVALID) return false; } if(!SecondMomentum.BufferInit(count, 0)) return false; if(!SecondMomentum.BufferCreate(OpenCL)) return false; //--- return true; }
Не забываем на каждом этапе контролировать процесс выполнения операций. И после успешного завершения всех выше указанных операций завершаем работу метода.
После инициализации мы переходе к методу прямого прохода feedForward. В параметрах данный метод получает лишь указатель на объект предыдущего нейронного слоя. И в теле метода мы сразу проверяем актуальность полученного указателя.
bool CNeuronMultiModel::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(NeuronOCL) == POINTER_INVALID) return false;
Для выполнения всех операций прямого прохода, предусмотренных алгоритмом работы нейронного слоя, мы уже создали кернел в программе OpenCL. И сейчас нам предстоит передать необходимы данные в кернел и вызвать его выполнение.
Вначале мы определим пространство задач. Выше мы определились использовать двухмерное пространство задач. В первом измерении укажем количество нейронов на выходе одной модели, а во втором — количество таких моделей. При инициализации класса мы не сохраняли количество нейронов в слое одной модели. Поэтому сейчас для определения размерности первого измерения пространства задач мы разделим общее количество нейронов на выходе нашего слоя на количество моделей в ансамбле. Со вторым измерением проще. Здесь есть у нас отдельная переменная с количеством моделей в ансамбле.
uint global_work_offset[2] = {0, 0}; uint global_work_size[2]; global_work_size[0] = Output.Total() / iModels; global_work_size[1] = iModels;
После определения пространства задач передадим необходимые исходные данные в параметры кернела. При этом обязательно проверяем результат выполнения операций.
if(!OpenCL.SetArgumentBuffer(def_k_FFMultiModels, def_k_ff_matrix_w, getWeightsIndex())) { printf("Error of set parameter kernel FeedForward: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FFMultiModels, def_k_ff_matrix_i, NeuronOCL.getOutputIndex())) { printf("Error of set parameter kernel FeedForward: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FFMultiModels, def_k_ff_matrix_o, Output.GetIndex())) { printf("Error of set parameter kernel FeedForward: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FFMultiModels, def_k_ff_inputs, NeuronOCL.Neurons() / iModels)) { printf("Error of set parameter kernel FeedForward: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FFMultiModels, def_k_ff_activation, (int)activation)) { printf("Error of set parameter kernel FeedForward: %d; line %d", GetLastError(), __LINE__); return false; }
Обратите внимание, что для указания кернела мы используем вновь созданный идентификатор нашего нового кернела. А для указания параметров используются идентификаторы соответствующего кернела базового полносвязного слоя. Это возможно благодаря сохранению всех параметров кернела и их последовательности.
После передачи всех параметров нам остаётся лишь отправить кернел в очередь выполнения.
if(!OpenCL.Execute(def_k_FFMultiModels, 2, global_work_offset, global_work_size)) { printf("Error of execution kernel FeedForward: %d", GetLastError()); return false; } //--- return true; }
Проверяем корректность выполнения всех операций и завершаем работу метода.
Далее мы переходим к работе над методами обратного прохода. Первым рассмотрим метод распределения градиента ошибки calcHiddenGradients. Как и при прямом проходе, в параметрах метода мы получаем указатель на объект предыдущего нейронного слоя. И сразу, в теле метода, проверяем актуальность полученного указателя.
bool CNeuronMultiModel::calcHiddenGradients(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(NeuronOCL) == POINTER_INVALID) return false;
Следующим этапом определяем пространство задач. Здесь все аналогично методу прямого прохода.
uint global_work_offset[2] = {0, 0}; uint global_work_size[2]; global_work_size[0] = NeuronOCL.Neurons() / iModels; global_work_size[1] = iModels;
И затем передаём исходные данные в параметры кернела.
if(!OpenCL.SetArgumentBuffer(def_k_HGMultiModels, def_k_chg_matrix_w, getWeightsIndex())) { printf("Error of set parameter kernel calcHiddenGradients: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HGMultiModels, def_k_chg_matrix_g, getGradientIndex())) { printf("Error of set parameter kernel calcHiddenGradients: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HGMultiModels, def_k_chg_matrix_o, NeuronOCL.getOutputIndex())) { printf("Error of set parameter kernel calcHiddenGradients: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HGMultiModels, def_k_chg_matrix_ig, NeuronOCL.getGradientIndex())) { printf("Error of set parameter kernel calcHiddenGradients: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_HGMultiModels, def_k_chg_outputs, Neurons() / iModels)) { printf("Error of set parameter kernel calcHiddenGradients: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_HGMultiModels, def_k_chg_activation, NeuronOCL.Activation())) { printf("Error of set parameter kernel calcHiddenGradients: %d; line %d", GetLastError(), __LINE__); return false; }
Как можно заметить, здесь довольно стандартный алгоритм организации работы кернела программы OpenCL, который мы уже не раз реализовывали. Но есть нюанс с передачей идентификатора модели для обучения. Нам предстоит выбрать случайный номер модели для обучения. Для этого мы воспользуемся генератором псевдослучайных чисел. Но при этом мы не должны забывать, что именно для этой модели мы должны на следующем этапе обновить матрицу весов. Поэтому полученный случайный идентификатор модели мы сохраним в ранее созданную переменную iUpdateModel. Ее значением мы сможем воспользоваться при обновлении матрицы весов.
iUpdateModel = (int)MathRound(MathRand() / 32767.0 * (iModels - 1)); if(!OpenCL.SetArgument(def_k_HGMultiModels, def_k_chg_model, iUpdateModel)) { printf("Error of set parameter kernel calcHiddenGradients: %d; line %d", GetLastError(), __LINE__); return false; }
После успешной передачи всех параметров отправляем кернел в очередь выполнения и завершаем работу метода.
if(!OpenCL.Execute(def_k_HGMultiModels, 2, global_work_offset, global_work_size)) { printf("Error of execution kernel CalcHiddenGradient: %d", GetLastError()); return false; } //--- return true; }
Алгоритм метода обновления матрицы весов полностью повторяет шаги подготовки и постановки кернела в очередь выполнения и не содержит "подводных камней". Поэтому позвольте не задерживаться на его описании. С его полным кодом можно ознакомиться во вложении.
Для работы с файлами используются методы Save и Load. Их алгоритм довольно прост. Дело в том, что в новом классе мы создаем лишь две переменные: количество моделей в ансамбле и идентификатор обучаемой модели. Только первая переменная содержит гиперпараметр, который нам предстоит сохранить. Процесс сохранения всех унаследованных объектов и переменных уже организован в методах родительского класса. Там же созданы все необходимые контроли. Поэтому для сохранения данных нам достаточно сначала вызвать аналогичный метод родительского класса, а затем сохранить значение лишь одного гиперпараметра.
bool CNeuronMultiModel::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false; if(FileWriteInteger(file_handle, iModels) <= 0) return false; //--- return true; }
Аналогично организована работа по загрузке данных из файла.
На этом мы завершаем работу с кодом нового класса. С полным кодом всех его методов можно познакомиться во вложении.
Но перед его использованием нам необходимо совершить ещё ряд действий в коде нашей библиотеки. Прежде всего нам необходимо создать константы для идентификации кернелов и добавленных параметров.
#define def_k_FFMultiModels 46 ///< Index of the kernel of the multi-models neuron to calculate feed forward #define def_k_HGMultiModels 47 ///< Index of the kernel of the multi-models neuron to calculate hiden gradient #define def_k_chg_model 6 ///< Number of model to calculate #define def_k_UWMultiModels 48 ///< Index of the kernel of the multi-models neuron to update weights #define def_k_uwa_model 9 ///< Number of model to update
Затем добавляем:
- блок создания нового типа нейронного слоя в методе CNet::Create;
- новый тип слоя в метод CLayer::CreateElement;
- новый тип в диспетчерский метод прямого прохода базового класса нейронной сети;
- новый тип в диспетчерский метод обратного прохода CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject).
Мы построили класс для параллельной работы нескольких независимых полносвязных слоев, что позволяет нам создавать ансамбли моделей. Но это лишь одна часть, а не весь алгоритм исследования через несогласие. Для реализации полного алгоритма мы создадим новый класс моделей CEVD, по аналогии с модулем внутреннего любопытства. В структуре классов можно найти много общего. Это наблюдается в названии методов и переменных. Мы видим буфер воспроизведения опыта CReplayBuffer. Есть две внутренние модели cTargetNet и cForwardNet, но нет инверсной модели. И в качестве cForwardNet мы будем использовать ансамбль моделей. Различия, как всегда, в деталях.
//+------------------------------------------------------------------+ //| Exploration via Disagreement | //+------------------------------------------------------------------+ class CEVD : protected CNet { protected: uint iMinBufferSize; uint iStateEmbedingLayer; double dPrevBalance; bool bUseTargetNet; bool bTrainMode; //--- CNet cTargetNet; CReplayBuffer cReplay; CNet cForwardNet; virtual bool AddInputData(CArrayFloat *inputVals); public: CEVD(); CEVD(CArrayObj *Description, CArrayObj *Forward); bool Create(CArrayObj *Description, CArrayObj *Forward); ~CEVD(); int feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true); bool backProp(int batch, float discount = 0.999f); int getAction(int state_size = 0); float getRecentAverageError() { return recentAverageError; } bool Save(string file_name, bool common = true); bool Save(string dqn, string forward, bool common = true); virtual bool Load(string file_name, bool common = true); bool Load(string dqn, string forward, uint state_layer, bool common = true); //--- virtual int Type(void) const { return defEVD; } virtual bool TrainMode(bool flag) { bTrainMode = flag; return (CNet::TrainMode(flag) && cForwardNet.TrainMode(flag));} virtual bool GetLayerOutput(uint layer, CBufferFloat *&result) { return CNet::GetLayerOutput(layer, result); } //--- virtual void SetStateEmbedingLayer(uint layer) { iStateEmbedingLayer = layer; } virtual void SetBufferSize(uint min, uint max); };
Мы добавляем переменную bTrainMode, чтобы разделить алгоритм на процесс эксплуатации и обучения. Добавляем флаг bUseTargetNet, так как отказались от постоянного обновления cTargetNet пред каждым пакетом обновления модели. Также мы внесли изменения в алгоритм методов. Но обо всем по порядку.
Методы прямого прохода и определения действия агента получили деление алгоритма на процессы эксплуатации и обучения. Это связано с тем, что в процессе обучения мы хотим заставить агента максимально исследовать окружающую среду. В процессе эксплуатации мы, наоборот, хотим исключить излишние риски и следовать только внутренней политике. Давайте посмотрим, как это реализовано.
В начале метод прямого прохода построен аналогично соответствующему методу блока внутреннего любопытства. В параметрах мы получаем исходное состояние системы. Дополняем его данными о состоянии счета и открытых позициях. И вызываем метод прямого прохода обучаемой модели.
int CEVD::feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true) { if(!AddInputData(inputVals)) return -1; //--- if(!CNet::feedForward(inputVals, window, tem)) return -1;
Но далее алгоритм выбора действия разделяется на 2 потока: обучения и эксплуатации. В режиме обучения мы считываем скрытое (сжатое) состояние окружающей среды из обучаемой модели и осуществляем прямой проход нашего ансамбля динамических моделей. Напомню, что в отличии от модуля внутреннего любопытства, мы смотрим прогноз состояния не для одного конкретного действия, а сразу для всего спектра возможных действий. И только после успешного прямого прохода Forward ансамбля мы вызываем метод определения оптимального действия. С данным методом мы познакомимся чуть позже.
int action = -1; if(bTrainMode) { CBufferFloat *state; //if(!GetLayerOutput(1, state)) // return -1; if(!GetLayerOutput(iStateEmbedingLayer, state)) return -1; if(!cForwardNet.feedForward(state, 1, false)) { delete state; return -1; } double balance = AccountInfoDouble(ACCOUNT_BALANCE); double reward = (dPrevBalance == 0 ? 0 : balance - dPrevBalance); dPrevBalance = balance; action = getAction(state.Total()); delete state; if(action < 0 || action > 3) return -1; if(!cReplay.AddState(inputVals, action, reward)) return -1; }
После успешного определения действия мы добавляем набор состояния в буфер воспроизведения опыта.
В режиме эксплуатации мы не совершаем лишних действий, а только определяем оптимальное действие на основании внутренней политики агента и завершаем работу метода.
else action = getAction(); //--- return action; }
Алгоритм метода определения оптимального действия также разделен на 2 ветки: обучения и эксплуатация.
int CEVD::getAction(int state_size = 0) { CBufferFloat *temp; //--- получаем результат обучаемой модели. CNet::getResults(temp); if(!temp) return -1;
В начале метода мы загружаем результат прямого прохода обучаемой модели. И далее, в случае обучения модели, мы корректируем данное значение на значение дисперсии прогнозов ансамбля динамических моделей по каждому возможному действию. Для этого мы выгружаем результат работы ансамбля сначала в вектор, а затем трансформируем вектор в матрицу. В полученной матрице каждая отдельная строка будет представлять прогнозное состояние системы для отдельного действия. Только в нашей матрице содержатся предсказания от всех моделей ансамбля. Для удобства обработки результатов мы разделим матрицу горизонтально на несколько равных матриц меньшего размера. Число таких матриц будет равно числу моделей в ансамбле. И каждая такая матрица будет иметь размерность строк раной спектру возможных действий нашего агента.
Теперь мы можем воспользоваться матричными операциями и сначала найти матрицу средних значений по каждому отдельному действию отдельного компонента состояния. А затем посчитать дисперсию отклонений прогнозных матриц от средней. Среднее значение дисперсии по каждому действию мы добавим к прогнозным значениям вознаграждения обучаемой модели. В этом месте можно использовать коэффициент для баланса исследования и эксплуатации. С целью максимального исследования окружающей среды можно использовать только дисперсию прогнозных значений, без ориентирования на ожидаемое вознаграждение. Таким образом мы стимулируем модель к максимальному изучению окружающей среды без воздействия на политику агента.
//--- в режиме обучения делаем поправку на "любопытство" if(bTrainMode && state_size > 0) { vector<float> model; matrix<float> forward; cForwardNet.getResults(model); forward.Init(1, model.Size()); forward.Row(model, 0); temp.GetData(model); //--- int actions = (int)model.Size(); forward.Reshape(forward.Cols() / state_size, state_size); matrix<float> ensemble[]; if(!forward.Hsplit(forward.Rows() / actions, ensemble)) return -1; matrix<float> means = ensemble[0]; int total = ArraySize(ensemble); for(int i = 1; i < total; i++) means += ensemble[i]; means = means / total; for(int i = 0; i < total; i++) ensemble[i] -= means; means = MathPow(ensemble[0], 2.0); for(int i = 1 ; i < total; i++) means += MathPow(ensemble[i], 2.0); model += means.Sum(1) / total; temp.AssignArray(model); }
В процессе эксплуатации модели мы не делаем никаких поправок, а определяем оптимальное действие по принципу максимизации ожидаемо награды.
//--- return temp.Argmax(); }
С полным кодом метода можно ознакомиться во вложении.
Стоит немного остановиться ещё на методе обратного прохода. Для исключения лишних итераций в процессе эксплуатации модели метод обратного прохода при отсутствии флага обучения модели сразу завершает свою работу. Это позволяет быстро переходить из режима обучения модели в тестовый режим без изменения кода советника.
bool CEVD::backProp(int batch, float discount = 0.999000f) { //--- if(cReplay.Total() < (int)iMinBufferSize || !bTrainMode) return true;
После прохождения блока контролей мы создаем необходимые локальные переменные.
//--- CBufferFloat *state1, *state2, *targetVals = new CBufferFloat(); vector<float> target, actions, st1, st2, result; matrix<float> forward; double reward; int action;
И после проведения подготовительной работы мы организовываем цикл обучения моделей в размере пакета, который был указан в параметрах метода.
//--- цикл обучения в размере batch for(int i = 0; i < batch; i++) { //--- получаем случайное состояние и реплай буфера if(!cReplay.GetRendomState(state1, action, reward, state2)) return false; //--- прямой проход обучаемой моделм ("текущее" состояие) if(!CNet::feedForward(state1, 1, false)) return false;
В теле цикла мы сначала получаем набор случайного состояния из буфера воспроизведения опыта и осуществляем прямой проход обучаемой модели с полученным состоянием.
getResults(target); //--- выгружаем эмбединг состояния if(!GetLayerOutput(iStateEmbedingLayer, state1)) return false; //--- прямой проход target net if(!cTargetNet.feedForward(state2, 1, false)) return false;
После выполнения прямого прохода обучаемой модели мы сохраняем полученный результат и скрытое состояние.
С помощью Target Net мы аналогичным способом получаем эмбединг последующего состояния системы.
//--- корректировка вознаграждения if(bUseTargetNet) { cTargetNet.getResults(targetVals); reward += discount * targetVals.Maximum(); } target[action] = (float)reward; if(!targetVals.AssignArray(target)) return false; //--- обратный проход обучаемой модели CNet::backProp(targetVals);
При необходимости мы корректируем внешнее вознаграждение системы на прогнозное значение Target Net и осуществляем обратный проход обучаемой модели.
На следующем этапе мы проводим обучение ансамбля моделей на полученных выше эмбедингах двух последующих состояний.
//--- прямой проход forward net - прогноз следующего состояния if(!cForwardNet.feedForward(state1, 1, false)) return false; //--- выгружаем эмбединг "будущего" состояния if(!cTargetNet.GetLayerOutput(iStateEmbedingLayer, state2)) return false;
Вначале мы осуществляем прямой проход ансамбля моделей с эмбедингом первого состояния.
Затем мы выгружаем результаты прямого прохода и на их базе подготавливаем целевые значения, путем замены вектора совершенного действия на эмбединг последующего состояния, полученного с помощью Target Net.
Для этого мы результаты прямого прохода ансамбля моделей переводим в матрицу с количеством столбцов равным эмбедингу состояния. Мы помним, что в матрице содержатся результаты всего ансамбля моделей. Поэтому организовываем цикл и заменяем прогнозное состояние на целевое для совершенного действия во всех моделях ансамбля.
//--- подготовка целей forward net cForwardNet.getResults(result); forward.Init(1, result.Size()); forward.Row(result, 0); forward.Reshape(result.Size() / state2.Total(), state2.Total()); int ensemble = (int)(forward.Rows() / target.Size()); //--- копируем целевое состояние в матрицу целей ансамбля state2.GetData(st2); for(int r = 0; r < ensemble; r++) forward.Row(st2, r * target.Size() + action);
На первый взгляд, замена целевого состояния во всех моделях идет в разрез с идеей обучения моделей ансамбля на разных данных. Но я напомню, что мы организовали случайный выбор модели в методе обратного прохода класса CNeuronMultiModel. И на данном этапе мы не знаем какая модель будет обучаться. Поэтому мы подготовим целевые значения для всех моделей. А выбор модели для обучения будет осуществлен позже.
//--- обратный проход foward net targetVals.AssignArray(forward); cForwardNet.backProp(targetVals); } //--- delete state1; delete state2; delete targetVals; //--- return true; }
В завершение итераций в теле цикла обучения мы осуществляем обратный проход ансамбля динамических Forward моделей с подготовленными данными. Следует обратить внимание, что при подготовке целевых значений мы изменили только целевые значения отдельного действия. Остальные мы оставили на уровне прогнозных значений. Это позволяет нам при осуществлении обратного прохода получить градиент ошибки только конкретного действия. По остальным направлениям мы ожидаем получить нулевую ошибку.
После успешного завершения итераций цикла мы удаляем ненужные объекты и завершаем работу метода.
Остальные методы класса построены аналогично соответствующим методам модуля внутреннего любопытства. С их полным кодом можно ознакомиться во вложении.
3. Тестирование
После создания необходимых классов и их методов мы переходим к тестированию проделанной работы. Для проверки работы функционала созданных классов мы создадим советник "EVDRL-learning.mq5". Как и ранее, советник мы создадим на основе советника из прошлой статьи. На этот раз мы не будем вносить изменения в архитектуру обучаемой модели. Вместо этого мы изменим класс используемой модели. Заменим модуль внутреннего любопытства на блок исследования через несогласие.
//+------------------------------------------------------------------+ //| Includes | //+------------------------------------------------------------------+ #include "EVD.mqh" ........... ........... ........... ........... //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CEVD StudyNet;
Таже мы внесем изменения в метод описания архитектуры моделей. Здесь мы удалим описание архитектуры инверсной модели и внесем правки в архитектуру Forward модели. На последней стоит немного остановиться. Ранее для форвард модели мы использовали перцептрон с одним скрытым слоем. Создадим подобную архитектуру для моделей ансамбля.
При решении задачи "в лоб" мы должны создать слой исходных данных с размером буфера достаточным для всех моделей и 2 последовательных слоя нашего нового класса ансамбля моделей CNeuronMultiModel. Но обратите внимание, что все модели ансамбля используют одно и тоже состояние системы. А значит, для обслуживания такого ансамбля нам необходимо каждый раз в слое исходных данных повторять столько раз один набор данных, сколько моделей будет в нашем ансамбле. На мой взгляд, это является неэффективным использованием памяти нашего OpenCL-контекста, несет дополнительные затраты времени на конкатенирование большого буфера исходных данных и вместе с тем увеличивает затраты времени на передачу большого объема данных из оперативной памяти устройства в память OpenCL-контекста.
Намного эффективнее было бы организовать обращение всех моделей к одному небольшому буферу данных, который содержит только одну копию состояния системы. Но мы не предусмотрели такой вариант при создании метода прямого прохода нашего класса CNeuronMultiModel.
Но давайте посмотрим на архитектуру нашего базового полносвязного нейронного слоя. В нем каждый нейрон имеет свой вектор весовых коэффициентов, независимый от других нейронов этого слоя. Практически это ансамбль независимых моделей размером в один нейрон. А значит, мы можем использовать один базовый полносвязный нейронный слой в качестве скрытого слоя для всех моделей нашего ансамбля. Нам лишь надо организовать нейронный слой достаточного размера, чтобы обеспечить все модели нашего ансамбля данными.
Таким образом, для нашего ансамбля Forward моделей мы создаем слой исходных данных в размере 100 элементов. Именно такой размер сжатого представления состояния системы мы получаем от основной модели. Напомню, что в данном случае мы не добавляем вектор действия, так как ожидаем получить от модели прогнозные состояния для всего спектра возможных действий.
Далее мы будем использовать ансамбль из 5 моделей. В качестве скрытого слоя мы создаем один полносвязный нейронный слой из 1000 элементов (по 200 нейронов на каждую модель).
И за ним следует наш новый слой ансамбля моделей. Здесь мы указываем следующее описание нейронного слоя:
- Тип нейронного слоя (descr.type) defNeuronMultiModels;
- Количество нейронов в одной модели (descr.count) 400 (по 100 элементов на описания состояния каждого из 4 возможных действий;
- Количество нейронов в предыдущем слоя для 1 модели (descr.window ) 200;
- Количество моделей в ансамбле (descr.step) 5;
- Функция активации (descr.activation) TANH (гиперболический тангенс, должна соответствовать функции активации слоя эмбединга в основной модели;
- Метод оптимизации (descr.optimization) ADAM (единственно возможный для данного типа нейронного слоя.)
bool CreateDescriptions(CArrayObj *Description, CArrayObj *Forward) { //--- ........... ........... //--- if(!Forward) { Forward = new CArrayObj(); if(!Forward) return false; } //--- Model ........... ........... ........... ........... //--- Forward Forward.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 100; descr.window = 0; descr.activation = None; descr.optimization = ADAM; if(!Forward.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 1000; descr.activation = TANH; descr.optimization = ADAM; if(!Forward.Add(descr)) { delete descr; return false; } //--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMultiModels; descr.count = 400; descr.window = 200; descr.step = 5; descr.activation = TANH; descr.optimization = ADAM; if(!Forward.Add(descr)) { delete descr; return false; } //--- return true; }
Обучение и тестирование модели мы проводили без изменения условий: пара EURUSD, таймфрейм H1, параметры индикаторов по умолчанию.
По результатам тестового обучения надо сказать, что обучения ансамбля моделей требует больше времени, чем обучения одной Forward модели. При этом можно наблюдать как вначале модель довольно хаотично совершает действия. В процессе обучения эта хаотичность снижается.
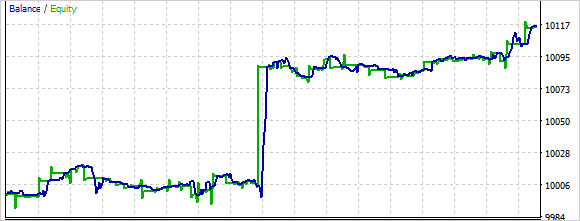
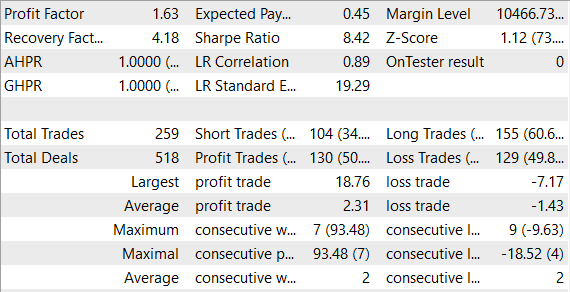
В целом, в процессе тестирования модель смогла получить прибыль.
Заключение
При обучении моделей с подкреплением изучение окружающей среды остается важной проблемой. В этой статье был представлен еще один подход к этой проблеме — исследование через несогласие. Агент обучается в режиме онлайн на данных, которые он собирает сам в процессе взаимодействия со средой, используя метод оптимизации политики. В то же время, после каждого взаимодействия агента со средой, ансамбль моделей обновляется, что позволяет агенту обновлять свою внутреннюю модель о среде на каждом шаге и получать более точные прогнозы о состояниях среды в будущем.
Была создана и протестирована модель на реальных данных в тестере стратегий MetaTrader 5. В результате тестирования моделью была получена прибыль. Что позволяет предположить о возможном потенциале развития данного направления. В то же время обучение и тестирование модели проводилось на довольно коротком временном отрезке. Для использования модели в реальной торговле потребуется дополнительное обучение модели на расширенных исторических данных.
Ссылки
- Self-Supervised Exploration via Disagreement
- Нейросети — это просто (Часть 35): Модуль внутреннего любопытства (Intrinsic Curiosity Module)
- Нейросети — это просто (Часть 36): Реляционные модели обучения с подкреплением (Relational Reinforcement Learning)
- Нейросети — это просто (Часть 37): Разреженное внимание (Sparse Attention)
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | EVDRL-learning.mq5 | Советник | Советник для обучения модели |
| 2 | EVD.mqh | Библиотека класса | Библиотека класса организации работы исследования через несогласия |
| 2 | ICM.mqh | Библиотека класса | Библиотека класса организации работы модуля внутреннего любопытства |
| 3 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 4 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL |
…
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
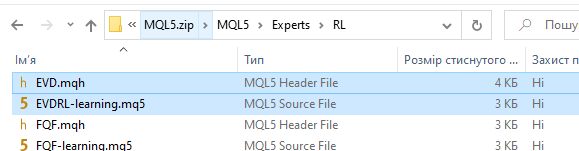
По вашей ссылке нет указанного советника!!! Там только старый из прошлой статьи. Я сперва думал, что вы просто название забыли изменить при копировании, а при сравнении обнаружил полное совпадение кода!!! КАРАУЛ!!!
В архиве внизу статьи приложена полный комплект файлов. Там есть советники из предыдущих статей. Но есть и указанный в статье советник.
Извините, еще один дилетантский вопрос. Советник не совершил ни одной сделки в тестере. На графике пока тоже просто висит без признаков активности. Почему?
И еще. Данные индикаторов используются только как дополнительный фильтр при совершении сделки?