Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
Noch sehr alt, aber ich denke, interessante Informationen über den Erhalt von Zecken vor der Verarbeitung.
https://www.mql5.com/ru/forum/102066/page9
Mit diesem Beitrag verneige ich mich vor den Mathematikern.
Betrachten Sie die Wahrscheinlichkeitsverteilungen der Zeitintervalle (in Sekunden) zwischen echten Tick-Kursen.
Für das Paar AUDCAD:
Für das Paar AUDCHF:
Ich wage zu behaupten, dass die Werte der Wahrscheinlichkeitsdichtefunktion (Spalte "Wahrscheinlichkeit") nahezu identisch sein werden, wenn die Anzahl der akzeptierten Ticks auf 1.000.000 steigt.
Hypothese - wir haben gerade die Zeitskala des Forex-Marktes vor uns. Die Arbeit (Daten empfangen, Berechnungen durchführen) muss auf dieser Zeitskala erfolgen, nicht auf der einheitlichen oder exponentiellen.
Bitte helfen Sie mir, die analytische Formel für die Wahrscheinlichkeitsdichtefunktion dieser Verteilung zu bestimmen! Und als Konsequenz - die Formel für den Generator von Zufallszahlen dieser Verteilung.
Herzliche Grüße,
Alexander_K
Die Verteilung der inkrementellen Geschwindigkeiten: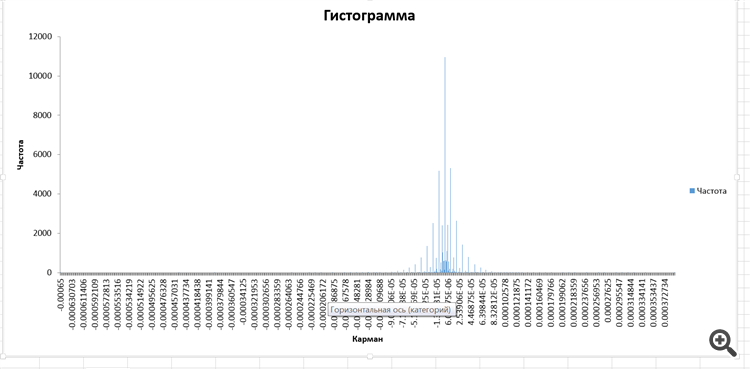
Ich habe keine Ahnung, was es ist. Aber, interessant.
Eine inkrementelle Geschwindigkeitsverteilung:
Ich habe keine Ahnung, was es ist. Aber, interessant.
Es sieht aus wie ein zweiseitiges Exponential mit Diskontinuitätsrauschen.
Laplace-Verteilung
...
Bitte helfen Sie mir, die analytische Formel für die Wahrscheinlichkeitsdichtefunktion dieser Verteilung zu bestimmen! Daraus ergibt sich die Formel für den Zufallszahlengenerator dieser Verteilung.
Herzliche Grüße,
Alexander_K
Simulation einer Zufallsvariablen mit vorgegebenem Verteilungsgesetz
Alexander, bitte senden Sie mir die Rohdaten, und ich werde versuchen, eine Verteilung zu finden.
Hallo Denis.
Auf Blatt 2 sind die Spalten zur besseren Übersichtlichkeit benannt.
Eine inkrementelle Geschwindigkeitsverteilung:
Ich habe keine Ahnung, was es ist. Aber, interessant.
Es sieht aus wie ein zweiseitiges Exponential mit Diskontinuitätsrauschen.
Laplace-Verteilung.
Nein, auf keinen Fall - es handelt sich weder um die Laplace-Verteilung noch um eine einseitige geometrische Verteilung.
Ich dachte, es wäre das hier:
mit der Formel:
aber es hat nicht gepasst...
Mit diesem Beitrag verneige ich mich vor den Mathematikern.
Betrachten Sie die Wahrscheinlichkeitsverteilungen der Zeitintervalle (in Sekunden) zwischen echten Tick-Kursen.
Für das Paar AUDCAD:
Für das Paar AUDCHF:
Ich wage zu behaupten, dass die Werte der Wahrscheinlichkeitsdichtefunktion (Spalte "Wahrscheinlichkeit") nahezu identisch sein werden, wenn die Anzahl der akzeptierten Ticks auf 1.000.000 steigt.
Hypothese - wir haben gerade die Zeitskala des Forex-Marktes vor uns. Die Arbeit (Daten empfangen, Berechnungen durchführen) muss auf dieser Zeitskala erfolgen und nicht auf der einheitlichen oder exponentiellen.
Bitte helfen Sie mir, die analytische Formel für die Wahrscheinlichkeitsdichtefunktion dieser Verteilung zu bestimmen! Und als Konsequenz - die Formel für den Generator von Zufallszahlen dieser Verteilung.
Herzliche Grüße,
Alexander_K
Es gibt eine Hypothese: "Nachts gibt es weniger Ticks und tagsüber mehr Ticks, so dass der Preis tagsüber mehr und nachts weniger in einer Minute zurücklegen kann", was zutrifft, wenn man davon ausgeht, dass der Preis immer ungefähr die gleiche Strecke pro Tick zurücklegt.
Am besten messen Sie die durchschnittliche Entfernung, die ein Kurs pro Tick zu verschiedenen Tageszeiten zurücklegt.