Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
>> OK. Hier sind die Daten.Wir scheinen uns missverstanden zu haben. Meine Meinung über Anomalien bezieht sich nicht auf den Generator, sondern auf den Markt. Konstruieren Sie eine Verteilung der ersten Inkremente und überzeugen Sie sich selbst.
Nun, für das kugelförmige Pferd im Vakuum, d. h. für eine garantierte Normalverteilung, ist es unwahrscheinlich. Nun, die echten sind keine Pferde in einem Vakuum. Es gibt 5 oder 6 oder sogar 10 S.C.E..
Onkel, bitte, hier ist noch ein Bild des Pfunds von 1971, die Tagebücher. Es mag einen einzelnen Ausfallschritt geben (und den gibt es übrigens nicht :), das Wichtigste ist, dass er nicht zu einem Muster wird. Oder?
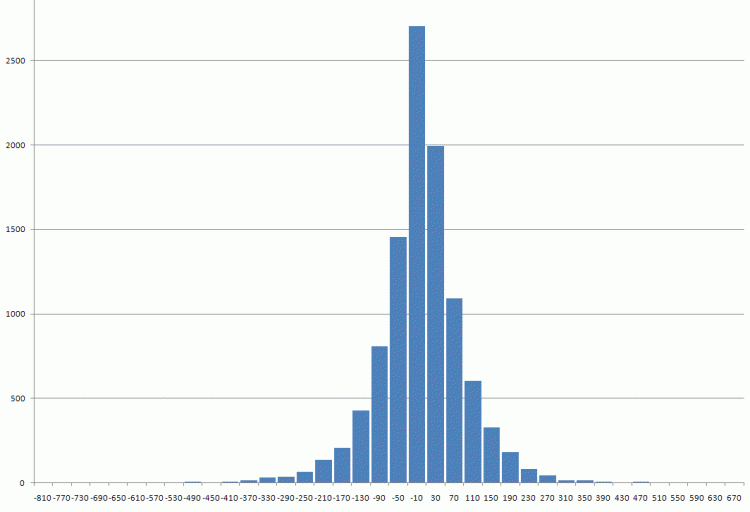
Daten zur Überprüfung sind beigefügt.Erste Pfunddifferenzen seit 1971.
>>S. Vielleicht sollte er auf Stationarität geprüft werden :)
Onkel, bitte, hier ist noch ein Bild des Pfunds von 1971, die Tagebücher. Es mag einen einzelnen Ausfallschritt geben (und den gibt es übrigens nicht :), das Wichtigste ist, dass er nicht zu einem Muster wird. Oder?
Die Daten für die Prüfung sind beigefügt.Die ersten Unterschiede im Pfund seit 1971
Ich würde es eine Laplace-Verteilung nennen.
Ich würde es die Laplace-Verteilung nach Augenmaß nennen
Der Schlüssel ist, dass es keine 5-6-10 Sigmas gibt. Ansonsten ja, aber Sie müssen es testen. Und doch könnte es in Ordnung sein.Ilja, hier ein Vorschlag: Nähen Sie diese Verteilung durch eine Normalverteilung an. Und dann sehen Sie, wie sehr sich das echte Histogramm und die Annäherung der Gaußschen Kurve voneinander unterscheiden. Beschränken Sie sich nicht auf drei Sigmas, sondern suchen Sie mindestens zehn.
Eine weitere triviale Prüfung: Berechnen Sie die ersten Momente dieser Verteilung und vergleichen Sie sie mit den Momenten der Normalverteilung.
Das Phänomen der "fat tails" in Finanzreihen ist seit langem bekannt. Was wollen Sie mir beweisen?
Ilja, hier ein Vorschlag: Nähen Sie diese Verteilung durch eine Normalverteilung an. Und dann sehen Sie, wie sehr sich das echte Histogramm und die Annäherung der Gaußschen Kurve voneinander unterscheiden. Beschränken Sie sich nicht auf drei Sigmas, sondern suchen Sie mindestens zehn.
Eine weitere triviale Prüfung: Berechnen Sie die ersten Momente dieser Verteilung und vergleichen Sie sie mit den Momenten der Normalverteilung.
Das Phänomen der "fat tails" in Finanzreihen ist seit langem bekannt. Was wollen Sie mir beweisen?
Die Rede war von 5-6-10 RMS. Ich kann kein Muster in ihrem Aussehen erkennen.
Der Schlüssel ist, dass es keine 5-6-10 Sigmas gibt. So wie es ist, ja, aber es muss getestet werden. Und doch könnte es normal sein.ist höchst unwahrscheinlich. Normalverteilungen findet man in der Regel in der Natur, wo eine "große" Zufallsvariable die Summe einer großen Anzahl von "kleinen" Zufallsvariablen ist, die auf eine bestimmte Weise (aber identisch) verteilt sind. Ein Paradebeispiel dafür ist die Brownsche Bewegung, der im nächsten Thema bereits so viele Seiten gewidmet wurden. Im Falle des Marktes ist das Gesetz der Preisbildung weit davon entfernt, denn um ein normales Gesetz zu erhalten, bedarf es einer sehr großen Anzahl von äußeren "Störungen", die der Hauptfaktor bei der Bildung der Verteilung sein müssen. Aber wir glauben doch nicht, dass die Preisbildung auf dem Markt Lärm ist, oder?
In einem Diagramm, rein visuell, werden Sie diese 5-6-10 nicht sehen.
Irgendwo hatte ich sogar eine Tabelle, die die Unterschiede aufzeigt. Nimmt man die ersten beiden Momente der Verteilung und betrachtet sie als Momente der Annäherung an die Normalverteilung, so lässt sich die Differenz der Häufigkeiten um 3, 4, 5 usw. Sigmas leicht berechnen.
Ich erinnere mich nicht an die genauen Zahlen, aber die Häufigkeit der realen 3-Sigma-Abweichung ist 3-4 mal höher als die Gaußsche (Gaußsche 0,3%, reale mehr als 1%). Die 4-Sigma-Abweichung tritt in der Realität etwa 15-mal häufiger auf als die Gaußsche Abweichung, bei 5-Sigma beträgt der Unterschied Dutzende, wenn nicht Hunderte Male. Und so weiter.
Solange Sie die Risiken nicht abschätzen, ist es Ihnen egal, ob es sich um eine Gaußsche Verteilung handelt oder nicht.
P.S. Übrigens scheint es so, als ob LTCM laut Taleb genau deshalb zusammengebrochen ist, weil die Risiken unterschätzt wurden. Eine Abweichung von 10 Sigma wurde als vernachlässigbar seltenes Ereignis betrachtet. Und genau das ist geschehen.
Ich erinnere mich nicht an die genauen Zahlen, aber die reale 3-Sigma-Abweichungshäufigkeit ist 3-4 mal so hoch wie die Gaußsche (Gaußsche 0,3%, reale mehr als 1%). Die 4-Sigma-Abweichung tritt in der Realität etwa 15-mal häufiger auf als die Gaußsche Abweichung, bei 5-Sigma-Abweichungen beträgt der Unterschied ein Dutzend Mal. Und so weiter.
...was wiederum ein Beweis für Laplace ist.
Solange Sie die Risiken nicht abschätzen, ist es Ihnen egal, ob es sich um eine Gaußsche Verteilung handelt oder nicht.
Können Sie mir bitte sagen, wie ich bei der Risikobewertung vorgehen soll?