Die praktische Anwendung von Korrelationen im Handel

Inhaltsverzeichnis

• Einführung
• Das Konzept der Korrelation
• Arten von Korrelationen
• Implementierung von Indikatoren
• Korrelationsbasiertes Handelssystem
• Testen des Handelssystems
• Ergebnisse
• Schlussfolgerungen

Einführung

Die Essenz des Handels ist mit der Notwendigkeit verbunden, zukünftige Marktentwicklungen vorherzusagen, und so hängt der potenzielle Gewinn stark von der Genauigkeit einer solchen Vorhersage ab. Zu Beginn meines Artikels Handelsideen basierend auf der Kursrichtung und der Bewegungsgeschwindigkeit habe ich folgende Idee beschrieben: Jede Bewegung ist durch ihre Richtung, Beschleunigung und Geschwindigkeit charakterisiert. Gleiches gilt für die Preisbewegung der Devisen und in anderen Märkten.

Jede Bewegung hat bestimmte Eigenschaften, die den Beginn der Bewegung, eine bestimmte Geschwindigkeit, Trägheit und Ende anzeigen. Erfolgreiche Handelsstrategien sind diejenigen, die den Beginn der Bewegung so schnell wie möglich erkennen und in den Markt eintreten sowie das Ende dieser Bewegung eindeutig identifizieren können. Dennoch kann keine Strategie die Ein- und Austrittspunkte mit absoluter Gewissheit bestimmen. Es geht hier um eine günstige Gelegenheiten und Wahrscheinlichkeiten. Daher werden wir in diesem Artikel eines der Instrumente der Wahrscheinlichkeitstheorie, die Korrelation, die im Rahmen der Finanzmärkte angewendet werden, betrachten.

Das Konzept der Korrelation

Die Korrelation ist eine statistische Beziehung zwischen zwei oder mehr Zufallsvariable (oder Mengen, die im akzeptablen Maß als zufällig angesehen werden können). Ändert sich eine oder ändern sich mehrere Variablen, führt das zu systematischen Änderungen der anderen gekoppelten Variablen. Das mathematische Maß für die Korrelation zweier Zufallsvariablen ist der Korrelationskoeffizient. Wenn die Änderung einer Zufallsvariablen nicht zu einer regelmäßigen Änderung der anderen Zufallsvariablen führt, sondern u.U. zu einer Änderung einer anderen statistischen Eigenschaft dieser Zufallsvariablen, wird eine solche Beziehung nicht als Korrelation betrachtet, obwohl sie statistisch sein könnte.

Die Werte des Korrelationskoeffizienten variiert von -1 bis +1. Je weiter der Korrelationswert von 0 entfernt ist, desto stärker ist die Abhängigkeit zwischen den untersuchten Variablen. Und wenn der Wert nach 1 tendiert, wird die Korrelation als positiv bezeichnet. Wenn der Wert nach -1 tendiert, nennt man die Korrelation negativ. Bei positiver Korrelation führt ein Anstieg einer der Variablen zu einem Anstieg der zweiten. Im Falle der negativen Korrelation führt das Fallen eines Wertes auch zum Fallen des zweiten Wertes.

Auf anderen Gebieten helfen Korrelationen, die Abhängigkeit einer Variablen von der zweiten Variablen basierend auf den verfügbaren Daten zu identifizieren. Wie kann eine Korrelation im Finanzmarkthandel helfen? 

Betrachten wir Abb.1 und die markierte Abwärtsbewegung.

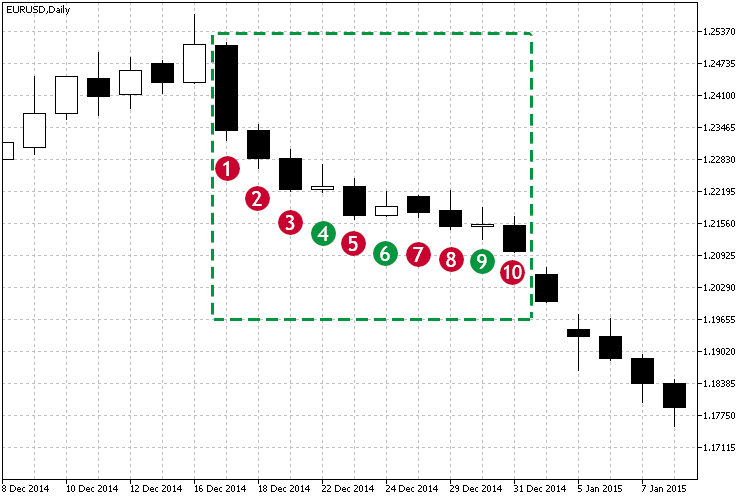
Abb.1 Beispiel eines Abwärtstrends.

Wie aus der markierten Zone ersichtlich ist, beginnend mit der Kerze #1, liegen die meisten Schlusskurse unter dem Eröffnungskurs, und jeder Schlusskurs liegt unter dem vorherigen. So sinkt der Preis. Visuell ist zu erkennen, dass es einen Abwärtstrend gibt. Aber wie können wir verstehen, ob die Abhängigkeit stark ist? Außerdem ist der Trend nicht perfekt: Es gab kleine Bewegungen der Kerzen 4, 6 und 9 sich nach oben zu bewegen. Wie kann hier eine Korrelation hilfreich sein? In diesem Fall gibt der Korrelationskoeffizient die Stärke der aktuellen Bewegung an. Basierend auf Beobachtungen der Korrelationskoeffizienten im Zeitverlauf können wir mehrere Schlussfolgerungen ziehen:

• Die Stärke des aktuellen Trends - direkt basierend auf dem aktuellen Wert der Korrelation.
• Die Dauer des Trends - basierend auf der Beobachtung des gewählten Schwellenwertes im Zeitverlauf. Zum Beispiel liegt der Schwellenwert über 0,75 und fällt nicht unter 3-4 Kerzen.

Arten von Korrelationen

Die folgenden Arten von Korrelationen helfen bei der Definition der Abhängigkeit zwischen den analysierten Variablen:

1. Linear und nichtlinear. Eine lineare Korrelation bezieht sich auf eine Abhängigkeit, bei der ein Wert steigt oder fällt und der zweite sich immer um denselben Faktor entsprechend ändert. Eine nichtlinearer Abhängigkeit führt die Änderung einer Variable nicht zu einer linearen Änderung in der anderen, sondern muss durch andere Funktionen beschrieben werden.
2. Positive und negative Korrelationen beziehen sich auf das Vorzeichen dieser Abhängigkeit. Im Falle einer positiven Korrelation führt das Wachstum in einer der Variablen zum Wachstum der anderen.

Abb.1 zeigt das Beispiel einer linearen Korrelation. Als nächstes betrachten wir verschiedene Arten von Berechnungen und Methoden zur Bestimmung der Interdependenz zweier Variablen.

Der Lineare Korrelationskoeffizient (Pearson-Korrelationskoeffizient)

Diese Berechnungsmethode ermöglicht es, die direkte Beziehung zwischen Variablen anhand ihrer absoluten Werte zu identifizieren. Die Berechnung ist so organisiert, dass, wenn die Beziehung zwischen den Variablen linear ist, der Pearson-Koeffizient genau das anzeigt. Im Kontext der Finanzmärkte würde diese Beziehung das Vorhandensein von Bewegungen in die eine oder andere Richtung in der Zeit bedeuten. Die Pearson-Korrelation wird nach der folgenden Formel berechnet:

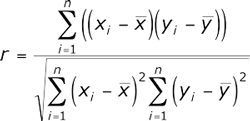
Berechnen wir nun den Pearson-Korrelationskoeffizienten für die in Abb.1 dargestellten Daten und die Abhängigkeit der Schlusskurse im Zeitverlauf messen. Dazu geben wir die Daten in die Tabelle ein:

Schlusskurs	Kerzennummer
1.23406	1
1.22856	2
1.22224	3
1.22285	4
1.21721	5
1.21891	6
1.21773	7
1.21500	8
1.21546	9
1.20995	10

Die ganze Berechnung zeigt das nächste Bild.

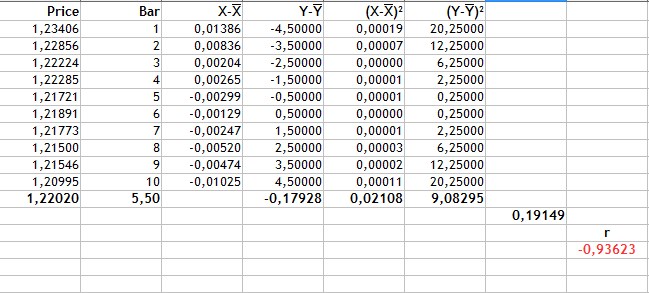
Abb.2 Berechnung des Korrelationskoeffizienten von Pearson.

Die Berechnung erfolgt in der folgenden Reihenfolge:

1. Zuerst werden die Durchschnittswerte des Preises und der Kerzen berechnet. Diese sind 1.22020 und 5.5.
2. Dann werden wir für jeden Variablentyp (Spalten 3-4) eine Abweichung vom Mittelwert berechnen. 
3. Der Wert von -0,17928 ist die Summe aus dem Produkt der Preisabweichungen und der Kerzennummer. Das ist der Zähler der Formel.
4. Die Spalten 5 und 6 sind die Quadrate der Abweichungen. Die Werte von 0.02108 und 9.08295 sind die Quadratwurzeln der Summe der quadrierten Abweichungen.
5. Der Nenner in der Formel oder das Produkt aus der Summe der quadrierten Abweichungen ist gleich 0,19149. 
6. Damit ist der Pearson-Korrelationskoeffizient -0,93623.

Diese Ergebnis zeigt, dass es eine starke lineare negative Abhängigkeit gibt.

Der Rang-Korrelationskoeffizient nach Spearman

Dieses Berechnungsverfahren ermöglicht die Bestimmung einer direkten linearen Beziehung zwischen Zufallsvariablen. Die Bewertung basiert nicht auf den Zahlenwerten der analysierten Elemente, sondern auf den entsprechenden Rängen. Auch seine Werte variieren von -1 bis 1. Der Absolutwert kennzeichnet die Nähe der Verbindung, während das Vorzeichen die Richtung dieser Verbindung zwischen den beiden Elementen angibt. Sie wird nach der folgenden Formel berechnet:

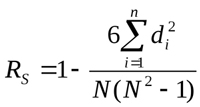
wobei di die Rangdifferenz im Beispiel ist. Betrachten wir ein Beispiel zur Berechnung der Rangkorrelation für die in Abb.1 dargestellten Daten und geben die Werte in eine neue Tabelle ein:

Schlusskurs	Kerzennummer	Rang des Schlusskurses	Rangnummer der Kerze
1.23406	1	10	1
1.22856	2	9	2
1.22224	3	7	3
1.22285	4	8	4
1.21721	5	4	5
1.21891	6	6	6
1.21773	7	5	7
1.21500	8	2	8
1.21546	9	3	9
1.20995	10	1	10

Wie aus der Tabelle ersichtlich, haben wir die Werte nach den Schlusskursen gereiht: Rang 1 hat dem niedrigsten Wert erhalten, und so weiter. Mit Hilfe der Formel berechnen wir die Differenz der D-Ränge der untersuchten Merkmale und verwenden die erhaltenen Werte in der Formel. 

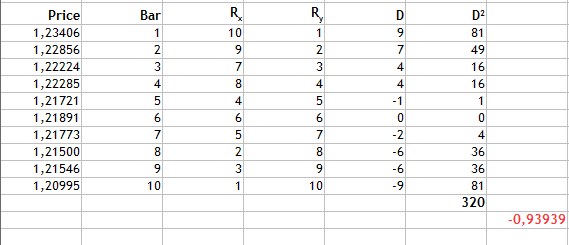
Abb.3 Berechnung des Rang-Korrelationskoeffizienten nach Spearmans.

Wie aus Abb.3 ersichtlich ist, finden wir die Differenz der Ränge, finden dann die Summe der quadrierten resultierenden Unterschiede und erhalten 320. Wir ersetzen die erhaltenen Werte durch die Formel und erhalten ein Ergebnis von -0.93939.

Basierend auf dem resultierenden Wert des Korrelationskoeffizienten können wir die gleiche Schlussfolgerung ziehen: eine starke lineare negative Bewegung. In diesem Fall ist die Nähe der Verbindung mit dem Pearson-Korrelationskoeffizienten vergleichbar. Allerdings ist folgendes zu beachten: Diese Berechnungsmethode hat einen Nachteil. Unvergleichbare Werte von Differenzen können den gleichen Werten von Rangdifferenzen entsprechen. So ist beispielsweise die Reihenfolge von Kerzen vergleichbar, während die Werte der Preisränge nicht einmal annähernd gleich sind, obwohl die Variation des Preises eher gering ist und sich um Tausendstel unterscheidet. Daher ist diese Berechnungsmethode in diesem Fall sinnvoll.

Rang-Korrelationskoeffizient nach Kendall

Wie der Koeffizient nach Spearman ist auch Kendalls Rang-Korrelationskoeffizient das Maß für die lineare Beziehung zwischen Zufallsvariablen. Die Werte der analysierten Elemente werden ähnlich geordnet, obwohl die Berechnungsmethode anders ist. Die folgende Formel zur Berechnung des Koeffizienten wird hier verwendet:

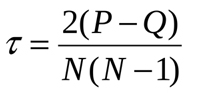
Wobei P die Summe der Übereinstimmungen ist und Q die Summe der Invertierungen. Um die Bedeutung zu verstehen, betrachten wir noch einmal das Beispiel in Abb.1. Zunächst sortieren wir die Tabellendaten wie folgt:

Schlusskurs	Kerzennummer	Rang des Schlusskurses	Rangnummer der Kerze
1.20995	10	1	10
1.21500	8	2	8
1.21546	9	3	9
1.21721	5	4	5
1.21773	7	5	7
1.21891	6	6	6
1.22224	3	7	3
1.22285	4	8	4
1.22856	2	9	2
1.23406	1	10	1

Die Tabelle wird also nach 'Rang des Schlusskurses' sortiert. Danach bestimmen wir die Anzahl der Ränge, die höher sind als die aktuelle, beginnend mit der ersten Zeile im Feld 'Rangnummer der Kerze'. Der erste Wert ist 10, also überprüfen wir es - es gibt keine Ränge über eins. Dann sehen wir 8 an und finde den höheren Rang 9. Und so weiter. Diese sind P passende Werte. 

Dann berechnen wir die niedrigeren Ränge. Für 10 gibt es 9 niedrigere Ränge, weil es der höchste ist. 8 wird sieben niedrigere Ränge haben — 5,7,6,6,3,4,2,1. Dies sind Q Invertierungen. Fügen wir den resultierenden Wert zu einer Tabelle hinzu und berechnen den Koeffizienten:

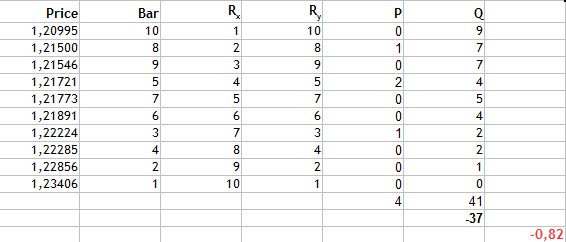
Abb.4 Berechnung des Kendall-Rangkorrelationskoeffizienten.

Dann fassen wir die resultierenden übereinstimmende Werte und Invertierungswerte zusammen. Ihre Differenz ist gleich -37. Durch Einfügen dieses Wertes in die Formel erhalten wir den Wert des Kendall-Koeffizienten: -0,82. Es ist wieder eine starke negative Korrelation. Das Ergebnis deutet jedoch darauf hin, dass diese Methode selektiver ist als die beiden vorherigen, da der Absolutwert kleiner ist.

Der Vorzeichenkorrelationskoeffizient nach Fechner

Diese Methode basiert auf der Bewertung des Konsistenzgrades in den Richtungen der Wertabweichungen vom Mittelwert und der Berechnung der den Werten entsprechenden Anzeichen von Abweichungen. Die Berechnungsformel ist sehr einfach:

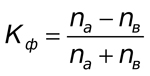
Hier ist Na die Anzahl der Übereinstimmungen nach dem Vorzeichen, Nb die Anzahl der Nichtübereinstimmungen. Nun berechnen wir den Korrelationskoeffizienten für unser Beispiel der Abb.1. 

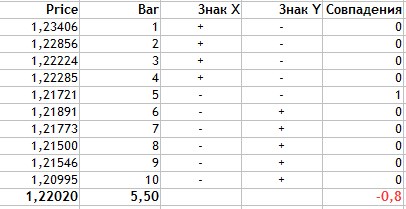
Abb.4 Berechnung des Korrelationskoeffizienten nach Fechner.

Die Berechnung wird wie folgt durchgeführt:

1. Es werden durchschnittliche Datenwerte für zwei Merkmale ermittelt. Dies ist 1.2202 für den Preis und 5.5 für die Kerzen.
2. In der Spalte Vorzeichen X setzen wir '+', wenn der aktuelle Preiswert größer als der Durchschnitt ist und '-', wenn der Preis unterdurchschnittlich ist.
3. Das Gleiche gilt für die Anzahl der Kerzen.
4. Dann müssen wir für die beiden Merkmale (Preis und Kerzen) die passenden Vorzeichen berechnen.
5. Wie aus der Tabelle ersichtlich ist, passten die Werte nur einmal und damit Na = 1, während Nb = 9.
6. Diese erhaltenen Werte werden in der Formel ersetzt.

Wie Sie sehen können, ist die Methode für den Korrelationskoeffizienten nach Fechner recht einfach. Das Ergebnis ist -0,8. Auch dies ist ein Hinweis auf eine stark negative Beziehung zwischen dem Schlusskurs und der Kerzenanzahl.

Implementierung von Indikatoren

Lassen Sie uns nun alle Methoden zur Korrelationsberechnung in der Sprache MQL5 implementieren. 

Korrelationskoeffizient nach Pearson

Da der Pearson-Koeffizient nach einer großen Formel berechnet wird, ist die Berechnung in zwei Stufen unterteilt, die Berechnung des Zählers und des Nenners.

//+------------------------------------------------------------------+
//| Berechnung des Zählers                                           |
//+------------------------------------------------------------------+
double Numerator(double &Ranks[],int N)
  {
//----
   double Y[],dx[],dy[],mx=0.0,my=0.0,sum=0.0,sm=0.0;
   ArrayResize(Y,N);
   ArrayResize(dx,N);
   ArrayResize(dy,N);

   int n=N;
   for(int i=0; i<N; i++)
     {
      Y[i]=n;
      n--;
     }

   mx=Average(Y);
   my=Average(Ranks);

   for(int j=0;j<N;j++)
     {
      dx[j]=Y[j]-mx;
      dy[j]=Ranks[j]-my;
      sm+=dx[j]*dy[j];
     }
   return sm;
  }
//+------------------------------------------------------------------+
//| Berechnung des Nenners                                           |
//+------------------------------------------------------------------+
double Denominator(double &Ranks[],int N)
  {
//----
   double Y[],dx2[],dy2[],mx=0.0,my=0.0,sum=0.0,smx2=0.0,smy2=0.0;
   ArrayResize(Y,N);
   ArrayResize(dx2,N);
   ArrayResize(dy2,N);

   int n=N;
   for(int i=0; i<N; i++)
     {
      Y[i]=n;
      n--;
     }

   mx=Average(Y);
   my=Average(Ranks);

   for(int j=0;j<N;j++)
     {
      dx2[j]=MathPow(Y[j]-mx,2);
      dy2[j]=MathPow(Ranks[j]-my,2);
      smx2+=dx2[j];
      smy2+=dy2[j];
     }
   return(MathSqrt(smx2*smy2));
  }

Die endgültige Logik und Methode der Berechnung für eine Darstellung als Indikator sieht wie folgt aus:

//+------------------------------------------------------------------+
//| Funktion des nutzerdefinierten Indikators                        |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,    // Anzahl der Bars in der Historie ab der aktuellen Bar
                const int prev_calculated,// Anzahl der bereits berechneten Bars
                const int begin,          // Index für den Array price[] für den Beginn
                const double &price[]
                )

  {
   if(rates_total<rangeN+begin)
      return(0);
   int limit;

   if(prev_calculated>rates_total || prev_calculated<=0)
     {
      limit=rates_total-2-rangeN-begin;
      if(begin>0)
         PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin);
     }
   else
      limit=rates_total-prev_calculated;

   ArraySetAsSeries(price,true);

   for(int i=0; i<=limit; i++)
     {
      for(int k=0; k<rangeN; k++)
         PriceInt[k]=price[k+i];
      ExtLineBuffer[i]=PearsonCalc(PriceInt,rangeN);
     }

   return(rates_total);
  }

//+------------------------------------------------------------------+
//| Berechnung des Korrelationskoeffizient nach Pearson              |
//+------------------------------------------------------------------+
double PearsonCalc(double &Ranks[],int N)
  {
   double ch,zn;
   ch=Numerator(Ranks,N);
   zn=Denominator(Ranks,N);
   return (ch/zn);
  }

Der Rang-Korrelationskoeffizient nach Spearman

Für einen Indikator auf Basis dieser Berechnungsmethode verwenden wir bereits existierenden Code von hier. 

//+------------------------------------------------------------------+
//| Funktion des nutzerdefinierten Indikators                        |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,    // Anzahl der Bars in der Historie ab der aktuellen Bar
                const int prev_calculated,// Anzahl der bereits berechneten Bars
                const int begin,          // Index für den Array price[] für den Beginn
                const double &price[]
                )

  {
   if(rates_total<rangeN+begin)
      return(0);
   int limit;

   if(prev_calculated>rates_total || prev_calculated<=0)
     {
      limit=rates_total-2-rangeN-begin;
      if(begin>0)
         PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin);
     }
   else
      limit=rates_total-prev_calculated;

   ArraySetAsSeries(price,true);

   for(int i=limit; i>=0; i--)
     {
      for(int k=0; k<rangeN; k++)
         PriceInt[k]=int(price[i+k]*multiply);

      RankPrices(TrueRanks,PriceInt);
      ExtLineBuffer[i]=SpearmanCalc(R2,rangeN);
     }

   return(rates_total);
  }
//+------------------------------------------------------------------+
//| Berechnung des Korrelationskoeffizient nach Spearman             |
//+------------------------------------------------------------------+
double SpearmanCalc(double &Ranks[],int N)
  {
//----
   double sumd2=0.0;

   for(int i=0; i<N; i++)
      sumd2+=MathPow(Ranks[i]-i-1,2);

   return(1-6*sumd2/(N*(MathPow(N,2)-1)));
  }

Rang-Korrelationskoeffizient nach Kendall

Für die Berechnung dieser Methode verwenden wir die internen Reserven von MQL5 selbst. Wir werden nämlich die integrierte, mathematische Statistik-Bibliothek verwenden.

//+------------------------------------------------------------------+
//| Funktion des nutzerdefinierten Indikators                        |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,    // Anzahl der Bars in der Historie ab der aktuellen Bar
                const int prev_calculated,// Anzahl der bereits berechneten Bars
                const int begin,          // Index für den Array price[] für den Beginn
                const double &price[]
                )

  {
   if(rates_total<rangeN+begin)
      return(0);
   int limit;

   if(prev_calculated>rates_total || prev_calculated<=0)
     {
      limit=rates_total-2-rangeN-begin;

      if(begin>0)
         PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin);
     }
   else
      limit=rates_total-prev_calculated;

   ArraySetAsSeries(price,true);

   for(int i=0; i<=limit; i++)
     {
      for(int k=0; k<rangeN; k++)
         PriceInt[k]=price[k+i];
      ExtLineBuffer[i]=KendallCalc(PriceInt,rangeN);
     }

   return(rates_total);
  }
//+------------------------------------------------------------------+
//| Berechnung des Korrelationskoeffizient nach Kendall              |
//+------------------------------------------------------------------+
double KendallCalc(double &Ranks[],int N)
  {
   double Y[],t;
   ArrayResize(Y,N);

   int n=N;
   for(int i=0; i<N; i++)
     {
      Y[i]=n;
      n--;
     }
   MathCorrelationKendall(Ranks,Y,t);
   return (t);
  }
//+------------------------------------------------------------------+

Der Vorzeichenkorrelationskoeffizient nach Fechner

Diese Methode basiert auf dem Ermitteln der übereinstimmenden Vorzeichen von Abweichungen vom Durchschnittswert. Dann werden die übereinstimmende Vorzeichen gezählt.

//+------------------------------------------------------------------+
//| Funktion des nutzerdefinierten Indikators                        |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,    // Anzahl der Bars in der Historie ab der aktuellen Bar
                const int prev_calculated,// Anzahl der bereits berechneten Bars
                const int begin,          // Index für den Array price[] für den Beginn
                const double &price[]
                )

  {
   if(rates_total<rangeN+begin)
      return(0);
   int limit;

   if(prev_calculated>rates_total || prev_calculated<=0)
     {
      limit=rates_total-2-rangeN-begin;
      if(begin>0)
         PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin);
     }
   else
      limit=rates_total-prev_calculated;

   ArraySetAsSeries(price,true);
   for(int i=0; i<=limit; i++)
     {
      for(int k=0; k<rangeN; k++)
         PriceInt[k]=price[k+i];
      ExtLineBuffer[i]=FechnerCalc(PriceInt,rangeN);
     }

   return(rates_total);
  }
//+------------------------------------------------------------------+
//| Berechnung des Korrelationskoeffizient nach Fechner              |
//+------------------------------------------------------------------+
double FechnerCalc(double &Ranks[],int N)
  {
   double Y[],res,mx,my,sum=0.0,markx[],marky[];
   double Na=0.0,Nb=0.0;
   ArrayResize(Y,N);
   ArrayResize(markx,N);
   ArrayResize(marky,N);

   int n=N;
   for(int i=0; i<N; i++)
     {
      Y[i]=n;
      n--;
     }

   mx=Average(Y);
   my=Average(Ranks);

   for(int j=0; j<N; j++)
     {
      markx[j]=(Y[j]>mx)?1:-1;
      marky[j]=(Ranks[j]>my)?1:-1;
      if(markx[j]==marky[j])
         Na++;
      else
         Nb++;
     }

   res=(Na-Nb)/(Na+Nb);
   return (res);
  }

Abbildung 6 zeigt alle vier Methoden zur Berechnung der Korrelation zwischen dem Schlusskursen der Kerzen und der Zeit. Für alle Indikatoren ist der Zeitraum von 10 eingestellt, so dass Sie die Funktionsweise unter ähnlichen Bedingungen beurteilen können.

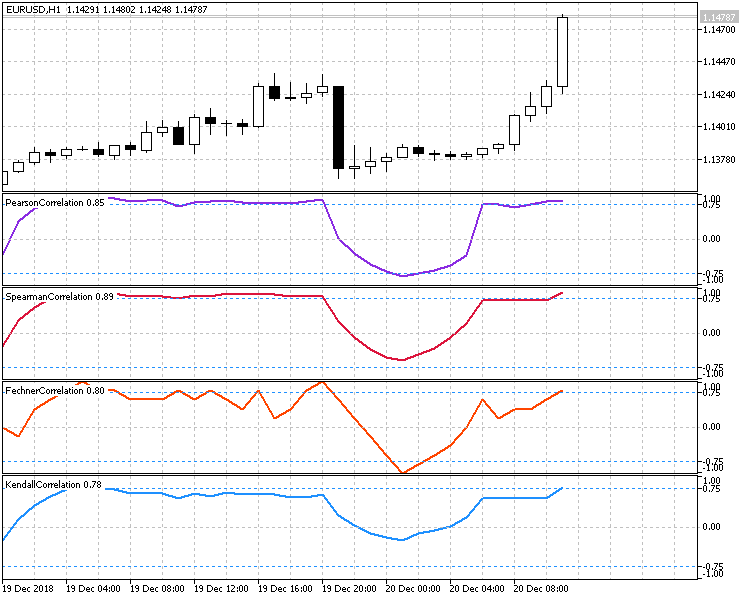
Abb.6 Vergleich der verschiedenen Berechnungsmethoden.

Korrelationsbasiertes Handelssystem

Bei der Erstellung einer auf Korrelationen basierenden Handelsstrategie sollten Sie die Indikatorspezifika und Berechnungsmethoden sorgfältig analysieren sowie mögliche Risiken und ungünstige Markteintrittsbedingungen identifizieren.

Die Verwendung großer Zeiträume wird wie für fast alle Indikatoren nicht empfohlen, da der Indikator die Ausführung verzögert. Sie könnten auch bei starken Trendwenden eine schwache Korrelationen aufweisen, da sie die Werte bereits abgeschlossener Gegenbewegungen berücksichtigen.

Da Indikatoren nicht den aktuellen Preis, sondern die Summe mehrerer Werte über einen Zeitraum analysieren, sollte der aktuelle Korrelationswert nicht als absolute Schätzung betrachtet werden. Die Korrelationsdynamik sollte analysiert werden. Dies kann mit Oszillatoren geschehen, die den aktuellen und den vorherigen Wert des Korrelationskoeffizienten verwenden.  

Daher wird unsere Strategie das Verhalten des Korrelationskoeffizienten-basierten Oszillators analysieren und nach einem Ausbruch aus vordefinierten Niveaus suchen. Die folgenden beiden Optionen sind möglich:

• Der Koeffizient fällt. Verkaufen, wenn der positive Koeffizient fällt und einen vordefinierten Schwellenwert durchbricht. Kaufen, wenn der negative Koeffizient steigt und den symmetrischen Schwellenwert durchbricht, der positive ist.
• Der Koeffizient steigt. Verkaufen, wenn der Koeffizient im negativen Bereich fällt und ein vordefinierten Schwellenwert durchbricht. Kaufen, wenn der Koeffizient steigt und ein symmetrischen, positiven Schwellenwert durchbricht.

Mögliche Einstiegspunkte werden in den folgenden Screenshots dargestellt.

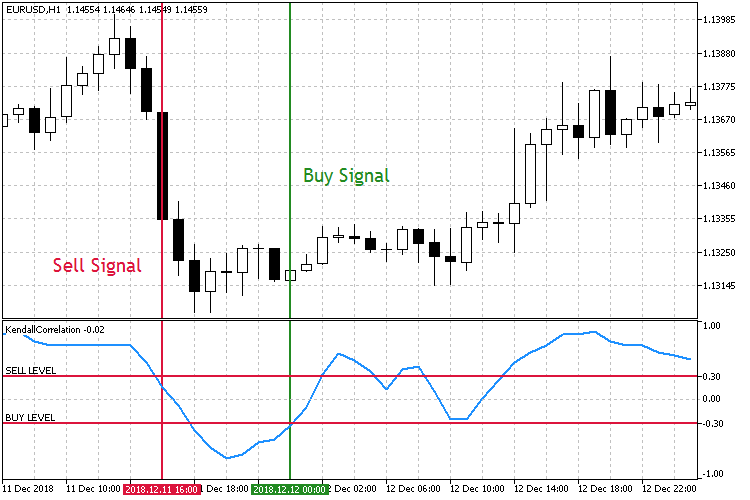
Abb.7 Den fallenden Korrelationskoeffizienten handeln.

Wie aus der Abbildung ersichtlich ist, gibt es zwei symmetrische Schwellenwerte für den Korrelationskoeffizienten: Sell Level 0.3 und Buy Level -0.3. Wenn der Verkaufswert nach unten gebrochen ist, verkaufen wir. Wir kaufen, wenn der Kaufwert nach oben durchbrochen wird.

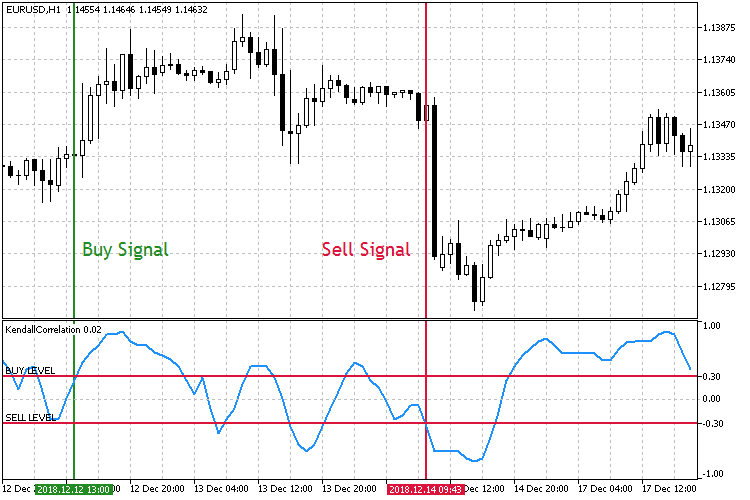
Abb.8 Den steigenden Korrelationskoeffizienten handeln.  

Im zweiten Handelsmodus in Abb. 8 sind die Schwellenwerte für die Positionseröffnungen umgekehrt. Diesmal, wenn das Kaufniveau nach oben durchbrochen ist, wird eine Kaufposition eröffnet. Eine Verkaufsorder wird eröffnet, wenn das Verkaufsniveau nach unten gebrochen ist. 

Für die Implementierung in einem Expert Advisor benötigen wir die oben genannten Strategien und die Wahl einer geeigneten Korrelationsberechnungsmethode.

//+------------------------------------------------------------------+
//| Enumeration der Berechnungsmodi                                  |
//+------------------------------------------------------------------+
enum Strategy_type
  {
   DECREASE = 1,           // Fallend       
   INCREASE                // Steigend
  };
//+------------------------------------------------------------------+
//| Enumeration der Berechnungsmethoden der Korrelationen            |
//+------------------------------------------------------------------+
enum Corr_method
  {
   PEARSON = 1,            //Pearson       
   SPEARMAN,               //Spearman
   KENDALL,                //Kendall
   FECHNER                 //Fechner
  };

Zusätzlich zu den EA-Parametern fügen wir folgende Eingaben hinzu: Auswahl der Berechnungsmethode, der Strategie, der Schlüsselebene und des einstellbaren Arbeitszeitraums.

//+------------------------------------------------------------------+
//| Expert Advisor Eingabeparameter                                  |
//+------------------------------------------------------------------+
input    string               Inp_EaComment="Correlation Strategy";        //EA Kommentar
input    double               Inp_Lot=0.01;                                //Lot
input    MarginMode           Inp_MMode=LOT;                               //MM

//--- Auswahl der Korrelationsberechnungsmethode und des Strategietyps
input    Corr_method          Inp_Corr_method=1;                           //Korrelationsmethode
input    Strategy_type        Inp_Strategy_type=1;                         //Strategietype

//--- EA Parameter
input    string               Inp_Str_label="===EA parameters===";         //Kennzeichnung
input    int                  Inp_MagicNum=1111;                           //Magicnummer
input    int                  Inp_StopLoss=40;                             //Stop-Loss(points)
input    int                  Inp_TakeProfit=60;                           //Take-Profit(points)
//--- Indicator parameters 
input    int                  Inp_RangeN=10;                               //Rangberechnung
input    double               Inp_KeyLevel=0.2;                            //Schwellenwert    
input    ENUM_TIMEFRAMES      Inp_Timeframe=PERIOD_CURRENT;                //Arbeitszeitrahmen

Die Korrektheit der Schwellenwerte wird bei der Initialisierung des EAs überprüft: Die Ebene muss zwischen 0 und 1 liegen, da für die Schwellenwerte ein Absolutwert verwendet werden.

//--- Überprüfung des Schwellenwertes
   if(Inp_KeyLevel>1 || Inp_KeyLevel<0)
     {
      Print(Inp_EaComment,": Incorrect key level!");
      return(INIT_FAILED);
     }

Definition der Berechnungsmethode gemäß dem Eingabeparameter:

//--- 
   switch(Inp_Corr_method)
     {
      case 1:
         ind_type="Correlation\\PearsonCorrelation";
         break;
      case 2:
         ind_type="Correlation\\SpearmanCorrelation";
         break;
      case 3:
         ind_type="Correlation\\KendallCorrelation";
         break;
      case 4:
         ind_type="Correlation\\FechnerCorrelation";
         break;
      default:
         break;
     }
//--- Erstzellen des Indikatorhandles 
   InpInd_Handle=iCustom(Symbol(),Inp_Timeframe,ind_type,Inp_RangeN);
   if(InpInd_Handle==INVALID_HANDLE)
     {
      Print(Inp_EaComment,": Fehler beim Erhalt des Indikatorhandles");
      Print("Handle = ",InpInd_Handle,"  error = ",GetLastError());
      return(INIT_FAILED);
     }

Danach können wir die Eröffnungsbedingungen festlegen:

//+------------------------------------------------------------------+
//| Experten Funktion OnTick                                         |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Datenabfrage für die Berechnung

   if(!GetIndValue())
      return;

   if(!Trade.IsOpenedByMagic(Inp_MagicNum))
     {
      //--- Eröffnen einer Position wegen eines Kaufsignals
      if(BuySignal())
         Trade.BuyPositionOpen(Symbol(),Inp_Lot,Inp_StopLoss,Inp_TakeProfit,Inp_MagicNum,Inp_EaComment);
      //--- Eröffnen einer Position wegen eines Verkaufssignals
      if(SellSignal())
         Trade.SellPositionOpen(Symbol(),Inp_Lot,Inp_StopLoss,Inp_TakeProfit,Inp_MagicNum,Inp_EaComment);
     }
  }
//+------------------------------------------------------------------+
//| Kaufbedingungen                                                  |
//+------------------------------------------------------------------+
bool BuySignal()
  {
   bool res=false;
   if(Inp_Strategy_type==1)
      res=(corr[1]>Inp_KeyLevel && corr[0]<Inp_KeyLevel)?true:false;
   else if(Inp_Strategy_type==2)
      res=(corr[0]>Inp_KeyLevel && corr[1]<Inp_KeyLevel)?true:false;
   return res;
  }
//+------------------------------------------------------------------+
//| Verkaufsbedingungen                                              |
//+------------------------------------------------------------------+
bool SellSignal()
  {
   bool res=false;
   if(Inp_Strategy_type==1)
      res=(corr[1]<-Inp_KeyLevel && corr[0]>-Inp_KeyLevel)?true:false;
   else if(Inp_Strategy_type==2)
      res=(corr[0]<-Inp_KeyLevel && corr[1]>-Inp_KeyLevel)?true:false;
   return res;
  }

Tests

Der Expert Advisor wir mit folgenden Parametern getestet:

• Zeitraum: für den Modus des Aufwärtstrends 01.01.2015 — 01.12.2018.
• Währungspaar EURUSD.
• Ausführung: Ohne Verzögerung. Dies sind keine hochfrequenten Handelsstrategien, so dass der Effekt von Verzögerungen sehr gering wäre.
  
• Test: 1 Minute OHLC. Vortests an realen Ticks zeigen fast die gleichen Ergebnisse. 
  
• Einlage: 1000 USD.
• Test: 1 Minute OHLC. Vortests mit realen Ticks zeigen fast die gleichen Ergebnisse.
• Server: MetaQuotes-Demo.
• Kurse: 5 Dezimalstellen.

Parameter für die Tests und Optimierung.

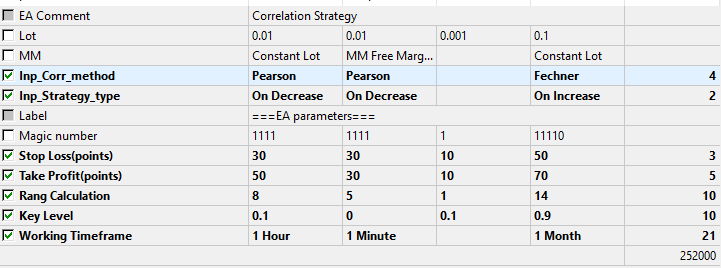
Abb.9 Die Optimierungsparameter.

Die Optimierung wird helfen, festzustellen, welche der Berechnungsmethoden und Strategiearten besser geeignet ist. Die Tests und die Optimierungen führten zu folgenden Ergebnissen.

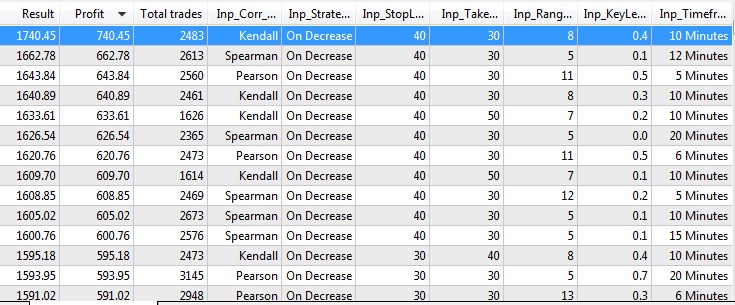
Abb.10 Test- und Optimierungsergebnisse.

Lassen Sie uns nun den EA mit den besten Optimierungsparametern testen.

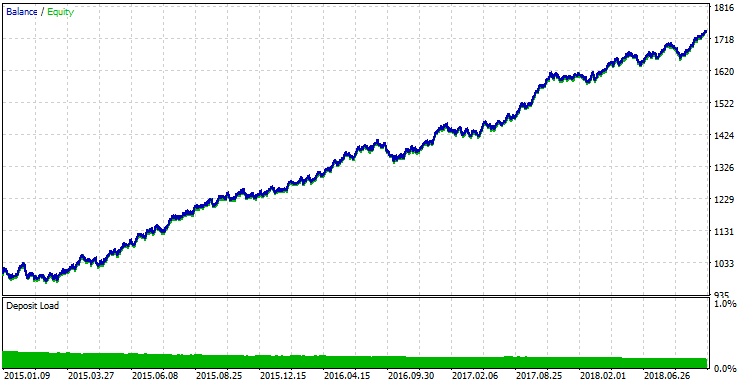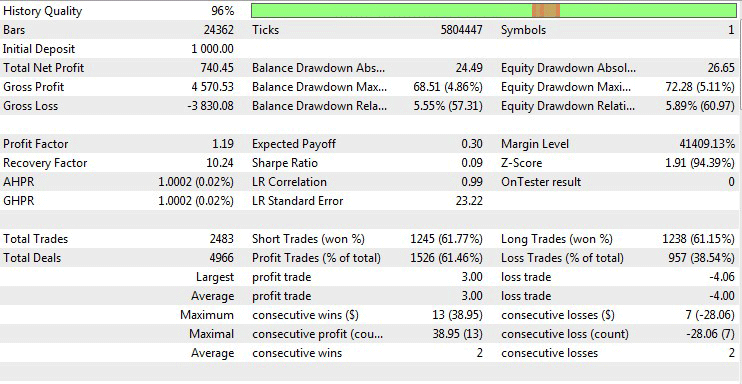
Abb.11 Testergebnis mit den besten Optimierungsparametern.

Ergebnisse

Basierend auf den erzielten Ergebnissen können wir folgende Schlüsse ziehen:

• Die besten Ergebnisse werden bei fallendem Korrelationskoeffizienten im Modus On Decrease erzielt. Dieses Ergebnis lässt sich nur dadurch erklären, dass der Oszillator bei fallendem Koeffizienten schneller auf Marktbewegungen reagiert. Wie bereits erwähnt, weisen Oszillatoren, die auf Korrelationskoeffizienten basieren (insbesondere solche mit großen Perioden), eine signifikante Verzögerung auf.
• Die einfachste Berechnungsmethode (Fechner-Koeffizient) findet sich nicht unter den Top 20 Ergebnissen. Das beste Ergebnis mit dieser Methode liegt nur auf Platz 99. 
• Die besten Ergebnisse wurden bei kleinen Zeitfenstern mit engem Take Profit und Stop Loss erzielt.
• Es wurden keine Abhängigkeiten der Gewinnsumme von der ausgewählten Periode und der Schlüsselstufe gefunden. Es herrschen jedoch kleinere Perioden vor und die untere Grenze des Optimierungsbereichs mit der Periode 5 wird ständig unter den besten Ergebnissen gefunden. Dies ist eine weitere Bestätigung dafür, dass korrelationsbasierte Indikatoren eine große Verzögerung und über einen längeren Zeitraum ein schlechteres Ergebnis erzielen.

Schlussfolgerungen

Das angehängte Archiv enthält alle besprochenen Dateien, die sich in den entsprechenden Ordnern befinden. Für den ordnungsgemäßen Betrieb müssen Sie lediglich den Ordner MQL5 in den Terminalverzeichnis speichern.

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Deklaration
1	Correlation.mq5	EA	Der Expert Advisor mit den 4 Berechnungsmethoden der Korrelationen und 2 Strategien, die darauf basieren.
2	Trade.mqh	Bibliothek	Eine Klasse mit den Handelsfunktionen
3	FechnerCorrelation.mq5	Indikator	Indikator des Korrelationskoeffizienten nach Fechner
4	KendallCorrelation.mq5	Indikator	Indikator des Korrelationskoeffizienten nach Kendall
5	PearsonCorrelation.mq5	Indikator	Indikator des Korrelationskoeffizienten nach Pearson
6	SpearmanCorrelation.mq5	Indikator	Indikator des Korrelationskoeffizienten nach Spearman