
Tiefe neuronale Netzwerke (Teil V). Bayes'sche Optimierung von DNN-Hyperparametern
Inhalt
- Einführung
- 1. Bestimmung der optimalen Hyperparameter des DNN (darch)
- Generierung der Quelldatensätze
- Entfernen von statistisch unbedeutenden Prädiktoren
- Bestimmung der zu optimierenden DNN-Hyperparameter und deren Wertebereiche
- Definition der Funktionen für das Pretraining und der Feinabstimmung für den DNN
- Definition der Fitnessfunktion zur Optimierung
- Berechnung der optimalen Parameter der DNN
- 2. Training und Test des DNN mit den optimalen Parametern
- 3. Analyse der Ergebnisse des DNN-Tests mit den optimalen Parametern
- 4. Weiterführende Tests der Modelle mit optimalen Parametern
- Schlussfolgerung
- Anwendung
Einführung
Der vorherige Artikel betrachtete ein Basismodell und das DNN-Modell mit Standardparametern. Die Klassifizierungsqualität dieses Modells erwies sich als unbefriedigend. Was kann getan werden, um die Qualität der Klassifizierung zu verbessern?
- Optimierung der DNN-Hyperparameter
- Verbesserung der DNN-Regulierung
- Erhöhung der Anzahl der Trainingsstichproben
- Ändern der Struktur des neuronalen Netzes
Alle aufgeführten Möglichkeiten zur Verbesserung der bestehenden DNN werden in diesem und den kommenden Artikeln berücksichtigt. Beginnen wir mit der Optimierung der Hyperparameter des Netzwerks.
1. Bestimmung der optimalen Hyperparameter der DNN
Im allgemeinen Fall lassen sich die Hyperparameter des neuronalen Netzes in zwei Gruppen einteilen: global und lokal (Knoten). Zu den globalen Hyperparametern gehören die Anzahl der verdeckten Schichten, die Anzahl der Neuronen in jeder Schicht, der Grad des Lernens, der Impuls, die Initialisierung der Neuronengewichte. Lokale Hyperparameter — Schichttyp, Aktivierungsfunktion, Dropout/Dropconnect und andere Regularisierungsparameter.
Die Struktur der Hyperparameter-Optimierung ist in der Abbildung dargestellt:
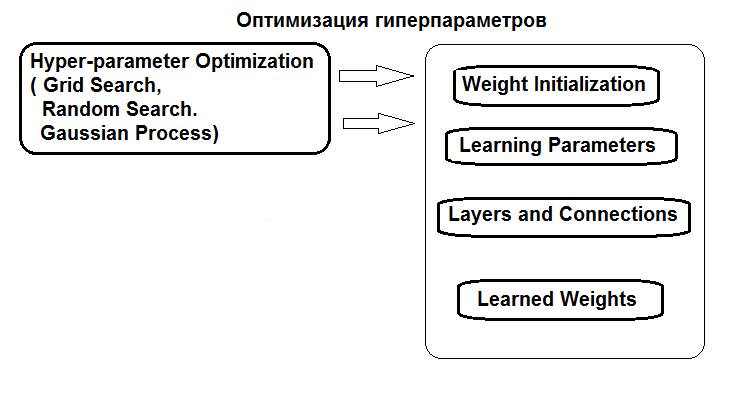
Abb. 1. Struktur der Hyperparameter des neuronalen Netzes und Optimierungsmethoden
Hyperparameter können auf drei Arten optimiert werden:
- Rastersuche: Für jeden Hyperparameter wird ein Vektor mit mehreren Festwerten definiert. Anschließend wird das Modell mit der Funktion caret::train() oder einem benutzerdefinierten Skript auf alle Kombinationen von Hyperparameterwerten trainiert. Danach wird das Modell mit den besten Werten für die Klassifizierungsqualität ausgewählt. Seine Parameter werden als optimal angesehen. Der Nachteil dieser Methode ist, dass die Definition eines Werterasters eher das Optimum verfehlt.
- Genetische Optimierung: stochastische Suche nach den besten Parametern mittels genetischer Algorithmen. Mehrere Algorithmen der genetischen Optimierung wurden ausführlich früher diskutiert. Sie werden daher nicht wiederholt.
- Und schließlich die Bayes'sche Optimierung. Sie wird in diesem Artikel verwendet werden.
Der Bayes'sche Ansatz beinhaltet Gaußsche Prozesse und MCMC. Es wird das Paket rBayesianOptimization (Version 1.1.0) verwendet. Die Theorie der angewandten Methoden ist in der Literatur weit verbreitet und wird z.B. in diesem Artikel beschrieben.
Um eine Bayes'sche Optimierung durchzuführen, ist es notwendig:
- Bestimmen der Fitnessfunktion;
- Bestimmen der Liste und der Grenzen der Änderungen in den Hyperparametern.
Die Fitnessfunktion (FF) sollte eine Qualitätskennzahl (Optimierungskriterium, Skalar) liefern, die während der Optimierung maximiert werden soll, und die vorhergesagten Werte der Zielfunktion. FF liefert den Wert von mean(F1) — dem Durchschnittswert von F1 für zwei Klassen. Das DNN-Modell wird mit Pretraining trainiert.
Generierung der Quelldatensätze
Für die Experimente wird die neue Version von MRO 3.4.2 verwendet. Es enthält mehrere neue Pakete, die bisher nicht verwendet wurden.
Starten wir RStudio, gehen dann zu GitHub/Part_I, um die Datei Cotir.RData mit Kursen des Terminals herunterzuladen, und holen zuletzt die Datei FunPrepareData.R mit Funktionen zu Datenaufbereitung von GitHub/Part_IV.
Bisher wurde festgestellt, dass ein Datensatz mit kalkulatorischen Ausreißern und normalisierten Daten bessere Ergebnisse im Training mit Pretraining ermöglicht. Wir könnten auch die anderen zuvor betrachteten Vorverarbeitungsmöglichkeiten testen.
Bei der Einteilung in Teilmengen für pretrain/train/val/test nutzen wir die erste Möglichkeit, die Klassifizierungsqualität zu verbessern — die Anzahl der Proben für das Training zu erhöhen. Die Anzahl der Stichproben in der Teilmenge pretrain wird auf 4000 erhöht.
#----Prepare------------- library(anytime) library(rowr) library(darch) library(rBayesianOptimization) library(foreach) library(magrittr) #source(file = "FunPrepareData.R") #source(file = "FUN_Optim.R") #---prepare---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt, 4000, 1000, 500, 100, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) preproc <- PreNorm(DTcap, meth = meth) DTcap.n <- NormData(DTcap, preproc = preproc) }, env)
Durch Ändern des Parameters start in der Funktion SplitData() ist es möglich, Sätze zu erhalten, die um den Betrag des Starts verschoben sind. Dies ermöglicht es, die Qualität in verschiedenen Teilen der Preisspanne in der Zukunft zu überprüfen und festzustellen, wie sie sich in der Geschichte verändert.
Entfernen von statistisch unbedeutenden Prädiktoren
Entfernen von zwei statistisch insignifikanten Variablen c(v.rstl, v.pcci). Sie wurden im vorherigen Artikel dieser Serie definiert.
##---Data DT-------------- require(foreach) evalq({ foreach(i = 1:4) %do% { DTcap.n[[i]] %>% dplyr::select(-c(v.rstl, v.pcci)) } -> DT list(pretrain = DT[[1]], train = DT[[2]], val = DT[[3]], test = DT[[4]]) -> DT }, env)
Erstellen von Datensätzen (pretrain/train/test/test1) für Pretraining, Feinabstimmung und dem Testen, erfasst in der Liste X.
#-----Data X------------------
evalq({
list(
pretrain = list(
x = DT$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$pretrain$Class %>% as.data.frame()
),
train = list(
x = DT$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$train$Class %>% as.data.frame()
),
test = list(
x = DT$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$val$Class %>% as.data.frame()
),
test1 = list(
x = DT$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$test$Class %>% as.vector()
)
) -> X
}, env)
Die Sätze für die Experimente sind fertig.
Eine Funktion wird benötigt, um die Metriken aus den Testergebnissen zu berechnen. Der Wert von mean(F1) wird als Optimierungskriterium (Maximierung) verwendet. Wir Laden diese Funktion in die env-Umgebung.
evalq( #input actual & predicted vectors or actual vs predicted confusion matrix # https://github.com/saidbleik/Evaluation/blob/master/eval.R Evaluate <- function(actual=NULL, predicted=NULL, cm=NULL){ if (is.null(cm)) { actual = actual[!is.na(actual)] predicted = predicted[!is.na(predicted)] f = factor(union(unique(actual), unique(predicted))) actual = factor(actual, levels = levels(f)) predicted = factor(predicted, levels = levels(f)) cm = as.matrix(table(Actual = actual, Predicted = predicted)) } n = sum(cm) # number of instances nc = nrow(cm) # number of classes diag = diag(cm) # number of correctly classified instances per class rowsums = apply(cm, 1, sum) # number of instances per class colsums = apply(cm, 2, sum) # number of predictions per class p = rowsums / n # distribution of instances over the classes q = colsums / n # distribution of instances over the predicted classes #accuracy accuracy = sum(diag) / n #per class recall = diag / rowsums precision = diag / colsums f1 = 2 * precision * recall / (precision + recall) #macro macroPrecision = mean(precision) macroRecall = mean(recall) macroF1 = mean(f1) #1-vs-all matrix oneVsAll = lapply(1:nc, function(i){ v = c(cm[i,i], rowsums[i] - cm[i,i], colsums[i] - cm[i,i], n - rowsums[i] - colsums[i] + cm[i,i]); return(matrix(v, nrow = 2, byrow = T))}) s = matrix(0, nrow = 2, ncol = 2) for (i in 1:nc) {s = s + oneVsAll[[i]]} #avg accuracy avgAccuracy = sum(diag(s))/sum(s) #micro microPrf = (diag(s) / apply(s,1, sum))[1]; #majority class mcIndex = which(rowsums == max(rowsums))[1] # majority-class index mcAccuracy = as.numeric(p[mcIndex]) mcRecall = 0*p; mcRecall[mcIndex] = 1 mcPrecision = 0*p; mcPrecision[mcIndex] = p[mcIndex] mcF1 = 0*p; mcF1[mcIndex] = 2 * mcPrecision[mcIndex] / (mcPrecision[mcIndex] + 1) #random accuracy expAccuracy = sum(p*q) #kappa kappa = (accuracy - expAccuracy) / (1 - expAccuracy) #random guess rgAccuracy = 1 / nc rgPrecision = p rgRecall = 0*p + 1 / nc rgF1 = 2 * p / (nc * p + 1) #rnd weighted rwgAccurcy = sum(p^2) rwgPrecision = p rwgRecall = p rwgF1 = p classNames = names(diag) if (is.null(classNames)) classNames = paste("C",(1:nc),sep = "") return(list( ConfusionMatrix = cm, Metrics = data.frame( Class = classNames, Accuracy = accuracy, Precision = precision, Recall = recall, F1 = f1, MacroAvgPrecision = macroPrecision, MacroAvgRecall = macroRecall, MacroAvgF1 = macroF1, AvgAccuracy = avgAccuracy, MicroAvgPrecision = microPrf, MicroAvgRecall = microPrf, MicroAvgF1 = microPrf, MajorityClassAccuracy = mcAccuracy, MajorityClassPrecision = mcPrecision, MajorityClassRecall = mcRecall, MajorityClassF1 = mcF1, Kappa = kappa, RandomGuessAccuracy = rgAccuracy, RandomGuessPrecision = rgPrecision, RandomGuessRecall = rgRecall, RandomGuessF1 = rgF1, RandomWeightedGuessAccurcy = rwgAccurcy, RandomWeightedGuessPrecision = rwgPrecision, RandomWeightedGuessRecall = rwgRecall, RandomWeightedGuessWeightedF1 = rwgF1))) }, env) #-------------------------
Die Funktion gibt eine Vielzahl von Metriken zurück, von denen momentan nur F1 notwendig ist.
Es wird ein neuronales Netzwerk mit zwei verdeckte Schichten verwendet, wie im vorherigen Teil des Artikels. DNN wird in zwei Stufen trainiert, mit Pretraining. Die möglichen Optionen sind:
- Pretraining:
- Trainieren nur von SRBM;
- Trainieren SRBM + die oberste Schicht des neuronalen Netzes.
- Feinabstimmung:
- Verwenden wir die Trainingsmethode backpropagation;
- Verwenden wir die Trainingsmethode rpropagation.
Jede der vier Trainingsoptionen hat einen anderen Satz von Hyperparametern zur Optimierung.
Definition der Hyperparameter für die Optimierung
Definieren wir die Liste der Hyperparameter mit den zu optimierenden Werten sowie deren Wertebereiche:
- n1, n2 — die Anzahl der Neuronen in jeder verdeckte Schicht Die Werte reichen von 1 bis 25. Vor der Zuführung zum Modell wird der Parameter mit 2 multipliziert, da er ein Vielfaches von 2 benötigt (poolSize). Dies ist notwendig für die Aktivierungsfunktion maxout.
- fact1, fact2 — Indizes der Aktivierungsfunktion für jede verdeckte Schicht, ausgewählt aus der Liste der Aktivierungsfunktionen, die durch den Vektor Fact <- c("tanhUnit", "maxoutUnit", "softplusUnit", "sigmoidUnit") definiert sind. Wir könnten auch weitere Funktionen hinzufügen.
- dr1, dr2 — der Dropout-Wert in jeder Schicht, Bereich von 0 bis 0,5.
- Lr.rbm — Level des StackedRBM-Trainings, Bereich von 0,01 bis 1,0 in der Pretraining-Phase.
- Lr.top — Trainingsniveau der obersten Schicht des neuronalen Netzes in der Vorschulungsphase, Bereich von 0,01 bis 1,0. Dieser Parameter ist nicht notwendig, um ein Pretraining durchzuführen, ohne die oberste Schicht des neuronalen Netzes zu trainieren.
- Lr.fine — Neuronales Netzwerk-Trainingsniveau in der Feinabstimmung bei Verwendung von Backpropagation, Bereich von 0,01 bis 1,0. Dieser Parameter ist bei Verwendung von rpropagation nicht erforderlich.
Eine detaillierte Beschreibung aller Parameter finden sich im vorherigen Artikel und in der Beschreibung des Pakets. Alle Parameter der Funktion darch() haben Standardwerte. Sie können in mehrere Gruppen eingeteilt werden.
- Globale Parameter. Wird sowohl zum Pretraining als auch zum Feinabstimmung eingesetzt.
- Die Parameter der Datenvorverarbeitung. Die Eigenschaften von caret::preProcess() werden verwendet.
- Parameter für SRBM. Wird nur für das Pretraining verwendet.
- Parameter von NN. Wird sowohl für das Pretraining als auch zur Feinabstimmung verwendet, kann aber für jede Stufe unterschiedliche Werte haben.
Die Standardwerte der Parameter können durch Angabe einer Liste ihrer neuen Werte oder durch explizites Schreiben in die Funktion darch() geändert werden. Hier eine kurze Beschreibung der zu optimierenden Hyperparameter.
Stellen wir zunächst die globalen Parameter von DNN ein, die für das Pretraining/Training üblich sind.
Ln <- c(0, 2*n1, 2*n2, 0) — Vektor, der angibt, dass ein 4-schichtiges, neuronales Netzwerk mit zwei verdeckten Schichten erzeugt werden soll. Die Anzahl der Neuronen in den Eingangs- und Ausgangsschichten wird aus den Eingangsdaten bestimmt, sie können nicht explizit angegeben werden. Die Anzahl der Neuronen in verdeckten Schichten beträgt 2*n1 bzw. 2*n2.
Definieren wir dann die Trainingsstufen für RBM (Lr.rbm), für die oberste Schicht von DNN beim Pretraining (Lr.top) und für alle Schichten bei der Feinabstimmung (Lr.fine).
fact1/fact2 — Indizes der Aktivierungsfunktion für jede verdeckte Schicht aus einer durch den Vektor Fact definierten Liste. Die Funktion softmax wird in der Ausgabeschicht verwendet.
dr1/dr2 — Dropout-Level in jeder ausgeblendeten Ebene.
darch.trainLayers — zeigt die zu trainierenden Schichten mit Pretraining und die zu trainierenden Schichten während der Feinabstimmung an.
Schreiben wir die Hyperparameter und deren Wertebereiche für jede der 4 Trainings-/Optimierungsoptionen. Zusätzlich werden die Parameter Bs.rbm = 100 (rbm.batchSize) und Bs.nn = 50 (darch.batchSize) extern gesetzt, um die besten Trainingsmöglichkeiten zu finden. Wenn sie verringert werden, verbessert sich die Klassifizierungsqualität, aber die Optimierungszeit erhöht sich erheblich.
#-2---------------------- evalq({ #--InitParams--------------------- Fact <- c("tanhUnit","maxoutUnit","softplusUnit", "sigmoidUnit") wUpd <- c("weightDecayWeightUpdate", "maxoutWeightUpdate", "weightDecayWeightUpdate", "weightDecayWeightUpdate") #---SRBM + RP---------------- bonds1 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0)#, ) #---SRBM + BP---------------- bonds2 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0), Lr.fine = c(0.01, 1.0) ) #---SRBM + upperLayer + BP---- bonds3 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0), Lr.top = c(0.01, 1.0), Lr.fine = c(0.01, 1.0) ) #---SRBM + upperLayer + RP----- bonds4 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0), Lr.top = c(0.01, 1.0) ) Bs.rbm <- 100L Bs.nn <- 50L },envir = env)
Definition der Funktion für das Pretraining und der Feinabstimmung
DNN wird mit allen vier Optionen trainiert. Alle dafür notwendigen Funktionen stehen im Skript FUN_Optim.R, das vor dem Start von Berechnungen mit Git/PartV heruntergeladen werden sollte.
Die Funktionen für das Pretraining und die Feinabstimmung für jede Option:
- pretrainSRBM(Ln, fact1, fact2, dr1, dr2, Lr.rbm) — Pretraining nur des SRBM
- pretrainSRBM_topLayer(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) — Pretraining SRBM + obere Schicht (Backpropagation)
- fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) — Feinabstimmung des DNN mittels rpropagation
- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) — Feinabstimmung des DNN mittels Backpropagation
Um den Artikel nicht mit der Auflistung ähnlicher Funktionen zu überladen, wird nur die Option mit Pretraining (SRBM + topLayer) + RP(Feinabstimmung rpropagation) berücksichtigt. In vielen Versuchen zeigte diese Option in den meisten Fällen das beste Ergebnis. Die Funktionen für andere Optionen sind ähnlich.
# SRBM + upper Layer (backpropagation) pretrainSRBM_topLayer <- function(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) # SRBM + upper Layer (backpropagation) { darch( x = X$pretrain$x, y = X$pretrain$y, xValid = X$train$x, yValid = X$train$y, #=====constant====================================== layers = Ln, paramsList = list(), darch = NULL, shuffleTrainData = T, seed = 54321, logLevel = "WARN", #FATAL, ERROR, WARN, DEBUG, and TRACE. #--optimization parameters---------------------------------- darch.unitFunction = c(Fact[fact1], Fact[fact2], "softmaxUnit"), darch.weightUpdateFunction = c(wUpd[fact1], wUpd[fact2], "weightDecayWeightUpdate"), rbm.learnRate = Lr.rbm, bp.learnRate = Lr.top, darch.dropout = c(0, dr1, dr2), #=== params RBM ============== rbm.numEpochs = 30L, rbm.allData = T, rbm.batchSize = Bs.rbm, rbm.consecutive = F, rbm.errorFunction = mseError, #rmseError rbm.finalMomentum = 0.9, rbm.initialMomentum = 0.5, rbm.momentumRampLength = 1, rbm.lastLayer = -1, rbm.learnRateScale = 1, rbm.numCD = 1L, rbm.unitFunction = tanhUnitRbm, rbm.updateFunction = rbmUpdate, rbm.weightDecay = 2e-04, #=== parameters NN ======================== darch.numEpochs = 30L, darch.batchSize = Bs.nn, darch.trainLayers = c(FALSE, FALSE,TRUE ), darch.fineTuneFunction = "backpropagation", #rpropagation bp.learnRateScale = 1, #0.99 #--weight----------------- generateWeightsFunction = generateWeightsGlorotUniform, # generateWeightsUniform (default), # generateWeightsGlorotUniform, # generateWeightsHeUniform. # generateWeightsNormal, # generateWeightsGlorotNormal, # generateWeightsHeNormal, darch.weightDecay = 2e-04, normalizeWeights = T, normalizeWeightsBound = 15, #--parameters regularization----------- darch.dither = F, darch.dropout.dropConnect = F, darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2L, darch.maxout.unitFunction = "exponentialLinearUnit", darch.elu.alpha = 2, darch.returnBestModel = T #darch.returnBestModel.validationErrorFactor = 0, ) }
In dieser Funktion werden die Werte des Datensatzes X$train zur Validierung verwendet.
Funktion zur Feinabstimmung mit rpropagation. Neben den Parametern wird dieser Funktion eine vortrainierte Struktur Dnn übergeben.
fineTuneRP <- function(Ln, fact1, fact2, dr1, dr2, Dnn) # rpropagation { darch( x = X$train$x, y = X$train$y, #xValid = X$test$x, yValid = X$test$y, xValid = X$test$x %>% head(250), yValid = X$test$y %>% head(250), #=====constant====================================== layers = Ln, paramsList = list(), darch = Dnn, shuffleTrainData = T, seed = 54321, logLevel = "WARN", #FATAL, ERROR, WARN, DEBUG, and TRACE. rbm.numEpochs = 0L, #--optimization parameters---------------------------------- darch.unitFunction = c(Fact[fact1], Fact[fact2], "softmaxUnit"), darch.weightUpdateFunction = c(wUpd[fact1], wUpd[fact2], "weightDecayWeightUpdate"), darch.dropout = c(0, dr1, dr2), #=== parameters NN ======================== darch.numEpochs = 50L, darch.batchSize = Bs.nn, darch.trainLayers = c(TRUE,TRUE, TRUE), darch.fineTuneFunction = "rpropagation", #"rpropagation" "backpropagation" #=== params RPROP ====== rprop.decFact = 0.5, rprop.incFact = 1.2, rprop.initDelta = 1/80, rprop.maxDelta = 50, rprop.method = "iRprop+", rprop.minDelta = 1e-06, #--weight----------------- darch.weightDecay = 2e-04, normalizeWeights = T, normalizeWeightsBound = 15, #--parameters regularization----------- darch.dither = F, darch.dropout.dropConnect = F, darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2L, darch.maxout.unitFunction = "exponentialLinearUnit", darch.elu.alpha = 2, darch.returnBestModel = T #darch.returnBestModel.validationErrorFactor = 0, ) }
Hier werden die ersten 250 Werte des X$test-Sets als Validierungsdaten verwendet. Alle Funktionen für alle Trainingsoptionen sollten in die env-Umgebung geladen werden.
Definition der Fitnessfunktion
Verwenden wir diese beiden Funktionen, um eine Fitnessfunktion zu schreiben, die für die Optimierung von Hyperparametern erforderlich ist. Er liefert den Wert des Optimierungskriteriums Score = mean(F1), das optimiert werden soll, und die vorhergesagten Werte der Zielfunktion Ypred.
#---SRBM + upperLayer + RP---- fitnes4.DNN <- function(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) { Ln <- c(0, 2*n1, 2*n2, 0) #-- pretrainSRBM_topLayer(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) -> Dnn fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) -> Dnn predict(Dnn, newdata = X$test$x %>% tail(250) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(250) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics$F1 %>% mean() return(list(Score = Score, Pred = Ypred) }
Bestimmung der optimalen Parameter für DNN
Die Optimierungsfunktion BayesianOptimization() wird mit 10 Anfangspunkten im Raum der zufällig erhaltenen Hyperparameter gestartet. Trotz der Tatsache, dass die Berechnung auf allen Prozessorkernen (Intel MKL) parallelisiert wird, dauert es immer noch sehr lange und hängt von der Anzahl der Iterationen und der Größe der 'Batchsize' ab. Um Zeit zu sparen, beginnen wir mit 10 Iterationen. Wenn die Ergebnisse in Zukunft nicht zufriedenstellend sind, kann die Optimierung fortgesetzt werden, indem die optimalen Werte des vorherigen Optimierungslaufs als Ausgangswerte verwendet werden.
Trainingsvariante SRBM + RP
#---SRBM + RP---------------- evalq( OPT_Res1 <- BayesianOptimization(fitnes1.DNN, bounds = bonds1, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env) Best Parameters Found: Round = 7 n1 = 22.0000 n2 = 2.0000 fact1 = 3.0000 fact2 = 2.0000 dr1 = 0.4114 dr2 = 0.4818 Lr.rbm = 0.7889 Value = 0.7531
Betrachten wir die erhaltenen Varianten der optimalen Parameter und F1 sehen. Die Funktion BayesianOptimization() gibt mehrere Werte zurück: die besten Parameterwerte Best_Par, den besten Wert des Optimierungskriteriums für diese optimalen Parameter — Best_Value, Optimierungshistorie — History und die erhaltenen Vorhersagen nach allen Iterationen — Pred. Sehen wir uns die Geschichte der Optimierung an, indem wir sie in absteigender Reihenfolge nach 'Wert' sortieren.
evalq({
OPT_Res1 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init1
best.init1
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Value
1 22 2 3 2 0.41136623 0.48175897 0.78886312 0.7531204
2 23 8 4 2 0.16814464 0.16221565 0.08381839 0.7485614
3 19 17 3 3 0.17274258 0.46809117 0.72698789 0.7485614
4 25 25 4 2 0.30039573 0.26894463 0.11226139 0.7473266
5 11 24 3 2 0.31564303 0.11091751 0.40387209 0.7462520
6 1 6 3 4 0.36876218 0.17403265 0.90387675 0.7450260
7 25 25 3 1 0.06872059 0.42459582 0.40072731 0.7447972
8 1 25 4 1 0.24871843 0.18593687 0.31920691 0.7445628
9 18 1 4 3 0.49846810 0.38517469 0.51115471 0.7423566
10 13 25 4 1 0.37052548 0.07603925 0.87100360 0.7402597
Das ist ein gutes Ergebnis. Führen wir noch einen weiteren Optimierungslauf durch, aber mit den Werten des vorherigen Laufs best_init1, um 10 Punkte im Raum der Hyperparameter zu initialisieren.
evalq( OPT_Res1.1 <- BayesianOptimization(fitnes1.DNN, bounds = bonds1, init_grid_dt = best.init1, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env) Best Parameters Found: Round = 1 n1 = 4.0000 n2 = 1.0000 fact1 = 1.0000 fact2 = 4.0000 dr1 = 0.1870 dr2 = 0.0000 Lr.rbm = 0.9728 Value = 0.7608
Schauen wir auf die 10 besten Werten.
evalq({
OPT_Res1.1 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init1
best.init1
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Value
1 4 1 1 4 0.18701522 2.220446e-16 0.9728164 0.7607811
2 3 24 1 4 0.12698982 1.024231e-01 0.5540933 0.7549180
3 5 5 1 3 0.07366640 2.630144e-01 0.2156837 0.7542661
4 1 18 1 4 0.41907554 4.641130e-02 0.6092082 0.7509800
5 1 23 1 4 0.25279461 1.365197e-01 0.2957633 0.7504026
6 4 25 4 1 0.09500347 3.083338e-01 0.2522729 0.7488496
7 17 3 3 3 0.36117416 3.162195e-01 0.4214501 0.7458489
8 13 4 3 3 0.22496776 1.481455e-01 0.4448280 0.7437376
9 21 24 1 3 0.36154287 1.335931e-01 0.6749752 0.7435897
10 5 11 3 3 0.29627244 3.425604e-01 0.1251956 0.7423566
Nicht nur das beste Ergebnis hat sich verbessert, sondern auch die Qualitätszusammensetzung der Top 10, die "Value"-Statistik ist gestiegen. Die Optimierung kann mehrmals wiederholt werden, indem verschiedene Ausgangspunkte ausgewählt werden (z.B. für die schlechtesten 10 Werte optimieren, usw.).
Für diese Trainingsvariante sind die folgenden Hyperparameter am besten geeignet:
> env$OPT_Res1.1$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm 4.0000 1.0000 1.0000 4.0000 0.1870 0.0000 0.9728
Interpretieren wir das. Die folgenden optimalen Parameter wurden ermittelt:
- die Anzahl der Neuronen der ersten verdeckten Schicht - 2*n1 = 8
- die Anzahl der Neuronen der zweiten verdeckten Schicht - 2*n2 = 2
- Aktivierungsfunktion der ersten verdeckten Schicht Fact[fact1] ="tanhdUnit".
- Aktivierungsfunktion der zweiten verdeckten Schicht Fact[fact2] = "sigmoidUnit".
- Dropout-Level der ersten verdeckten Schicht dr1 = 0,187
- Dropout-Level der zweiten verdeckten Schicht dr2 = 0.0
- Trainingsstand von SRBM bei der Vorbildung Lr.rbm = 0,9729
Neben einem allgemein guten Ergebnis wurde eine interessante Struktur DNN (10-8-2-2-2) gebildet.
Trainingsvariante SRBM + BP
#---SRBM + BP---------------- evalq( OPT_Res2 <- BayesianOptimization(fitnes2.DNN, bounds = bonds2, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env)
Schauen wir auf die 10 besten Ergebnisse.
> evalq({
+ OPT_Res2 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
+ dplyr::select(-Round) -> best.init2
+ best.init2
+ }, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.fine Value
1 23 24 2 1 0.45133494 0.14589979 0.89897498 0.2325569 0.7612619
2 3 24 4 3 0.07673542 0.42267387 0.59938522 0.4376796 0.7551184
3 15 13 4 1 0.32812018 0.45708556 0.09472489 0.8220925 0.7516732
4 7 18 3 1 0.15980725 0.12045896 0.82638047 0.2752569 0.7473167
5 7 23 3 3 0.37716019 0.23287775 0.61652190 0.9749432 0.7440724
6 21 23 3 1 0.22184400 0.08634275 0.08049532 0.3349808 0.7440647
7 23 8 3 4 0.26182910 0.11339229 0.31787446 0.9639373 0.7429621
8 5 2 1 1 0.25633998 0.27587931 0.17733507 0.4987357 0.7429471
9 1 24 1 2 0.12937722 0.22952235 0.19549144 0.6538553 0.7426660
10 18 8 4 1 0.44986721 0.28928018 0.12523905 0.2441150 0.7384895
Das Ergebnis ist gut, eine weitere Optimierung ist nicht von Nöten.
Die besten Hyperparameter dieser Variante:
> env$OPT_Res2$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.fine 23.0000 24.0000 2.0000 1.0000 0.4513 0.1459 0.8990 0.2326
Trainingsvariante SRBM + upperLayer + BP
#---SRBM + upperLayer + BP---- evalq( OPT_Res3 <- BayesianOptimization(fitnes3.DNN, bounds = bonds3, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env)Best Parameters Found: Round = 20 n1 = 24.0000 n2 = 5.0000 fact1 = 1.0000 fact2 = 2.0000 dr1 = 0.4060 dr2 = 0.2790 Lr.rbm = 0.9586 Lr.top = 0.8047 Lr.fine = 0.8687 Value = 0.7697
Schauen wir auf die 10 besten Ergebnisse.
evalq({
OPT_Res3 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init3
best.init3
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top Lr.fine Value
1 24 5 1 2 0.40597650 0.27897269 0.9585567 0.8046758 0.86871454 0.7696970
2 24 13 1 1 0.02456308 0.08652276 0.9807432 0.8033236 0.87293155 0.7603146
3 7 8 3 3 0.24115850 0.42538540 0.5970306 0.2897183 0.64518524 0.7543239
4 9 15 3 3 0.14951302 0.04013773 0.3734516 0.2499858 0.14993060 0.7521897
5 4 20 3 3 0.45660260 0.12858958 0.8280872 0.1998107 0.08997839 0.7505357
6 21 6 3 1 0.38742051 0.12644262 0.5145560 0.3599426 0.24159111 0.7403176
7 22 3 1 1 0.13356602 0.12940396 0.1188595 0.8979277 0.84890568 0.7369316
8 7 18 3 4 0.44786101 0.33788727 0.4302948 0.2660965 0.75709349 0.7357294
9 25 13 2 1 0.02456308 0.08652276 0.9908265 0.8065841 0.87293155 0.7353894
10 24 17 1 1 0.23273972 0.01572794 0.9193522 0.6654211 0.26861297 0.7346243
Das Ergebnis ist gut, eine weitere Optimierung ist nicht von Nöten.
Die besten Hyperparameter dieser Trainingsvariante:
> env$OPT_Res3$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top Lr.fine 24.0000 5.0000 1.0000 2.0000 0.4060 0.2790 0.9586 0.8047 0.8687
Variant of training SRBM + upperLayer + RP
#---SRBM + upperLayer + RP---- evalq( OPT_Res4 <- BayesianOptimization(fitnes4.DNN, bounds = bonds4, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env)Best Parameters Found: Round = 15 n1 = 23.0000 n2 = 7.0000 fact1 = 3.0000 fact2 = 1.0000 dr1 = 0.3482 dr2 = 0.4726 Lr.rbm = 0.0213 Lr.top = 0.5748 Value = 0.7625
Die besten 10 Varianten der Hyperparameter:
evalq({
OPT_Res4 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init4
best.init4
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top Value
1 23 7 3 1 0.34823851 0.4726219 0.02129964 0.57482890 0.7625131
2 24 13 3 1 0.38677878 0.1006743 0.72237324 0.42955366 0.7560023
3 1 1 4 3 0.17036760 0.1465872 0.40598393 0.06420964 0.7554773
4 23 7 3 1 0.34471936 0.4726219 0.02129964 0.57405944 0.7536946
5 19 16 3 3 0.25563914 0.1349885 0.83913339 0.77474220 0.7516732
6 8 12 3 1 0.23000115 0.2758919 0.54359416 0.46533472 0.7475112
7 10 8 3 1 0.23661048 0.4030048 0.15234740 0.27667214 0.7458489
8 6 19 1 2 0.18992796 0.4779443 0.98278107 0.84591090 0.7391758
9 11 10 1 2 0.47157135 0.2730922 0.86300945 0.80325083 0.7369316
10 18 21 2 1 0.05182149 0.3503253 0.55296502 0.86458533 0.7359324
Das Ergebnis ist gut, eine weitere Optimierung ist nicht von Nöten.
Nehmen wir die besten Hyperparameter dieser Trainingsvariante:
> env$OPT_Res4$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top 23.0000 7.0000 3.0000 1.0000 0.3482 0.4726 0.0213 0.5748
Training und Test des DNN mit den optimalen Parametern
Betrachten wir die Metriken, die wir durch das Testen der Varianten erhalten haben.
Variante SRBM + RP
Um den DNN mit den optimalen Parametern zu testen, erstellen wir uns eine spezielle Funktion. Es wird hier gezeigt, nur für diese Trainingsvariante. Bei anderen Varianten ist es ähnlich.
#---SRBM + RP---------------- test1.DNN <- function(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm) { Ln <- c(0, 2*n1, 2*n2, 0) #-- pretrainSRBM(Ln, fact1, fact2, dr1, dr2, Lr.rbm) -> Dnn fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(250) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(250) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) return(list(Score = Score, Pred = Ypred, Dnn = Dnn, Dnn.opt = Dnn.opt)) }
Die Parameter der Funktion test1.DNN() sind die zuvor ermittelten optimalen Hyperparameter. Führen wir anschließend ein Pretraining mit der Funktion pretrainSRBM() durch, wir erhalten eine vortrainierte DNN, die später der Funktion der Feinabstimmung fineTuneRP() zugeführt wird, was zu einer trainierten Dnn.opt führt. Mit diesem Dnn.opt und den letzten 250 Werten des Datensatzes X$test erhalten wir die vorhergesagten Werte der Zielfunktion Ypred. Mit Hilfe der vorhergesagten Ypred und den tatsächlichen Werten der Zielfunktion yTest können wir mit der Funktion Evaluate() eine Reihe von Metriken berechnen. Hier stehen Ihnen mehrere Optionen zur Auswahl von Metriken zur Verfügung. Als Ergebnis erzeugt die Funktion eine Liste der folgenden Objekte: Score — Testmetriken, Pred — vorhergesagte Werte der Zielfunktion, Dnn — vortrainierte DNN, Dnn.opt — voll trainierte DNN.
Testen und betrachten wir das Ergebnis mit Hyperparametern, die nach zusätzlicher Optimierung erhalten wurden:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res1.1$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Ln <- c(0, 2*n1, 2*n2, 0)
#---train/test--------
Res1 <- test1.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm)
}, env)
env$Res1$Score
Accuracy Precision Recall F1
-1 0.74 0.718 0.724 0.721
1 0.74 0.759 0.754 0.757
Das Ergebnis ist schlechter nach der ersten Optimierung, eine Überanpassung ist evident. Tests mit der initialen Werten der Hyperparameter:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res1$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Ln <- c(0, 2*n1, 2*n2, 0)
#---train/test--------
Res1 <- test1.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm)
}, env)
env$Res1$Score
Accuracy Precision Recall F1
-1 0.756 0.757 0.698 0.726
1 0.756 0.755 0.806 0.780
Das Ergebnis ist gut. Zeichnen wir eine Grafik des Trainingsablaufes:
plot(env$Res1$Dnn.opt, type = "class")
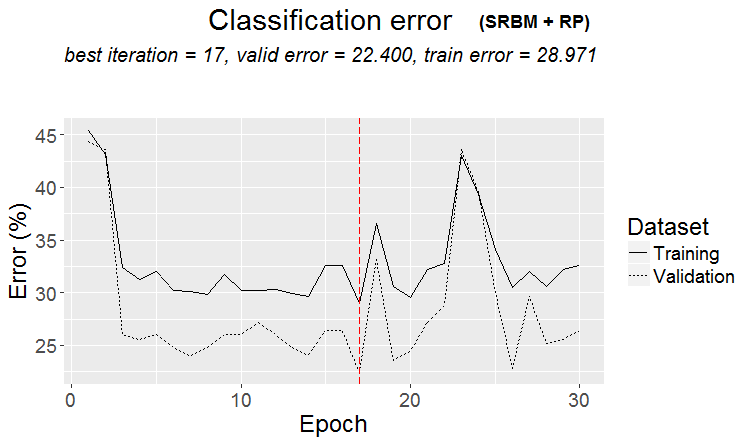
Abb. 2. Trainingsablauf von DNN mit der Variante SRBM + RP
Wie aus der Abbildung ersichtlich, ist der Fehler auf dem Validierungssatz geringer als der Fehler auf dem Trainingssatz. Das bedeutet, dass das Modell nicht überdimensioniert ist und eine gute Verallgemeinerungsfähigkeit besitzt. Die rote senkrechte Linie zeigt die Ergebnisse des Modells an, das als das beste gilt und nach dem Training als Ergebnis zurückgegeben wird.
Für die anderen drei Trainingsvarianten werden nur die Ergebnisse von Berechnungen und Verlaufsgrafik ohne weitere Angaben zur Verfügung gestellt. Alles wird ähnlich berechnet.
Variante SRBM + BP
Tests:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res2$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]; Lr.fine = best.par[8]
Ln <- c(0, 2*n1, 2*n2, 0)
#----train/test-------
Res2 <- test2.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine)
}, env)
env$Res2$Score
Accuracy Precision Recall F1
-1 0.768 0.815 0.647 0.721
1 0.768 0.741 0.873 0.801
Man könnte sagen, das Ergebnis ist exzellent. Schauen wir uns den Trainingsablauf an:
plot(env$Res2$Dnn.opt, type = "class")
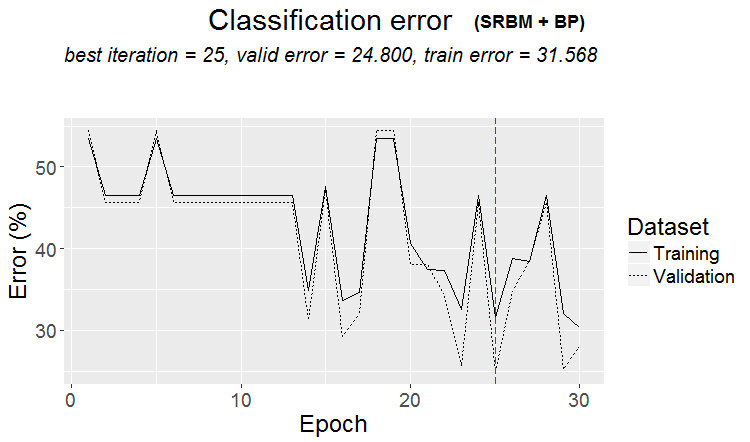
Abb. 3. Trainingsablauf von DNN mit der Variante SRBM + BP
Variante SRBM + upperLayer + BP
Tests:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res3$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Lr.top = best.par[8]
Lr.fine = best.par[9]
Ln <- c(0, 2*n1, 2*n2, 0)
#----train/test-------
Res3 <- test3.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top, Lr.fine)
}, env)
env$Res3$Score
Accuracy Precision Recall F1
-1 0.772 0.771 0.724 0.747
1 0.772 0.773 0.813 0.793
Exzellentes Ergebnis. zu bedenken ist, dass die Verwendung des Mittelwerts F1 als Optimierungskriterium zur gleichen Qualität für beide Klassen führt, trotz des Ungleichgewichts zwischen ihnen.
Grafik des Trainingsablaufes:
plot(env$Res3$Dnn.opt, type = "class")
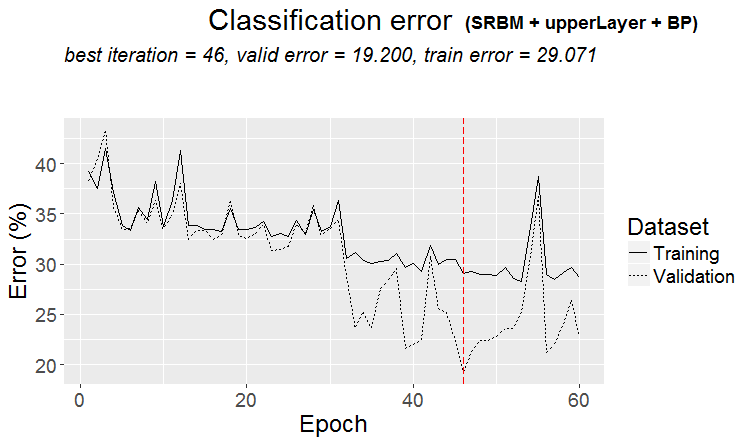
Abb. 4. Trainingsablauf von DNN mittels der Variante SRBM + upperLayer + BP
Variante SRBM + upperLayer + RP
Tests:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res4$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Lr.top = best.par[8]
Ln <- c(0, 2*n1, 2*n2, 0)
#----train/test-------
Res4 <- test4.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top)
}, env)
env$Res4$Score
Accuracy Precision Recall F1
-1 0.768 0.802 0.664 0.726
1 0.768 0.747 0.858 0.799
Ein sehr gutes Ergebnis. Schauen wir uns die Grafik des Trainingsablaufes an:
plot(env$Res4$Dnn.opt, type = "class")
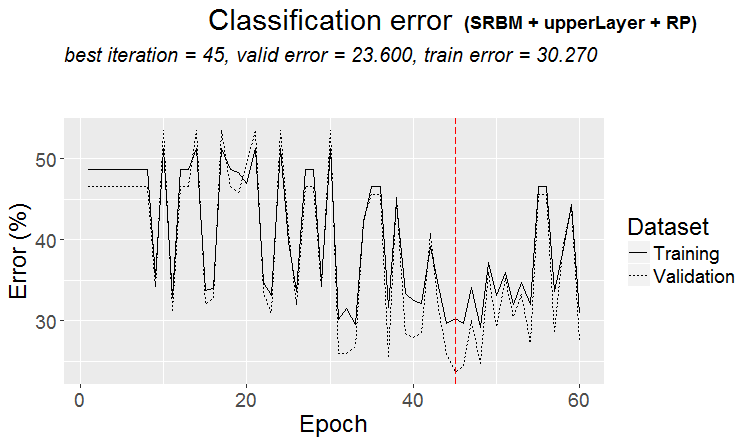
Abb. 5. Trainingsablauf von DNN mittels der Variante SRBM + upperLayer + RP
Analyse der Ergebnisse des DNN-Tests mit den optimalen Parametern
Die Ergebnisse des Trainings und Testens der DNN-Modelle, die von verschiedenen Varianten mit optimierten Hyperparametern trainiert wurden, liefern gute Ergebnisse mit einer Genauigkeit von 75 (+/-5)%. Der Klassifizierungsfehler von 25% ist stabil, hängt nicht von der Trainingsmethode ab und deutet darauf hin, dass die Struktur der Daten in einem Viertel der Fälle nicht mit der Struktur der Zielfunktion übereinstimmt. Das gleiche Ergebnis wurde bei der Untersuchung des Vorhandenseins von verrauschten Stichproben im Quelldatensatz beobachtet. Dort lag ihre Zahl ebenfalls bei etwa 25% und war nicht von den Methoden der Transformation der Prädiktoren abhängig. Das ist normal. Frage: Wie kann man die Vorhersage verbessern, ohne in die Falle der Überanpassung zu geraten? Es gibt mehrere Möglichkeiten:
- Mit einem Ensemble von neuronalen Netzen, bestehend aus den besten Modellen, die von 4 Varianten trainiert wurden;
- Verwendung von Ensembles neuronaler Netze, die aus 10 besten Modellen bestehen, die während der Optimierung durch jede Trainingsvariante erhalten werden;
- Benennen der verrauschten Daten in den Trainingsdaten mit einer zusätzlichen Klasse "0" und diese Zielfunktion (mit drei Klassen с("-1", "0", "1")) verwenden, um das DNN-Modell zu trainieren;
- Benennen der falsch klassifizierten Stichproben mit der zusätzlichen Klasse "0" und diese Zielfunktion (mit drei Klassen с("-1", "0", "1")) verwenden, um das DNN-Modell zu trainieren.
Das Erstellen, Trainieren und Verwenden der Ensembles werden im nächsten Artikel dieser Reihe ausführlich behandelt.
Das Experiment mit der Umbenennung des verrauschten Datensatzes verdient eine eigene Studie und geht über den Rahmen dieses Artikels hinaus. Die Idee ist einfach. Mit der Funktion ORBoostFilter::NoiseFiltersR, die im vorherigen Teil beschrieben wurde, werden die verrauschten Daten in den Trainings- und Validierungssätzen gleichzeitig ermittelt. In der Zielfunktion werden die Werte der diesen Stichproben entsprechenden Klassen ("-1"/"1") durch die Klasse "0" ersetzt. Das heißt, die Zielfunktion hat drei Klassen. Auf diese Weise versuchen wir, dem Modell beizubringen, verrauschte Stichproben nicht zu klassifizieren, das sie in der Regel den Klassifizierungsfehler verursachen. Gleichzeitig gehen wir davon aus, dass der entgangene Gewinn kein Verlust ist.
Weiterführende Tests der Modelle mit optimalen Parametern
Überprüfen wir, wie lange die optimalen Parameter von DNN Ergebnisse mit akzeptabler Qualität für die Tests von "zukünftigen" Kursen liefern. Der Test wird in der nach den vorangegangenen Optimierungen und Tests verbleibenden Umgebung wie folgt durchgeführt.
Verwenden wir ein bewegliches Fenster von 1350 Bars, Train = 1000, Test = 350 (für die Validierung — die ersten 250 Proben, für die Prüfung — die letzten 100 Proben) mit Schrittweite 100, um die Daten nach den ersten (4000 + 100) Bars, die für das Vortraining verwendet werden, durchzugehen. Machen wir 10 Schritte "vorwärts". Bei jedem Schritt werden zwei Modelle trainiert und getestet:
- Erstens — mit dem vortrainierten DNN, d.h. es wird bei jedem Schritt eine Feinabstimmung auf einen neuen Bereich durchgeführt;
- Zweitens — ein zusätzliches Training der DNN.opt, die nach der Optimierung in der Feinabstimmung erhalten wurde, auf einem neuen Bereich.
#---prepare----
evalq({
step <- 1:10
dt <- PrepareData(Data, Open, High, Low, Close, Volume)
DTforv <- foreach(i = step, .packages = "dplyr" ) %do% {
SplitData(dt, 4000, 1000, 350, 10, start = i*100) %>%
CappingData(., impute = T, fill = T, dither = F, pre.outl = pre.outl)%>%
NormData(., preproc = preproc) -> DTn
foreach(i = 1:4) %do% {
DTn[[i]] %>% dplyr::select(-c(v.rstl, v.pcci))
} -> DTn
list(pretrain = DTn[[1]],
train = DTn[[2]],
val = DTn[[3]],
test = DTn[[4]]) -> DTn
list(
pretrain = list(
x = DTn$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$pretrain$Class %>% as.data.frame()
),
train = list(
x = DTn$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$train$Class %>% as.data.frame()
),
test = list(
x = DTn$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$val$Class %>% as.data.frame()
),
test1 = list(
x = DTn$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$test$Class %>% as.vector()
)
)
}
}, env)
Führen wir den ersten Teil des Vorwärtstests mit den vortrainierten DNN und den optimalen Hyperparametern aus der Trainingsvariante SRBM + upperLayer + BP durch.
#----#---SRBM + upperLayer + BP---- evalq({ #--BestParams-------------------------- best.par <- OPT_Res3$Best_Par %>% unname # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine n1 = best.par[1]; n2 = best.par[2] fact1 = best.par[3]; fact2 = best.par[4] dr1 = best.par[5]; dr2 = best.par[6] Lr.rbm = best.par[7] Lr.top = best.par[8] Lr.fine = best.par[9] Ln <- c(0, 2*n1, 2*n2, 0) foreach(i = step, .packages = "darch" ) %do% { DTforv[[i]] -> X if(i==1) Res3$Dnn -> Dnn #----train/test------- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(100) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) } -> Score3_dnn }, env)
Die zweite Stufe des Vorwärtstests verwendet Dnn.opt, das durch die Optimierung erhalten wurde:
evalq({
foreach(i = step, .packages = "darch" ) %do% {
DTforv[[i]] -> X
if(i==1) {Res3$Dnn.opt -> Dnn}
#----train/test-------
fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt
predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred
yTest <- X$test$y[ ,1] %>% tail(100)
#numIncorrect <- sum(Ypred != yTest)
#Score <- 1 - round(numIncorrect/nrow(xTest), 2)
Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>%
round(3)
} -> Score3_dnnOpt
}, env)
Zum Vergleich der Testergebnisse tragen wir sie in eine Tabelle ein:
env$Score3_dnn env$Score3_dnnOpt
| iter | Score3_dnn | Score3_dnnOpt |
|---|---|---|
| Accuracy Precision Recall F1 | Accuracy Precision Recall F1 | |
| 1 | -1 0.76 0.737 0.667 0.7 1 0.76 0.774 0.828 0.8 |
-1 0.77 0.732 0.714 0.723 1 0.77 0.797 0.810 0.803 |
| 2 | -1 0.79 0.88 0.746 0.807 1 0.79 0.70 0.854 0.769 |
-1 0.78 0.836 0.78 0.807 1 0.78 0.711 0.78 0.744 |
| 3 | -1 0.69 0.807 0.697 0.748 1 0.69 0.535 0.676 0.597 |
-1 0.67 0.824 0.636 0.718 1 0.67 0.510 0.735 0.602 |
| 4 | -1 0.71 0.738 0.633 0.681 1 0.71 0.690 0.784 0.734 |
-1 0.68 0.681 0.653 0.667 1 0.68 0.679 0.706 0.692 |
| 5 | -1 0.56 0.595 0.481 0.532 1 0.56 0.534 0.646 0.585 |
-1 0.55 0.578 0.500 0.536 1 0.55 0.527 0.604 0.563 |
| 6 | -1 0.61 0.515 0.829 0.636 1 0.61 0.794 0.458 0.581 |
-1 0.66 0.564 0.756 0.646 1 0.66 0.778 0.593 0.673 |
| 7 | -1 0.67 0.55 0.595 0.571 1 0.67 0.75 0.714 0.732 |
-1 0.73 0.679 0.514 0.585 1 0.73 0.750 0.857 0.800 |
| 8 | -1 0.65 0.889 0.623 0.733 1 0.65 0.370 0.739 0.493 |
-1 0.68 0.869 0.688 0.768 1 0.68 0.385 0.652 0.484 |
| 9 | -1 0.55 0.818 0.562 0.667 1 0.55 0.222 0.500 0.308 |
-1 0.54 0.815 0.55 0.657 1 0.54 0.217 0.50 0.303 |
| 10 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 |
-1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 |
Die Tabelle zeigt, dass die ersten beiden Schritte zu guten Ergebnissen führen. Die Qualität ist in den ersten beiden Schritten beider Varianten eigentlich gleich, und dann fällt sie ab. Daher kann davon ausgegangen werden, dass DNN nach der Optimierung und Prüfung die Qualität der Klassifizierung auf dem Niveau der Testdaten auf mindestens 200-250 folgenden Bars beibehält.
Es gibt viele weitere Kombinationen für das zusätzliche Training von Modellen für die Vorwärtstests, die in dem vorhergehenden Artikel und zahlreichen, einstellbaren Hyperparametern erwähnt wurden.
Schlussfolgerung
- Das Paket darch v.0.12 bietet Zugriff auf eine riesige Liste von DNN-Hyperparametern und bietet großartige Möglichkeiten für die Tiefen- und Feinabstimmung.
- Die Verwendung des Bayes'schen Ansatzes zur Optimierung der DNN-Hyperparameter bietet eine große Auswahl an Modellen mit guter Qualität, die zur Erstellung von Ensembles verwendet werden können.
- Die Optimierung der Hyperparametern von DNN mit der Bayes'schen Methode verbessert die Qualität der Klassifizierung um 7-10%.
- Um das beste Ergebnis zu erzielen, ist es notwendig, mehrere Optimierungen (10 - 20) durchzuführen, gefolgt von der Auswahl des besten Ergebnisses.
- Der Optimierungsprozess kann Schritt für Schritt fortgesetzt werden, wobei die in den Vorläufen gewonnenen Parameter als Ausgangswerte herangezogen werden.
- Die Verwendung von Hyperparametern, die bei der Optimierung im DNN gewonnen werden, stellt sicher, dass die Qualität der Klassifizierung eines Vorwärtstests auf der Testebene im Abschnitt mit der Länge gleich dem Datensatz des Tests beibehalten wird.
Zur weiteren Verbesserung ist es sinnvoll, die Liste der optimierten Parameter um die Trainingsfunktion rpropagation in 4 Varianten, die Normalisierung der Neuronengewichte in den verdeckten Schichten normalizeWeights(TRUE, FALSE) und die obere Grenze dieser Normalisierung normalizeWeightsBound zu ergänzen. Wir könnten auch mit anderen Parametern experimentieren, bei der Annahme, dass das die Klassifikationsqualität des Modells beeinflussen könnte. Einer der Hauptvorteile des Paketes darch ist der Zugriff auf alle Parameter des neuronalen Netzes. Es ist möglich, experimentell zu bestimmen, wie sich jeder Parameter auf die Klassifizierungsqualität auswirkt.
Trotz erheblicher Zeitkosten ist der Einsatz der Bayes'schen Optimierung ratsam.
Die Verwendung eines Ensembles neuronaler Netze scheint eine weitere Möglichkeit zu sein, die Qualität der Klassifizierung zu verbessern. Diese Möglichkeit der Verstärkung in verschiedenen Varianten wird im nächsten Teil des Artikels diskutiert.
Anwendung
GitHub/PartV contains:
1. FUN_Optim.R — Funktionen, die für die Durchführung aller in diesem Artikel beschriebenen Berechnungen benötigt werden.
2. RUN_Optim.R — die in diesem Artikel durchgeführten Berechnungen.
3. SessionInfo. txt — Pakete, die von der Berechnungen verwendet werden.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/4225
 ZUP - Universeller ZigZag mit Pesavento-Mustern. Suche nach Mustern
ZUP - Universeller ZigZag mit Pesavento-Mustern. Suche nach Mustern
 Geschwindigkeitsvergleich von sich selbst speichernden Indikatoren
Geschwindigkeitsvergleich von sich selbst speichernden Indikatoren
 Synchronisierung mehrerer Charts eines Symbols auf verschiedenen Zeitrahmen
Synchronisierung mehrerer Charts eines Symbols auf verschiedenen Zeitrahmen
 Wie erstellt man ein grafisches Panel beliebiger Komplexität?
Wie erstellt man ein grafisches Panel beliebiger Komplexität?
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.