
Tiefe neuronale Netzwerke (Teil IV). Erstellen, trainieren und testen eines Modells des neuronalen Netzes
Inhalt
- Einführung
- 1. Eine kurze Beschreibung der Fähigkeiten des Paketes
- 1.1. Funktionen zu Initialisierung der Neuronen
- 1.2. Funktion zur Aktivierung der Neuronen
- 1.3. Trainingsmethoden
- 1.4. Methoden zur Regulierung und Stabilisierung
- 1.5. Methoden und Parameter zum Training eines RBM
- 1.6. Methoden und Parameter zum Training eines DNN
- 2. Testen der Qualität der Arbeit eines DNN in Abhängigkeit der verwendeten Parameter
- 2.1. Experimente
- 2.1.1. Eingangsdaten (Vorbereitung)
- 2.1.2. Basismodell der Vergleiche
- 2.1.3. Struktur eines DNN
- 2.1.4. Trainingsvarianten
- 2.2. Ergebnisanalyse
- Schlussfolgerung
- Anwendung
Einführung
Die wesentlichen Studien- und Anwendungsgebiete
Derzeit gibt es zwei Hauptströme in der Untersuchung und Anwendung von tiefen neuronalen Netzen. Sie unterscheiden sich in der Herangehensweise an die Initialisierung der Neuronengewichte in verdeckten Schichten.
Ansatz 1: Neuronale Netzwerke reagieren sehr empfindlich auf die Methode der Initialisierung von Neuronen in verdeckten Schichten, vor allem wenn die Anzahl der verdeckte Schichten steigt (größer als 3). Professor G. Hynton versuchte als Erster, dieses Problem zu lösen. Die Idee hinter seinem Ansatz war es, die Gewichte der Neuronen in verdeckten Schichten mit den Gewichten zu initiieren, die während des unbeaufsichtigten Trainings von autoassoziativen neuronalen Netzen in Form von RBM (Restricted Boltzmann Maschine) oder AE (Autoencoder) gewonnen wurden. Diese gestapelten RBM (SRBM) und gestapelten AE (SAE) werden mit einem großen Spektrum an nicht markierten Daten trainiert. Ziel eines solchen Trainings ist es, verdeckte Strukturen (Darstellungen, Bilder) und Zusammenhänge in den Daten aufzudecken. Die Initialisierung von Neuronen mit Gewichten eines MLP (multi-layer perceptron), die während des Vortrainings (pretraining) gewonnen werden, versetzt MLP in einen Lösungsraum ganz nahe dem optimale. Damit kann die Anzahl der gekennzeichneten Daten und der Durchläufe beim anschließenden Feintuning (Training) des MLP verringert werden. Dies sind für viele Anwendungsbereiche in der Praxis, insbesondere bei der Verarbeitung von vielen Daten, äußerst wichtige Vorteile.
Ansatz 2: Eine weitere Gruppe von Wissenschaftlern unter der Leitung von Yoshua Benjio schuf spezifische Methoden der Initialisierung von verdeckten Neuronen, spezifische Funktionen der Aktivierung, Methoden der Stabilisierung und Training. Der Erfolg dieser Richtung ist mit einer umfangreichen Entwicklung von tiefen faltungsneuronalen Netzen und rekurrenten neuronalen Netzen (DCNN, RNN) verbunden. Solche neuronalen Netzwerke zeigten eine hohe Effizienz bei der Bilderkennung, Analyse und Klassifizierung von Texten sowie bei der Übersetzung gesprochener Sprache aus einer Sprache in eine andere. Ideen und Methoden, die für diese neuronalen Netze entwickelt wurden, kamen auch bei MLP zum Einsatz.
Derzeit werden beide Ansätze werden aktiv genutzt. Zu beachten ist, dass neuronale Netze mit Vortraining bei nahezu gleichen Ergebnissen weniger Rechenleistung und weniger Proben für das Training benötigen. Das ist ein wichtiger Vorteil. Ich persönlich bevorzuge tiefe neuronale Netze mit Vortraining. Ich glaube, dass die Zukunft dem unüberwachten Lernen gehört.
Pakete in der Sprache R, die es ermöglichen, DNN zu entwickeln und zu verwenden
R verfügt über eine Reihe von Paketen zur Erstellung und Verwendung von DNN mit unterschiedlichem Komplexitätsgrad und einer Reihe von Funktionen.
Pakete, die das Erstellen, Trainieren und Testen eines DNN mit Vortraining ermöglichen:
- deepnet ist ein einfaches Paket, das nicht viele Einstellungen und Parameter bietet. Es ermöglicht die Erstellung von neuronalen Netzen der Typen SAE mit Vortraining und SRBM. Im vorherigen Artikel haben wir einen funktionierenden Experten mit diesem Paket besprochen. Die Verwendung eines RBM für das Vortraining führt zu weniger stabilen Ergebnissen. Dieses Paket eignet sich für die erste Begegnung mit diesem Thema und das Erlernen der Besonderheiten solcher Netzwerke. Mit dem richtigen Ansatz, kann es ein Experte verwenden. RcppDL ist eine Version dieses Paketes, die in C++ leicht gekürzt ist.
- darch v.0.12 ist ein komplexes, flexibles Paket mit vielen Parametern und Einstellungsmöglichkeiten. Die empfohlenen Einstellungen sind voreingestellt. Dieses Paket ermöglicht es, ein neuronales Netz beliebiger Komplexität und Konfiguration zu erstellen und einzurichten. Es verwendet SRBM für das Vortraining. Dieses Paket ist für fortgeschrittene Benutzer. Wir werden dessen Möglichkeiten später im Detail besprechen.
Unten sind Pakete, die es ermöglichen, ein DNN ohne Vortraining zu erstellen, zu trainieren und zu testen:
- H2O ist ist ein Paket zur Verarbeitung großer Datenmengen (>1M Zeilen und >1K Spalten). Das darin verwendete tiefe, neuronale Netz hat ein entwickeltes Regularisierungssystem. Seine Fähigkeiten übersteigen unsere Notwendigkeiten, aber das sollte niemanden davon abhalten, es zu nutzen.
- mxnet ermöglicht nicht nur MLP, sondern auch komplexe, rekurrente Netze, verschachtelte, neuronale Netzwerke und des Typs LSTM. Dieses Paket hat ein API für mehrere Sprachen, einschließlich R und Python. Die Philosophie des Paketes unterscheidet sich von den oben genannten. Dies liegt daran, dass die Entwickler hauptsächlich Pakete für Python geschrieben haben. Das Paket mxnet für R ist verkleinert und hat weniger Funktionen als das Paket für Python. Das macht dieses Paket aber nicht schlechter.
Das Thema der tiefen und rekurrenten Netze ist in der Python-Umgebung gut entwickelt. Es gibt viele interessante Pakete für den Aufbau von neuronalen Netzen dieser Art, die in R nicht existieren. Dies sind Pakete in R, die es erlauben, Programme/Module auszuführen, die in Python geschrieben wurden:
- PythonInR und reticulate sind zwei Pakete, die es ermöglichen, beliebigen Python-Code in R auszuführen. Dazu muss Python 2/3 auf Ihrem Computer installiert sein.
- kerasr ist eine Schnittstelle für R für eine beliebte Bibliothek des tiefen Lernens ('deep learning') Keras.
- tensorflow ist ein Paket, das den Zugriff auf die vollständige API von TensorFow in der R-Umgebung ermöglicht.
Vor Kurzem hat Microsoft die Bibliothek cntk v.2.1(Computatinal Network Toolkit) auf GitHub veröffentlicht. Es kann als Backend für einen vergleichbaren Keras verwendet werden. Es wird empfohlen, es mit unseren Problemen zu testen.
Yandex hält es aktuell bereit - dessen eigene Bibliothek CatBoost ist Open-Source verfügbar. Diese Bibliothek kann für Trainingsmodelle mit unterschiedlichen Datentypen verwendet werden. Dazu gehören Daten, die sich nur schwer als Zahlen darstellen lassen, z. B. Wolkentypen und Warenarten. Der Quellcode, die Dokumentation, Benchmarks und die notwendigen Hilfsmittel sind bereits auf GitHub veröffentlicht unter der Lizenz von Apache 2.0. Obwohl es sich hierbei nicht um ein neuronales Netze handelt, sondern um Bäume, ist es ratsam, den Algorithmus zu testen, zumal er die API von R enthält.
1. Eine kurze Beschreibung der Fähigkeiten des Paketes
Das Paket darch ver. 0.12.0 bietet eine breite Palette an Funktionen die es Ihnen nicht nur ermöglichen, ein Modell zu erstellen und zu trainieren, sondern es auch auf Ihre Bedürfnisse und Vorlieben zuzuschneiden. Wesentliche Änderungen wurden in der Version des Pakets (0.10.0) eingeführt, die im vorherigen Artikel behandelt wurde. Neue Aktivierungs-, Initialisierungs- und Stabilisierungsfunktionen wurden hinzugefügt. Das bemerkenswert Neue ist jedoch, dass alles zu einer Funktion darch() gebracht wurde, die gleichzeitig Konstruktor ist. Grafikkarten werden unterstützt. Nach dem Training gibt die Funktion ein Objekt der Klasse DArch zurück. Die Struktur des Objektes ist in Abb. 1 dargestellt. Die Funktionen predict() und darchTest() geben eine Vorhersage über die neuen Daten oder Klassifikationsmetriken zurück.

Abb. 1. Die Struktur des Objektes DArch
Alle Parameter haben Standardwerte. Diese Werte sind in der Regel nicht optimal. Alle diese Parameter können in drei Gruppen aufgeteilt - allgemeine, für RBM und für NN. Mit einige davon werden wir später im Detail beschäftigen.
| Funktionen | Typen |
|---|---|
| Funktionen zur Initialisierung |
|
| Funktionen zur Aktivierung |
|
| Funktionen zum Training |
|
| Niveaus des Trainings |
|
| Funktionen zur Stabilisierung |
|
| Momentum |
|
| Abbruchkriterium |
|
Ein tiefes neuronales Netz besteht aus n RBM (n = Schichten -1), die zu einem autoassoziativen Netz (SRBM) verbunden sind, und den eigentlichen neuronalen Netzen MLP mit mehreren Schichten. Das schichtweise Training von RBM ist ein unbeaufsichtigtes Training mit nicht gekennzeichneten Daten. Die Feinabstimmung des neuronalen Netzes erfordert eine Überwachung und erfolgt auf markierten Daten.
Die Aufteilung dieser Trainingsphasen mit Parametern gibt uns die Möglichkeit, Daten verschiedener Volumina (nicht unterschiedlicher Struktur!!) zu nutzen und mehrere, fein abgestimmte Modelle auf der Basis eines Vortrainings zu erhalten. Sind die Daten für Vor- und Feinabstimmung gleich, kann das Training in einem Zug durchgeführt werden, ohne es in zwei Stufen einzuteilen. Das Vortraining kann übersprungen werden (rbm.numEpochs = 0; darch.numEpochs = 10)). In diesem Fall können Sie nur ein mehrschichtiges neuronales Netzwerk verwenden oder nur RBM trainieren (rbm. numEpochs = 10; darch. numEpochs = 0). Sie haben weiterhin Zugriff auf alle internen Parameter.
Das trainierte neuronale Netz kann beliebig oft mit neue Daten trainiert werden. Dies ist nur bei einer begrenzten Anzahl von Modellen möglich. Das Strukturdiagramm eines tiefen neuronalen Netzes, das von komplexen eingeschränkten Boltzmann-Maschinen (DNRBM) initialisiert wurde, ist in Abb. 2. dargestellt.
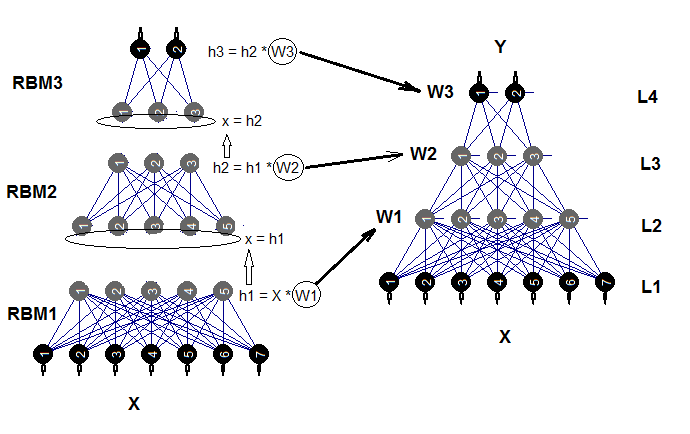
Abb. 2. Das Strukturdiagramm von DNSRBM
1.1. Funktionen zu Initialisierung der Neuronen
Es gibt zwei Hauptfunktionen zur Initialisierung der Neuronen im Programmpaket.
- generateWeightsUniform() verwendet die Funktion runif(n, min, max) und ist wie folgt umgesetzt:
> generateWeightsUniform function (numUnits1, numUnits2, weights.min = getParameter(".weights.min", -0.1, ...), weights.max = getParameter(".weights.max", 0.1, ...), ...) { matrix(runif(numUnits1 * numUnits2, weights.min, weights.max), nrow = numUnits1, ncol = numUnits2) } <environment: namespace:darch>
numUnits1 ist die Anzahl der Neuronen in der vorhergehenden Schicht und numUnits2 ist die Anzahl der Neuronen in der aktuellen Schicht.
- generateWeightsNormal() verwendet die Funktion rnorm(n, mean, sd) und ist wie folgt umgesetzt:
> generateWeightsNormal function (numUnits1, numUnits2, weights.mean = getParameter(".weights.mean", 0, ...), weights.sd = getParameter(".weights.sd", 0.01, ...), ...) { matrix(rnorm(numUnits1 * numUnits2, weights.mean, weights.sd), nrow = numUnits1, ncol = numUnits2) } <environment: namespace:darch>
Weitere vier Funktionen verwenden diese beiden, aber definieren min, max, mean und sd mit spezifischen Funktionen. Sie können sie studieren, wenn sie den Funktionsnamen ohne Klammern in das Terminal eingeben.
1.2. Funktion zur Aktivierung der Neuronen
Zusammen mit Standardfunktionen zur Aktivierung bietet das Paket eine breite Palette von neuen an. Hier sind einige von Ihnen:
x <- seq(-5, 5, 0.1) par(mfrow = c(2,3)) plot(x, y = 1/(1 + exp(-x)), t = "l", main = "sigmoid") abline(v = 0, col = 2) plot(x, y = tanh(x), t = "l", main = "tanh") abline(v = 0, h = 0, col = 2) plot(x, y = log(1 + exp(x)), t = "l", main = "softplus"); abline(v = 0, col = 2) plot(x, y = ifelse(x > 0, x ,exp(x) - 1), t = "l", main = "ELU") abline(h = 0, v = 0, col = 2) plot(x, y = ifelse(x > 0, x , 0), t = "l", main = "ReLU") abline(h = 0, v = 0, col = 2) par(mfrow = c(1,1))
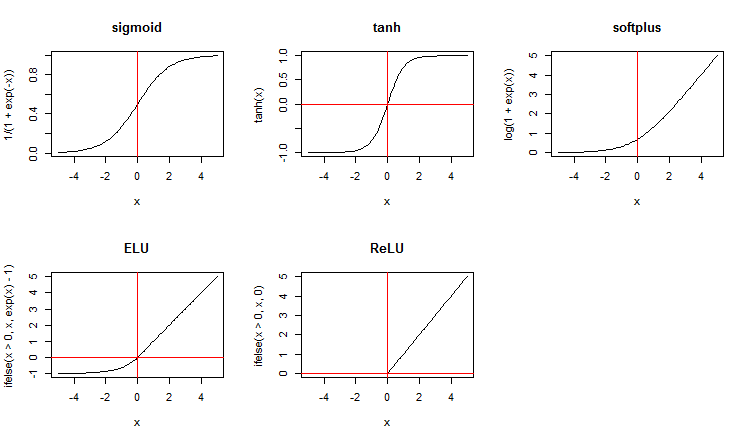
Abb. 3. Funktion zur Aktivierung der Neuronen
Betrachten wir die Aktivierungsfunktion maxout separat. Diese Funktionen kommt vom Convolutional Netz. Die verdeckte Schicht des neuronalen Netzes ist in Module der Größe des poolSize unterteilt. Die Anzahl der Neuronen in der verdeckten Schicht muss durch die Größe des Pools teilbar sein. Für das Training wird ein Neuron mit einer maximalen Aktivierung aus dem Pool ausgewählt und an den Eingang gesendet. Die Aktivierungsfunktion der Neuronen im Pool wird separat eingestellt. Einfach gesagt handelt es um eine Doppelschicht (convoluted + Maxpooling) mit eingeschränkten Möglichkeiten in der Filtrationsstufe. Gemäß verschiedener Veröffentlichungen, soll es zusammen mit dropout gute Ergebnisse erzielen. Abb. 4. zeigt das Schema der verdeckten Schicht mit 8 Neuronen und zwei Poolgrößen.
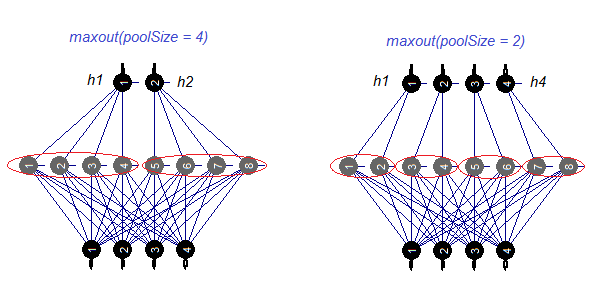
Abb. 4. Die Aktivierungsfunktion maxout
1.3. Trainingsmethoden
Leider gibt es nur zwei Trainingsmethoden im Paket - Backpropagation und rprop der Basisversion und der verbesserte mit der Aktualisierung der Gewichte während der Backpropagation und ohne sie. Es besteht auch die Möglichkeit, mit Hilfe des Multiplikators bp.learnRateScale. das Niveau des Trainings zu ändern.
1.4. Methoden zur Regulierung und Stabilisierung
- dropout ist ein Löschen (Nullsetzen der Gewichte) eines Teils der Neuronen der verdeckten Schicht während des Trainings. Neuronen werden in einer zufälligen Reihenfolge auf Null gesetzt. Die relative Anzahle der Neuronen, die gelöscht werden, ist definiert durch den Parameter darch.dropout. Die Zahl der Gelöschten in jeder Schicht kann unterschiedlich sein. Die Löschmaske kann für jeden Batchjob oder jeden Durchlauf erstellt werden.
- dropconnect Deaktiviert Verbindungen zwischen Neuronen der aktuellen Schicht und den Neuronen der vorhergehenden Schicht. Die Verbindungen werden in einer zufälligen Reihenfolge deaktiviert. Die relative Anzahl der zu deaktivierenden Verbindungen wird durch den gleichen Parameter darch.dropout (gewöhnlich nicht größer als 0,5) definiert. Gemäß verschiedener Veröffentlichungen, soll dropconnect bessere Ergebnisse als dropout erzielen.
- dither ist ein Weg ein Retraining durch Schwankungen der Eingangsdaten zu verhindern.
- weightDecay das Gewicht jedes Neurons wird mit (1 — weightDecay) vor der Aktualisierung multipliziert.
- normalizeWeights ist ein Weg, die Eingangsgewichte mit einer möglichen Obergrenze (L2 norm) zu normalisieren
Die ersten drei Methoden werden nur einzeln angewendet.
1.5. Methoden und Parameter zum Training eines RBM
Sie haben zwei Möglichkeiten, eine SRBM zu trainieren. Entweder wird eine RBM einzeln in rbm.numEpochs trainiert abwechselnd jedes RBM für jeweils einen Durchlauf trainiert. Die Auswahl einer dieser Methoden erfolgt durch den Parameter rbm.consecutive:. TRUE oder der Standard wählt die erste Methode und FALSE die zweite Methode. Abb. 5 zeigt ein Schema des Trainings in zwei Varianten. Mit dem rbm.lastLayer kann festgelegt werden, bei welcher Schicht der SRBM das Vortraining gestoppt werden soll. Wenn 0, sollen alle Schichten trainiert werden, und wenn (-1) bleibt die obere Schicht untrainiert. Dies ist sinnvoll, da die obere Schicht separat trainiert werden muss und es viel länger dauert. Andere Parameter bedürfen keiner zusätzlichen Erläuterung.
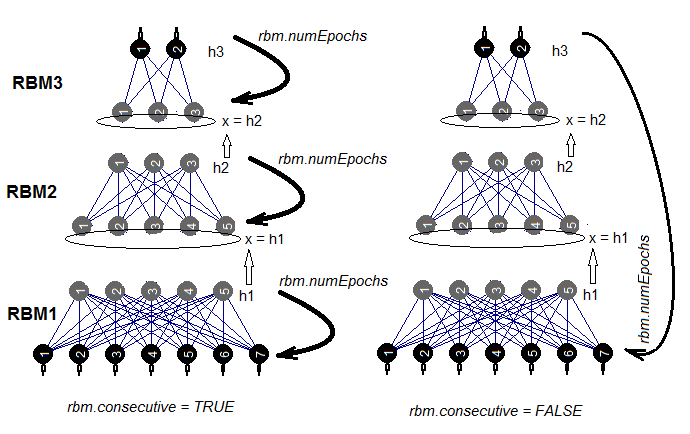
Abb. 5. Zwei Methoden des Trainings einer SRBM
1.6. Methoden und Parameter zum Training eines DNN
Ein DNN kann auf zwei Arten trainiert werden - mit und ohne Vortraining. Die Parameter, die in diesen Methoden verwendet werden, sind völlig unterschiedlich. Für ein Training mit Vortraining ist es daher nicht sinnvoll, bestimmte Initialisierungs- und Regularisierungsmethoden zu verwenden. Tatsächlich kann der Einsatz dieser Methoden das Ergebnis verschlechtern. Der Grund dafür ist, dass die Gewichte der Neuronen in den verdeckten Schichten nach einem Vortraining in der Nähe optimaler Werte platziert werden und nur eine geringfügige Feinabstimmung nötig ist. Um das gleiche Ergebnis im Training ohne Vortraining zu erreichen, müssen alle zur Verfügung stehenden Methoden der Initialisierung und Regularisierung genutzt werden. Normalerweise dauert das Training eines neuronalen Netzes auf diese Weise länger.
Wir werden uns also auf das Training mit Vortraining konzentrieren. Normalerweise geschieht dies in zwei Phasen.
- Training einer SRBM mit einer großen Menge nicht gekennzeichneter Daten. Die Parameter des Vortraining werden separat bestimmt. Als Ergebnis haben wir ein neuronales Netzwerk, das durch Gewichte einer SRBM initiiert wurde. Dann wird die obere Schicht des neuronalen Netzes mit gekennzeichneten Daten mit eigenen Trainingsparametern trainiert. Auf diese Weise haben wir ein neuronales Netz mit einer trainierten, oberen Schicht und Anfangsgewichten in den unteren Schichten. Sichern Sie es als eigenständiges Objekt zur weiteren Verwendung.
- In der zweiten Phase werden wir einige gekennzeichneten Stichproben, ein niedriges Trainingsniveau und eine kleine Anzahl von Trainingsdurchläufen für alle Schichten des neuronalen Netzes verwenden. Dies ist eine Feinabstimmung des Netzes. Das neuronale Netz ist trainiert.
Die Möglichkeit das Vortraining in Feinabstimmung und weiteren Trainings aufzuteilen, bietet eine unglaubliche Flexibilität bei der Erstellung von Trainingsalgorithmen nicht nur für ein DNN, sondern auch für die Ausbildung von DNN-Komitees. Abb. 6. vertritt mehrere Varianten der Trainings von DNN und DNN-Komitees.
- Variante а. Sichern des DNN in jedem Durchlauf der Feinabstimmung. Auf diese Weise haben wir eine Reihe von DNNs mit einem unterschiedlichen Grad des Trainings. Später kann jedes dieser neuronalen Netze einzeln oder als Teil eines Komitees genutzt werden. Der Nachteil dieses Szenarios besteht darin, dass alle DNNs auf den gleichen Daten trainiert werden, da alle die gleichen Trainingsparameter hatten.
- Variante b. Die Feinabstimmung des initiierten DNNs parallel zu verschiedenen Datensätzen (gleitende Fenster, wachsende Fenster etc.) und verschiedenen Parametern. Als Ergebnis erhalten wir ein DNN, das weniger korrelierte Vorhersagen erzeugt als das der Variante а.
- Variante c Feinabstimmung des eingeleiteten DNNs mit unterschiedlichen Datensätzen und Parametern. Sichern Sie die Zwischenmodelle. Das haben wir weiter oben weiteres Training genannt. Dies kann immer dann durchgeführt werden, wenn genügend neue Daten vorhanden sind.
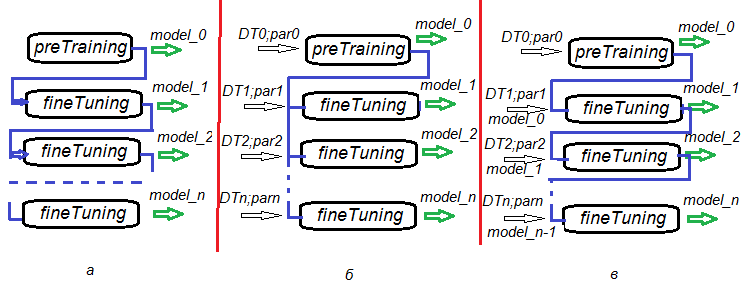
Abb. 6. Varianten das Trainings eines DNNs
2. Prüfung der Ergebnisqualität eines DNNs in Abhängigkeit von den verwendeten Parametern.
2.1. Experimente
2.1.1. Eingangsdaten (Vorbereitung)
Wir verwenden Daten und Funktionen aus den früheren Artikeln (1, 2, 3) . Dort haben wir verschiedene Varianten der vorbereitende Datenaufbereitung ausführlich besprochen. Ich werde kurz auf die Phasen der vorbereitende Bearbeitung eingehen, die wir durchführen werden. OHLCV ist die Ausgangsdaten, wie bisher. Die Eingangsdaten sind digitale Filter und die Ausgangsdaten sind ZigZag. Funktionen und das Bild des Arbeitsbereichs Cotir.RData können genutzt werden.
Die Etappen der Datenaufbereitung werden in getrennten Funktionen zusammengefasst:
- PrepareData() — erstellt den ersten Datensatz und bereinigt ihn von NA;
- SplitData() — teilt den anfänglichen Daten in die Datensätze pretrain, train, val, test;
- CappingData() — Ausreißer in allen Teilmengen identifizieren und begrenzen.
Um den Platz im Artikel zu sparen, werde ich diese Funktionen hier auflisten. Sie können von GitHub heruntergeladen werden, da sie in früheren Artikeln ausführlich behandelt wurden. Wir werden uns die Ergebnisse später ansehen. Wir werden nicht alle Methoden der Datentransformation im Vorfeld diskutieren. Viele von ihnen sind bekannt und weit verbreitet. Wir verwenden eine weniger bekannte Methode der Diskretisierung (überwacht und unbeaufsichtigt). Im zweiten Artikel besprachen wir zwei Pakete für eine kontrollierter Diskretisierung (discretization und smbinning). Sie enthalten verschiedene Diskretisierungsalgorithmen.
Wir werden verschiedene Methoden untersuchen, die kontinuierliche Variablen in Intervalle (bin) aufgeteilt werden können und wie diese diskretisierten Variablen in Modellen verwendet werden können.
Was ist "binning"?
Binning (in Intervalle aufteilen) ist ein Ausdruck in Bewertungsmodellen. Es ist bekannt als Diskretisierung im maschinellen Lernen. Dies ist ein Prozess, bei dem eine kontinuierliche Variable in eine endliche Anzahl von Intervallen (bins) umgewandelt wird. Dies hilft, seine Verteilung und Beziehung zur binären Zielvariablen zu verstehen. Die in diesem Prozess erzeugten Intervalle können zu Merkmalen der Vorhersage für die Verwendung in Modellen werden.
Warum binning?
Trotz einiger Vorbehalte gegenüber binning, hat es bedeutende Vorteile.
- Es erlaubt es, fehlende Daten (NA) und andere spezifische Berechnungen (z. B. Division durch Null) in das Modell einzubinden.
- Es kontrolliert oder mildert die Auswirkungen von Ausreißern auf das Modell.
- Es löst das Problem verschiedener Skalen in Prädiktoren, wodurch die gewichtete Koeffizienten im Endmodell vergleichbar werden.
Unbeaufsichtigte Diskretisierung
Die unbeaufsichtigte Diskretisierung teilt eine kontinuierliche Funktion in Intervalle (bins) auf, ohne weitere Informationen zu berücksichtigen. Für diese Einteilung gibt zwei Möglichkeiten. Es gibt Intervalle gleicher Länge und solche gleicher Häufigkeit.
| Option |
Ziel |
Beispiel |
Nachteil |
|---|---|---|---|
| Intervalle gleicher Länge |
Verstehen der Verteilung der Variablen |
Klassisches Histogramm mit gleichlangen Intervallen, die mithilfe verschiedener Regeln (Sturges, Rice usw) |
Die Anzahl der Datensätze in den Intervallen kann zu klein für eine korrekte Berechnung sein |
| Intervalle gleicher Häufigkeit |
Analysieren der Beziehung mit den binären Zielvariablen durch Indikatoren wie "bad rate" |
Quartile oder Perzentile | Ausgewählte Trennpunkte (cutoff) können die Differenz zwischen den Intervallen beim Vergleich mit den Zielvariable nicht maximieren |
Überwachte Diskretisierung
Die überwachte Diskretisierung teilt die kontinuierliche Variable in Intervallen auf, die in die Zielvariable projiziert werden. Die Schlüsselidee hierbei ist es, solche Trennpunkte zu finden, die den Unterschied zwischen den Gruppen maximieren.
Mit Hilfe von Algorithmen wie ChiMerge oder Rekursives Partitionieren können Analytiker in Sekundenschnelle die optimale Punkte finden und ihre Beziehung zur Zielvariablen mit Hilfe von Indizes wie Gewicht der Evidenz (WoE) und Informationswert (IV) bewerten.
WoE kann als Instrument zur Transformation von Prädiktoren in der Vorverarbeitungsphase für Algorithmen des überwachten Lernens eingesetzt werden. Während der Diskretisierung von Prädiktoren können wir sie durch ihre neuen nominalen Variablen oder mit den Werten ihrer WoE ersetzen. Die zweite Variante ist interessant, weil sie es erlaubt, nominalen Variablen (Faktoren) in Dummyvariablen umzuwandeln. Dies führt zu einer deutlichen Verbesserung der Qualität der Klassifizierung.
WOE und IV spielen bei der Datenanalyse zwei verschiedene Rollen:
- WOE beschreibt die Beziehung zwischen der prädiktiven Variable und der binären Zielvariablen.
- IV misst die Stärke dieser Beziehungen.
Finden wir heraus, was die Diagramme und Formeln zeigen. Wir erinnern uns an das Diagramm der Variablen v.fatl, die in 10 gleichhäufige Teilbereiche aus dem zweiten Teil des Artikels aufgeteilt wurde.
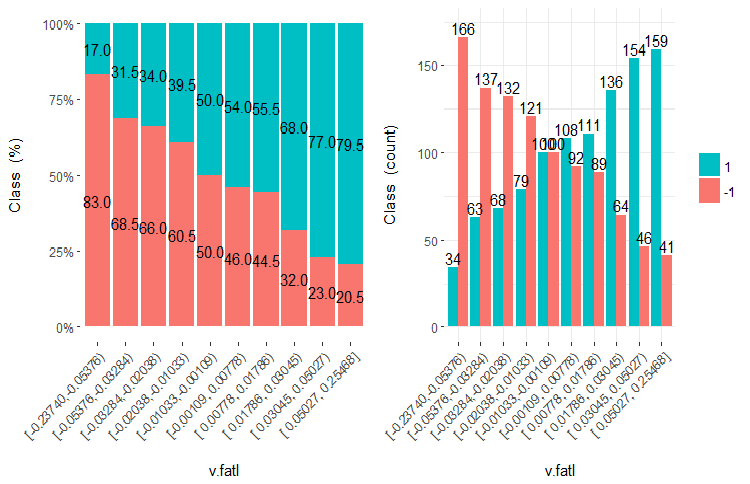
Abb. 7. Die Variable v.fatl aufgeteilt in 10 gleichhäufige Teilbereiche
Die Vorhersagequalität der Daten (WOE)
Wie Sie sehen können, hat jedes Intervall Stichproben, die in die Klasse "1" und Klasse "-1"kommen. Die Vorhersagefähigkeit der WoEi-Intervalle wird nach folgender Formel berechnet
WoEi = ln(Gi/Bi)*100
wobei:
Gi — relative Häufigkeit von "gut" (in unserem Fall "gut" = "1") Stichproben in jedem Feld der Variablen;
Bi — relative Häufigkeit von "schlecht" (in unserem Fall "schlecht" = "-1") Stichproben in jedem Intervall der Variablen.
Wenn WoEi = 1, d. h. die Anzahl der "guten" und "schlechten" Elemente in diesem Intervall ist ungefähr gleich, dann ist die Vorhersagefähigkeit dieses Intervall 0. Wenn die "guten" Stichproben die schlechtere Stichproben überwiegen, ist WOE > 0 und umgekehrt.
Informationswert (IV)
Dies ist das häufigste Maß für die Bestimmung der Signifikanz von Variablen und die Messung des Unterschieds in der Verteilung von "guten" und "schlechten" Stichproben. Der Informationswert kann mit folgender Formel berechnet werden:
IV = ∑ (Gi – Bi) ln (Gi/Bi)
Der Informationswert einer Variablen entspricht der Summe aller Intervalle der Variablen. Die Werte dieses Koeffizienten können wie folgt interpretiert werden:
- below 0,02 — statistisch unbedeutende Variable;
- 0,02 – 0,1 — statistisch schwach Variable;
- 0,1 – 0,3 — statistisch signifikante Variable;
- 0,3 und darüber — statistisch bedeutende, starke Variable.
Anschließend werden die Intervalle nach verschiedenen Algorithmen und Optimierungskriterien zusammengeführt bzw. aufgeteilt, um den Unterschied zwischen diesen Intervalle so groß wie möglich zu machen. Das Paket smbinning verwendet z. B. "Rekursives Partitioning" zur Kategorisierung numerischer Werte und die Informationswerte zur Ermittlung optimaler Trennpunkte. Das Paket discretization löst dieses Problem mit ChiMerge und MDL. Dabei ist zu beachten, dass die Trennpunkte aus dem Datensatz train ermittelt werden und zur Unterteilung der Datensätze test und val verwendet werden. .
Es gibt mehrere Pakete, die es erlauben, numerische Variablen auf die eine oder andere Weise zu diskretisieren. es sind dies discretization, smbinning, Information, InformationValue and woebinning. Wir müssen den Datensatz test diskretisieren und dann die Datensätze val und test anhand dieser Informationen aufteilen. Wir wollen auch eine visuelle Kontrolle der Ergebnisse. Wegen dieser Anforderungen habe ich mich für das Paket woebinning entschieden.
Das Paket teilt numerische Werte und Faktoren automatisch auf und bindet sie an die binäre Zielvariable. Hier werden zwei Ansätze verfolgt:
- Die Implementierung feiner und grober Klassifizierungen vereinigt nacheinander diskrete Klassen und Niveaus;
- Ein baumartiges Ansatz, der durch Iteration der ersten Intervalle binär aufteilt.
Beide Verfahren vereinigen Intervalle, basierend auf ähnlichen Werten von WOE, und stoppen auf Basis der IV-Kriterien. Das Paket kann sowohl mit eigenständigen Variablen als auch mit dem gesamten Daten verwendet werden. Dies bietet flexible Werkzeuge für das Studium der verschiedenen Lösungen des Aufteilens und für ihre Anwendung auf neue Daten.
Führen wir die Berechnung durch. Wir haben bereits Kurse aus dem Terminal in unsere Arbeitsumgebung geladen (oder eine Momentaufnahme des Arbeitsbereichs Cotir.RData aus GitHub). Ablauf der Berechnungen und dem Ergebnis:
- PrepareData() — erstellt den Anfangsdatensatz dt[7906,14], befreie ihn von NA. Der Datensatz enthält den Zeitstempel Data, Eingangsvariablen(12) und die Zielvariable Class (Faktor mit zwei Niveaus "-1" und "+1").
- SplitData() — Teilen der Daten dt[] in die Datensätze train, val, test im Verhältnis 2000/1000/500/500, und Kombinieren in DT[4, 4000, 14].
- CappingData() — Erkennen und Begrenzen der Ausreißer in allen Datensätzen und erhalten den Datensatz DTcap[4, 4000, 14]. Obwohl Diskretisierung gegenüber Ausreißern tolerant ist, werden wir sie begrenzen. Wenn Sie experimentieren wollen, können Sie dies auslassen. Wie Sie sich erinnern können, sind die Parameter der Ausreißern (pre.outl) in der Untermenge des Vortrainings definiert. Die Datensätze train/val/test werden mit diesen Parametern verarbeitet.
- NormData() — Normalisierung der Datensätze mit der Methode spatialSing aus dem Paket caret. Ähnlich dem Begrenzen der Ausreißer werden die Parameter der Normalisierung (preproc) in der Untermenge des Vortrainings definiert. Die Datensätze train/val/test werden mit diesen Parametern verarbeitet. Als Ergebnis erhalten wir DTcap.n[4, 4000, 14].
- DiscretizeData() — Definieren der Parameter der Diskretisierung (preCut), die Qualität der Variablen und ihrer Intervalle aus Sicht von WOE und IV.
evalq({
dt <- PrepareData(Data, Open, High, Low, Close, Volume)
DT <- SplitData(dt, 2000, 1000, 500,500)
pre.outl <- PreOutlier(DT$pretrain)
DTcap <- CappingData(DT, impute = T, fill = T, dither = F,
pre.outl = pre.outl)
preproc <- PreNorm(DTcap, meth = meth)
DTcap.n <- NormData(DTcap, preproc = preproc)
preCut <- PreDiscret(DTcap.n)
}, env)
Schreiben wir die Diskretisierungsdaten aller Variablen in eine Tabelle und schauen sie uns an:
evalq(tabulate.binning <- woe.binning.table(preCut), env) > env$tabulate.binning $`WOE Table for v.fatl` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.3904381926 154 7.7% 130 24 13.2% 2.4% 15.6% 171.3 0.185 2 <= -0.03713814085 769 38.5% 498 271 50.4% 26.8% 35.2% 63.2 0.149 3 <= 0.1130198981 308 15.4% 141 167 14.3% 16.5% 54.2% -14.5 0.003 4 <= Inf 769 38.5% 219 550 22.2% 54.3% 71.5% -89.7 0.289 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.626 $`WOE Table for ftlm` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.2344708291 462 23.1% 333 129 33.7% 12.7% 27.9% 97.2 0.204 2 <= -0.01368798447 461 23.1% 268 193 27.1% 19.1% 41.9% 35.2 0.028 3 <= 0.1789073635 461 23.1% 210 251 21.3% 24.8% 54.4% -15.4 0.005 4 <= Inf 616 30.8% 177 439 17.9% 43.4% 71.3% -88.4 0.225 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.463 $`WOE Table for rbci` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.1718377948 616 30.8% 421 195 42.6% 19.3% 31.7% 79.4 0.185 2 <= -0.09060410462 153 7.6% 86 67 8.7% 6.6% 43.8% 27.4 0.006 3 <= 0.3208178176 923 46.2% 391 532 39.6% 52.6% 57.6% -28.4 0.037 4 <= Inf 308 15.4% 90 218 9.1% 21.5% 70.8% -86.1 0.107 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.335 $`WOE Table for v.rbci` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.1837437563 616 30.8% 406 210 41.1% 20.8% 34.1% 68.3 0.139 2 <= 0.03581374495 461 23.1% 253 208 25.6% 20.6% 45.1% 22.0 0.011 3 <= 0.2503922644 461 23.1% 194 267 19.6% 26.4% 57.9% -29.5 0.020 4 <= Inf 462 23.1% 135 327 13.7% 32.3% 70.8% -86.1 0.161 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.331 $`WOE Table for v.satl` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.01840058612 923 46.2% 585 338 59.2% 33.4% 36.6% 57.3 0.148 2 <= 0.3247097195 769 38.5% 316 453 32.0% 44.8% 58.9% -33.6 0.043 3 <= 0.4003869443 154 7.7% 32 122 3.2% 12.1% 79.2% -131.4 0.116 4 <= Inf 154 7.7% 55 99 5.6% 9.8% 64.3% -56.4 0.024 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.330 $`WOE Table for v.stlm` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.4030051922 154 7.7% 118 36 11.9% 3.6% 23.4% 121.1 0.102 2 <= -0.1867821117 462 23.1% 282 180 28.5% 17.8% 39.0% 47.3 0.051 3 <= 0.1141896118 615 30.8% 301 314 30.5% 31.0% 51.1% -1.8 0.000 4 <= Inf 769 38.5% 287 482 29.0% 47.6% 62.7% -49.4 0.092 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.244 $`WOE Table for pcci` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.1738420887 616 30.8% 397 219 40.2% 21.6% 35.6% 61.9 0.115 2 <= -0.03163945242 307 15.3% 165 142 16.7% 14.0% 46.3% 17.4 0.005 3 <= 0.2553612644 615 30.8% 270 345 27.3% 34.1% 56.1% -22.1 0.015 4 <= Inf 462 23.1% 156 306 15.8% 30.2% 66.2% -65.0 0.094 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.228 $`WOE Table for v.ftlm` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.03697698898 923 46.2% 555 368 56.2% 36.4% 39.9% 43.5 0.086 2 <= 0.2437475615 615 30.8% 279 336 28.2% 33.2% 54.6% -16.2 0.008 3 <= Inf 462 23.1% 154 308 15.6% 30.4% 66.7% -66.9 0.099 5 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.194 $`WOE Table for v.rftl` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.1578370554 616 30.8% 372 244 37.7% 24.1% 39.6% 44.6 0.060 2 <= 0.1880959621 768 38.4% 384 384 38.9% 37.9% 50.0% 2.4 0.000 3 <= 0.3289762494 308 15.4% 129 179 13.1% 17.7% 58.1% -30.4 0.014 4 <= Inf 308 15.4% 103 205 10.4% 20.3% 66.6% -66.4 0.065 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.140 $`WOE Table for stlm` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.4586732186 154 7.7% 60 94 6.1% 9.3% 61.0% -42.5 0.014 2 <= -0.1688696056 462 23.1% 266 196 26.9% 19.4% 42.4% 32.9 0.025 3 <= 0.2631157075 922 46.1% 440 482 44.5% 47.6% 52.3% -6.7 0.002 4 <= 0.3592235072 154 7.7% 97 57 9.8% 5.6% 37.0% 55.6 0.023 5 <= 0.4846279843 154 7.7% 81 73 8.2% 7.2% 47.4% 12.8 0.001 6 <= Inf 154 7.7% 44 110 4.5% 10.9% 71.4% -89.2 0.057 8 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.122 $`WOE Table for v.rstl` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.4541701981 154 7.7% 94 60 9.5% 5.9% 39.0% 47.3 0.017 2 <= -0.3526306487 154 7.7% 62 92 6.3% 9.1% 59.7% -37.1 0.010 3 <= -0.2496412214 154 7.7% 53 101 5.4% 10.0% 65.6% -62.1 0.029 4 <= -0.08554320418 307 15.3% 142 165 14.4% 16.3% 53.7% -12.6 0.002 5 <= 0.360854678 923 46.2% 491 432 49.7% 42.7% 46.8% 15.2 0.011 6 <= Inf 308 15.4% 146 162 14.8% 16.0% 52.6% -8.0 0.001 8 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.070 $`WOE Table for v.pcci` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.4410911486 154 7.7% 92 62 9.3% 6.1% 40.3% 41.9 0.013 2 <= -0.03637567714 769 38.5% 400 369 40.5% 36.5% 48.0% 10.5 0.004 3 <= 0.1801156117 461 23.1% 206 255 20.9% 25.2% 55.3% -18.9 0.008 4 <= 0.2480148615 154 7.7% 84 70 8.5% 6.9% 45.5% 20.6 0.003 5 <= 0.3348752487 154 7.7% 67 87 6.8% 8.6% 56.5% -23.7 0.004 6 <= 0.4397404288 154 7.7% 76 78 7.7% 7.7% 50.6% -0.2 0.000 7 <= Inf 154 7.7% 63 91 6.4% 9.0% 59.1% -34.4 0.009 9 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.042
Die Tabelle zeigt für jede Variable folgende Werte:
- Final.Bin — Intervallgrenzen;
- Total.Count — Gesamtzahl der Elemente in den Intervallen;
- Total.Distr — Relative Anzahl der Elemente in den Intervallen;
- 0.Count — Anzahl der Elemente der Klasse "0";
- 1.Count — Anzahl der Elemente der Klasse "1";
- 0.Distr — — Relative Anzahl der Elemente der Klasse "0";
- 1.Distr — Relative Anzahl der Elemente der Klasse "1";
- 1.Rate — Prozentsatz der Anzahl der Elemente der Klasse "1" zur Anzahl der Elemente der Klasse "0";
- WOE — Vorhersagefähigkeit der Intervalle;
- IV — Statistische Signifikanz der Intervalle.
Grafisch ist das besser zu erkennen. Anzeige der Diagramme von WOE aller Variablen in aufsteigender Ordnung ihrer IV-Werte auf Basis dieser Tabelle:
> evalq(woe.binning.plot(preCut), env)
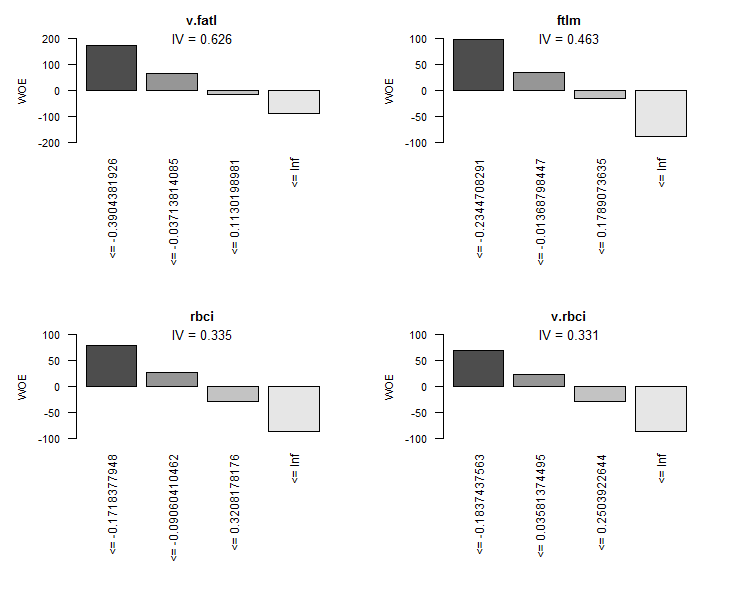
Abb. 8. WOE der 4 besten Variablen
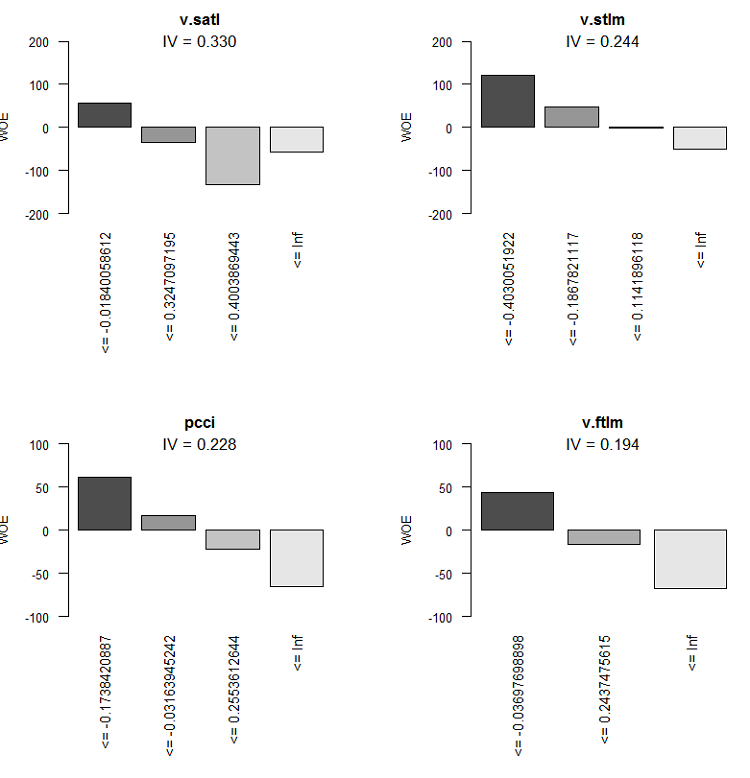
Abb. 9. WOE der Variablen 5 - 8
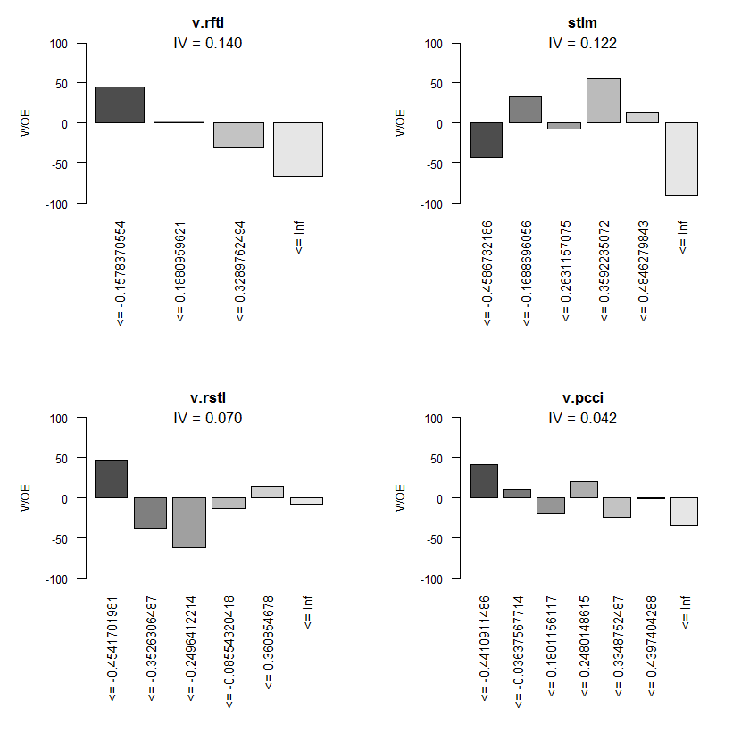
Abb. 10. WOE der Variablen 9 - 12
Jetzt das Diagramm der Gesamtklassifizierung der Variablen gemäß ihrer Informationssignifikanz IV.
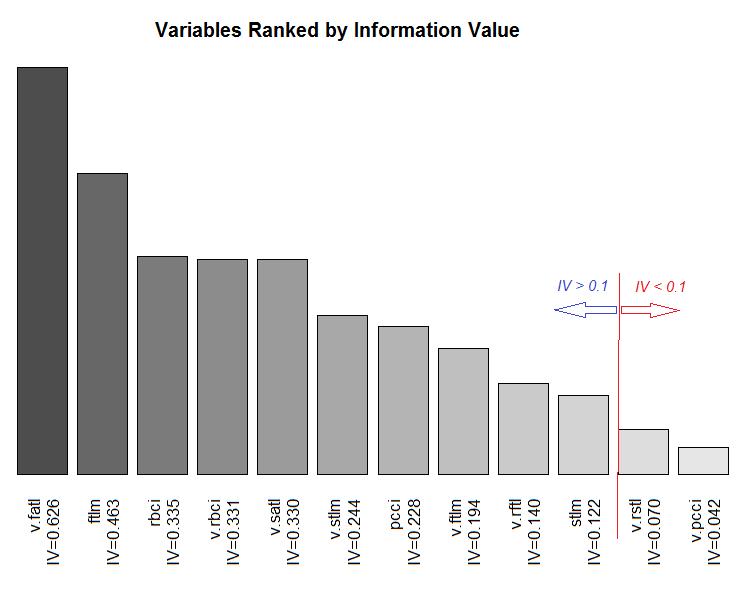
Abb. 11. Variablenklassifizierung nach ihrem IV
Wir werden die beiden insignifikanten Variablen v.rstl und v.pcci nicht verwenden, für die gilt IV < 0,1. Wir können aus den Diagrammen erkennen, dass von den 10 signifikanten Variablen nur v.satl und stlm eine nichtlineare Beziehung mit der Zielvariablen haben. Andere Variablen haben eine lineare Beziehung.
Weitere Experimente müssen wir drei Datensätze anlegen. Sie sind:
- DTbin ist ein Datensatz, in dem fortlaufende numerische Prädiktoren in Faktoren umgewandelt werden, deren Anzahl der Niveaus gleich der Anzahl der Intervalle ist, in die sie aufgeteilt werden;
- DTdum ist ein Datensatz, in dem Faktor-Prädiktoren des Datensatzes DTbin in Dummy-Binärvariablen transformiert werden;
- DTwoe ist ein Datensatz, bei dem Faktor-Prädiktoren in numerische Variablen umgewandelt werden, indem ihre Werte durch die WOE-Werte dieser Werte ersetzt werden.
Der erste Datensatz DTbin wird für das Training und dem Erhalt von Metriken des Basismodells benötigt. Der zweite und der dritte Datensatz werden für das Training des DNN und den Vergleich der Effizienz dieser beiden Transformationsmethoden verwendet.
Die Funktion woe.binning.deploy() des Paketes woebinning ermöglicht es uns, das Problem relativ leicht zu lösen. Folgenden Daten müssen der Funktion übergeben werden:
- Der Datenrahmen mit Prädiktoren und der Zielvariablen, die die Werte 0 oder 1 haben müssen;
- Parameter der Diskretisierung, die aus der vorherigen Berechnung ermittelt wurde (preCut);
- Die Variablennamen, die kategorisiert werden müssen. Wenn alle Variablen kategorisiert werden sollen, muss nur der Name des Datenrahmens angegeben werden;
- Angabe des minimalen IV, für Variablen, die nicht kategorisiert werden sollen;
- Angabe zusätzlicher Variablen (außer den kategorisierten), die wir erhalten wollen. Es gibt zwei Varianten - "woe" und "dum".
Die Funktion gibt einen Datenrahmen mit den initialen Variablen, den kategorisierten Variablen und den zusätzliche Variablen (falls angegeben) zurück. Die Namen neu erstellter Variablen werden durch Hinzufügen eines entsprechenden Präfixes oder Suffixes zum Namen der initialen Variablen erzeugt. So sind die Präfixe aller weiteren Variablen "dum" oder "woe" und kategorisierte Variablen haben das Suffix "binned". Schreiben wir eine Funktion DiscretizeData(), die den ursprünglichen Datensatz mittels woe.binning.deploy() transformiert.
DiscretizeData <- function(X, preCut, var){ require(foreach) require(woeBinning) DTd <- list() foreach(i = 1:length(X)) %do% { X[[i]] %>% select(-Data) %>% targ.int() %>% woe.binning.deploy(preCut, min.iv.total = 0.1, add.woe.or.dum.var = var) -> res return(res) } -> DTd list(pretrain = DTd[[1]] , train = DTd[[2]] , val = DTd[[3]] , test = DTd[[4]] ) -> DTd return(DTd) }
Die Eingangsparameter der Funktion sind die Anfangsdaten (list X) mit pretrain/train/val/test, die Parameter der Diskretisierung preCut und der Typ der zusätzlichen Variablen (string var).
Die Funktion entfernt die Variable "Data" aus jeder Liste und ersetzt den Zielfaktor "Class" durch das numerische Ziel "Cl". Basierend auf diesem, sendet es woe.binning.deploy() an den Eingang der Funktion. Zusätzlich spezifizieren wir den minimalen IV = 0.1 als Eingabeparameter, um die Variablen in die Ausgabe aufzunehmen. Als Ergebnis erhalten wir eine Liste mit den gleichen Daten pretrain/train/val/test. In jeder Liste werden kategorisierte Variablen und, falls gewünscht, zusätzliche Variablen den Ausgangsvariablen hinzugefügt. Lassen Sie uns alle benötigten Datensätze berechnen und die Rohdaten aus DTcap.n denen hinzufügen.
evalq({
require(dplyr)
require(foreach)
DTbin = DiscretizeData(DTcap.n, preCut = preCut, var = "")
DTwoe = DiscretizeData(DTcap.n, preCut = preCut, var = "woe")
DTdum = DiscretizeData(DTcap.n, preCut = preCut, var = "dum")
X.woe <- list()
X.bin <- list()
X.dum <- list()
foreach(i = 1:length(DTcap.n)) %do% {
DTbin[[i]] %>% select(contains("binned")) -> X.bin[[i]]
DTdum[[i]] %>% select(starts_with("dum")) -> X.dum[[i]]
DTwoe[[i]] %>% select(starts_with("woe")) %>%
divide_by(100) -> X.woe[[i]]
return(list(bin = X.bin[[i]], woe = X.woe[[i]],
dum = X.dum[[i]], raw = DTcap.n[[i]]))
} -> DTcut
list(pretrain = DTcut[[1]],
train = DTcut[[2]],
val = DTcut[[3]],
test = DTcut[[4]] ) -> DTcut
rm(DTwoe, DTdum, X.woe, X.bin, X.dum)
},
env)
Da WOE ein Prozentwert ist, können wir das WOE durch 100 dividieren und Werte von Variablen erhalten, die ohne zusätzliche Normalisierung an die Eingänge des neuronalen Netzes gesendet werden können. Betrachten wir die Struktur des so erhaltenen Liste, zum Beispiel DTcut$val.
> env$DTcut$val %>% str() List of 4 $ bin:'data.frame': 501 obs. of 10 variables: ..$ v.fatl.binned: Factor w/ 5 levels "(-Inf,-0.3904381926]",..: 1 1 3 2 4 3 4 4 4 4 ... ..$ ftlm.binned : Factor w/ 5 levels "(-Inf,-0.2344708291]",..: 2 1 1 1 2 2 3 4 4 4 ... ..$ rbci.binned : Factor w/ 5 levels "(-Inf,-0.1718377948]",..: 2 1 2 1 2 3 3 3 4 4 ... ..$ v.rbci.binned: Factor w/ 5 levels "(-Inf,-0.1837437563]",..: 1 1 3 2 4 3 4 4 4 4 ... ..$ v.satl.binned: Factor w/ 5 levels "(-Inf,-0.01840058612]",..: 1 1 1 1 1 1 1 1 1 2 ... ..$ v.stlm.binned: Factor w/ 5 levels "(-Inf,-0.4030051922]",..: 2 2 3 2 3 2 3 3 4 4 ... ..$ pcci.binned : Factor w/ 5 levels "(-Inf,-0.1738420887]",..: 1 1 4 2 4 2 4 2 2 3 ... ..$ v.ftlm.binned: Factor w/ 4 levels "(-Inf,-0.03697698898]",..: 1 1 3 2 3 2 3 3 2 2 ... ..$ v.rftl.binned: Factor w/ 5 levels "(-Inf,-0.1578370554]",..: 2 1 1 1 1 1 1 2 2 2 ... ..$ stlm.binned : Factor w/ 7 levels "(-Inf,-0.4586732186]",..: 2 2 2 2 1 1 1 1 1 2 ... $ woe:'data.frame': 501 obs. of 10 variables: ..$ woe.v.fatl.binned: num [1:501] 1.713 1.713 -0.145 0.632 -0.897 ... ..$ woe.ftlm.binned : num [1:501] 0.352 0.972 0.972 0.972 0.352 ... ..$ woe.rbci.binned : num [1:501] 0.274 0.794 0.274 0.794 0.274 ... ..$ woe.v.rbci.binned: num [1:501] 0.683 0.683 -0.295 0.22 -0.861 ... ..$ woe.v.satl.binned: num [1:501] 0.573 0.573 0.573 0.573 0.573 ... ..$ woe.v.stlm.binned: num [1:501] 0.473 0.473 -0.0183 0.473 -0.0183 ... ..$ woe.pcci.binned : num [1:501] 0.619 0.619 -0.65 0.174 -0.65 ... ..$ woe.v.ftlm.binned: num [1:501] 0.435 0.435 -0.669 -0.162 -0.669 ... ..$ woe.v.rftl.binned: num [1:501] 0.024 0.446 0.446 0.446 0.446 ... ..$ woe.stlm.binned : num [1:501] 0.329 0.329 0.329 0.329 -0.425 ... $ dum:'data.frame': 501 obs. of 41 variables: ..$ dum.v.fatl.-Inf.-0.3904381926.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.v.fatl.-0.03713814085.0.1130198981.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.v.fatl.-0.3904381926.-0.03713814085.binned: num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.v.fatl.0.1130198981.Inf.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.ftlm.-0.2344708291.-0.01368798447.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.ftlm.-Inf.-0.2344708291.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.ftlm.-0.01368798447.0.1789073635.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.ftlm.0.1789073635.Inf.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ....................................................................................... ..$ dum.stlm.-Inf.-0.4586732186.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.stlm.-0.1688696056.0.2631157075.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.stlm.0.2631157075.0.3592235072.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.stlm.0.3592235072.0.4846279843.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.stlm.0.4846279843.Inf.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... $ raw:'data.frame': 501 obs. of 14 variables: ..$ Data : POSIXct[1:501], format: "2017-02-23 15:30:00" "2017-02-23 15:45:00" ... ..$ ftlm : num [1:501] -0.223 -0.374 -0.262 -0.31 -0.201 ... ..$ stlm : num [1:501] -0.189 -0.257 -0.271 -0.389 -0.473 ... ..$ rbci : num [1:501] -0.0945 -0.1925 -0.1348 -0.1801 -0.1192 ... ..$ pcci : num [1:501] -0.5714 -0.2602 0.4459 -0.0478 0.2596 ... ..$ v.fatl: num [1:501] -0.426 -0.3977 0.0936 -0.1512 0.1178 ... ..$ v.satl: num [1:501] -0.35 -0.392 -0.177 -0.356 -0.316 ... ..$ v.rftl: num [1:501] -0.0547 -0.2065 -0.3253 -0.4185 -0.4589 ... ..$ v.rstl: num [1:501] 0.0153 -0.0273 -0.0636 -0.1281 -0.15 ... ..$ v.ftlm: num [1:501] -0.321 -0.217 0.253 0.101 0.345 ... ..$ v.stlm: num [1:501] -0.288 -0.3 -0.109 -0.219 -0.176 ... ..$ v.rbci: num [1:501] -0.2923 -0.2403 0.1909 0.0116 0.2868 ... ..$ v.pcci: num [1:501] -0.0298 0.3738 0.6153 -0.5643 0.2742 ... ..$ Class : Factor w/ 2 levels "-1","1": 1 1 1 1 2 2 2 2 2 1 ...
Wie Sie sehen können, enthält die bin 10 Faktorvariablen mit unterschiedlicher Anzahl von Ebenen. Sie enden mit dem Suffix "binned". woe enthält 10 Variablen, deren Faktorstufen durch ihre WOE ersetzt werden (sie haben das Präfix "woe"). dum hat 41 numerische Variablen dummy mit Werten (0, 1), erhalten aus den Faktorvariablen durch durch einen eins zu eins Codierung (sie haben das Präfix "dum"). raw hat 14 Variablen. Es sind Zeitstempel (Data), Zielfaktoren (Class:Factor) und 12 Prädiktoren.
Wir haben alle Daten, die wir für weitere Experimente brauchen. Die unten aufgeführten Objekte sollten sich mittlerweile in der Umgebung env befinden. Wir speichern den Arbeitsbereich mit diesen Objekten in der Datei PartIV.RData.
> ls(env) [1] "Close" "Data" "dt" "DT" "DTbin" "DTcap" "DTcap.n" "DTcut" "High" [10] "i" "Low" "Open" "pre.outl" "preCut" "preproc" "Volume"
2.1.2. Basismodell der Vergleiche
Wir verwenden das Modell OneR aus dem Paket OneR als Basismodell. Dieses Modell ist einfach, zuverlässig und leicht zu interpretieren. Informationen über den Algorithmus finden Sie in der Paketbeschreibung. Dieses Modell funktioniert nur mit Intervalldaten. Das Paket enthält Hilfsfunktionen, die in unterschiedlicher Weise numerische Variablen diskretisieren. Da wir bereits Prädiktoren in Faktoren transformiert, die wir nicht benötigen.
Jetzt werde ich die Berechnung im Folgenden erklären. Erstellen der Datensätze train/val/test durch das extrahieren der entsprechenden Listen von DTcut und fügen wir ihnen die Zielvariable Class hinzu. Wir trainieren das Modell mit dem Datensatz train.
> evalq({
+ require(OneR)
+ require(dplyr)
+ require(magrittr)
+ train <- cbind(DTcut$train$bin, Class = DTcut$train$raw$Class) %>% as.data.frame()
+ val <- cbind(DTcut$val$bin, Class = DTcut$val$raw$Class) %>% as.data.frame()
+ test <- cbind(DTcut$test$bin, Class = DTcut$test$raw$Class) %>% as.data.frame()
+ model <- OneR(data = train, formula = NULL, ties.method = "chisq", #c("first","chisq"
+ verbose = TRUE) #FALSE, TRUE
+ }, env)
Loading required package: OneR
Attribute Accuracy
1 * v.satl.binned 63.14%
2 v.fatl.binned 62.64%
3 ftlm.binned 62.54%
4 pcci.binned 61.44%
5 v.rftl.binned 59.74%
6 v.rbci.binned 58.94%
7 rbci.binned 58.64%
8 stlm.binned 58.04%
9 v.stlm.binned 57.54%
10 v.ftlm.binned 56.14%
---
Chosen attribute due to accuracy
and ties method (if applicable): '*'
Warning message:
In OneR(data = train, formula = NULL, ties.method = "chisq", verbose = TRUE) :
data contains unused factor levels
Das Modell wählt die Variable v.satl.binned mit einer Grundgenauigkeit von 63.14% als Basis für das Erstellen der Regeln. Schauen wir auf die allgemeinen Informationen über dies Modell:
> summary(env$model) Call: OneR(data = train, formula = NULL, ties.method = "chisq", verbose = FALSE) Regeln: If v.satl.binned = (-Inf,-0.01840058612] then Class = -1 If v.satl.binned = (-0.01840058612,0.3247097195] then Class = 1 If v.satl.binned = (0.3247097195,0.4003869443] then Class = 1 If v.satl.binned = (0.4003869443, Inf] then Class = 1 Accuracy: 632 of 1001 instances classified correctly (63.14%) Contingency table: v.satl.binned Class (-Inf,-0.01840058612] (-0.01840058612,0.3247097195] (0.3247097195,0.4003869443] (0.4003869443, Inf] Sum -1 * 325 161 28 37 551 1 143 * 229 * 35 * 43 450 Sum 468 390 63 80 1001 --- Maximum in each column: '*' Pearson's Chi-squared test: X-squared = 74.429, df = 3, p-value = 4.803e-16
Grafische Darstellung der Trainingsergebnisse:
plot(env$model)

Abb. 12. Verteilung der Kategorien der Variablen v.satl.binned durch die Klassen dieses Modells
Die Genauigkeit der Vorhersage im Training ist nicht sehr hoch. Mal sehen, welche Genauigkeit das Modell mit dem Datensatz val zeigt:
> evalq(res.val <- eval_model(predict(model, val %>% as.data.frame()), val$Class), + env) Confusion matrix (absolute): Actual Prediction -1 1 Sum -1 106 87 193 1 100 208 308 Sum 206 295 501 Confusion matrix (relative): Actual Prediction -1 1 Sum -1 0.21 0.17 0.39 1 0.20 0.42 0.61 Sum 0.41 0.59 1.00 Accuracy: 0.6267 (314/501) Error rate: 0.3733 (187/501) Error rate reduction (vs. base rate): 0.0922 (p-value = 0.04597)
und der Datensatz test:
> evalq(res.test <- eval_model(predict(model, test %>% as.data.frame()), test$Class), + env) Confusion matrix (absolute): Actual Prediction -1 1 Sum -1 130 102 232 1 76 193 269 Sum 206 295 501 Confusion matrix (relative): Actual Prediction -1 1 Sum -1 0.26 0.20 0.46 1 0.15 0.39 0.54 Sum 0.41 0.59 1.00 Accuracy: 0.6447 (323/501) Error rate: 0.3553 (178/501) Error rate reduction (vs. base rate): 0.1359 (p-value = 0.005976)
Die Ergebnisse sind nicht besonders ermutigend. Die Verminderung der Fehler zeigt wie die Genauigkeit gestiegen ist im Verhältnis zur Basisniveau (0.5). Ein niedriger Wert für p (<0.05) zeigt, dass das Modell fähig ist, Vorhersagen zu erstellen, die besser sind als das Basisnieveau. Die Genauigkeit des Datensatzes test 0.6447 (323/501), der höher ist als der des Datensatzes val. Der Datensatz test ist weiter weg vom Datensatz train als val. Dies Ergebnis wird unser Referenzpunkt für die Vergleiche der Vorhersagen unserer zukünftigen Modelle.
2.1.3. Struktur eines DNN
Zum Training und Testen werden wir drei Datensätze verwenden:
- DTcut$$raw — 12 Eingabevariablen (begrenzte Ausreißer und normalisiert).
- DTcut$$dum — 41 binäre Variablen
- DTcut$$woe — 10 numerische Variablen.
Bei allen Mengen wenden wir die Zielvariable Class = Faktor mit zwei Ebenen an. Struktur der neuronalen Netze:
- DNNraw - layers = c(12, 16, 8(2), 2), Aktivierungsfunktionen c(tanh, maxout(lin), softmax)
- DNNwoe - layers = c(10, 16, 8(2), 2), Aktivierungsfunktionen c(tanh, maxout(lin), softmax)
- DNNdum - layers = c(41, 50, 8(2), 2), Aktivierungsfunktionen c(ReLU, maxout(ReLU), softmax)
Die folgende Abbildung zeigt die Struktur des neuronalen Netzes DNNwoe. Das neuronales Netz besteht aus einer Eingab-, zwei verdeckten und einer Ausgabeschicht. Die beiden anderen neuronale Netze (DNNdum, DNNraw) haben einen ähnlichen Aufbau. Sie unterscheiden sich jedoch in der Anzahl der Neuronen in den Schichten und in den Aktivierungsfunktionen.
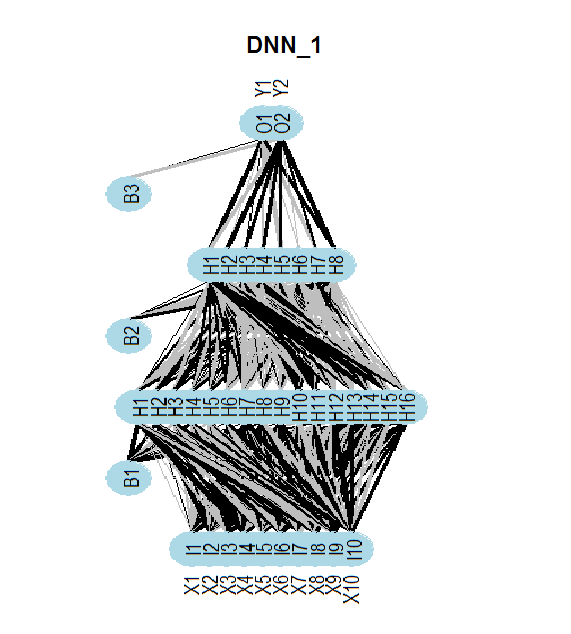
Abb. 13. Die Struktur des neuronalen Netzes DNNwoe
2.1.4. Trainingsvarianten
Mit einem Vortraining
Das Training umfasst zwei Phasen:
- Vortraining des SRBM mit dem Datensatz /pretrain gefolgt durch das Training nur der obersten Schicht des neuronalen Netzes, Validierung mit dem Datensatz train und den Parametern — par_0;
- Feinabstimmung des gesamten Netzes mit den Datensätzen train/val und den Parametern par_1.
Wir können die Zwischenmodelle der Feinabstimmung speichern, aber es ist nicht zwingend notwendig. Das Modell mit den besten Trainingsergebnisse ist zu speichern. Die Parameter dieser beiden Stufen sollten enthalten:
- par_0 — Die allgemeine Parameter des neuronalen Netzes, die Trainingsparameter des RBM und die Trainingsparameter der oberen Schicht des DNN;
- par_1 — Die Parameter des Trainings aller Ebenen des DNN.
Alle Parameter von DArch haben Standardwerte. Benötigen wir in einer bestimmten Trainingsphase verschiedene Parameter, so können wir diese durch eine Liste setzen, mit der die voreingestellten Parameter überschrieben werden. Nach der ersten Trainingsphase erhalten wir die Struktur des DArch mit Parametern und Trainingsergebnissen (Trainingsfehler, Testfehler etc.) sowie das neuronale Netz, das mit den Gewichten des trainierten SRBM initiiert wird. Um die zweite Trainingsphase abzuschließen, müssen die in der ersten Trainingsphase gewonnene Struktur von DArch in die Parameterliste für diese Trainingsphase aufnehmen. Natürlich benötigen wir einen Datensatz für das Trainings und die Validierung.
Betrachten wir die Parameter, die für die ersten Phase des Trainings erforderlich sind (Vortraining von SRBM und Training der oberen Schicht des neuronalen Netzes) und führen es durch:
##=====CODE I etap=========================== evalq({ require(darch) require(dplyr) require(magrittr) Ln <- c(0, 16, 8, 0)# // die Anzahl der Ein- und Ausgangsneuronen wird im Datensatz automatisch identifiziert nEp_0 <- 25 #------------------ par_0 <- list( layers = Ln, # // Herausnehmen dieses Parameters aus der Liste (der Einfachheit halber) seed = 54321,# // falls wir identische Daten während der Initialisierung erhalten logLevel = 5, # // welche Informationsleistung wir benötigen # params RBM======================== rbm.consecutive = F, # each RBM is trained one epoch at a time rbm.numEpochs = nEp_0, rbm.batchSize = 50, rbm.allData = TRUE, rbm.lastLayer = -1, # // kein Training der oberen Schicht des SRBM rbm.learnRate = 0.3, rbm.unitFunction = "tanhUnitRbm", # params NN ======================== darch.batchSize = 50, darch.numEpochs = nEp_0,# // Herausnehmen dieses Parameters aus der Liste, der Einfachheit halber darch.trainLayers = c(F,F,T), #обучать //nur die oberste Schicht darch.unitFunction = c("tanhUnit","maxoutUnit", "softmaxUnit"), bp.learnRate = 0.5, bp.learnRateScale = 1, darch.weightDecay = 0.0002, darch.dither = F, darch.dropout = c(0.1,0.2,0.1), darch.fineTuneFunction = backpropagation, #rpropagation normalizeWeights = T, normalizeWeightsBound = 1, darch.weightUpdateFunction = c("weightDecayWeightUpdate", "maxoutWeightUpdate", "weightDecayWeightUpdate"), darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2, darch.maxout.unitFunction = "linearUnit") #--------------------------- DNN_default <- darch(darch = NULL, paramsList = par_0, x = DTcut$pretrain$woe %>% as.data.frame(), y = DTcut$pretrain$raw$Class %>% as.data.frame(), xValid = DTcut$train$woe %>% as.data.frame(), yValid = DTcut$train$raw$Class %>% as.data.frame() ) }, env)Ergebnis nach Abschluss der ersten Trainingsphase:
........................... INFO [2017-09-11 14:12:19] Classification error on Train set (best model): 31.95% (639/2000) INFO [2017-09-11 14:12:19] Train set (best model) Cross Entropy error: 1.233 INFO [2017-09-11 14:12:19] Classification error on Validation set (best model): 35.86% (359/1001) INFO [2017-09-11 14:12:19] Validation set (best model) Cross Entropy error: 1.306 INFO [2017-09-11 14:12:19] Best model was found after epoch 3 INFO [2017-09-11 14:12:19] Final 0.632 validation Cross Entropy error: 1.279 INFO [2017-09-11 14:12:19] Final 0.632 validation classification error: 34.42% INFO [2017-09-11 14:12:19] Fine-tuning finished after 5.975 secs
Zweite Trainingsphase des neuronalen Netzes:
##=====CODE II etap=========================== evalq({ require(darch) require(dplyr) require(magrittr) nEp_1 <- 100 bp.learnRate <- 1 par_1 <- list( layers = Ln, seed = 54321, logLevel = 5, rbm.numEpochs = 0,# SRBM is not to be trained! darch.batchSize = 50, darch.numEpochs = nEp_1, darch.trainLayers = c(T,T,T), #TRUE, darch.unitFunction = c("tanhUnit","maxoutUnit", "softmaxUnit"), bp.learnRate = bp.learnRate, bp.learnRateScale = 1, darch.weightDecay = 0.0002, darch.dither = F, darch.dropout = c(0.1,0.2,0.1), darch.fineTuneFunction = backpropagation, #rpropagation backpropagation normalizeWeights = T, normalizeWeightsBound = 1, darch.weightUpdateFunction = c("weightDecayWeightUpdate", "maxoutWeightUpdate", "weightDecayWeightUpdate"), darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2, darch.maxout.unitFunction = exponentialLinearUnit, darch.elu.alpha = 2) #------------------------------ DNN_1 <- darch( darch = DNN_default, paramsList = par_1, x = DTcut$train$woe %>% as.data.frame(), y = DTcut$train$raw$Class %>% as.data.frame(), xValid = DTcut$val$woe %>% as.data.frame(), yValid = DTcut$val$raw$Class %>% as.data.frame() ) }, env)
Ergebnis nach der zweiten Trainingsphase:
........................... INFO [2017-09-11 15:48:37] Finished epoch 100 of 100 after 0.279 secs (3666 patterns/sec) INFO [2017-09-11 15:48:37] Classification error on Train set (best model): 31.97% (320/1001) INFO [2017-09-11 15:48:37] Train set (best model) Cross Entropy error: 1.225 INFO [2017-09-11 15:48:37] Classification error on Validation set (best model): 31.14% (156/501) INFO [2017-09-11 15:48:37] Validation set (best model) Cross Entropy error: 1.190 INFO [2017-09-11 15:48:37] Best model was found after epoch 96 INFO [2017-09-11 15:48:37] Final 0.632 validation Cross Entropy error: 1.203 INFO [2017-09-11 15:48:37] Final 0.632 validation classification error: 31.44% INFO [2017-09-11 15:48:37] Fine-tuning finished after 37.22 secs
Diagramm der Änderung des Vorhersagefehlers während der zweiten Trainingsphase:
plot(env$DNN_1, y = "raw")
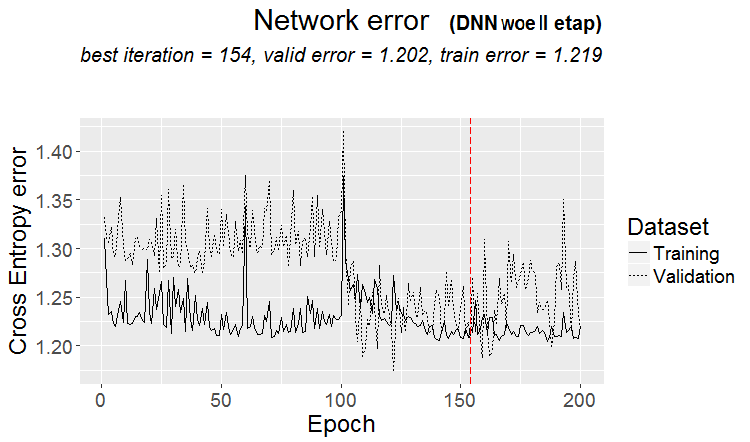
Abb. 14. Änderung des Klassifikationsfehlers während der zweiten Trainingsphase:
Betrachten wir den Klassifikationsfehler des finalen Modells mit dem Datensatz test:
#-----------
evalq({
xValid = DTcut$test$woe %>% as.data.frame()
yValid = DTcut$test$raw$Class %>% as.vector()
Ypredict <- predict(DNN_1, newdata = xValid, type = "class")
numIncorrect <- sum(Ypredict != yValid)
cat(paste0("Incorrect classifications on all examples: ", numIncorrect, " (",
round(numIncorrect/nrow(xValid)*100, 2), "%)\n"))
caret::confusionMatrix(yValid, Ypredict)
}, env)
Incorrect classifications on all examples: 166 (33.13%)
Confusion Matrix and Statistics
Reference
Prediction -1 1
-1 129 77
1 89 206
Accuracy : 0.6687
95% CI : (0.6255, 0.7098)
No Information Rate : 0.5649
P-Value [Acc > NIR] : 1.307e-06
Kappa : 0.3217
Mcnemar's Test P-Value : 0.3932
Sensitivity : 0.5917
Specificity : 0.7279
Pos Pred Value : 0.6262
Neg Pred Value : 0.6983
Prevalence : 0.4351
Detection Rate : 0.2575
Detection Prevalence : 0.4112
Balanced Accuracy : 0.6598
'Positive' Class : -1
#----------------------------------------
Die Genauigkeit dieses Datensatzes (woe) mit diesen Parametern, die alles andere als optimal sind, ist viel höher als die Genauigkeit des Basismodells. Durch die Optimierung der Hyperparameter des DNNs besteht ein signifikantes Potenzial zur Erhöhung der Genauigkeit. Bei einer erneuten Berechnung kann es passieren, dass die Daten nicht exakt mit denen aus dem Artikel übereinstimmen.
Wir wollen unsere Skripte in eine kompaktere Form bringen, um weitere Berechnungen mit anderen Datensätzen durchführen zu können. Schreiben wir eine Funktion für den Datensatz woe:
#------------------- DNN.train.woe <- function(param, X){ require(darch) require(magrittr) darch( darch = NULL, paramsList = param[[1]], x = X[[1]]$woe %>% as.data.frame(), y = X[[1]]$raw$Class %>% as.data.frame(), xValid = X[[2]]$woe %>% as.data.frame(), yValid = X[[2]]$raw$Class %>% as.data.frame() ) %>% darch( ., paramsList = param[[2]], x = X[[2]]$woe %>% as.data.frame(), y = X[[2]]$raw$Class %>% as.data.frame(), xValid = X[[3]]$woe %>% as.data.frame(), yValid = X[[3]]$raw$Class %>% as.data.frame() ) -> Darch return(Darch) }
Wiederholen der Berechnung für den Datensatz DTcut$$woe in kompakter Form:
evalq({
require(darch)
require(magrittr)
Ln <- c(0, 16, 8, 0)
nEp_0 <- 25
nEp_1 <- 25
rbm.learnRate = c(0.5,0.3,0.1)
bp.learnRate <- c(0.5,0.3,0.1)
list(par_0, par_1) %>% DNN.train.woe(DTcut) -> Dnn.woe
xValid = DTcut$test$woe %>% as.data.frame()
yValid = DTcut$test$raw$Class %>% as.vector()
Ypredict <- predict(Dnn.woe, newdata = xValid, type = "class")
numIncorrect <- sum(Ypredict != yValid)
cat(paste0("Incorrect classifications on all examples: ", numIncorrect, " (",
round(numIncorrect/nrow(xValid)*100, 2), "%)\n"))
caret::confusionMatrix(yValid, Ypredict) -> cM.woe
}, env)
Ausführen der Berechnung mit dem Datensatz DTcut$$raw:
#-------------------------
DNN.train.raw <- function(param, X){
require(darch)
require(magrittr)
darch( darch = NULL, paramsList = param[[1]],
x = X[[1]]$raw %>% tbl_df %>% select(-c(Data, Class)),
y = X[[1]]$raw$Class %>% as.data.frame(),
xValid = X[[2]]$raw %>% tbl_df %>% select(-c(Data, Class)),
yValid = X[[2]]$raw$Class %>% as.data.frame()
) %>%
darch( ., paramsList = param[[2]],
x = X[[2]]$raw %>% tbl_df %>% select(-c(Data, Class)),
y = X[[2]]$raw$Class %>% as.data.frame(),
xValid = X[[3]]$raw %>% tbl_df %>% select(-c(Data, Class)),
yValid = X[[3]]$raw$Class %>% as.data.frame()
) -> Darch
return(Darch)
}
#-------------------------------
evalq({
require(darch)
require(magrittr)
Ln <- c(0, 16, 8, 0)
nEp_0 <- 25
nEp_1 <- 25
rbm.learnRate = c(0.5,0.3,0.1)
bp.learnRate <- c(0.5,0.3,0.1)
list(par_0, par_1) %>% DNN.train.raw(DTcut) -> Dnn.raw
xValid = DTcut$test$raw %>% tbl_df %>% select(-c(Data, Class))
yValid = DTcut$test$raw$Class %>% as.vector()
Ypredict <- predict(Dnn.raw, newdata = xValid, type = "class")
numIncorrect <- sum(Ypredict != yValid)
cat(paste0("Incorrect classifications on all examples: ", numIncorrect, " (",
round(numIncorrect/nrow(xValid)*100, 2), "%)\n"))
caret::confusionMatrix(yValid, Ypredict) -> cM.raw
}, env)
#----------------------------
Unten sind die Ergebnisse und das Diagramm der Änderungen der Klassifikationsfehler dieses Datensatzes:
> env$cM.raw
Confusion Matrix and Statistics
Reference
Prediction -1 1
-1 133 73
1 86 209
Accuracy : 0.6826
95% CI : (0.6399, 0.7232)
No Information Rate : 0.5629
P-Value [Acc > NIR] : 2.667e-08
Kappa : 0.3508
Mcnemar's Test P-Value : 0.3413
Sensitivity : 0.6073
Specificity : 0.7411
Pos Pred Value : 0.6456
Neg Pred Value : 0.7085
Prevalence : 0.4371
Detection Rate : 0.2655
Detection Prevalence : 0.4112
Balanced Accuracy : 0.6742
'Positive' Class : -1
#--------------------------------------
plot(env$Dnn.raw, y = "raw")
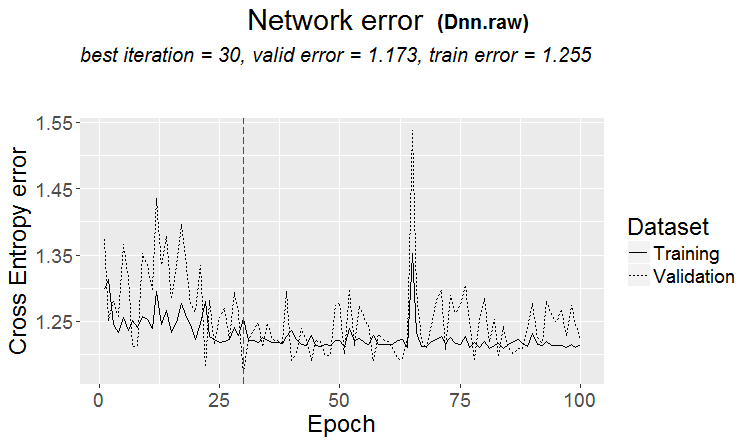
Abb. 15. Klassifizierungsfehler der zweiten Phase
Ich war nicht in der Lage, das neuronale Netzwerk mit den Daten von DTcut$$dum trainieren. Versuchen Sie es selbst. Geben Sie z. B. die Daten von DTcut$$$bin ein und ordnen Sie in den Trainingsparametern an, dass Prädiktoren in Dummies umgewandelt werden.
Training ohne Vortraining
Trainieren wir das neuronale Netz ohne Vortraining mit den gleichen Daten (woe, raw) mit den Datensätzen Vortrain/train/val. Scheuen wir und das Ergebnis an.
#-------WOE---------------- evalq({ require(darch) require(magrittr) Ln <- c(0, 16, 8, 0) nEp_1 <- 100 bp.learnRate <- c(0.5,0.7,0.1) #--param---------------- par_1 <- list( layers = Ln, seed = 54321, logLevel = 5, rbm.numEpochs = 0,# SRBM is not to be trained! darch.batchSize = 50, darch.numEpochs = nEp_1, darch.trainLayers = c(T,T,T), #TRUE, darch.unitFunction = c("tanhUnit","maxoutUnit", "softmaxUnit"), bp.learnRate = bp.learnRate, bp.learnRateScale = 1, darch.weightDecay = 0.0002, darch.dither = F, darch.dropout = c(0.0,0.2,0.1), darch.fineTuneFunction = backpropagation, #rpropagation backpropagation normalizeWeights = T, normalizeWeightsBound = 1, darch.weightUpdateFunction = c("weightDecayWeightUpdate", "maxoutWeightUpdate", "weightDecayWeightUpdate"), darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2, darch.maxout.unitFunction = exponentialLinearUnit, darch.elu.alpha = 2) #--train--------------------------- darch( darch = NULL, paramsList = par_1, x = DTcut[[1]]$woe %>% as.data.frame(), y = DTcut[[1]]$raw$Class %>% as.data.frame(), xValid = DTcut[[2]]$woe %>% as.data.frame(), yValid = DTcut[[2]]$raw$Class %>% as.data.frame() ) -> Dnn.woe.I #---test-------------------------- xValid = DTcut$val$woe %>% as.data.frame() yValid = DTcut$val$raw$Class %>% as.vector() Ypredict <- predict(Dnn.woe.I, newdata = xValid, type = "class") numIncorrect <- sum(Ypredict != yValid) cat(paste0("Incorrect classifications on all examples: ", numIncorrect, " (", round(numIncorrect/nrow(xValid)*100, 2), "%)\n")) caret::confusionMatrix(yValid, Ypredict) -> cM.woe.I }, env) #---------Ris16------------------------------------ plot(env$Dnn.woe.I, type = "class") env$cM.woe.I
Metrik:
....................................................... INFO [2017-09-14 10:38:01] Classification error on Train set (best model): 28.7% (574/2000) INFO [2017-09-14 10:38:01] Train set (best model) Cross Entropy error: 1.140 INFO [2017-09-14 10:38:02] Classification error on Validation set (best model): 35.86% (359/1001) INFO [2017-09-14 10:38:02] Validation set (best model) Cross Entropy error: 1.299 INFO [2017-09-14 10:38:02] Best model was found after epoch 67 INFO [2017-09-14 10:38:02] Final 0.632 validation Cross Entropy error: 1.241 INFO [2017-09-14 10:38:02] Final 0.632 validation classification error: 33.23% INFO [2017-09-14 10:38:02] Fine-tuning finished after 37.13 secs Incorrect classifications on all examples: 150 (29.94%) > env$cM.woe.I Confusion Matrix and Statistics Reference Prediction -1 1 -1 144 62 1 88 207 Accuracy : 0.7006 95% CI : (0.6584, 0.7404) No Information Rate : 0.5369 P-Value [Acc > NIR] : 5.393e-14 Kappa : 0.3932 Mcnemar's Test P-Value : 0.04123 Sensitivity : 0.6207 Specificity : 0.7695 Pos Pred Value : 0.6990 Neg Pred Value : 0.7017 Prevalence : 0.4631 Detection Rate : 0.2874 Detection Prevalence : 0.4112 Balanced Accuracy : 0.6951 'Positive' Class : -1
Diagramm der Änderung der Klassifizierungsfehler während des Trainings:
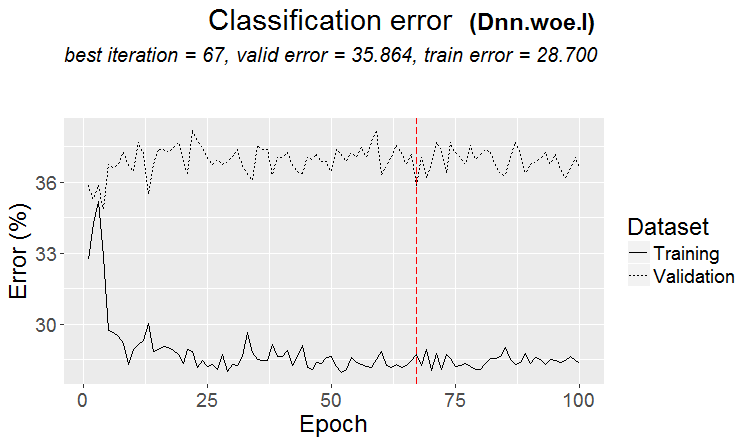
Abb. 16. Änderung der Klassifizierungsfehler ohne Vortraining mit den Datensätzen $woe set
Dasselbe mit den Daten /raw:
evalq({
require(darch)
require(magrittr)
Ln <- c(0, 16, 8, 0)
nEp_1 <- 100
bp.learnRate <- c(0.5,0.7,0.1)
#--param-----------------------------
par_1 <- list(
layers = Ln,
seed = 54321,
logLevel = 5,
rbm.numEpochs = 0,# SRBM is not to be trained!
darch.batchSize = 50,
darch.numEpochs = nEp_1,
darch.trainLayers = c(T,T,T), #TRUE,
darch.unitFunction = c("tanhUnit","maxoutUnit", "softmaxUnit"),
bp.learnRate = bp.learnRate,
bp.learnRateScale = 1,
darch.weightDecay = 0.0002,
darch.dither = F,
darch.dropout = c(0.1,0.2,0.1),
darch.fineTuneFunction = backpropagation, #rpropagation backpropagation
normalizeWeights = T,
normalizeWeightsBound = 1,
darch.weightUpdateFunction = c("weightDecayWeightUpdate",
"maxoutWeightUpdate",
"weightDecayWeightUpdate"),
darch.dropout.oneMaskPerEpoch = T,
darch.maxout.poolSize = 2,
darch.maxout.unitFunction = exponentialLinearUnit,
darch.elu.alpha = 2)
#---train------------------------------
darch( darch = NULL, paramsList = par_1,
x = DTcut[[1]]$raw %>% tbl_df %>% select(-c(Data, Class)) ,
y = DTcut[[1]]$raw$Class %>% as.vector(),
xValid = DTcut[[2]]$raw %>% tbl_df %>% select(-c(Data, Class)) ,
yValid = DTcut[[2]]$raw$Class %>% as.vector()
) -> Dnn.raw.I
#---test--------------------------------
xValid = DTcut[[3]]$raw %>% tbl_df %>% select(-c(Data, Class))
yValid = DTcut[[3]]$raw$Class %>% as.vector()
Ypredict <- predict(Dnn.raw.I, newdata = xValid, type = "class")
numIncorrect <- sum(Ypredict != yValid)
cat(paste0("Incorrect classifications on all examples: ", numIncorrect, " (",
round(numIncorrect/nrow(xValid)*100, 2), "%)\n"))
caret::confusionMatrix(yValid, Ypredict) -> cM.raw.I
}, env)
#---------Ris17----------------------------------
env$cM.raw.I
plot(env$Dnn.raw.I, type = "class")
Metrik:
INFO [2017-09-14 11:06:13] Classification error on Train set (best model): 30.75% (615/2000) INFO [2017-09-14 11:06:13] Train set (best model) Cross Entropy error: 1.189 INFO [2017-09-14 11:06:13] Classification error on Validation set (best model): 33.67% (337/1001) INFO [2017-09-14 11:06:13] Validation set (best model) Cross Entropy error: 1.236 INFO [2017-09-14 11:06:13] Best model was found after epoch 45 INFO [2017-09-14 11:06:13] Final 0.632 validation Cross Entropy error: 1.219 INFO [2017-09-14 11:06:13] Final 0.632 validation classification error: 32.59% INFO [2017-09-14 11:06:13] Fine-tuning finished after 35.47 secs Incorrect classifications on all examples: 161 (32.14%) > #---------Ris17---------------------------------- > env$cM.raw.I Confusion Matrix and Statistics Reference Prediction -1 1 -1 140 66 1 95 200 Accuracy : 0.6786 95% CI : (0.6358, 0.7194) No Information Rate : 0.5309 P-Value [Acc > NIR] : 1.283e-11 Kappa : 0.3501 Mcnemar's Test P-Value : 0.02733 Sensitivity : 0.5957 Specificity : 0.7519 Pos Pred Value : 0.6796 Neg Pred Value : 0.6780 Prevalence : 0.4691 Detection Rate : 0.2794 Detection Prevalence : 0.4112 Balanced Accuracy : 0.6738 'Positive' Class : -1
Diagramm der Änderung der Klassifizierungsfehler:
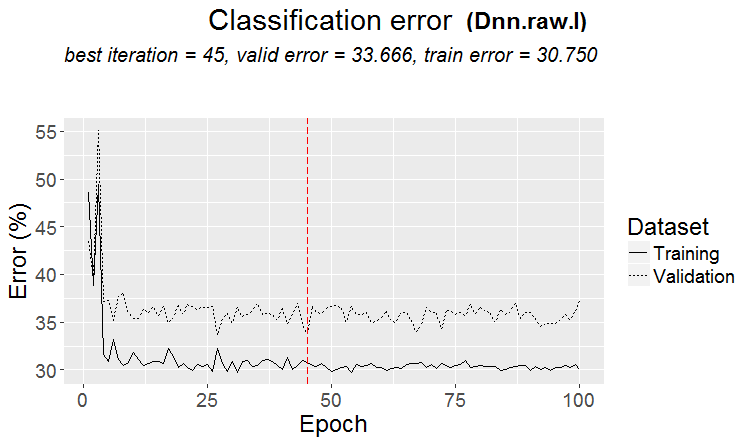
Abb. 17. Änderung der Klassifizierungsfehler ohne Vortraining mit den Datensatz $raw
2.2. Ergebnisanalyse
Erstellen wir eine Tabelle mit beiden Ergebnissen:
| Type des Trainings | Datensatz /woe | Datensatz /raw: |
|---|---|---|
| Mit einem Vortraining | 0.6687 (0.6255 - 0.7098) | 0.6826(0.6399 - 0.7232) |
| Ohne Vortraining | 0.7006(0.6589 - 0.7404) | 0.6786(0.6359 - 0.7194) |
Der Klassifizierungsfehler beim Vortraining ist in beiden Datensätzen nahezu gleich. Er liegt im Bereich von 30+/-4%. Trotz eines geringeren Fehlers ist aus dem Diagramm der Änderung des Klassifizierungsfehler ersichtlich, dass es während des Trainings ohne Vortraining eine Umschulung gab (der Fehler an den Datensätzen val und test ist deutlich größer als der Trainingsfehler). Deshalb werden wir in unseren weiteren Experimenten das Training mit Vortraining einsetzen.
Das Ergebnis ist nicht viel größer als das Ergebnis des Basismodells. Wir können die Eigenschaften durch die Optimierung einiger Hyperparameter zu verbessern. Wir werden dies im nächsten Artikel angehen.
Schlussfolgerung
Trotz der Einschränkungen (z. B. nur zwei grundlegende Trainingsmethoden), erlaubt das Paket darch die Erstellung von neuronalen Netzen unterschiedlicher Struktur und Parameter.
Dieses Paket ist ein gutes Werkzeug für das tiefgreifende Studium neuronaler Netze.
Die Schwächen eines DNNs ist vor allem durch die Verwendung der Standardparameter oder Parameter in der Nähe von ihnen erklärt. Der Datensatz woe zeigte keine Vorteile gegenüber raw. Deshalb werden wir im nächsten Artikel:
- Einen Teil der vorher ermittelten Hyperparameter in DNN.woe optimieren;
- Ein DNN unter Verwendung der Bibliothek TensorFlow erstellen, testen und die Ergebnisse mit DNN (darch) vergleichen;
- Eine Gruppe von neuronalen Netzen unterschiedlicher Art (Sacking, Stacking) erstellen und sehen, ob sich dadurch die Qualität von Vorhersagen verbessert.
Anwendung
GitHub/PartIV contains:
- FunPrepareData.R — Funktionen zur Datenaufbereitung
- RunPrepareData.R — Skripte zur Datenaufbereitung
- Experiment.R — Skripte für die Durchführung der Experimente
- Part_IV.RData — Eine Momentaufnahme des Arbeitsbereichs mit allen Objekten, die nach der Datenaufbereitungsphase erhalten wurden
- SessionInfo.txt — Information über verwendete Software
- Darch_default.txt — Liste der Parameter der Struktur von DArch mit den Standardwerten
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/3473
 Cross-Plattform Expert Advisor: Stopps
Cross-Plattform Expert Advisor: Stopps
 Tiefe neuronale Netzwerke (Teil III). Stichprobenauswahl und Verminderung der Dimensionen
Tiefe neuronale Netzwerke (Teil III). Stichprobenauswahl und Verminderung der Dimensionen
 Risikobewertung durch die Abfolge von Positionen von Finanzanlagen
Risikobewertung durch die Abfolge von Positionen von Finanzanlagen
 Tiefe neuronale Netzwerke (Teil II). Ausarbeitung und Auswahl von Prädiktoren
Tiefe neuronale Netzwerke (Teil II). Ausarbeitung und Auswahl von Prädiktoren
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.