
Verwendung von selbstorganisierenden Karten (Kohonenkarten) in MetaTrader 5
Einleitung
Eine selbstorganisierende Karte (self-organizing map, SOM) ist eine Art künstliches neuronales Netzwerk, das durch einen nicht überwachten Lernprozess eingelernt wird, um eine zweidimensionale, diskretisierte Darstellung des Eingaberaums der Einlernbeispiele, die als Karte bezeichnet wird, zu erstellen.
Diese Karten sind nützlich für die Klassifizierung und Visualisierung niederdimensionaler Ansichten von hochdimensionalen Daten, ähnlich der multidimensionalen Skalierung. Dieses Modell wurde zuerst durch den finnischen Professor Teuvo Kohonen als künstliches neuronales Netzwerk beschrieben und wird manchmal Kohonenkarte genannt.
Es stehen zahlreiche Algorithmen zur Verfügung. Wir befolgen den unter http://www.ai-junkie.com zu findenden Code. Zur Visualisierung der Daten im MetaTrader 5 Client Terminal nutzen wir die Bibliothek cIntBMP für die Erstellung von BMP-Bildern. In diesem Beitrag werden wir mehrere einfache Anwendungsbeispiele von Kohonenkarten betrachten.
1. Selbstorganisierende Karten
Die selbstorganisierenden Karten wurden erstmals von Teuvo Kohonen im Jahre 1982 beschrieben. Im Gegensatz zu vielen neuronalen Netzwerken benötigen sie keine absolute Entsprechung zwischen Eingabe- und Ziel-Ausgabedaten. Dieses neuronale Netzwerk wird durch einen unüberwachten Lernprozess eingelernt.
Die SOM lässt sich formal als nichtlineare, geordnete, geglättete Abbildung hochdimensionaler Eingabedaten auf die Elemente eines herkömmlichen, niederdimensionalen Arrays beschreiben. Im einfachsten Fall erstellt sie ein Ähnlichkeitsdiagramm von Eingabedaten.
Die SOM konvertiert die nichtlinearen statistischen Beziehungen zwischen hochdimensionalen Daten in eine einfache geometrische Beziehung ihrer Abbildungspunkte auf einem herkömmlichen zweidimensionalen Knotenraster. SOM-Karten können für die Klassifizierung und Visualisierung von hochdimensionalen Daten genutzt werden.
1,1. Netzwerkarchitektur
Eine einfache Kohonenkarte in Form eines Rasters aus 16 Knoten (je 4x4 davon sind mit einem 3-dimensionalen Eingabevektor verbunden) ist in Abb. 1. dargestellt.
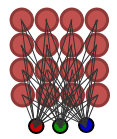
Abbildung 1. Einfache Kohonenkarte (16 Knoten)
Jeder Knoten hat x- und y-Koordinaten im Raster und einen auf Basis des Eingabevektors definierten Gewichtungsvektor.
1,2. Einlernalgorithmus
Im Gegensatz zu vielen anderen Typen von neuronalen Netzwerken benötigt die SOM keine festgelegte Zielausgabe. Stattdessen wird der Rasterbereich, in dem die Knotengewichtung dem Eingabevektor entspricht, selektiv optimiert, um den Daten der Klasse, zu der der Eingabevektor gehört, näher zu entsprechen.
Ausgehend von einer anfänglichen Verteilung zufälliger Gewichtungen und über viele Durchläufe bildet die SOM schließlich eine Karte aus stabilen Zonen. Jede Zone ist effektiv ein Merkmalsklassifikator, also können Sie sich die grafische Darstellung als eine Art Karte des Eingaberaums vorstellen.
Die Einlernung geschieht in vielen Schritten und über mehrere Durchläufe:
- Die Gewichtungen jedes Knotens werden mit zufälligen Werten initialisiert.
- Ein Vektor wird zufällig aus dem Satz der Einlerndaten ausgewählt.
- Jeder Knoten wird untersucht, um zu berechnen, welche Gewichtungen dem Eingabevektor am ähnlichsten sind. Der ausgewählte Knoten ist allgemein als Best Matching Unit (BMU) bekannt.
- Der Radius der Umgebung der BMU wird berechnet. Am Anfang entspricht dieser Wert dem Radius des Rasters, wird aber mit jedem Schritt verkleinert.
- Für jeden Knoten innerhalb des Radius der BMU werden die Knotengewichtungen angepasst, damit sie dem Eingabevektor ähnlicher sind. Je näher sich ein Knoten an der BMU befindet, desto wichtiger sind seine Gewichtungen.
- Schritt 2 wird N Mal wiederholt.
Die Details finden Sie unter http://www.ai-junkie.com.
2. Fallstudien
2,1. Beispiel 1. "Hello World!" in SOM
Das klassische Beispiel einer Kohonenkarte ist die Clusterung von Farben.
Nehmen wir an, wir haben einen Satz von 8 Farben. Jede von ihnen wird als dreidimensionaler Vektor im RGB-Farbmodell dargestellt.
-
 Rot: (255,0,0);
Rot: (255,0,0);  Grün: (0.128,0);
Grün: (0.128,0); Blau: (0,0,255);
Blau: (0,0,255); Dunkelgrün: (0.100,0);
Dunkelgrün: (0.100,0); Dunkelblau: (0,0,139);
Dunkelblau: (0,0,139); Gelb: (255.255,0);
Gelb: (255.255,0); Orange: (255.165,0);
Orange: (255.165,0); Violett: (128,0,128).
Violett: (128,0,128).
Bei der Arbeit mit Kohonenkarten in der MQL5-Sprache befolgen wir das objektorientierte Paradigma.
Wir brauchen zwei Klassen: Die Klasse CSOMNode für einen Knoten des regulären Rasters und CSOM, eine Klasse eines neuronalen Netzwerks.
//+------------------------------------------------------------------+ //| CSOMNode class | //+------------------------------------------------------------------+ class CSOMNode { protected: int m_x1; int m_y1; int m_x2; int m_y2; double m_x; double m_y; double m_weights[]; public: //--- class constructor CSOMNode(); //--- class destructor ~CSOMNode(); //--- node initialization void InitNode(int x1,int y1,int x2,int y2); //--- return coordinates of the node's center double X() const { return(m_x);} double Y() const { return(m_y);} //--- returns the node coordinates void GetCoordinates(int &x1,int &y1,int &x2,int &y2); //--- returns the value of weight_index component of weight's vector double GetWeight(int weight_index); //--- returns the squared distance between the node weights and specified vector double CalculateDistance(double &vector[]); //--- adjust weights of the node void AdjustWeights(double &vector[],double learning_rate,double influence); };
Die Umsetzung der Klassenmethoden finden Sie in som_ex1.mq5. Der Code hat zahlreiche Kommentare, wir konzentrieren uns auf die Idee.
Die Beschreibung der CSOM-Klasse sieht so aus:
//+------------------------------------------------------------------+ //| CSOM class | //+------------------------------------------------------------------+ class CSOM { protected: //--- class for using of bmp images cIntBMP m_bmp; //--- grid mode int m_gridmode; //--- bmp image size int m_xsize; int m_ysize; //--- number of nodes int m_xcells; int m_ycells; //--- array with nodes CSOMNode m_som_nodes[]; //--- total items in training set int m_total_training_sets; //--- training set array double m_training_sets_array[]; protected: //--- radius of the neighbourhood (used for training) double m_map_radius; //--- time constant (used for training) double m_time_constant; //--- initial learning rate (used for training) double m_initial_learning_rate; //--- iterations (used for training) int m_iterations; public: //--- class constructor CSOM(); //--- class destructor ~CSOM(); //--- net initialization void InitParameters(int iterations,int xcells,int ycells,int bmpwidth,int bmpheight); //--- finds the best matching node, closest to the specified vector int BestMatchingNode(double &vector[]); //--- train method void Train(); //--- render method void Render(); //--- shows the bmp image on the chart void ShowBMP(bool back); //--- adds a vector to training set void AddVectorToTrainingSet(double &vector[]); //--- shows the pattern title void ShowPattern(double c1,double c2,double c3,string name); //--- adds a pattern to training set void AddTrainPattern(double c1,double c2,double c3); //--- returns the RGB components of the color void ColToRGB(int col,int &r,int &g,int &b); //--- returns the color by RGB components int RGB256(int r,int g,int b) const {return(r+256*g+65536*b); } //--- deletes image from the chart void NetDeinit(); };
Die Verwendung der CSOM-Klasse ist einfach:
CSOM KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ void OnInit() { MathSrand(200); //--- initialize net, 10000 iterations will be used for training //--- the net contains 15x20 nodes, bmp image size 400x400 KohonenMap.InitParameters(10000,15,20,400,400); //-- add RGB-components of each color from training set KohonenMap.AddTrainPattern(255, 0, 0); // Red KohonenMap.AddTrainPattern( 0,128, 0); // Green KohonenMap.AddTrainPattern( 0, 0,255); // Blue KohonenMap.AddTrainPattern( 0,100, 0); // Dark green KohonenMap.AddTrainPattern( 0, 0,139); // Dark blue KohonenMap.AddTrainPattern(255,255, 0); // Yellow KohonenMap.AddTrainPattern(255,165, 0); // Orange KohonenMap.AddTrainPattern(128, 0,128); // Purple //--- train net KohonenMap.Train(); //--- render map to bmp KohonenMap.Render(); //--- show patterns and titles for each color KohonenMap.ShowPattern(255, 0, 0,"Red"); KohonenMap.ShowPattern( 0,128, 0,"Green"); KohonenMap.ShowPattern( 0, 0,255,"Blue"); KohonenMap.ShowPattern( 0,100, 0,"Dark green"); KohonenMap.ShowPattern( 0, 0,139,"Dark blue"); KohonenMap.ShowPattern(255,255, 0,"Yellow"); KohonenMap.ShowPattern(255,165, 0,"Orange"); KohonenMap.ShowPattern(128, 0,128,"Purple"); //--- show bmp image on the chart KohonenMap.ShowBMP(false); //--- }
Das Ergebnis wird in Abb. 2 dargestellt.
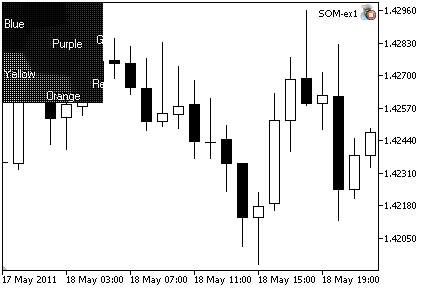
Abbildung 2. Ausgabe des Expert Advisors SOM_ex1.mq5
Die Dynamiken der Einlernung der Kohonenkarte werden in Abb. 3 dargestellt (siehe Schritte unter dem Bild):
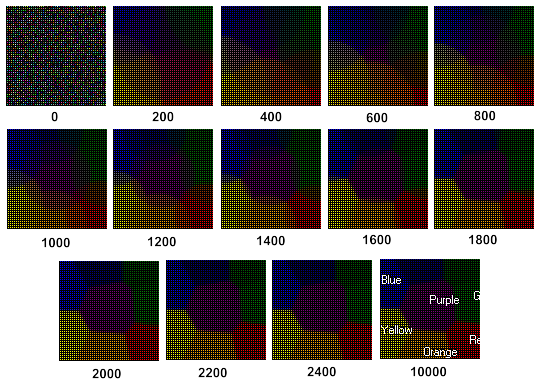
Abbildung 3. Dynamiken des Einlernens der Kohonenkarte
Aus Abb. 3 ist ersichtlich, dass die Kohonenkarte nach 2400 Schritten entsteht.
Wenn wir ein Raster aus 300 Knoten erstellen und die Bildgröße mit 400x400 festlegen:
//--- lattice of 15x20 nodes, image size 400x400 KohonenMap.InitParameters(10000,15,20,400,400);
erhalten wir das in Abb. 4 dargestellte Bild:
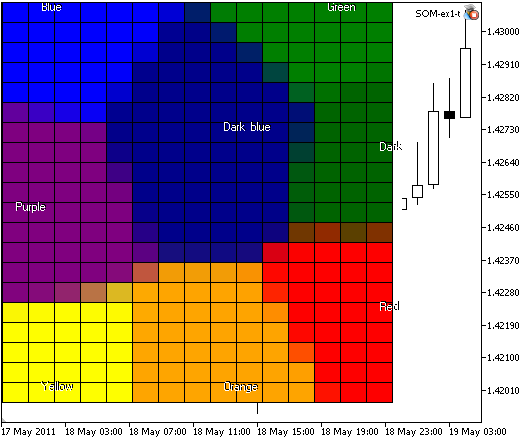
Abbildung 4. Kohonenkarte mit 300 Knoten, Bildgröße 400x400
Wenn Sie das Buch Visual Explorations in Finance: with Self-Organizing Maps von Guido Deboeck und Teuvo Kohonen lesen, werden Sie daran erinnert, dass Rasterknoten auch als sechseckige Zellen dargestellt werden können. Durch eine Anpassung des Codes des Expert Advisors können wir eine weitere Visualisierung umsetzen.
Das Ergebnis von SOM-ex1-hex.mq5 wird in Abb. 5 dargestellt:
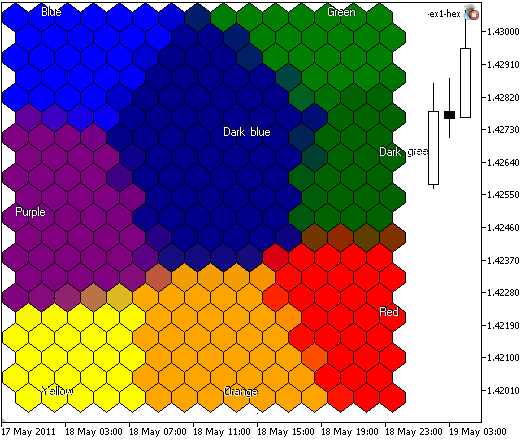
Abbildung 5. Kohonenkarte mit 300 Knoten, Bildgröße 400x400, Darstellung der Knoten als sechseckige Zellen
In dieser Version können wir die Anzeige von Zellenrändern durch die Verwendung von Eingabeparametern definieren:
// input parameter, used to show hexagonal cells input bool HexagonalCell=true; // input parameter, used to show borders input bool ShowBorders=true;
In einigen Fällen benötigen wir keine Anzeige der Zellenränder. Wenn Sie ShowBorders=false festlegen, erhalten Sie das folgende Bild (siehe Abb. 6):
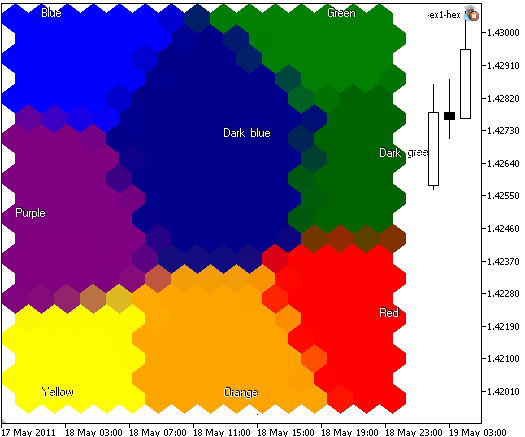
Abb. 6. Kohonenkarte mit 300 Knoten, Bildgröße 400x400, Darstellung der Knoten als sechseckige Zellen, Zellenränder deaktiviert
Im ersten Beispiel haben wir 8 Farben im Einlernsatz mit festgelegten Farbkomponenten verwendet. Wir können den Einlernsatz erweitern und die Festlegung von Farbkomponenten vereinfachen, indem wir die CSOM-Klasse um zwei Methoden erweitern.
Beachten Sie, dass die Kohonenkarten in diesem Fall einfach sind, weil es nur wenige Farben gibt, die im Farbraum getrennt sind. Als Ergebnis erhalten wir die lokalisierten Cluster.
Ein Problem entsteht, wenn wir mehr Farben mit näheren Farbkomponenten betrachten.
2,2. Beispiel 2. Nutzung von Web-Farben als Einlernmuster
In MQL5 sind die Web-Farben vordefinierte Konstanten.
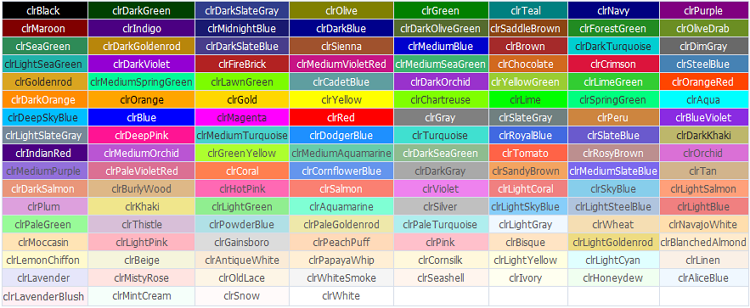
Abbildung 7. Web-Farben
Was wäre, wenn wir den Kohonen-Algorithmus auf einen Vektorsatz mit ähnlichen Komponenten anwenden?
Wir können die von der CSOM-Klasse abgeleitete Klasse CSOMWeb erstellen:
//+------------------------------------------------------------------+ //| CSOMWeb class | //+------------------------------------------------------------------+ class CSOMWeb : public CSOM { public: //--- adds a color to training set (used for colors, instead of AddTrainPattern) void AddTrainColor(int col); //--- method of showing of title of the pattern (used for colors, instead of ShowPattern) void ShowColor(int col,string name); };
Wie Sie sehen können, haben wir zwei neue Methoden hinzugefügt, um die Arbeit mit Farben zu vereinfachen. Die explizite Festlegung von Farbkomponenten ist nicht mehr erforderlich.
Die Umsetzung der Klasse sieht so aus:
//+------------------------------------------------------------------+ //| Adds a color to training set | //| (used for colors, instead of AddTrainPattern) | //+------------------------------------------------------------------+ void CSOMWeb::AddTrainColor(int col) { double vector[]; ArrayResize(vector,3); int r=0; int g=0; int b=0; ColToRGB(col,r,g,b); vector[0]=r; vector[1]=g; vector[2]=b; AddVectorToTrainingSet(vector); ArrayResize(vector,0); } //+------------------------------------------------------------------+ //| Method of showing of title of the pattern | //| (used for colors, instead of ShowPattern) | //+------------------------------------------------------------------+ void CSOMWeb::ShowColor(int col,string name) { int r=0; int g=0; int b=0; ColToRGB(col,r,g,b); ShowPattern(r,g,b,name); }
Alle Web-Farben können im Array web_colors[] kombiniert werden:
//--- web colors array color web_colors[132]= { clrBlack, clrDarkGreen, clrDarkSlateGray, clrOlive, clrGreen, clrTeal, clrNavy, clrPurple, clrMaroon, clrIndigo, clrMidnightBlue, clrDarkBlue, clrDarkOliveGreen, clrSaddleBrown, clrForestGreen, clrOliveDrab, clrSeaGreen, clrDarkGoldenrod, clrDarkSlateBlue, clrSienna, clrMediumBlue, clrBrown, clrDarkTurquoise, clrDimGray, clrLightSeaGreen, clrDarkViolet, clrFireBrick, clrMediumVioletRed, clrMediumSeaGreen, clrChocolate, clrCrimson, clrSteelBlue, clrGoldenrod, clrMediumSpringGreen, clrLawnGreen, clrCadetBlue, clrDarkOrchid, clrYellowGreen, clrLimeGreen, clrOrangeRed, clrDarkOrange, clrOrange, clrGold, clrYellow, clrChartreuse, clrLime, clrSpringGreen, clrAqua, clrDeepSkyBlue, clrBlue, clrMagenta, clrRed, clrGray, clrSlateGray, clrPeru, clrBlueViolet, clrLightSlateGray, clrDeepPink, clrMediumTurquoise, clrDodgerBlue, clrTurquoise, clrRoyalBlue, clrSlateBlue, clrDarkKhaki, clrIndianRed, clrMediumOrchid, clrGreenYellow, clrMediumAquamarine, clrDarkSeaGreen, clrTomato, clrRosyBrown, clrOrchid, clrMediumPurple, clrPaleVioletRed, clrCoral, clrCornflowerBlue, clrDarkGray, clrSandyBrown, clrMediumSlateBlue, clrTan, clrDarkSalmon, clrBurlyWood, clrHotPink, clrSalmon, clrViolet, clrLightCoral, clrSkyBlue, clrLightSalmon, clrPlum, clrKhaki, clrLightGreen, clrAquamarine, clrSilver, clrLightSkyBlue, clrLightSteelBlue, clrLightBlue, clrPaleGreen, clrThistle, clrPowderBlue, clrPaleGoldenrod, clrPaleTurquoise, clrLightGray, clrWheat, clrNavajoWhite, clrMoccasin, clrLightPink, clrGainsboro, clrPeachPuff, clrPink, clrBisque, clrLightGoldenrod, clrBlanchedAlmond, clrLemonChiffon, clrBeige, clrAntiqueWhite, clrPapayaWhip, clrCornsilk, clrLightYellow, clrLightCyan, clrLinen, clrLavender, clrMistyRose, clrOldLace, clrWhiteSmoke, clrSeashell, clrIvory, clrHoneydew, clrAliceBlue, clrLavenderBlush, clrMintCream, clrSnow, clrWhite };
Die OnInit()-Funktion hat die einfache Form:
CSOMWeb KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ void OnInit() { MathSrand(200); int total_web_colors=ArraySize(web_colors); //--- initialize net, 10000 iterations will be used for training //--- the net contains 15x20 nodes, bmp image size 400x400 KohonenMap.InitParameters(10000,50,50,500,500); //-- add all web colors to training set for(int i=0; i<total_web_colors; i++) { KohonenMap.AddTrainColor(web_colors[i]); } //--- train net KohonenMap.Train(); //--- render map to bmp KohonenMap.Render(); //--- show patterns and titles for each color for(int i=0; i<total_web_colors; i++) { KohonenMap.ShowColor(web_colors[i],ColorToString(web_colors[i],true)); } //--- show bmp image on the chart KohonenMap.ShowBMP(false); }
Wenn wir som-ex2-hex.mq5 ausführen, erhalten wir das in Abb. 8 dargestellte Bild.
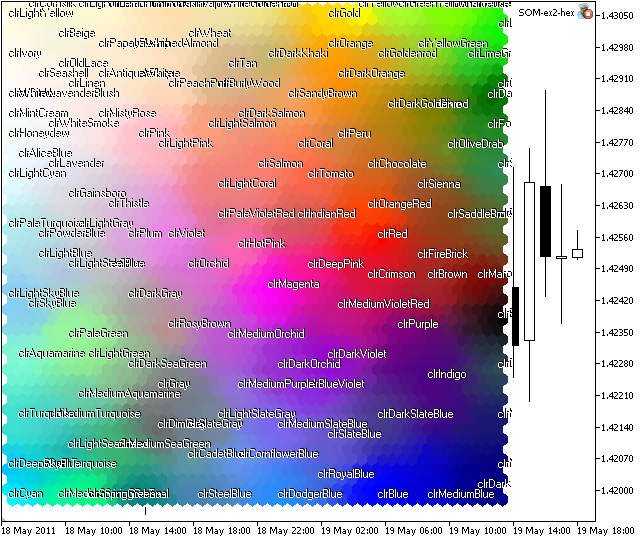
Abbildung 8. Kohonenkarte für Web-Farben
Wie Sie sehen können, gibt es einige Cluster, doch einige Farben (wie xxxBlue) befinden sich in unterschiedlichen Bereichen.
Der Grund dafür ist die Struktur des Einlernsatzes: Es gibt viele Vektoren mit nahen Komponenten.
2,3. Beispiel 3. Clusterung von Produkten
Als Nächstes betrachten wir ein einfaches Beispiel, in dem fünfundzwanzig verschiedene Lebensmittel in Ähnlichkeitsbereichen auf Basis der drei Parameter Eiweiß, Kohlenhydrat und Fett gruppiert werden sollen.
| Lebensmittel | Eiweiß | Kohlehydrat | Fett | |
|---|---|---|---|---|
| 1 | Äpfel | 0,4 | 11,8 | 0,1 |
| 2 | Avocado | 1,9 | 1,9 | 19,5 |
| 3 | Bananen | 1,2 | 23,2 | 0,3 |
| 4 | Rindersteak | 20,9 | 0 | 7,9 |
| 5 | Big Mac | 13 | 19 | 11 |
| 6 | Paranüsse | 15,5 | 2,9 | 68,3 |
| 7 | Brot | 10,5 | 37 | 3,2 |
| 8 | Butter | 1 | 0 | 81 |
| 9 | Käse | 25 | 0,1 | 34,4 |
| 10 | Käsekuchen | 6,4 | 28,2 | 22,7 |
| 11 | Kekse | 5,7 | 58,7 | 29,3 |
| 12 | Corn Flakes | 7 | 84 | 0,9 |
| 13 | Eier | 12,5 | 0 | 10,8 |
| 14 | Brathähnchen | 17 | 7 | 20 |
| 15 | Pommes | 3 | 36 | 13 |
| 16 | Heiße Schokolade | 3,8 | 19,4 | 10,2 |
| 17 | Peperoni | 20,9 | 5,1 | 38,3 |
| 18 | Pizza | 12,5 | 30 | 11 |
| 19 | Schweinefleischpastete | 10,1 | 27,3 | 24,2 |
| 20 | Kartoffeln | 1,7 | 16,1 | 0,3 |
| 21 | Reis | 6,9 | 74 | 2,8 |
| 22 | Backhähnchen | 26,1 | 0,3 | 5,8 |
| 23 | Zucker | 0 | 95,1 | 0 |
| 24 | Tunfischsteak | 25,6 | 0 | 0,5 |
| 25 | Wasser | 0 | 0 | 0 |
Tabelle 1. Eiweiß, Kohlenhydrate und Fett von 25 Lebensmitteln.
Dies ist eine interessante Aufgabe, weil die Eingabevektoren unterschiedliche Werte haben und jede Komponente über einen eigenen Wertebereich verfügt. Dies ist für die Visualisierung wichtig, weil wir das RGB-Farbmodell mit Komponenten zwischen 0 und 255 anwenden.
Glücklicherweise sind die Eingabevektoren in diesem Fall ebenfalls 3-dimensional, sodass wir das RGB-Farbmodell für die Visualisierung der Kohonenkarte nutzen können.
//+------------------------------------------------------------------+ //| CSOMFood class | //+------------------------------------------------------------------+ class CSOMFood : public CSOM { protected: double m_max_values[]; double m_min_values[]; public: void Train(); void Render(); void ShowPattern(double c1,double c2,double c3,string name); };
Wie Sie sehen können, haben wir die Arrays m_max_values[] und m_min_values[] für die Speicherung der Höchst- und Mindestwerte der Einlernsätze hinzugefügt. Für die Visualisierung im RGB-Farbmodell wird die "Skalierung" benötigt, also haben wir die Methoden Train(), Render() und ShowPattern() neu bestimmt.
Die Suche nach den Höchst- und Mindestwerten ist in der Methode Train() enthalten.
//--- find minimal and maximal values of the training set ArrayResize(m_max_values,3); ArrayResize(m_min_values,3); for(int j=0; j<3; j++) { double maxv=m_training_sets_array[3+j]; double minv=m_training_sets_array[3+j]; for(int i=1; i<m_total_training_sets; i++) { double v=m_training_sets_array[3*i+j]; if(v>maxv) {maxv=v;} if(v<minv) {minv=v;} } m_max_values[j]=maxv; m_min_values[j]=minv; Print(j,"m_min_value=",m_min_values[j],"m_max_value=",m_max_values[j]); }
Um die Komponenten im RGB-Farbmodell anzuzeigen, müssen wir die Methode Render() anpassen:
// int r = int(m_som_nodes[ind].GetWeight(0)); // int g = int(m_som_nodes[ind].GetWeight(1)); // int b = int(m_som_nodes[ind].GetWeight(2)); int r=int ((255*(m_som_nodes[ind].GetWeight(0)-m_min_values[0])/(m_max_values[0]-m_min_values[0]))); int g=int ((255*(m_som_nodes[ind].GetWeight(1)-m_min_values[1])/(m_max_values[1]-m_min_values[1]))); int b=int ((255*(m_som_nodes[ind].GetWeight(2)-m_min_values[2])/(m_max_values[2]-m_min_values[2])));
Das Ergebnis von som_ex3.mq5 wird in Abb. 9 dargestellt.
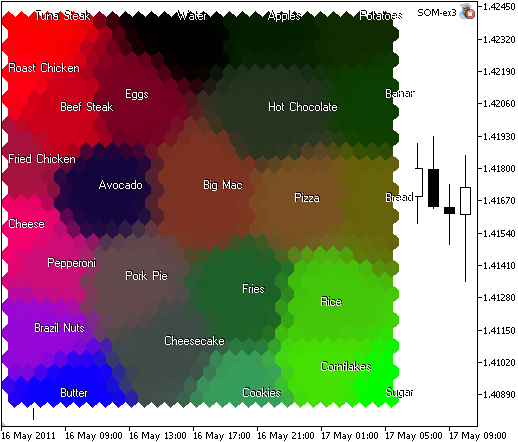
Abbildung 9. Lebensmittelkarte, gruppiert in Ähnlichkeitsbereiche auf Basis von Eiweiß, Kohlehydraten und Fett
Analyse der Komponenten. In der Karte ist ersichtlich, dass Zucker, Reis und Corn Flakes aufgrund des Kohlenhydrats (2. Komponente) in Grün dargestellt werden. Die Butter ist in der blauen Zone, weil sie viel Fett (3. Komponente) enthält. Rindersteak, Backhähnchen und Tunfischsteak enthalten viel Eiweiß (1. Komponente, rot).
Sie können den Einlernsatz durch das Hinzufügen neuer Lebensmittel aus den Tabellen der Lebensmittelzusammensetzung (alternative Tabelle) erweitern.
Wie Sie sehen können, ist das Problem für die "reinen" R-, G- und B-Richtungen gelöst. Doch wie sieht es bei anderen Lebensmitteln mit mehreren gleichen (oder weitestgehend gleichen) Bestandteilen aus? Im Weiteren betrachten wir die Komponente Ebenen. Diese ist äußerst nützlich, insbesondere in Fällen, in denen die Eingabevektoren mehr als 3 Dimensionen haben.
2,4. Beispiel 4. 4-dimensionaler Fall. Der Fisher'sche Iris-Datensatz. CMYK
Bei der Visualisierung dreidimensionaler Vektoren gibt es keine Probleme. Die Ergebnisse sind dank des für die Visualisierung von Farbkomponenten verwendeten RGB-Farbmodells klar.
Bei der Arbeit mit hochdimensionalen Daten müssen wir einen Weg finden, sie zu visualisieren. Die einfachste Lösung ist die Darstellung als Farbverlaufskarte (beispielsweise Schwarz-Weiß), deren Farben proportional zur Vektorlänge sind. Die andere Variante ist die Nutzung eines anderen Farbraums. In diesem Beispiel betrachten wir das CMYK-Farbmodell für den Fisher'schen Iris-Datensatz. Es gibt noch eine bessere Lösung, die wir später betrachten werden.
Der Iris-Datensatz oder der Fisher'sche Iris-Datensatz ist ein multivariater Datensatz, der von R. Fisher (1936) als Beispiel für die Diskriminanzanalyse eingeführt wurde. Der Datensatz besteht aus 50 Exemplaren von jeder der drei Gattungen der Schwertlilien (Iris setosa, Iris virginica und Iris versicolor).
Vier Merkmale jedes Exemplars, die Länge und Breite des Kelchblatts und des Blütenblatts, wurden in Zentimetern gemessen.

Abbildung 10. Schwertlilie
Jedes Exemplar weist 4 Merkmale auf:
- Länge des Kelchblatts;
- Breite des Kelchblatts;
- Länge des Blütenblatts;
- Breite des Blütenblatts.
Den Iris-Datensatz finden Sie in SOM_ex4.mq5.
In diesem Beispiel nutzen wir den Zwischenfarbraum CMYK für die Darstellung, d. h. wir betrachten die Gewichtungen des Knotens als Vektoren im CMYK-Raum. Für die Visualisierung der Ergebnisse wird die Konvertierung von CMYK in RGB genutzt. Die neue Methode int CSOM::CMYK2Col(uchar c,uchar m,uchar y,uchar k) wird der CSOM-Klasse hinzugefügt, die in der Methode CSOM::Render() verwendet wird. Genauso müssen wir die Klassen anpassen, damit sie 4-dimensionale Vektoren unterstützen.
Das Ergebnis wird in Abb. 11 dargestellt.
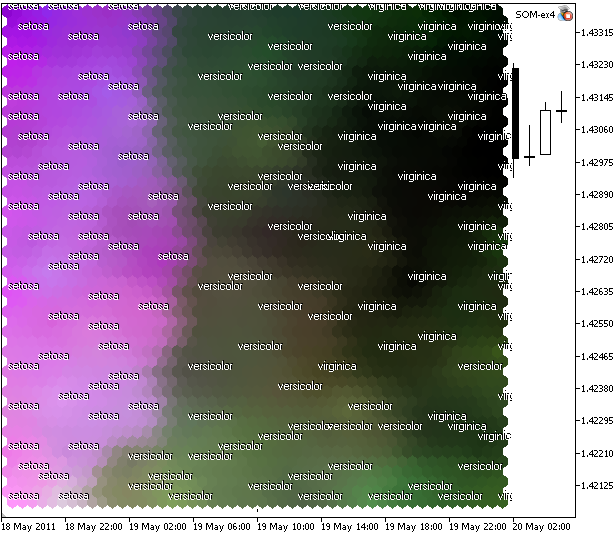
Abbildung 11. Kohonenkarte des Iris-Datensatzes, dargestellt im CMYK-Farbmodell
Was sehen wir? Wir verfügen nicht über die vollständige Clusterung (aufgrund der Merkmale der Aufgabe), doch man sieht eine lineare Trennung der Iris setosa.
Der Grund für diese lineare Trennung der setosa ist der hohe Anteil der Komponente "Magenta" (2. Komponente) im CMYK-Raum.
2,6. Analyse der Komponentenebenen
Anhand der vorhergehenden Beispiele (Clusterung von Lebensmittel- und Iris-Daten) sieht man, dass es ein Problem mit der Datenvisualisierung gibt.
Für die Lebensmittelaufgabe haben wir zum Beispiel die Kohonenkarte mithilfe der Informationen über bestimmte Farben (Rot, Grün, Blau) analysiert. Zusätzlich zu den Grund-Clustern gab es bestimmte Lebensmittel mit mehreren Komponenten. Zusätzlich wird die Analyse erschwert, wenn die Komponenten weitestgehend gleich sind.
Die Ebenen der Komponenten liefern uns die Möglichkeit, die relative Intensität für jedes der Lebensmittel zu sehen.
Wir müssen die Instanzen der Klasse CIntBMP (Array m_bmp[]) in die CSOM-Klasse einfügen und die entsprechenden Abbildungsmethoden anpassen. Ebenso benötigen wir eine Farbverlaufskarte, um die Intensität jeder Komponente zu visualisieren (niedrigere Werte werden in Blau, höhere in Rot angezeigt):
![]()
Abbildung 12. Verlaufspalette
Wir haben das Array Palette[768] und die Methoden GetPalColor() und Blend() hinzugefügt. Die Darstellung von Knoten befindet sich in der Methode RenderCell().
Iris-Datensatz
Die Ergebnisse von som-ex4-cpr.mq5 werden in Abb. 13 dargestellt.
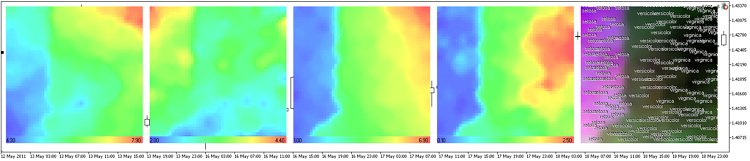
Abbildung 13. Komponentenebenen-Darstellung des Iris-Datensatzes
In diesem Fall haben wir ein Raster mit 30x30 Knoten verwendet, die Bildgröße beträgt 300x300.
Die Komponentenebenen spielen eine wichtige Rolle bei der Korrelationssuche: Durch den Vergleich dieser Ebenen können sogar nur teilweise korrelierende Variablen durch eine Sichtprüfung gefunden werden. Dies ist einfacher, wenn die Komponentenebenen neu angeordnet werden, sodass die korrelierenden nahe beieinander sind. Auf diese Weise lassen sich interessante Kombinationen von Komponenten für die weitere Untersuchung einfach auswählen.
Betrachten wir die Komponentenebenen (Abb. 14).
Die Werte der Maximum- und Minimum-Komponenten werden in der Farbverlaufstabelle gezeigt.
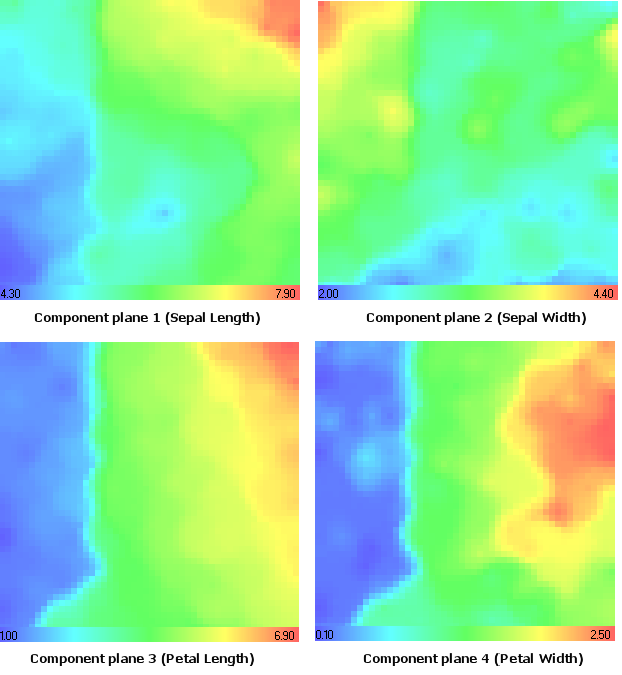
Abbildung 14. Iris-Datensatz. Komponentenebenen
Alle diese im CMYK-Farbmodell dargestellten Komponentenebenen werden in Abb. 15 gezeigt.

Abbildung 15. Iris-Datensatz. Kohonenkarte im CMYK-Farbmodell
Betrachten wir den Iris-Typ setosa. Mithilfe der Analyse der Komponentenebenen (Abb. 14) kann man erkennen, dass er Minimal-Werte in der 1. (Länge des Kelchblatts), 3. (Länge des Blütenblatts) und 4. (Breite des Blütenblatts) Komponentenebene aufweist.
Auffallend ist, dass er Maximal-Werte in der 2. Komponentenebene (Breite des Kelchblatts) aufweist – das gleiche Ergebnis, das wir im CMYK-Farbmodell (Magenta-Komponente, Abb. 15) erhalten haben.
Clusterung von Lebensmitteln
Betrachten wir nun die Aufgabe der Clusterung von Lebensmitteln mithilfe der Analyse von Komponentenebenen (som-ex3-cpr.mq5).
Das Ergebnis wird in Abb. 16 präsentiert (30x30 Knoten, Bildgröße 300x300, sechseckige Zellen ohne Grenzen).
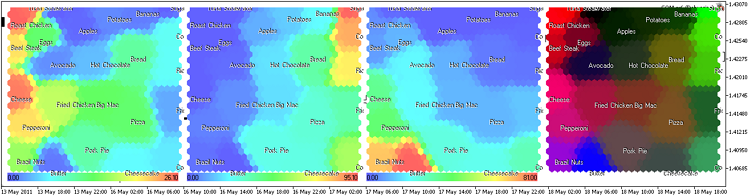
Abbildung 16. Kohonenkarte für Lebensmittel, Darstellung der Komponentenebenen
Wir haben die Anzeige von Titeln in der Methode ShowPattern() der Klasse CSOM hinzugefügt (Eingabeparameter ShowTitles=true).
Die Komponentenebenen (Eiweiß, Kohlenhydrat, Fett) sehen so aus:
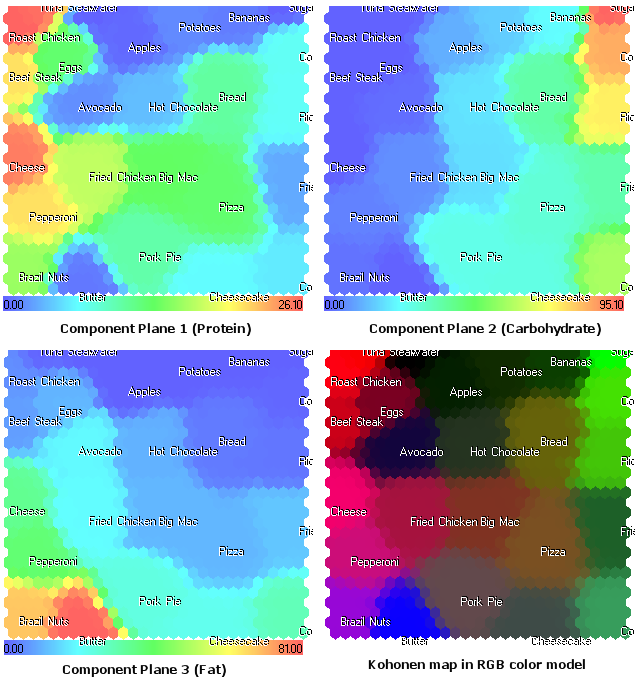
Abbildung 17. Kohonenkarte für Lebensmittel. Komponentenebenen und RGB-Farbmodell
Die in Abb. 17 gezeigte Darstellung der Komponentenebenen ermöglicht eine neue Ansicht der Struktur der Lebensmittelkomponenten. Zudem liefert sie zusätzliche Informationen, die im in Abb. 9 gezeigten RGB-Farbmodell nicht sichtbar sind.
Beispielsweise sehen wir nun, dass Käse sich in der 1. Komponentenebene (Eiweiß) befindet. Im RGB-Farbmodell wird er aufgrund des Fettes (2. Komponente) mit einer Farbe nahe an Magenta dargestellt.
2,5. Umsetzung der Komponentenebenen bei beliebigen Dimensionen
In den Beispielen, die wir betrachtet haben, war die Dimension fix und der Algorithmus der Visualisierung war bei verschiedenen Darstellungsarten (RGB- und CMYK-Farbmodelle) unterschiedlich.
Nun können wir den Algorithmus für beliebige Dimensionen verallgemeinern, doch in diesem Fall visualisieren wir nur die Komponentenebenen. Das Programm muss die beliebigen Daten aus einer CSV-Datei laden können.
Die Datei food.csv sieht beispielsweise so aus:
Protein;Carbohydrate;Fat;Title 0.4;11.8;0.1;Apples 1.9;1.9;19.5;Avocado 1.2;23.2;0.3;Bananas 20.9;0.0;7.9;Beef Steak 13.0;19.0;11.0;Big Mac 15.5;2.9;68.3;Brazil Nuts 10.5;37.0;3.2;Bread 1.0;0.0;81.0;Butter 25.0;0.1;34.4;Cheese 6.4;28.2;22.7;Cheesecake 5.7;58.7;29.3;Cookies 7.0;84.0;0.9;Cornflakes 12.5;0.0;10.8;Eggs 17.0;7.0;20.0;Fried Chicken 3.0;36.0;13.0;Fries 3.8;19.4;10.2;Hot Chocolate 20.9;5.1;38.3;Pepperoni 12.5;30.0;11.0;Pizza 10.1;27.3;24.2;Pork Pie 1.7;16.1;0.3;Potatoes 6.9;74.0;2.8;Rice 26.1;0.3;5.8;Roast Chicken 0.0;95.1;0.0;Sugar 25.6;0.0;0.5;Tuna Steak 0.0;0.0;0.0;Water
Die erste Zeile der Datei enthält die Namen (Titel) des Vektors der Eingabedaten. Die Titel werden für die Unterscheidung der Komponentenebenen benötigt. Wir werden ihre Namen im Farbverlaufs-Panel darstellen.
Der Name des Musters befindet sich in der letzten Spalte, in unserem Fall handelt es sich um den Namen des Lebensmittels.
Der Code von SOM.mq5 (Funktion OnInit) wurde vereinfacht:
CSOM KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { MathSrand(200); //--- load patterns from file if(!KohonenMap.LoadTrainDataFromFile(DataFileName)) { Print("Error in loading data for training."); return(1); } //--- train net KohonenMap.Train(); //--- render map KohonenMap.Render(); //--- show patterns from training set KohonenMap.ShowTrainPatterns(); //--- show bmp on the chart KohonenMap.ShowBMP(false); return(0); }
Der Name der Datei, die die Einlernmuster enthält, wird im Eingabeparameter DataFileName angegeben, in unserem Fall "food.csv".
Das Ergebnis wird in Abb. 18 dargestellt.

Abbildung 18. Kohonenkarte für Lebensmittel mit schwarz-weißem Farbverlaufsschema
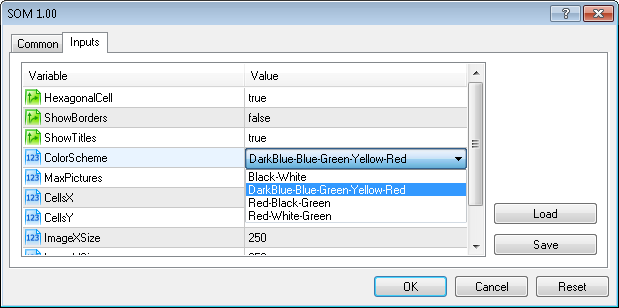
Wir haben ebenso den Eingabeparameter ColorScheme für die Auswahl des Farbverlaufsschemas hinzugefügt.
Derzeit sind 4 Farbschemata verfügbar (ColorScheme=0,1,2,4=Schwarz-Weiß, Dunkelblau-Blau-Grün-Gelb-Rot, Rot-Schwarz-Grün, Rot-Weiß-Grün).

Sie können Ihr eigenes Schema einfach durch Hinzufügen des Farbverlaufs in der Methode CSOM::InitParameters() hinzufügen.
Das Farbschema kann aus den Eingabeparametern des Expert Advisors ausgewählt werden:
Auf ähnliche Weise können wir den Iris-Datensatz (iris-fisher.csv) vorbereiten:
Sepal length;Sepal width;Petal length;Petal width;Title 5.1;3.5;1.4;0.2;setosa 4.9;3.0;1.4;0.2;setosa 4.7;3.2;1.3;0.2;setosa 4.6;3.1;1.5;0.2;setosa 5.0;3.6;1.4;0.2;setosa 5.4;3.9;1.7;0.4;setosa 4.6;3.4;1.4;0.3;setosa 5.0;3.4;1.5;0.2;setosa 4.4;2.9;1.4;0.2;setosa 4.9;3.1;1.5;0.1;setosa 5.4;3.7;1.5;0.2;setosa 4.8;3.4;1.6;0.2;setosa 4.8;3.0;1.4;0.1;setosa 4.3;3.0;1.1;0.1;setosa 5.8;4.0;1.2;0.2;setosa 5.7;4.4;1.5;0.4;setosa 5.4;3.9;1.3;0.4;setosa 5.1;3.5;1.4;0.3;setosa 5.7;3.8;1.7;0.3;setosa 5.1;3.8;1.5;0.3;setosa 5.4;3.4;1.7;0.2;setosa 5.1;3.7;1.5;0.4;setosa 4.6;3.6;1.0;0.2;setosa 5.1;3.3;1.7;0.5;setosa 4.8;3.4;1.9;0.2;setosa 5.0;3.0;1.6;0.2;setosa 5.0;3.4;1.6;0.4;setosa 5.2;3.5;1.5;0.2;setosa 5.2;3.4;1.4;0.2;setosa 4.7;3.2;1.6;0.2;setosa 4.8;3.1;1.6;0.2;setosa 5.4;3.4;1.5;0.4;setosa 5.2;4.1;1.5;0.1;setosa 5.5;4.2;1.4;0.2;setosa 4.9;3.1;1.5;0.2;setosa 5.0;3.2;1.2;0.2;setosa 5.5;3.5;1.3;0.2;setosa 4.9;3.6;1.4;0.1;setosa 4.4;3.0;1.3;0.2;setosa 5.1;3.4;1.5;0.2;setosa 5.0;3.5;1.3;0.3;setosa 4.5;2.3;1.3;0.3;setosa 4.4;3.2;1.3;0.2;setosa 5.0;3.5;1.6;0.6;setosa 5.1;3.8;1.9;0.4;setosa 4.8;3.0;1.4;0.3;setosa 5.1;3.8;1.6;0.2;setosa 4.6;3.2;1.4;0.2;setosa 5.3;3.7;1.5;0.2;setosa 5.0;3.3;1.4;0.2;setosa 7.0;3.2;4.7;1.4;versicolor 6.4;3.2;4.5;1.5;versicolor 6.9;3.1;4.9;1.5;versicolor 5.5;2.3;4.0;1.3;versicolor 6.5;2.8;4.6;1.5;versicolor 5.7;2.8;4.5;1.3;versicolor 6.3;3.3;4.7;1.6;versicolor 4.9;2.4;3.3;1.0;versicolor 6.6;2.9;4.6;1.3;versicolor 5.2;2.7;3.9;1.4;versicolor 5.0;2.0;3.5;1.0;versicolor 5.9;3.0;4.2;1.5;versicolor 6.0;2.2;4.0;1.0;versicolor 6.1;2.9;4.7;1.4;versicolor 5.6;2.9;3.6;1.3;versicolor 6.7;3.1;4.4;1.4;versicolor 5.6;3.0;4.5;1.5;versicolor 5.8;2.7;4.1;1.0;versicolor 6.2;2.2;4.5;1.5;versicolor 5.6;2.5;3.9;1.1;versicolor 5.9;3.2;4.8;1.8;versicolor 6.1;2.8;4.0;1.3;versicolor 6.3;2.5;4.9;1.5;versicolor 6.1;2.8;4.7;1.2;versicolor 6.4;2.9;4.3;1.3;versicolor 6.6;3.0;4.4;1.4;versicolor 6.8;2.8;4.8;1.4;versicolor 6.7;3.0;5.0;1.7;versicolor 6.0;2.9;4.5;1.5;versicolor 5.7;2.6;3.5;1.0;versicolor 5.5;2.4;3.8;1.1;versicolor 5.5;2.4;3.7;1.0;versicolor 5.8;2.7;3.9;1.2;versicolor 6.0;2.7;5.1;1.6;versicolor 5.4;3.0;4.5;1.5;versicolor 6.0;3.4;4.5;1.6;versicolor 6.7;3.1;4.7;1.5;versicolor 6.3;2.3;4.4;1.3;versicolor 5.6;3.0;4.1;1.3;versicolor 5.5;2.5;4.0;1.3;versicolor 5.5;2.6;4.4;1.2;versicolor 6.1;3.0;4.6;1.4;versicolor 5.8;2.6;4.0;1.2;versicolor 5.0;2.3;3.3;1.0;versicolor 5.6;2.7;4.2;1.3;versicolor 5.7;3.0;4.2;1.2;versicolor 5.7;2.9;4.2;1.3;versicolor 6.2;2.9;4.3;1.3;versicolor 5.1;2.5;3.0;1.1;versicolor 5.7;2.8;4.1;1.3;versicolor 6.3;3.3;6.0;2.5;virginica 5.8;2.7;5.1;1.9;virginica 7.1;3.0;5.9;2.1;virginica 6.3;2.9;5.6;1.8;virginica 6.5;3.0;5.8;2.2;virginica 7.6;3.0;6.6;2.1;virginica 4.9;2.5;4.5;1.7;virginica 7.3;2.9;6.3;1.8;virginica 6.7;2.5;5.8;1.8;virginica 7.2;3.6;6.1;2.5;virginica 6.5;3.2;5.1;2.0;virginica 6.4;2.7;5.3;1.9;virginica 6.8;3.0;5.5;2.1;virginica 5.7;2.5;5.0;2.0;virginica 5.8;2.8;5.1;2.4;virginica 6.4;3.2;5.3;2.3;virginica 6.5;3.0;5.5;1.8;virginica 7.7;3.8;6.7;2.2;virginica 7.7;2.6;6.9;2.3;virginica 6.0;2.2;5.0;1.5;virginica 6.9;3.2;5.7;2.3;virginica 5.6;2.8;4.9;2.0;virginica 7.7;2.8;6.7;2.0;virginica 6.3;2.7;4.9;1.8;virginica 6.7;3.3;5.7;2.1;virginica 7.2;3.2;6.0;1.8;virginica 6.2;2.8;4.8;1.8;virginica 6.1;3.0;4.9;1.8;virginica 6.4;2.8;5.6;2.1;virginica 7.2;3.0;5.8;1.6;virginica 7.4;2.8;6.1;1.9;virginica 7.9;3.8;6.4;2.0;virginica 6.4;2.8;5.6;2.2;virginica 6.3;2.8;5.1;1.5;virginica 6.1;2.6;5.6;1.4;virginica 7.7;3.0;6.1;2.3;virginica 6.3;3.4;5.6;2.4;virginica 6.4;3.1;5.5;1.8;virginica 6.0;3.0;4.8;1.8;virginica 6.9;3.1;5.4;2.1;virginica 6.7;3.1;5.6;2.4;virginica 6.9;3.1;5.1;2.3;virginica 5.8;2.7;5.1;1.9;virginica 6.8;3.2;5.9;2.3;virginica 6.7;3.3;5.7;2.5;virginica 6.7;3.0;5.2;2.3;virginica 6.3;2.5;5.0;1.9;virginica 6.5;3.0;5.2;2.0;virginica 6.2;3.4;5.4;2.3;virginica 5.9;3.0;5.1;1.8;virginica
Das Ergebnis wird in Abb. 19 dargestellt.

Abbildung 19. Iris-Datensatz. Komponentenebenen mit Rot-Schwarz-Grün-Farbschema (ColorScheme=2, iris-fisher.csv)
Nun verfügen wir über ein Werkzeug für reale Anwendungen.
2,6. Beispiel 5. Markt-Heatmaps
Selbstorganisierende Karten können für Karten von Marktbewegungen verwendet werden. Manchmal wird ein globales Bild des Marktes benötigt. Dafür ist die Markt-Heatmap ein sehr hilfreiches Werkzeug. Die Aktien werden abhängig von Wirtschaftssektoren kombiniert.
Die aktuelle Farbe der Aktie hängt von der der aktuellen Wachstumsrate (in %) ab:

Abbildung 20. Markt-Heatmap für Aktien aus S&P500
Die wöchentliche Markt-Heatmap der Aktien aus S&P (http://finviz.com) wird in Abb. 20 dargestellt. Die Farbe hängt von der Wachstumsrate (in %) ab:
![]()
Die Größe des Aktienrechtecks hängt von der Marktkapitalisierung ab. Die gleiche Analyse lässt sich im MetaTrader 5 Client Terminal mithilfe der Kohonenkarten durchführen.
Die Grundidee ist, die Wachstumsraten (in %) für mehrere Timeframes zu benutzen. Wir verfügen über das Werkzeug für die Arbeit mit Kohonenkarten, also wird nur noch ein Script benötigt, das die Daten in einer .csv-Datei speichert.
Die Preisdaten zu CFD-Preisen von amerikanischen Aktien (#AA, #AIG, #AXP, #BA, #BAC, #C, #CAT, #CVX, #DD, #DIS, #EK, #GE, #HD, #HON, #HPQ, #IBM, #INTC, #IP, #JNJ, #JPM, #KFT, #KO, #MCD, #MMM, #MO, #MRK, #MSFT, #PFE, #PG, #T, #TRV, #UTX, #VZ, #WMT и #XOM) können dem MetaQuotes Demo-Server entnommen werden.
Das Script, das die Datei dj.csv erstellt, ist äußerst simpel:
//+------------------------------------------------------------------+ //| DJ.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" string s_cfd[35]= { "#AA","#AIG","#AXP","#BA","#BAC","#C","#CAT","#CVX","#DD","#DIS","#EK","#GE", "#HD","#HON","#HPQ","#IBM","#INTC","#IP","#JNJ","#JPM","#KFT","#KO","#MCD","#MMM", "#MO","#MRK","#MSFT","#PFE","#PG","#T","#TRV","#UTX","#VZ","#WMT","#XOM" }; //+------------------------------------------------------------------+ //| Returns price change in percents | //+------------------------------------------------------------------+ double PercentChange(double Open,double Close) { return(100.0*(Close-Open)/Close); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { ResetLastError(); int filehandle=FileOpen("dj.csv",FILE_WRITE|FILE_ANSI); if(filehandle==INVALID_HANDLE) { Alert("Error opening file"); return; } //--- MqlRates MyRates[]; ArraySetAsSeries(MyRates,true); string t="M30;M60;M90;M120;M150;M180;M210;M240;Title"; FileWrite(filehandle,t); Print(t); int total_symbols=ArraySize(s_cfd); for(int i=0; i<total_symbols; i++) { string cursymbol=s_cfd[i]; int copied1=CopyRates(cursymbol,PERIOD_M30,0,8,MyRates); if(copied1>0) { string s=""; s=s+DoubleToString(PercentChange(MyRates[1].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[2].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[3].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[4].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[5].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[6].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[7].open,MyRates[0].close),3)+";"; s=s+cursymbol; Print(s); FileWrite(filehandle,s); } else { Print("Error in request of historical data on symbol ",cursymbol); return; } } Alert("OK"); FileClose(filehandle); } //+------------------------------------------------------------------+
Die historischen Daten müssen heruntergeladen werden. Dies können Sie mithilfe des Scripts DownloadHistory automatisch ausführen.
Als Ergebnis des Scripts dj.mq5 erhalten wir die Datei dj.csv mit den folgenden Daten:
M30;M60;M90;M120;M150;M180;M210;M240;Title 0.063;-0.564;-0.188;0.376;0.251;0.313;0.627;0.439;#AA -0.033;0.033;0.067;-0.033;0.067;-0.133;0.266;0.533;#AIG -0.176;0.039;0.039;0.274;0.196;0.215;0.430;0.646;#AXP -0.052;-0.328;-0.118;0.315;0.223;0.367;0.288;0.328;#BA -0.263;-0.351;-0.263;0.000;-0.088;0.088;0.000;-0.088;#BAC -0.224;-0.274;-0.374;-0.100;-0.274;-0.224;-0.324;-0.598;#C -0.069;-0.550;-0.079;0.766;0.727;0.638;0.736;0.589;#CAT -0.049;-0.168;0.099;0.247;0.187;0.049;0.355;0.266;#CVX 0.019;-0.058;0.058;0.446;0.174;0.349;0.136;-0.329;#DD -0.073;-0.219;-0.146;0.267;0.170;0.292;0.170;0.267;#DIS -1.099;-1.923;-1.099;0.275;0.275;0.275;-0.549;-1.374;#EK -0.052;-0.310;-0.103;0.362;0.258;0.362;0.465;0.258;#GE -0.081;-0.244;-0.326;-0.136;0.081;0.326;0.489;0.489;#HD -0.137;-0.427;-0.171;0.427;0.445;0.342;0.325;0.359;#HON -0.335;-0.363;-0.112;0.112;0.168;0.307;0.475;0.251;#HPQ 0.030;-0.095;0.065;0.190;0.071;0.214;0.279;0.327;#IBM 0.000;-0.131;-0.044;-0.088;-0.044;0.000;0.000;0.044;#INTC -0.100;-0.200;-0.166;0.100;-0.067;0.033;-0.532;-0.798;#IP -0.076;0.076;0.259;0.473;0.427;0.336;0.336;-0.076;#JNJ -0.376;-0.353;-0.494;-0.259;-0.423;-0.329;-0.259;-0.541;#JPM -0.057;-0.086;-0.029;0.086;0.114;0.057;0.257;-0.114;#KFT 0.059;-0.030;0.119;0.282;0.119;0.193;0.208;-0.119;#KO -0.109;-0.182;0.206;0.352;0.279;0.473;0.521;0.194;#MCD -0.043;-0.195;-0.151;0.216;0.270;0.227;0.411;0.206;#MMM -0.036;-0.072;0.072;0.144;-0.072;-0.108;0.108;0.072;#MO 0.081;-0.081;0.027;0.081;-0.054;0.027;-0.027;-0.108;#MRK 0.083;0.083;0.041;0.331;0.083;0.248;0.166;0.041;#MSFT 0.049;0.000;0.243;0.680;0.194;0.243;0.340;0.097;#PFE -0.045;0.060;0.104;0.015;-0.179;-0.149;-0.224;-0.224;#PG 0.097;-0.032;0.000;0.129;0.129;0.064;0.097;0.064;#T -0.277;-0.440;-0.326;-0.358;-0.537;-0.619;-0.570;-0.733;#TRV -0.081;-0.209;0.035;0.325;0.198;0.093;0.128;-0.035;#UTX 0.054;0.000;0.054;0.190;0.136;0.326;0.380;0.353;#VZ -0.091;-0.091;-0.036;0.036;-0.072;0.000;0.145;-0.127;#WMT -0.062;-0.211;0.087;0.198;0.186;0.050;0.347;0.508;#XOM
Nach dem Start von som.mq5 (ColorScheme=3, CellsX=30, CellsY=30, ImageXSize=200, ImageXSize=200, DataFileName="dj.csv") erhalten wir 8 Bilder, von denen jedes den Zeitintervallen 30, 60, 90, 120, 150, 180, 210 und 240 Minuten entspricht.
Die Kohonenkarten der Daten der Marktwachstumsrate (amerikanische Aktien) in den letzten 4 Stunden der Handelssitzung am 23. Mai 2011 sind in Abb. 21 dargestellt.
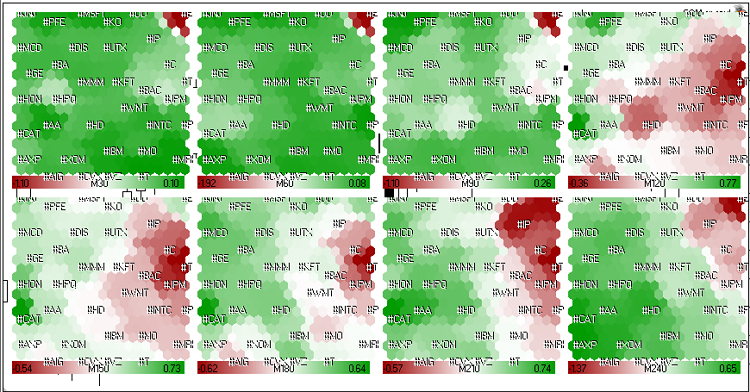
Abbildung 21. Kohonenkarten für amerikanische Aktien (letzte 4 Stunden der Handelssitzung am 23. Mai 2011).
Aus Abb. 21 ist ersichtlich, dass die Dynamiken von #C (Citigroup Inc.), #T (AT&T Inc.), #JPM (JPMorgan Chase & Co) und #BAC (Bank of America) ähnlich sind. Sie wurden in einem langfristigen roten Cluster gruppiert.
In den letzten 1,5 Stunden (M30, M60, M90) wurden ihre Dynamiken grün, im Allgemeinen (M240) befanden sich die Aktien im roten Bereich.
Mithilfe von Kohonenkarten können wir die relativen Dynamiken von Aktien visualisieren und somit Gewinner und Verlierer und deren Umgebung finden. Elemente mit ähnlichen Daten bilden Cluster.
Wie wir in Abb. 21a sehen, war der Preis der Aktien von Citigroup Inc führend beim Fallen. Im Allgemeinen befanden sich alle Aktien von Finanzunternehmen im roten Bereich.
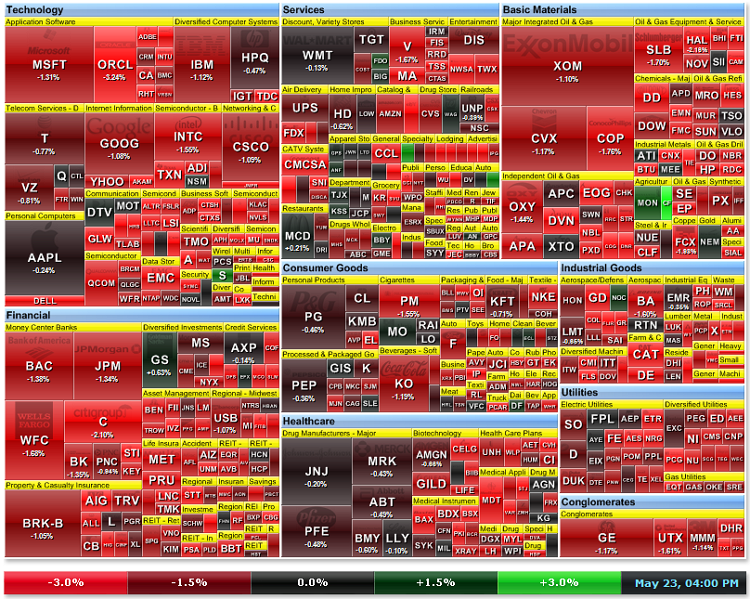
Abb. 21a Markt-Heatmap von 23. Mai 2011 (Quelle: http://finviz.com)
Auf ähnliche Weise können wir die Kohonenkarten des FOREX-Marktes berechnen (Abb. 22):
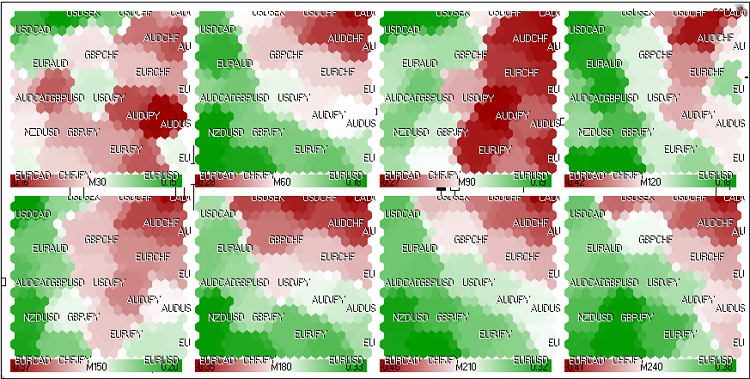
Abbildung 22. Kohonenkarte des FOREX-Marktes (24. Mai 2011, europäische Sitzung)
Es wurden die folgenden Paare verwendet: EURUSD, GBPUSD, USDCHF, USDJPY, USDCAD, AUDUSD, NZDUSD, USDSEK, AUDNZD, AUDCAD, AUDCHF, AUDJPY, CHFJPY, EURGBP, EURAUD, EURCHF, EURJPY, EURNZD, EURCAD, GBPCHF, GBPJPY, CADCHF.
Die Wachstumsraten werden mithilfe des Scripts fx.mq5 in die Datei fx.csv exportiert.
M30;M60;M90;M120;M150;M180;M210;M240;Title 0.058;-0.145;0.045;-0.113;-0.038;-0.063;0.180;0.067;EURUSD 0.046;-0.100;0.078;0.094;0.167;0.048;0.123;0.160;GBPUSD -0.048;0.109;-0.142;-0.097;-0.219;-0.143;-0.277;-0.236;USDCHF 0.042;0.097;0.043;-0.024;-0.009;-0.067;0.024;0.103;USDJPY -0.045;0.162;0.155;0.239;0.217;0.246;0.157;0.227;USDCAD 0.095;-0.126;-0.018;-0.141;-0.113;-0.062;0.081;-0.005;AUDUSD 0.131;-0.028;0.167;0.096;-0.013;0.147;0.314;0.279;NZDUSD -0.047;0.189;-0.016;0.107;0.084;0.076;-0.213;-0.133;USDSEK -0.034;-0.067;-0.188;-0.227;-0.102;-0.225;-0.234;-0.291;AUDNZD 0.046;0.039;0.117;0.102;0.097;0.170;0.234;0.216;AUDCAD 0.057;-0.016;-0.158;-0.226;-0.328;-0.215;-0.180;-0.237;AUDCHF 0.134;-0.020;0.024;-0.139;-0.124;-0.127;0.107;0.098;AUDJPY 0.083;-0.009;0.184;0.084;0.208;0.082;0.311;0.340;CHFJPY 0.025;-0.036;-0.030;-0.200;-0.185;-0.072;0.058;-0.096;EURGBP -0.036;-0.028;0.061;0.010;0.074;-0.006;0.088;0.070;EURAUD 0.008;-0.049;-0.098;-0.219;-0.259;-0.217;-0.094;-0.169;EURCHF 0.096;-0.043;0.085;-0.124;-0.049;-0.128;0.206;0.157;EURJPY -0.073;-0.086;-0.119;-0.211;-0.016;-0.213;-0.128;-0.213;EURNZD 0.002;0.009;0.181;0.119;0.182;0.171;0.327;0.284;EURCAD -0.008;0.004;-0.077;-0.015;-0.054;-0.127;-0.164;-0.080;GBPCHF 0.079;-0.005;0.115;0.079;0.148;-0.008;0.144;0.253;GBPJPY 0.013;-0.060;-0.294;-0.335;-0.432;-0.376;-0.356;-0.465;CADCHF
Zusätzlich zu den Preisen können Sie die Werte der Indikatoren in unterschiedlichen Timeframes benutzen.
2,6. Beispiel 6. Analyse der Optimierungsergebnisse
Der Strategietester des MetaTrader 5 Client Terminals liefert eine Möglichkeit, die Struktur des Parameterraums zu erforschen und den besten Satz der Strategieparameter zu finden. Sie können auch die Ergebnisse der Optimierung mithilfe der Option "Export to XML (MS Office Excel)" aus dem Kontextmenü der Registerkarte "Optimization Results" exportieren.
Die Testerstatistiken sind ebenfalls in den Ergebnissen der Optimierung enthalten (41 Spalten):
- Ergebnis
- Profit
- Gross Profit
- Gross Loss
- Withdrawal
- Expected Payoff
- Profit Factor
- Recovery Factor
- Sharpe Ratio
- Margin Level
- Custom
- Minimal Balance
- Balance DD Maximal
- Balance DD Maximal (%)
- Balance DD Relative
- Balance DD Relative (%)
- Minimal Equity
- Equity DD Maximal
- Equity DD Maximal (%)
- Equity DD Relative
- Equity DD Relative (%)
- Abschluss
- Abschlüsse
- Short Trades
- Profit Short Trades
- Long Trades
- Profit Long Trades
- Profit Trades
- Loss Trades
- Max profit trade
- Max loss trade
- Max consecutive wins
- Max consecutive wins ($)
- Max consecutive profit
- Max consecutive profit count
- Max consecutive losses
- Max consecutive losses ($)
- Max consecutive loss
- Max consecutive loss count
- Avg consecutive wins
- Avg consecutive losses
Durch den Gebrauch der Testerstatistiken wird die Analyse des Parameterraums unterstützt. Wichtig ist, dass viele Parameter der Statistik eng miteinander verknüpft sind und von den Ergebnissen der Handelsperformance abhängen.
Beispielsweise haben die besten Handelsergebnisse die höchsten Werte bei den Parametern Profit, Profit Factor, Recovery Factor und Sharpe Ratio. Dies ermöglicht es uns, sie für die Analyse der Ergebnisse zu nutzen.
Ergebnisse der Optimierung des Expert Advisors MovingAverage.mq5
In diesem Kapitel betrachten wir die Analyse der Ergebnisse der Optimierung des Expert Advisors MovingAverage.mq5, der im Standardpaket des MetaTrader 5 Client Terminals enthalten ist. Dieser Expert Advisor basiert auf der Überkreuzung des Preises und des Indikators des gleitenden Mittelwerts. Er hat zwei Eingabeparameter: MovingPeriod und MovingShift, d. h. wir erhalten als Ergebnis eine XML-Datei mit 43 Spalten.
Wir werden nicht den 43-dimensionalen Parameterraum betrachten. Am interessantesten für uns sind:
- Profit;
- Profit Factor;
- Recovery Factor;
- Sharpe Ratio;
- Trades;
- ProfitTrades(%);
- MovingPeriod;
- MovingShift;
Beachten Sie, dass wir den Parameter ProfitTrades (%) hinzugefügt haben (fehlt in den Ergebnissen). Er steht für den prozentualen Anteil der gewinnbringenden Abschlüsse und ist das Ergebnis der Teilung von ProfitTrades (28) durch Trades (22), multipliziert mit 100.
Erstellen wir die Datei optim.csv mit 9 Spalten für 400 Sätze von Eingabeparametern des MetaTrader 5 Strategietesters.
Profit;Profit Factor;Recovery Factor;Sharpe Ratio;Trades;ProfitTrades(%);MovingPeriod;MovingShift;Title -372.3;0.83;-0.51;-0.05;71;28.16901408;43;6;43 -345.79;0.84;-0.37;-0.05;66;27.27272727;50;6;50 ...
Beachten Sie, dass wir den Wert von MovingPeriod als Spalte Title verwendet haben. Er wird zum "Markieren" der Muster in den Kohonenkarten genutzt.
Im Strategietester haben wir die Werte von MovingPeriod und MovingShift mit den folgenden Parametern optimiert:
- Symbol – EURUSD,
- Zeitraum – H1,
- Tick-Erzeugungsmodus – "1-minütiger OHLC",
- Testintervall – 2011.01.01-2011.05.24,
- Optimierung – Schnell (genetischer Algorithmus),
- Optimierung – Balance max.
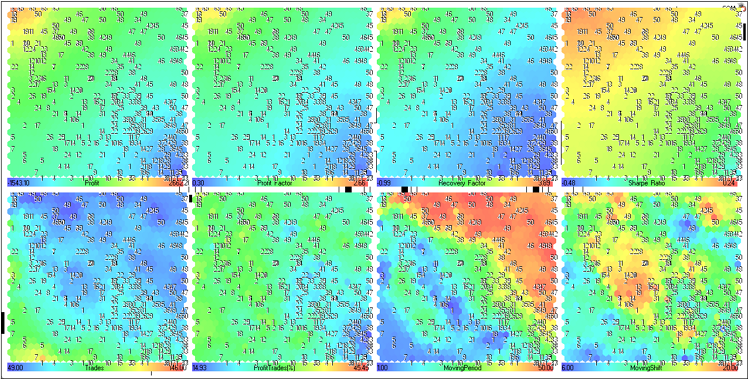
Abbildung 23. Kohonenkarte der Ergebnisse der Optimierung des EA MovingAverage (Darstellung als Komponentenebene)
Betrachten wir die Komponentenebenen der oberen Reihe (Profit, Profit Factor, Recovery Factor und Sharpe Ratio).
Sie werden in Abb. 24 kombiniert.
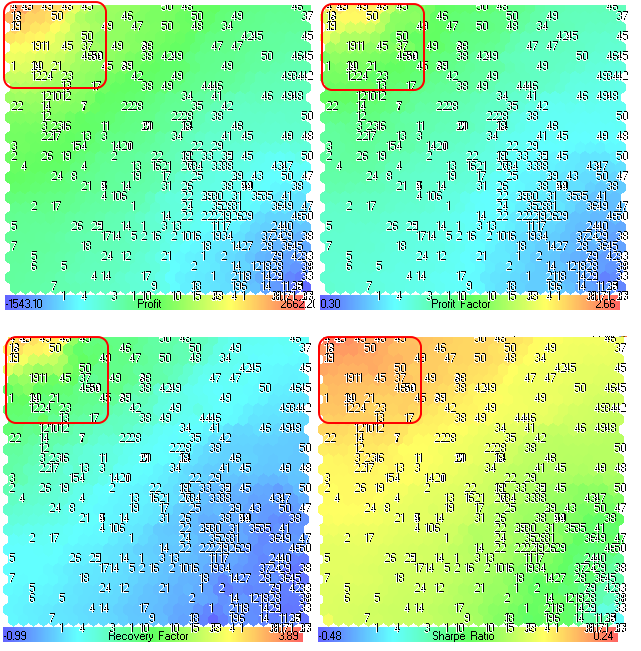
Abbildung 24. Komponentenebenen für die Parameter Profit, Profit Factor, Recovery Factor und Sharpe Ratio
Als Erstes müssen wir die Regionen mit den besten Optimierungsergebnissen finden.
Aus Abb. 24 geht hervor, dass sich die Regionen mit den höchsten Werten in der linken oberen Ecke befinden. Die Zahlen entsprechen dem Mittelungszeitraum des Indikators des gleitenden Mittelwerts (Parameter MovingPeriod, den wir als Titel verwendet haben). Die Position der Zahlen ist bei allen Komponentenebenen gleich. Jede Komponentenebene hat ihren eigenen Wertebereich, die Werte werden im Farbverlaufs-Panel wiedergegeben.
Die besten Optimierungsergebnisse haben die höchsten Werte für Profit, Profit Factor, Recovery Factor und Sharpe Ratio. Somit verfügen wir über Informationen über die Regionen auf der Karte (skizziert in Abb. 24).
Die Komponentenebenen für Trades, ProfitTrades(%), MovingPeriod und MovingShift werden in Abb. 25 präsentiert.
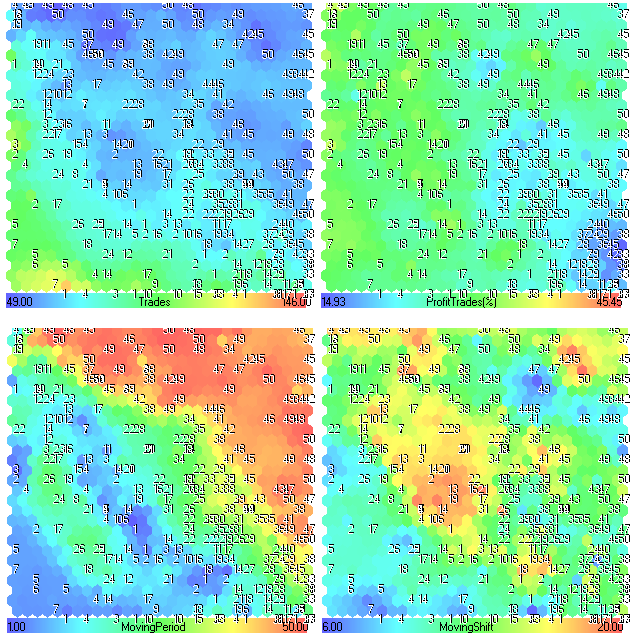
Abbildung 25. Komponentenebenen für die Parameter Trades, ProfitTrades(%), MovingPeriod und MovingShift
Analyse der Komponentenebenen
Auf den ersten Blick gibt es keine interessanten Informationen. Die ersten 4 Komponentenebenen (Profit, Profit Factor, Recovery Factor und Sharpe Ratio) sehen ähnlich aus, weil sie direkt von der Performance des Handelssystems abhängig sind.
Aus Abb. 24 ist ersichtlich, dass der Bereich links oben sehr interessant ist (beispielsweise lassen sich die besten Ergebnisse erzielen, wenn wir MovingPeriod zwischen 45 und 50 festlegen).
Der Expert Advisor wurde auf einem stündlichen Timeframe von EURUSD getestet, seine Strategie war trendbasiert. Wir können diese Werte als "Trendgedächtnis" des Marktes betrachten. Falls diese Annahme wahr ist, entspricht das Trendgedächtnis des Marktes für die erste Jahreshälfte 2011 2 Tagen.
Betrachten wir die anderen Komponentenebenen.
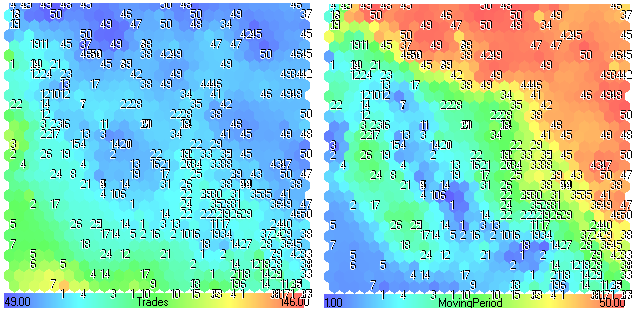
Abbildung 26. Komponentenebenen von Trades-MovingPeriod
Anhand von Abb. 26 können wir erkennen, dass geringere Werte von MovingPeriod (blaue Bereiche) zu höheren Werten von Trades (gelb-rote Bereiche) führen. Wenn der Zeitraum des gleitenden Mittelwerts kurz ist, gibt es viele Überkreuzungen (Abschlüsse).
Dies sehen wir auch in der Komponentenebene von Trades (grüne Bereiche mit Zahlen unter 20).
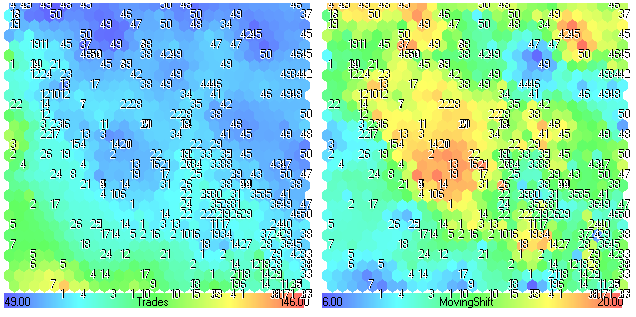
Abbildung 27. Komponentenebenen von Trades-MovingShift
Die Menge der Abschlüsse sinkt (blaue Bereiche) mit steigendem MovingShift (gelb-rote Bereiche). Anhand des Vergleichs der Komponentenebenen von MovingShift und Abb. 24 sieht man, dass der Parameter MovingShift für die Performance dieser Handelsstrategie nicht sehr wichtig ist.
Der Anteil gewinnbringender Abschlüsse ProfitTrades(%) hängt nicht direkt von MovingPeriod oder MovingShift ab, sondern ist ein integrales Merkmal des Handelssystems. In anderen Worten: Die Analyse seiner Korrelation mit Eingangsparametern hat keine Bedeutung.
Komplexere Handelsstrategien können auf ähnliche Art analysiert werden. Sie müssen den/die wichtigsten Parameter Ihres Handelssystems finden und sie als Titel benutzen.
Fazit
Der wichtigste Vorteil der selbstorganisierenden Karten ist die Möglichkeit, hochdimensionale Daten zweidimensional und diskretisiert darzustellen. Daten mit ähnlichen Merkmalen formen Cluster, was die Analyse von Korrelationen vereinfacht.
Details und weitere Anwendungsmöglichkeiten finden Sie in dem hervorragenden Buch Visual Explorations in Finance: with Self-Organizing Maps von Guide Deboeck und Teuvo Kohonen.
Anhang
Nach der Veröffentlichung der russischen Version schlug Alex Sergeev eine verbesserte Version von Klassen vor (SOM_Alex-Sergeev_en.zip).
Änderungsliste:
1. Die Anzeige von Bildern hat sich geändert: cIntBMP::Show(int aX, int aY, string aBMPFileName, string aObjectName, bool aFromImages=true)
2. Funktion zum Öffnen des Verzeichnisses mit Bildern hinzugefügt:
#import "shell32.dll" int ShellExecuteW(int hwnd, string oper, string prog, string param, string dir, int show); #import input bool OpenAfterAnaliz=true; // open folder with maps after finish
Änderungen in der Klasse CSOM:
- Methode CSOM::HideChart hinzugefügt – blendet Diagramme aus.
- Klassenmitglieder m_chart, m_wnd, m_x0, m_y0 hinzugefügt – (Diagramm, Fenster und Koordinaten für die Anzeige von Bildern).
+ Präfix m_sID hinzugefügt – Objektnamen. Das Präfix nutzt den Dateinamen, standardmäßig wird das Präfix "SOM" verwendet. - Alle Karten werden in den Ordner mit dem Namen m_sID gespeichert.
- Die Namen von bmp-Dateien werden anhand des Spaltennamen der Muster vergeben.
- Methode CSOM::ShowBMP angepasst (Karten werden in \Files anstatt \Images gespeichert, was viel schneller ist).
- CSOM::NetDeinit geändert in CSOM::HideBMP.
- Methode CSOM::ReadCSVData angepasst, die erste Spalte enthält Titel.
- Flag zum Anzeigen von Zwischenkarten in CSOM::Train(bool bShowProgress) hinzugefügt.
- Die Anzeige von Zwischenkarten in CSOM::Train wird alle 2 Sekunden ausgeführt (anstatt eines Durchlaufs), der Fortschritt wird mithilfe des Kommentars im Diagramm angezeigt.
- Namen einiger Variablen optimiert, Klassenmethoden nach Kategorie sortiert.
Die Zeichnung von bmp ist ein sehr langsamer Prozess. Wenn Sie es nicht wirklich brauchen, zeichnen Sie sie nicht jedes Mal.
Das Beispiel von SOM-Bildern mit Optimierungsergebnissen ist im Archiv beinhaltet.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/283
 Erstellen benutzerdefinierter Optimierungskriterien für Expert Advisors
Erstellen benutzerdefinierter Optimierungskriterien für Expert Advisors
 Statistische Schätzungen
Statistische Schätzungen
 Methode der Flächeninhalte
Methode der Flächeninhalte
 Tracing, Debugging und strukturelle Analyse von Quellcodes
Tracing, Debugging und strukturelle Analyse von Quellcodes
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.