Utilizzo di feature map auto-organizzanti (mappe Kohonen) su MetaTrader 5
297
0
Introduzione
Una feature map auto-organizzante (SOM) è un tipo di rete neurale artificiale che viene addestrata utilizzando l'apprendimento non supervisionato per produrre una rappresentazione discretizzata bidimensionale dello spazio di input dei campioni di addestramento, chiamato mappa.
Queste mappe sono utili per la classificazione e la visualizzazione di viste a bassa dimensione di dati ad alta dimensione, simile al ridimensionamento multidimensionale. Il modello è stato descritto per la prima volta come una rete neurale artificiale dal professore finlandese Teuvo Kohonen, ed è talvolta chiamato mappa di Kohonen.
Ci sono molti algoritmi disponibili, seguiremo il codice presentato su http://www.ai-junkie.com. Per visualizzare i dati nel client terminal MetaTrader 5 utilizzeremo cIntBMP, una libreria per la creazione di immagini BMP. In questo articolo considereremo alcune semplici applicazioni di Kohonen Maps.
1. Feature map auto-organizzanti
Le feature map auto-organizzanti sono state descritte per la prima volta da Teuvo Kohonen nel 1982. A differenza di molte reti neurali, non hanno bisogno di una corrispondenza uno a uno tra i dati di input e di output di destinazione. Questa rete neurale viene addestrata utilizzando l'apprendimento non supervisionato.
La SOM può essere descritta formalmente come una mappatura non lineare, ordinata e uniforme di dati di input ad alta dimensione sugli elementi di un array regolare a bassa dimensione. Nella sua forma base produce un grafico di somiglianza dei dati di input.
La SOM converte le relazioni statistiche non lineari tra i dati ad alta dimensione in una semplice relazione geometrica dei punti dell'immagine su una normale griglia bidimensionale di nodi. Le mappe SOM (Self-Organizing Map) possono essere utilizzate per la classificazione e la visualizzazione di dati ad alta dimensionalità.
1.1. Architettura di rete
La Fig.1 mostra una semplice mappa di Kohonen come griglia di 16 nodi (4x4 ciascuno di essi è connesso con un vettore di input tridimensionale).
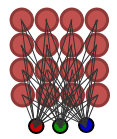
Figura 1. Mappa di Kohonen semplice (16 nodi)
Ogni nodo ha coordinate (x,y) nel reticolo e vettore dei pesi con componenti, definiti in base al vettore di input.
1.2. Algoritmo di apprendimento
A differenza di molti altri tipi di reti neurali, la SOM non necessita di un output di destinazione da specificare. Invece, dove i pesi dei nodi corrispondono al vettore di input, quell'area del reticolo viene ottimizzata selettivamente per assomigliare più da vicino ai dati per la classe di cui il vettore di input è membro.
Da una distribuzione iniziale di pesi casuali e su molte iterazioni, il SOM alla fine si stabilizza in una mappa di zone stabili. Ogni zona è effettivamente un classificatore di caratteristiche, quindi puoi pensare all'output grafico come a un tipo di mappa delle caratteristiche dello spazio di input.
L'addestramento avviene in più fasi e in più iterazioni:
- I pesi di ogni nodo sono inizializzati con valori casuali.
- Un vettore viene scelto casualmente dall'insieme dei dati di addestramento.
- Ogni nodo viene esaminato per calcolare quali pesi sono più simili al vettore di input. Il nodo vincente è comunemente noto come Best Matching Unit (BMU).
- Viene calcolato il raggio dell'intorno della BMU. Inizialmente, questo valore è impostato sul raggio del reticolo, ma senza dimish ad ogni passo.
- Per tutti i nodi trovati all'interno del raggio di BMU, i pesi del nodo vengono regolati per renderli più simili al vettore di input. Più un nodo è vicino alla BMU, più i suoi pesi vengono avvisati.
- Ripetere il passaggio 2 per N iterazioni.
I dettagli possono essere trovati http://www.ai-junkie.com.
2. Casi studio
2.1. Esempio 1. "Ciao mondo!" su SOM
Il classico esempio di mappa di Kohonen è un problema di clustering dei colori.
Supponiamo di avere un set di 8 colori, ognuno dei quali è rappresentato come un vettore tridimensionale nel modello a colori RGB.
-
Rosso: (255,0,0); 
Verde: (0,128,0);
Blu: (0,0,255);
Verde scuro: (0,100,0);
Blu scuro: (0,0,139);
Giallo: (255,255,0);
Arancione: (255,165,0);
Viola: (128,0,128).
Lavorando con le mappe Kohonen con il linguaggio MQL5, seguiremo il paradigma orientato agli oggetti.
Abbiamo bisogno di due classi: Classe CSOMNode per un nodo della griglia regolare e CSOM, che è una classe di rete neurale.
//+------------------------------------------------------------------+ //| CSOMNode class | //+------------------------------------------------------------------+ class CSOMNode { protected: int m_x1; int m_y1; int m_x2; int m_y2; double m_x; double m_y; double m_weights[]; public: //--- class constructor CSOMNode(); //--- class destructor ~CSOMNode(); //--- node initialization void InitNode(int x1,int y1,int x2,int y2); //--- return coordinates of the node's center double X() const { return(m_x);} double Y() const { return(m_y);} //--- returns the node coordinates void GetCoordinates(int &x1,int &y1,int &x2,int &y2); //--- returns the value of weight_index component of weight's vector double GetWeight(int weight_index); //--- returns the squared distance between the node weights and specified vector double CalculateDistance(double &vector[]); //--- adjust weights of the node void AdjustWeights(double &vector[],double learning_rate,double influence); };
L'implementazione dei metodi di classe può essere trovata in som_ex1.mq5. Il codice ha molti commenti e noi ci concentreremo sull'idea.
La descrizione della classe CSOM ha il seguente aspetto:
//+------------------------------------------------------------------+ //| CSOM class | //+------------------------------------------------------------------+ class CSOM { protected: //--- class for using of bmp images cIntBMP m_bmp; //--- grid mode int m_gridmode; //--- bmp image size int m_xsize; int m_ysize; //--- number of nodes int m_xcells; int m_ycells; //--- array with nodes CSOMNode m_som_nodes[]; //--- total items in training set int m_total_training_sets; //--- training set array double m_training_sets_array[]; protected: //--- radius of the neighbourhood (used for training) double m_map_radius; //--- time constant (used for training) double m_time_constant; //--- initial learning rate (used for training) double m_initial_learning_rate; //--- iterations (used for training) int m_iterations; public: //--- class constructor CSOM(); //--- class destructor ~CSOM(); //--- net initialization void InitParameters(int iterations,int xcells,int ycells,int bmpwidth,int bmpheight); //--- finds the best matching node, closest to the specified vector int BestMatchingNode(double &vector[]); //--- train method void Train(); //--- render method void Render(); //--- shows the bmp image on the chart void ShowBMP(bool back); //--- adds a vector to training set void AddVectorToTrainingSet(double &vector[]); //--- shows the pattern title void ShowPattern(double c1,double c2,double c3,string name); //--- adds a pattern to training set void AddTrainPattern(double c1,double c2,double c3); //--- returns the RGB components of the color void ColToRGB(int col,int &r,int &g,int &b); //--- returns the color by RGB components int RGB256(int r,int g,int b) const {return(r+256*g+65536*b); } //--- deletes image from the chart void NetDeinit(); };
L'uso della classe CSOM è semplice:
CSOM KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ void OnInit() { MathSrand(200); //--- initialize net, 10000 iterations will be used for training //--- the net contains 15x20 nodes, bmp image size 400x400 KohonenMap.InitParameters(10000,15,20,400,400); //-- add RGB-components of each color from training set KohonenMap.AddTrainPattern(255, 0, 0); // Red KohonenMap.AddTrainPattern( 0,128, 0); // Green KohonenMap.AddTrainPattern( 0, 0,255); // Blue KohonenMap.AddTrainPattern( 0,100, 0); // Dark green KohonenMap.AddTrainPattern( 0, 0,139); // Dark blue KohonenMap.AddTrainPattern(255,255, 0); // Yellow KohonenMap.AddTrainPattern(255,165, 0); // Orange KohonenMap.AddTrainPattern(128, 0,128); // Purple //--- train net KohonenMap.Train(); //--- render map to bmp KohonenMap.Render(); //--- show patterns and titles for each color KohonenMap.ShowPattern(255, 0, 0,"Red"); KohonenMap.ShowPattern( 0,128, 0,"Green"); KohonenMap.ShowPattern( 0, 0,255,"Blue"); KohonenMap.ShowPattern( 0,100, 0,"Dark green"); KohonenMap.ShowPattern( 0, 0,139,"Dark blue"); KohonenMap.ShowPattern(255,255, 0,"Yellow"); KohonenMap.ShowPattern(255,165, 0,"Orange"); KohonenMap.ShowPattern(128, 0,128,"Purple"); //--- show bmp image on the chart KohonenMap.ShowBMP(false); //--- }
Il risultato è presentato in Fig 2.
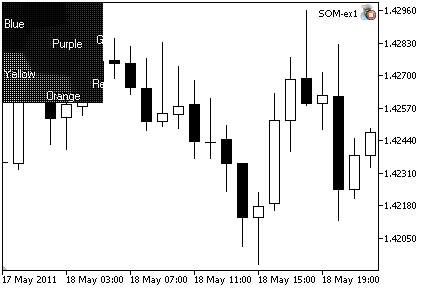
Figura 2. Figura 2. L'output dell'Expert Advisor SOM_ex1.mq5
La dinamica dell'apprendimento della mappa di Kohonen è presentata nella Fig.3 (vedi i passaggi sotto l'immagine):
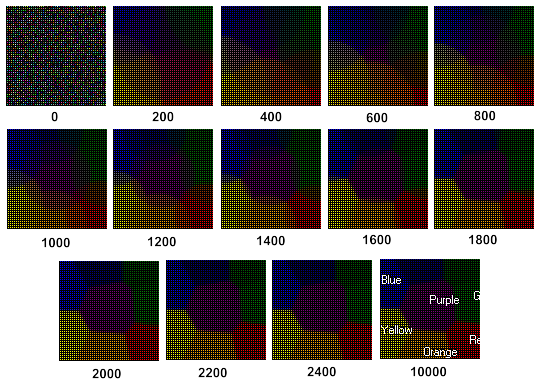
Figura 3. Le dinamiche dell'apprendimento della mappa di Kohonen
Nella Fig.3 possiamo vedere che la Mappa di Kohonen si è formata dopo 2400 passaggi.
Se creiamo il reticolo di 300 nodi e specifichiamo la dimensione dell'immagine come 400x400:
//--- lattice of 15x20 nodes, image size 400x400 KohonenMap.InitParameters(10000,15,20,400,400);
otterremo l'immagine, presentata nella Fig.4:
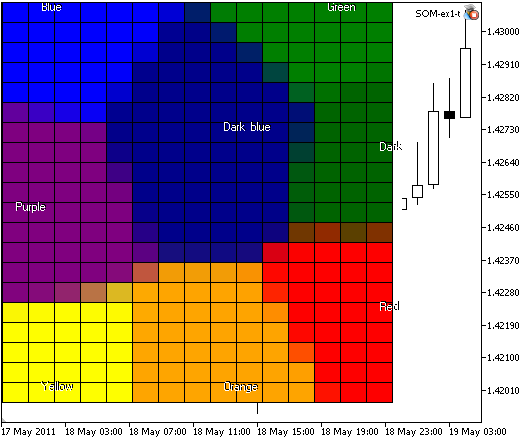
Figura 4. La mappa di Kohonen con 300 nodi, dimensione immagine 400x400
Se hai letto il libro Visual Explorations in Finance: with Self-Organizing Maps, scritto da Guido Deboeck e Teuvo Kohonen, ti ricorderai che i nodi reticolari possono anche essere rappresentati come celle esagonali. Modificando il codice dell'Expert Advisor, possiamo implementare un'altra visualizzazione.
Il risultato di SOM-ex1-hex.mq5 è presentato nella Fig.5:
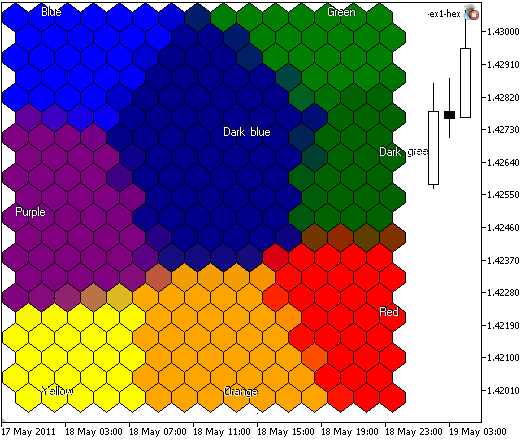
Figura 5. La mappa di Kohonen con 300 nodi, dimensione immagine 400x400, i nodi sono rappresentati in celle esagonali
In questa versione possiamo definire la visualizzazione dei bordi delle celle utilizzando i parametri di input:
// input parameter, used to show hexagonal cells input bool HexagonalCell=true; // input parameter, used to show borders input bool ShowBorders=true;
In alcuni casi non abbiamo bisogno di mostrare i bordi della cella e, se specifichi ShowBorders=false, otterrai la seguente immagine (vedi Fig.6):
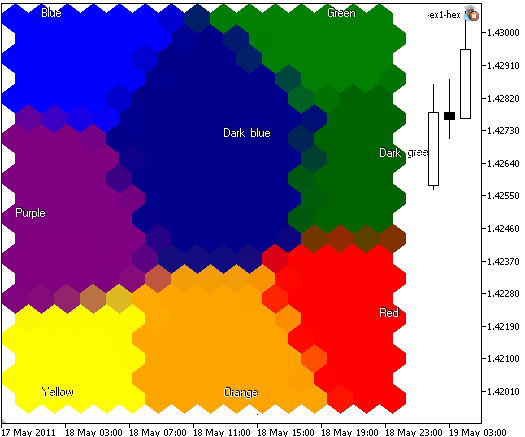
Fig.6. Mappa di Kohonen con 300 nodi, immagine 400x400, nodi tracciati come celle esagonali, bordi delle celle disabilitati
Nel primo esempio abbiamo usato 8 colori nel training set con i componenti di colore specificati. Possiamo estendere il training set e semplificare la specifica dei componenti del colore aggiungendo due metodi alla classe CSOM.
Da notare che in questo caso le mappe Kohonen sono semplici perché ci sono solo pochi colori, separati nello spazio colore. Di conseguenza, abbiamo dei cluster localizzati.
Il problema si presenta se consideriamo più colori con componenti di colore più vicini.
2.2. Esempio 2. Utilizzo dei Web-color come campioni di addestramento
Nel linguaggio MQL5 i Web-color sono costanti predefinite.
Figura 7. I Web-color
E se applicassimo l'algoritmo di Kohonen a un insieme di vettori con componenti simili?
Possiamo creare una classe CSOMWeb, derivata dalla classe CSOM:
//+------------------------------------------------------------------+ //| CSOMWeb class | //+------------------------------------------------------------------+ class CSOMWeb : public CSOM { public: //--- adds a color to training set (used for colors, instead of AddTrainPattern) void AddTrainColor(int col); //--- method of showing of title of the pattern (used for colors, instead of ShowPattern) void ShowColor(int col,string name); };
Come vedi, per semplificare il lavoro con i colori, abbiamo aggiunto due nuovi metodi. Adesso non è più necessaria la specifica esplicita dei componenti del colore.
L'implementazione dei metodi di classe si presenta come segue:
//+------------------------------------------------------------------+ //| Adds a color to training set | //| (used for colors, instead of AddTrainPattern) | //+------------------------------------------------------------------+ void CSOMWeb::AddTrainColor(int col) { double vector[]; ArrayResize(vector,3); int r=0; int g=0; int b=0; ColToRGB(col,r,g,b); vector[0]=r; vector[1]=g; vector[2]=b; AddVectorToTrainingSet(vector); ArrayResize(vector,0); } //+------------------------------------------------------------------+ //| Method of showing of title of the pattern | //| (used for colors, instead of ShowPattern) | //+------------------------------------------------------------------+ void CSOMWeb::ShowColor(int col,string name) { int r=0; int g=0; int b=0; ColToRGB(col,r,g,b); ShowPattern(r,g,b,name); }
Tutti i web-color possono essere combinati nell'array web_colors[]:
//--- web colors array color web_colors[132]= { clrBlack, clrDarkGreen, clrDarkSlateGray, clrOlive, clrGreen, clrTeal, clrNavy, clrPurple, clrMaroon, clrIndigo, clrMidnightBlue, clrDarkBlue, clrDarkOliveGreen, clrSaddleBrown, clrForestGreen, clrOliveDrab, clrSeaGreen, clrDarkGoldenrod, clrDarkSlateBlue, clrSienna, clrMediumBlue, clrBrown, clrDarkTurquoise, clrDimGray, clrLightSeaGreen, clrDarkViolet, clrFireBrick, clrMediumVioletRed, clrMediumSeaGreen, clrChocolate, clrCrimson, clrSteelBlue, clrGoldenrod, clrMediumSpringGreen, clrLawnGreen, clrCadetBlue, clrDarkOrchid, clrYellowGreen, clrLimeGreen, clrOrangeRed, clrDarkOrange, clrOrange, clrGold, clrYellow, clrChartreuse, clrLime, clrSpringGreen, clrAqua, clrDeepSkyBlue, clrBlue, clrMagenta, clrRed, clrGray, clrSlateGray, clrPeru, clrBlueViolet, clrLightSlateGray, clrDeepPink, clrMediumTurquoise, clrDodgerBlue, clrTurquoise, clrRoyalBlue, clrSlateBlue, clrDarkKhaki, clrIndianRed, clrMediumOrchid, clrGreenYellow, clrMediumAquamarine, clrDarkSeaGreen, clrTomato, clrRosyBrown, clrOrchid, clrMediumPurple, clrPaleVioletRed, clrCoral, clrCornflowerBlue, clrDarkGray, clrSandyBrown, clrMediumSlateBlue, clrTan, clrDarkSalmon, clrBurlyWood, clrHotPink, clrSalmon, clrViolet, clrLightCoral, clrSkyBlue, clrLightSalmon, clrPlum, clrKhaki, clrLightGreen, clrAquamarine, clrSilver, clrLightSkyBlue, clrLightSteelBlue, clrLightBlue, clrPaleGreen, clrThistle, clrPowderBlue, clrPaleGoldenrod, clrPaleTurquoise, clrLightGray, clrWheat, clrNavajoWhite, clrMoccasin, clrLightPink, clrGainsboro, clrPeachPuff, clrPink, clrBisque, clrLightGoldenrod, clrBlanchedAlmond, clrLemonChiffon, clrBeige, clrAntiqueWhite, clrPapayaWhip, clrCornsilk, clrLightYellow, clrLightCyan, clrLinen, clrLavender, clrMistyRose, clrOldLace, clrWhiteSmoke, clrSeashell, clrIvory, clrHoneydew, clrAliceBlue, clrLavenderBlush, clrMintCream, clrSnow, clrWhite };
La funzione OnInit() ha una forma semplice:
CSOMWeb KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ void OnInit() { MathSrand(200); int total_web_colors=ArraySize(web_colors); //--- initialize net, 10000 iterations will be used for training //--- the net contains 15x20 nodes, bmp image size 400x400 KohonenMap.InitParameters(10000,50,50,500,500); //-- add all web colors to training set for(int i=0; i<total_web_colors; i++) { KohonenMap.AddTrainColor(web_colors[i]); } //--- train net KohonenMap.Train(); //--- render map to bmp KohonenMap.Render(); //--- show patterns and titles for each color for(int i=0; i<total_web_colors; i++) { KohonenMap.ShowColor(web_colors[i],ColorToString(web_colors[i],true)); } //--- show bmp image on the chart KohonenMap.ShowBMP(false); }
Se avviamo som-ex2-hex.mq5, otterremo l'immagine, presentata nella Fig.8.
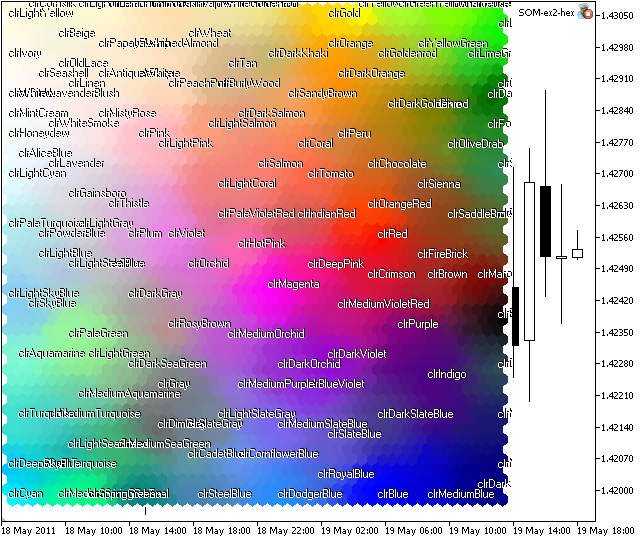
Figura 8. Mappa di Kohonen per i Web-color
Come vedi, ci sono alcuni cluster, ma alcuni colori (come xxxBlue) si trovano in regioni diverse.
Il motivo sta nella struttura del training set: ci sono molti vettori con componenti vicine.
2.3. Esempio 3. Clustering dei prodotti
Successivamente, considereremo un semplice esempio che tenterà di raggruppare venticinque alimenti in regioni di somiglianza, sulla base di tre parametri, che sono proteine, carboidrati e grassi.
| Cibo | Proteine | Carboidrati | Grassi | |
|---|---|---|---|---|
| 1 | Mele | 0,4 | 11,8 | 0,1 |
| 2 | Avocado | 1,9 | 1,9 | 19,5 |
| 3 | Banane | 1,2 | 23,2 | 0,3 |
| 4 | Bistecca di manzo | 20,9 | 0 | 7,9 |
| 5 | Big Mac | 13 | 19 | 11 |
| 6 | Noci brasiliane | 15,5 | 2,9 | 68,3 |
| 7 | Pane | 10,5 | 37 | 3,2 |
| 8 | Burro | 1 | 0 | 81 |
| 9 | Formaggio | 25 | 0,1 | 34,4 |
| 10 | Cheesecake | 6,4 | 28,2 | 22,7 |
| 11 | Biscotti | 5,7 | 58,7 | 29,3 |
| 12 | Cereali | 7 | 84 | 0,9 |
| 13 | Uova | 12,5 | 0 | 10,8 |
| 14 | Pollo fritto | 17 | 7 | 20 |
| 15 | Patatine fritte | 3 | 36 | 13 |
| 16 | Cioccolata calda | 3,8 | 19,4 | 10,2 |
| 17 | Salame piccante | 20,9 | 5,1 | 38,3 |
| 18 | Pizza | 12,5 | 30 | 11 |
| 19 | Pasticcio di maiale | 10,1 | 27,3 | 24,2 |
| 20 | Patate | 1,7 | 16,1 | 0,3 |
| 21 | Riso | 6,9 | 74 | 2,8 |
| 22 | Pollo arrosto | 26,1 | 0,3 | 5,8 |
| 23 | Zucchero | 0 | 95,1 | 0 |
| 24 | Bistecca di tonno | 25,6 | 0 | 0,5 |
| 25 | Acqua | 0 | 0 | 0 |
Tabella 1. Proteine, carboidrati e grassi per 25 alimenti.
Questo problema è interessante, perché i vettori di input hanno valori diversi e ogni componente ha il proprio intervallo di valori. È importante per la visualizzazione, perché utilizziamo il modello di colore RGB con componenti che variano da 0 a 255.
Fortunatamente, in questo caso anche i vettori di input sono tridimensionali e possiamo utilizzare il modello di colore RGB per la visualizzazione della mappa di Kohonen.
//+------------------------------------------------------------------+ //| CSOMFood class | //+------------------------------------------------------------------+ class CSOMFood : public CSOM { protected: double m_max_values[]; double m_min_values[]; public: void Train(); void Render(); void ShowPattern(double c1,double c2,double c3,string name); };
Come puoi vedere, abbiamo aggiunto gli array m_max_values[] e m_min_values[] per l'archiviazione dei valori massimi e minimi del set di addestramento. Per la visualizzazione nel modello a colori RGB, è necessario il "ridimensionamento" e così abbiamo sovraccaricato i metodi Train(), Render() e ShowPattern().
La ricerca dei valori massimo e minimo è implementata nel metodo Train().
//--- find minimal and maximal values of the training set ArrayResize(m_max_values,3); ArrayResize(m_min_values,3); for(int j=0; j<3; j++) { double maxv=m_training_sets_array[3+j]; double minv=m_training_sets_array[3+j]; for(int i=1; i<m_total_training_sets; i++) { double v=m_training_sets_array[3*i+j]; if(v>maxv) {maxv=v;} if(v<minv) {minv=v;} } m_max_values[j]=maxv; m_min_values[j]=minv; Print(j,"m_min_value=",m_min_values[j],"m_max_value=",m_max_values[j]); }
Per mostrare i componenti nel modello di colore RGB, dobbiamo modificare il metodo Render():
// int r = int(m_som_nodes[ind].GetWeight(0)); // int g = int(m_som_nodes[ind].GetWeight(1)); // int b = int(m_som_nodes[ind].GetWeight(2)); int r=int ((255*(m_som_nodes[ind].GetWeight(0)-m_min_values[0])/(m_max_values[0]-m_min_values[0]))); int g=int ((255*(m_som_nodes[ind].GetWeight(1)-m_min_values[1])/(m_max_values[1]-m_min_values[1]))); int b=int ((255*(m_som_nodes[ind].GetWeight(2)-m_min_values[2])/(m_max_values[2]-m_min_values[2])));
Il risultato di som_ex3.mq5 è presentato nella Fig.9.
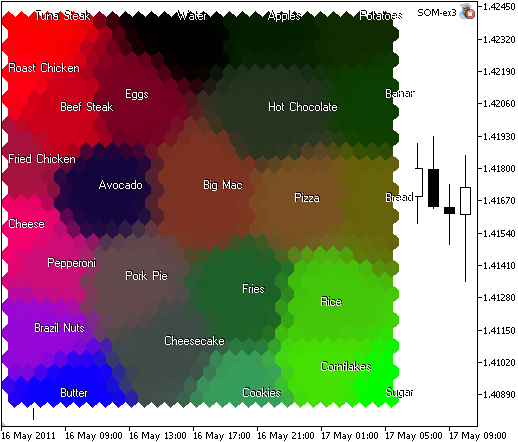
Figura 9. Mappa alimentare, raggruppata in regioni di somiglianza, basata su proteine, carboidrati e grassi
Analisi dei componenti. Si può vedere dalla mappa che zucchero, riso e cereali sono tracciati con il colore verde a causa dei carboidrati (2° componente). Il burro è nella zona verde, ha molti grassi (3° componente). Molte proteine (1° componente, in rosso) sono contenute nella bistecca di manzo, nel pollo arrosto e nella bistecca di tonno.
Puoi estendere il set di formazione aggiungendo nuovo cibo dalle Tabelle di composizione degli alimenti (tabella alternativa).
Come vedete, il problema è risolto per le direzioni R,G,B "pure". Che dire di altri alimenti con diversi componenti uguali (o per lo più uguali)? Più avanti considereremo i piani dei componenti, molto utili specialmente per i casi in cui i vettori di input hanno dimensione maggiore di 3.
2.4. Esempio 4. Caso quadridimensionale. Set di dati dell’iris di Fisher. CMYK
Per i vettori tridimensionali, non ci sono problemi con la visualizzazione. I risultati sono chiari grazie al modello di colore RGB, utilizzato per visualizzare i componenti del colore.
Quando lavoriamo con dati ad alta dimensionalità, dobbiamo trovare il modo per visualizzarli. La soluzione semplice è tracciare una mappa gradiente (ad esempio, Nero/Bianco), con colori, proporzionali alla lunghezza del vettore. L'altro modo è usare un altro color space. In questo esempio considereremo il modello di colore CMYK per il set di dati dell’iris di Fisher. Esista una soluzione migliore e in seguito la prenderemo in considerazione.
Il set di data dell’Iris o Iris di Fisher è un set di dati multivariato introdotto da R. Fisher (1936) come esempio di analisi discriminante. Il set di dati è costituito da 50 campioni di ciascuna delle tre specie di fiori di Iris (Iris setosa, Iris virginica e Iris versicolor).
Sono state misurate quattro caratteristiche da ciascun campione, ovvero la lunghezza e la larghezza del sepalo e del petalo in centimetri.
Figura 10. Iris
Ogni campione ha 4 caratteristiche:
- lunghezza del sepalo;
- Larghezza del sepalo;
- Lunghezza del petalo;
- Larghezza del petalo.
Il set di dati dell’Iris è disponibile in SOM_ex4.mq5.
In questo esempio utilizzeremo lo spazio colore CMYK intermedio per la stampa, ovvero considereremo i pesi del nodo come vettori nello spazio CMYK. Per visualizzare i risultati viene utilizzata la conversione CMYK->RGB. Un nuovo metodo, int CSOM::CMYK2Col(uchar c,uchar m,uchar y,uchar k), viene aggiunto alla classe CSOM e utilizzato nel metodo CSOM::Render(). Inoltre, dobbiamo modificare le classi per supportare i vettori a 4 dimensioni.
Il risultato è presentato nella Fig.11.
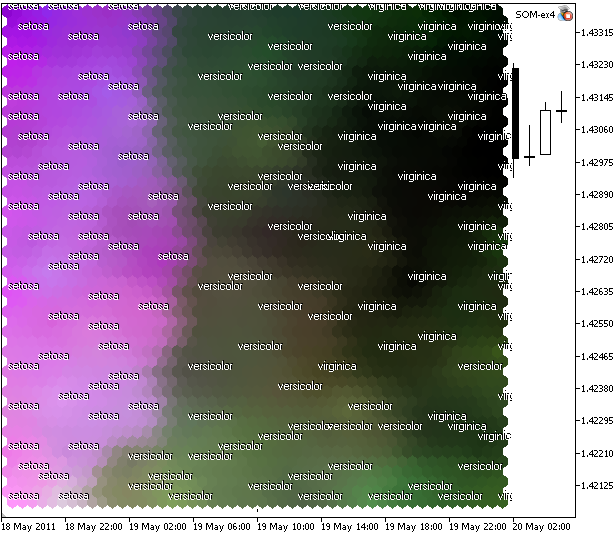
Figura 11. Mappa di Kohonen per il set di dati dell’Iris, tracciato in un modello di colore CMYK
Cosa vediamo? Non abbiamo il clustering completo (a causa delle caratteristiche del problema), ma si può vedere la separazione lineare dell’Iris setosa.
La ragione di questa separazione lineare dell’Iris setosa sta nel grande componente "Magenta" (2°) nello spazio CMYK.
2.6. Analisi del Piano dei componenti
Si può vedere dagli esempi precedenti (clustering di dati di cibo e iris) come ci sia un problema con la visualizzazione dei dati.
Ad esempio, per il problema alimentare abbiamo analizzato la Mappa di Kohonen utilizzando le informazioni su determinati colori (rosso, verde, blu). Oltre ai cluster di base, c'erano alcuni alimenti con diversi componenti. Inoltre, l'analisi diventa difficile se i componenti sono per lo più uguali.
I piani dei componenti offrono la possibilità di vedere l'intensità relativa per ciascuno degli alimenti.
Dobbiamo aggiungere le istanze della classe CIntBMP (array m_bmp[]) nella classe CSOM e modificare i metodi di rendering corrispondenti. Inoltre, abbiamo bisogno di una mappa del gradiente per visualizzare l'intensità di ciascun componente (i valori più bassi mostrati con il colore blu, i valori più alti mostrati con il rosso):
Figura 12. Tavola dei gradienti
Abbiamo aggiunto l'array Palette[768], i metodi GetPalColor() e Blend(). Il disegno di un nodo viene posizionato nel metodo RenderCell().
Set di dati dell'iride
I risultati di som-ex4-cpr.mq5 sono presentati nella Fig.13.
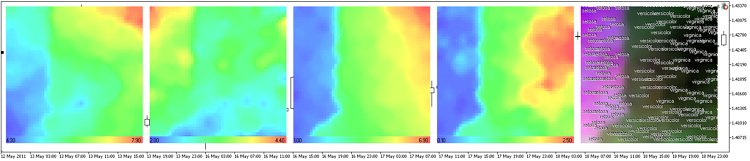
Figura 13. Rappresentazione dei piani dei componenti del set di dati dell'iride
In questo caso utilizziamo la griglia con nodi 30x30, dimensione immagine 300x300.
I piani dei componenti svolgono un ruolo importante nel rilevamento della correlazione: da confrontare questi piani anche parzialmente correlando le variabili può essere rilevata mediante ispezione visiva. Questo è più facile se i piani dei componenti vengono riorganizzati in modo che quelli correlati siano vicini l'uno all'altro. In questo modo, è facile selezionare interessanti combinazioni di componenti per ulteriori indagine.
Consideriamo i piani dei componenti (Fig.14).
I valori dei componenti massimo e minimo sono mostrati nella tabella dei gradienti.
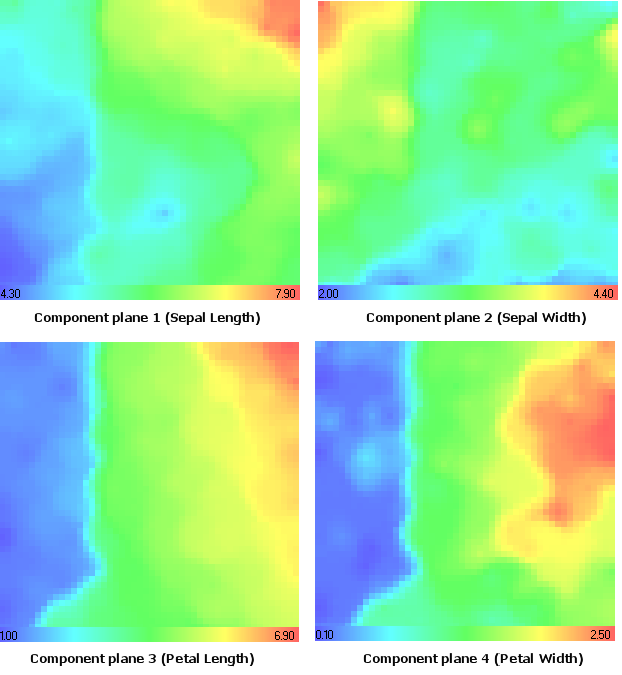
Figura 14. Insieme di dati dell'iride. Piani dei componenti
Tutti i piani dei componenti rappresentati nel modello a colori CMYK sono mostrati nella Fig.15.
Figura 15. Insieme di dati dell'iride. Mappa di Kohonen nel modello di colore CMYK
Ricordiamo il tipo iris setosa. Utilizzando l'analisi del piano dei componenti (Fig. 14) si può vedere che ha valori minimi nei piani del primo (lunghezza del sepalo), terzo (lunghezza del petalo) e quarto (larghezza del petalo).
È notevole che abbia valori massimi nel piano del 2° componente (Larghezza del sepalo), lo stesso risultato che abbiamo ottenuto nel modello a colori CMYK (componente Magenta, Fig.15).
Clustering alimentare
Consideriamo ora il problema del clustering degli alimenti utilizzando l'analisi del piano dei componenti (som-ex3-cpr.mq5).
Il risultato è presentato nella Fig.16 (30x30 nodi, dimensione immagine 300x300, celle esagonali senza bordi).
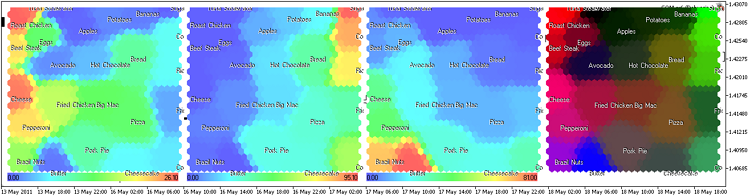
Figura 16. Mappa di Kohonen per il cibo, rappresentazione del piano dei componenti
Abbiamo aggiunto l'opzione di visualizzazione dei titoli nel metodo ShowPattern() della classe CSOM (parametro di input ShowTitles=true).
I piani dei componenti (proteine, carboidrati, grassi) hanno il seguente aspetto:
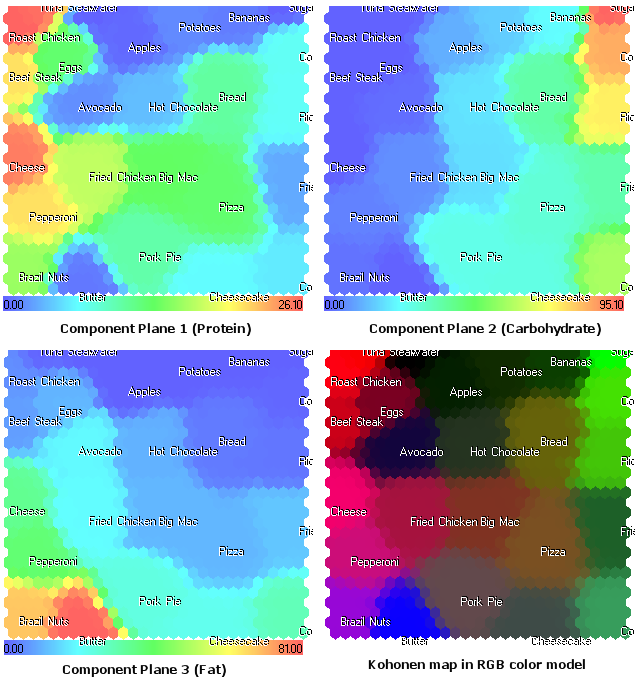
Figura 17. Mappa di Kohonen per gli alimenti. Piani dei componenti e modello di colore RGB
La rappresentazione del piano dei componenti, mostrata nella Fig.17, apre una nuova visuale sulla struttura dei componenti degli alimenti. Inoltre, fornisce informazioni aggiuntive che non possono essere viste nel modello di colore RGB, presentato nella Fig.9.
Ad esempio, adesso vediamo il formaggio nel piano del 1° componente (proteine). Nel modello di colore RGB è invece mostrato con il colore vicino al magenta a causa del grasso (2° componente).
2.5. Implementazione dei piani dei componenti per il caso di dimensione arbitraria
Gli esempi che abbiamo considerato hanno alcune caratteristiche specifiche, la dimensione è stata fissata e l'algoritmo di visualizzazione era diverso per le diverse rappresentazioni (modelli di colore RGB e CMYK).
Ora possiamo generalizzare l'algoritmo per le dimensioni arbitrarie, ma in questo caso visualizzeremo solo i piani dei componenti. Il programma deve essere in grado di caricare i dati arbitrari dal file CSV.
Ad esempio, il file food.csv ha il seguente aspetto:
Protein;Carbohydrate;Fat;Title 0.4;11.8;0.1;Apples 1.9;1.9;19.5;Avocado 1.2;23.2;0.3;Bananas 20.9;0.0;7.9;Beef Steak 13.0;19.0;11.0;Big Mac 15.5;2.9;68.3;Brazil Nuts 10.5;37.0;3.2;Bread 1.0;0.0;81.0;Butter 25.0;0.1;34.4;Cheese 6.4;28.2;22.7;Cheesecake 5.7;58.7;29.3;Cookies 7.0;84.0;0.9;Cornflakes 12.5;0.0;10.8;Eggs 17.0;7.0;20.0;Fried Chicken 3.0;36.0;13.0;Fries 3.8;19.4;10.2;Hot Chocolate 20.9;5.1;38.3;Pepperoni 12.5;30.0;11.0;Pizza 10.1;27.3;24.2;Pork Pie 1.7;16.1;0.3;Potatoes 6.9;74.0;2.8;Rice 26.1;0.3;5.8;Roast Chicken 0.0;95.1;0.0;Sugar 25.6;0.0;0.5;Tuna Steak 0.0;0.0;0.0;Water
La prima riga del file contiene i nomi (titoli) del vettore di dati di input. I titoli sono necessari per distinguere i piani dei componenti. Stamperemo i loro nomi nel pannello del gradiente.
Il nome del pattern si trova nell'ultima colonna. Nel nostro caso è il nome del cibo.
Il codice di SOM.mq5 (funzione OnInit) è semplificato:
CSOM KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { MathSrand(200); //--- load patterns from file if(!KohonenMap.LoadTrainDataFromFile(DataFileName)) { Print("Error in loading data for training."); return(1); } //--- train net KohonenMap.Train(); //--- render map KohonenMap.Render(); //--- show patterns from training set KohonenMap.ShowTrainPatterns(); //--- show bmp on the chart KohonenMap.ShowBMP(false); return(0); }
Il nome del file con i modelli di addestramento è specificato nel parametro di input DataFileName, nel nostro caso "food.csv".
Il risultato è mostrato nella Fig.18.
Figura 18. Mappa di Kohonen del cibo in combinazione di colori sfumati bianco/nero
Inoltre, abbiamo aggiunto il parametro di input ColorScheme per la selezione dello schema gradiente.
Al momento sono disponibili 4 combinazioni di colori (ColorScheme=0,1,2,4=Nero-Bianco, Blu Scuro-Blu-Verde-Giallo-Rosso, Rosso-Nero-Verde, Rosso-Bianco-Verde).
Puoi facilmente aggiungere il tuo schema aggiungendo il gradiente nel metodo CSOM::InitParameters().
La combinazione di colori può essere selezionata dai parametri di input dell’Expert Advisor:
Allo stesso modo possiamo preparare il set di dati dell’Iris (iris-fisher.csv):
Sepal length;Sepal width;Petal length;Petal width;Title 5.1;3.5;1.4;0.2;setosa 4.9;3.0;1.4;0.2;setosa 4.7;3.2;1.3;0.2;setosa 4.6;3.1;1.5;0.2;setosa 5.0;3.6;1.4;0.2;setosa 5.4;3.9;1.7;0.4;setosa 4.6;3.4;1.4;0.3;setosa 5.0;3.4;1.5;0.2;setosa 4.4;2.9;1.4;0.2;setosa 4.9;3.1;1.5;0.1;setosa 5.4;3.7;1.5;0.2;setosa 4.8;3.4;1.6;0.2;setosa 4.8;3.0;1.4;0.1;setosa 4.3;3.0;1.1;0.1;setosa 5.8;4.0;1.2;0.2;setosa 5.7;4.4;1.5;0.4;setosa 5.4;3.9;1.3;0.4;setosa 5.1;3.5;1.4;0.3;setosa 5.7;3.8;1.7;0.3;setosa 5.1;3.8;1.5;0.3;setosa 5.4;3.4;1.7;0.2;setosa 5.1;3.7;1.5;0.4;setosa 4.6;3.6;1.0;0.2;setosa 5.1;3.3;1.7;0.5;setosa 4.8;3.4;1.9;0.2;setosa 5.0;3.0;1.6;0.2;setosa 5.0;3.4;1.6;0.4;setosa 5.2;3.5;1.5;0.2;setosa 5.2;3.4;1.4;0.2;setosa 4.7;3.2;1.6;0.2;setosa 4.8;3.1;1.6;0.2;setosa 5.4;3.4;1.5;0.4;setosa 5.2;4.1;1.5;0.1;setosa 5.5;4.2;1.4;0.2;setosa 4.9;3.1;1.5;0.2;setosa 5.0;3.2;1.2;0.2;setosa 5.5;3.5;1.3;0.2;setosa 4.9;3.6;1.4;0.1;setosa 4.4;3.0;1.3;0.2;setosa 5.1;3.4;1.5;0.2;setosa 5.0;3.5;1.3;0.3;setosa 4.5;2.3;1.3;0.3;setosa 4.4;3.2;1.3;0.2;setosa 5.0;3.5;1.6;0.6;setosa 5.1;3.8;1.9;0.4;setosa 4.8;3.0;1.4;0.3;setosa 5.1;3.8;1.6;0.2;setosa 4.6;3.2;1.4;0.2;setosa 5.3;3.7;1.5;0.2;setosa 5.0;3.3;1.4;0.2;setosa 7.0;3.2;4.7;1.4;versicolor 6.4;3.2;4.5;1.5;versicolor 6.9;3.1;4.9;1.5;versicolor 5.5;2.3;4.0;1.3;versicolor 6.5;2.8;4.6;1.5;versicolor 5.7;2.8;4.5;1.3;versicolor 6.3;3.3;4.7;1.6;versicolor 4.9;2.4;3.3;1.0;versicolor 6.6;2.9;4.6;1.3;versicolor 5.2;2.7;3.9;1.4;versicolor 5.0;2.0;3.5;1.0;versicolor 5.9;3.0;4.2;1.5;versicolor 6.0;2.2;4.0;1.0;versicolor 6.1;2.9;4.7;1.4;versicolor 5.6;2.9;3.6;1.3;versicolor 6.7;3.1;4.4;1.4;versicolor 5.6;3.0;4.5;1.5;versicolor 5.8;2.7;4.1;1.0;versicolor 6.2;2.2;4.5;1.5;versicolor 5.6;2.5;3.9;1.1;versicolor 5.9;3.2;4.8;1.8;versicolor 6.1;2.8;4.0;1.3;versicolor 6.3;2.5;4.9;1.5;versicolor 6.1;2.8;4.7;1.2;versicolor 6.4;2.9;4.3;1.3;versicolor 6.6;3.0;4.4;1.4;versicolor 6.8;2.8;4.8;1.4;versicolor 6.7;3.0;5.0;1.7;versicolor 6.0;2.9;4.5;1.5;versicolor 5.7;2.6;3.5;1.0;versicolor 5.5;2.4;3.8;1.1;versicolor 5.5;2.4;3.7;1.0;versicolor 5.8;2.7;3.9;1.2;versicolor 6.0;2.7;5.1;1.6;versicolor 5.4;3.0;4.5;1.5;versicolor 6.0;3.4;4.5;1.6;versicolor 6.7;3.1;4.7;1.5;versicolor 6.3;2.3;4.4;1.3;versicolor 5.6;3.0;4.1;1.3;versicolor 5.5;2.5;4.0;1.3;versicolor 5.5;2.6;4.4;1.2;versicolor 6.1;3.0;4.6;1.4;versicolor 5.8;2.6;4.0;1.2;versicolor 5.0;2.3;3.3;1.0;versicolor 5.6;2.7;4.2;1.3;versicolor 5.7;3.0;4.2;1.2;versicolor 5.7;2.9;4.2;1.3;versicolor 6.2;2.9;4.3;1.3;versicolor 5.1;2.5;3.0;1.1;versicolor 5.7;2.8;4.1;1.3;versicolor 6.3;3.3;6.0;2.5;virginica 5.8;2.7;5.1;1.9;virginica 7.1;3.0;5.9;2.1;virginica 6.3;2.9;5.6;1.8;virginica 6.5;3.0;5.8;2.2;virginica 7.6;3.0;6.6;2.1;virginica 4.9;2.5;4.5;1.7;virginica 7.3;2.9;6.3;1.8;virginica 6.7;2.5;5.8;1.8;virginica 7.2;3.6;6.1;2.5;virginica 6.5;3.2;5.1;2.0;virginica 6.4;2.7;5.3;1.9;virginica 6.8;3.0;5.5;2.1;virginica 5.7;2.5;5.0;2.0;virginica 5.8;2.8;5.1;2.4;virginica 6.4;3.2;5.3;2.3;virginica 6.5;3.0;5.5;1.8;virginica 7.7;3.8;6.7;2.2;virginica 7.7;2.6;6.9;2.3;virginica 6.0;2.2;5.0;1.5;virginica 6.9;3.2;5.7;2.3;virginica 5.6;2.8;4.9;2.0;virginica 7.7;2.8;6.7;2.0;virginica 6.3;2.7;4.9;1.8;virginica 6.7;3.3;5.7;2.1;virginica 7.2;3.2;6.0;1.8;virginica 6.2;2.8;4.8;1.8;virginica 6.1;3.0;4.9;1.8;virginica 6.4;2.8;5.6;2.1;virginica 7.2;3.0;5.8;1.6;virginica 7.4;2.8;6.1;1.9;virginica 7.9;3.8;6.4;2.0;virginica 6.4;2.8;5.6;2.2;virginica 6.3;2.8;5.1;1.5;virginica 6.1;2.6;5.6;1.4;virginica 7.7;3.0;6.1;2.3;virginica 6.3;3.4;5.6;2.4;virginica 6.4;3.1;5.5;1.8;virginica 6.0;3.0;4.8;1.8;virginica 6.9;3.1;5.4;2.1;virginica 6.7;3.1;5.6;2.4;virginica 6.9;3.1;5.1;2.3;virginica 5.8;2.7;5.1;1.9;virginica 6.8;3.2;5.9;2.3;virginica 6.7;3.3;5.7;2.5;virginica 6.7;3.0;5.2;2.3;virginica 6.3;2.5;5.0;1.9;virginica 6.5;3.0;5.2;2.0;virginica 6.2;3.4;5.4;2.3;virginica 5.9;3.0;5.1;1.8;virginica
Il risultato è mostrato nella Fig.19.
Figura 19. Insieme di dati dell'iride. Piani dei componenti nella combinazione di colori Rosso-Nero-Verde (ColorScheme=2, iris-fisher.csv)
Ora abbiamo uno strumento per le applicazioni reali.
2.6. Esempio 5. Mappe termica di mercato
Le feature map auto-organizzanti possono essere utilizzate per le mappe dei movimenti di mercato. A volte è necessaria un'immagine globale del mercato, e la mappa termica di mercato è uno strumento molto utile. I titoli sono combinati insieme a seconda dei settori economici.
Il colore attuale delle scorte dipende dal tasso di crescita attuale (in %):
Figura 20. Mappa termica di mercato per le azioni da S&P500
La mappa termica di mercato settimanale delle azioni di S&P (http://finviz.com) è mostrata nella Fig.20. Il colore dipende dal tasso di crescita (in %):
La dimensione del rettangolo azionario dipende dalla capitalizzazione di mercato. La stessa analisi può essere eseguita nel client terminal MetaTrader 5 utilizzando le mappe di Kohonen.
L'idea è di utilizzare i tassi di crescita (in %) per più periodi di tempo. Abbiamo lo strumento per lavorare con le mappe di Kohonen, quindi l'unica cosa che ci occorre è lo script, il quale salva i dati in un file .csv.
I dati sui prezzi dei CFD delle azioni americane (#AA, #AIG, #AXP, #BA, #BAC, #C, #CAT, #CVX, #DD, #DIS, #EK, #GE, #HD, # HON, #HPQ, #IBM, #INTC, #IP, #JNJ, #JPM, #KFT, #KO, #MCD, #MMM, #MO, #MRK, #MSFT, #PFE, #PG, #T, #TRV, #UTX, #VZ, #WMT e #XOM) possono essere trovati sul server Demo di MetaQuotes.
Lo script che prepara il file dj.csv è molto semplice:
//+------------------------------------------------------------------+ //| DJ.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" string s_cfd[35]= { "#AA","#AIG","#AXP","#BA","#BAC","#C","#CAT","#CVX","#DD","#DIS","#EK","#GE", "#HD","#HON","#HPQ","#IBM","#INTC","#IP","#JNJ","#JPM","#KFT","#KO","#MCD","#MMM", "#MO","#MRK","#MSFT","#PFE","#PG","#T","#TRV","#UTX","#VZ","#WMT","#XOM" }; //+------------------------------------------------------------------+ //| Returns price change in percents | //+------------------------------------------------------------------+ double PercentChange(double Open,double Close) { return(100.0*(Close-Open)/Close); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { ResetLastError(); int filehandle=FileOpen("dj.csv",FILE_WRITE|FILE_ANSI); if(filehandle==INVALID_HANDLE) { Alert("Error opening file"); return; } //--- MqlRates MyRates[]; ArraySetAsSeries(MyRates,true); string t="M30;M60;M90;M120;M150;M180;M210;M240;Title"; FileWrite(filehandle,t); Print(t); int total_symbols=ArraySize(s_cfd); for(int i=0; i<total_symbols; i++) { string cursymbol=s_cfd[i]; int copied1=CopyRates(cursymbol,PERIOD_M30,0,8,MyRates); if(copied1>0) { string s=""; s=s+DoubleToString(PercentChange(MyRates[1].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[2].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[3].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[4].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[5].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[6].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[7].open,MyRates[0].close),3)+";"; s=s+cursymbol; Print(s); FileWrite(filehandle,s); } else { Print("Error in request of historical data on symbol ",cursymbol); return; } } Alert("OK"); FileClose(filehandle); } //+------------------------------------------------------------------+
I dati cronologici devono essere scaricati. Puoi farlo automaticamente usando lo script DownloadHistory.
Come risultato dello script dj.mq5, otterremo il dj.csv con i seguenti dati:
M30;M60;M90;M120;M150;M180;M210;M240;Title 0.063;-0.564;-0.188;0.376;0.251;0.313;0.627;0.439;#AA -0.033;0.033;0.067;-0.033;0.067;-0.133;0.266;0.533;#AIG -0.176;0.039;0.039;0.274;0.196;0.215;0.430;0.646;#AXP -0.052;-0.328;-0.118;0.315;0.223;0.367;0.288;0.328;#BA -0.263;-0.351;-0.263;0.000;-0.088;0.088;0.000;-0.088;#BAC -0.224;-0.274;-0.374;-0.100;-0.274;-0.224;-0.324;-0.598;#C -0.069;-0.550;-0.079;0.766;0.727;0.638;0.736;0.589;#CAT -0.049;-0.168;0.099;0.247;0.187;0.049;0.355;0.266;#CVX 0.019;-0.058;0.058;0.446;0.174;0.349;0.136;-0.329;#DD -0.073;-0.219;-0.146;0.267;0.170;0.292;0.170;0.267;#DIS -1.099;-1.923;-1.099;0.275;0.275;0.275;-0.549;-1.374;#EK -0.052;-0.310;-0.103;0.362;0.258;0.362;0.465;0.258;#GE -0.081;-0.244;-0.326;-0.136;0.081;0.326;0.489;0.489;#HD -0.137;-0.427;-0.171;0.427;0.445;0.342;0.325;0.359;#HON -0.335;-0.363;-0.112;0.112;0.168;0.307;0.475;0.251;#HPQ 0.030;-0.095;0.065;0.190;0.071;0.214;0.279;0.327;#IBM 0.000;-0.131;-0.044;-0.088;-0.044;0.000;0.000;0.044;#INTC -0.100;-0.200;-0.166;0.100;-0.067;0.033;-0.532;-0.798;#IP -0.076;0.076;0.259;0.473;0.427;0.336;0.336;-0.076;#JNJ -0.376;-0.353;-0.494;-0.259;-0.423;-0.329;-0.259;-0.541;#JPM -0.057;-0.086;-0.029;0.086;0.114;0.057;0.257;-0.114;#KFT 0.059;-0.030;0.119;0.282;0.119;0.193;0.208;-0.119;#KO -0.109;-0.182;0.206;0.352;0.279;0.473;0.521;0.194;#MCD -0.043;-0.195;-0.151;0.216;0.270;0.227;0.411;0.206;#MMM -0.036;-0.072;0.072;0.144;-0.072;-0.108;0.108;0.072;#MO 0.081;-0.081;0.027;0.081;-0.054;0.027;-0.027;-0.108;#MRK 0.083;0.083;0.041;0.331;0.083;0.248;0.166;0.041;#MSFT 0.049;0.000;0.243;0.680;0.194;0.243;0.340;0.097;#PFE -0.045;0.060;0.104;0.015;-0.179;-0.149;-0.224;-0.224;#PG 0.097;-0.032;0.000;0.129;0.129;0.064;0.097;0.064;#T -0.277;-0.440;-0.326;-0.358;-0.537;-0.619;-0.570;-0.733;#TRV -0.081;-0.209;0.035;0.325;0.198;0.093;0.128;-0.035;#UTX 0.054;0.000;0.054;0.190;0.136;0.326;0.380;0.353;#VZ -0.091;-0.091;-0.036;0.036;-0.072;0.000;0.145;-0.127;#WMT -0.062;-0.211;0.087;0.198;0.186;0.050;0.347;0.508;#XOM
Dopo aver lanciato som.mq5(ColorScheme=3, CellsX=30,CellsY=30, ImageXSize=200, ImageXSize=200, DataFileName="dj.csv"), otterremo 8 immagini, ognuna delle quali corrisponde agli intervalli di tempo di 30, 60, 90, 120, 150, 180, 210 e 240 minuti.
Le mappe di Kohonen dei dati sui tassi di crescita del mercato (azioni americane) delle ultime 4 ore della sessione di negoziazione del 23 maggio 2011 sono presentate in Fig.21.
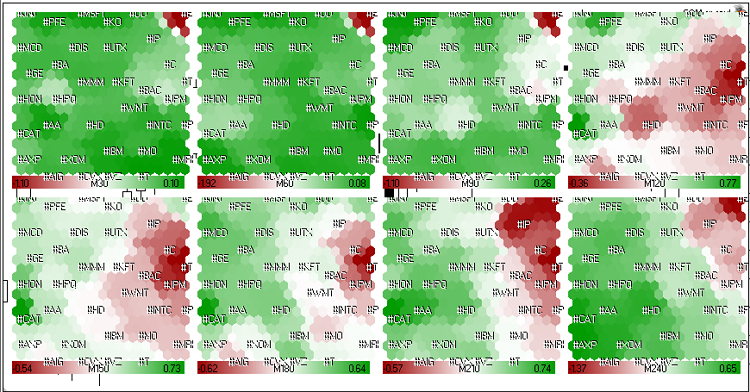
Figura 21. Mappe di Kohonen per le azioni americane (ultime 4 ore della sessione di negoziazione del 23 maggio 2011).
Si può vedere dalla Fig.21 che le dinamiche di #C (Citigroup Inc.), #T (AT&T Inc.), #JPM (JPMorgan Chase & Co), #BAC (Bank of America) sono simili. Si sono raggruppati in un cluster rosso a lungo termine.
Durante le ultime 1,5 ore (M30, M60, M90) la sua dinamica è diventata verde, ma generalmente (M240) le azioni erano nella zona rossa.
Utilizzando le mappe di Kohonen, possiamo visualizzare le dinamiche relative delle azioni, trovare i leader e i perdenti e il loro ambiente. Gli elementi con dati simili formano i cluster.
Come si vede dalla Fig.21a, il prezzo delle azioni Citigroup Inc è stato il leader del ribasso. In generale, tutti i titoli delle società finanziarie erano in zona rossa.
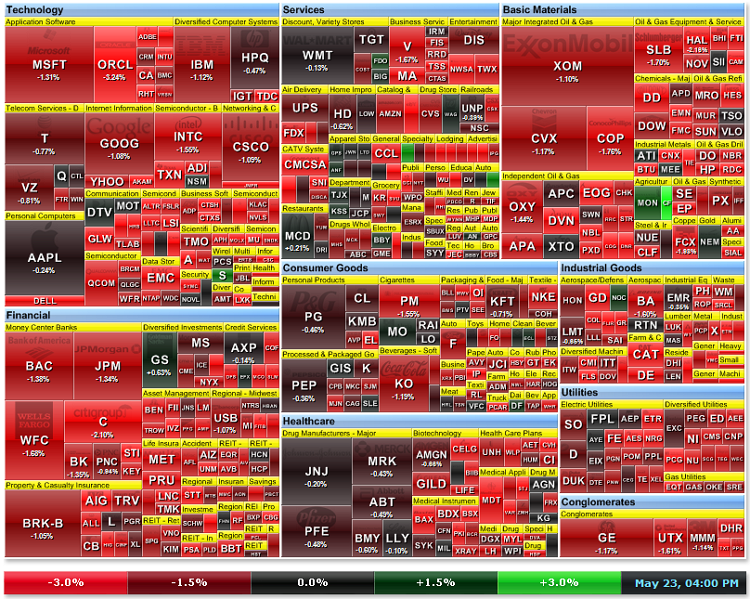
Figura 21a. Mappa termica di mercato del 23 maggio 2011 http://finviz.com)
Allo stesso modo, possiamo calcolare le mappe di Kohonen del mercato FOREX (Fig.22):
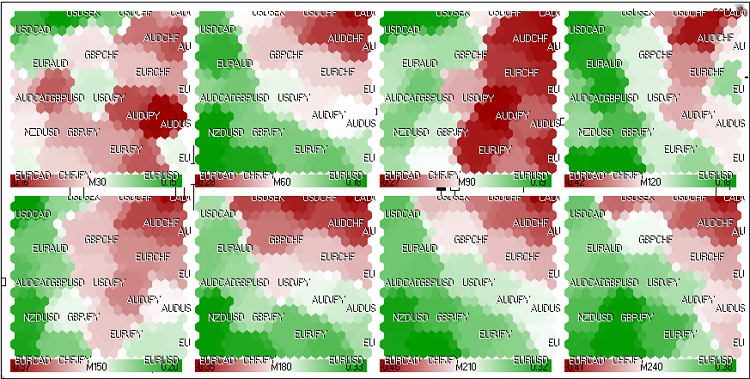
Figura 22. Mappa di Kohonen per il mercato FOREX (24 maggio 2011, sessione europea)
Vengono utilizzate le seguenti coppie: EURUSD, GBPUSD, USDCHF, USDJPY, USDCAD, AUDUSD, NZDUSD, USDSEK, AUDNZD, AUDCAD, AUDCHF, AUDJPY, CHFJPY, EURGBP, EURAUD, EURCHF, EURJPY, EURNZD, EURCAD, GBPCHF, GBPJPY, CADCHF.
I tassi di crescita vengono esportati in fx.csv utilizzando lo script fx.mq5.
M30;M60;M90;M120;M150;M180;M210;M240;Title 0.058;-0.145;0.045;-0.113;-0.038;-0.063;0.180;0.067;EURUSD 0.046;-0.100;0.078;0.094;0.167;0.048;0.123;0.160;GBPUSD -0.048;0.109;-0.142;-0.097;-0.219;-0.143;-0.277;-0.236;USDCHF 0.042;0.097;0.043;-0.024;-0.009;-0.067;0.024;0.103;USDJPY -0.045;0.162;0.155;0.239;0.217;0.246;0.157;0.227;USDCAD 0.095;-0.126;-0.018;-0.141;-0.113;-0.062;0.081;-0.005;AUDUSD 0.131;-0.028;0.167;0.096;-0.013;0.147;0.314;0.279;NZDUSD -0.047;0.189;-0.016;0.107;0.084;0.076;-0.213;-0.133;USDSEK -0.034;-0.067;-0.188;-0.227;-0.102;-0.225;-0.234;-0.291;AUDNZD 0.046;0.039;0.117;0.102;0.097;0.170;0.234;0.216;AUDCAD 0.057;-0.016;-0.158;-0.226;-0.328;-0.215;-0.180;-0.237;AUDCHF 0.134;-0.020;0.024;-0.139;-0.124;-0.127;0.107;0.098;AUDJPY 0.083;-0.009;0.184;0.084;0.208;0.082;0.311;0.340;CHFJPY 0.025;-0.036;-0.030;-0.200;-0.185;-0.072;0.058;-0.096;EURGBP -0.036;-0.028;0.061;0.010;0.074;-0.006;0.088;0.070;EURAUD 0.008;-0.049;-0.098;-0.219;-0.259;-0.217;-0.094;-0.169;EURCHF 0.096;-0.043;0.085;-0.124;-0.049;-0.128;0.206;0.157;EURJPY -0.073;-0.086;-0.119;-0.211;-0.016;-0.213;-0.128;-0.213;EURNZD 0.002;0.009;0.181;0.119;0.182;0.171;0.327;0.284;EURCAD -0.008;0.004;-0.077;-0.015;-0.054;-0.127;-0.164;-0.080;GBPCHF 0.079;-0.005;0.115;0.079;0.148;-0.008;0.144;0.253;GBPJPY 0.013;-0.060;-0.294;-0.335;-0.432;-0.376;-0.356;-0.465;CADCHF
Oltre ai prezzi, puoi utilizzare i valori degli indicatori in tempi diversi.
2.6. Esempio 6. Cache dei risultati di ottimizzazione
Lo Strategy Tester del client terminal MetaTrader 5 offre l'opportunità di esplorare la struttura dello spazio dei parametri e trovare il miglior set di parametri della strategia. Inoltre è possibile esportare i risultati di ottimizzazione utilizzando l'opzione "Export to XML (MS Office Excel)" dal menu contestuale della scheda "Optimization Results".
Le statistiche del tester sono incluse anche nei risultati di ottimizzazione (41 colonne):
- Risultato
- Profitto
- Profitto lordo
- Perdita lorda
- Prelievo
- Profitto previsto
- Fattore di profitto
- Fattore di recupero
- Indice di Sharpe
- Livello di margine
- Personalizza
- Saldo minimo
- Saldo DD Massimo
- Saldo DD Massimo (%)
- Saldo DD Relativo
- Saldo DD Relativo (%)
- Equità minima
- Capitale DD Massimo
- Capitale DD Massimo (%)
- Equità DD Relativa
- Equità DD Relativa (%)
- Trade
- Operazioni
- Short Trade
- Profitto Short Trade
- Long Trade
- Profitto Long Trade
- Profit Trade
- Loss Trade
- Trading con profitto massimo
- Trading con perdita massima
- Numero massimo di vittorie consecutive
- Vittorie consecutive massime ($)
- Massimo profitto consecutivo
- Conteggio massimo di profitto consecutivo
- Massime perdite consecutive
- Massime perdite consecutive ($)
- Massima perdita consecutiva
- Numero massimo di perdite consecutive
- Media vittorie consecutive
- Media perdite consecutive
L'uso delle statistiche del tester consente di aiutare nell'analisi dello spazio dei parametri. È notevole che molti parametri della statistica siano strettamente correlati e dipendano dai risultati delle prestazioni di trading.
Ad esempio, i migliori risultati di trading hanno i valori più grandi dei parametri Profitto, Fattore di profitto, Fattore di recupero e Indice di Sharpe. Questo permette di utilizzarli nell'analisi dei risultati.
Risultati di ottimizzazione dell’Expert Advisor MovingAverage.mq5
In questo capitolo considereremo l'analisi dei risultati di ottimizzazione di dell’Expert Advisor MovingAverage.mq5, incluso nel pacchetto standard del client terminal MetaTrader 5. Questo Expert Advisor si basa sull'incrocio di prezzo e indicatore di media mobile. Ha due parametri di input: MovingPeriod e MovingShift, cioè avremo il file XML con 43 colonne come risultato.
Non considereremo lo spazio dei parametri a 43 dimensioni. I più interessanti sono:
- Profitto;
- Fattore di profitto;
- Fattore di recupero;
- Indice di Sharpe;
- Trade;
- ProfitTrades(%);
- MovingPeriod;
- MovingShift;
Da notare che abbiamo aggiunto il parametro ProfitTrades (%) (assente nei risultati). Indica la percentuale di operazioni redditizie e calcolate come risultato della divisione di ProfitTrades (28) per Trade (22), moltiplicato per 100..
Prepariamo il file optim.csv con 9 colonne per 400 set di parametri di input dello Strategy Tester di MetaTrader 5.
Profit;Profit Factor;Recovery Factor;Sharpe Ratio;Trades;ProfitTrades(%);MovingPeriod;MovingShift;Title -372.3;0.83;-0.51;-0.05;71;28.16901408;43;6;43 -345.79;0.84;-0.37;-0.05;66;27.27272727;50;6;50 ...
Da notare che abbiamo utilizzato il valore di MovingPeriod come colonna Titolo e verrà utilizzato per "segnare" i modelli sulle mappe di Kohonen.
Nello Strategy Tester abbiamo ottimizzato i valori di MovingPeriod e MovingShift con i seguenti parametri:
- Symbol=EURUSD
- PERIOD_H1
- Modalità di generazione del segno di spunta - "1 Minute OHLC",
- Intervallo di prova - 2011.01.01-2011.05.24,
- Ottimizzazione - Veloce (algoritmo genetico),
- Ottimizzazione - Bilanciamento max.
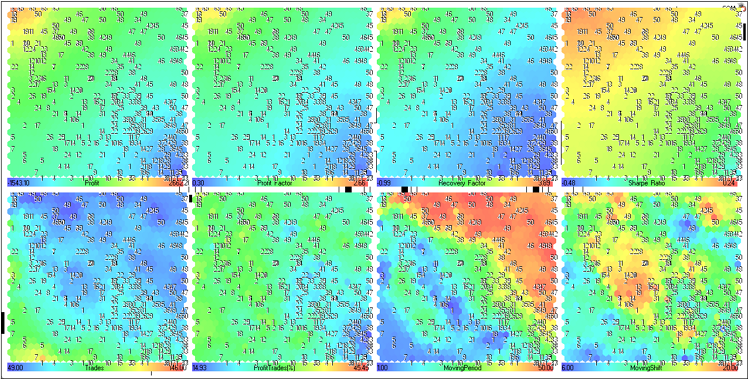
Figura 23. Mappa di Kohonen per i risultati di ottimizzazione dell’EA MovingAverage (rappresentazione del piano dei componenti)
Consideriamo i piani dei componenti della riga superiore (Profitto, Fattore di profitto, Fattore di recupero и Indice di Sharpe).
Sono combinati nella Fig.24.
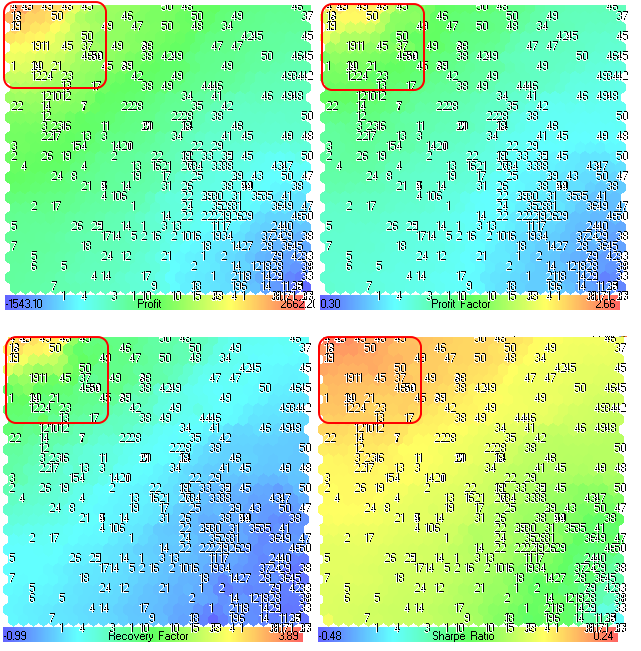
Figura 24. Piani dei componenti per i parametri Profitto, Fattore di profitto, Fattore di recupero e Indice di Sharpe
La prima cosa di cui avevamo bisogno è trovare le regioni con i migliori risultati di ottimizzazione.
Si può vedere dalla Fig.24 che le regioni con i valori massimi si trovano nell'angolo in alto a sinistra. I numeri corrispondono al periodo di media dell'indicatore Moving Average (parametro MovingPeriod, lo abbiamo usato come titolo). La posizione dei numeri è la stessa per tutti i piani dei componenti. Ogni piano dei componenti ha il proprio intervallo di valori, i quali sono stampati nel pannello dei gradienti.
I migliori risultati di ottimizzazione hanno i valori più grandi di Profitto, Fattore di profitto, Fattore di recupero e Indice di Sharpe, quindi abbiamo delle informazioni sulle regioni sulla mappa (delineate nella Fig.24).
I piani dei componenti per Trades, ProfitTrades(%), MovingPeriod e MovingShift sono mostrati nella Fig.25.
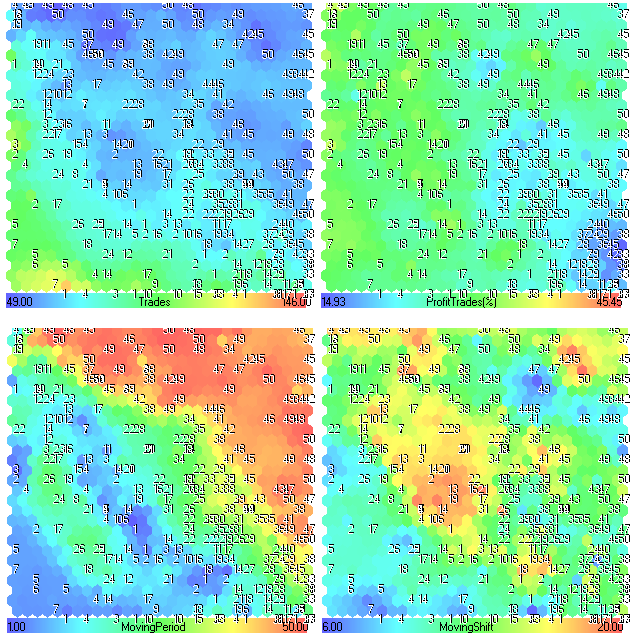
Figura 25. Piani dei componenti per i parametri Trades, ProfitTrades(%), MovingPeriod e MovingShift
Analisi del piano dei componenti
A prima vista, non ci sono informazioni interessanti. I primi 4 piani dei componenti (Profitto, Fattore di profitto, Fattore di recupero e Indice di Sharpe) sembrano simili perché dipendono direttamente dalle prestazioni del sistema di trading.
Come si può vedere dalla Fig.24, la regione in alto a sinistra è molto interessante (per esempio, si possono ottenere risultati migliori se impostiamo MovingPeriod da 45 a 50).
L'Expert Advisor è stato testato su un intervallo di tempo orario di EURUSD e la sua strategia è basata sul trend. Possiamo considerare questi valori come una memoria di "trend di mercato". Se è vero, la memoria dell'andamento del mercato per la prima metà del 2011 è pari a 2 giorni.
Consideriamo altri piani dei componenti.
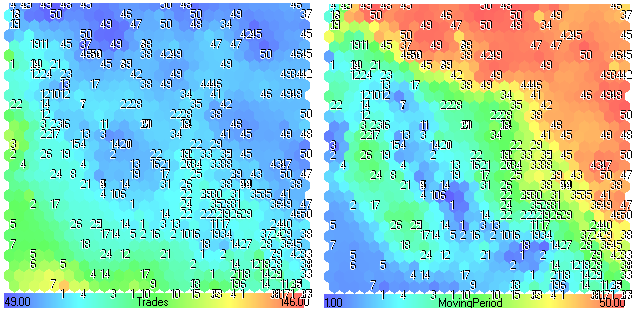
Figura 26. Piani dei componenti Trades-MovingPeriod
Guardando alla Fig.26, possiamo vedere che i valori più bassi di MovingPeriod (regioni blu) portano a valori maggiori di Trades (regioni giallo-rosse). Se il periodo della media mobile è basso, ci sono molti crossover (trade).
Inoltre, possiamo vedere questo fatto sul piano dei componenti Trade (regioni verdi con numeri inferiori a 20).
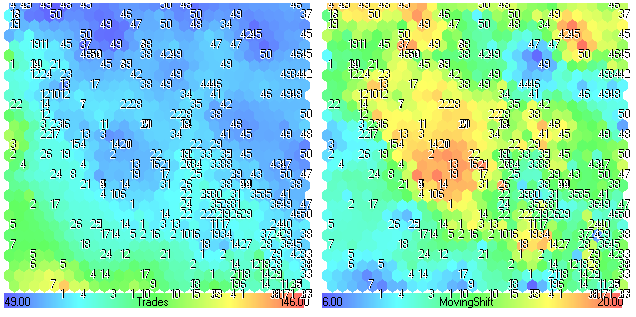
Figura 27. Piani dei componenti Trades-MovingShift
Il numero di operazioni diminuisce (regioni blu) all'aumentare del MovingShift (regioni giallo-rosse). Confrontando i piani dei componenti per MovingShift e la Fig.24, si può vedere che il parametro MovingShift non è molto importante per le prestazioni di questa strategia di trading.
La percentuale di operazioni redditizie ProfitTrades(%) non dipende direttamente da MovingPeriod o MovingShift, ma è una caratteristica integrale del sistema di trading. In altre parole, l'analisi della sua correlazione con i parametri di input non ha alcun significato.
Le strategie di trading più complesse possono essere analizzate in modo simile. Devi trovare i parametri più importanti del tuo sistema di trading e usarli come titolo.
Conclusione
Il vantaggio principale delle mappe di funzioni auto-organizzanti è l'opportunità di produrre una rappresentazione discretizzata bidimensionale di dati ad alta dimensione. I dati con caratteristiche simili formano cluster, il che semplifica l'analisi di correlazione.
Altri dettagli e applicazioni possono essere trovati nell'eccellente libro Visual Explorations in Finance: with Self-Organizing Maps di Guido Deboeck e Teuvo Kohonen.
Appendice
Dopo la pubblicazione della versione russa, Alex Sergeev ha proposto la versione migliorata delle classi (SOM_Alex-Sergeev_en.zip).
Elenco modifiche:
1. La visualizzazione delle immagini è cambiata: cIntBMP::Show(int aX, int aY, string aBMPFileName, string aObjectName, bool aFromImages=true)
2. È stata aggiunta la funzione per aprire la cartella con le immagini:
#import "shell32.dll" int ShellExecuteW(int hwnd, string oper, string prog, string param, string dir, int show); #import input bool OpenAfterAnaliz=true; // open folder with maps after finish
Modifiche alla classe CSOM:
- È stato aggiunto il metodo CSOM::HideChart per nascondere il grafico.
- Sono stati aggiunti i membri della classe m_chart, m_wnd, m_x0, m_y0 - (grafico, finestra e coordinate per mostrare le immagini).
+ m_sID - prefisso dei nomi degli oggetti. Il prefisso utilizza il nome del file, per impostazione predefinita viene utilizzato il prefisso "SOM". - Tutte le mappe vengono salvate nella cartella con nome m_sID.
- I file bmp sono denominati in base al nome della colonna dei modelli.
- Modificato il metodo CSOM::ShowBMP (mappe salvate nella cartella \Files invece di \Images, funziona molto più velocemente).
- Il CSOM::NetDeinit è cambiato in CSOM::HideBMP.
- Modificato il metodo CSOM::ReadCSVData, la prima colonna contiene i titoli.
- Aggiunto un flag per mostrare le mappe intermedie su CSOM::Train(bool bShowProgress).
- La visualizzazione delle mappe intermedie su CSOM::Train viene eseguita ogni 2 secondi (anziché l'iterazione), l'avanzamento viene mostrato sul grafico tramite il Commento.
- Nomi ottimizzati di alcune variabili, metodi di classe ordinati per categoria.
Il disegno di bmp è un processo molto lento. Se non ne hai davvero bisogno, non disegnarlo ogni volta.
L'esempio di immagini SOM con risultati di ottimizzazione è incluso nell'archivio.
Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/283
Creazione di criteri personalizzati di ottimizzazione degli Expert Advisor
Stime statistiche
Il Wizard MQL5 per principianti
Tracciamento, debug e analisi strutturale del codice sorgente
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso