
Was ist Martingale?
Was ist Martingale?
Wenn Sie "Martingale" in das Suchfeld einer Suchmaschine eingeben, erhalten Sie eine große Anzahl an Seiten mit einer Beschreibung dieses Systems. Es ist interessant, dass Sie, neben anderen, auf Webseiten von Online-Casinos stoßen werden, die versichern, dass dieses System funktioniert, und alles was Sie tun müssen, ist die Nummer Ihrer Kreditkarte anzugeben und anzufangen Geld zu scheffeln. Was merkwürdig ist - sind die Casinos bereit so einfach ihr Geld abzugeben? Wenn das Martingale wirklich so gut funktioniert, warum sind nicht alle Casinos längst pleite gegangen?
Also, was ist Martingale? Hier ist die Definition von Wikipedia:
- Ein Spiel beginnt mit einem bestimmten minimalen Einsatz,
- Nach jedem Verlust soll der Einsatz so erhöht werden, dass der Gewinn alle vorherigen Verluste abdeckt, plus eines kleinen Gewinns,
- Im Falle des Gewinns, kehrt der Spieler zurück zum minimalen Einsatz.
Wo wird Martingale verwendet?
Das einfachste Glücksspiel um Martingale zu untersuchen ist der Münzwurf. Die Chancen zu gewinnen oder zu verlieren sind gleich - der Spiele gewinnt, wenn die Münze Kopf zeigt und verliert wenn sie Zahl zeigt. Das Martingale System funktioniert bei diesem Spiel auf die folgende Weise:
- Beginnen Sie das Spiel mit einem kleinen Einsatz,
- Nach jedem Verlust verdoppeln Sie den Einsatz,
- Im Falle des Gewinns, kehren Sie zurück zu dem Minimalen Einsatz.
Das Martingale System kann auch beim Spielen von Roulette verwendet werden, mit Einsätzen auf Rot oder Schwarz. Die Chancen sind geringer als 50/50, weil auch die Null dabei ist, aber immer noch sehr nah dran.
Wird es auf Trading angewandt, kann die folgende Variante des Spiel verwendet werden. Analog zu einem Münzwurf, öffnen wir eine Position in eine beliebige Richtung (Short oder Long), Mit Stop-Loss und Take-Profit in gleichem Abstand zum Eröffnungskurs. Wenn wir die Position in eine zufällige Richtung öffnen, ist die Wahrscheinlichkeit von Gewinn und Verlust analog - 50/50. Also, in diesem Artikel beschreibe ich nur das klassische Problem des Münzwurfs und der Verdoppelung des Einsatzes bei einem Verlust.
Mathematischer Teil
Führen wir eine mathematische Berechnung über die Abhängigkeit der Verlustwahrscheinlichkeit gegenüber dem möglichen Gewinn mit dem Martingale System durch. Wir verwenden die folgenden Symbole:
- Set – eine Reihe von Würfen, die mit einem Gewinn enden. Das heißt, alle Würfe, ausgenommen der letzte, verlieren. Bei dem ersten Wurf ist der Einsatz minimal, bei jedem nächsten Wurf wird der Einsatz verdoppelt,
- Q – anfängliche Einlage
- q – Preis der Start-Wette
- k – maximale Anzahl an Würfen (verlierend) in einer Reihe, die in den Bankrott führen (angenommen nach k Würfen ist die Einlage gleich Null).
Da wir nach jedem Verlust-Wurf verdoppeln, können wir folgende Gleichung ableiten:
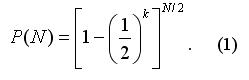
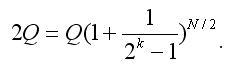
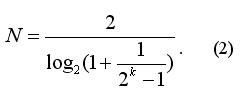
Wenn wir N nicht als Ganzzahl betrachten (runden Sie die Ergebnisse von Kapitalwert (2) nicht zu einer Ganzzahl), dann ist hängt P(N) nicht von k ab und ist gleich 1/2 (Sie können das leicht überprüfen, mit Einfügen von (2) in (1) mit den einfachsten Eigenschaften von Logarithmen). Das heißt, die Verwendung von Martingale bietet keine Vorteile. Wir könnten auch unser gesamtes Kapital Q einsetzen, und der Gewinn wäre wahrscheinlich der gleiche (1/2).
Schlussfolgerung aus dem Mathematischen Teil
Ehrlich gesagt, zu Beginn dieses Artikels, bei der Vorbereitung der Berechnungen, habe ich erwartet, dass Martingale die Wahrscheinlichkeit des Verlusts erhöhen wird. Es erwies sich als falsch und das Verlustrisiko erhöht sich nicht. Trotzdem beschreibt der Artikel anschaulich die Bedeutungslosigkeit der Verwendung von Martingale.
Expert Advisor
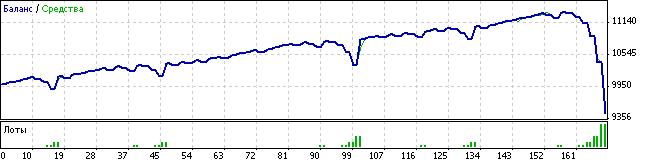
Nach dem Erhalt der obigen Formeln, war das erste was ich tat, das Schreiben eines kleinen Programms, das den Vorgang des Münzwurf-Spiels simuliert und die Abhängigkeit der Verlustwahrscheinlichkeit (P) von dem Koeffizienten k abfasst. Nach der Prüfung fand ich, dass die Programmergebnisse (es kann "ein Experiment" genannt werden) sich mit den mathematischen Berechnungen deckenNatürlich, die ideale Variante wäre es einen Expert Advisor zu schreiben, der nach den selben Regeln handelt wie bei dem Münzwurf, und sicherstellt, dass theoretische und experimentelle Daten identisch sind. Es ist allerdings unmöglich, weil der Anfangseinsatz mit dieser Formel berechnet wird:
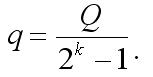
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/1481
 Kursprognose mit Neuralen Netzen
Kursprognose mit Neuralen Netzen
 Praktische Verwendung eines Virtual Private Server (VPS) für Autotrading
Praktische Verwendung eines Virtual Private Server (VPS) für Autotrading
 MQL4 Sprache für Einsteiger. Schwierige Fragen in Einfachen Sätzen.
MQL4 Sprache für Einsteiger. Schwierige Fragen in Einfachen Sätzen.
 Handelssignal über RSS Feed senden
Handelssignal über RSS Feed senden
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.