¿Qué es un Martingale? y ¿es razonable usarlo?

¿Qué es Martingale?

Si escribimos "martingale" en el cuadro de un buscador, este nos devolverá un gran número de páginas con la descripción de este sistema. Es interesante que, entre otras, encontraremos sitios web de casinos en línea, que garantiza que este sistema funciona, y todo lo que necesitamos es introducir el número de nuestra tarjeta de crédito para empezar a recoger el dinero. Pero lo que es extraño es ¿están los casinos preparados para dar su dinero con tanta facilidad? Si el Martingale funciona realmente tan bien, entonces ¿por qué no ha quebrado todos los casinos?

Entonces, ¿qué es Martingale? Esta es la definición de la Wikipedia:

El Martingale es un sistema de apuestas en los juegos de azar. El significado es el siguiente:

• Un juego comienza con una apuesta mínima;
• Después de cada pérdida, la apuesta debe incrementarse, por lo que al ganar pueden recuperarse todas las pérdidas anteriores más un pequeño beneficio;
• En caso de ganar, un jugador vuelve a la apuesta mínima.

(Traducción del ruso hecha por MetaQuotes Software Corp.)Aquí puede encontrar más información: https://en.wikipedia.org/wiki/Martingale_system

¿Dónde se usa Martingale?

El juego de azar más sencillo para el análisis, Martingale es un hoyuelo. Los opciones de ganar y perder son idénticas: el jugador gana si sale cara en una moneda y pierde si sale cruz. El sistema Martingale para este juego funciona de esta forma:

• Se inicia el juego con una pequeña apuesta;
• Después de cada pérdida se dobla la apuesta;
• En caso de ganar, un jugador vuelve a la apuesta mínima.

El Martingale también puede usarse al jugar a la ruleta, apostando al rojo o al negro. Las opciones son menores que el 50/50, ya que también está el cero, pero aún está muy cerca.

Al aplicarlo al trading, puede usarse la siguiente variante del juego. Al igual que cuando lanzamos una moneda, abrimos una posición en cualquier dirección (corta o larga) con stop-loss y take-profit equidistantes del precio de la transacción. Cuando abrimos la posición en una dirección aleatoria, la probabilidad de beneficio y pérdida es la misma: 50/50. En este artículo describiré solo el problema clásico de lanzar una moneda doblando la apuesta al perder.

Parte matemática

Vamos a realizar un cálculo matemático de la dependencia de la probabilidad de pérdida respecto al posible beneficio en el juego con una moneda usando el sistema Martingale. Vamos a presentar los símbolos siguientes:

• Set – un conjunto de tiradas que terminan con una ganadora. Es decir, todas las tiradas son perdedoras excepto la última. En la primera tirada la apuesta es mínima, y en cada tirada siguiente del conjunto se dobla la apuesta;
• Q – depósito inicial;
• q – precio de la apuesta inicial;
• k – número máximo de tiradas (perdedoras) en el conjunto, que llevan a la bancarrota (se supone que después de k tiradas el depósito es igual a cero).

Como doblamos la apuesta después de cada tirada perdedora, podemos obtener la siguiente ecuación:

Cada conjunto con la cantidad de tiradas menos k-1 devuelve el beneficio q. Como la probabilidad de ganar en una tirada = ½, la longitud promedio del conjunto es 2*. Vamos a llamar P(N) a la probabilidad de que no se produzca la bancarrota en N tiradas. Como N son aproximadamente N/2 conjuntos (la longitud promedio del conjunto es 2), y la probabilidad de ganar en el conjunto es (1/2)^k-1 , luego

Obtenemos la función de la dependencia de ganar en N. Pero el número total de tiradas (N) no nos informa lo suficiente, por lo que vamos a intentar vincular N con un beneficio esperado. Supongamos que en el resultado queremos doblar nuestro capital. Como en el conjunto, cada vez que ganamos q=Q/(2^k-1), el beneficio total se calcula de acuerdo con la regla del interés compuesto (puede consultar información adicional sobre el interés compuesto aquí):

Después de algunas transformaciones sencillas obtenemos la siguiente fórmula para N:

Después de calcular la probabilidad del beneficio P(N) usando las igualdades (1)-(2) obtenemos los resultados siguientes:

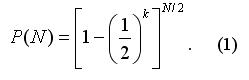
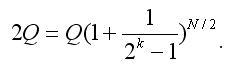
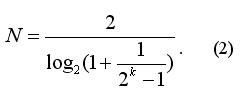
Si tenemos en cuenta N como si no fuera entero (no redondeamos los resultados de la igualdad (2) a un número entero), entonces P(N) no depende de k y es igual a 1/2 (puede verificarlo fácilmente, insertando (2) en (1) y usando las propiedades más simples de los logaritmos). Es decir, usar Martingale no proporciona ninguna ventaja. Podríamos también apostar todo nuestro capital Q y la probabilidad de ganar sería la misma (1/2).

Conclusiones de la parte matemática

Hablando francamente, el comienzo de la preparación de los cálculos para este artículo, esperaba que Martingale incrementara la probabilidad de pérdidas. Parecía ser incorrecto y el riesgo de pérdida no aumentaba. Aunque este artículo describe con mucha claridad la inutilidad de usar Martingale.

Asesor Experto

Después de obtener las fórmulas anteriores, lo primero que hice fue escribir un pequeño programa que emulaba el proceso de juego de hoyuelos y que elaboraba estadísticas sobre la dependencia de la posibilidad de pérdida (P) del coeficiente k. Después de la comprobación, encontré que los resultados del programa (puede llamarse "un experimento") coinciden con los cálculos matemáticos.
Por supuesto, la variante ideal sería escribir un asesor experto que operase con las mismas reglas que en los hoyuelos y asegurarnos que los datos teóricos y los experimentales son idénticos. Pero es imposible, ya que la apuesta inicial se calcula usando la fórmula:

Y en Forex podemos "apostar" solo una suma múltiplo de 1/10 de un lote. Por esta razón, es imposible escribir un asesor experto que proporcione claramente las fórmulas anteriores. No obstante, para completar el análisis aún podemos escribir un asesor experto usando Martingale. Pero aquí la apuesta inicial se fijará en 0,1 de un lote. De forma análoga, la apuesta se doblará con una pérdida y volverá a la inicial con un beneficio. Como se describió al comienzo del artículo, se abrirá una transacción de la forma siguiente: se abre una transacción en una dirección aleatoria con la probabilidad del 50 % y stoploss y takeprofit se fijan a una misma distancia.

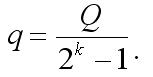
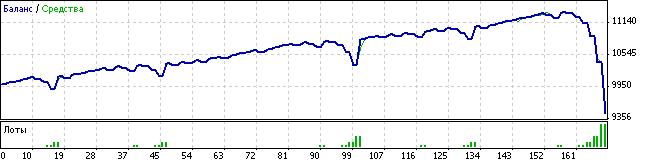
La captura de pantalla anterior muestra los resultados de la prueba de este asesor experto. Como ve, aunque la dirección general de la curva es ascendente, de vez en cuando sufre grandes caídas. Como resultado de la última caída, el asesor experto deja de operar, ya que el balance no es suficiente para la siguiente apuesta con un lote duplicado. Y en el momento de la parada, el balance es positivo: esta es la diferencia con el cálculo teórico en la "parte matemática".
Nota final Los archivos adjuntos contienen la captura de pantalla de todos los cálculos matemáticos necesarios y el asesor experto.