Kategorientheorie in MQL5 (Teil 15) : Funktoren mit Graphen

Einführung

Im vorigen Artikel haben wir uns angesehen, wie Konzepte, die in früheren Artikeln behandelt wurden, wie lineare Ordnungen, als Kategorien betrachtet werden können und warum ihre „Morphismen“ Funktoren darstellen, wenn sie sich auf andere Kategorien beziehen. In diesem Artikel werden wir die Illustrationen aus dem vorherigen Artikel vertiefen, indem wir uns ansehen, wie Graphentheorie von ähnlichem Nutzen sein können wie die im vorherigen Artikel besprochenen linearen Ordnungen. Um Graphen zu verwenden, werden wir die MQL5-Kalenderdaten als Graphen und damit als Kategorie rekonstruieren. Dies wird ein wichtiger Schwerpunkt sein. Ziel dieses Artikels ist es daher, wie in unserem vorangegangenen Artikel, das Volatilitätsprognosepotenzial von Funktoren zwischen zwei Kategorien aufzuzeigen. In diesem Fall ist unsere Domänenkategorie jedoch ein Graph, während die Codomäne die Volatilitätswerte des S&P 500 (nicht VIX) in einer Zeitreihenvorordnung enthält.

Rekonstituieren von MQL5-Kalender-Feed-Daten als Graph

Der MQL5-Wirtschaftskalender wurde bereits behandelt, als wir die Kategorientheorie mit Datenbankschemata in Verbindung brachten, sodass eine erneute Einführung seiner Relevanz für Händler hier nicht angebracht ist. Um ihn als Graphen, eine Folge von Kanten und Knoten, darzustellen, muss zunächst eine Vorauswahl der Nachrichten getroffen werden, die wir in unsere Kategorie aufnehmen wollen. Wie aus der Website des Wirtschaftskalenders ersichtlich ist, gibt es eine Vielzahl von Punkten, aus denen man wählen kann. Wenn wir jedoch beschließen, nur vier auszuwählen, basierend auf einer losen Hypothese, die sie wie im folgenden Diagramm zeigt, verbindet:

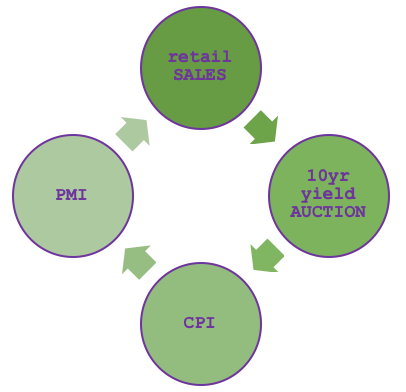
Dann würde unsere Hypothese besagen, dass die Einzelhandelsumsätze von den PMI-Zahlen der Produzenten abhängen, die wiederum vom Verbraucherpreisindex abgeleitet sind, der wiederum davon abhängt, wie gut die Treasury-Auktionen gelaufen sind, deren Ergebnisse ebenfalls auf den Einzelhandelsumsätzen beruhen. Es handelt sich also um einen einfachen Zyklus, dessen Wahrheitsgehalt nicht Gegenstand des Artikels ist, sondern vielmehr dazu dient, eine mögliche Zusammenstellung als Graph aus den Daten des Wirtschaftskalenders zu veranschaulichen.

Graphen bieten den Vorteil, dass sie komplexe, miteinander verbundene Systeme vereinfachen, indem sie zwei übersichtliche Tabellen erstellen, von denen eine die Paarungen der Knotenpunkte enthält und die andere als Index der Knotenpunkte dient. Ein Graph kann als Kategorie betrachtet werden, da die Eckpunkte als Objekte (Domänen) angesehen werden können und die Kanten als Morphismen dienen. Nebenbei bemerkt: Der Unterschied zu einer linearen Ordnung, wie sie im vorigen Artikel betrachtet wurde, liegt, wie der Name schon sagt, in der Linearität. Graphen sind in der Regel für komplexere Verbindungen geeignet, bei denen ein Objekt/ein Bereich mit mehr als einem Objekt verbunden sein kann.

Anstatt also einzelne Objekte in dieser Kategorie mit Objekten in der Kategorie S&P-Volatilität zu paaren, wie wir es im vorherigen Artikel über lineare Aufträge getan haben, werden wir die Zeilen der Scheitelpunktpaare mit der Kategorie S&P paaren. Dies bedeutet, dass es kein Isomorphismus sein kann, da mehrere Zeilen an ein einziges Objekt (Datenpunkt) in der S&P gebunden sind, da die S&P zeitbasiert ist. Das bedeutet auch, dass unsere Domänenobjekte aus vier Elementen bestehen werden (die letzten Werte jedes der vier Elemente im Zyklus).

Kategorientheorie und Funktoren - eine Zusammenfassung

Die Kategorientheorie hat viele Anwendungen, wie bereits in den bisherigen Artikeln erwähnt, aber die meisten öffentlichen Referenzen neigen dazu, sich auf die algebraische Topologie zu konzentrieren, und das könnte an den ursprünglichen Autoren dieses Themas liegen, weshalb die Anwendung auf den Handel über MQL5 neu erscheinen mag. In der Tat neigen die meisten Händler, die mit MQL5 vertraut sind, dazu, neuronale Netze zu verwenden, um einen Vorteil für ihre Systeme zu entwickeln, vielleicht, weil sie sie sie über einen längeren Zeitraum studiert haben und mit den Kategorien verglichen haben, aber das sollte nicht davon abhalten, auch Kategorien zu erforschen, weil das Endergebnis ist, dass die meisten Händler nach einem Vorteil suchen und wenn ein System oder eine Methode zu häufig vorkommt, dann sind die Chancen, einen zu finden, geringer.

Funktoren (Mathematik) sind, wie bereits in unserem letzten Artikel erwähnt, in Wirklichkeit Morphismen zwischen Kategorien. Diese „Morphismen“ verbinden nicht nur die Objekte in zwei Kategorien, sondern sie verbinden auch die Homomorphismen zwischen den Kategorien.

Im letzten Artikel haben wir zwei Szenarien getestet, wobei wir zum einen die Objektverknüpfung zwischen zwei Kategorien und zum anderen die Morphismusverknüpfung zwischen denselben Kategorien berücksichtigt haben. Ein Funktor ist ein Protokoll von beiden. Für unsere Zwecke untersuchten wir die Unterschiede zwischen den beiden, indem wir jeweils einen der beiden einsetzten, und erstellten für beide Berichte von Strategietestern, die die relative Bedeutung bei der Prognose der NASDAQ-Volatilität hervorhoben. In Anbetracht des kurzen Testzeitraums vom 1. Januar 2020 bis zum 15. März desselben Jahres konnten keine Schlussfolgerungen darüber gezogen werden, welche Zuordnung besser ist, aber der Unterschied in den Ergebnissen deutete auf eine hohe Sensitivität hin und damit auf die Notwendigkeit, eine der beiden hervorzuheben.

Erstellung einer Kategorie der S&P 500-Volatilität

Die Erfassung und Verarbeitung unserer SP500-Volatilitätsdaten ist unkompliziert und ähnelt der Art und Weise, wie wir im letzten Artikel die Volatilität für den NASDAQ gemessen haben. Der CBOE Volatility Index (VIX) ist ein anderer Indikator als der, den wir hier betrachten, und es ist wichtig, dass die Leser dies beachten. Der aktuelle Volatilitätswert wird also bei jedem neuen Balken gemäß der nachstehenden Aufstellung neu berechnet:

      double _float_value=0.0;
      //where R is an instance of MqlRates...
      _float_value=(R.high-R.low)/Point();

Wie bereits erwähnt, wird der S&P unsere Codomain bilden, wobei die Objekte, die die Volatilitätswerte erfassen, eine Objektmenge bilden und die Morphismen zwischen ihnen die relative Veränderung zwischen den Volatilitätswerten erfassen. Die Initialisierung dieser Kategorie könnte wie folgt gehandhabt werden:

//+------------------------------------------------------------------+
//|   Get SP500-100 data from symbol (NDX100 for this broker).       | 
//|   Load it into SP500 category.                                   |
//+------------------------------------------------------------------+
void SetSP500(MqlRates &R)
   {
      _hmorph_sp500.Let();
      
      double _float_value=0.0;
      
      _float_value=(R.high-R.low)/Point();
      
      _element_value.Let();_element_value.Cardinality(1);_element_value.Set(0,DoubleToString(_float_value));
      _domain_sp500.Cardinality(1);_domain_sp500.Set(0,_element_value);
      
      //_category_sp500.Domains(_category_sp500.Domains()+1);
      _category_sp500.SetDomain(_category_sp500.Domains(),_domain_sp500);  
   }

Wie wir in unserem letzten Artikel gesehen haben, könnten wir, wenn wir eine Domäne mit einer Verzögerung auf diese Codomäne abbilden können, eine gewisse Vorhersagekraft für die Volatilität des S&P 500 erhalten. Wie im letzten Artikel werden wir die Objekt- und Morphismus-Funktoren separat mit identischen Signal- und Geldmanagement-Setups testen, um die Empfindlichkeit zu messen.

Funktoren des Wirtschaftskalenders für den S&P 500

Wir werden die Kategorie der Wirtschaftskalenderdaten anhand der nachstehenden Liste erstellen:

//+------------------------------------------------------------------+
//|   Get Ocean data from file defined in input.                     | 
//|   Load it into Ocean category.                                   |
//+------------------------------------------------------------------+
void SetEconomic(MqlRates &R)
   {
      datetime _time=R.time;
      
      int _elements=1;
      
      _e_retail.Let();
      SampleEvents(_time,_e_retail,IntToCountry(__country),__currency,TYPE_RETAIL_SALES);//printf(__FUNCSIG__+"...retail. ");
      
      _e_cpi.Let();
      string _cpi_time="";_e_retail.Get(0,_cpi_time);
      SampleEvents(StringToTime(_cpi_time),_e_cpi,IntToCountry(__country),__currency,TYPE_CPI);//printf(__FUNCSIG__+"...cpi. ");
      
      _e_auction.Let();
      string _auction_time="";_e_cpi.Get(0,_auction_time);
      SampleEvents(StringToTime(_auction_time),_e_auction,IntToCountry(__country),__currency,TYPE_AUCTION_10YR);//printf(__FUNCSIG__+"...auction. ");
      
      _e_pmi.Let();
      string _pmi_time="";_e_auction.Get(0,_pmi_time);
      SampleEvents(StringToTime(_pmi_time),_e_pmi,IntToCountry(__country),__currency,TYPE_PMI);//printf(__FUNCSIG__+"...pmi. ");
      
       _domain_economic.Cardinality(__ECON);
       _domain_economic.Set(0,_e_retail);
       _domain_economic.Set(1,_e_cpi);
       _domain_economic.Set(2,_e_auction);
       _domain_economic.Set(3,_e_pmi);
      
       _category_economic.SetDomain(_category_economic.Domains(),_domain_economic);
   }

Jedes Objekt in diesem Bereich hat zwei Scheitelpunkte, die die gepaarten Kalenderwerte darstellen, von denen mindestens einer im Zeitbereich des Volatilitätswerts im Codomain liegt. Da diese Wirtschaftsdaten in Abständen von etwa einem Monat veröffentlicht werden, werden wir den Test im monatlichen Zeitrahmen durchführen. Wie im vorangegangenen Artikel wird unser Funktorzuordnung Koeffizienten für jeden Datenpunkt im Objekt haben. Der Unterschied besteht darin, dass wir mit der Möglichkeit konfrontiert sind, dass mehrere Objekte auf dieselbe Volatilität in der Codomain abgebildet werden. Im Idealfall müssen wir den Koeffizienten (für eine lineare Abbildung) von jedem Objekt separat ermitteln und für die Vorhersage verwenden. Das bedeutet, dass sie zwangsläufig widersprüchliche Projektionen zusätzlich zu den von der Morphismusabbildung gelieferten liefern. Für die Zwecke dieses Artikels könnten wir daher jeden Funktor, der die Kalenderdaten auf die S&P-Kategorie abbildet, abwägen und die Summe der Punktprodukte nehmen, um den Volatilitätswert zu ermitteln.

Die praktische Anwendung der Funktoren erfolgt wie im vorangegangenen Artikel in zwei Alternativen, wobei wir in der ersten Iteration die Objekte und in der nächsten die Morphismen abbilden werden. Die Zuordnung der Objekte von der Funktion Output() wird sein:

//+------------------------------------------------------------------+
//| Get Forecast value, forecast for next change in price bar range. |
//+------------------------------------------------------------------+
double GetObjectsForecast(MqlRates &R)
   {
      double _output=0.0;
      
      //econ init
      SetEconomic(R);
      
      //sp500 init
      SetSP500(R);
      
      matrix _domain;
      vector _codomain,_inputs;
      
      _domain.Init(__ECON+1,__ECON);
      
      for(int r=0;r<__ECON+1;r++)
      {
         CDomain<string> _d;_d.Let();
         _category_economic.GetDomain(_category_economic.Domains()-r-1,_d);
         
         for(int c=0;c<__ECON;c++)
         {
            CElement<string> _e; _d.Get(c,_e);
            
            string _s; _e.Get(1,_s);
            
            _domain[r][c]=StringToDouble(_s);
         }
      }
      
      _codomain.Init(__ECON);
      
      for(int r=0;r<__ECON;r++)
      {
         CDomain<string> _d;_d.Let();
         _category_sp500.GetDomain(_category_sp500.Domains()-r-1,_d);
         
         CElement<string> _e; _d.Get(0,_e);
         
         string _s; _e.Get(0,_s);
            
         _codomain[r]=StringToDouble(_s);
      }
      
      _inputs.Init(__ECON);_inputs.Fill(__constant_morph);
      
      M(_domain,_codomain,_inputs,_output,1);
      
      return(_output);
   }

Unsere Morphismus-zu-Morphismus-Zuordnung wird auch anders gehandhabt, indem wir die Morphismen zwischen den Scheitelpunkten, wie durch das Änderungsdelta definiert, auf den Morphismus zwischen den Volatilitätsdatenpunkten der S&P, wie ebenfalls durch den Änderungswert definiert, abbilden. Dies wird wie folgt gehandhabt:

//+------------------------------------------------------------------+
//|   Get Forecast value, forecast for next change in price bar range. |
//+------------------------------------------------------------------+
double GetMorphsForecast(MqlRates &R)
   {
      ...
      
      for(int r=0;r<__ECON+1;r++)
      {
         ...
         
         for(int c=0;c<__ECON;c++)
         {
            CElement<string> _e_new; _d_new.Get(c,_e_new);
            
            string _s_new; _e_new.Get(1,_s_new);
            
            CElement<string> _e_old; _d_old.Get(c,_e_old);
            
            string _s_old; _e_old.Get(1,_s_old);
            
            _domain[r][c]=StringToDouble(_s_new)-StringToDouble(_s_old);
         }
      }
      
      _codomain.Init(__ECON);
      
      for(int r=0;r<__ECON;r++)
      {
         ...
         
         CElement<string> _e_new; _d_new.Get(0,_e_new);
         
         string _s_new; _e_new.Get(0,_s_new);
         
         CElement<string> _e_old; _d_old.Get(0,_e_old);
         
         string _s_old; _e_old.Get(0,_s_old);
         
         _codomain[r]=StringToDouble(_s_new)-StringToDouble(_s_old);
      }
      
      _inputs.Init(__ECON);_inputs.Fill(__constant_morph);
      
      M(_domain,_codomain,_inputs,_output,1);
      
      return(_output);
   }

Die Darstellung als Diagramm dieser beiden Teile des Funktors wird sich ebenfalls leicht von dem unterscheiden, was wir im letzten Artikel behandelt haben, da unsere Beziehung nicht mehr isomorph sein wird, wie es damals der Fall war. Wir können die Zuordnung von Objekt zu Objekt wie folgt veranschaulichen:

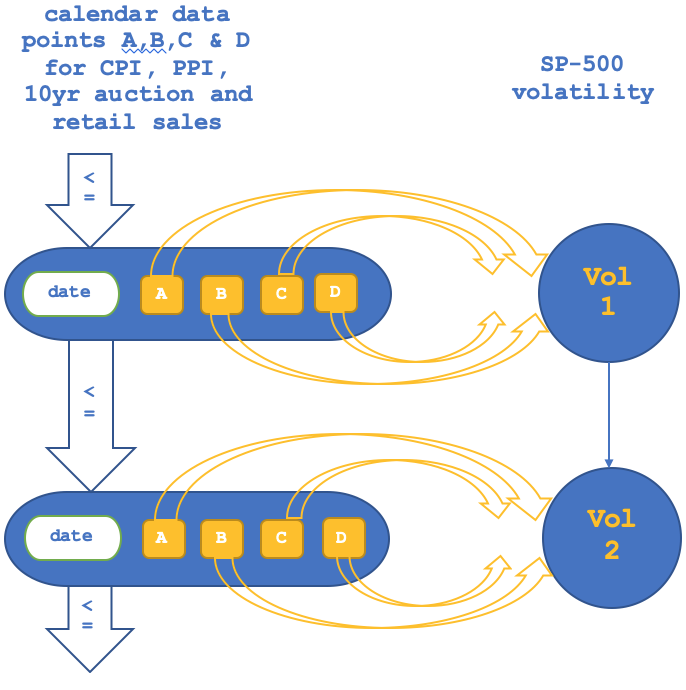
Und so sieht der Morphismus zu Morphismus aus:

Es ist bedauerlich, dass der Strategietester von MQL5 keine Tests mit Zugriff auf wirtschaftliche Kalenderereignisse ermöglicht. Viele Leistungsgewinne, die sich aus der Entwicklung robusterer Handelssysteme ergeben, bleiben auf dem Tisch liegen. Da wir dies als Skript kodiert haben, können wir bestenfalls die voraussichtliche Änderung der Volatilität auf der Grundlage unserer Prognose ausgeben. Wenn Sie einige Verlaufsdaten durchgehen, können Sie einen Eindruck davon gewinnen, wie genau unsere Prognosen sind.

Nichtsdestotrotz, wenn wir unser Skript ausführen, das auf den vom Broker bereitgestellten Preisdaten basiert, sind wir in der Lage, unsere beiden Kategorien aus dem Graph der Kalenderdaten und aus der Volatilität des SP500 sowie ihrem Verbindungsfunktor zu konstruieren, und wir erhalten die folgenden Protokolle, die Projektionen zur Volatilität erstellen. Die Zuordnung vom Objekt-zu-Objekt-Funktor druckt die Protokolle:

2023.07.30 13:45:47.035 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: 0.00000000, on: 2020.01.01 00:00, with actual being: 54260.00000000
2023.07.30 13:45:47.134 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: 0.00000000, on: 2020.02.01 00:00, with actual being: 95438.00000000
2023.07.30 13:45:47.265 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: 0.00000000, on: 2020.03.01 00:00, with actual being: 53588.00000000
2023.07.30 13:45:47.392 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: 0.00000000, on: 2020.04.01 00:00, with actual being: 30352.00000000
2023.07.30 13:45:47.512 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: 0.00000000, on: 2020.05.01 00:00, with actual being: 29694.00000000
2023.07.30 13:45:47.644 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -716790.11376869, on: 2020.06.01 00:00, with actual being: 21905.00000000
2023.07.30 13:45:47.740 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -12424.22112077, on: 2020.07.01 00:00, with actual being: 26509.00000000
2023.07.30 13:45:47.852 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: 53612.17123096, on: 2020.08.01 00:00, with actual being: 37890.00000000




...

2023.07.30 13:45:50.294 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -27774.72154618, on: 2022.09.01 00:00, with actual being: 42426.00000000
2023.07.30 13:45:50.377 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: 46751.59791572, on: 2022.10.01 00:00, with actual being: 39338.00000000
2023.07.30 13:45:50.487 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -19820.29385469, on: 2022.11.01 00:00, with actual being: 37305.00000000
2023.07.30 13:45:50.593 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -5370.60103622, on: 2022.12.01 00:00, with actual being: 30192.00000000
2023.07.30 13:45:50.700 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -4662833.98425755, on: 2023.01.01 00:00, with actual being: 25359.00000000
2023.07.30 13:45:50.795 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: 33455.47933459, on: 2023.02.01 00:00, with actual being: 30681.00000000
2023.07.30 13:45:50.905 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -40357.22273603, on: 2023.03.01 00:00, with actual being: 12502.00000000
2023.07.30 13:45:51.001 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -37676.03496283, on: 2023.04.01 00:00, with actual being: 18835.00000000
2023.07.30 13:45:51.094 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -54634.02723538, on: 2023.05.01 00:00, with actual being: 28877.00000000
2023.07.30 13:45:51.178 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -35897.40757724, on: 2023.06.01 00:00, with actual being: 23306.00000000
2023.07.30 13:45:51.178 ct_15_w (SPX500,MN1)    void OnStart() corr is: 0.36053106 with morph constant as: 50000.00000000

Während Morphismus zu Morphismus das Folgende ausgibt:

2023.07.30 13:47:38.737 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: 0.00000000, on: 2020.01.01 00:00, with actual being: 54260.00000000
2023.07.30 13:47:38.797 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: 0.00000000, on: 2020.02.01 00:00, with actual being: 95438.00000000
2023.07.30 13:47:38.852 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: 0.00000000, on: 2020.03.01 00:00, with actual being: 53588.00000000
2023.07.30 13:47:38.906 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: 0.00000000, on: 2020.04.01 00:00, with actual being: 30352.00000000
2023.07.30 13:47:39.010 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: 0.00000000, on: 2020.05.01 00:00, with actual being: 29694.00000000
2023.07.30 13:47:39.087 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: -2482719.31391738, on: 2020.06.01 00:00, with actual being: 21905.00000000




...

2023.07.30 13:47:41.541 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: -86724.54189079, on: 2022.11.01 00:00, with actual being: 37305.00000000
2023.07.30 13:47:41.661 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: -126817.99564744, on: 2022.12.01 00:00, with actual being: 30192.00000000
2023.07.30 13:47:41.793 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: -198737.93199622, on: 2023.01.01 00:00, with actual being: 25359.00000000
2023.07.30 13:47:41.917 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: -280104.88246660, on: 2023.02.01 00:00, with actual being: 30681.00000000
2023.07.30 13:47:42.037 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: 24129.34336223, on: 2023.03.01 00:00, with actual being: 12502.00000000
2023.07.30 13:47:42.157 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: 4293.73674465, on: 2023.04.01 00:00, with actual being: 18835.00000000
2023.07.30 13:47:42.280 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: 763492.31964126, on: 2023.05.01 00:00, with actual being: 28877.00000000
2023.07.30 13:47:42.401 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: -30298.30836734, on: 2023.06.01 00:00, with actual being: 23306.00000000
2023.07.30 13:47:42.401 ct_15_w (SPX500,MN1)    void OnStart() corr is: 0.03400012 with morph constant as: 50000.00000000

Einige Punkte aus den obigen Protokollen sind erwähnenswert. Erstens: Die ersten fünf Monate weisen alle einen Null auf. Ich denke, das liegt daran, dass nicht genügend Preisdaten vorliegen, um vollständige Berechnungen durchzuführen, wie es manchmal bei vielen Indikatoren der Fall ist. Zweitens sind negative Werte Teil der Prognosen, doch wir suchen lediglich nach einem streng positiven Wert, um anzugeben, wie hoch unsere Volatilität im nächsten Balken sein wird. Dies könnte darauf zurückzuführen sein, dass wir niedrige Volatilitätswerte nicht richtig einschätzen können, da wir die Regressionstools der MQL5-Bibliothek verwenden, die Identitätsmatrizen bei der Lösung für unsere Mehrfachkoeffizienten (vier) verwenden. Eine Umgehung dieses Problems könnte darin bestehen, negative Werte mit Hilfe einer Funktion wie der unten vorgeschlagenen zu normalisieren.

//+------------------------------------------------------------------+
//| Normalizes negative projections to positive number.              |
//+------------------------------------------------------------------+
double NormalizeForecast(double NegativeValue,double CurrentActual,double PreviousActual,double PreviousForecast)
   {
      return(CurrentActual+(((CurrentActual-NegativeValue)/CurrentActual)*fabs(PreviousActual-PreviousForecast)));
   }

Wenn wir nun unser Skript ausführen und die Korrelation zwischen unseren Projektionen und den tatsächlichen Werten überprüfen, werden wir mit Sicherheit unterschiedliche Ergebnisse erhalten, zumal die Gleichungskonstante ein sehr empfindlicher Wert ist, der in hohem Maße bestimmt, welche Ausgaben und Projektionen wir am Ende erhalten. Für die nachstehend erstellten Protokolle setzen wir ihn auf Null. Zuerst führen wir den Objekt-zu-Objekt-Funktor aus:

2023.07.30 14:43:42.224 ct_15_w_n (SPX500,MN1)  void OnStart() Objects forecast is: 15650.00000000, on: 2020.01.01 00:00, with actual being: 54260.00000000

...

2023.07.30 14:43:45.895 ct_15_w_n (SPX500,MN1)  void OnStart() Objects forecast is: 15718.63125861, on: 2023.03.01 00:00, with actual being: 12502.00000000
2023.07.30 14:43:45.957 ct_15_w_n (SPX500,MN1)  void OnStart() Objects forecast is: 12187.53007421, on: 2023.04.01 00:00, with actual being: 18835.00000000
2023.07.30 14:43:46.026 ct_15_w_n (SPX500,MN1)  void OnStart() Objects forecast is: 19185.80075759, on: 2023.05.01 00:00, with actual being: 28877.00000000
2023.07.30 14:43:46.129 ct_15_w_n (SPX500,MN1)  void OnStart() Objects forecast is: 11544.54076238, on: 2023.06.01 00:00, with actual being: 23306.00000000
2023.07.30 14:43:46.129 ct_15_w_n (SPX500,MN1)  void OnStart() correlation is: 0.46195608 with morph constant as: 0.00000000

Und dann führen wir unser Skript aus, während wir Projektionen auf der Grundlage des Morphismus-zu-Morphismus-Funktors vornehmen, wiederum mit der gleichen Gleichungskonstante von Null.

2023.07.30 14:45:54.257 ct_15_w_n (SPX500,MN1)  void OnStart() Morphs forecast is: 54260.00000000, on: 2020.02.01 00:00, with actual being: 95438.00000000

...

2023.07.30 14:45:57.449 ct_15_w_n (SPX500,MN1)  void OnStart() Morphs forecast is: 257937.92970615, on: 2023.05.01 00:00, with actual being: 28877.00000000
2023.07.30 14:45:57.527 ct_15_w_n (SPX500,MN1)  void OnStart() Morphs forecast is: 679078.55629755, on: 2023.06.01 00:00, with actual being: 23306.00000000
2023.07.30 14:45:57.527 ct_15_w_n (SPX500,MN1)  void OnStart() correlation is: -0.03589660 with morph constant as: 0.00000000

Wir erhalten eine etwas höhere Korrelation von 0,46 gegenüber dem Wert von 0,3, den wir ohne Normalisierung erhielten. Dies könnte auf einige Vorteile der Normalisierung hinweisen, aber in unserem Fall wurde die Eingabekonstante von 50000 geändert, und wie bereits erwähnt, reagieren die Prognosen und damit die Korrelation sehr empfindlich darauf. Da wir nur eine einzige Eingabe haben, könnten wir diesen Wert optimieren, um aussagekräftigere Ergebnisse zu erhalten.

Auswirkungen auf die Wirtschaftsbeteiligten

Ein übersehener Wert der Kategorientheorie für die Finanzanalyse ist meiner Meinung nach das Transferlernen. Der Link, den wir soeben geteilt haben, führt Sie zu Wikipedia, wo Sie eine Einführung erhalten, aber was man nicht so leicht erkennen kann, ist der Nutzen, den wir aus unseren Anwendungen hier ziehen würden. Aus unseren obigen Tests ergaben sich Koeffizienten zwischen der Abbildung des Objektfunktor und der Abbildung des Morphismus. Der Prozess der Ermittlung dieser Koeffizienten ist zwangsläufig rechenintensiv, insbesondere wenn die Optimierung, wie man idealerweise erwarten würde, über lange historische Zeiträume im Strategietester von MQL5 erfolgt.

Da die Funktorkoeffizienten jedoch Teil einer Hypothese sind, die oben als Zyklus vorgestellt wurde, kann argumentiert werden, dass diese Koeffizienten, die auf eine bestimmte Weise für die USD-Währungswerte aus dem Wirtschaftskalender wirken, ebenso wirksam sein könnten, wenn es um EUR-Wirtschaftskalenderwerte zur EURO-STOXX-Volatilität oder GBP-Werte zur FTSE-Volatilität geht. Dies stellt eine Liste möglicher Kombinationen dar, und wo unsere Funktoren von unschätzbarem Wert sind, ist die Verwendung von Koeffizienten, die aus einer langwierigen, rechenintensiven Optimierung gewonnen wurden, und deren Anwendung auf eine dieser Alternativen, die auf dem Papier, basierend auf unserer Hypothese, bessere als durchschnittliche Ergebnisse liefern könnten.

Um dies zu veranschaulichen, verwenden wir die unten aufgeführten Eingaben:

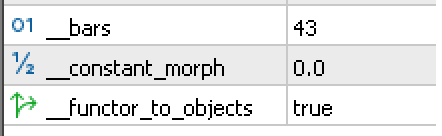
Lassen Sie uns einige Tests mit alternativen Währungen und ihren jeweiligen Aktienindizes durchführen. Wenn wir mit den Werten des EUR-Wirtschaftskalenders aus Deutschland in einer Kategorie beginnen, die durch einen Funktor mit der DAX30-Volatilitätskategorie gepaart ist, dann erhalten wir mit den obigen Einstellungen den folgenden Testergebnisbericht:

2023.07.30 15:12:25.655	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 75550.00000000, on: 2020.01.01 00:00, with actual being: 210640.00000000
2023.07.30 15:12:25.727	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 210640.00000000, on: 2020.02.01 00:00, with actual being: 431320.00000000

...

2023.07.30 15:12:28.445	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 144734.23693128, on: 2022.09.01 00:00, with actual being: 154697.00000000
2023.07.30 15:12:28.539	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 171908.69769099, on: 2022.10.01 00:00, with actual being: 156643.00000000
2023.07.30 15:12:28.648	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 298789.42486333, on: 2022.11.01 00:00, with actual being: 99044.00000000
2023.07.30 15:12:28.753	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 178962.89317906, on: 2022.12.01 00:00, with actual being: 137604.00000000
2023.07.30 15:12:28.901	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 440957.33259197, on: 2023.01.01 00:00, with actual being: 55544.00000000
2023.07.30 15:12:29.032	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 143198.91357580, on: 2023.02.01 00:00, with actual being: 124659.00000000
2023.07.30 15:12:29.151	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 24327.24201304, on: 2023.03.01 00:00, with actual being: 48737.00000000
2023.07.30 15:12:29.267	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 167059.32862279, on: 2023.04.01 00:00, with actual being: 69888.00000000
2023.07.30 15:12:29.357	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 67301.73632062, on: 2023.05.01 00:00, with actual being: 74073.00000000
2023.07.30 15:12:29.470	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 87406.10063493, on: 2023.06.01 00:00, with actual being: 104992.00000000
2023.07.30 15:12:29.470	ct_15_w_n (GER30,MN1)	void OnStart() correlation is: 0.02260757 with morph constant as: 0.00000000

Für GBP und den FTSE-100 ergibt sich folgendes Bild:

2023.07.30 15:12:45.341	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 45860.00000000, on: 2020.01.01 00:00, with actual being: 109780.00000000
2023.07.30 15:12:45.381	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 109780.00000000, on: 2020.02.01 00:00, with actual being: 210420.00000000
2023.07.30 15:12:45.420	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 210420.00000000, on: 2020.03.01 00:00, with actual being: 87250.00000000
2023.07.30 15:12:45.466	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 87250.00000000, on: 2020.04.01 00:00, with actual being: 58380.00000000
2023.07.30 15:12:45.508	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 1581489.63705309, on: 2020.05.01 00:00, with actual being: 58370.00000000

...

2023.07.30 15:12:46.685	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 153576.16806574, on: 2023.01.01 00:00, with actual being: 30453.00000000
2023.07.30 15:12:46.710	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 222058.94934174, on: 2023.02.01 00:00, with actual being: 77051.00000000
2023.07.30 15:12:46.739	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 50993.02046828, on: 2023.03.01 00:00, with actual being: 30780.00000000
2023.07.30 15:12:46.784	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 66795.26430874, on: 2023.04.01 00:00, with actual being: 45453.00000000
2023.07.30 15:12:46.832	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 75492.86146563, on: 2023.05.01 00:00, with actual being: 28845.00000000
2023.07.30 15:12:46.876	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 92298.50964858, on: 2023.06.01 00:00, with actual being: 49472.00000000
2023.07.30 15:12:46.876	ct_15_w_n (UK100,MN1)	void OnStart() correlation is: 0.14415363 with morph constant as: 0.00000000

Aus unseren ersten Protokollen geht hervor, dass wir zwar in der Lage sind, Prognosen zu erstellen, diese aber aufgrund der begrenzten Verwendung von Kalenderdaten im Strategietester nicht glaubwürdig verifizieren können. Unsere Hypothese hat sich eindeutig nicht bewahrheitet, und offen gesagt war die oben ermittelte Korrelation von 0,46 für USD und SP500 kaum aussagekräftig. 

In der Tat ist der Korrelationswert eine vorläufige „Lösung“, da er nur als ein sehr früher Indikator dafür dient, wie zuverlässig die Vorhersagen sind oder sein könnten, abhängig von der Wahl des Inputs, der in unserem Fall vor allem der Koeffizient der linearen Beziehung zwischen der Domänenkategorie und ihrer Codomäne ist. Langfristige und zuverlässigere Optionen wären der manuelle Export dieser Wirtschaftskalenderdaten entweder als csv-Datei, die von einem Expertenberater gelesen werden kann, oder sogar in eine Datenbank zur besseren Aufbewahrung. Mit beiden Optionen kann man über die idealen langen Zeiträume richtige Tests durchführen.

Neben der Volatilitätsprognose als Mittel zur Bestimmung des idealen Stop-Loss könnten wir auch einen systematischen Ansatz für die Positionsgrößenbestimmung verfolgen. Um dies mit unserer Methodik zu erreichen, nehmen wir an, dass wir eine ungebundene Kategorie von Zeitreihendaten haben, die den Handelsverlauf eines bestimmten Wertpapiers darstellt, wobei jedes Objekt in der Kategorie ein bestimmtes Handelsergebnis repräsentiert und die Pfeile (Morphismen) zwischen den Objekten Änderungen dieser Ergebnisse im Zeitverlauf darstellen.

Um diese Kategorie bei der Festlegung oder Vorhersage der idealen Positionsgröße für ein Handelssystem zu verwenden, würden wir sie über einen Funktor auf eine andere Kategorie einer Zeitreihe idealer Positionsgrößen auf der Grundlage tatsächlicher Handelsergebnisse und vielleicht der daraus resultierenden Volatilität abbilden. Wenn der Handel zum Beispiel ein Verlust war, würde das Objekt zu diesem Zeitpunkt in der Kategorie eine kleine Positionsgröße protokollieren, während es bei einem korrekten Handel eine größere Größe protokollieren würde. Die Volatilität könnte als zusätzlicher Faktor dafür dienen, wie viel kleiner oder größer eine Position ist, je nach der während des Handels erfassten Volatilität. Die Skalierung könnte also so aussehen, dass bei Verlusten die ideale Positionsgröße im Verhältnis zum Volatilitätswert noch stärker reduziert wird. Wenn das Handelsergebnis ein Gewinn ist, wird die ideale Positionsgröße ebenfalls im Verhältnis zur Volatilität erhöht. Der Zuordnungs-Funktor würde erwartungsgemäß eine Verzögerung aufweisen, sodass z. B. ein jetziges Handelsergebnis mit einer Positionsgröße für die nächste Periode verknüpft ist.

Der Funktor würde nicht nur die Handelsergebnisse mit der antizipierten idealen Positionsgröße verknüpfen, sondern auch die Morphismen zwischen den Handelsergebnissen mit den Morphismen zwischen der idealen Positionsgröße. Wie wir im letzten Artikel und auch oben gesehen haben, kann das eine das andere überprüfen, aber eine aufschlussreichere Frage könnte sein, wie die Abbildungsfunktion die Domäne mit der Codomäne verbindet.

Bisher haben wir sehr einfache Koeffizienten verwendet, die auf Regressionen aus früheren Ergebnissen beruhen. Wie Sie der beigefügten Quelle am Ende dieses und des vorherigen Artikels entnehmen können, sind wir davon ausgegangen, dass eine einfache Konstante und ein Koeffizient zum Domänenwert addiert wurden, um den Codomain-Wert zu erhalten, was man als einfache lineare Beziehung interpretieren könnte. Neben einer linearen Beziehung könnten die Domänenwerte aber auch über eine quadratische Beziehung auf die Codomain abgebildet werden, wobei wir, wenn der höchste Exponent zwei ist, einen zusätzlichen Koeffizienten haben, der mit dem Domänenwert zum Quadrat multipliziert wird, um das verknüpfte Codomain-Gegenstück zu erhalten. Und je mehr Exponenten man verwendet, desto mehr Koeffizienten benötigt man für die Definition der Funktorzurordnung.

Eine Alternative zu diesem einfachen und vermutlich fehleranfälligen Ansatz könnte darin bestehen, dass ein künstliches neuronales Netz die Homomorphismuszuordung zwischen den beiden Bereichen definiert. Dies müsste sowohl für die Objekte als auch für die Morphismen geschehen und würde beim Training mit großen Datenmengen in den meisten Fällen zu genaueren Ergebnissen führen. Aber abgesehen von der Frage der Genauigkeit ist es intuitiv der richtige Ansatz, da neuronale Netze gut darin sind, mehrere Eingaben zu verarbeiten und eine einzige Ausgabe zu erzeugen, wie es in diesem Fall der Fall wäre.

Schlussfolgerung

Zusammenfassend lässt sich sagen, dass die wichtigsten Punkte, die hier behandelt wurden, die Zusammenstellung von Wirtschaftskalenderdaten als Graph, die Betrachtung dieses Graphs als Kategorie und, wie in unserem vorherigen Artikel, die Verwendung einer Beziehung der Funktoren, die der Volatilität des S&P 500 nachgelagert ist, um Prognosen für die Volatilität des S&P 500 zu erstellen, waren. Wir verwenden diese Projektionen, um die Trailing-Stops offener Positionen zu verschieben, wie es in diesen Serien der Fall war. Neben der Anpassung des Stop-Loss von offenen Positionen können wir die Funktor-Beziehung nutzen, um die Positionsgröße von neuen Aufträgen festzulegen oder sogar das Einstiegssignal für jedes handelbare Wertpapier zu definieren. Diese Serie verzichtet auf die letzten beiden Beispiele, soweit es um die Zusammenstellung eines Expert Advisors mit dem IDE-Assistenten geht, da ich der Meinung bin, dass der Leser besser in der Lage ist, diese Konzepte auf seine eigene Strategie abzustimmen. Was wir bis hierher ebenfalls gelernt haben, ist die Definition des Morphing und nun auch von Funktorrelationen. Wir haben grobe, inkrementelle Werte verwendet, die eine lineare oder quadratische Beziehung von der Domäne zur Codomäne haben könnten, aber auch künstliche neuronale Netze könnten bei der Definition dieser Zuordnung verwendet werden. Darauf könnten wir in den nächsten Artikeln eingehen.