MetaTrader 5 / テスター
English Русский 中文 Español Deutsch Português
preview
MQL5の圏論（第15回）：関手とグラフ

MQL5の圏論（第15回）：関手とグラフ

MetaTrader 5 — テスター | 6 10月 2023, 14:41
331 0
Stephen Njuki
Stephen Njuki

はじめに

前回の記事では、線形順序のようなこれまでに取り上げた概念をどのように圏として見ることができるのか、そしてなぜその「射」が他の圏と関連するときに関手を構成するのかについて見てきました。この記事では、グラフが、前回の記事で見た線形順序のような使い方ができることを見て、前回の記事のイラストを発展させます。グラフを使うために、MQL5のカレンダーデータをグラフ、つまり圏として再構成します。これは重要な焦点となるでしょう。したがって、この記事の目的は、前回の記事と同様に、2つの圏間の関手によるボラティリティ予測の可能性を実証することです。ただし、この場合、始域はグラフであり、終域はS&P500のボラティリティ値（VIXではない）を時系列に並べたものです。


MQL5カレンダーフィードデータをグラフとして再構成する

MQL5の経済指標カレンダーについては、圏論とデータベーススキーマを関連づけたときに説明したので、トレーダーとの関連性をここで改めて紹介することは適切ではありません。これをグラフ、つまり辺と頂点の列として表現するには、まず、圏に含めるニュースのサブセットを事前に選択する必要があります。経済指標カレンダーのWebサイトを見れば明らかなようにたくさんの項目から選ぶことができますが、下図のように、それらを結びつける緩やかな仮説に基づいて、例えば4つだけを選ぶことにします。


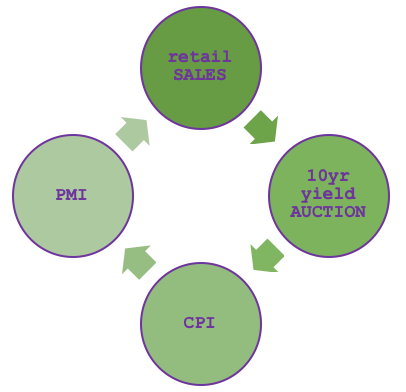
そうすると、私たちの仮説は、小売売上高は生産者PMIの数値の関数であり、生産者PMIはCPIに由来し、そのCPIは国庫入札のパフォーマンスの良し悪しに由来し、そのパフォーマンスも小売売上高に基づくと主張することになります。つまり、これは単なるサイクルであり、その真偽は記事の主題ではなく、経済指標カレンダーのデータから考えられるグラフの構成を説明するためのものです。

グラフには、頂点のペアの1つと頂点のインデックスとして機能する2つの単純なテーブルを作成することで複雑な相互接続システムを簡素化できるという利点があります。グラフを圏と見なすことができるのは、頂点をオブジェクト（始域）、辺を射と見なすことができるからです。余談ですが、前回の記事で見た線形順序とこれがどう違うかというと、その名の通り直線性です。グラフは、オブジェクトや始域が複数のオブジェクトに接続できるような、より複雑な接続に対応する傾向があります。

そこで、前回の線形順序の記事のように、この圏の個々のオブジェクトをS&Pのボラティリティ圏のオブジェクトとペアリングするのではなく、頂点のペアの行をS&Pの圏とペアリングすることにします。これは、S&Pが時間ベースであることを考慮すると、複数の行がS&P内の単一のオブジェクト（データポイント）と対になるようにバインドされているため、同型写像であることはできないことを意味します。また、始域オブジェクトが4つの要素（サイクル内の4項目のそれぞれの最新値）を構成することになります。


圏論と関手

これまでの記事ですでに述べたように、圏論には多くの応用例がありますが、公開されているほとんどの参考文献は代数位相幾何学に焦点を当てる傾向があり、これはこの主題の元の著者によるものである可能性があります。これが、MQL5を介した取引への応用が斬新に見えるかもしれない理由です。実際、MQL5に精通しているほとんどのトレーダーは、ニューラルネットワークを使用してシステムのエッ ジを効かせる傾向があります。おそらく、ニューラルネットワークは、圏に比べて長い期間にわたって研究されているからでしょう。これは、圏の探索を妨げるものではありません。要するに、ほとんどのトレーダーは優位性を求めており、システムや手法があまりにも一般的であれば、優位性を見つける確率は低くなるからです。

前回の記事ですでに述べたように、関手は事実上、圏間の射です。これらの「射」は、単に2つの圏のオブジェクトを結びつけるだけでなく、圏間の同型性も結びつけます。

前回の記事では、2つの圏間のオブジェクト連結を使用するシナリオと、同じ圏間の射の連結を考慮するシナリオの2つをテストしました。関手は両者の対数ですが、ここでの目的では、一度にひとつずつ関与することで両者の違いを探り、ナスダックのボラティリティを予測する上での相対的な重要性を強調したそれぞれのストラテジーテスターレポートを作成しました。2020年1月1日から同年3月15日までという短いテスト期間であったため、どちらの写像が優れているかという結論は導き出すことができませんでしたが、結果の違いは高い感度を示しており、どちらかを強調する必要性を示しています。


S&P500のボラティリティの圏の作成

SP500のボラティリティデータの収集と処理は、前回の記事でNASDAQのボラティリティを測定した方法と同様で、単純明快です。VIX指数は、ここで検討するものとは別の指標であることにご注意ください。現在のボラティリティの数値は、以下のリストに従って、新しいバーごとに再計算されます。

      double _float_value=0.0;
      //where R is an instance of MqlRates...
      _float_value=(R.high-R.low)/Point();


すでに述べたように、S&Pは、ボラティリティの値を1つのオブジェクトセットとしてとらえるオブジェクトと、それらの間の射がボラティリティの測定値間の相対的な変化をとらえることによって、終域を形成します。この圏の初期化は以下のように処理できます。

//+------------------------------------------------------------------+
//|   Get SP500-100 data from symbol (NDX100 for this broker).       | 
//|   Load it into SP500 category.                                   |
//+------------------------------------------------------------------+
void SetSP500(MqlRates &R)
   {
      _hmorph_sp500.Let();
      
      double _float_value=0.0;
      
      _float_value=(R.high-R.low)/Point();
      
      _element_value.Let();_element_value.Cardinality(1);_element_value.Set(0,DoubleToString(_float_value));
      _domain_sp500.Cardinality(1);_domain_sp500.Set(0,_element_value);
      
      //_category_sp500.Domains(_category_sp500.Domains()+1);
      _category_sp500.SetDomain(_category_sp500.Domains(),_domain_sp500);  
   }


前回の記事で見たように、始域をこの終域に遅れて写像することができれば、S&P500のボラティリティの予測能力を得ることができるでしょう。前回の記事と同様に、感度を測るために、同一のシグナルとマネーマネージメントのセットアップで、オブジェクトの関手と射の関手を別々にテストします。


経済指標カレンダーからS&P500への関手

以下のリストを使って、経済指標カレンダーデータの圏を構築します。

//+------------------------------------------------------------------+
//|   Get Ocean data from file defined in input.                     | 
//|   Load it into Ocean category.                                   |
//+------------------------------------------------------------------+
void SetEconomic(MqlRates &R)
   {
      datetime _time=R.time;
      
      int _elements=1;
      
      _e_retail.Let();
      SampleEvents(_time,_e_retail,IntToCountry(__country),__currency,TYPE_RETAIL_SALES);//printf(__FUNCSIG__+"...retail. ");
      
      _e_cpi.Let();
      string _cpi_time="";_e_retail.Get(0,_cpi_time);
      SampleEvents(StringToTime(_cpi_time),_e_cpi,IntToCountry(__country),__currency,TYPE_CPI);//printf(__FUNCSIG__+"...cpi. ");
      
      _e_auction.Let();
      string _auction_time="";_e_cpi.Get(0,_auction_time);
      SampleEvents(StringToTime(_auction_time),_e_auction,IntToCountry(__country),__currency,TYPE_AUCTION_10YR);//printf(__FUNCSIG__+"...auction. ");
      
      _e_pmi.Let();
      string _pmi_time="";_e_auction.Get(0,_pmi_time);
      SampleEvents(StringToTime(_pmi_time),_e_pmi,IntToCountry(__country),__currency,TYPE_PMI);//printf(__FUNCSIG__+"...pmi. ");
      
       _domain_economic.Cardinality(__ECON);
       _domain_economic.Set(0,_e_retail);
       _domain_economic.Set(1,_e_cpi);
       _domain_economic.Set(2,_e_auction);
       _domain_economic.Set(3,_e_pmi);
      
       _category_economic.SetDomain(_category_economic.Domains(),_domain_economic);
   }


この始域の各オブジェクトは2つの頂点を持ち、対になったカレンダー値のうち、少なくとも1つは終域のボラティリティ値の時間範囲内にあります。この経済データは約1か月間隔で発表されるため、月次の時間枠でテストします。前回の記事と同様、関手の写像はオブジェクトの各データポイントに係数を持つことになります。ここでの違いは、終域の同じボラティリティに複数のオブジェクトが写像される可能性に直面することです。理想的には、各オブジェクトから（線形写像の）係数を個別に取得し、予測に使用する必要があります。つまり、射の写像によって提供される投影の上に、相反する投影を提供することになります。このため、本稿では、カレンダーデータからS&P圏に写像する各関手を計量し、すべての関手のドット積和をとってボラティリティ値に写像することにします。

前回の記事のように、関手の実際の応用では、2つの選択肢に従うことになります。最初の反復でオブジェクトを写像し、次の反復で射を写像します。Output()関数からのオブジェクトの写像は次のようになります。

//+------------------------------------------------------------------+
//| Get Forecast value, forecast for next change in price bar range. |
//+------------------------------------------------------------------+
double GetObjectsForecast(MqlRates &R)
   {
      double _output=0.0;
      
      //econ init
      SetEconomic(R);
      
      //sp500 init
      SetSP500(R);
      
      matrix _domain;
      vector _codomain,_inputs;
      
      _domain.Init(__ECON+1,__ECON);
      
      for(int r=0;r<__ECON+1;r++)
      {
         CDomain<string> _d;_d.Let();
         _category_economic.GetDomain(_category_economic.Domains()-r-1,_d);
         
         for(int c=0;c<__ECON;c++)
         {
            CElement<string> _e; _d.Get(c,_e);
            
            string _s; _e.Get(1,_s);
            
            _domain[r][c]=StringToDouble(_s);
         }
      }
      
      _codomain.Init(__ECON);
      
      for(int r=0;r<__ECON;r++)
      {
         CDomain<string> _d;_d.Let();
         _category_sp500.GetDomain(_category_sp500.Domains()-r-1,_d);
         
         CElement<string> _e; _d.Get(0,_e);
         
         string _s; _e.Get(0,_s);
            
         _codomain[r]=StringToDouble(_s);
      }
      
      _inputs.Init(__ECON);_inputs.Fill(__constant_morph);
      
      M(_domain,_codomain,_inputs,_output,1);
      
      return(_output);
   }


射から射への写像も、変化量デルタによって定義される頂点間の射を、同じく変化量によって定義されるS&Pのボラティリティデータポイント間の射に写像することによって、異なる方法で処理されます。これは以下のように処理されます。

//+------------------------------------------------------------------+
//|   Get Forecast value, forecast for next change in price bar range. |
//+------------------------------------------------------------------+
double GetMorphsForecast(MqlRates &R)
   {
      ...
      
      for(int r=0;r<__ECON+1;r++)
      {
         ...
         
         for(int c=0;c<__ECON;c++)
         {
            CElement<string> _e_new; _d_new.Get(c,_e_new);
            
            string _s_new; _e_new.Get(1,_s_new);
            
            CElement<string> _e_old; _d_old.Get(c,_e_old);
            
            string _s_old; _e_old.Get(1,_s_old);
            
            _domain[r][c]=StringToDouble(_s_new)-StringToDouble(_s_old);
         }
      }
      
      _codomain.Init(__ECON);
      
      for(int r=0;r<__ECON;r++)
      {
         ...
         
         CElement<string> _e_new; _d_new.Get(0,_e_new);
         
         string _s_new; _e_new.Get(0,_s_new);
         
         CElement<string> _e_old; _d_old.Get(0,_e_old);
         
         string _s_old; _e_old.Get(0,_s_old);
         
         _codomain[r]=StringToDouble(_s_new)-StringToDouble(_s_old);
      }
      
      _inputs.Init(__ECON);_inputs.Fill(__constant_morph);
      
      M(_domain,_codomain,_inputs,_output,1);
      
      return(_output);
   }


関手のこれら2つの部分の図式的表現も、前回の記事で取り上げたものとは若干異なります。なぜなら、ここでの関係は当時のようにもはや同型ではなくなるからです。オブジェクトからオブジェクトへの写像は次のように描けます。


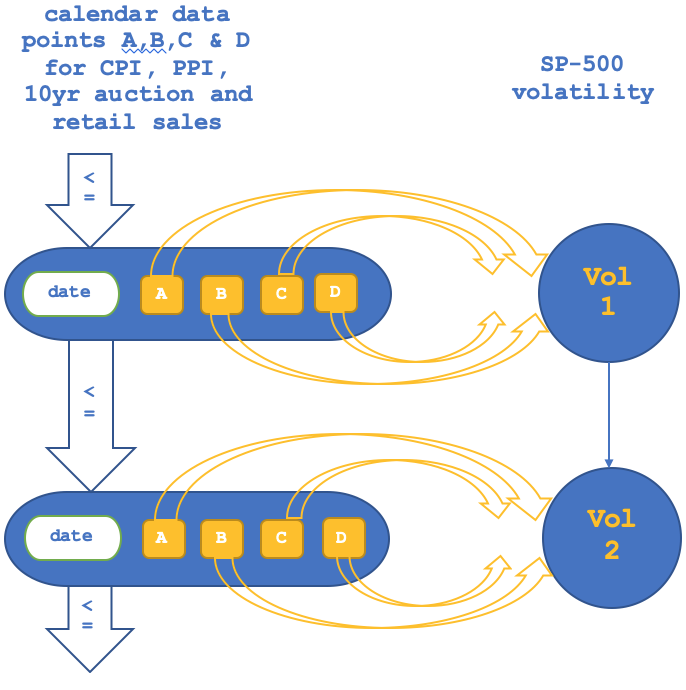
そして、射から射への写像は次のようになります。


MQL5のストラテジーテスターでは、残念ながら、経済指標カレンダーのイベントにアクセスしてテストすることができません。より堅牢な取引システムを開発することで得られるパフォーマンスの多くは、活用されていません。スクリプトとしてコード化した以上、できることは、予測に基づくボラティリティの変化予測を表示することです。履歴を反復すれば、予測の精度を知ることができます。

それでも、ブローカーから提供された価格データを基にしたスクリプトを実行すれば、カレンダーデータのグラフとSP500のボラティリティから2つの圏と、それらを接続する関手を構築することができます。ボラティリティを予測する以下のログを得ることができます。オブジェクトからオブジェクトへの関手の写像は以下のログを出力します。

2023.07.30 13:45:47.035 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: 0.00000000, on: 2020.01.01 00:00, with actual being: 54260.00000000
2023.07.30 13:45:47.134 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: 0.00000000, on: 2020.02.01 00:00, with actual being: 95438.00000000
2023.07.30 13:45:47.265 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: 0.00000000, on: 2020.03.01 00:00, with actual being: 53588.00000000
2023.07.30 13:45:47.392 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: 0.00000000, on: 2020.04.01 00:00, with actual being: 30352.00000000
2023.07.30 13:45:47.512 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: 0.00000000, on: 2020.05.01 00:00, with actual being: 29694.00000000
2023.07.30 13:45:47.644 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -716790.11376869, on: 2020.06.01 00:00, with actual being: 21905.00000000
2023.07.30 13:45:47.740 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -12424.22112077, on: 2020.07.01 00:00, with actual being: 26509.00000000
2023.07.30 13:45:47.852 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: 53612.17123096, on: 2020.08.01 00:00, with actual being: 37890.00000000




...

2023.07.30 13:45:50.294 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -27774.72154618, on: 2022.09.01 00:00, with actual being: 42426.00000000
2023.07.30 13:45:50.377 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: 46751.59791572, on: 2022.10.01 00:00, with actual being: 39338.00000000
2023.07.30 13:45:50.487 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -19820.29385469, on: 2022.11.01 00:00, with actual being: 37305.00000000
2023.07.30 13:45:50.593 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -5370.60103622, on: 2022.12.01 00:00, with actual being: 30192.00000000
2023.07.30 13:45:50.700 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -4662833.98425755, on: 2023.01.01 00:00, with actual being: 25359.00000000
2023.07.30 13:45:50.795 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: 33455.47933459, on: 2023.02.01 00:00, with actual being: 30681.00000000
2023.07.30 13:45:50.905 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -40357.22273603, on: 2023.03.01 00:00, with actual being: 12502.00000000
2023.07.30 13:45:51.001 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -37676.03496283, on: 2023.04.01 00:00, with actual being: 18835.00000000
2023.07.30 13:45:51.094 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -54634.02723538, on: 2023.05.01 00:00, with actual being: 28877.00000000
2023.07.30 13:45:51.178 ct_15_w (SPX500,MN1)    void OnStart() Objects forecast is: -35897.40757724, on: 2023.06.01 00:00, with actual being: 23306.00000000
2023.07.30 13:45:51.178 ct_15_w (SPX500,MN1)    void OnStart() corr is: 0.36053106 with morph constant as: 50000.00000000


射から射については次のようになります。

2023.07.30 13:47:38.737 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: 0.00000000, on: 2020.01.01 00:00, with actual being: 54260.00000000
2023.07.30 13:47:38.797 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: 0.00000000, on: 2020.02.01 00:00, with actual being: 95438.00000000
2023.07.30 13:47:38.852 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: 0.00000000, on: 2020.03.01 00:00, with actual being: 53588.00000000
2023.07.30 13:47:38.906 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: 0.00000000, on: 2020.04.01 00:00, with actual being: 30352.00000000
2023.07.30 13:47:39.010 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: 0.00000000, on: 2020.05.01 00:00, with actual being: 29694.00000000
2023.07.30 13:47:39.087 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: -2482719.31391738, on: 2020.06.01 00:00, with actual being: 21905.00000000




...

2023.07.30 13:47:41.541 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: -86724.54189079, on: 2022.11.01 00:00, with actual being: 37305.00000000
2023.07.30 13:47:41.661 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: -126817.99564744, on: 2022.12.01 00:00, with actual being: 30192.00000000
2023.07.30 13:47:41.793 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: -198737.93199622, on: 2023.01.01 00:00, with actual being: 25359.00000000
2023.07.30 13:47:41.917 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: -280104.88246660, on: 2023.02.01 00:00, with actual being: 30681.00000000
2023.07.30 13:47:42.037 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: 24129.34336223, on: 2023.03.01 00:00, with actual being: 12502.00000000
2023.07.30 13:47:42.157 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: 4293.73674465, on: 2023.04.01 00:00, with actual being: 18835.00000000
2023.07.30 13:47:42.280 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: 763492.31964126, on: 2023.05.01 00:00, with actual being: 28877.00000000
2023.07.30 13:47:42.401 ct_15_w (SPX500,MN1)    void OnStart() Morphs forecast is: -30298.30836734, on: 2023.06.01 00:00, with actual being: 23306.00000000
2023.07.30 13:47:42.401 ct_15_w (SPX500,MN1)    void OnStart() corr is: 0.03400012 with morph constant as: 50000.00000000


上記のログ出力から特筆すべき点がいくつかあります。まず、最初の5か月はすべてゼロが予測されています。これは、多くの指標に見られるように、完全な計算をするのに十分な価格データがないためだと思います。次に、予測にはマイナスの値もありますが、ここでは、次のバーでのボラティリティを示すために、厳密にプラスの値を探しているだけです。これは、多重係数（4つ）を解く際に恒等行列を使用するMQL5ライブラリの回帰ツールを使用しているため、低いボラティリティの値をサイズ化できなかったことが原因である可能性があります。これを回避するには、以下に提案するような関数を使って負の値を正規化する方法があります。

//+------------------------------------------------------------------+
//| Normalizes negative projections to positive number.              |
//+------------------------------------------------------------------+
double NormalizeForecast(double NegativeValue,double CurrentActual,double PreviousActual,double PreviousForecast)
   {
      return(CurrentActual+(((CurrentActual-NegativeValue)/CurrentActual)*fabs(PreviousActual-PreviousForecast)));
   }


ここでスクリプトを実行し、予測値と実際の値の相関を確認すれば、異なる結果が得られるに違いありません。特に方程式定数は、最終的に得られる出力や予測を大きく左右する非常に微妙な値だからです。以下に生成されるログではゼロに設定しています。まず、オブジェクトからオブジェクトへの関手を実行します。

2023.07.30 14:43:42.224 ct_15_w_n (SPX500,MN1)  void OnStart() Objects forecast is: 15650.00000000, on: 2020.01.01 00:00, with actual being: 54260.00000000

...

2023.07.30 14:43:45.895 ct_15_w_n (SPX500,MN1)  void OnStart() Objects forecast is: 15718.63125861, on: 2023.03.01 00:00, with actual being: 12502.00000000
2023.07.30 14:43:45.957 ct_15_w_n (SPX500,MN1)  void OnStart() Objects forecast is: 12187.53007421, on: 2023.04.01 00:00, with actual being: 18835.00000000
2023.07.30 14:43:46.026 ct_15_w_n (SPX500,MN1)  void OnStart() Objects forecast is: 19185.80075759, on: 2023.05.01 00:00, with actual being: 28877.00000000
2023.07.30 14:43:46.129 ct_15_w_n (SPX500,MN1)  void OnStart() Objects forecast is: 11544.54076238, on: 2023.06.01 00:00, with actual being: 23306.00000000
2023.07.30 14:43:46.129 ct_15_w_n (SPX500,MN1)  void OnStart() correlation is: 0.46195608 with morph constant as: 0.00000000


次に、やはり同じ方程式定数ゼロを使用して、射から射への関手に基づいた射影を作成しながらスクリプトを実行します。

2023.07.30 14:45:54.257 ct_15_w_n (SPX500,MN1)  void OnStart() Morphs forecast is: 54260.00000000, on: 2020.02.01 00:00, with actual being: 95438.00000000

...

2023.07.30 14:45:57.449 ct_15_w_n (SPX500,MN1)  void OnStart() Morphs forecast is: 257937.92970615, on: 2023.05.01 00:00, with actual being: 28877.00000000
2023.07.30 14:45:57.527 ct_15_w_n (SPX500,MN1)  void OnStart() Morphs forecast is: 679078.55629755, on: 2023.06.01 00:00, with actual being: 23306.00000000
2023.07.30 14:45:57.527 ct_15_w_n (SPX500,MN1)  void OnStart() correlation is: -0.03589660 with morph constant as: 0.00000000


正規化なしで得られた0.3という数値に対し、0.46というわずかに高い相関が得られました。これは正規化による利点を示している可能性がありますが、ここでは入力定数が50000から変更されており、前述の通り、予測とそれによる相関はその影響を非常に受けやすくなります。入力は1つだけなので、ストラテジーテスターを適切に実行すれば、この値を最適化し、より有意義な結果が得られる可能性があります。


トレーダーへの影響

私が思うに、金融分析における圏論の見落としがちな価値は、転移学習です。先ほどのリンクはウィキペディアで紹介されているものですが、このリンクから簡単に推測できないのは、ここでの応用によって私たちが得るメリットです。上記のテストから、オブジェクト関手の写像と射の写像の間の係数を導き出しました。MQL5のストラテジーテスターで、理想的とされるように、長い過去期間にわたって最適化を行う場合、これらの係数を求めるプロセスは、特に計算集約的となるに違いありません。

しかし、関手係数は、上記のサイクルとして提示された一連の仮説の一部であるため、経済指標カレンダーの米ドル通貨値に対して特定の方法で機能しているこれらの係数は、EURO-STOXXボラティリティのEUR経済指標カレンダーの値や、FTSEボラティリティのGBP値に対しても同様に有効であると主張することができます。これは可能な組み合わせのリストを示すものであり、ここでの関手が貴重なものとなるのは、1回の長時間にわたる計算集中型の最適化から得られた係数を使用し、仮説に基づき、理論上は平均以上の結果をもたらす可能性のあるこれらの選択肢のいずれかに適用するときです。

これを説明するために、以下の入力を使用します。


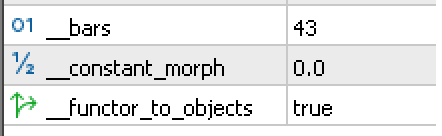
代替通貨とそれぞれの株価指数を使っていくつかテストしてみましょう。DAX30ボラティリティ圏と関手で対になった圏でドイツから得たEUR経済指標カレンダーの値から始めると、上記の設定で以下のようなテスターレポートが得られます。

2023.07.30 15:12:25.655	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 75550.00000000, on: 2020.01.01 00:00, with actual being: 210640.00000000
2023.07.30 15:12:25.727	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 210640.00000000, on: 2020.02.01 00:00, with actual being: 431320.00000000

...

2023.07.30 15:12:28.445	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 144734.23693128, on: 2022.09.01 00:00, with actual being: 154697.00000000
2023.07.30 15:12:28.539	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 171908.69769099, on: 2022.10.01 00:00, with actual being: 156643.00000000
2023.07.30 15:12:28.648	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 298789.42486333, on: 2022.11.01 00:00, with actual being: 99044.00000000
2023.07.30 15:12:28.753	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 178962.89317906, on: 2022.12.01 00:00, with actual being: 137604.00000000
2023.07.30 15:12:28.901	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 440957.33259197, on: 2023.01.01 00:00, with actual being: 55544.00000000
2023.07.30 15:12:29.032	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 143198.91357580, on: 2023.02.01 00:00, with actual being: 124659.00000000
2023.07.30 15:12:29.151	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 24327.24201304, on: 2023.03.01 00:00, with actual being: 48737.00000000
2023.07.30 15:12:29.267	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 167059.32862279, on: 2023.04.01 00:00, with actual being: 69888.00000000
2023.07.30 15:12:29.357	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 67301.73632062, on: 2023.05.01 00:00, with actual being: 74073.00000000
2023.07.30 15:12:29.470	ct_15_w_n (GER30,MN1)	void OnStart() Objects forecast is: 87406.10063493, on: 2023.06.01 00:00, with actual being: 104992.00000000
2023.07.30 15:12:29.470	ct_15_w_n (GER30,MN1)	void OnStart() correlation is: 0.02260757 with morph constant as: 0.00000000


GBPとFTSE-100については、次のようになります。

2023.07.30 15:12:45.341	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 45860.00000000, on: 2020.01.01 00:00, with actual being: 109780.00000000
2023.07.30 15:12:45.381	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 109780.00000000, on: 2020.02.01 00:00, with actual being: 210420.00000000
2023.07.30 15:12:45.420	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 210420.00000000, on: 2020.03.01 00:00, with actual being: 87250.00000000
2023.07.30 15:12:45.466	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 87250.00000000, on: 2020.04.01 00:00, with actual being: 58380.00000000
2023.07.30 15:12:45.508	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 1581489.63705309, on: 2020.05.01 00:00, with actual being: 58370.00000000

...

2023.07.30 15:12:46.685	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 153576.16806574, on: 2023.01.01 00:00, with actual being: 30453.00000000
2023.07.30 15:12:46.710	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 222058.94934174, on: 2023.02.01 00:00, with actual being: 77051.00000000
2023.07.30 15:12:46.739	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 50993.02046828, on: 2023.03.01 00:00, with actual being: 30780.00000000
2023.07.30 15:12:46.784	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 66795.26430874, on: 2023.04.01 00:00, with actual being: 45453.00000000
2023.07.30 15:12:46.832	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 75492.86146563, on: 2023.05.01 00:00, with actual being: 28845.00000000
2023.07.30 15:12:46.876	ct_15_w_n (UK100,MN1)	void OnStart() Objects forecast is: 92298.50964858, on: 2023.06.01 00:00, with actual being: 49472.00000000
2023.07.30 15:12:46.876	ct_15_w_n (UK100,MN1)	void OnStart() correlation is: 0.14415363 with morph constant as: 0.00000000


最初のログから明らかなように、予測はできても、ストラテジーテスターのカレンダーデータの使用が限られているため、信頼できる検証はできません。率直に言って、米ドルとSP500の上記の0.46の相関は決定的なものではありませんでした。 

実際、相関値は一時的な「解」です。これは、予測がどの程度信頼できるか、または入力の選択に応じて予測がどの程度信頼できるかを示す非常に初期の指標としてのみ機能するからです。入力の選択に応じて、予測は主に圏の始域とその終域間の線形関係の係数の1つになります。長期的かつ信頼性の高いオプションは、この経済指標カレンダーのデータを手動でエクスポートし、csvファイルとしてエキスパートアドバイザー(EA)に読み込ませるか、より安全に保管するためにデータベースに保存することです。どちらのオプションを選んでも、理想的に、長期にわたって適切なテストを実施することができます。

理想的なストップロスを決定する手段としてボラティリティを予測するだけでなく、ポジションサイジングにも体系的なアプローチを持ちたいと思うかもしれません。これを実現するために、ここでの手法では、特定の証券の取引履歴である時系列データの非有界な圏があるとします。圏内の各オブジェクトは特定の取引結果を表し、オブジェクト間の矢印（射）は、時間を通じて記録されたこれらの結果に対する変化を表します。

取引システムの理想的なポジションサイズを設定または予測するためにこの圏を使用するには、関手によって、実際の取引結果に基づく理想的なポジションサイズの時系列の別の圏に写像します。例えば、その取引が損失であった場合、圏内のその時点のオブジェクトは小さなポジションサイズを記録し、正確であった場合は大きなサイズを記録することになります。ボラティリティは、取引中に記録されたボラティリティによって、ポジションがどれだけ増減するかを示す追加的な要因として機能する可能性があります。そのため、取引が損失となった場合、ボラティリティの数値に比例して理想的なポジションサイズがさらに縮小されるようなスケーリングが可能です。同様に、取引結果がプラスであれば、理想的なポジションサイズもボラティリティに比例して再び拡大されます。この関手の写像には、例えば現在の取引結果が次の期間のポジションサイジングに結びつけるというようなラグが予想されます。

この関手は、取引結果と予想される理想的なポジションサイズだけでなく、取引結果間の射と理想的なポジションサイズ間の射をも結びつけることになります。過去の記事で見てきたように、また上記でも見てきたように、一方は他方を確認することができますが、より洞察的な質問は、写像関数がどのように始域と終域を結びつけるかということです。

ここまでは、過去の結果から回帰した非常に基本的な係数を用いてきました。この記事と前回の記事の末尾にある添付のソースからわかるように、単純な定数をと始域値への係数を加えて、単純な線形関係と解釈できるような終域値を得ると仮定しました。しかし、線形関係以外に、始域値は2次関係を介して終域に写像される可能性があります。この場合、最高指数が2であれば、リンクされた終域に到達するために、始域値の2乗に乗算される余分な係数があります。そしてもちろん、指数を多く使えば使うほど、関手写像を定義するのに必要な係数が増えます。

ただし、この単純で間違いなくエラーを起こしやすいアプローチに代わるものとして、ニューラルネットワークに2つの始域間の同型写像を定義させることができます。これはオブジェクトと射の両方に対して行う必要があり、ほとんどの場合、大量のデータに対する訓練からより正確な結果が得られるはずです。 しかし、精度の問題はさておき、この場合に当てはまるように、ニューラルネットワークは複数の入力を受け取り、単一の出力を生成することに長けているため、これは直感的には正しいアプローチです。


結論

まとめると、ここで取り上げた主なポイントは、経済指標カレンダーのデータをグラフとして構成すること、このグラフを圏として見ること、そして前回の記事と同様に、S&P500のボラティリティに遅行する関手関係を利用してS&P500のボラティリティの予測を行うことです。本連載でやってきたように、これらの予測をポジションのトレーリングストップを移動させるために使用します。ポジションのストップロスを調整する以外にも、関手の関係を使って新規注文のポジションサイズを設定したり、取引可能な証券のエントリシグナルを定義したりすることもできます。本連載では、IDEウィザードを使用してEAを組み立てることに関する限り、最後の2つの例は避けています。これらの概念を自分の戦略に合わせて微調整するのに読者の方が適していると思うからです。また、ここまでで得られたのは、射の定義と関手関係の定義です。始域から終域への線形または二次関係を持つ粗い増分値を使ってきましたが、ニューラルネットワークもこの写像を定義するのに使うことができます。それについては、今後の記事で見ていくことにします。


MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/13033

添付されたファイル |
ZIPをダウンロード
ct_14_1s.mqh (73.52 KB)
ct_15_w.mq5 (17.23 KB)
ct_15_w_n.mq5 (18.41 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
MQL5の圏論（第16回）：多層パーセプトロンと関手 MQL5の圏論（第16回）：多層パーセプトロンと関手
本連載16回目となる今回は、関手と、それが人工ニューラルネットワークを使ってどのように実装できるかを見ていきます。当連載ではこれまで、ボラティリティを予測するというアプローチをとってきましたが、今回はポジションのエントリーとエグジットのシグナルを設定するためのカスタムシグナルクラスの実装を試みます。
RSIディープスリームーブ取引手法 RSIディープスリームーブ取引手法
MetaTrader 5でRSIディープスリームーブ取引テクニックを紹介します。この記事は、株式、通貨、商品などの証券の強さと勢いを測定するために使用されるテクニカル分析指標であるRSIに基づくいくつかの取引テクニックを紹介する新しい一連の研究に基づいています。
回帰指標を用いたONNXモデルの評価 回帰指標を用いたONNXモデルの評価
回帰とは、ラベル付けされていない例から実際の値を予測するタスクのことです。いわゆる回帰メトリクスは、回帰モデルの予測精度を評価するために使用されます。
ニューラルネットワークが簡単に（第37回）：スパースアテンション(Sparse Attention) ニューラルネットワークが簡単に（第37回）：スパースアテンション(Sparse Attention)
前回は、アテンションメカニズムをアーキテクチャーに用いたリレーショナルモデルについて説明しました。これらのモデルの特徴の1つは、コンピューティングリソースを集中的に利用することです。今回は、セルフアテンションブロック内部の演算回数を減らす仕組みの1つについて考えてみたいと思います。これにより、モデルの一般的なパフォーマンスが向上します。