从理论到实践 - 页 547 1...540541542543544545546547548549550551552553554...1981 新评论 Aleksey Nikolayev 2018.09.10 11:52 #5461 Novaja: 也许有人能告诉我分布在对数尺度上是怎样的,我正在寻找,但找不到。不用找了,安装R和R-Studio,做任何你想做的图。 Vladimir 2018.09.10 15:34 #5462 Novaja: 也许有人能告诉我分布在对数尺度上是怎样的,我正在寻找。感兴趣。也找不到,虽然相对频率直方图上的范围并不总是很直观地代表它们所绘制的数据。但我在http://www.math.wm.edu/~leemis/chart/UDR/UDR.html 上看到了一个非常有趣的数字,其中有不同类型的分布彼此之间的联系。我从未见过同时有这么多的分配。为收集他们的财产做了大量的工作。而他们之间的相互安排又是怎样的布局,使箭头不长不短......。 P.S. 事实证明,在该网站上,你可以在这个图中找到每个分布的pdf文本,其中有其参数的公式,并可以进入所需的VIKI。一整本参考书。 Univariate Distribution Relationship Chart Larry Leemiswww.math.wm.edu A clickable diagram of probability distributions and their relationships Aleksey Nikolayev 2018.09.10 16:16 #5463 Vladimir:有趣的是。也找不到,虽然相对频率直方图上的范围远不总是它们所绘制的数据的良好视觉表现。但我在http://www.math.wm.edu/~leemis/chart/UDR/UDR.html 上看到了一个非常有趣的数字,其中有不同类型分布之间的联系。我从未见过同时有这么多的分配。为收集他们的财产做了大量的工作。而他们之间的相互安排又是怎样的布局,才能使箭头不至于长而断...... P.S. 事实证明,在该网站上,你也可以找到这个数字的搜索,每个分布的PDF文本,其参数的公式,和访问所需的VIKI。一整本参考书。我没有看到皮尔逊分布。这将使箭矢的排列变得非常困难。 Violetta Novak 2018.09.10 17:24 #5464 所以它在中间,卡方,顺便说一下,我在hubra上的一篇文章的评论中看到这个图。谢谢。(笑)。 Alexander_K2 2018.09.10 17:39 #5465 巫师回来了...。 我洗去喜悦和悲伤的泪水...... 对我来说,这已经太晚了;对那些受苦的人来说,现在是给他们希望的时候了。 Aleksey Nikolayev 2018.09.10 18:08 #5466 Novaja: 所以它是在中间,chi-square,顺便说一下,我在hubra的一篇文章的评论中看到这个方案。谢谢你。不,皮尔逊分布 是一个比chi-squared更广泛的概念。我没有白写箭的可能问题。 secret 2018.09.10 21:10 #5467 Vizard_: 还没有一个阶段性的画像... avtomat分部有很多这样的人) Alexander_K 2018.09.11 04:23 #5468 Vizard_:我在等待米沙尼老师的视频。但到目前为止,只学会了射击麻雀))))。可能是在准备什么...他通过努力工作赚取存款...显然,作为一个看门人。就像Fa。 Alexander_K 2018.09.11 04:34 #5469 Vizard_: 而医生已经消失了...总之,夏天已经对我们的队伍造成了伤害。 Vitaly Muzichenko 2018.09.11 08:01 #5470 Uladzimir Izerski:这就是人们赚取面包的方式。但它很迅速。理论是好的,但实践是失败的) 1...540541542543544545546547548549550551552553554...1981 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
也许有人能告诉我分布在对数尺度上是怎样的,我正在寻找,但找不到。
不用找了,安装R和R-Studio,做任何你想做的图。
也许有人能告诉我分布在对数尺度上是怎样的,我正在寻找。
感兴趣。也找不到,虽然相对频率直方图上的范围并不总是很直观地代表它们所绘制的数据。但我在http://www.math.wm.edu/~leemis/chart/UDR/UDR.html 上看到了一个非常有趣的数字,其中有不同类型的分布彼此之间的联系。我从未见过同时有这么多的分配。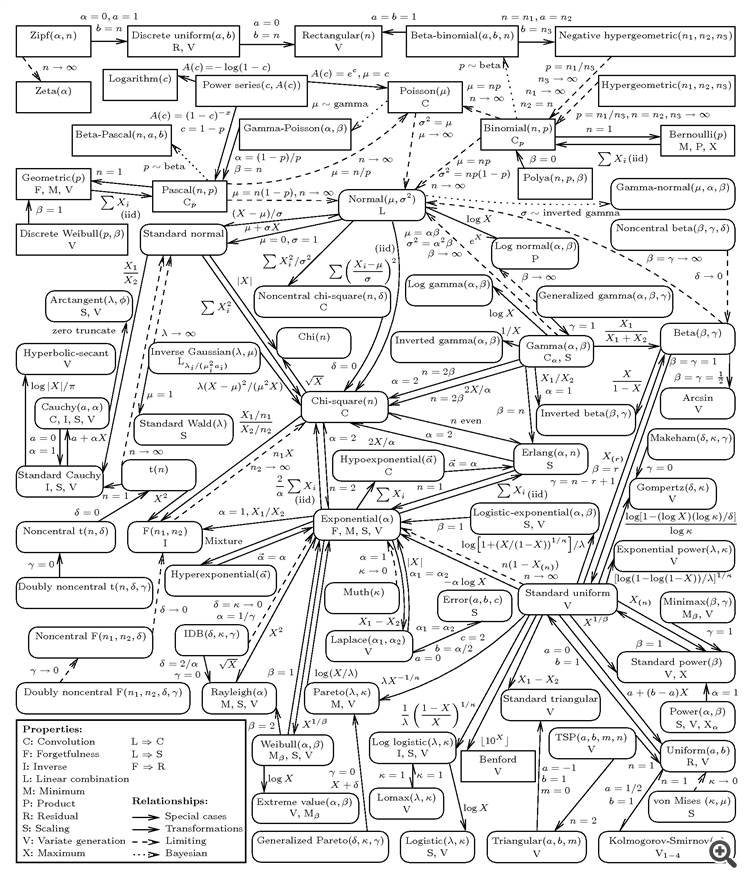
为收集他们的财产做了大量的工作。而他们之间的相互安排又是怎样的布局,使箭头不长不短......。
P.S. 事实证明,在该网站上,你可以在这个图中找到每个分布的pdf文本,其中有其参数的公式,并可以进入所需的VIKI。一整本参考书。
有趣的是。也找不到,虽然相对频率直方图上的范围远不总是它们所绘制的数据的良好视觉表现。但我在http://www.math.wm.edu/~leemis/chart/UDR/UDR.html 上看到了一个非常有趣的数字,其中有不同类型分布之间的联系。我从未见过同时有这么多的分配。
为收集他们的财产做了大量的工作。而他们之间的相互安排又是怎样的布局,才能使箭头不至于长而断......
P.S. 事实证明,在该网站上,你也可以找到这个数字的搜索,每个分布的PDF文本,其参数的公式,和访问所需的VIKI。一整本参考书。
我没有看到皮尔逊分布。这将使箭矢的排列变得非常困难。
巫师回来了...。
我洗去喜悦和悲伤的泪水......
对我来说,这已经太晚了;对那些受苦的人来说,现在是给他们希望的时候了。
所以它是在中间,chi-square,顺便说一下,我在hubra的一篇文章的评论中看到这个方案。谢谢你。
不,皮尔逊分布 是一个比chi-squared更广泛的概念。我没有白写箭的可能问题。
还没有一个阶段性的画像...
我在等待米沙尼老师的视频。但到目前为止,只学会了射击麻雀))))。可能是在准备什么...
他通过努力工作赚取存款...显然,作为一个看门人。就像Fa。
而医生已经消失了...总之,夏天已经对我们的队伍造成了伤害。
这就是人们赚取面包的方式。但它很迅速。
理论是好的,但实践是失败的)