Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет. Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
Mathemat>>: Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет. Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
Компьютер подсчитал :) Если гирьки можно ставить на обе чашки одновременно, то задача имеет 2136 решений (можно уравновесить ровно 63 груза). Действительно все решения содержат гирьку с весом 1.
Mathemat>>: Доказательство того, что минимальная - 1, несложно: максимально возможный вес равен сумме всех шести чисел, а тот, что ближайший к нему, равен сумме пяти (шесть без минимальной гирьки). Разница между максимальным и ближайшим к нему весом должна быть равна 1. Следовательно, минимальная равна 1. ihor, доказано, надеюсь? Ага, слезно просим программку.
P.S. Вероятно, предполагается, что гири можно ставить только на одну чашку весов. На другой - груз.
Одно решение очевидно: 1, 2, 4, 8, 16, 32.
1、2、4、8、16、32 - 单一答案
如果任何重量小于2^n,总重量将小于63。
如果多了,用这些壶铃可以获得的重量序列就会有差距。
有趣的是,如果砝码可以同时放在两个杯子上,这个问题就变得相当困难和有趣了。 这就是我想折磨的人。但我不知道解决方案。
,尽管在任何情况下,事实证明,权重的最小权重是1。但这并不自动意味着他们会到2的程度。
接下来(第10)。
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
我不太清楚最小壶铃数为1
也许两个壶铃2和3也会起作用。
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
计算机已经做了计算 :)
如果砝码可以同时放在两个杯子上,该问题有2136个解决方案(正好有63个砝码可以被平衡)。
事实上,所有的解决方案都包含一个1的权重。
Компьютер подсчитал :)
Если гирьки можно ставить на обе чашки одновременно, то задача имеет 2136 решений (можно уравновесить ровно 63 груза).
Действительно все решения содержат гирьку с весом 1.
你会公布节目吗?求你了,求你了!
是的,含泪要求提供一个方案。
Доказательство того, что минимальная - 1, несложно: максимально возможный вес равен сумме всех шести чисел, а тот, что ближайший к нему, равен сумме пяти (шесть без минимальной гирьки). Разница между максимальным и ближайшим к нему весом должна быть равна 1. Следовательно, минимальная равна 1. ihor, доказано, надеюсь?
Ага, слезно просим программку.
我错了1。
方案中没有什么有趣的东西,只是简单的过冲。
#include <stdio.h>
#define COUNT 63
bool isOK(int v0,int v1,int v2,int v3,int v4,int v5){
bool arr[COUNT]。
for(int i=0;i<COUNT;i++) arr[i]=false。
// 1 - 在一个杯子上,0 - 不涉及重量 - 1 - 在第二个杯子上
for(int i0=-1;i0<=1;i0++)
for(int i1=-1;i1<=1;i1++)
for(int i2=-1;i2<=1;i2++)
for(int i3=-1;i3<=1;i3++)
for(int i4=-1;i4<=1;i4++)
for(int i5=-1;i5<=1;i5++) {
int ves=v0*i0+v1*i1+v2*i2+v3*i3+v4*i4+v5*i5;
if(ves > COUNT) 返回false。
如果(ves>0) arr[ves-1]=true。
}
for(int i=0;i<COUNT;i++)
if(!arr[i]) return false;
返回true。
}
main(){
for(int i0=1;i0<COUNT;i0++)
for(int i1=i0;i1<=COUNT-i0;i1++)
for(int i2=i1;i2<=COUNT-i0-i1;i2++)
for(int i3=i2;i3<=COUNT-i0-i1-i2;i3++)
for(int i4=i3;i4<=COUNT-i0-i1-i2-i3;i4++)
for(int i5=i4;i5<=COUNT-i0-i1-i2-i3-i4;i5++)
如果(isOK(i0,i1,i2,i3,i4,i5))
printf("%d %d %d %d %d %d\n",i0,i1,i2,i3,i4,i5)。
}
Следующая (10-й):
该证明没有太多严谨性,但很正确。
让我们介绍一下顶点坐标的符号,如图所示。对于蓝色是一个正方形
x1-x2=y1-y4 。
y1-y2=x1-x2。
以及
x3-x4=y2-y3。
y4-y3=x2-x3。
从前两个方程中,如果我们回忆一下图形方程,我们可以得到
x4-x2=A(sinx2-sinx4),
从第三和第四次
x3-x1=A(sinx1-sinx3).
由于除了最小方格数之外,对方格没有任何限制,我们将只考虑方格围绕原点对称的情况。但此时x4=-x2,x3=-x1,正弦也一样。我们的方程式将采取的形式。
sin(2*x2)/(2*x2)=1/A
sin(2*x1)/(2*x1)=1/A
回顾一下从x2和x1站在左手边的函数图。要做到这一点,请看图:该图在正数和负数x处都有递减的极值。显然,通过逐渐减少A的数量,我们可以得到我们所需要的许多根,包括1978年和更多。
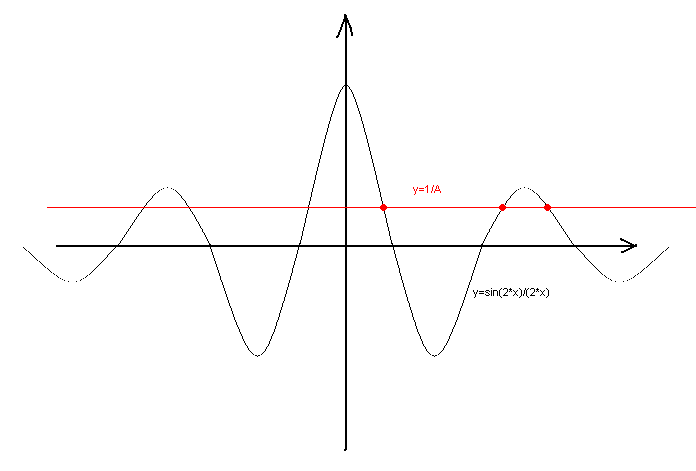
得到的根是不同的,以一种纯粹的非理性的方式相互联系着。我不需要详细证明这种情况下的正方形是不成对的。