Применение метода собственных координат к анализу структуры неэкстенсивных статистических распределений
8 505
26
Оглавление
- Введение
- 1. Q-Gaussian в эконометрике
- 2. Собственные координаты
- 3. Неэкстенсивные вероятностные распределения
- 4. If it looks like a cat... it might not be a cat
- Заключение
- Литература
- Приложение. Анализ распределения SP500 при помощи Q-Gaussian
Введение
В 1988 году Константино Тсаллис (Constantino Tsallis) предложил обобщение статистической механики Больцмана-Гиббса-Шеннона (Boltzmann-Gibbs-Shannon) [1], в котором было введено понятие неэкстенсивной энтропии (nonextensive entropy).
Важным следствием обобщения энтропии оказалось существование новых типов распределений [2], играющих ключевую роль в новой статистической механике (Q-Exponential и Q-Gaussian):
Выяснилось, что при помощи данных распределений могут быть описаны множество экспериментальных данных [3-6] систем с длительной памятью, дальнодействующими силами и сильнокоррелированных систем.
Энтропия очень сильно связана с информацией [7]. Обобщение статистической механики на базе теории информации было построено в работах [8-9]. Новая неэкстенсивная статистическая механика оказалась очень полезной для эконометрики [10-17]. Например, распределение Q-Gaussian хорошо описывает широкие крылья (хвосты) распределений приращений котировок финансовых инструментов (q~1.5), при этом на больших масштабах (месяцы, годы), большинство распределений приращений финансовых временных рядов превращаются в нормальное распределение (q=1) [10].
Естественно было ожидать, что подобное обобщение статистической механики приведет к аналогу центральной предельной теоремы для q-Gaussian распределений. В работе [18] было показано, что это не так - предельное распределение суммы сильнокоррелированных случайных переменных аналитически отличается от q-Gaussian.
Однако возникла проблема другого рода: оказалось, что численные значения полученного точного решения очень близки к Q-Gaussian ("numerically similar, analytically different"). Для анализа отличий между функциями и получения наилучших параметров Q-Gaussian в [18] использовалось разложение в ряд. Отношение данных функций привело к степенному разложению по параметру q, характеризующему степень неэкстенсивности системы.
Центральной проблемой прикладной статистики является проблема принятия статистических гипотез (hypotesis admission problem). Долгое время считалось, что эта проблема не может быть решена [19-20]. Для этого нужен специальный инструмент (вроде электронного микроскопа), позволяющий увидеть больше, чем доступно методами современной прикладной статистики.
В работе [21] был предложен метод собственных координат (eigencoordinates), который позволяет осуществить погружение на более глубокий уровень - анализ структурных свойств функциональных зависимостей. Этот очень красивый метод может быть использован для решения множества задач. В работе [22] были построены операторные разложения функций, соответствующих указанным выше неэкстенсивным распределениям.
В данной статье мы рассмотрим метод собственных координат и разберем примеры его практического использования. Статья содержит множество формул, но они важны для понимания сути метода. Повторив все расчеты, вы сможете самостоятельно построить функциональные разложения для интересующих вас функций.
1. Q-Gaussian в эконометрике
Распределение Q-Gaussian играет очень важную роль в эконометрике [4,10-17].
Общее представление об уровне современных исследований можно найти в докладах Dr. Claudio Antonini "q-Gaussians in Finance" [23] и "The Use of the q-Gaussian Distribution in Finance" [24].
Приведем кратко основные результаты.
Рис. 1. Методология науки (Слайд 4 "The Use of the q-Gaussian Distribution in Finance")
Основные особенности финансовых временных рядов приведены на рис. 2:
Рис 2. Свойства финансовых временных рядов (Слайд 3 "The Use of the q-Gaussian Distribution in Finance")
Множество теоретических моделей, используемых для описания финансовых временных рядов, приводят к Q-Gaussian распределению:
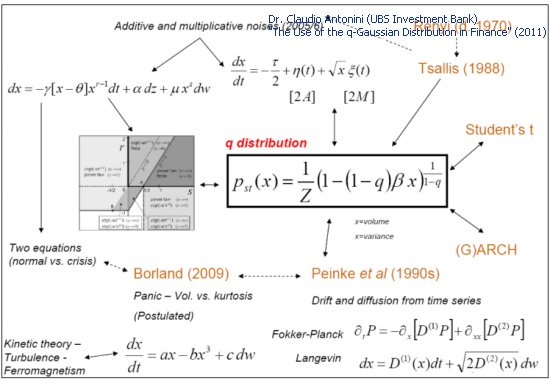
Рис 3. Теоретические модели и Q-Gaussian (Слайд 27 "The Use of the q-Gaussian Distribution in Finance")
Q-Gaussian также используется для феноменологического описания распределений котировок):
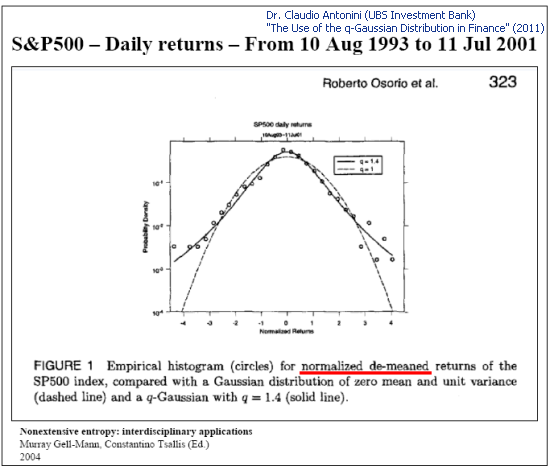
Рис 4. Пример анализа S&P 500 daily returns (Слайд 8 "The Use of the q-Gaussian Distribution in Finance")
При работе с реальными данными возникает проблема идентификации функций:
Рис. 5. Проблема идентификации функции распределения (Слайд 14 "q-Gaussians in Finance")
В обоих докладах Dr. Claudio Antonini подчеркивается важность корректной идентификации функций для построения адекватных моделей физических процессов:
Рис. 6. Выводы докладов "q-Gaussians in Finance" и "The Use of the q-Gaussian Distribution in Finance (Dr. Claudio Antonini, 2010, 2011)
- q-Gaussian Stock Price Dynamics, (Michael English, 2008)
- q-Gaussian European Options (Michael English, 2008)
- q-Gaussian Random Deviates & Distribution, (Michael English, 2008)
- q-Gaussian Portfolios (Michael English, 2008)
- q-Gaussian Risk Measures (Michael English, 2008)
- Expected Value & Value at Risk for Lognormal Asset (Michael English, 2008)
2. Собственные координаты
Разложение по собственным координатам имеет вид:
где C1…CN – константы, а X1(t),..,XN(t) - "собственные координаты".
Такие линейные разложения очень удобны и часто применяются при анализе данных. Например, в логарифмическом масштабе показательная функция превращается в прямую линию (ее наклон легко вычисляется при помощи линейной регрессии). Таким образом, для нахождения параметров функции нет необходимости проведения нелинейной оптимизации (fitting).
Однако для более сложных функций (например, суммы двух экспонент) логарифмический масштаб уже не поможет – функция не будет выглядеть как прямая. Для нахождения коэффициентов функции потребуется нелинейная оптимизация.
Бывают случаи, когда экспериментальные данные с одинаковой точностью можно объяснить при помощи нескольких функций, каждой из которых соответствуют различные модели физических процессов. Какую функцию выбрать? Какая из них наиболее адекватно покажет реальность за пределами экспериментальных данных?
Для анализа сложных систем (например, финансовых временных рядов) корректная идентификация функций очень важна - каждому из распределений соответствует свой физический процесс, выбор адекватной модели поможет глубже понять динамику и общие свойства сложных систем.
Прикладная статистика [19, 20] говорит о том, что не существует критерия, позволяющего отвергнуть неверную статистическую гипотезу. Метод собственных координат открывает новый взгляд на данную проблему (hypothesis admission problem).
Функцию, используемую для описания экспериментальных данных, можно рассматривать как решение некоторого дифференциального уравнения. Его форма определяет структуру разложения по собственным координатам.
Особенность разложения по собственным координатам заключается в том, что все данные, порожденные функцией Y(t), в базисе собственных координат X1(t)..XN(t) функции Y(t) линейны по построению. Данные, сгенерированные любой другой функцией F(t), в данном базисе уже не будут иметь вид прямой линии (они будут выглядеть линейными в базисе собственных координат функции F(t)).
Это обстоятельство позволяет произвести точную идентификацию функций, значительно упрощая работу со статистическими гипотезами.
2.1. Метод собственных координат
Идея метода заключается в том, чтобы построить собственные координаты Xk(t) в виде операторов, построенных на базе функции Y(t).
Это можно сделать при помощи математического анализа, собственные координаты Xk(t) примут вид интегральных сверток, а строение разложения будет определяться структурой дифференциального уравнения, которому удовлетворяет функция Y(t). Далее возникнет проблема нахождения коэффициентов C1.. CN.
При разложении по ортогональным базисам (например, для нахождения коэффициентов преобразования Фурье) коэффициенты разложения находятся путем проектирования вектора на базис – нужный результат получается за счет ортогональности базисных функций.
В нашем случае такой способ не подходит - об ортогональности X1(t)… XN(t) информации нет.
2.2. Расчет коэффициентов разложения методом наименьших квадратов
Расчет коэффициентов Ck можно осуществить методом наименьших квадратов. Эта задача сведется к решению системы линейных уравнений.
Пусть:
Реально для каждого измерения 
есть ошибка 
:
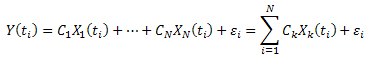
Минимизируем сумму квадратов отклонений:
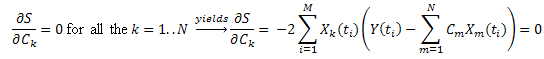
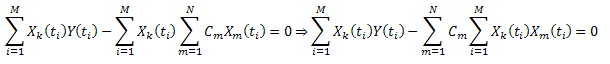
Введя обозначение: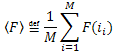 
, ее можно записать в виде:
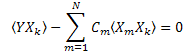
Таким образом, получается система линейных уравнений на C1...CN (k=1..N):
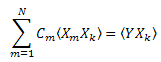
Матрица "корреляторов" симметрична: 
.
В некоторых случаях разложение по собственным координатам удобно строить в интегральном виде:
Это позволяет уменьшить роль ошибок (за счет усреднения), однако требует дополнительных вычислений.
2.3. Пример разложения функции R(x)
Рассмотрим пример разложения по собственным координатам следующей функции:
Данная функция порождает несколько статистических распределений [21]:
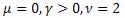- нормальное (гауссово) распределение;
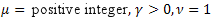- распределение Пуассона;
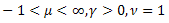- Gamma-распределение;
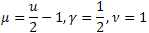- распределение 
;
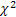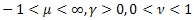- распределение Штауфера (Schtauffer), включающее в себя распределение Вейбулла (Weibull) как частный случай 
.
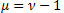Кроме того, она также удобна для описания релаксационных процессов:
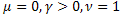- обычная экспоненциальная функция;
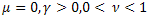- растянутая (stretched) экспоненциальная функция;
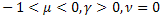- степенная релаксационная функция.
Продифференцировав R(x) по x, получим:
Умножим обе части на x:
Преобразуем 
:
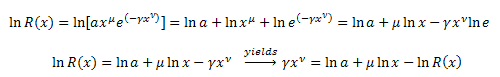
Подставим в уравнение:
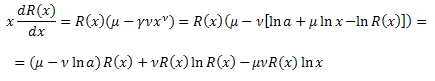
Получили дифференциальное уравнение для функции R(x):
Проинтегрируем обе части по x в интервале [xm,x]:
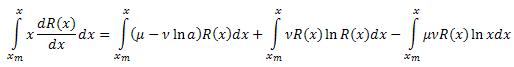
Левую часть выражения интегрируем по частям:
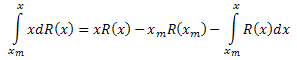
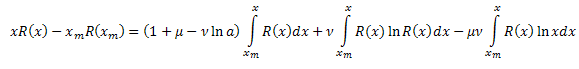
Таким образом, получили:
где:
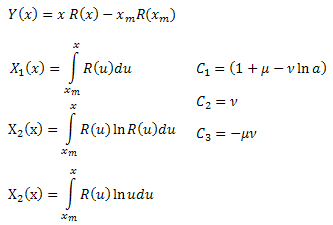
Вычислив коэффициенты 
, можно найти параметры функции 
. Четвертый параметр 
можно найти из выражения для R(x).
2.4. Программная реализация
Для расчета коэффициентов разложения потребуется решение системы линейных уравнений. Работу с матрицами удобно выделить в виде отдельного класса CMatrix (файл CMatrix.mqh). При помощи методов данного класса можно установить параметры матрицы, значения матричных элементов, а также решить систему линейных уравнений методом Гаусса.
//+------------------------------------------------------------------+ //| CMatrix class | //+------------------------------------------------------------------+ class CMatrix { double m_matrix[]; int m_rows; int m_columns; public: void SetSize(int nrows,int ncolumns); double Get(int i,int j); void Set(int i,int j,double val); void GaussSolve(double &v[]); void Test(); };
Приведем пример скрипта (EC_Example1.mq5), осуществляющего расчет собственных координат и параметров функции R(x).
//+------------------------------------------------------------------+ //| EC_Example1.mq5 | //| Copyright 2012, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2012, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #include <CMatrix.mqh> //+------------------------------------------------------------------+ //| CECCalculator | //+------------------------------------------------------------------+ class CECCalculator { protected: int m_size; //--- x[i] double m_x[]; //--- y[i] double m_y[]; //--- матрица CMatrix m_matrix; //--- Y[i] double m_ec_y[]; //--- собственные координаты X1[i],X2[i],X3[i] double m_ec_x1[]; double m_ec_x2[]; double m_ec_x3[]; //--- коэффициенты C1,C2,C3 double m_ec_coefs[]; //--- функция f1=Y-C2*X2-C3*X3 double m_f1[]; //--- функция f2=Y-C1*X1-C3*X3 double m_f2[]; //--- функция f3=Y-C1*X1-C2*X2 double m_f3[]; private: //--- функция для генерации данных double R(double x,double a,double mu,double gamma,double nu); //--- расчет интеграла double Integrate(double &x[],double &y[],int ind); //--- расчет функции Y(x) void CalcY(double &y[]); //--- расчет функции X1(x) void CalcX1(double &x1[]); //--- расчет функции X2(x) void CalcX2(double &x2[]); //--- расчет функции X3(x) void CalcX3(double &x3[]); //--- расчет коррелятора double Correlator(int ind1,int ind2); public: //--- метод генерации набора данных тестовой функции x[i],y[i] void GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu); //--- загрузка данных из файла bool LoadData(string filename); //--- сохранение данных в файл bool SaveData(string filename); //--- сохранение результатов расчета void SaveResults(string filename); //--- расчет собственных координат void CalcEigenCoordinates(); //--- расчет коэффициентов линейного разложения void CalcEigenCoefficients(); //--- расчет параметров функции void CalculateParameters(); //--- расчет функций f1,f2,f3 void CalculatePlotFunctions(); }; //+------------------------------------------------------------------+ //| Функция R(x) | //+------------------------------------------------------------------+ double CECCalculator::R(double x,double a,double mu,double gamma,double nu) { return(a*MathExp(mu*MathLog(MathAbs(x)))*MathExp(-gamma*MathExp(nu*MathLog(MathAbs(x))))); } //+------------------------------------------------------------------+ //| Метод генерации набора данных x[i],y[i] тестовой функции R(x) | //+------------------------------------------------------------------+ void CECCalculator::GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu) { if(size<=0) return; if(x1>=x2) return; m_size=size; ArrayResize(m_x,m_size); ArrayResize(m_y,m_size); double delta=(x2-x1)/(m_size-1); //--- for(int i=0; i<m_size; i++) { m_x[i]=x1+i*delta; m_y[i]=R(m_x[i],a,mu,gamma,nu); } }; //+------------------------------------------------------------------+ //| Метод загрузки данных из .CSV-файла | //+------------------------------------------------------------------+ bool CECCalculator::LoadData(string filename) { int filehandle=FileOpen(filename,FILE_CSV|FILE_READ|FILE_ANSI,'\r'); if(filehandle==INVALID_HANDLE) { Alert("Error in open of file ",filename,", error",GetLastError()); return(false); } m_size=0; while(!FileIsEnding(filehandle)) { string str=FileReadString(filehandle); if(str!="") { string astr[]; StringSplit(str,';',astr); if(ArraySize(astr)==2) { ArrayResize(m_x,m_size+1); ArrayResize(m_y,m_size+1); m_x[m_size]=StringToDouble(astr[0]); m_y[m_size]=StringToDouble(astr[1]); m_size++; } else { m_size=0; return(false); } } } FileClose(filehandle); return(true); } //+------------------------------------------------------------------+ //| Метод сохранения данных в .CSV-файл | //+------------------------------------------------------------------+ bool CECCalculator::SaveData(string filename) { if(m_size==0) return(false); if(ArraySize(m_x)!=ArraySize(m_y)) return(false); if(ArraySize(m_x)==0) return(false); int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI,'\r'); if(filehandle==INVALID_HANDLE) { Alert("Error in open of file ",filename,", error",GetLastError()); return(false); } for(int i=0; i<ArraySize(m_x); i++) { string s=DoubleToString(m_x[i],8)+";"; s+=DoubleToString(m_y[i],8)+";"; s+="\r"; FileWriteString(filehandle,s); } FileClose(filehandle); return(true); } //+------------------------------------------------------------------+ //| Метод расчета интеграла | //+------------------------------------------------------------------+ double CECCalculator::Integrate(double &x[],double &y[],int ind) { double sum=0; for(int i=0; i<ind-1; i++) sum+=(x[i+1]-x[i])*(y[i+1]+y[i])*0.5; return(sum); } //+------------------------------------------------------------------+ //| Метод расчета функции Y(x) | //+------------------------------------------------------------------+ void CECCalculator::CalcY(double &y[]) { if(m_size==0) return; ArrayResize(y,m_size); for(int i=0; i<m_size; i++) y[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0]; }; //+------------------------------------------------------------------+ //| Метод расчета функции X1(x) | //+------------------------------------------------------------------+ void CECCalculator::CalcX1(double &x1[]) { if(m_size==0) return; ArrayResize(x1,m_size); for(int i=0; i<m_size; i++) x1[i]=Integrate(m_x,m_y,i); } //+------------------------------------------------------------------+ //| Метод расчета функции X2(x) | //+------------------------------------------------------------------+ void CECCalculator::CalcX2(double &x2[]) { if(m_size==0) return; double tmp[]; ArrayResize(tmp,m_size); for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_y[i])); ArrayResize(x2,m_size); for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,tmp,i); } //+------------------------------------------------------------------+ //| Метод расчета функции X3(x) | //+------------------------------------------------------------------+ void CECCalculator::CalcX3(double &x3[]) { if(m_size==0) return; double tmp[]; ArrayResize(tmp,m_size); for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_x[i])); ArrayResize(x3,m_size); for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i); } //+------------------------------------------------------------------+ //| Метод расчета собственных координат | //+------------------------------------------------------------------+ void CECCalculator::CalcEigenCoordinates() { CalcY(m_ec_y); CalcX1(m_ec_x1); CalcX2(m_ec_x2); CalcX3(m_ec_x3); } //+------------------------------------------------------------------+ //| Метод расчета коррелятора | //+------------------------------------------------------------------+ double CECCalculator::Correlator(int ind1,int ind2) { if(m_size==0) return(0); if(ind1<=0 || ind1>4) return(0); if(ind2<=0 || ind2>4) return(0); //--- double arr1[]; double arr2[]; ArrayResize(arr1,m_size); ArrayResize(arr2,m_size); //--- switch(ind1) { case 1: ArrayCopy(arr1,m_ec_x1,0,0,WHOLE_ARRAY); break; case 2: ArrayCopy(arr1,m_ec_x2,0,0,WHOLE_ARRAY); break; case 3: ArrayCopy(arr1,m_ec_x3,0,0,WHOLE_ARRAY); break; case 4: ArrayCopy(arr1,m_ec_y,0,0,WHOLE_ARRAY); break; } switch(ind2) { case 1: ArrayCopy(arr2,m_ec_x1,0,0,WHOLE_ARRAY); break; case 2: ArrayCopy(arr2,m_ec_x2,0,0,WHOLE_ARRAY); break; case 3: ArrayCopy(arr2,m_ec_x3,0,0,WHOLE_ARRAY); break; case 4: ArrayCopy(arr2,m_ec_y,0,0,WHOLE_ARRAY); break; } //--- double sum=0; for(int i=0; i<m_size; i++) { sum+=arr1[i]*arr2[i]; } sum=sum/m_size; return(sum); }; //+------------------------------------------------------------------+ //| Метод расчета коэффициентов линейного разложения | //+------------------------------------------------------------------+ void CECCalculator::CalcEigenCoefficients() { //--- установка размера матрицы 3x4 m_matrix.SetSize(3,4); //--- расчет матрицы корреляторов for(int i=3; i>=1; i--) { string s=""; for(int j=1; j<=4; j++) { double corr=Correlator(i,j); m_matrix.Set(i,j,corr); s=s+" "+DoubleToString(m_matrix.Get(i,j)); } Print(i," ",s); } //--- решение системы линейных уравнений m_matrix.GaussSolve(m_ec_coefs); //--- показываем решение - полученные коэффициенты C1,..CN for(int i=ArraySize(m_ec_coefs)-1; i>=0; i--) Print("C",i+1,"=",m_ec_coefs[i]); }; //+------------------------------------------------------------------+ //| Метод расчета параметров функции a,mu,nu,gamma | //+------------------------------------------------------------------+ void CECCalculator::CalculateParameters() { if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;} //--- calculate a double a=MathExp((1-m_ec_coefs[0])/m_ec_coefs[1]-m_ec_coefs[2]/(m_ec_coefs[1]*m_ec_coefs[1])); //--- calculate mu double mu=-m_ec_coefs[2]/m_ec_coefs[1]; //--- calculate nu double nu=m_ec_coefs[1]; //--- calculate gamma double arr1[],arr2[]; ArrayResize(arr1,m_size); ArrayResize(arr2,m_size); double corr1=0; double corr2=0; for(int i=0; i<m_size; i++) { arr1[i]=MathPow(m_x[i],nu); arr2[i]=MathLog(MathAbs(m_y[i]))-MathLog(a)-mu*MathLog(m_x[i]); corr1+=arr1[i]*arr2[i]; corr2+=arr1[i]*arr1[i]; } double gamma=-corr1/corr2; //--- Print("a=",a); Print("mu=",mu); Print("nu=",nu); Print("gamma=",gamma); }; //+------------------------------------------------------------------+ //| Метод расчета функций | //| f1=Y-C2*X2-C3*X3 | //| f2=Y-C1*X1-C3*X3 | //| f3=Y-C1*X1-C2*X2 | //+------------------------------------------------------------------+ void CECCalculator::CalculatePlotFunctions() { if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;} //--- ArrayResize(m_f1,m_size); ArrayResize(m_f2,m_size); ArrayResize(m_f3,m_size); //--- for(int i=0; i<m_size; i++) { //--- plot function f1=Y-C2*X2-C3*X3 m_f1[i]=m_ec_y[i]-m_ec_coefs[1]*m_ec_x2[i]-m_ec_coefs[2]*m_ec_x3[i]; //--- plot function f2=Y-C1*X1-C3*X3 m_f2[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[2]*m_ec_x3[i]; //--- plot function f3=Y-C1*X1-C2*X2 m_f3[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[1]*m_ec_x2[i]; } } //+------------------------------------------------------------------+ //| Метод сохранение результатов расчета | //+------------------------------------------------------------------+ void CECCalculator::SaveResults(string filename) { if(m_size==0) return; int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI); if(filehandle==INVALID_HANDLE) { Alert("Error in open of file ",filename," for writing, error",GetLastError()); return; } for(int i=0; i<m_size; i++) { string s=DoubleToString(m_x[i],8)+";"; s+=DoubleToString(m_y[i],8)+";"; s+=DoubleToString(m_ec_y[i],8)+";"; s+=DoubleToString(m_ec_x1[i],8)+";"; s+=DoubleToString(m_f1[i],8)+";"; s+=DoubleToString(m_ec_x2[i],8)+";"; s+=DoubleToString(m_f2[i],8)+";"; s+=DoubleToString(m_ec_x3[i],8)+";"; s+=DoubleToString(m_f3[i],8)+";"; s+="\r"; FileWriteString(filehandle,s); } FileClose(filehandle); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { CECCalculator ec; //--- подготовка данных модельной функции ec.GenerateData(100,0.25,15.25,1.55,1.05,0.15,1.3); //--- сохранение в файл ec.SaveData("ex1.csv"); //--- расчет собственный координат ec.CalcEigenCoordinates(); //--- расчет коэффициентов ec.CalcEigenCoefficients(); //--- расчет параметров ec.CalculateParameters(); //--- расчет функций f1,f2,f3 ec.CalculatePlotFunctions(); //--- сохранение результатов в файл ec.SaveResults("ex1-results.csv"); }
2.5. Результаты расчета модельной функции R(x)
В качестве модельных данных сгенерируем 100 значений функции R(x) в интервале от [0.25,15.25]
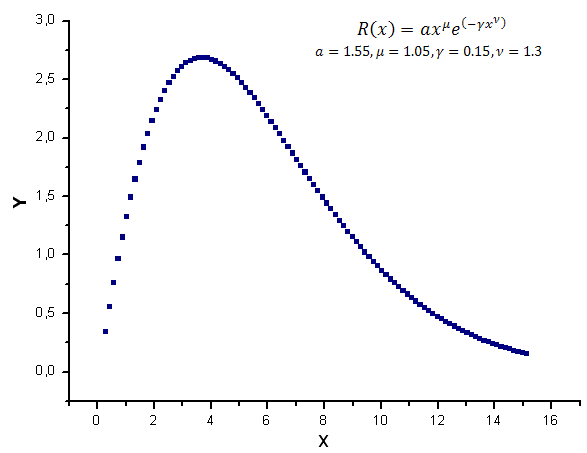
Рис 7. Модельная функция, используемая для расчета
На базе этих данных строятся функции Y(x) и ее разложение по функциям X1(x), X2(x), X3(x).
На рис. 8 приведена функция Y(x) и ее "собственные координаты" X1(x), X2(x), X3(x).
Рис 8. Общий вид функции Y(x) и собственных координат X1(x), X2(x), X3(x)
Следует обратить внимание на гладкость данных функций, она обусловлена интегральной природой операторов X1(x), X2(x), X3(x).
После расчета функций Y(x), X1(x), X2(x), X3(x) составляется матрица корреляторов, затем решаются уравнения на коэффициенты C1, C2, C3, далее через них находятся расчетные параметры функции R(x):
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) gamma=0.2769402213886906 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) nu=1.126643424450548 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) mu=1.328595266178149 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) a=1.637687667818532 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C1=1.772838639779728 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C2=1.126643424450548 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C3=-1.496853120395737 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 1 221.03637620 148.53278281 305.48547011 101.93843241 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 2 148.53278281 101.63995012 202.85142688 74.19784681 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 3 305.48547011 202.85142688 429.09345292 127.82779760
Проверим линейность построенного разложения. Для этого нужно вычислить 3 функции:
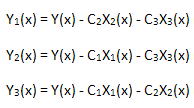
каждая из которых проектируются в свой базис собственных координат X1(x), X2(x), X3(x):
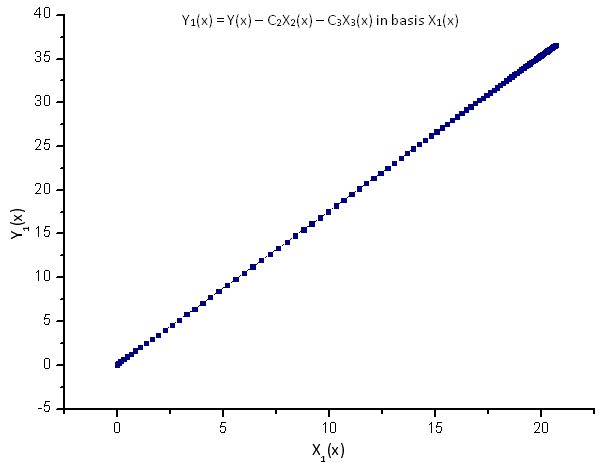
Рис 9. Представление функции Y1(x) в базисе X1(x)
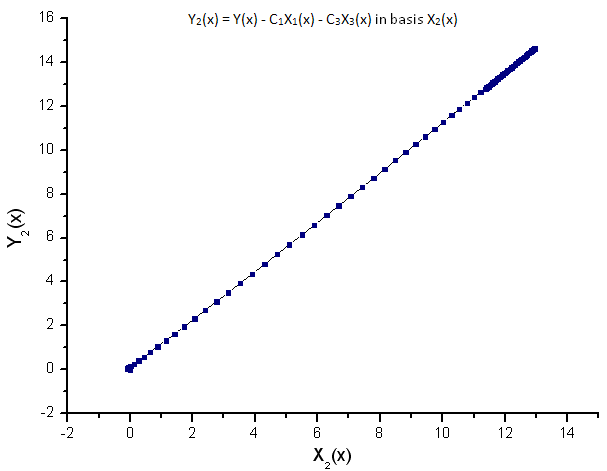
Рис 10. Представление функции Y2(x) в базисе X2(x)
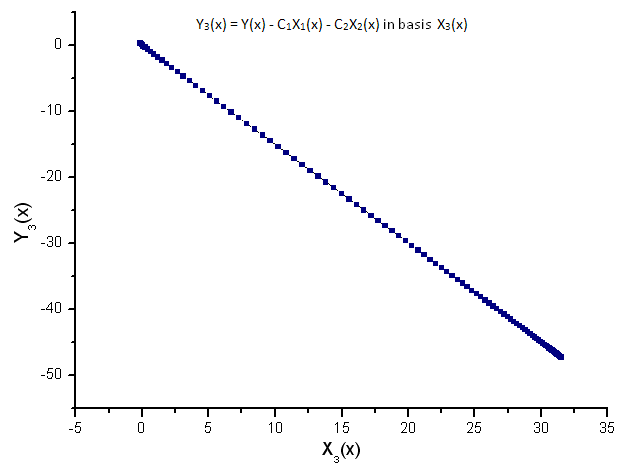
Рис. 11. Представление функции Y3(x) в базисе X3(x)
Линейная зависимость построенных функций свидетельствует о том, что ряд данных, приведенный на рис. 7, точно соответствует функции R(x).
Любая другая функция (даже близкая по форме), представленная в собственных координатах R(x), уже не будет иметь линейный вид. Этот факт позволяет идентифицировать функции.
Точность расчета численных значений параметров модельной функции можно повысить, если увеличить количество точек до 10000 (интервал тот же):
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) gamma=0.1508739336762316 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) nu=1.298316173744703 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) mu=1.052364487161627 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) a=1.550281229466634 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C1=1.483135479113404 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C2=1.298316173744703 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C3=-1.36630183435649 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 1 225.47846911 151.22066473 311.86134419 104.65062550 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 2 151.22066473 103.30005101 206.66297964 76.03285182 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 3 311.86134419 206.66297964 438.35625824 131.91955339
В данном случае параметры функции найдены с более высокой точностью.
2.6. Влияние шума
Реальные экспериментальные данные всегда содержат шум.
В методе GenerateData() класса ECCCalculator заменим:
m_y[i]=R(m_x[i],a,mu,gamma,nu);
на
m_y[i]=R(m_x[i],a,mu,gamma,nu)+0.25*MathRand()/32767.0;
добавив случайный шум, приблизительно равный 10% от максимального значения функции.
Результат работы скрипта EC_Example1-noise.mq5:
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) gamma=0.4013079343855266 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) nu=0.9915044018913447 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) mu=1.403541951457922 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) a=2.017238416806171 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C1=1.707774107235756 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C2=0.9915044018913447 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C3=-1.391618023109698 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 1 254.45082565 185.19087989 354.25574000 125.17343164 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 2 185.19087989 136.81028987 254.92996885 97.14705491 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 3 354.25574000 254.92996885 501.76021715 159.49440494
График модельной функции со случайным шумом приведен на рис. 12.
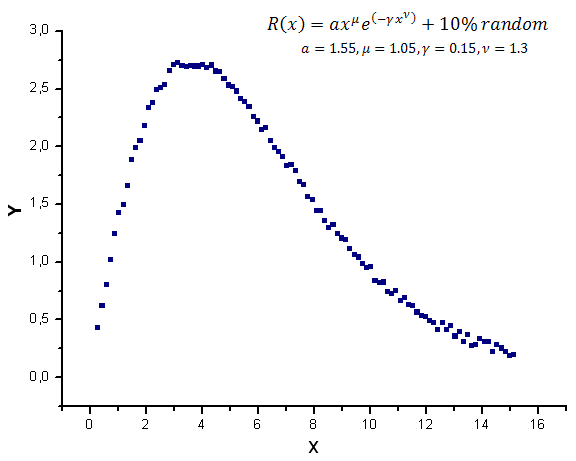
Рис 12. Модельная функция с шумом, используемая для расчета
Рис 13. Общий вид функции Y(x) и собственных координат X1(x), X2(x), X3(x)
Функции X1(x), X2(x) и X3(x), выступающие в качестве "собственных координат" по-прежнему выглядят гладкими, однако Y(x), построенная как их линейная комбинация, выглядит иначе (рис. 13).
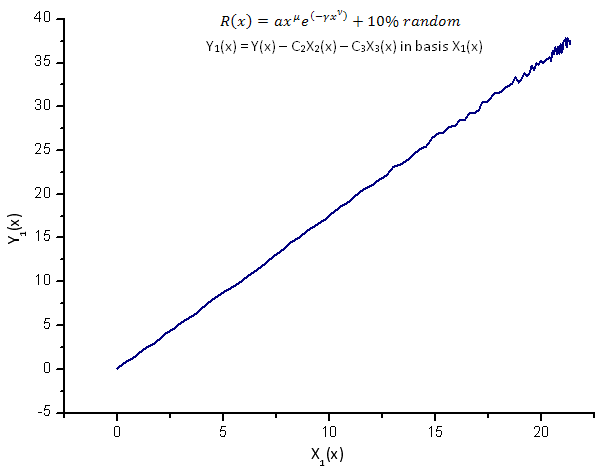
Рис 14. Представление функции Y1(x) в базисе X1(x)
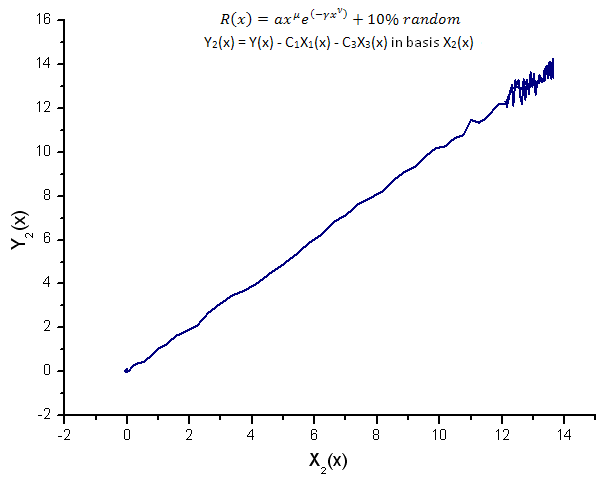
Рис 15. Представление функции Y2(x) в базисе X2(x)
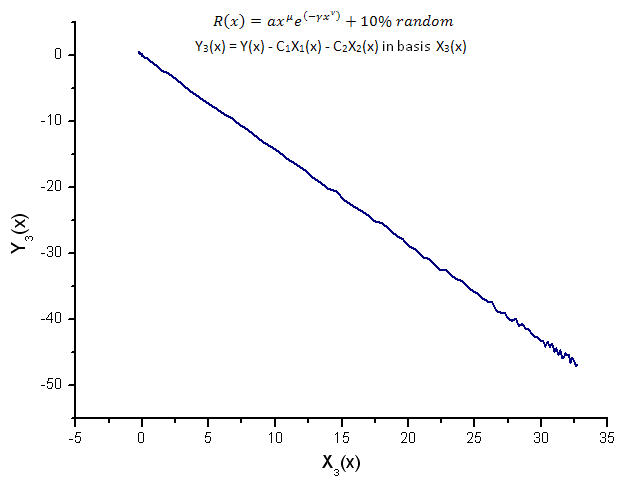
Рис 16. Представление функции Y3(x) в базисе X3(x)
Представление функций Y1(x),Y2(x) и Y3(x) в базисе собственных координат (рис. 8-10) по-прежнему имеет линейную форму, однако вокруг прямой можно заметить флуктуации, обусловленные наличием шума. Наиболее ярко это проявляется для больших X, при которых сигнал/шум становится минимальным.
В данном случае шумовые компоненты лежат по обе стороны от прямой, поэтому в таких случаях удобно использовать интегральный вид разложения по собственным координатам (раздел. 2.2).
3. Неэкстенсивные вероятностные распределения
Обобщение статистической механики приводит к распределениям [2, 22]:
где 
, 
.
Распределение q-Exponential является частным случаем функции P1(x), распределение q-Gaussian является частным случаем функции P2(x).
3.1. Разложение по собственным координатам функции P1(x)
Продифференцируем P1(x):
Полученное дифференциальное уравнение имеет вид:
Проинтегрируем от [xm,x]:
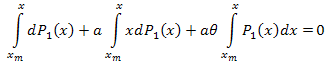
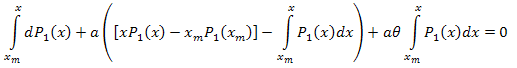
Таким образом:
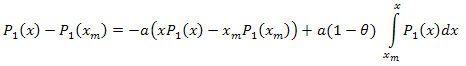
Разложение по собственным координатам имеет вид:
где:
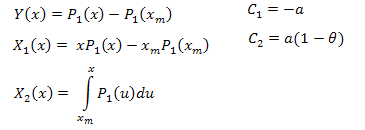
Функции для расчета выглядят следующим образом (скрипт EC_Example2.mq5):
//+------------------------------------------------------------------+ //| CalcY | //+------------------------------------------------------------------+ void CECCalculator::CalcY(double &y[]) { if(m_size==0) return; ArrayResize(y,m_size); //--- Y=P(x)-P(xm) for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0]; }; //+------------------------------------------------------------------+ //| CalcX1 | //+------------------------------------------------------------------+ void CECCalculator::CalcX1(double &x1[]) { if(m_size==0) return; ArrayResize(x1,m_size); //--- X1=x*P(x)-xm*P(xm) for(int i=0; i<m_size; i++) x1[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0]; } //+------------------------------------------------------------------+ //| CalcX2 | //+------------------------------------------------------------------+ void CECCalculator::CalcX2(double &x2[]) { if(m_size==0) return; ArrayResize(x2,m_size); //--- X2=Integrate(P1(x)) for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,m_y,i); }
На этот раз матрица корреляторов имеет размерность 2x3, значения параметров a и theta функции P1(x) определяются через коэффициенты С1 и C2. Численное значение параметра B можно найти из условия нормировки.
Результат расчета модельной функции P1(x,1,0.5,2), интервал x [0,10], количество точек 1000:
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) theta=1.986651299600245 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) a=0.5056083906174813 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C1=-0.5056083906174813 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C2=-0.4988591756915261 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 1 0.15420524 0.48808959 -0.32145543 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 2 0.48808959 1.79668322 -1.14307410Функция P1(x) и ее разложение по собственным координатам приведены на рис. 17-20.
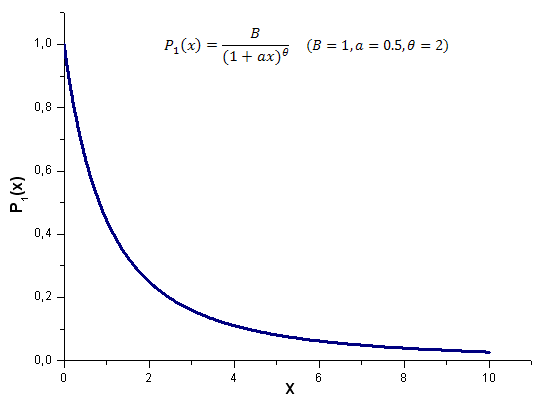
Рис. 17. Модельная функция P1(x, 1, 0.5, 2), используемая для расчета, 1000 точек
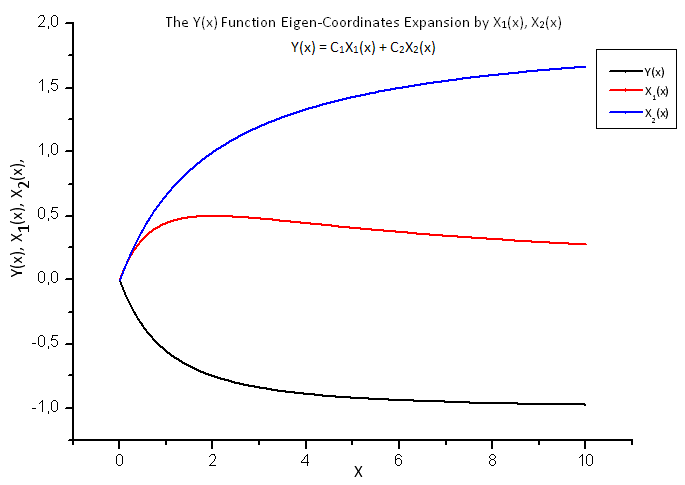
Рис. 18. Общий вид функции Y(x) и собственных координат X1(x) и X2(x)
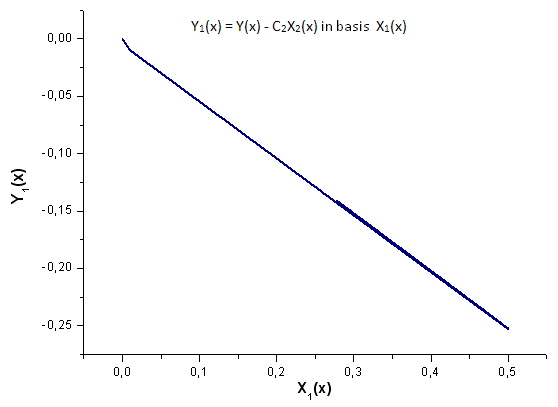
Рис 19. Представление функции Y1(x) в базисе X1(x)
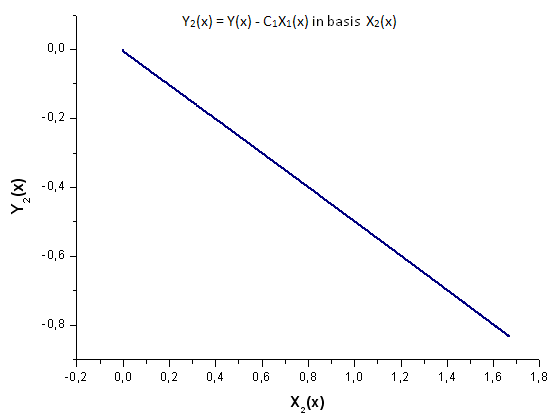
Рис 20. Представление функции Y2(x) в базисе X2(x)
Обратите внимание на рис. 19. В самом начале графика и во второй трети графика имеет место небольшая деформация линейной зависимости. Это связано с особенностями построенного разложения - X1(x) не имеет интегральной природы).
3.2. Разложение по собственным координатам функции P2(x)
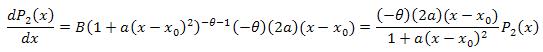
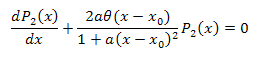
Дифференциальное уравнение:
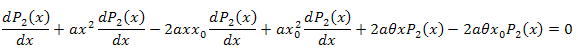
Интегрируем по x в интервале [xm,x]:
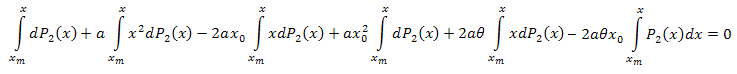
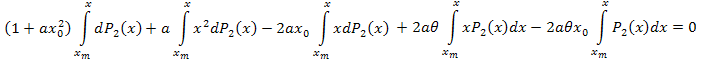
Используя интегрирование по частям, имеем:
Упростим:
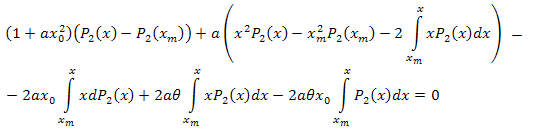
После алгебраических преобразований получим:
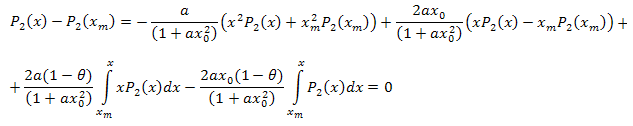
Таким образом, получили разложение:
где:
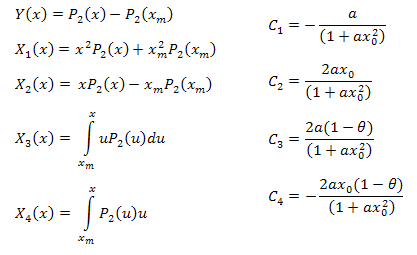
Параметры функции можно вычислить по формулам:
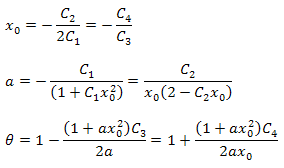
Следует обратить внимание на то, что в полученном разложении имеет место дополнительное соотношение между параметрами. Этот факт можно использовать для контроля правильности выбора функции для анализа. Для данных, точно соответствующих функции P2(x), эти соотношения справедливы всегда.
Численное значение параметра B определяется из условия нормировки.
Функции для расчета собственных координат (EC_Example3.mq5):
//+------------------------------------------------------------------+ //| CalcY | //+------------------------------------------------------------------+ void CECCalculator::CalcY(double &y[]) { if(m_size==0) return; ArrayResize(y,m_size); for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0]; }; //+------------------------------------------------------------------+ //| CalcX1 | //+------------------------------------------------------------------+ void CECCalculator::CalcX1(double &x1[]) { if(m_size==0) return; ArrayResize(x1,m_size); //--- X1=(x^2)*P2(x)+(xm)^2*P2(xm) for(int i=0; i<m_size; i++) x1[i]=(m_x[i]*m_x[i])*m_y[i]+(m_x[0]*m_x[0])*m_y[0]; } //+------------------------------------------------------------------+ //| CalcX2 | //+------------------------------------------------------------------+ void CECCalculator::CalcX2(double &x2[]) { if(m_size==0) return; ArrayResize(x2,m_size); //--- X2=(x)*P2(x)-(xm)*P2(xm) for(int i=0; i<m_size; i++) x2[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0]; } //+------------------------------------------------------------------+ //| CalcX3 | //+------------------------------------------------------------------+ void CECCalculator::CalcX3(double &x3[]) { if(m_size==0) return; double tmp[]; ArrayResize(tmp,m_size); for(int i=0; i<m_size; i++) tmp[i]=m_x[i]*m_y[i]; //--- X3=Integrate(X*P2(x)) ArrayResize(x3,m_size); for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i); } //+------------------------------------------------------------------+ //| CalcX4 | //+------------------------------------------------------------------+ void CECCalculator::CalcX4(double &x4[]) { if(m_size==0) return; //--- X4=Integrate(P2(x)) ArrayResize(x4,m_size); for(int i=0; i<m_size; i++) x4[i]=Integrate(m_x,m_y,i); }
Результат расчета модельной функции P2(x) (B=1, a=0.5, theta=2, x0=1) 1000 точек:
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: theta=2.260782711057654 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: theta=2.076195813531546 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: a=0.4557937139014854 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: a=0.4977821155774935 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: x0=1.043759816231049 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: x0=0.8909465007003451 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C1=-0.3567992171618368 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C2=0.6357780279659221 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C3=-0.7679716475618039 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C4=0.8015779457297644 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1 1.11765877 0.60684314 1.34789126 1.28971267 -0.01429928 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2 0.60684314 0.37995888 0.55974145 0.58899739 0.06731011 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 3 1.34789126 0.55974145 3.00225771 2.54531927 -0.39043224 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 4 1.28971267 0.58899739 2.54531927 2.20595917 -0.27218168Функция P2(x) и ее разложение по собственным координатам приведены на рис. 21-26.
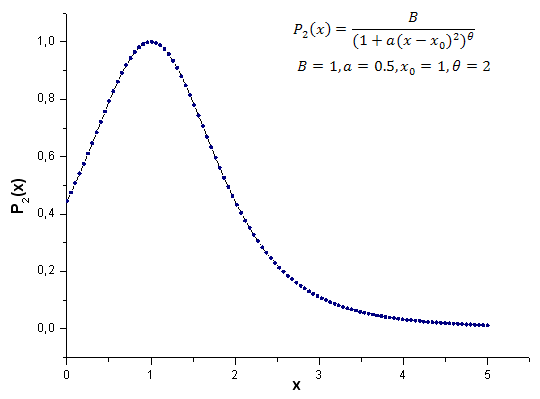
Рис 21. Модельная функция P2(x,1,0.5,2,1), используемая для расчета, 100 точек
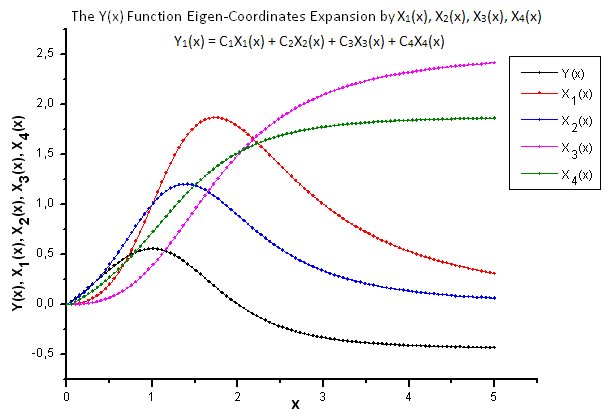
Рис 22. Общий вид функции Y(x) и собственных координат X1(x), X2(x), X3(x), X4(x)
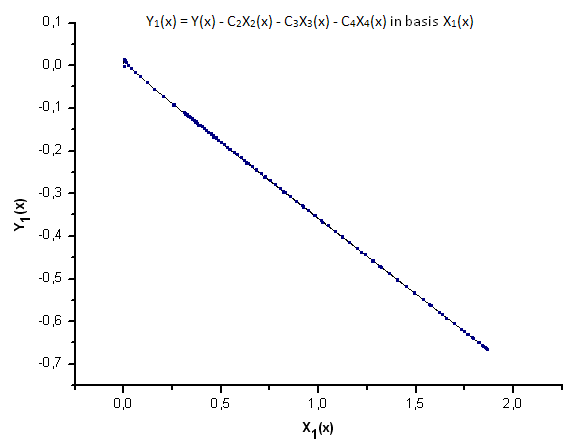
Рис 23. Представление функции Y1(x) в базисе X1(x)
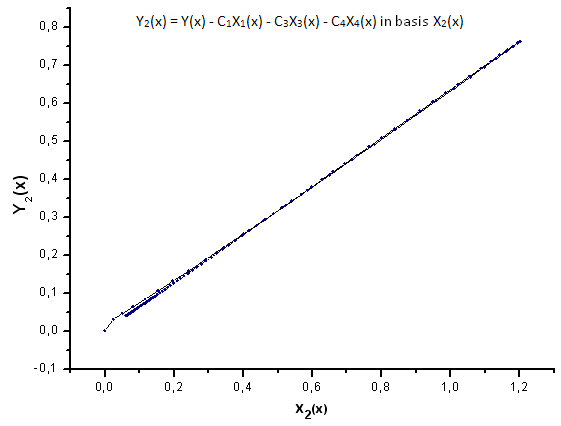
Рис 24. Представление функции Y2(x) в базисе X2(x)
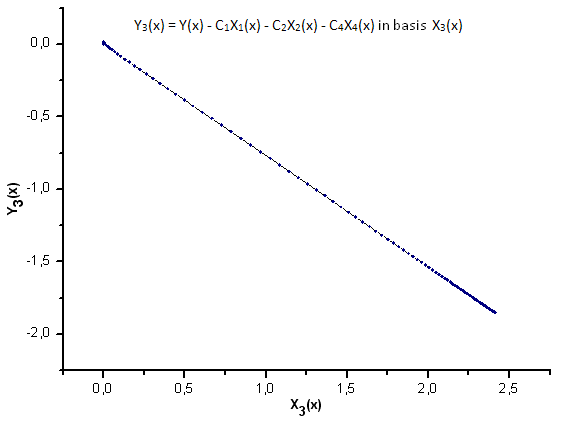
Рис 25. Представление функции Y3(x) в базисе X3(x)
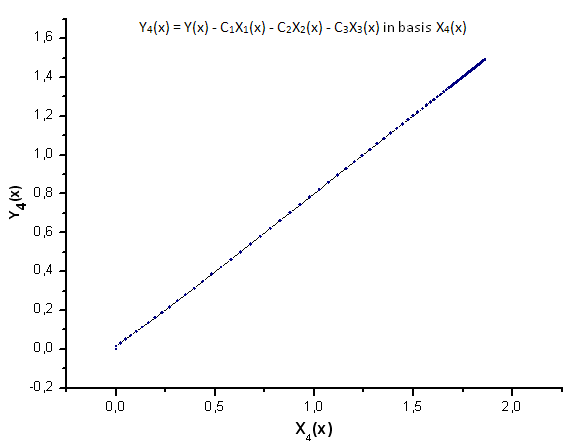
Рис 26. Представление функции Y4(x) в базисе X4(x)
4. If it looks like a cat... it might not be a cat
Семейство q-Gaussian распределений лежит в самом сердце неэкстенсивной статистической механики, поэтому казалось естественным ожидать, что оно появится в обобщении центральной предельной теоремы. Главным аргументом в его пользу были энтропийные соображения [26].
Однако в статье [18, доклад] показано,что распределения типа q-Gaussian не являются универсальными, тем самым подвергнув сомнению их особую роль в качестве предельных распределений.
Например, функция (аналитическое решение одной из задач):
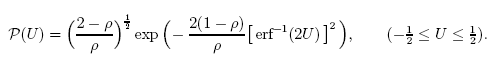
с очень хорошей точностью описывается при помощи q-Gaussian распределения.
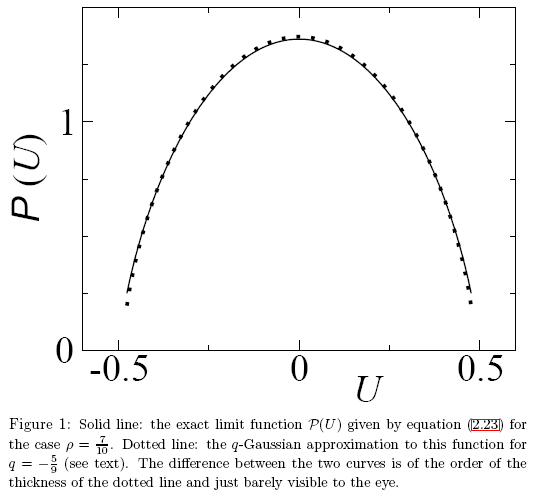
Рис. 27. Пример из статьи "A note on q-Gaussians and non-Gaussians in statistical mechanics"
В данном случае аналитически разные функции имеют близкие численные значения, поэтому невооруженным глазом сложно найти отличия. Необходим точный метод идентификации функций. Метод собственных координат позволяет красиво решить эту задачу.
Рассмотрим пример разложения по собственным координатам функции P(U) и покажем, чем именно она отличается от q-Gaussian. Визуально функции очень похожи (рис. 27).
Сгенерируем сигнал (100 значений функции P(U)) и "спроектируем" его на систему собственных координат функции P2(x), построенную в разделе 3.2.
Скрипт Hilhorst-Schehr-problem.mq5 выполняет расчет функции P(U) и построение ряда данных, которые сохраняются в файле MQL5\Files\test-data.csv. Анализ этих данных производится скриптом EC_Example3_Test.mq5.
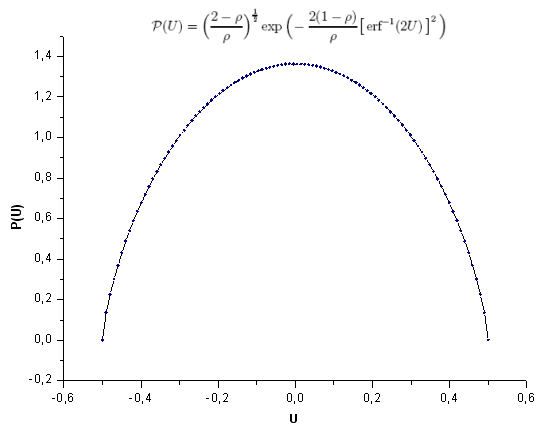
Рис. 28. Модельная функция P(U), 100 точек
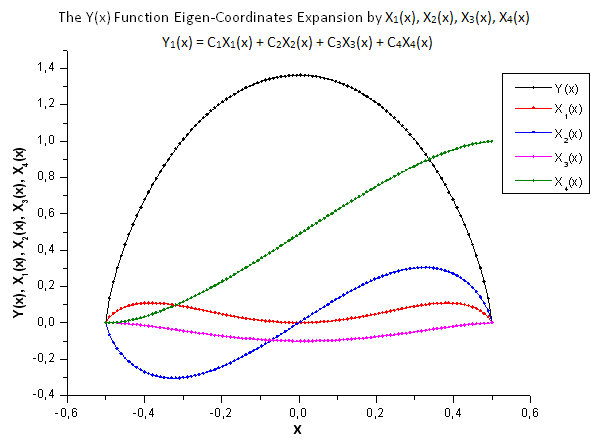
Рис 29. Общий вид функции Y(x) и собственных координат X1(x), X2(x), X3(x), X4(x)
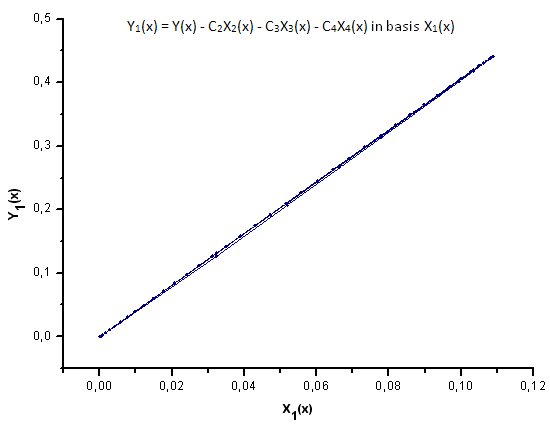
Рис 30. Представление функции Y1(x) в базисе X1(x)
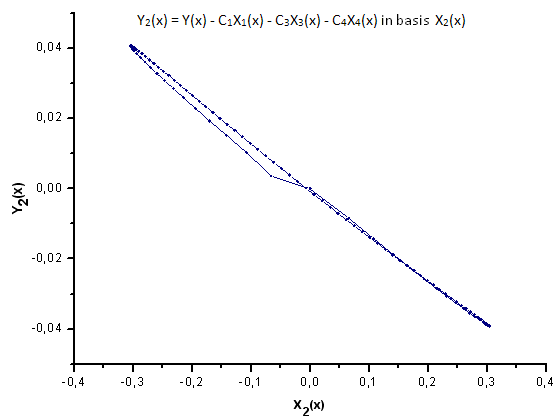
Рис 31. Представление функции Y2(x) в базисе X2(x)
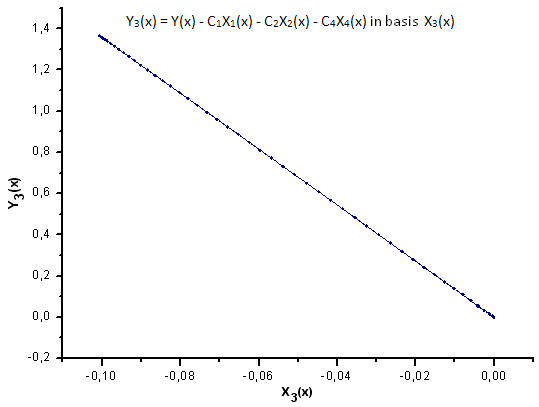
Рис 32. Представление функции Y3(x) в базисе X3(x)
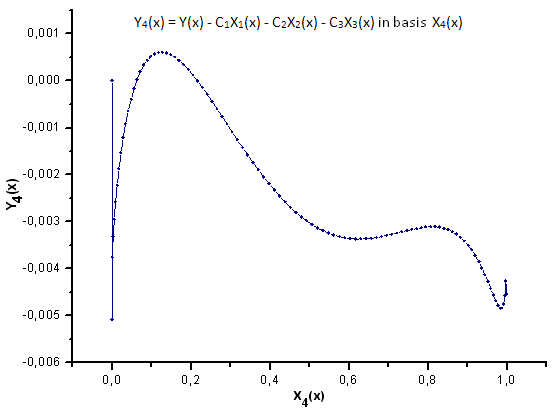
Рис 33. Представление функции Y4(x) в базисе X4(x)
Как видно из рис. 30-33, по координатам X1(x), X2(x) и X3(x) функции P2(x) и P(U) очень похожи - наблюдается хорошая линейная зависимость между Xi(x) и Yi(x). Существенное отличие проявляется в компоненте X4(x) (рис. 33).
Отсутствие линейной зависимости для компоненты X4(x) доказывает тот факт, что набор данных, порожденный P(U), несмотря на визуальное сходство с распределением q-Gaussian, таковым не является.
Можно по-другому взглянуть на функции (рис. 34-37), построив совместно Xi(x) и Yi(x).
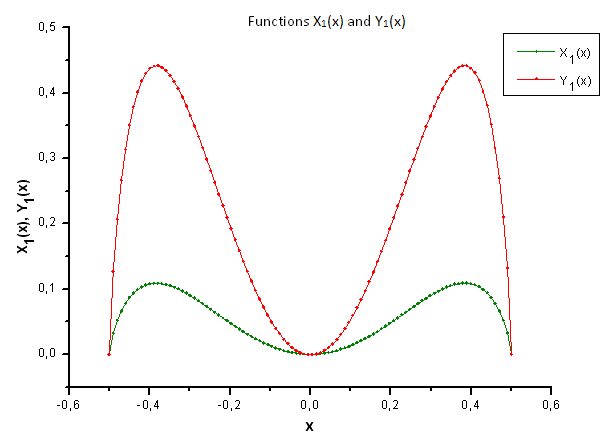
Рис 34. Общий вид функций X1(x) и Y1(x)
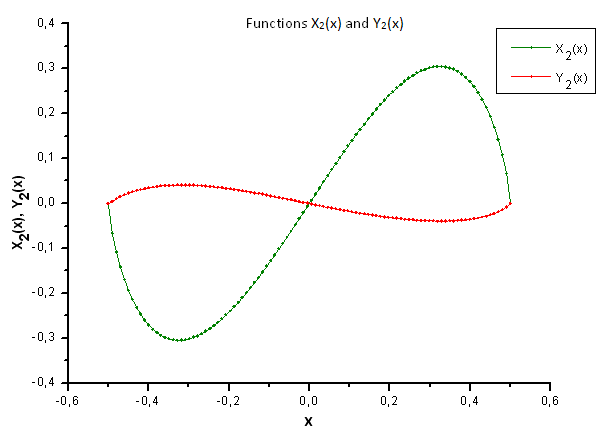
Рис 35. Общий вид функций X2(x) и Y2(x)
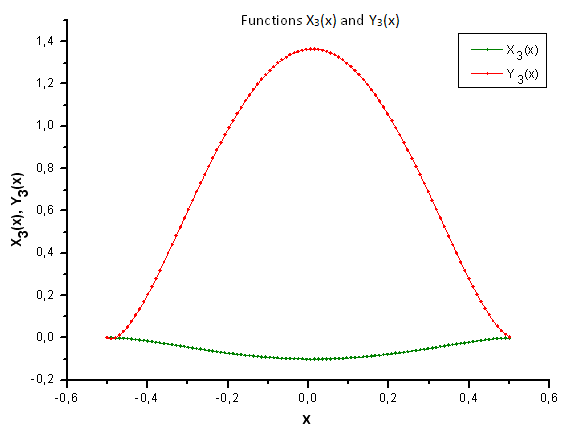
Рис 36. Общий вид функций X3(x) и Y3(x)
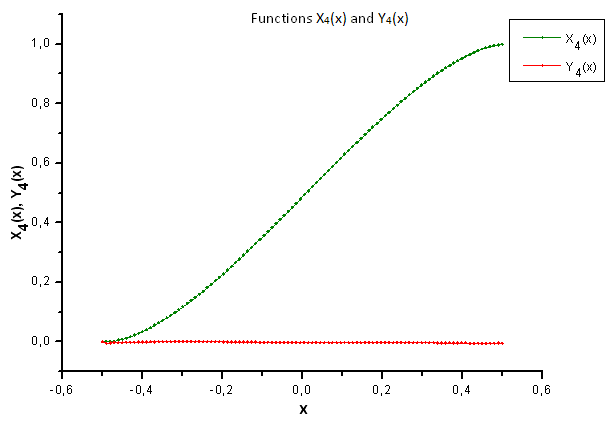
Рис 37. Общий вид функций X4(x) и Y4(x)
Как видно из рис. 37, при проектировании данных, сгенерированных функцией P(U) на собственные координаты функции P2(x), проявилось различие в структуре компоненты X4(x). Таким образом, можно точно сказать, что экспериментальные данные не соответствуют функции P2(x).
Расчет (EC_Example3_test) подтверждает этот факт:
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: theta=1.034054797050629 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: theta=-0.6736146397139184 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: a=199.3574440289263 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: a=-4.052181367572913 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: x0=-0.0003278538628371299 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: x0=0.0161122975924721 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C1=4.056448634458822 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C2=-0.1307174151339552 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C3=-13.57786363975563 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C4=-0.004451555043369697 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1 0.00465975 0.00000000 -0.00218260 0.02762761 0.04841405 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2 0.00000000 0.04841405 -0.00048835 0.06788438 0.00000001 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 3 -0.00218260 -0.00048835 0.00436149 -0.02811625 -0.06788437 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 4 0.02762761 0.06788438 -0.02811625 0.35379820 0.48337994
Также нарушились соотношения между параметрами.
Заключение
Метод собственных координат - уникальный инструмент анализа структурных свойств функциональных зависимостей, позволяющий значительно упросить анализ и интерпретацию данных.
Идея метода заключается в построении из набора экспериментальных данных {xi,yi} новых функций, соответствующих предполагаемой модели. Форма операторных разложений определяется структурой дифференциального уравнения, которому удовлетворяет функция, выступающая в качестве "кандидата" на описание данных. Если функция выбрана верно (native function), то функциональные разложения, построенные на данных {xi,yi}, в базисе собственных координат примут линейный вид. Отклонения от линейности в базисе собственных координат "функции-кандидата" свидетельствуют о том, что данные {xi,yi} не могли быть порождены данной функцией, и построенная модель не является правильной.
В некоторых сложных случаях функция-кандидат и "нативная" функция бывают похожи настолько, что большая часть построенных разложений оказывается линейной. Тем не менее, при помощи метода собственных координат удается найти различие между этими функциями, которое проявляется в нарушении линейности разложения - в примере Хилхорста и Шера различие проявилось в последнем члене разложения при проектировании на X4(x).
Эта информация также может быть полезна - в дифференциальном уравнении (раздел 3.2), которому удовлетворяет функция P2(x), данный член соответствует линейной части по P2(x). При феноменологическом описании экспериментальных данных ("ищем решение в виде q-Gaussian") это не так интересно, однако если модель базируется на дифференциальных уравнениях (рис. 3), то можно лучше понять роль каждого из механизмов, учитываемых в моделях физических процессов.
Литература
- C. Tsallis, "Possible Generalization of Boltzmann-Gibbs Statistics", Journal of Statistical Physics, Vol. 52, Nos. 1/2, 1988.
- C. Tsallis, "Nonextensive statistics: Theoretical, experimental and computational evidences and connections". Brazilian Journal of Physics, (1999) vol. 29. p.1.
- C. Tsallis, "Some comments on Boltzmann-Gibbs statistical mechanics", Chaos, Solitons & Fractals Volume 6, 1995, pp. 539–559.
- Europhysics News "Special Issue: Nonextensive statistical mechanics: new trends, new perspectives", Vol. 36 No. 6 (November-December 2005).
- M. Gell-Mann, C. Tsallis, "Nonextensive Entropy: Interdisciplinary Applications", Oxford University Press, 15.04.2004, 422 p.
- Constantino Tsallis, официальный сайт Nonextensive Statistical Mechanics and Thermodynamics.
- Чумак О.В, "Энтропии и фракталы в анализе данных", М.-Ижевск: НИЦ "Регулярная и хаотическая динамика", Институт компьютерных исследований, 2011. - 164 с.
- Qiuping A. Wang, "Incomplete statistics and nonextensive generalizations of statistical mechanics", Chaos, Solitons and Fractals, 12(2001)1431-1437.
- Qiuping A. Wang, "Extensive generalization of statistical mechanics based on incomplete information theory", Entropy, 5(2003).
- Lisa Borland, "Long-range memory and nonextensivity in financial markets", Europhysics News 36, 228-231 (2005)
- T. S. Biró, R. Rosenfeld, "Microscopic Origin of Non-Gaussian Distributions of Financial Returns", Physica A: Statistical Mechanics and its Applications, Vol. 387, Nr. 7 (Mar 1, 2008) , p. 1603-1612 (preprint).
- S. M. D. Queiros, C. Anteneodo, C. Tsallis, "Power-law distributions in economics: a nonextensive statistical approach", Proceedings of SPIE (2005) Volume: 5848, Publisher: SPIE, Pages: 151-164, (preprint)
- R Hanel, S Thurner, "Derivation of power-law distributions within standard statistical mechanics", Physica A: Statistical Mechanics and its Applications (2005), Volume: 351, Issue: 2-4, Publisher: Elsevier, Pages: 260-268. (preprint)
- A K Rajagopal, Sumiyoshi Abe, "Statistical mechanical foundations of power-law distributions", Physica D: Nonlinear Phenomena (2003), Volume: 193, Issue: 1-4, Pages: 19 (preprint)
- T. Kaizoji, "An interacting-agent model of financial markets from the viewpoint of nonextensive statistical mechanics", Physica A: Statistical Mechanics and its Applications, Vol. 370, N. 1 (Oct 1, 2006) , p. 109-113. (preprint)
- V. Gontis, J. Ruseckas, A. Kononovičius, "A long-range memory stochastic model of the return in financial markets", Physica A: Statistical Mechanics and its Applications 389 (2010) 100-106. (preprint)
- H.E. Roman, M. Porto, "Self-generated power-law tails in probability distributions", Physical Review E - Statistical, Nonlinear and Soft Matter Physics (2001), Volume: 63, Issue: 3 Pt 2, Pages: 036-128.
- H. J. Hilhorst, G. Schehr, "A note on q-Gaussians and non-Gaussians in statistical mechanics" (2007, препринт, презентация).
- D. J. Hudson, "Lectures on elementary statistics and probability", CERN-63-29, Geneva : CERN, 1963. - 101 p.
- D. J. Hudson, "Statistics lectures II : maximum likelihood and least squares theory", CERN-64-18. - Geneva : CERN, 1964. - 115 p.
- R. R. Nigmatullin, "Eigen-coordinates: New method of analytical functions identification in experimental measurements", Applied Magnetic Resonance Volume 14, Number 4 (1998), 601-633.
- R.R. Nigmatullin, "Recognition of nonextensive statistical distributions by the eigencoordinates method", Physica A: Statistical Mechanics and its Applications Volume 285, Issues 3–4, 1 October 2000, pp. 547–565.
- C. Antonini "q-Gaussians in Finance" (2010).
- C. Antonini, "The Use of the q-Gaussian Distribution in Finance" (2011).
- L. G. Moyano, C. Tsallis, M. Gell-Mann, "Numerical indications of a q-generalised central limit theorem", Europhysics Letters 73, 813-819, 2006, (preprint).
- T. Dauxois, "Non-Gaussian distributions under scrutiny", J. Stat. Mech. (2007) N08001. (preprint)
Приложение. Анализ распределения SP500 при помощи Q-Gaussian
Рассмотрим классический пример (рис. 4) по объяснению распределения SP500 при помощи q-Gaussian (функция P2(x)).
Дневные данные по ценам закрытия SP500 брались по ссылке: http://wikiposit.org/w?filter=Finance/Futures/Indices/S__and__P%20500/
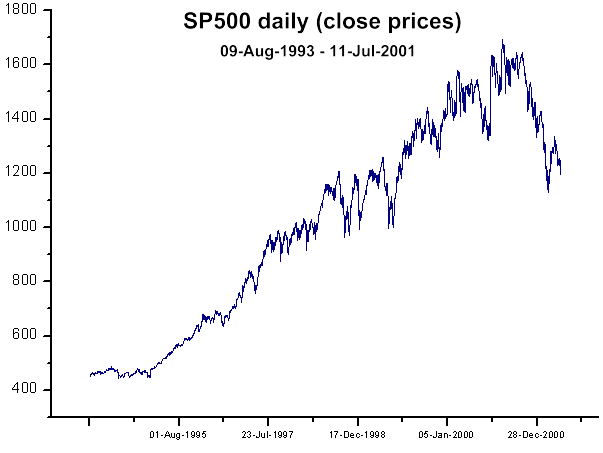
Рис. 38. График дневных цен закрытия SP500
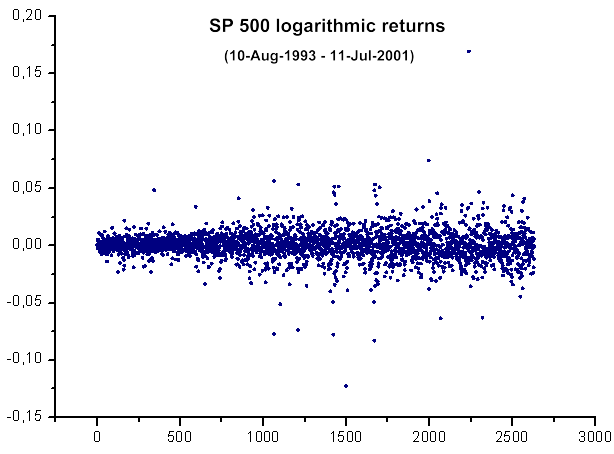
Рис. 39. График логарифма приращений дневных котировок SP500
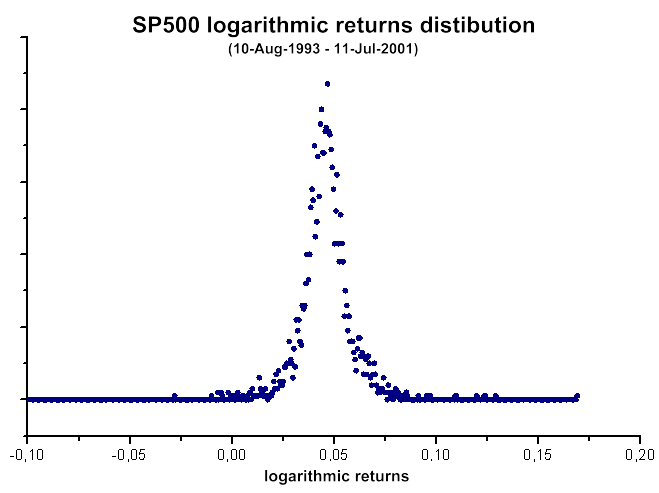
Рис. 40. Распределение логарифма приращений дневных котировок SP500
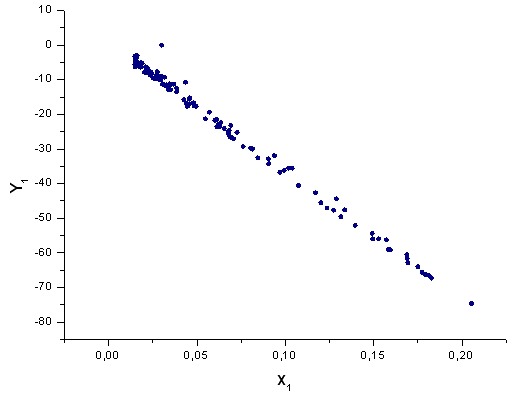
Рис. 41. Представление функции Y1(x) в базисе X1(x)
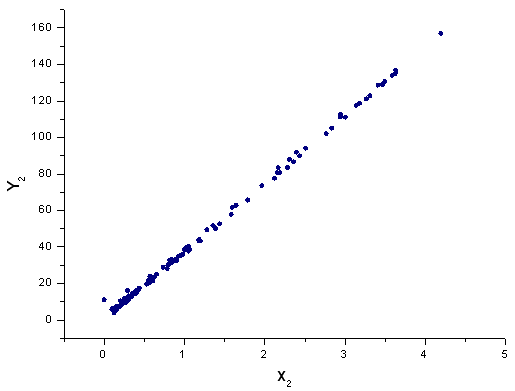
Рис. 42. Представление функции Y2(x) в базисе X2(x)
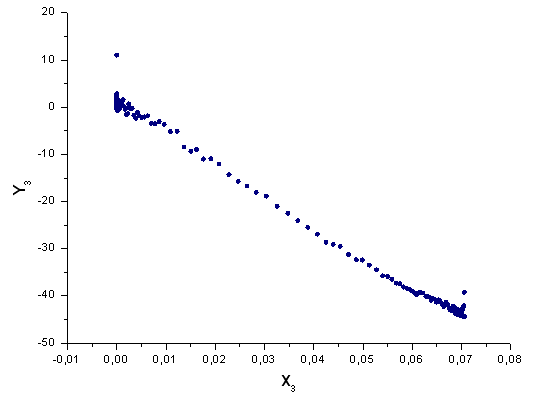
Рис. 43. Представление функции Y3(x) в базисе X3(x)
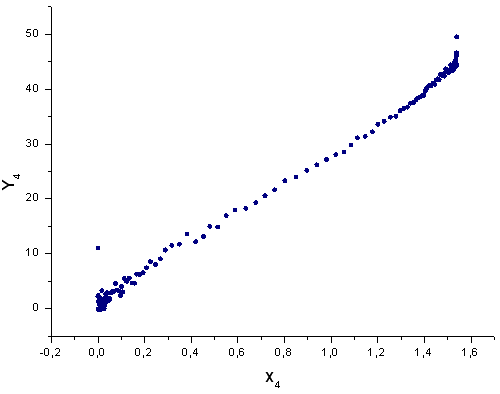
Рис. 44. Представление функции Y4(x) в базисе X4(x)
Для проверки файл SP500-data.csv нужно скопировать в папку \Files\, далее запустить CalcDistr_SP500.mq5 (расчет распределения) и затем q-gaussian-SP500.mq5 (анализ методом собственных координат)
Результаты расчета:
2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 2: theta=1.770125768485269 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 1: theta=1.864132228192338 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 2: a=2798.166930885822 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 1: a=8676.207867097581 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 2: x0=0.04567518783335043 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 1: x0=0.0512505923716428 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) C1=-364.7131366394939 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) C2=37.38352859698793 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) C3=-630.3207508306047 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) C4=28.79001868944634 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 1 0.00177913 0.03169294 0.00089521 0.02099064 0.57597695 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 2 0.03169294 0.59791579 0.01177430 0.28437712 11.55900584 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 3 0.00089521 0.01177430 0.00193200 0.04269286 0.12501732 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 4 0.02099064 0.28437712 0.04269286 0.94465120 3.26179090 2012.06.29 20:01:09 CalcDistr_SP500 (EURUSD,D1) checking distibution cnt=2632.0 n=2632 2012.06.29 20:01:09 CalcDistr_SP500 (EURUSD,D1) Min=-0.1229089015984444 Max=0.1690557338964631 range=0.2919646354949075 size=2632 2012.06.29 20:01:09 CalcDistr_SP500 (EURUSD,D1) Total data=2633
Оценки параметра q, полученные методом собственных координат (q=1+1/theta): q~1,55. В примере (рис. 4) q~1.4.
Координаты X1 и X2 чувствительные по своей природе, на X3 и X4 хвосты слегка деформированы, но не настолько, чтобы считать q-gaussian неверной функцией.
Вывод: в целом эти данные неплохо проецируются на q-gaussian, данные брались как есть, но усреднение все-же присутствует, поскольку SP500-индексный инструмент и использовались дневные графики.
Знакомство с методом эмпирической модовой декомпозиции
Визуализируй стратегию в тестере MetaTrader 5
MetaTrader 4 на Mac OS
200 usd за вашу статью по алготрейдингу!
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Спасибо за интересные вопросы, думаю, они далеко не простые.
Математическое благообразие не является нашей целью, есть надежда в том, что статистические свойства могут дать информацию о рынке. Каждый конкретный инструмент имеет свои свойства, если они оказываются постоянными, то это и есть его характеристика. Серьезные прорывы в понимании мира появились именно после обнаружения инвариантов.
1. Распределение показывает, на чьей стороне статистическое преимущество. Например, с SP500 распределение сдвинуто вправо и график показывает тренд.2. Единственным критерием истины является эксперимент. Но его можно использовать не только для подтверждения разумности теорий, а наоборот - нужно сделать так, чтобы он дал нам по шапке - только так можно выйти за рамки существующих представлений - важно найти место, где именно мы заблуждаемся. В этом смысле распределения могут подсказать, где они теряют смысл - нужно считать и смотреть.
Я не знаю правильный ответ, хрустального шара у меня нет (везде смотрел), он должен быть у кого-то из вас.
Давайте делиться опытом, проверять идеи и обсуждать результаты - вместе гораздо проще найти правильный ответ.
Да, это конечно козырной валет, но хотелось бы ещё даму и короля.
Как распределение может ответить на следующие вопросы:
имея в арсенале методы отвечающие на эти вопросы, можно считать что переход от академических поисков к практике завершён.
Хотя меня терзают смутные сомнения что распределение отвечает и на вопрос определения тренда.
Я в другой теме приводил скрины на которых явно видно зарождающийся тренд внутри более старого, те мелкое движение которое вписывается в старый тренд и не приводит к статистическим возмущениям, в последствии становиться первой опорной линией для описания нового тренда.
Я думаю что вложенность трендов очень сложная задача для распознавания которая стоит того чтоб ей занимались.
Поскольку методы распознавания могут сильно двинуть процесс понимания эволюции тренда и дать ответ на вопрос который все подразумевают но никто пока не дал ответа "а что такое тренд?".
А то ведь парадоксальная ситуация, все его видят, но никто не знает определения, прям НЛО какое то :)
Я в другой теме приводил скрины на которых явно видно зарождающийся тренд внутри более старого, те мелкое движение которое вписывается в старый тренд и не приводит к статистическим возмущениям, в последствии становиться первой опорной линией для описания нового тренда.
Quantum:
Каждый конкретный инструмент имеет свои свойства, если они оказываются постоянными, то это и есть его характеристика. Серьезные прорывы в понимании мира появились именно после обнаружения инвариантов.
Увы, но свойства инструментов постоянно меняются. Очень мало свойств, каких то закономерностей, которые существуют годами.
Quantum:
1. Распределение показывает, на чьей стороне статистическое преимущество. Например, с SP500 распределение сдвинуто вправо и график показывает тренд.Если взять отрезок времени где SP500 сначала идет вниз а потом вверх, то вероятно (хорошо бы проверить) получится симметричная кривая.
Здесь нет тренда, если по распределению смотреть, а между тем там будет две прекрасные возможности заработать, сначала шорт, потом лонг. В этом недостаток распределений, у них нет понятия времени, или развития процесса во времени. А на рынке это очень важно, смотреть динамику.
Можно конечно не брать инструмент весь, а порубить его на интервалы и построить для них распределения, получится нечто похожее на набор маркет профилей (что то типа свечного графика, только вместо свечек будут распределения). В таком случае мы опять придем к известной задаче о разладке процесса. Точнее, задаче скорейшего определения разладки процесса.
Quantum:
2. Единственным критерием истины является эксперимент. Но его можно использовать не только для подтверждения разумности теорий, а наоборот - нужно сделать так, чтобы он дал нам по шапке - только так можно выйти за рамки существующих представлений - важно найти место, где именно мы заблуждаемся. В этом смысле распределения могут подсказать, где они теряют смысл - нужно считать и смотреть.
Где, в какой теме, такие рисунки выложены?
Почему-то вспомнился принцип фальсифицируемости.
Ищи не то, что подтверждает, а то, что опровергает.
Статью еще не читал.