일반화된 통계 분포의 구조 분석에 고유값 좌표계 적용하기
207
0
목차
- 개요
- 1. 계량 경제학의 가우스 q-분포
- 2. 고유값 좌표
- 3. 일반화된 확률 분포
- 4. 고양이처럼 보이면 고양이가 아닐지도 몰라요
- 결론
- 참고 자료
- 부록 가우스 q-분포를 이용한 S&P 500 일간 수익률 분석
개요
1988년, 콘스탄티노 뜨살리스(Constantino Tsallis) Boltzmann-Gibbs-Shannon 통계역학[1]을 일반화한 비확장 엔트로피의 개념을 소개했습니다.
엔트로피의 일반화로 통계역학에서 아주 중요한 역할을 하는 두 가지 분포 형식[2], q-지수 분포와 가우스-q 분포가 나타났죠.
이러한 분포 유형은 장기 기억, 장거리 힘 및 강한 상관 관계를 포함하는 시스템의 대부분의 실험 데이터를 설명하는 데 사용할 수 있다는 것이 밝혀졌습니다.
엔트로피는 정보와 관련이 깊죠[7]. 참고 자료 [8, 9]에 정보 이론을 기반으로 한 통계역학 일반화에 대한 설명이 포함되어 있습니다. 이 일반화된 통계역학은 계량 경제학에서 매우 유용하게 쓰이게 됐죠[10~17]. 예를 들어 가우스-q 분포는 금융 상품 시세 증분의 분포에서 나타나는 넓은 꼬리에 대한 설명이라고 볼 수 있죠(q~1.5). 재무 시계열의 증분 분포는 대부분의 경우 스케일이 증가하면서 정규 분포(q=1)를 따르게 됩니다.
통계 역학의 이러한 일반화는 가우스-q 분포에 대한 중심 극한 정리와 유사한 결과를 가져올 것으로 자연스레 예상되었는데요. 그러나 강한 상관 관계를 갖는 임의의 변수들의 합의 극한 분포는 가우스-q 분포와 분석적으로 다른 것으로 증명됐습니다[18].
하지만 또 다른 문제도 발생했죠. 분포의 수치값이 가우스-q 분포의 수치값과 매우 유사하게 나타난 겁니다. 함수의 차이를 분석하고 가우스-q 분포의 최적 변수를 구하기 위해 참고자료 [18]에서 급수 확장이 이용되었습니다. 함수들 간의 관계는 q 매개 변수를 멱급수로 만들었고 이는 시스템의 비확장성 정도를 나타냅니다.
응용통계학의 가장 큰 문제는 통계적 가설을 인정하는 것이죠. 오랜동안 해결 불가능한 문제로 치부되어 왔고[19~20], 현대 응용통계학이 아닌 다른 특수한 도구가 필요할 것으로 예상되었죠.
참고 자료 [21]의 고유값 좌표계는 함수 릴레이션의 구조적 특성에 대한 한층 깊은 분석을 가능케 합니다. 여러 문제를 해결할 수 있는 아주 훌륭한 방법이죠. 위의 비확장 분포에 해당하는 연산자 전개 함수는 참고 자료 [22]에서 찾아볼 수 있습니다.
본문은 고유값 좌표계와 그 실제 적용의 예시를 다룹니다. 고유값 좌표계의 핵심이 되는 여러 공식도 포함하고 있죠. 이 공식들을 이해하고 나면 여러분이 원하는 함수에 대한 전개 함수를 만들 수 있을 겁니다.
1. 계량 경제학의 가우스 q-분포
가우스 q-분포는 계량경제학에서 아주 중요한 역할을 합니다[4,10-17].
현재 연구 수준은 참고 자료 [23], [24]에 나와 있습니다.
주요 결과를 개괄하겠습니다.
그림 1. 과학적 방법론(슬라이드 4: The Use of the q-Gaussian Distribution in Finance)
금융 시계열의 주요 특성은 그림 2에 나타나 있습니다.
그림 2. 금융 시계열 특성(슬라이드 3: The Use of the q-Gaussian Distribution in Finance)
금융 시계열을 설명하는 이론들은 대부분 가우스-q 분포로 이어집니다.
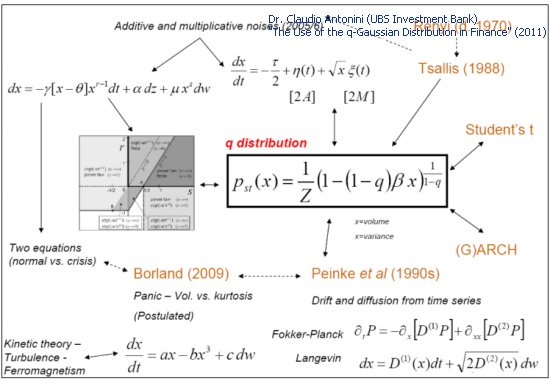
그림 3. 이론적 모델과 가우스 q-분포(슬라이드 27: The Use of the q-Gaussian Distribution in Finance)
가우스 q-분포는 시세 분포의 현상학적 설명에도 이용되죠.
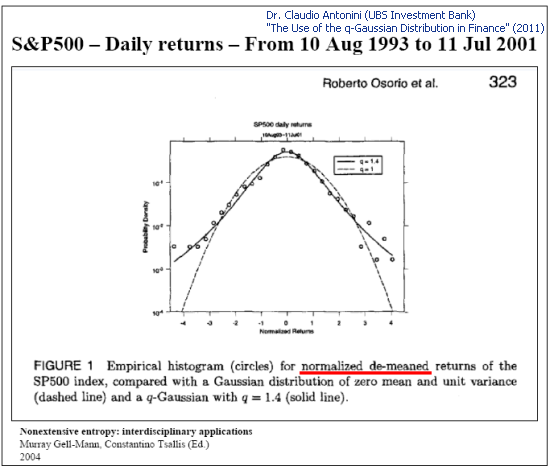
그림. 4. S&P 일간 수익률 샘플 분석(슬라이드 8: The Use of the q-Gaussian Distribution in Finance)
실제 데이터 적용 시 함수 식별에 문제가 발생합니다.
그림 5. 밀도 함수 식별 문제(슬라이드 14: q-Gaussians in Finance)
Claudio Antonini 박사는 실제 현상에 적합한 모델 구축에 있어 함수의 올바른 식별의 중요성을 강조합니다.
그림 6. 'q-Gaussians in Finance' 및 'The Use of the q-Gaussian Distribution in Finance'의 결론(Dr. Claudio Antonini, 2010, 2011)
- q-Gaussian Stock Price Dynamics, (Michael English, 2008)
- q-Gaussian European Options (Michael English, 2008)
- q-Gaussian Random Deviates & Distribution, (Michael English, 2008)
- q-Gaussian Portfolios (Michael English, 2008)
- q-Gaussian Risk Measures (Michael English, 2008)
- Expected Value & Value at Risk for Lognormal Asset (Michael English, 2008)
2. 고유값 좌표
고유값 좌표식은 다음과 같이 전개됩니다.
C1…CN은 정수이며 X1(t),..,XN(t)는 '고유값 좌표'가 됩니다.
이같은 선형 전개는 굉장히 편리하여 데이터 분석에도 자주 사용되죠. 예를 들어, 로그 스케일을 갖는 지수 함수를 직선으로 표현할 수 있습니다. 경사는 선형 회귀를 이용해 쉽게 구할 수 있죠. 따라서, 함수 매개 변수 설정을 위해 비선형 최적화를 실행할 필요가 없습니다.
하지만 보다 복잡한 함수를 다루게 되면 로그 눈금이 거의 도움이 되지 않죠. 함수가 더이상 직선으로 나타나지 않기 때문입니다. 따라서 함수의 계수를산출에 비선형 최적화가 필요하게 되죠.
서로 다른 물리적 프로세스 모델에 해당하는 함수를 이용해도 동등하게 실험 데이터를 분석할 수 있게 됩니다. 그렇다면 어떤 함수를 택하는 게 좋을까요? 어떤 함수가 보다 현실적인 결과를 가져올까요?
재무 시계열과 같은 복잡한 시스템 분석에 있어 올바른 함수 식별은 매우 중요합니다. 각각의 분포가 특정 물리적 프로세스에 해당하며 적합한 모델을 선택하면 시스템의 일반적 특성 및 그 역할을 보다 잘 이해할 수 있죠.
응용통계학[19, 20]에 따르면 틀린 통계적 가설을 기각하는 기준은 없습니다. 고유값 좌표계는 이에 대해 완전히 새로운 시각을 제안하죠.
실험 데이터 분석에 이용된 함수를 특정 미분방정식에 대한 해결책으로 보는 겁니다. 그 형식이 고유값 좌표 전개 구조를 결정하게 되죠.
고유값 좌표 전개의 특성 중 하나는 Y(t) 함수로 생성된 모든 데이터가 기저함수 X1(t)..XN(t)에 대해 선형 구조를 갖는다는 겁니다. 이 경우 F(t) 함수로 생성된 데이터는 선형 구조를 갖지 않습니다.
덕분에 함수를 정확하게 식별해 통계적 가설을 보다 용이하게 다룰 수 있게 되죠.
2.1. 고유값 좌표계
핵심은 고유값 좌표 Xk(t)를 기저함수 Y(t)를 갖는 연산자 형식으로 만드는 겁니다.
고유값 좌표 Xk(t)가 콘벌루션 형태를 띠며 그 전개는 함수 Y(t)를 값으로 갖는 미분방정식의 구조로 결정됩니다. 계수 C1.. CN의 판단에 대한 문제가 발생하기도 하는데요.
정규 직교 전개(예: 푸리에 변환 계수 산출)의 경우 계수는 벡터를 기반으로 산출되며 기저함수의 직교성 덕분에 원하는 결과를 구할 수 있게 됩니다.
우리의 경우 X1(t)… XN(t)의 직교성에 대한 정보가 없으므로 이는 적합한 방법이 아니죠.
2.2. 최소제곱법으로 팽창 계수 구하기
계수 Ck는 최소제곱법으로 산출 가능합니다. 일차 방정식 시스템을 풀면 되는데요.
다음을 가정합니다.
를 측정할 때마다 오류가 발생합니다
.
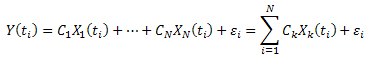
편차 제곱의 합의 값을 최소화합니다.
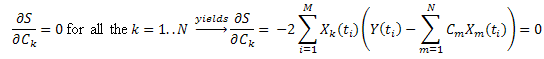
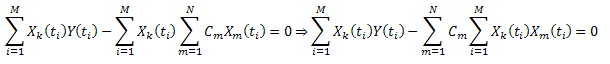
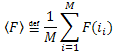를 이용하면 다음과 같이 쓸 수 있죠.
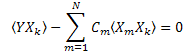
C1...CN(k=1..N)을 갖는 선형 방정식이 생성됩니다.
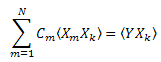
상관 행렬은 대칭을 이룹니다
.
적분을 이용한 고유값 좌표 전개가 더 편한 경우도 있습니다.
이 경우 평균값을 이용해 오류의 영향을 줄일 수는 있지만 추가적 연산을 필요로 하죠.
2.3. R(x) 함수 전개 예시
아래 함수에 대한 고유값 좌표 전개를 살펴보겠습니다.
해당 함수는 다양한 통계적 분포를 낳습니다[21].
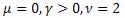-정규 분포(가우스 분포)
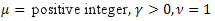-푸아송 분포
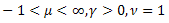-감마 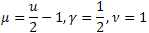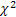분포
-
분포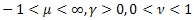
-베이불 분포를 포함하는 Schtauffer 분포
.
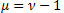완화 과정 설명에도 적합합니다.
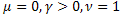- 일반 지수 함수
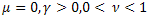- 늘어난 지수 함수
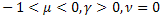- 응력 완화 함수
x에 대해 R(x)를 미분한 결과는 다음과 같습니다.
양쪽에 x를 곱합니다.
다음을 변환하세요.
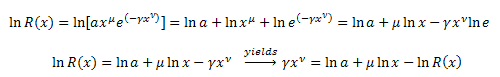
해당 수식에서 다음을 치환합니다.
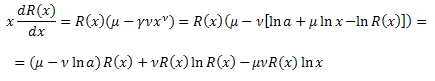
R(x) 함수에 대한 미분방정식은 다음과 같습니다.
인터벌 [xm,x]를 갖는 x에 대해 적분합니다.
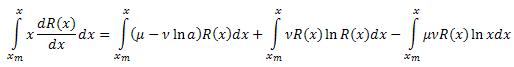
좌변을 적분합니다.
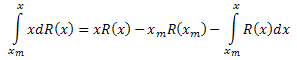
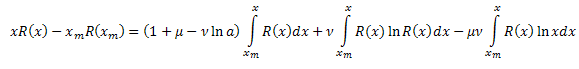
다음과 같은 결과가 나옵니다.
읽는 법
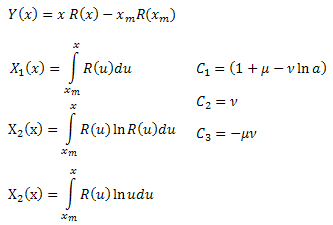
상관 계수를 계산하면
함수 매개 변수를 결정할 수 있습니다
. 네 번째 변수는 
R(x) 함수식에서 가져올 수 있죠.
2.4. 구현
팽창 계수를 구하려면 일차 방정식 시스템을 풀면 됩니다. 행렬을 보다 편하게 다루기 위해 별도의 클래스 CMatrix(CMatrix.mqh)를 생성합니다. 해당 클래스 메소드를 이용해 행렬 매개 변수와 엘리먼트 값을 설정하고 가우스 합을 이용해 일차 방정식을 풀 수 있습니다.
//+------------------------------------------------------------------+ //| CMatrix class | //+------------------------------------------------------------------+ class CMatrix { double m_matrix[]; int m_rows; int m_columns; public: void SetSize(int nrows,int ncolumns); double Get(int i,int j); void Set(int i,int j,double val); void GaussSolve(double &v[]); void Test(); };
R(x) 함수의 고유값 좌표 및 매개 변수를 산출하는 스크립트 예시를 살펴보겠습니다(EC_Example1.mq5).
//+------------------------------------------------------------------+ //| EC_Example1.mq5 | //| Copyright 2012, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2012, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #include <CMatrix.mqh> //+------------------------------------------------------------------+ //| CECCalculator | //+------------------------------------------------------------------+ class CECCalculator { protected: int m_size; //--- x[i] double m_x[]; //--- y[i] double m_y[]; //--- matrix CMatrix m_matrix; //--- Y[i] double m_ec_y[]; //--- eigen-coordinates X1[i],X2[i],X3[i] double m_ec_x1[]; double m_ec_x2[]; double m_ec_x3[]; //--- coefficients C1,C2,C3 double m_ec_coefs[]; //--- function f1=Y-C2*X2-C3*X3 double m_f1[]; //--- function f2=Y-C1*X1-C3*X3 double m_f2[]; //--- function f3=Y-C1*X1-C2*X2 double m_f3[]; private: //--- function for data generation double R(double x,double a,double mu,double gamma,double nu); //--- calculation of the integral double Integrate(double &x[],double &y[],int ind); //--- calculation of the function Y(x) void CalcY(double &y[]); //--- calculation of the function X1(x) void CalcX1(double &x1[]); //--- calculation of the function X2(x) void CalcX2(double &x2[]); //--- calculation of the function X3(x) void CalcX3(double &x3[]); //--- calculation of the correlator double Correlator(int ind1,int ind2); public: //--- method for generating the test function data set x[i],y[i] void GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu); //--- loading data from the file bool LoadData(string filename); //--- saving data into the file bool SaveData(string filename); //--- saving the calculation results void SaveResults(string filename); //--- calculation of the eigen-coordinates void CalcEigenCoordinates(); //--- calculation of the linear expansion coefficients void CalcEigenCoefficients(); //--- calculation of the function parameters void CalculateParameters(); //--- calculation of the functions f1,f2,f3 void CalculatePlotFunctions(); }; //+------------------------------------------------------------------+ //| Function R(x) | //+------------------------------------------------------------------+ double CECCalculator::R(double x,double a,double mu,double gamma,double nu) { return(a*MathExp(mu*MathLog(MathAbs(x)))*MathExp(-gamma*MathExp(nu*MathLog(MathAbs(x))))); } //+-----------------------------------------------------------------------+ //| Method for generating the data set x[i],y[i] of the test function R(x)| //+-----------------------------------------------------------------------+ void CECCalculator::GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu) { if(size<=0) return; if(x1>=x2) return; m_size=size; ArrayResize(m_x,m_size); ArrayResize(m_y,m_size); double delta=(x2-x1)/(m_size-1); //--- for(int i=0; i<m_size; i++) { m_x[i]=x1+i*delta; m_y[i]=R(m_x[i],a,mu,gamma,nu); } }; //+------------------------------------------------------------------+ //| Method for loading data from the .CSV file | //+------------------------------------------------------------------+ bool CECCalculator::LoadData(string filename) { int filehandle=FileOpen(filename,FILE_CSV|FILE_READ|FILE_ANSI,'\r'); if(filehandle==INVALID_HANDLE) { Alert("Error in open of file ",filename,", error",GetLastError()); return(false); } m_size=0; while(!FileIsEnding(filehandle)) { string str=FileReadString(filehandle); if(str!="") { string astr[]; StringSplit(str,';',astr); if(ArraySize(astr)==2) { ArrayResize(m_x,m_size+1); ArrayResize(m_y,m_size+1); m_x[m_size]=StringToDouble(astr[0]); m_y[m_size]=StringToDouble(astr[1]); m_size++; } else { m_size=0; return(false); } } } FileClose(filehandle); return(true); } //+------------------------------------------------------------------+ //| Method for saving data into the .CSV file | //+------------------------------------------------------------------+ bool CECCalculator::SaveData(string filename) { if(m_size==0) return(false); if(ArraySize(m_x)!=ArraySize(m_y)) return(false); if(ArraySize(m_x)==0) return(false); int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI,'\r'); if(filehandle==INVALID_HANDLE) { Alert("Error in open of file ",filename,", error",GetLastError()); return(false); } for(int i=0; i<ArraySize(m_x); i++) { string s=DoubleToString(m_x[i],8)+";"; s+=DoubleToString(m_y[i],8)+";"; s+="\r"; FileWriteString(filehandle,s); } FileClose(filehandle); return(true); } //+------------------------------------------------------------------+ //| Method for the calculation of the integral | //+------------------------------------------------------------------+ double CECCalculator::Integrate(double &x[],double &y[],int ind) { double sum=0; for(int i=0; i<ind-1; i++) sum+=(x[i+1]-x[i])*(y[i+1]+y[i])*0.5; return(sum); } //+------------------------------------------------------------------+ //| Method for the calculation of the function Y(x) | //+------------------------------------------------------------------+ void CECCalculator::CalcY(double &y[]) { if(m_size==0) return; ArrayResize(y,m_size); for(int i=0; i<m_size; i++) y[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0]; }; //+------------------------------------------------------------------+ //| Method for the calculation of the function X1(x) | //+------------------------------------------------------------------+ void CECCalculator::CalcX1(double &x1[]) { if(m_size==0) return; ArrayResize(x1,m_size); for(int i=0; i<m_size; i++) x1[i]=Integrate(m_x,m_y,i); } //+------------------------------------------------------------------+ //| Method for the calculation of the function X2(x) | //+------------------------------------------------------------------+ void CECCalculator::CalcX2(double &x2[]) { if(m_size==0) return; double tmp[]; ArrayResize(tmp,m_size); for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_y[i])); ArrayResize(x2,m_size); for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,tmp,i); } //+------------------------------------------------------------------+ //| Method for the calculation of the function X3(x) | //+------------------------------------------------------------------+ void CECCalculator::CalcX3(double &x3[]) { if(m_size==0) return; double tmp[]; ArrayResize(tmp,m_size); for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_x[i])); ArrayResize(x3,m_size); for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i); } //+------------------------------------------------------------------+ //| Method for the calculation of the eigen-coordinates | //+------------------------------------------------------------------+ void CECCalculator::CalcEigenCoordinates() { CalcY(m_ec_y); CalcX1(m_ec_x1); CalcX2(m_ec_x2); CalcX3(m_ec_x3); } //+------------------------------------------------------------------+ //| Method for the calculation of the correlator | //+------------------------------------------------------------------+ double CECCalculator::Correlator(int ind1,int ind2) { if(m_size==0) return(0); if(ind1<=0 || ind1>4) return(0); if(ind2<=0 || ind2>4) return(0); //--- double arr1[]; double arr2[]; ArrayResize(arr1,m_size); ArrayResize(arr2,m_size); //--- switch(ind1) { case 1: ArrayCopy(arr1,m_ec_x1,0,0,WHOLE_ARRAY); break; case 2: ArrayCopy(arr1,m_ec_x2,0,0,WHOLE_ARRAY); break; case 3: ArrayCopy(arr1,m_ec_x3,0,0,WHOLE_ARRAY); break; case 4: ArrayCopy(arr1,m_ec_y,0,0,WHOLE_ARRAY); break; } switch(ind2) { case 1: ArrayCopy(arr2,m_ec_x1,0,0,WHOLE_ARRAY); break; case 2: ArrayCopy(arr2,m_ec_x2,0,0,WHOLE_ARRAY); break; case 3: ArrayCopy(arr2,m_ec_x3,0,0,WHOLE_ARRAY); break; case 4: ArrayCopy(arr2,m_ec_y,0,0,WHOLE_ARRAY); break; } //--- double sum=0; for(int i=0; i<m_size; i++) { sum+=arr1[i]*arr2[i]; } sum=sum/m_size; return(sum); }; //+------------------------------------------------------------------+ //| Method for the calculation of the linear expansion coefficients | //+------------------------------------------------------------------+ void CECCalculator::CalcEigenCoefficients() { //--- setting the matrix size 3x4 m_matrix.SetSize(3,4); //--- calculation of the correlation matrix for(int i=3; i>=1; i--) { string s=""; for(int j=1; j<=4; j++) { double corr=Correlator(i,j); m_matrix.Set(i,j,corr); s=s+" "+DoubleToString(m_matrix.Get(i,j)); } Print(i," ",s); } //--- solving the system of the linear equations m_matrix.GaussSolve(m_ec_coefs); //--- displaying the solution - the obtained coefficients C1,..CN for(int i=ArraySize(m_ec_coefs)-1; i>=0; i--) Print("C",i+1,"=",m_ec_coefs[i]); }; //+--------------------------------------------------------------------+ //| Method for the calculation of the function parameters a,mu,nu,gamma| //+--------------------------------------------------------------------+ void CECCalculator::CalculateParameters() { if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;} //--- calculate a double a=MathExp((1-m_ec_coefs[0])/m_ec_coefs[1]-m_ec_coefs[2]/(m_ec_coefs[1]*m_ec_coefs[1])); //--- calculate mu double mu=-m_ec_coefs[2]/m_ec_coefs[1]; //--- calculate nu double nu=m_ec_coefs[1]; //--- calculate gamma double arr1[],arr2[]; ArrayResize(arr1,m_size); ArrayResize(arr2,m_size); double corr1=0; double corr2=0; for(int i=0; i<m_size; i++) { arr1[i]=MathPow(m_x[i],nu); arr2[i]=MathLog(MathAbs(m_y[i]))-MathLog(a)-mu*MathLog(m_x[i]); corr1+=arr1[i]*arr2[i]; corr2+=arr1[i]*arr1[i]; } double gamma=-corr1/corr2; //--- Print("a=",a); Print("mu=",mu); Print("nu=",nu); Print("gamma=",gamma); }; //+------------------------------------------------------------------+ //| Method for the calculation of the functions | //| f1=Y-C2*X2-C3*X3 | //| f2=Y-C1*X1-C3*X3 | //| f3=Y-C1*X1-C2*X2 | //+------------------------------------------------------------------+ void CECCalculator::CalculatePlotFunctions() { if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;} //--- ArrayResize(m_f1,m_size); ArrayResize(m_f2,m_size); ArrayResize(m_f3,m_size); //--- for(int i=0; i<m_size; i++) { //--- plot function f1=Y-C2*X2-C3*X3 m_f1[i]=m_ec_y[i]-m_ec_coefs[1]*m_ec_x2[i]-m_ec_coefs[2]*m_ec_x3[i]; //--- plot function f2=Y-C1*X1-C3*X3 m_f2[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[2]*m_ec_x3[i]; //--- plot function f3=Y-C1*X1-C2*X2 m_f3[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[1]*m_ec_x2[i]; } } //+------------------------------------------------------------------+ //| Method for saving the calculation results | //+------------------------------------------------------------------+ void CECCalculator::SaveResults(string filename) { if(m_size==0) return; int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI); if(filehandle==INVALID_HANDLE) { Alert("Error in open of file ",filename," for writing, error",GetLastError()); return; } for(int i=0; i<m_size; i++) { string s=DoubleToString(m_x[i],8)+";"; s+=DoubleToString(m_y[i],8)+";"; s+=DoubleToString(m_ec_y[i],8)+";"; s+=DoubleToString(m_ec_x1[i],8)+";"; s+=DoubleToString(m_f1[i],8)+";"; s+=DoubleToString(m_ec_x2[i],8)+";"; s+=DoubleToString(m_f2[i],8)+";"; s+=DoubleToString(m_ec_x3[i],8)+";"; s+=DoubleToString(m_f3[i],8)+";"; s+="\r"; FileWriteString(filehandle,s); } FileClose(filehandle); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { CECCalculator ec; //--- model function data preparation ec.GenerateData(100,0.25,15.25,1.55,1.05,0.15,1.3); //--- saving into the file ec.SaveData("ex1.csv"); //--- calculation of the eigen-coordinates ec.CalcEigenCoordinates(); //--- calculation of the coefficients ec.CalcEigenCoefficients(); //--- calculation of the parameters ec.CalculateParameters(); //--- calculation of the functions f1,f2,f3 ec.CalculatePlotFunctions(); //--- saving the results into the file ec.SaveResults("ex1-results.csv"); }
2.5. R(x) 함수 모델 계산 결과
[0.25,15.25]를 인터벌로 갖는 R(x) 함수 값 100개를 생성해 모델 데이터로 삼겠습니다.
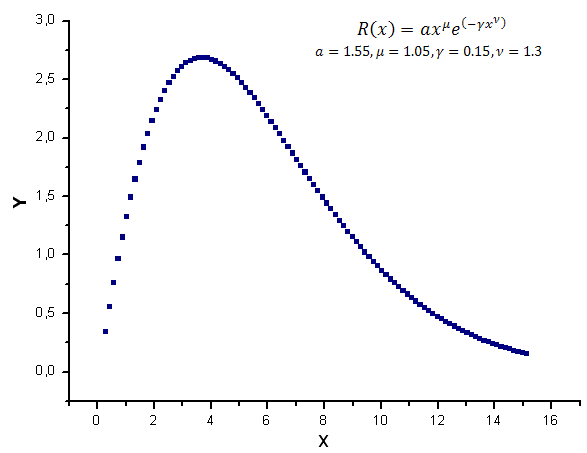
그림 7. 연산용 함수 모델
해당 데이터를 기반으로 Y(x) 함수가 플로팅되며 X1(x), X2(x) 및 X3(x) 함수의 전개가 이루어집니다.
그림 8은 함수 Y(x)와 그 고유값 좌표 X1(x), X2(x) 및 X3(x)를 나타냅니다.
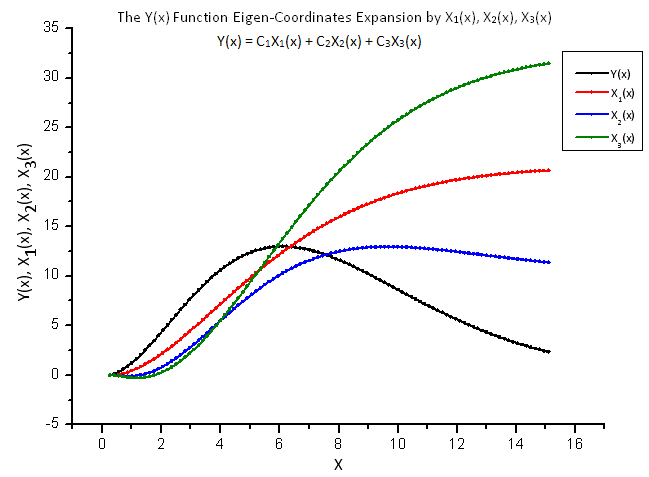
그림 8. Y(x) 함수와 고유값 좌표계 X1(x), X2(x), X3(x)의 일반형
X1(x), X2(x) 및 X3(x) 연산자의 미분적 특성에서 매끄러운 함수가 나타납니다.
함수 Y(x), X1(x), X2(x) 및 X3(x)의 연산 후 상관 행렬이 생성되며, 계수 C1, C2 및 C3에 대한 방정식이 해결되고 그에 따라 R(x) 함수 매개 변수가 설정됩니다.
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) gamma=0.2769402213886906 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) nu=1.126643424450548 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) mu=1.328595266178149 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) a=1.637687667818532 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C1=1.772838639779728 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C2=1.126643424450548 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C3=-1.496853120395737 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 1 221.03637620 148.53278281 305.48547011 101.93843241 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 2 148.53278281 101.63995012 202.85142688 74.19784681 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 3 305.48547011 202.85142688 429.09345292 127.82779760
이제 계산 결과의 선형성을 확인하겠습니다. 다음 3개 함수를 계산해야 합니다.
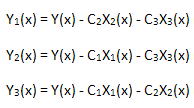
각 함수는 고유값 좌표 X1(x), X2(x) 및 X3(x)를 기저 함수로 갖습니다.
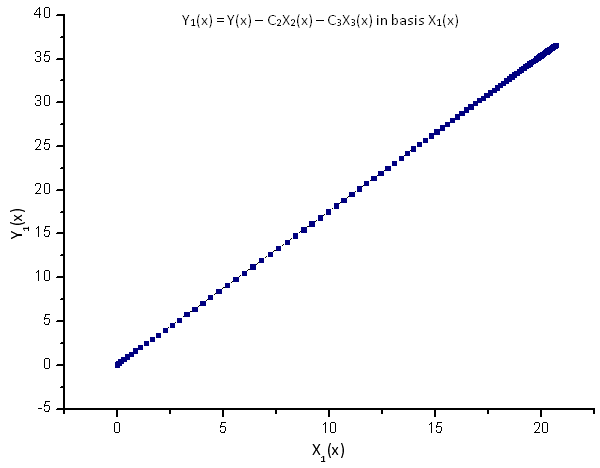
그림 9. 기저함수 X1(x)를 갖는 Y1(x)의 함수식
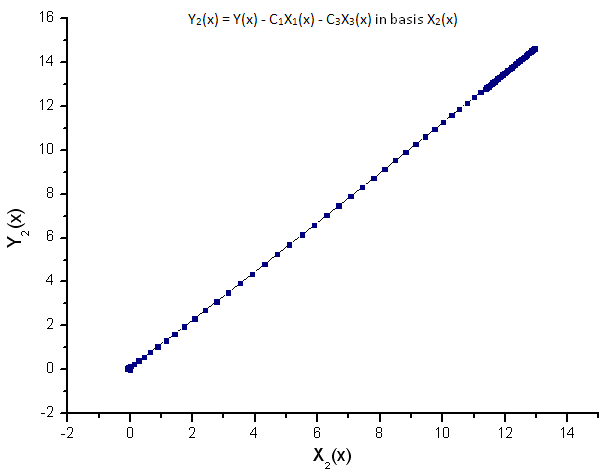
그림 10. 기저함수 X2(x)를 갖는 Y2(x)의 함수식
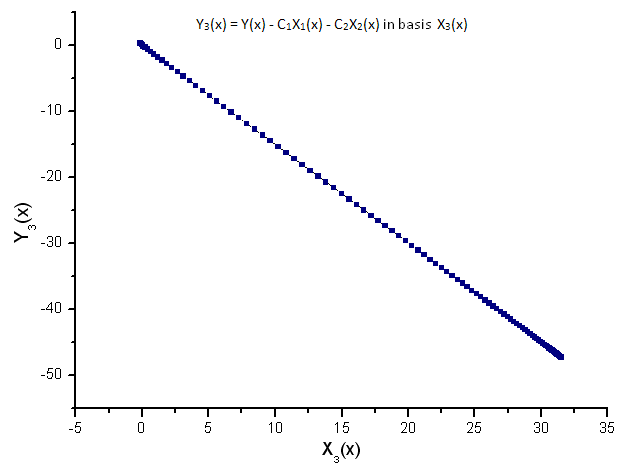
그림 11. 기저함수 X3(x)를 갖는 Y3(x)의 함수식
각 함수의 선형 종속성은 그림 7의 데이터 세트가 R(x) 함수에 완전히 일치함을 보여줍니다.
R(x) 고유값 좌표에 나타난 나머지 함수는 더이상 선형이 아니게 되죠. 덕분에 함수를 식별할 수 있게 됩니다.
동일한 인터벌을 유지하면서 포인트 개수를 10000으로 증가시키면 수치 계산의 정확도를 향상시킬 수 있습니다.
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) gamma=0.1508739336762316 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) nu=1.298316173744703 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) mu=1.052364487161627 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) a=1.550281229466634 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C1=1.483135479113404 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C2=1.298316173744703 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C3=-1.36630183435649 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 1 225.47846911 151.22066473 311.86134419 104.65062550 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 2 151.22066473 103.30005101 206.66297964 76.03285182 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 3 311.86134419 206.66297964 438.35625824 131.91955339
이 경우 함수 매개 변수가 보다 정확하게 계산된 것이죠.
2.6. 노이즈 효과
실제 실험 데이터에는 반드시 노이즈가 나타납니다.
ECCCalculator 클래스의 GenerateData() 메소드에서
m_y[i]=R(m_x[i],a,mu,gamma,nu);
다음을 수정합니다.
m_y[i]=R(m_x[i],a,mu,gamma,nu)+0.25*MathRand()/32767.0;
함수 최대 값의 약 10%가 되는 랜덤 노이즈를 추가합니다.
EC_Example1-noise.mq5 스크립트가 다음과 같이 나타납니다.
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) gamma=0.4013079343855266 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) nu=0.9915044018913447 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) mu=1.403541951457922 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) a=2.017238416806171 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C1=1.707774107235756 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C2=0.9915044018913447 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C3=-1.391618023109698 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 1 254.45082565 185.19087989 354.25574000 125.17343164 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 2 185.19087989 136.81028987 254.92996885 97.14705491 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 3 354.25574000 254.92996885 501.76021715 159.49440494
그림 12는 랜덤 노이즈가 반영된 함수 모델 차트입니다.
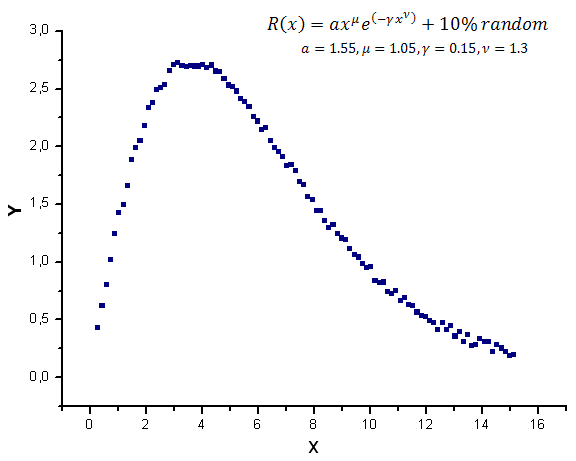
그림 12. 노이즈가 반영된 연산용 함수 모델
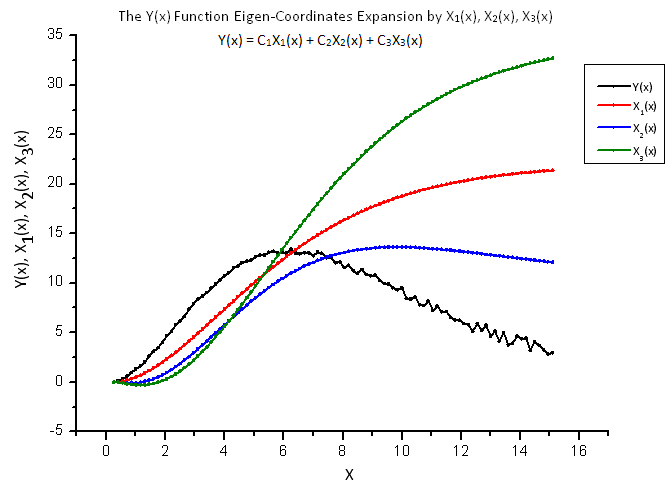
그림 13. Y(x) 함수와 고유값 좌표계 X1(x), X2(x), X3(x)의 일반형
고유값 좌표가 되는 함수 X1(x), X2(x) 및 X3(x)는 여전히 매끄럽게 나타납니다. 하지만 세 함수의 선형 결합인 Y(x)는 다르게 나타나네요(그림 13).
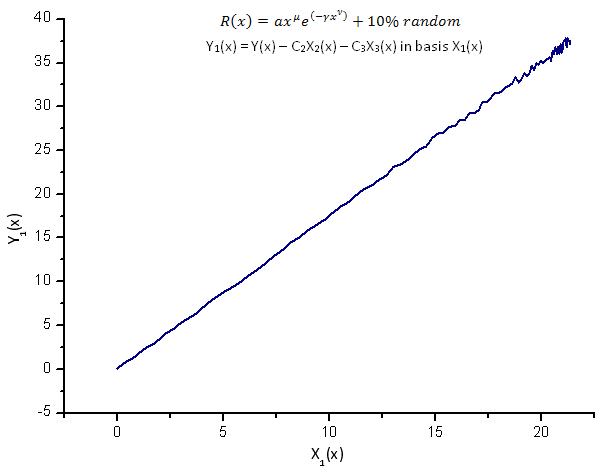
그림 14. 기저함수 X1(x)를 갖는 Y1(x)의 함수식
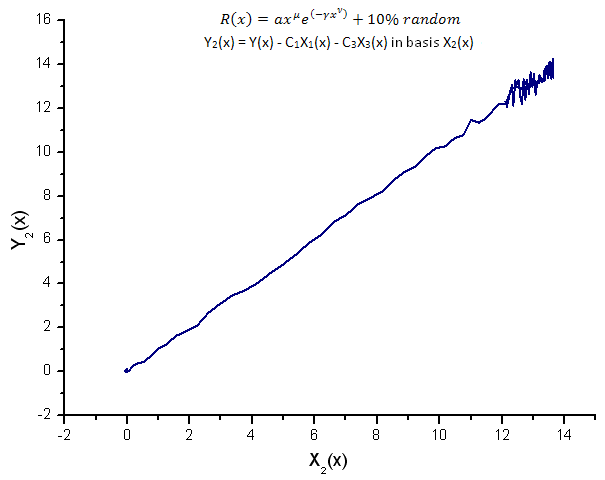
그림 15. 기저함수 X2(x)를 갖는 Y2(x)의 함수식
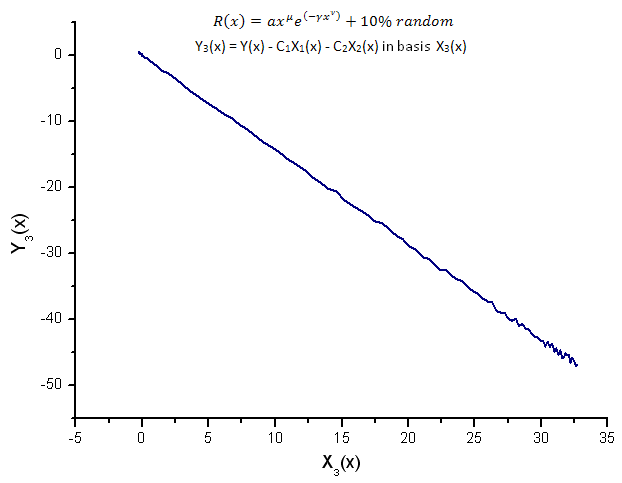
그림 16. 기저함수 X3(x)를 갖는 Y3(x)의 함수식
고유값 좌표를 기저함수로 갖는 Y1(x),Y2(x) 및 Y3(x)는(그림 8~10) 여전히 선형으로 나타나지만 노이즈로 인해 직선 주변으로 파동이 발생합니다. X값이 클수록 더 뚜렷하게 나타납니다.
이때 노이즈 컴포넌트는 직선의 양면에 위치하므로 고유 좌표 전개를 적분하는 것이 편리합니다.
3. 일반화된 확률 분포
통계역학의 일반화는 참고 자료 [2, 22]의 분포를 낳았습니다.
읽는 법
가우스 q-분포는 P2(x) 함수의 특수 케이스에 해당합니다.
3.1. P1(x) 함수 고유값 좌표 전개
P1(x)를 미분합니다.
다음과 같은 미분방정식이 도출됩니다.
인터벌 [xm,x]에 대해 적분합니다.
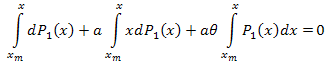
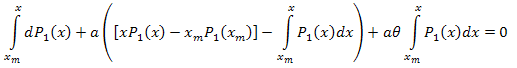
다음의 결과가 나옵니다.
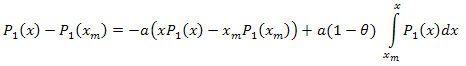
고유값 좌표식은 다음과 같이 전개됩니다.
읽는 법
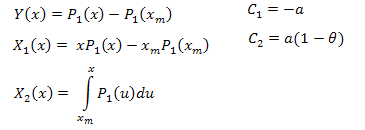
다음은 연산에 필요한 함수입니다(EC_Example2.mq5).
//+------------------------------------------------------------------+ //| CalcY | //+------------------------------------------------------------------+ void CECCalculator::CalcY(double &y[]) { if(m_size==0) return; ArrayResize(y,m_size); //--- Y=P(x)-P(xm) for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0]; }; //+------------------------------------------------------------------+ //| CalcX1 | //+------------------------------------------------------------------+ void CECCalculator::CalcX1(double &x1[]) { if(m_size==0) return; ArrayResize(x1,m_size); //--- X1=x*P(x)-xm*P(xm) for(int i=0; i<m_size; i++) x1[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0]; } //+------------------------------------------------------------------+ //| CalcX2 | //+------------------------------------------------------------------+ void CECCalculator::CalcX2(double &x2[]) { if(m_size==0) return; ArrayResize(x2,m_size); //--- X2=Integrate(P1(x)) for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,m_y,i); }
이 경우 상관 행렬의 크기는 2*3입니다. P1(x) 함수의 a와 θ값은 계수 С1 및 C2를 기반으로 산출됩니다. 매개 변수 B의 수치값은 정규화를 통해 얻어집니다.
아래는 인터벌 x [0,10]를 갖는 모델 함수 P1(x,1,0.5,2)의 연산 결과입니다. 사용된 포인트 개수는 1000개입니다.
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) theta=1.986651299600245 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) a=0.5056083906174813 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C1=-0.5056083906174813 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C2=-0.4988591756915261 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 1 0.15420524 0.48808959 -0.32145543 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 2 0.48808959 1.79668322 -1.14307410그림 17~20은 P1(x) 함수 및 그 고유값 좌표 전개를 나타냅니다.
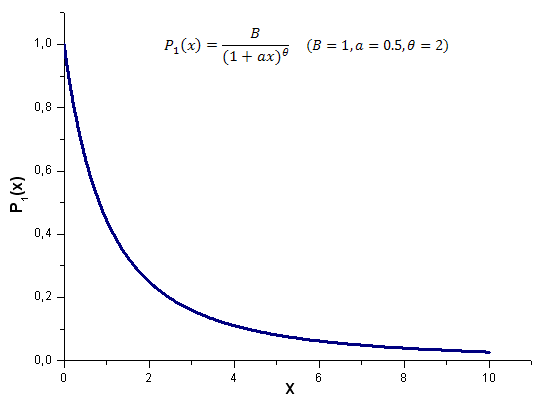
그림 17. 연산용 함수 모델 P1(x, 1, 0.5, 2), 1000 포인트
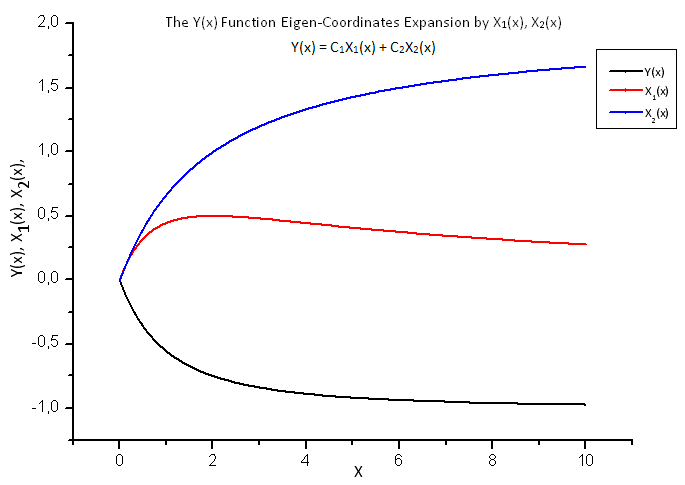
그림 18. Y(x) 함수와 고유값 좌표계 X1(x), X2(x)의 일반형
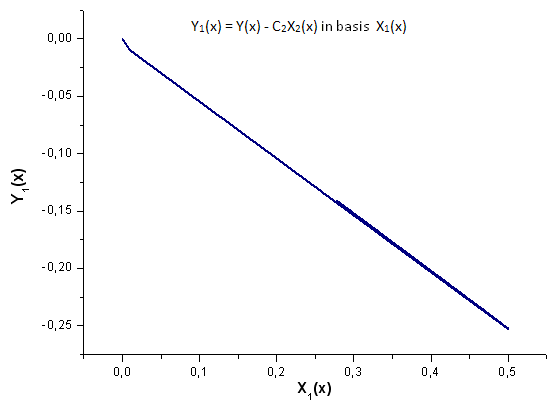
그림 19. 기저함수 X1(x)를 갖는 Y1(x)의 함수식
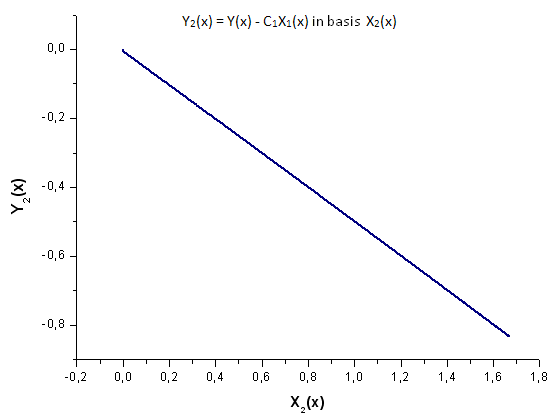
그림 20. 기저함수 X2(x)를 갖는 Y2(x)의 함수식
그림 19를 자세히 살펴볼게요. 차트 시작 지점과 2/3 지점에서 선형 종속성의 왜곡이 약간 일어납니다.
- X1(x)이 미분적 특성을 띠지 않기 때문입니다.
3.2. P2(x) 함수 고유값 좌표 전개
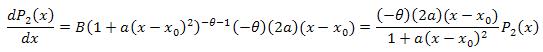
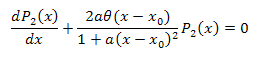
미분방정식
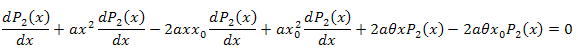
인터벌 [xm,x]를 갖는 x에 대해 적분합니다.
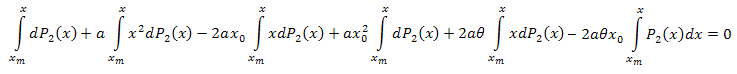
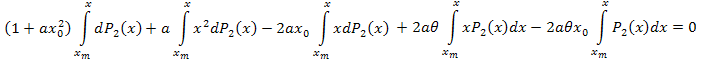
다음의 결과가 나옵니다.
단순화합니다.
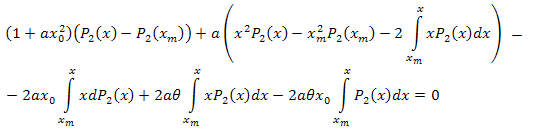
다음의 결과가 나옵니다.
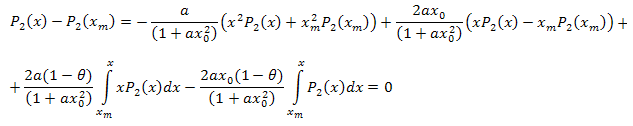
따라서 다음과 같이 전개됩니다.
읽는 법
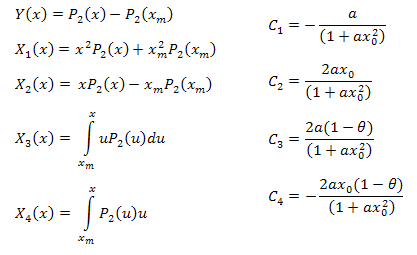
아래 공식을 이용해 함수의 변수를 구할 수 있습니다.
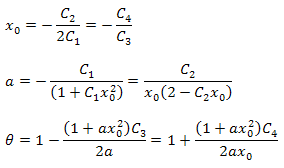
전개 결과 매개 변수 사이에 추가 관계가 생김을 알 수 있습니다. 이를 이용해 분석에 선택된 함수의 정확성을 확인할 수 있죠. P2(x) 함수에만 해당하는 데이터의 경우 늘 이런 관계가 관찰되죠.
매개 변수 B의 수치값은 정규화를 통해 얻어집니다.
고유값 좌표 연산에 필요한 함수는 다음과 같습니다(EC_Example3.mq5).
//+------------------------------------------------------------------+ //| CalcY | //+------------------------------------------------------------------+ void CECCalculator::CalcY(double &y[]) { if(m_size==0) return; ArrayResize(y,m_size); for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0]; }; //+------------------------------------------------------------------+ //| CalcX1 | //+------------------------------------------------------------------+ void CECCalculator::CalcX1(double &x1[]) { if(m_size==0) return; ArrayResize(x1,m_size); //--- X1=(x^2)*P2(x)+(xm)^2*P2(xm) for(int i=0; i<m_size; i++) x1[i]=(m_x[i]*m_x[i])*m_y[i]+(m_x[0]*m_x[0])*m_y[0]; } //+------------------------------------------------------------------+ //| CalcX2 | //+------------------------------------------------------------------+ void CECCalculator::CalcX2(double &x2[]) { if(m_size==0) return; ArrayResize(x2,m_size); //--- X2=(x)*P2(x)-(xm)*P2(xm) for(int i=0; i<m_size; i++) x2[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0]; } //+------------------------------------------------------------------+ //| CalcX3 | //+------------------------------------------------------------------+ void CECCalculator::CalcX3(double &x3[]) { if(m_size==0) return; double tmp[]; ArrayResize(tmp,m_size); for(int i=0; i<m_size; i++) tmp[i]=m_x[i]*m_y[i]; //--- X3=Integrate(X*P2(x)) ArrayResize(x3,m_size); for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i); } //+------------------------------------------------------------------+ //| CalcX4 | //+------------------------------------------------------------------+ void CECCalculator::CalcX4(double &x4[]) { if(m_size==0) return; //--- X4=Integrate(P2(x)) ArrayResize(x4,m_size); for(int i=0; i<m_size; i++) x4[i]=Integrate(m_x,m_y,i); }
아래는 P2(x) 모델 함수의 연산 결과입니다(B=1, a=0.5, theta=2, x0=1). 사용된 포인트 개수는 1000개입니다.
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: theta=2.260782711057654 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: theta=2.076195813531546 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: a=0.4557937139014854 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: a=0.4977821155774935 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: x0=1.043759816231049 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: x0=0.8909465007003451 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C1=-0.3567992171618368 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C2=0.6357780279659221 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C3=-0.7679716475618039 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C4=0.8015779457297644 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1 1.11765877 0.60684314 1.34789126 1.28971267 -0.01429928 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2 0.60684314 0.37995888 0.55974145 0.58899739 0.06731011 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 3 1.34789126 0.55974145 3.00225771 2.54531927 -0.39043224 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 4 1.28971267 0.58899739 2.54531927 2.20595917 -0.27218168그림 21~26은 함수 P2(x) 및 그 고유값 좌표 전개를 나타냅니다.
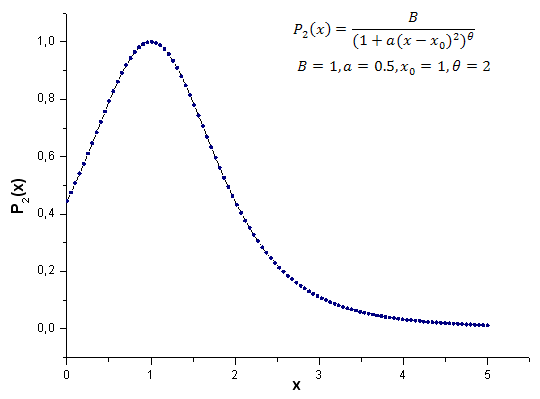
그림 21. 연산용 함수 모델 P2(x,1,0.5,2,1), 100 포인트
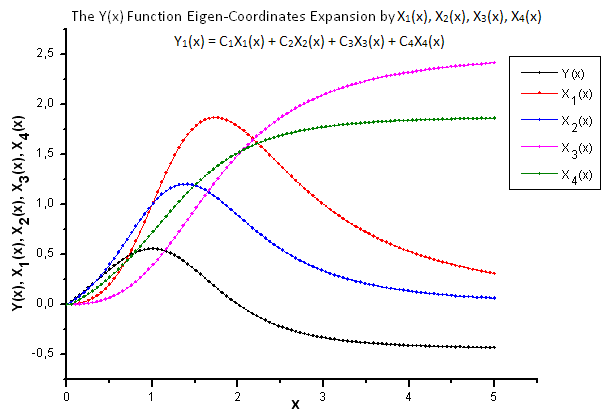
그림 22. Y(x) 함수와 고유값 좌표계 X1(x), X2(x), X3(x), X4(x)의 일반형
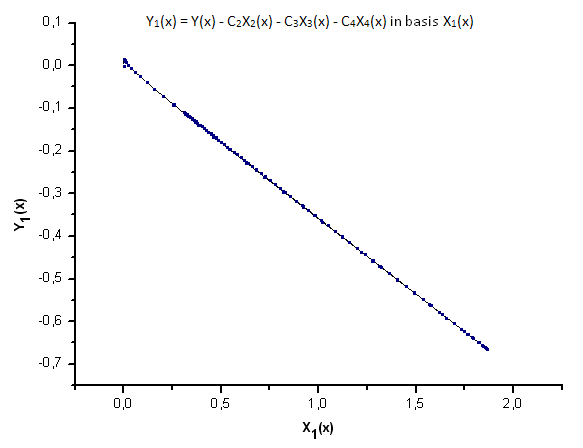
그림 23. 기저함수 X1(x)를 갖는 Y1(x)의 함수식
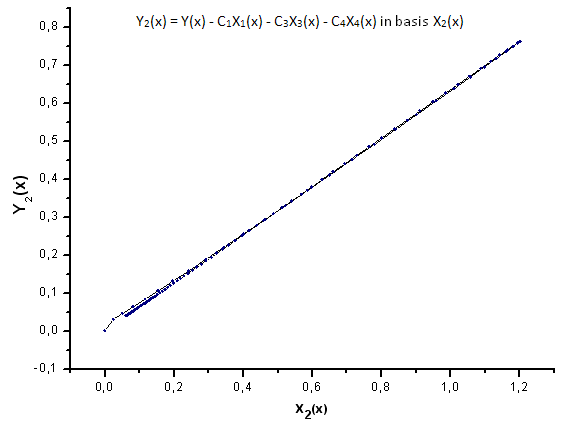
그림 24. 기저함수 X2(x)를 갖는 Y2(x)의 함수식
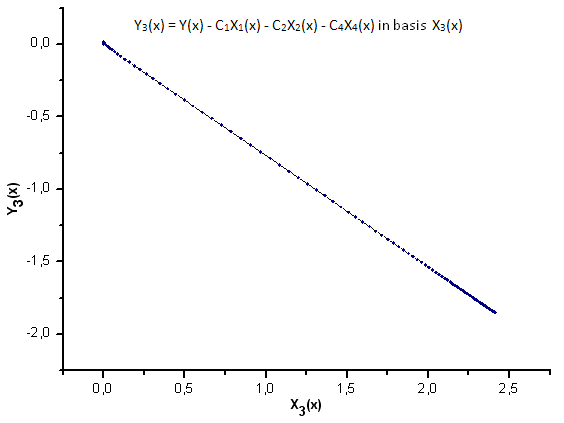
그림 25. 기저함수 X3(x)를 갖는 Y3(x)의 함수식
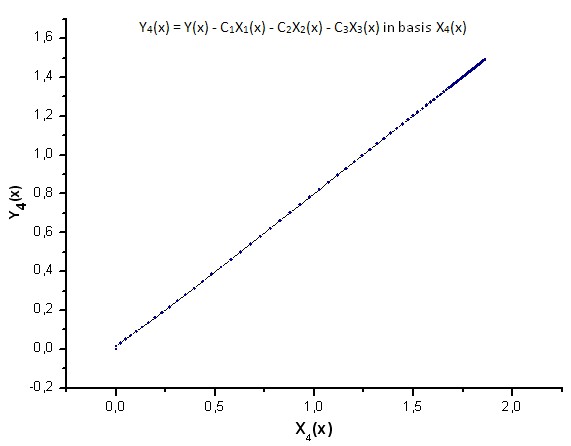
그림 26. 기저함수 X4(x)를 갖는 Y4(x)의 함수식
4. 고양이처럼 보이면... 고양이가 아닐지도 몰라요
가우스 q 계열의 분포는 일반화된 통계역학의 중심에 위치하므로 일반화된 중심 극한 정리에서도 관찰될 것으로 충분히 예상 가능합니다. 엔트로피 개념이 논거로 이용됐죠[26].
하지만 참고 자료 [18, presentation]에서 가우스 q 계열의 분포가 보편적이지 않음이 증명됐습니다. 따라서 극한 분포로서의 역할에 대한 의구심을 일으켰죠.
다음의 함수를 예로 들어 보겠습니다.
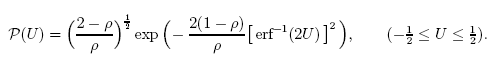
가우스-q 분포를 이용해 매우 정확하게 설명할 수 있습니다.
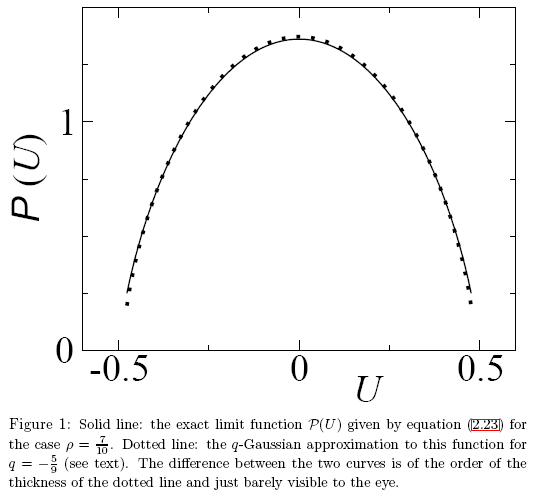
그림 27. 'A Note on q-Gaussians and Non-Gaussians in Statistical Mechanics' 발췌 예시
분석적으로 다른 함수지만 수치 값이 유사하므로 겉으로는 그 차이가 판단되지 않습니다. 정확한 함수 식별 방법이 필요하죠. 고유값 좌표계를 이용하면 이런 문제를 해결할 수 있는데요.
P(U) 함수 고유값 좌표 전개를 예로 들어 가우스 q-분포와의 차이점을 알아보겠습니다. 그냥 보기에는 매우 유사한 함수처럼 보입니다(그림 27).
시그널(P(U) 함수 값 100개)을 생성하고 앞서 3.2에서 그린 P2(x) 함수의 고유값 좌표 시스템에 '투영'해 보겠습니다.
Hilhorst-Schehr-problem.mq5 스크립트가 P(U) 함수를 계산하여 MQL5\Files\test-data.csv 파일에 데이터 세트를 생성합니다. 해당 데이터는 EC_Example3_Test.mq5로 분석됩니다.
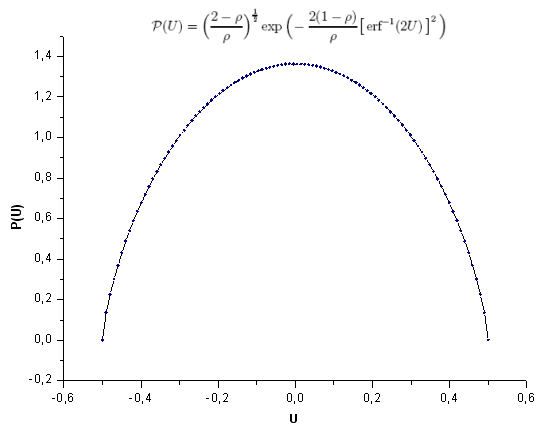
그림 28. 함수 모델 P(U), 100 포인트
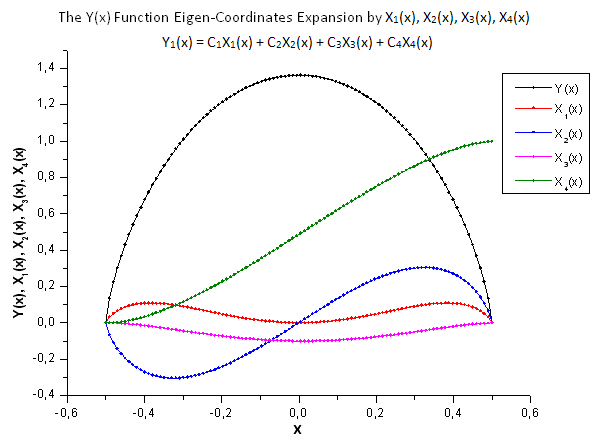
그림 29. Y(x) 함수와 고유값 좌표계 X1(x), X2(x), X3(x), X4(x)의 일반형
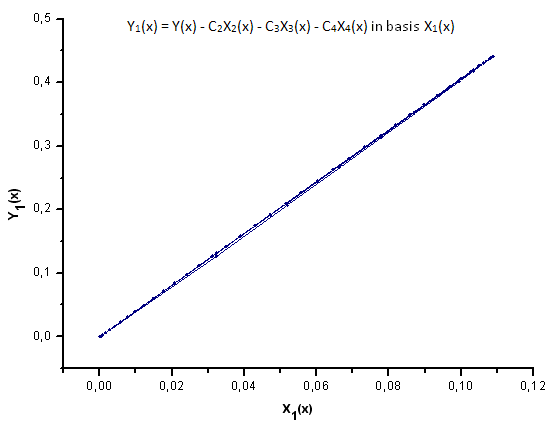
그림 30. 기저함수 X1(x)를 갖는 Y1(x)의 함수식
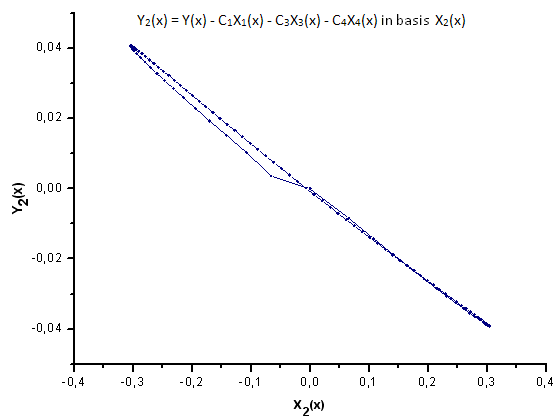
그림 31. 기저함수 X2(x)를 갖는 Y2(x)의 함수식
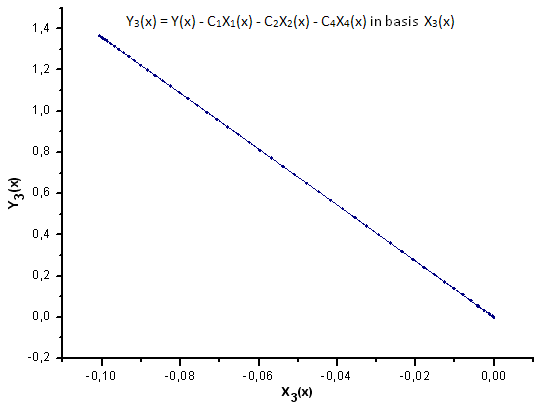
그림 32. 기저함수 X3(x)를 갖는 Y3(x)의 함수식
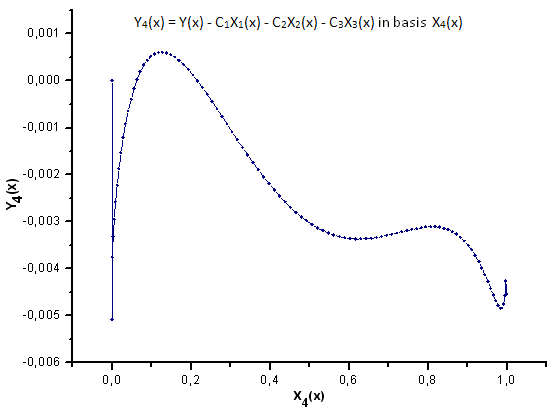
그림 33. 기저함수 X4(x)를 갖는 Y4(x)의 함수식
그림 30~33에서 확인 가능하듯 P2(x)와 P(U) 함수는 X1(x), X2(x) 및 X3(x) 좌표를 갖는 다는 점에서 매우 유사합니다. Xi(x)와 Yi(x) 사이의 선형 종속성을 확인할 수 있죠. 하지만 X4(x) 컴포넌트에서 큰 차이가 발생합니다(그림 33).
X4(x) 컴포넌트에 대한 선형 종속성의 부재가 P(U) 함수로 생성된 데이터 세트가 가우스 q-분포에 해당하지 않음을 증명합니다. 겉으로는 비슷하게 보여도 말이죠.
Xi(x)와 Yi(x)를 한번에 그려 다른 시점을 적용해 보겠습니다(그림 34~37).
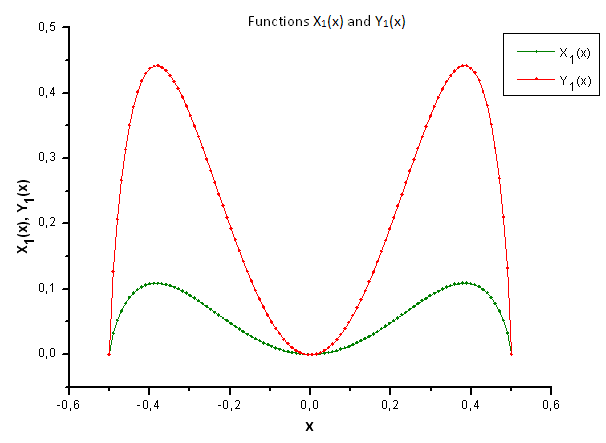
그림 34. X1(x) 함수와 Y1(x) 함수의 일반형
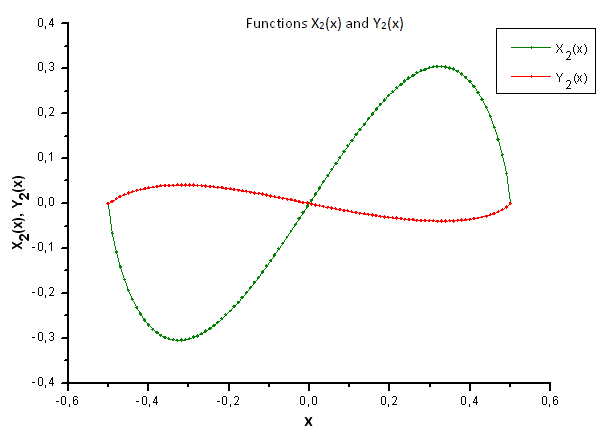
그림 35. X2(x) 함수와 Y2(x) 함수의 일반형
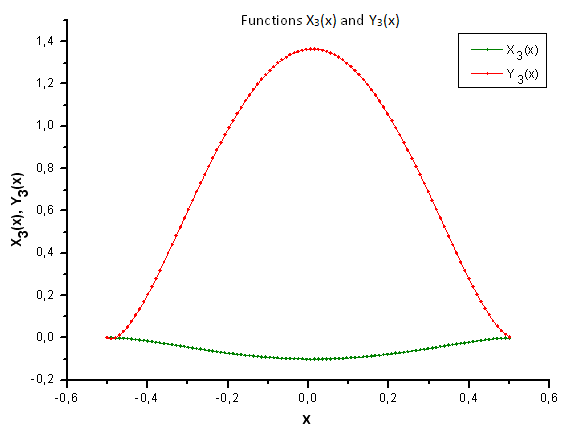
그림 36. X3(x) 함수와 Y3(x) 함수의 일반형
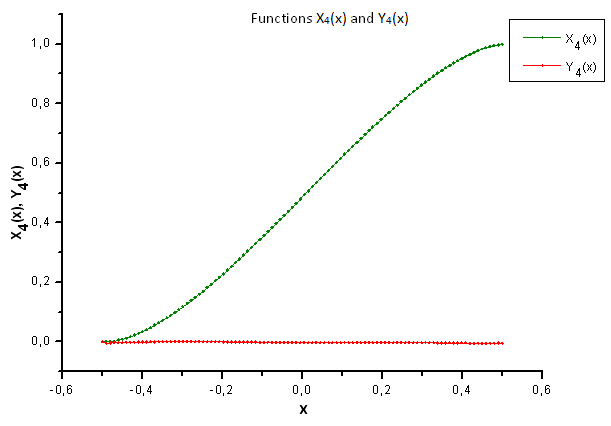
그림 37. X4(x) 함수와 Y4(x) 함수의 일반형
그림 37에서 확인 가능하듯 P2(x) 함수의 고유값 좌표에 P(U) 함수가 생성된 데이터를 투영하면 X4(x) 컴포넌트의 구조적 차이가 뚜렷하게 나타납니다. 따라서 실험 데이터가 P2(x) 함수와 일치하지 않음이 증명됩니다.
아래의 연산 결과 또한 이를 뒷받침하죠(EC_Example3_test).
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: theta=1.034054797050629 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: theta=-0.6736146397139184 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: a=199.3574440289263 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: a=-4.052181367572913 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: x0=-0.0003278538628371299 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: x0=0.0161122975924721 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C1=4.056448634458822 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C2=-0.1307174151339552 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C3=-13.57786363975563 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C4=-0.004451555043369697 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1 0.00465975 0.00000000 -0.00218260 0.02762761 0.04841405 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2 0.00000000 0.04841405 -0.00048835 0.06788438 0.00000001 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 3 -0.00218260 -0.00048835 0.00436149 -0.02811625 -0.06788437 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 4 0.02762761 0.06788438 -0.02811625 0.35379820 0.48337994
매개 변수 간의 관계 또한 약해졌습니다.
결론
고유값 좌표계는 함수 간 구조적 특성을 분석해 데이터 분석 및 해석을 간단하게 해주는 독특한 도구입니다.
실험 데이터 세트 {xi,yi}를 이용해 제안된 모델에 상응하는 새로운 함수를 만드는 게 핵심이죠. 연산자 전개 형식은 데이터 정의 '후보'로 쓰이는 함수 값을 갖는 미분방정식 구조에 의해 설정됩니다. 네이티브 함수의 경우 {xi,yi} 데이터를 이용해 연산된 함수는 선형으로 나타납니다. '후보 함수'의 고유값 좌표를 기반으로 한 선형의 편차는 {xi,yi} 데이터가 주어진 함수로 생성될 수 없으며 따라서 해당 모델이 부적합함을 나타냅니다.
몇몇 복잡한 경우에서는 네이티브 함수와 후보 함수가 매우 유사하게 나타나며 연산 결과의 대부분이 선형을 띠기도 합니다. 하지만 고유값 좌표계를 이용하면 함수 간의 차이를 식별할 수 있습니다. 선형성이 약화되기 때문이죠. Hilhorst와 Schehr의 예시가 X4(x) 함수를 투영하는 경우를 잘 설명했죠.
이는 P2(x) 함수 값을 갖는 미분방정식을 다룰 때에도 유용하게 쓰입니다. P2(x) 함수의 선형 부분에서 문제를 확인 가능하죠. 실험 데이터의 현상학적 설명에는 큰 도움이 되지 않을 수 있겠네요. 하지만 미분방정식을 기반으로 하는 모델의 경우(그림 3), 모델의 물리적 프로세스에 포함된 각 매커니즘의 역할을 이해하는 데에 도움이 될 겁니다.
참고 자료
- C. Tsallis, "Possible Generalization of Boltzmann-Gibbs Statistics", Journal of Statistical Physics, Vol. 52, Nos. 1/2, 1988.
- C. Tsallis, "Nonextensive Statistics: Theoretical, Experimental and Computational Evidences and Connections". Brazilian Journal of Physics, (1999) vol. 29. p.1.
- C. Tsallis, "Some Comments on Boltzmann-Gibbs Statistical Mechanics", Chaos, Solitons & Fractals Volume 6, 1995, pp. 539–559.
- Europhysics News "Special Issue: Nonextensive Statistical Mechanics: New Trends, New Perspectives", Vol. 36 No. 6 (November-December 2005).
- M. Gell-Mann, C. Tsallis, "Nonextensive Entropy: Interdisciplinary Applications", Oxford University Press, 15.04.2004, 422 p.
- Constantino Tsallis, the Official Website Nonextensive Statistical Mechanics and Thermodynamics.
- Chumak, O.V. "Entropy and Fractals in Data Analysis", М.-Izhevsk: RDC "Regular and Chaotic Dynamics", Institute for Computer Research, 2011. - 164 p.
- Qiuping A. Wang, "Incomplete Statistics and Nonextensive Generalizations of Statistical Mechanics", Chaos, Solitons and Fractals, 12(2001)1431-1437.
- Qiuping A. Wang, "Extensive Generalization of Statistical Mechanics Based on Incomplete Information Theory", Entropy, 5(2003).
- Lisa Borland, "Long-Range Memory and Nonextensivity in Financial Markets", Europhysics News 36, 228-231 (2005)
- T. S. Biró, R. Rosenfeld, "Microscopic Origin of Non-Gaussian Distributions of Financial Returns", Physica A: Statistical Mechanics and its Applications, Vol. 387, Nr. 7 (Mar 1, 2008) , p. 1603-1612 (preprint).
- S. M. D. Queiros, C. Anteneodo, C. Tsallis, "Power-Law Distributions in Economics: A Nonextensive Statistical Approach", Proceedings of SPIE (2005) Volume: 5848, Publisher: SPIE, Pages: 151-164, (preprint)
- R Hanel, S Thurner, "Derivation of Power-Law Distributions within Standard Statistical Mechanics", Physica A: Statistical Mechanics and its Applications (2005), Volume: 351, Issue: 2-4, Publisher: Elsevier, Pages: 260-268. (preprint)
- A K Rajagopal, Sumiyoshi Abe, "Statistical Mechanical Foundations of Power-Law Distributions", Physica D: Nonlinear Phenomena (2003), Volume: 193, Issue: 1-4, Pages: 19 (preprint)
- T. Kaizoji, "An Interacting-Agent Model of Financial Markets from the Viewpoint of Nonextensive Statistical Mechanics", Physica A: Statistical Mechanics and its Applications, Vol. 370, N. 1 (Oct 1, 2006) , p. 109-113. (preprint)
- V. Gontis, J. Ruseckas, A. Kononovičius, "A Long-Range Memory Stochastic Model of the Return in Financial Markets", Physica A: Statistical Mechanics and its Applications 389 (2010) 100-106. (preprint)
- H.E. Roman, M. Porto, "Self-Generated Power-Law Tails in Probability Distributions", Physical Review E - Statistical, Nonlinear and Soft Matter Physics (2001), Volume: 63, Issue: 3 Pt 2, Pages: 036-128.
- H. J. Hilhorst, G. Schehr, "A Note on q-Gaussians and Non-Gaussians in Statistical Mechanics" (2007, preprint, presentation).
- D. J. Hudson, "Lectures on Elementary Statistics and Probability", CERN-63-29, Geneva : CERN, 1963. - 101 p.
- D. J. Hudson, "Statistics Lectures II : Maximum Likelihood and Least Squares Theory", CERN-64-18. - Geneva : CERN, 1964. - 115 p.
- R. R. Nigmatullin, "Eigen-Coordinates: New Method of Analytical Functions Identification in Experimental Measurements", Applied Magnetic Resonance Volume 14, Number 4 (1998), 601-633.
- R.R. Nigmatullin, "Recognition of Nonextensive Statistical Distributions by the Eigencoordinates Method", Physica A: Statistical Mechanics and its Applications Volume 285, Issues 3–4, 1 October 2000, pp. 547–565.
- C. Antonini "q-Gaussians in Finance" (2010).
- C. Antonini, "The Use of the q-Gaussian Distribution in Finance" (2011).
- L. G. Moyano, C. Tsallis, M. Gell-Mann, "Numerical Indications of a q-Generalised Central Limit Theorem", Europhysics Letters 73, 813-819, 2006, (preprint).
- T. Dauxois, "Non-Gaussian Distributions under Scrutiny", J. Stat. Mech. (2007) N08001. (preprint)
부록 가우스 q-분포를 이용한 S&P 500 일간 수익률 분석
S&P 500 일간 수익률 분석(P2(x) 함수)에 대한 전형적인 가우스 q-분포 접근법의 예시를 살펴보겠습니다(그림 4).
http://wikiposit.org/w?filter=Finance/Futures/Indices/S__and__P%20500/에서 제공되는 일간 데이터를 이용했습니다.
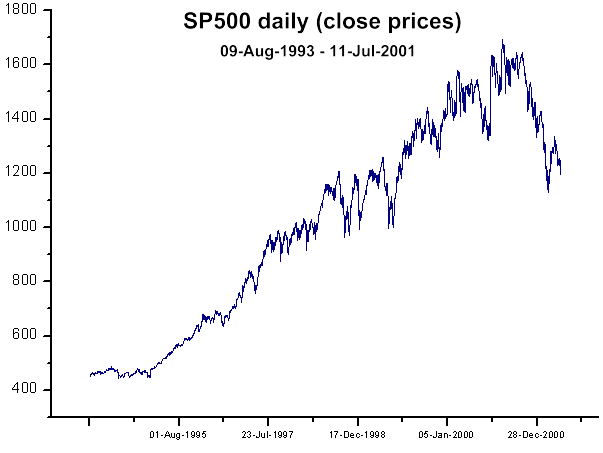
그림 38. S&P 500 일간 종가
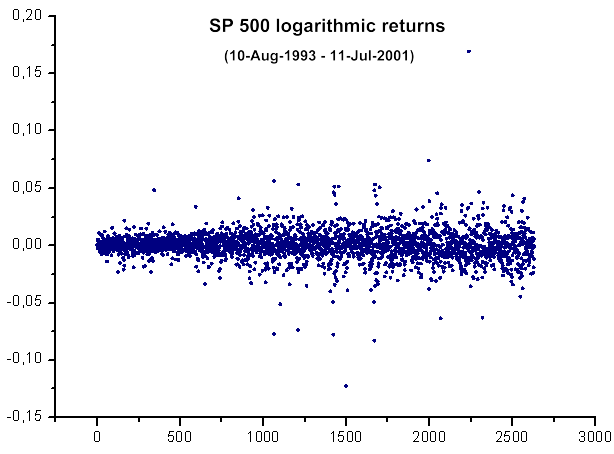
그림 39. S&P 500 로그 수익률
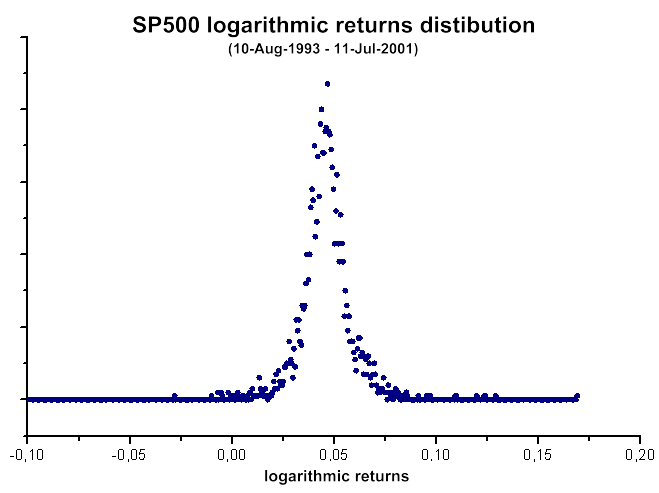
그림 40. S&P 500 로그 수익률 분포
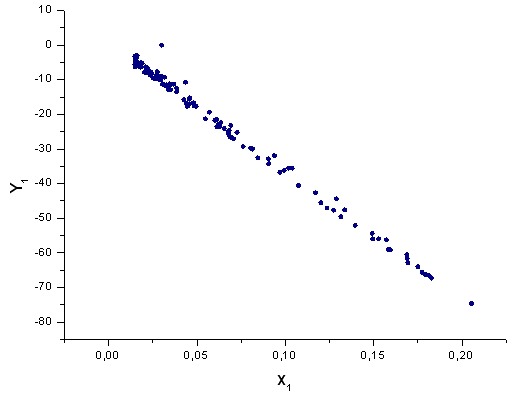
그림 41. 기저함수 X1(x)를 갖는 Y1(x)의 함수식
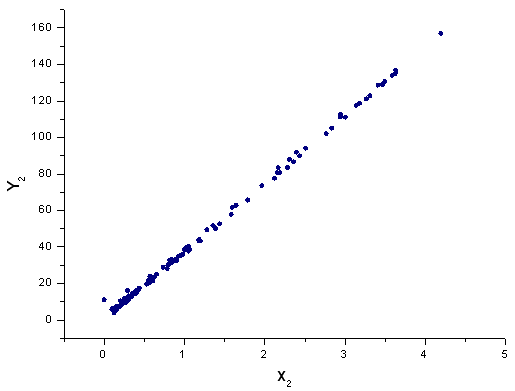
그림 42. 기저함수 X2(x)를 갖는 Y2(x)의 함수식
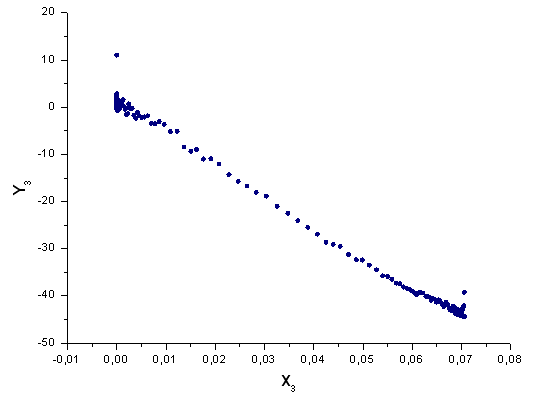
그림 43. 기저함수 X3(x)를 갖는 Y3(x)의 함수식
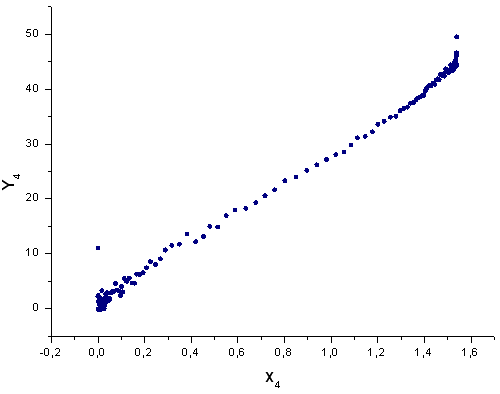
그림 44. 기저함수 X4(x)를 갖는 Y4(x)의 함수식
터미널에서 분석을 실행에 앞서 우선 SP500-data.csv 파일을 \Files\ 폴더에 위치시킵니다.
그 다음 다음의 두 스크립트를 실행합니다.
- CalcDistr_SP500.mq5(분포 계산)
- q-gaussian-SP500.mq5(고유값 좌표 분석)
2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 2: theta=1.770125768485269 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 1: theta=1.864132228192338 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 2: a=2798.166930885822 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 1: a=8676.207867097581 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 2: x0=0.04567518783335043 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 1: x0=0.0512505923716428 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) C1=-364.7131366394939 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) C2=37.38352859698793 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) C3=-630.3207508306047 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) C4=28.79001868944634 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 1 0.00177913 0.03169294 0.00089521 0.02099064 0.57597695 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 2 0.03169294 0.59791579 0.01177430 0.28437712 11.55900584 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 3 0.00089521 0.01177430 0.00193200 0.04269286 0.12501732 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 4 0.02099064 0.28437712 0.04269286 0.94465120 3.26179090 2012.06.29 20:01:09 CalcDistr_SP500 (EURUSD,D1) checking distibution cnt=2632.0 n=2632 2012.06.29 20:01:09 CalcDistr_SP500 (EURUSD,D1) Min=-0.1229089015984444 Max=0.1690557338964631 range=0.2919646354949075 size=2632 2012.06.29 20:01:09 CalcDistr_SP500 (EURUSD,D1) Total data=2633
고유값 좌표를 이용하여 산출된 q 예측값(q=1+1/theta): q~1,55
실제 보고된 값(그림 4): q~1.4
결론: 일반적으로 가우스-q 함수를 이용하여 위의 데이터를 설명할 수 있습니다. 문헌에서 확인할 수 있는 가우스 q-분포를 이용한 성공적인 자료 해석의 예입니다.
MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/412
경험적 모드 분해법의 기초
알고리즘 트레이딩 기사를 작성하고 200달러를 받으세요!
MetaTrader 모바일 터미널의 MetaQuotes ID
미지의 확률 밀도 함수에 대한 커널 밀도 추정
