MetaTrader 5 / Experts
English Русский 中文 Español Deutsch 日本語 Português 한국어 Français Türkçe
Applicazione del metodo delle auto-coordinate all'analisi strutturale di distribuzioni statistiche non estensive

Applicazione del metodo delle auto-coordinate all'analisi strutturale di distribuzioni statistiche non estensive

MetaTrader 5 — Experts | 11 gennaio 2022, 15:30
94 0
MetaQuotes
MetaQuotes

Contenuti


Introduzione

Nel 1988, Constantino Tsallis ha proposto la generalizzazione della meccanica statistica di Boltzmann-Gibbs-Shannon [1], dove ha presentato una nozione di entropia non estensiva.

Un'importante conseguenza della generalizzazione dell'entropia sembra essere l'esistenza di nuovi tipi di distribuzione [2] che giocano un ruolo chiave nella nuova meccanica statistica (Q-Esponenziale e Q-gaussiana):

distribuzioni statistiche non estensive

È stato scoperto che questi tipi di distribuzione possono essere utilizzati per descrivere una buona quantità di dati sperimentali in sistemi con memoria a lungo raggio, sistemi con forze a lungo raggio e sistemi fortemente correlati.

L'entropia è strettamente correlata all'informazione [7]. La generalizzazione della meccanica statistica basata sulla teoria dell'informazione è stata presentata in [8-9]. La nuova meccanica statistica non estensiva si è dimostrata molto utile per l'econometria [10-17]. Ad esempio, la distribuzione Q-Gaussiana descrive bene le ampie ali (code) delle distribuzioni degli incrementi delle quotazioni degli strumenti finanziari (q~1.5). Detto questo, la maggior parte delle distribuzioni di incrementi di serie temporali finanziarie si trasformano in distribuzioni normali (q=1) a scale più grandi (mesi, anni) [10].

Ci si aspettava naturalmente che tale generalizzazione della meccanica statistica risultasse in un analogo del teorema del limite centrale per le distribuzioni q-gaussiane. Ma questo si è dimostrato sbagliato in [18]: la distribuzione limite della somma di variabili casuali fortemente correlate è analiticamente diversa dalle q-gaussiane.

Si è presentato però un problema di altro tipo: è risultato che i valori numerici della soluzione esatta trovata erano molto vicini alla Q-gaussiana ("numericamente simile, analiticamente diverso"). Per analizzare le differenze tra le funzioni e ottenere i migliori parametri della distribuzione Q-gaussiana, è stato utilizzato uno sviluppo in serie in [18]. Le relazioni di queste funzioni hanno portato all'espansione di potenza nel parametro q che caratterizza il grado di non estensività del sistema.

Il problema principale delle statistiche applicate è il problema di accettare ipotesi statistiche. È stato a lungo considerato impossibile da risolvere [19-20], richiedendo uno strumento speciale (qualcosa come un microscopio elettronico) che permettesse di vedere più di ciò che è possibile usando i metodi della moderna statistica applicata.

Il metodo delle auto-coordinate introdotto in [21] ci permette di raggiungere un livello più profondo: l'analisi delle proprietà strutturali delle relazioni funzionali. Questo metodo molto buono può essere utilizzato per risolvere una varietà di problemi. Le espansioni di operatori di funzioni corrispondenti alle suddette distribuzioni non estensive sono state dimostrate in [22].

Questo articolo tratterà il metodo delle auto-coordinate ed esempi del suo uso pratico. Contiene molte formule che sono di grande importanza per comprendere l'essenza del metodo. Dopo aver ripetuto tutti i calcoli, sarai in grado di tracciare autonomamente le espansioni delle funzioni per le funzioni di interesse.

1. Q-gaussiane in econometria

La distribuzione Q-gaussiana gioca un ruolo molto importante in econometria [4,10-17].

Per avere una comprensione generale dell'attuale livello di ricerca, si può fare riferimento ai lavori del Dr. Claudio Antonini "q-Gaussians in Finance" [23] e "The Use of the q-Gaussian Distribution in Finance" [24].

Descriviamo brevemente i principali risultati.

Fig.1. Metodologia scientifica (Slide 4 "The Use of the q-Gaussian Distribution in Finance")

Fig.1. Metodologia scientifica (Slide 4 "The Use of the q-Gaussian Distribution in Finance")

I principali dettagli delle serie temporali finanziarie sono riportati nella Fig.2:

Fig.2. Proprietà delle serie cronologiche finanziarie (Slide 3 "The Use of the q-Gaussian Distribution in Finance")

Fig.2. Proprietà delle serie cronologiche finanziarie (Slide 3 "The Use of the q-Gaussian Distribution in Finance")

Molti modelli teorici utilizzati per descrivere le serie temporali finanziarie portano alla distribuzione Q-gaussiana:

Fig.3. Modelli teorici e Q-gaussiana (Slide 27 "The Use of the q-Gaussian Distribution in Finance")

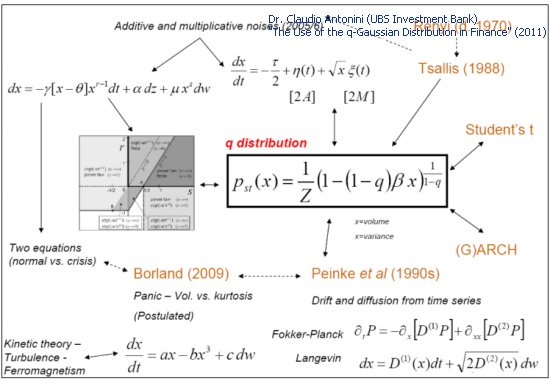
Fig.3. Modelli teorici e Q-gaussiana (Slide 27 "The Use of the q-Gaussian Distribution in Finance")

La distribuzione Q-gaussiana viene utilizzata anche per la descrizione fenomenologica delle distribuzioni delle virgolette:

Fig.4. Esempio di analisi dei rendimenti giornalieri dell'S&P 500 (Slide 8 "The Use of the q-Gaussian Distribution in Finance")

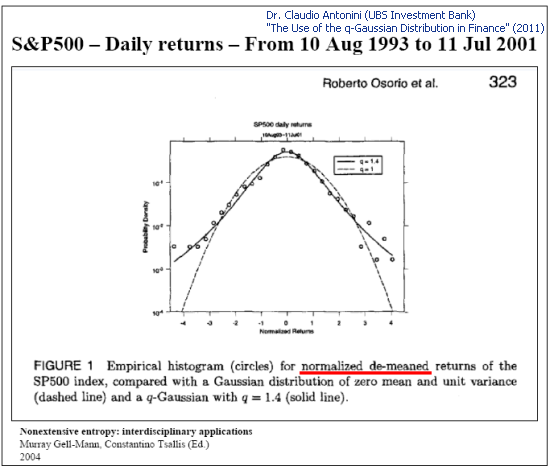
Fig.4. Esempio di analisi dei rendimenti giornalieri dell'S&P 500 (Slide 8 "The Use of the q-Gaussian Distribution in Finance")

Lavorare con dati reali pone un problema di identificazione delle funzioni:

Fig.5. Il problema dell'identificazione della funzione di distribuzione (Slide 14 "q-Gaussians in Finance")

Fig.5. Il problema dell'identificazione della funzione di distribuzione (Slide 14 "q-Gaussians in Finance")

Entrambi gli articoli del Dr. Claudio Antonini sottolineano l'importanza di una corretta individuazione delle funzioni per costruire modelli adeguati dei processi fisici:

Fig.6. Conclusioni tratte in "q-Gaussians in finance" e "The Use of the q-Gaussian Distribution in Finance" (Dr. Claudio Antonini, 2010, 2011)

Fig.6. Conclusioni tratte in "q-Gaussians in finance" e "The Use of the q-Gaussian Distribution in Finance" (Dr. Claudio Antonini, 2010, 2011)

Esempi di utilizzo delle statistiche q-gaussiane in finanza (fogli di lavoro + file MathCad):


2. Coordinate di Eigen

L'espansione in auto-coordinate è la seguente:

dove C1…CN sono le costanti e X1(t),..,XN(t) sono le "auto-coordinate".

Tali espansioni lineari sono molto convenienti e spesso utilizzate nell'analisi dei dati. Ad esempio, una funzione esponenziale su una scala logaritmica si trasforma in una retta (la sua pendenza può essere facilmente calcolata utilizzando la regressione lineare). Pertanto, non è necessaria un'ottimizzazione non lineare (fitting) per determinare i parametri della funzione.

La scala logaritmica sarà comunque di scarso aiuto quando si ha a che fare con funzioni più complesse (es. la somma di due esponenti) e la funzione non apparirà come una linea retta. Sarà necessaria un'ottimizzazione non lineare per determinare i coefficienti della funzione.

Ci sono casi in cui i dati sperimentali possono essere spiegati ugualmente bene usando diverse funzioni che corrispondono tutte a diversi modelli di processi fisici. Quale funzione scegliere? Quale fornirà un quadro più adeguato della realtà al di fuori dei dati sperimentali?

La corretta identificazione della funzione è fondamentale per l'analisi di sistemi complessi (es. serie temporali finanziarie): ogni distribuzione corrisponde a un determinato processo fisico e saremo in grado di comprendere meglio le dinamiche e le proprietà generali dei sistemi complessi avendo scelto un modello adeguato.

La statistica applicata [19, 20] afferma che non esiste alcun criterio che consenta di rifiutare un'ipotesi statistica errata. Il metodo delle auto-coordinate getta una luce completamente nuova su questo problema (accettazione dell'ipotesi).

La funzione utilizzata per la descrizione dei dati sperimentali può essere vista come una soluzione a una certa equazione differenziale. La sua forma determina la struttura dell'espansione in auto-coordinate.

Una caratteristica peculiare dell'espansione in auto-coordinate è che tutti i dati generati dalla funzione Y(t) sono di struttura lineare nella base in auto-coordinate X1(t)..XN(t) della funzione Y(t). I dati generati da qualsiasi altra funzione F(t) in questa base non appariranno più come una linea retta (appariranno lineari nella base in auto-coordinate della funzione F(t)).

Questo fatto permette di identificare con precisione le funzioni, facilitando così notevolmente il lavoro con ipotesi statistiche.


2.1. Il metodo delle auto-coordinate

Il concetto alla base del metodo è quello di costruire le auto-coordinate Xk(t) sotto forma di operatori basati sulla funzione Y(t).

Si può fare utilizzando l'analisi matematica per cui le auto-coordinate Xk(t) assumono la forma di convoluzioni integrali e l'espansione è determinata dalla struttura dell'equazione differenziale che è soddisfatta dalla funzione Y(t). Inoltre, un problema di determinazione dei coefficienti C1.. CN sorge.

Nell'espansione della base ortogonale (ad esempio quando si determinano i coefficienti della trasformata di Fourier), i coefficienti di espansione vengono calcolati proiettando il vettore sulla base e si ottiene il risultato desiderato grazie all'ortogonalità delle funzioni di base.

Questo non è adatto nel nostro caso in quanto non ci sono informazioni sull'ortogonalità di X1(t)… XN(t).


2.2. Calcolo dei coefficienti di espansione utilizzando il metodo dei minimi quadrati

I coefficienti Ck possono essere calcolati con il metodo dei minimi quadrati. Questo problema si riduce alla risoluzione di un sistema di equazioni lineari.

Supponi che:

Espansione in Coordinate Eigen

Praticamente, per ogni misurazione di c'è un errore:

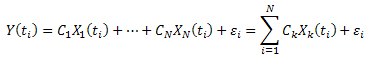
Riduci al minimo la somma delle deviazioni al quadrato:


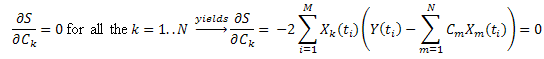
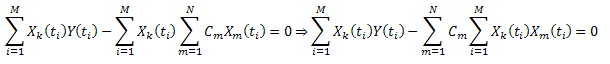
Introducendo la notazione: 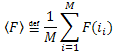media, può essere scritta come segue:

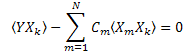
Quindi, otteniamo un sistema di equazioni lineari in C1...CN (k=1..N):

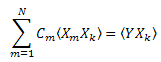
La matrice di "correlazione" è simmetrica: .

In alcuni casi, l'espansione in auto-coordinate può apparire più conveniente in forma integrale:

Consente di ridurre l'impatto degli errori (dovuti alla media) ma richiede calcoli aggiuntivi.


2.3. Un esempio dell'espansione della funzione R(x)

Diamo un'occhiata allo sviluppo in auto-coordinate della seguente funzione:

Questa funzione genera diverse distribuzioni statistiche [21]:

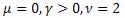  1. - la distribuzione normale (gaussiana);
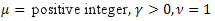  2. - la distribuzione di Poisson;
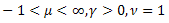  3. - la distribuzione gamma;
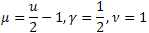  4. - la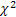 distribuzione;
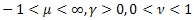  5. - La distribuzione di Schtauffer che include la distribuzione di Weibull come caso speciale.

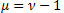Inoltre, è anche adatto per descrivere i processi di rilassamento:

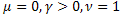  1. - la funzione esponenziale ordinaria;
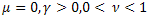  2. - la funzione esponenziale allungata;
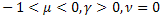  3. - la funzione di rilassamento del potere.

Avendo differenziato R(x) rispetto a x, abbiamo:


Moltiplica entrambi i membri per x:

Trasforma:

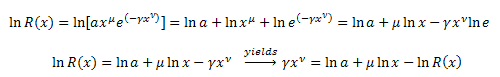
Sostituisci nell'equazione:

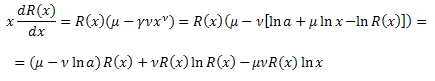
Otteniamo l'equazione differenziale per la funzione R(x):

Integra entrambi i membri rispetto a x sull'intervallo [xm,x]:


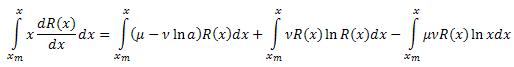
Integra il lato sinistro dell'equazione per parti:

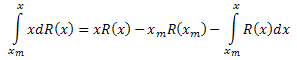
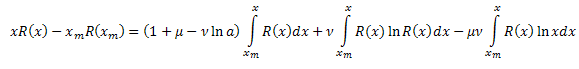
Di conseguenza, abbiamo:

dove:

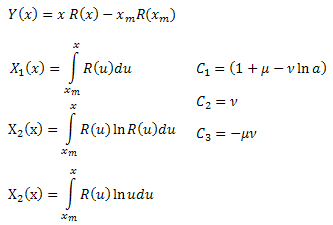
Calcolando i coefficienti, possiamo determinare i parametri della funzione. Il quarto parametro può essere derivato dalla formula per R(x).


2.4. Implementazione

Il calcolo dei coefficienti di dilatazione richiede la risoluzione del sistema di equazioni lineari. Per la comodità di lavorare con le matrici, può essere organizzato come una classe separata CMatrix (il file CMatrix.mqh). Utilizzando i metodi di questa classe, è possibile impostare i parametri della matrice, i valori degli elementi della matrice e risolvere il sistema di equazioni lineari utilizzando il metodo gaussiano.

//+------------------------------------------------------------------+
//| CMatrix class                                                    |
//+------------------------------------------------------------------+
class CMatrix
  {
   double            m_matrix[];
   int               m_rows;
   int               m_columns;
public:
   void              SetSize(int nrows,int ncolumns);
   double            Get(int i,int j);
   void              Set(int i,int j,double val);
   void              GaussSolve(double &v[]);
   void              Test();
  };

Diamo un esempio dello script (EC_Example1.mq5) che calcola le auto-coordinate ei parametri della funzione R(x).

//+------------------------------------------------------------------+
//|                                                  EC_Example1.mq5 |
//|                        Copyright 2012, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2012, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <CMatrix.mqh>
//+------------------------------------------------------------------+
//| CECCalculator                                                    |
//+------------------------------------------------------------------+
class CECCalculator
  {
protected:
   int               m_size;
   //--- x[i]
   double            m_x[];
   //--- y[i]
   double            m_y[];
   //--- matrix
   CMatrix           m_matrix;
   //--- Y[i]
   double            m_ec_y[];
   //--- eigen-coordinates X1[i],X2[i],X3[i]
   double            m_ec_x1[];
   double            m_ec_x2[];
   double            m_ec_x3[];
   //--- coefficients C1,C2,C3
   double            m_ec_coefs[];
   //--- function f1=Y-C2*X2-C3*X3
   double            m_f1[];
   //--- function f2=Y-C1*X1-C3*X3
   double            m_f2[];
   //--- function f3=Y-C1*X1-C2*X2
   double            m_f3[];
private:
   //--- function for data generation
   double            R(double x,double a,double mu,double gamma,double nu);
   //--- calculation of the integral
   double            Integrate(double &x[],double &y[],int ind);
   //--- calculation of the function Y(x)
   void              CalcY(double &y[]);
   //--- calculation of the function X1(x)
   void              CalcX1(double &x1[]);
   //--- calculation of the function X2(x)
   void              CalcX2(double &x2[]);
   //--- calculation of the function X3(x)
   void              CalcX3(double &x3[]);
   //--- calculation of the correlator
   double            Correlator(int ind1,int ind2);
public:
   //--- method for generating the test function data set x[i],y[i]
   void              GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu);
   //--- loading data from the file
   bool              LoadData(string filename);
   //--- saving data into the file
   bool              SaveData(string filename);
   //--- saving the calculation results
   void              SaveResults(string filename);
   //--- calculation of the eigen-coordinates
   void              CalcEigenCoordinates();
   //--- calculation of the linear expansion coefficients
   void              CalcEigenCoefficients();
   //--- calculation of the function parameters
   void              CalculateParameters();
   //--- calculation of the functions f1,f2,f3
   void              CalculatePlotFunctions();
  };
//+------------------------------------------------------------------+
//| Function R(x)                                                    |
//+------------------------------------------------------------------+
double CECCalculator::R(double x,double a,double mu,double gamma,double nu)
  {
   return(a*MathExp(mu*MathLog(MathAbs(x)))*MathExp(-gamma*MathExp(nu*MathLog(MathAbs(x)))));
  }
//+-----------------------------------------------------------------------+
//| Method for generating the data set x[i],y[i] of the test function R(x)|
//+-----------------------------------------------------------------------+
void CECCalculator::GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu)
  {
   if(size<=0) return;
   if(x1>=x2) return;
   m_size=size;
   ArrayResize(m_x,m_size);
   ArrayResize(m_y,m_size);
   double delta=(x2-x1)/(m_size-1);
//---
   for(int i=0; i<m_size; i++)
     {
      m_x[i]=x1+i*delta;
      m_y[i]=R(m_x[i],a,mu,gamma,nu);
     }
  };
//+------------------------------------------------------------------+
//| Method for loading data from the .CSV file                       |
//+------------------------------------------------------------------+
bool CECCalculator::LoadData(string filename)
  {
   int filehandle=FileOpen(filename,FILE_CSV|FILE_READ|FILE_ANSI,'\r');
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename,", error",GetLastError());
      return(false);
     }
   m_size=0;
   while(!FileIsEnding(filehandle))
     {
      string str=FileReadString(filehandle);
      if(str!="")
        {
         string astr[];
         StringSplit(str,';',astr);
         if(ArraySize(astr)==2)
           {
            ArrayResize(m_x,m_size+1);
            ArrayResize(m_y,m_size+1);
            m_x[m_size]=StringToDouble(astr[0]);
            m_y[m_size]=StringToDouble(astr[1]);
            m_size++;
           }
         else
           {
            m_size=0;
            return(false);
           }
        }
     }
   FileClose(filehandle);
   return(true);
  }
//+------------------------------------------------------------------+
//| Method for saving data into the .CSV file                        |
//+------------------------------------------------------------------+
bool CECCalculator::SaveData(string filename)
  {
   if(m_size==0) return(false);
   if(ArraySize(m_x)!=ArraySize(m_y)) return(false);
   if(ArraySize(m_x)==0) return(false);
   int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI,'\r');
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename,", error",GetLastError());
      return(false);
     }
   for(int i=0; i<ArraySize(m_x); i++)
     {
      string s=DoubleToString(m_x[i],8)+";";
      s+=DoubleToString(m_y[i],8)+";";
      s+="\r";
      FileWriteString(filehandle,s);
     }
   FileClose(filehandle);
   return(true);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the integral                       |
//+------------------------------------------------------------------+
double CECCalculator::Integrate(double &x[],double &y[],int ind)
  {
   double sum=0;
   for(int i=0; i<ind-1; i++) sum+=(x[i+1]-x[i])*(y[i+1]+y[i])*0.5;
   return(sum);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function Y(x)                  |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
   for(int i=0; i<m_size; i++) y[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the function X1(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
   for(int i=0; i<m_size; i++) x1[i]=Integrate(m_x,m_y,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function X2(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_y[i]));
   ArrayResize(x2,m_size);
   for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,tmp,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function X3(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX3(double &x3[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_x[i]));
   ArrayResize(x3,m_size);
   for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the eigen-coordinates              |
//+------------------------------------------------------------------+
void CECCalculator::CalcEigenCoordinates()
  {
   CalcY(m_ec_y);
   CalcX1(m_ec_x1);
   CalcX2(m_ec_x2);
   CalcX3(m_ec_x3);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the correlator                     |
//+------------------------------------------------------------------+
double CECCalculator::Correlator(int ind1,int ind2)
  {
   if(m_size==0) return(0);
   if(ind1<=0 || ind1>4) return(0);
   if(ind2<=0 || ind2>4) return(0);
//---
   double arr1[];
   double arr2[];
   ArrayResize(arr1,m_size);
   ArrayResize(arr2,m_size);
//---
   switch(ind1)
     {
      case 1: ArrayCopy(arr1,m_ec_x1,0,0,WHOLE_ARRAY); break;
      case 2: ArrayCopy(arr1,m_ec_x2,0,0,WHOLE_ARRAY); break;
      case 3: ArrayCopy(arr1,m_ec_x3,0,0,WHOLE_ARRAY); break;
      case 4: ArrayCopy(arr1,m_ec_y,0,0,WHOLE_ARRAY); break;
     }
   switch(ind2)
     {
      case 1: ArrayCopy(arr2,m_ec_x1,0,0,WHOLE_ARRAY); break;
      case 2: ArrayCopy(arr2,m_ec_x2,0,0,WHOLE_ARRAY); break;
      case 3: ArrayCopy(arr2,m_ec_x3,0,0,WHOLE_ARRAY); break;
      case 4: ArrayCopy(arr2,m_ec_y,0,0,WHOLE_ARRAY); break;
     }
//---
   double sum=0;
   for(int i=0; i<m_size; i++) { sum+=arr1[i]*arr2[i];  }
   sum=sum/m_size;
   return(sum);
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the linear expansion coefficients  |
//+------------------------------------------------------------------+
void CECCalculator::CalcEigenCoefficients()
  {
//--- setting the matrix size 3x4
   m_matrix.SetSize(3,4);
//--- calculation of the correlation matrix 
   for(int i=3; i>=1; i--)
     {
      string s="";
      for(int j=1; j<=4; j++)
        {
         double corr=Correlator(i,j);
         m_matrix.Set(i,j,corr);
         s=s+" "+DoubleToString(m_matrix.Get(i,j));
        }
      Print(i," ",s);
     }
//--- solving the system of the linear equations
   m_matrix.GaussSolve(m_ec_coefs);
//--- displaying the solution - the obtained coefficients C1,..CN 
   for(int i=ArraySize(m_ec_coefs)-1; i>=0; i--) Print("C",i+1,"=",m_ec_coefs[i]);
  };
//+--------------------------------------------------------------------+
//| Method for the calculation of the function parameters a,mu,nu,gamma|
//+--------------------------------------------------------------------+
void CECCalculator::CalculateParameters()
  {
   if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;}
//--- calculate a
   double a=MathExp((1-m_ec_coefs[0])/m_ec_coefs[1]-m_ec_coefs[2]/(m_ec_coefs[1]*m_ec_coefs[1]));
//--- calculate mu
   double mu=-m_ec_coefs[2]/m_ec_coefs[1];
//--- calculate nu
   double nu=m_ec_coefs[1];
//--- calculate gamma
   double arr1[],arr2[];
   ArrayResize(arr1,m_size);
   ArrayResize(arr2,m_size);
   double corr1=0;
   double corr2=0;
   for(int i=0; i<m_size; i++)
     {
      arr1[i]=MathPow(m_x[i],nu);
      arr2[i]=MathLog(MathAbs(m_y[i]))-MathLog(a)-mu*MathLog(m_x[i]);
      corr1+=arr1[i]*arr2[i];
      corr2+=arr1[i]*arr1[i];
     }
   double gamma=-corr1/corr2;
//---
   Print("a=",a);
   Print("mu=",mu);
   Print("nu=",nu);
   Print("gamma=",gamma);
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the functions                      |
//| f1=Y-C2*X2-C3*X3                                                 |
//| f2=Y-C1*X1-C3*X3                                                 |
//| f3=Y-C1*X1-C2*X2                                                 |
//+------------------------------------------------------------------+
void CECCalculator::CalculatePlotFunctions()
  {
   if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;}
//---
   ArrayResize(m_f1,m_size);
   ArrayResize(m_f2,m_size);
   ArrayResize(m_f3,m_size);
//---
   for(int i=0; i<m_size; i++)
     {
      //--- plot function f1=Y-C2*X2-C3*X3
      m_f1[i]=m_ec_y[i]-m_ec_coefs[1]*m_ec_x2[i]-m_ec_coefs[2]*m_ec_x3[i];
      //--- plot function f2=Y-C1*X1-C3*X3
      m_f2[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[2]*m_ec_x3[i];
      //--- plot function f3=Y-C1*X1-C2*X2
      m_f3[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[1]*m_ec_x2[i];
     }
  }
//+------------------------------------------------------------------+
//| Method for saving the calculation results                        |
//+------------------------------------------------------------------+
void CECCalculator::SaveResults(string filename)
  {
   if(m_size==0) return;
   int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI);
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename," for writing, error",GetLastError());
      return;
     }
   for(int i=0; i<m_size; i++)
     {
      string s=DoubleToString(m_x[i],8)+";";
      s+=DoubleToString(m_y[i],8)+";";
      s+=DoubleToString(m_ec_y[i],8)+";";
      s+=DoubleToString(m_ec_x1[i],8)+";";
      s+=DoubleToString(m_f1[i],8)+";";
      s+=DoubleToString(m_ec_x2[i],8)+";";
      s+=DoubleToString(m_f2[i],8)+";";
      s+=DoubleToString(m_ec_x3[i],8)+";";
      s+=DoubleToString(m_f3[i],8)+";";
      s+="\r";
      FileWriteString(filehandle,s);
     }
   FileClose(filehandle);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CECCalculator ec;
//--- model function data preparation
   ec.GenerateData(100,0.25,15.25,1.55,1.05,0.15,1.3);
//--- saving into the file
   ec.SaveData("ex1.csv");
//--- calculation of the eigen-coordinates
   ec.CalcEigenCoordinates();
//--- calculation of the coefficients
   ec.CalcEigenCoefficients();
//--- calculation of the parameters
   ec.CalculateParameters();
//--- calculation of the functions f1,f2,f3
   ec.CalculatePlotFunctions();
//--- saving the results into the file
   ec.SaveResults("ex1-results.csv");
  }

2.5. I risultati del calcolo della funzione del modello R(x)

Genereremo 100 valori della funzione R(x) nell'intervallo [0.25,15.25] come dati del modello

Fig.7. Funzione modello utilizzata per i calcoli

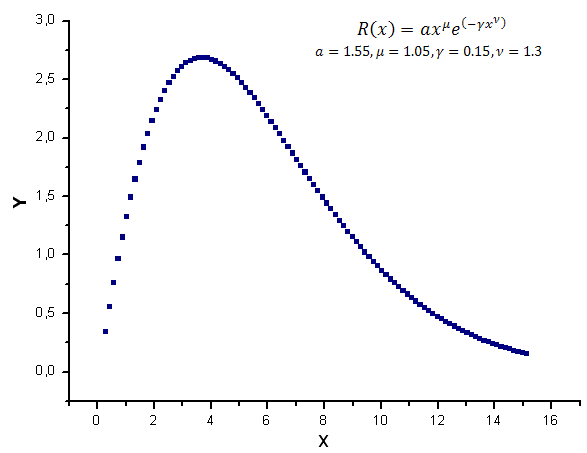
Fig.7. Funzione modello utilizzata per i calcoli

Questi dati forniscono la base per tracciare la funzione Y(x) e la sua espansione nelle funzioni X1(x), X2(x) e X3(x).

La Fig.8 mostra la funzione Y(x) e le sue "auto-coordinate" X1(x), X2(x) e X3(x).

Fig.8. Forma generale della funzione Y(x) e delle auto-coordinate X1(x), X2(x) e X3(x)

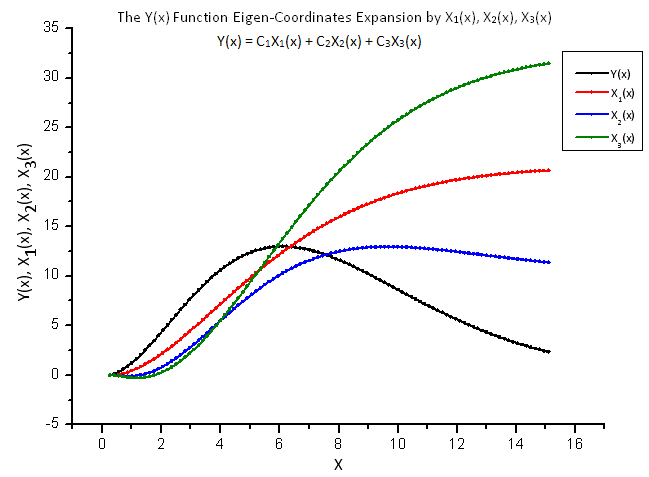
Fig.8. Forma generale della funzione Y(x) e delle auto-coordinate X1(x), X2(x) e X3(x)

Da notare l'uniformità di queste funzioni risultanti dalla natura integrale degli operatori X1(x), X2(x) e X3(x).

Dopo il calcolo delle funzioni Y(x), X1(x), X2(x) e X3(x), si costruisce la matrice di correlazione, si risolvono le equazioni per i coefficienti C1, C2 e C3 e i parametri della funzione R(x ) sono calcolati in base ai valori ottenuti:

2012.06.21 14:20:28 ec_example1 (EURUSD,H1) gamma=0.2769402213886906
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) nu=1.126643424450548
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) mu=1.328595266178149
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) a=1.637687667818532
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C1=1.772838639779728
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C2=1.126643424450548
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C3=-1.496853120395737
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 1  221.03637620 148.53278281 305.48547011 101.93843241
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 2  148.53278281 101.63995012 202.85142688 74.19784681
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 3  305.48547011 202.85142688 429.09345292 127.82779760

Verificheremo ora la linearità dell'espansione calcolata. A tal fine, dobbiamo calcolare 3 funzioni:

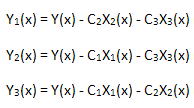
ciascuno dei quali è proiettato sulla base delle auto-coordinate X1(x), X2(x) e X3(x):

Fig.9. Rappresentazione della funzione Y1(x) nella base X1(x)

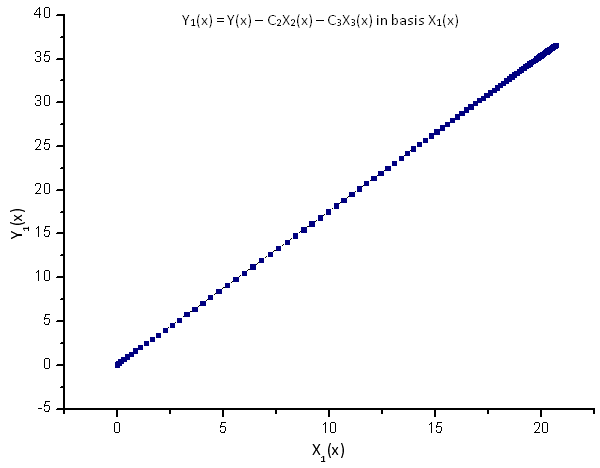
Fig.9. Rappresentazione della funzione Y1(x) nella base X1(x)

Fig.10. Rappresentazione della funzione Y2(x) nella base X2(x)

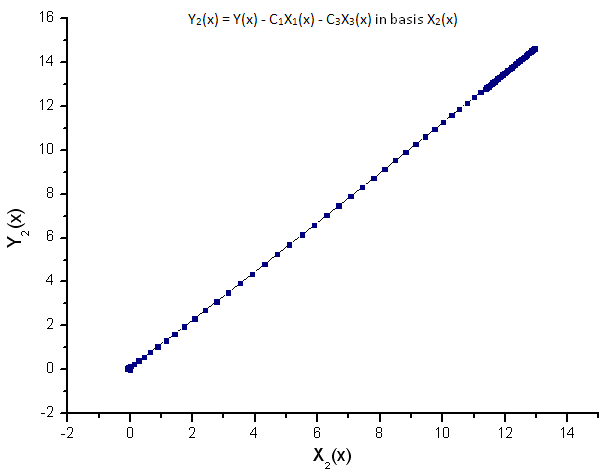
Fig.10. Rappresentazione della funzione Y2(x) nella base X2(x)

Fig.11. Rappresentazione della funzione Y3(x) nella base X3(x)

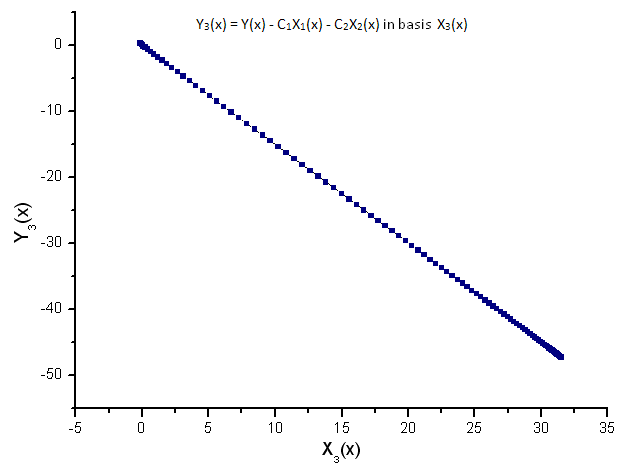
Fig.11. Rappresentazione della funzione Y3(x) nella base X3(x)

La dipendenza lineare delle funzioni tracciate suggerisce che la serie di dati in Fig.7 corrisponda strettamente alla funzione R(x).

Qualsiasi altra funzione (anche simile nella forma) rappresentata nelle auto-coordinate R(x) non avrà più una forma lineare. Questo fatto ci permette di identificare le funzioni.

La precisione del calcolo dei valori numerici dei parametri della funzione del modello può essere migliorata se il numero di punti viene aumentato a 10000 (mantenendo lo stesso intervallo):

2012.06.21 14:22:18 ec_example1 (EURUSD,H1) gamma=0.1508739336762316
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) nu=1.298316173744703
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) mu=1.052364487161627
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) a=1.550281229466634
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C1=1.483135479113404
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C2=1.298316173744703
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C3=-1.36630183435649
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 1  225.47846911 151.22066473 311.86134419 104.65062550
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 2  151.22066473 103.30005101 206.66297964 76.03285182
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 3  311.86134419 206.66297964 438.35625824 131.91955339

In questo caso, i parametri della funzione sono stati calcolati in modo più accurato.


2.6. Effetto rumore

I dati sperimentali reali contengono sempre rumore.

Nel metodo GenerateData() della classe ECCCalculator, sostituiamo:

m_y[i]=R(m_x[i],a,mu,gamma,nu);

insieme a

m_y[i]=R(m_x[i],a,mu,gamma,nu)+0.25*MathRand()/32767.0;

aggiungendo un rumore casuale, pari a circa il 10% del valore massimo della funzione.

Il risultato dello script EC_Example1-noise.mq5 è il seguente:

2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) gamma=0.4013079343855266
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) nu=0.9915044018913447
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) mu=1.403541951457922
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) a=2.017238416806171
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C1=1.707774107235756
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C2=0.9915044018913447
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C3=-1.391618023109698
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 1  254.45082565 185.19087989 354.25574000 125.17343164
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 2  185.19087989 136.81028987 254.92996885 97.14705491
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 3  354.25574000 254.92996885 501.76021715 159.49440494

Il grafico della funzione del modello con un rumore casuale è mostrato in Fig.12.

Fig.12. Funzione modello con rumore utilizzata per i calcoli

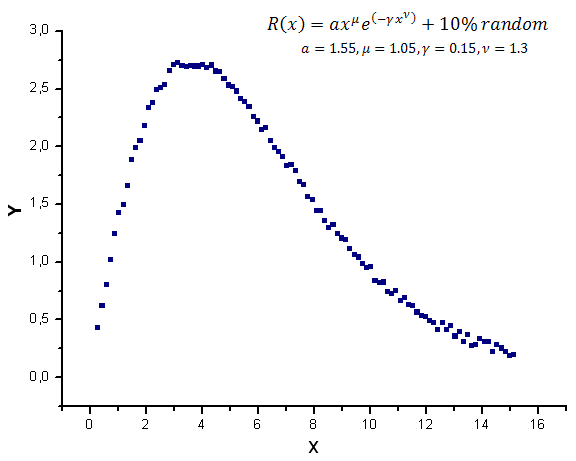
Fig.12. Funzione modello con rumore utilizzata per i calcoli

Fig.13. Forma generale della funzione Y(x) e delle auto-coordinate X1(x), X2(x) e X3(x)

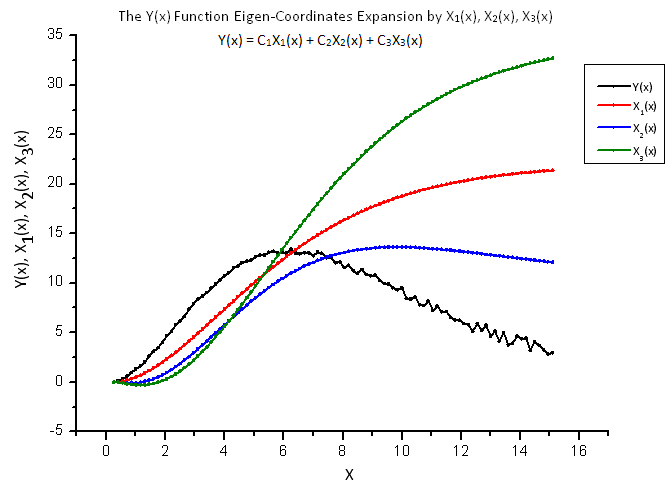
Fig.13. Forma generale della funzione Y(x) e delle auto-coordinate X1(x), X2(x) e X3(x)

Le funzioni X1(x), X2(x) e X3(x), le quali servono come "auto-coordinate", sembrano ancora lisce, tuttavia la Y(x) tracciata come loro combinazione lineare sembra essere diversa (Fig.13).

Fig.14. Rappresentazione della funzione Y1(x) nella base X1(x)

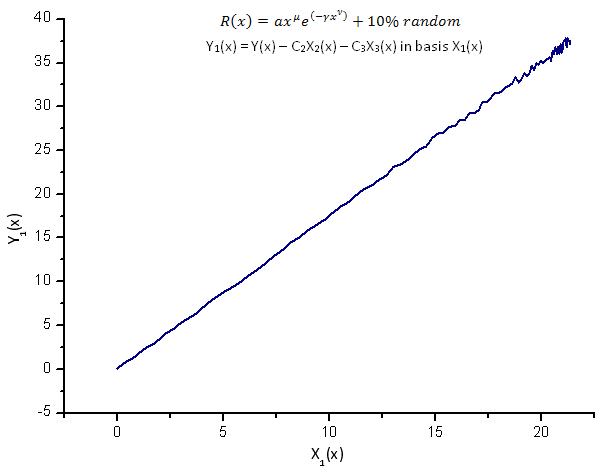
Fig.14. Rappresentazione della funzione Y1(x) nella base X1(x)

Fig.15. Rappresentazione della funzione Y2(x) nella base X2(x)

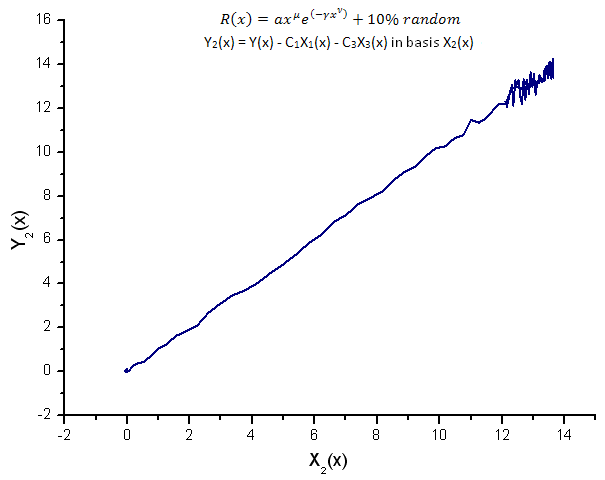
Fig.15. Rappresentazione della funzione Y2(x) nella base X2(x)

Fig.16. Rappresentazione della funzione Y3(x) nella base X3(x)

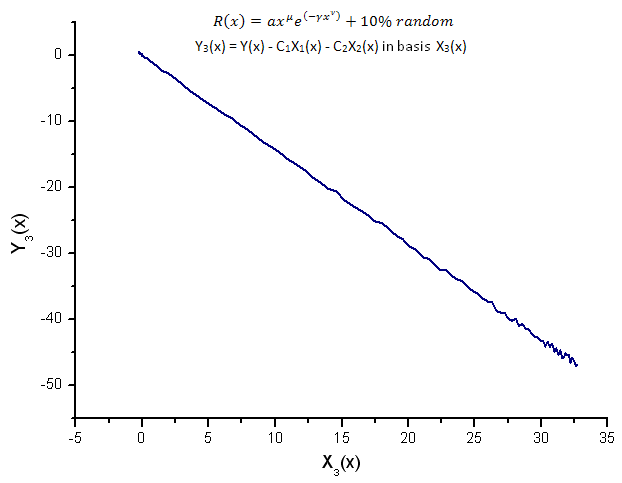
Fig.16. Rappresentazione della funzione Y3(x) nella base X3(x)

La rappresentazione delle funzioni Y1(x),Y2(x) e Y3(x) in base alle auto-coordinate (Figure 8-10) ha ancora una forma lineare, ma si possono notare fluttuazioni attorno alla retta dovute alla presenza di rumore. È più pronunciato rispetto alle X maggiori dove il segnale/rumore diventa minimo.

Qui le componenti del rumore giacciono su entrambi i lati della retta e in questo caso è quindi conveniente usare l'espansione integrale in auto-coordinate (Sezione 2.2).

 

3. Distribuzioni di probabilità non estese

La generalizzazione della meccanica statistica risulta nelle distribuzioni [2, 22]:

dove,.

La distribuzione q-gaussiana è un caso speciale della funzione P2(x).


3.1. L'espansione delle auto-coordinate della funzione P1(x)

Differenziamo P1(x):

L'equazione differenziale risultante è la seguente:

Integra sull'intervallo [xm,x]:

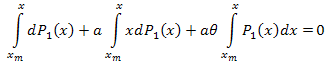
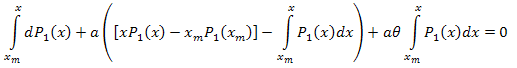
Perciò:

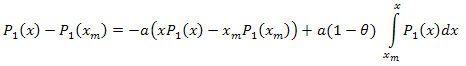
L'espansione in auto-coordinate è la seguente:

dove:

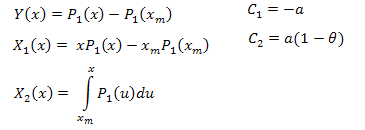
Le funzioni per i calcoli sono le seguenti (EC_Example2.mq5):

//+------------------------------------------------------------------+
//| CalcY                                                            |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
//--- Y=P(x)-P(xm)
   for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0];
  };
//+------------------------------------------------------------------+
//| CalcX1                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
//--- X1=x*P(x)-xm*P(xm)
   for(int i=0; i<m_size; i++) x1[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX2                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   ArrayResize(x2,m_size);
//--- X2=Integrate(P1(x)) 
   for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,m_y,i);
  }

Questa volta la dimensione della matrice di correlazione è 2x3; i valori dei parametri a e theta della funzione P1(x) sono determinati in base ai coefficienti С1 e C2. Il valore numerico del parametro B può essere ricavato dal requisito di normalizzazione.

Di seguito è riportato il risultato del calcolo della funzione del modello P1(x,1,0,5,2) nell'intervallo x [0,10]; il numero di punti utilizzati è 1000:

2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) theta=1.986651299600245
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) a=0.5056083906174813
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C1=-0.5056083906174813
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C2=-0.4988591756915261
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 1  0.15420524 0.48808959 -0.32145543
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 2  0.48808959 1.79668322 -1.14307410
La funzione P1(x) e la sua espansione in auto-coordinate sono mostrate nelle Figure 17-20.

Fig.17. Funzione modello P1(x, 1, 0.5, 2) utilizzata per i calcoli, 1000 punti

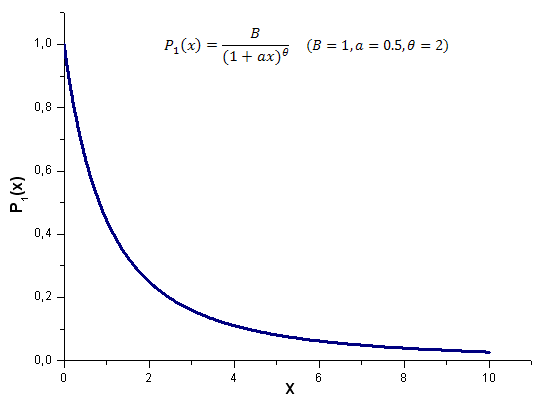
Fig.17. Funzione modello P1(x, 1, 0,5, 2) utilizzata per i calcoli, 1000 punti

Fig.18. Forma generale della funzione Y(x) e delle auto-coordinate X1(x) e X2(x)

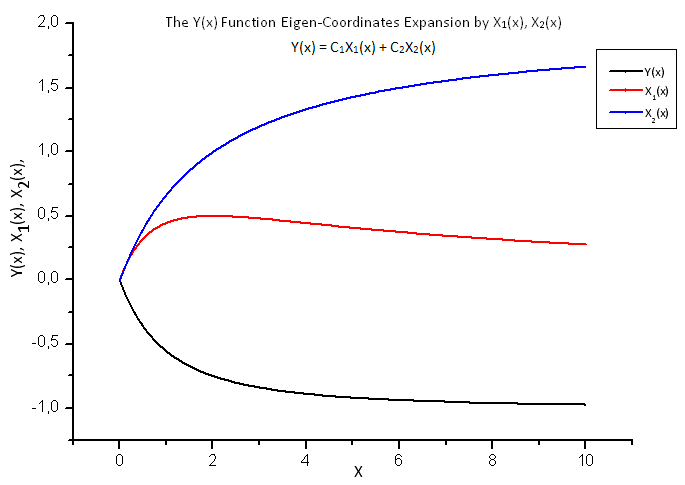
Fig.18. Forma generale della funzione Y(x) e delle auto-coordinate X1(x) e X2(x)

Fig.19. Rappresentazione della funzione Y1(x) nella base X1(x)

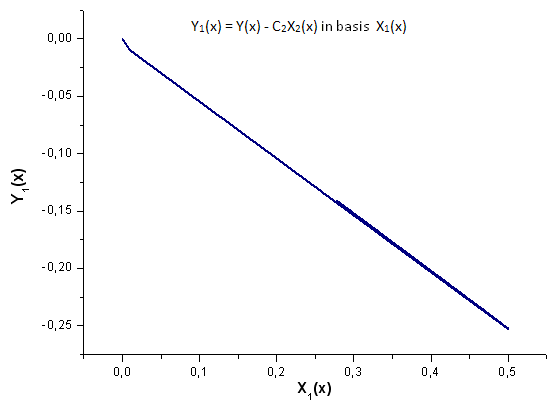
Fig.19. Rappresentazione della funzione Y1(x) nella base X1(x)

Fig.20. Rappresentazione della funzione Y2(x) nella base X2(x)

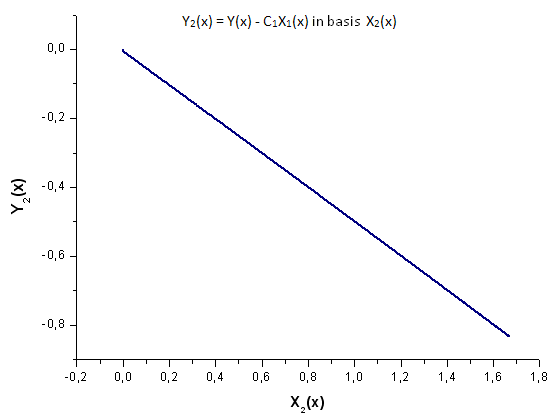
Fig.20. Rappresentazione della funzione Y2(x) nella base X2(x)

Dai un'occhiata da vicino alla Fig.19. C'è una leggera distorsione della dipendenza lineare all'inizio e nel secondo terzo del grafico.

Questo è associato alle peculiarità dell'espansione calcolata: X1(x) non è di natura integrale.


3.2. L'espansione delle auto-coordinate della funzione P2(x)

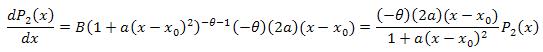
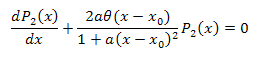
L'equazione differenziale:

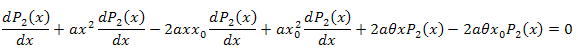
Integriamo rispetto a x sull'intervallo [xm,x]:

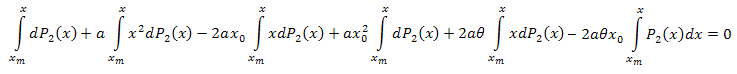
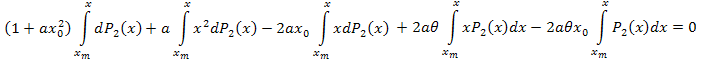
Integrando per parti si ha:

Semplifica:

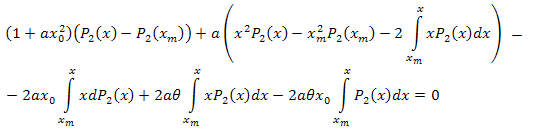
Seguendo le manipolazioni algebriche, otteniamo:

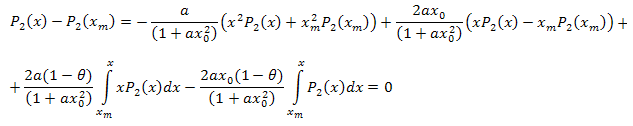
Pertanto, l'espansione risultante è la seguente:

dove:

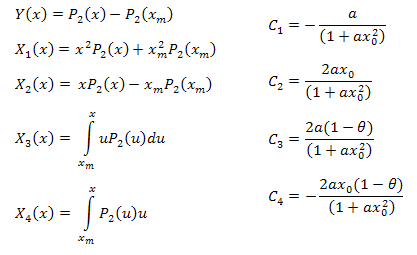
I parametri della funzione possono essere calcolati utilizzando le formule seguenti:

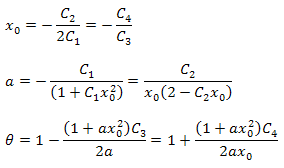
Va notato che esiste un'ulteriore relazione tra i parametri nell'espansione risultante. Questo fatto può essere utilizzato per verificare la correttezza della funzione selezionata per l'analisi. Queste relazioni sono sempre vere per i dati strettamente corrispondenti alla funzione P2(x).

Il valore numerico del parametro B può essere ricavato dal requisito di normalizzazione.

Le funzioni per il calcolo delle auto-coordinate sono le seguenti (EC_Example3.mq5):

//+------------------------------------------------------------------+
//| CalcY                                                            |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
   for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0];
  };
//+------------------------------------------------------------------+
//| CalcX1                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
   //--- X1=(x^2)*P2(x)+(xm)^2*P2(xm)
   for(int i=0; i<m_size; i++) x1[i]=(m_x[i]*m_x[i])*m_y[i]+(m_x[0]*m_x[0])*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX2                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   ArrayResize(x2,m_size);
   //--- X2=(x)*P2(x)-(xm)*P2(xm)
   for(int i=0; i<m_size; i++) x2[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX3                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX3(double &x3[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_x[i]*m_y[i];
   //--- X3=Integrate(X*P2(x)) 
   ArrayResize(x3,m_size);
   for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i);  
  }
//+------------------------------------------------------------------+
//| CalcX4                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX4(double &x4[])
  {
   if(m_size==0) return;
   //--- X4=Integrate(P2(x))
   ArrayResize(x4,m_size);
   for(int i=0; i<m_size; i++) x4[i]=Integrate(m_x,m_y,i);
  }

Di seguito è riportato il risultato del calcolo della funzione del modello P2(x) (B=1, a=0.5, theta=2, x0=1); il numero di punti utilizzato è 1000:

2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: theta=2.260782711057654
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: theta=2.076195813531546
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: a=0.4557937139014854
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: a=0.4977821155774935
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: x0=1.043759816231049
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: x0=0.8909465007003451
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C1=-0.3567992171618368
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C2=0.6357780279659221
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C3=-0.7679716475618039
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C4=0.8015779457297644
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1  1.11765877 0.60684314 1.34789126 1.28971267 -0.01429928
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2  0.60684314 0.37995888 0.55974145 0.58899739 0.06731011
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 3  1.34789126 0.55974145 3.00225771 2.54531927 -0.39043224
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 4  1.28971267 0.58899739 2.54531927 2.20595917 -0.27218168
La funzione P2(x) e la sua espansione in auto-coordinate sono mostrate nelle Figure 21-26.

Fig.21. Funzione modello P2(x,1,0.5,2,1) utilizzata per i calcoli, 100 punti

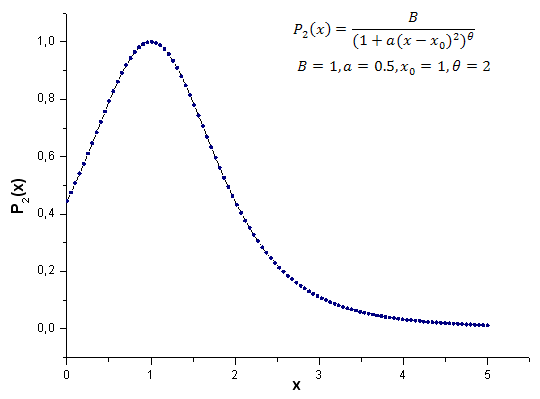
Fig.21. Funzione modello P2(x,1,0.5,2,1) utilizzata per i calcoli, 100 punti

Fig.22. Forma generale della funzione Y(x) e delle auto-coordinate X1(x), X2(x), X3(x) e X4(x)

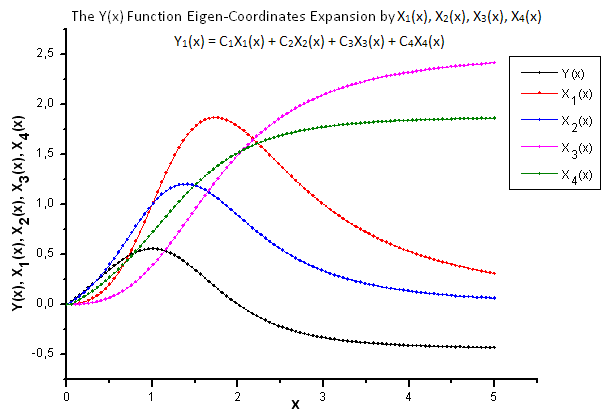
Fig.22. Forma generale della funzione Y(x) e delle auto-coordinate X1(x), X2(x), X3(x) e X4(x)

Fig.23. Rappresentazione della funzione Y1(x) nella base X1(x)

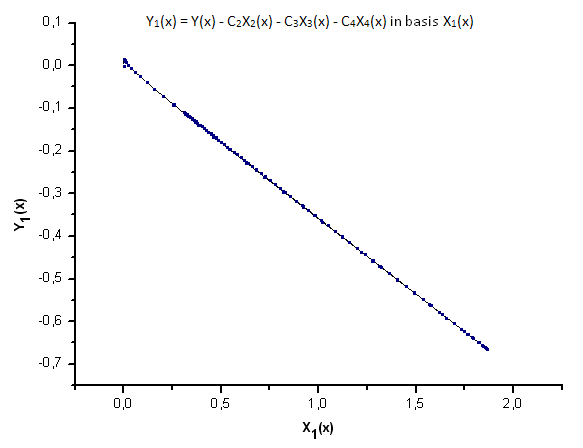
Fig.23. Rappresentazione della funzione Y1(x) nella base X1(x)

Fig.24. Rappresentazione della funzione Y2(x) nella base X2(x)

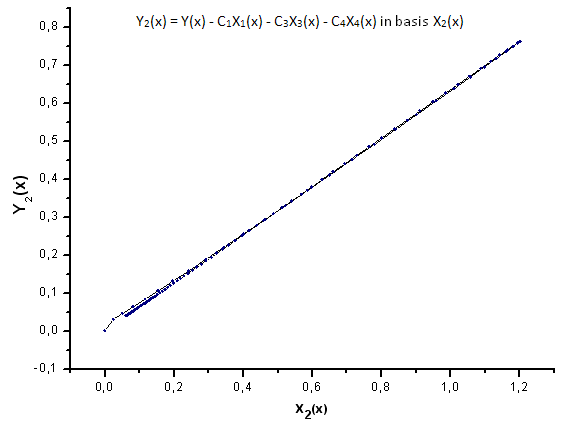
Fig.24. Rappresentazione della funzione Y2(x) nella base X2(x)

Fig.25. Rappresentazione della funzione Y3(x) nella base X3(x)

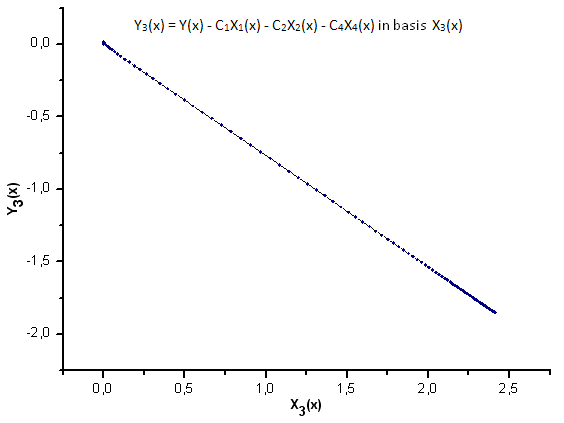
Fig.25. Rappresentazione della funzione Y3(x) nella base X3(x)

Fig.26. Rappresentazione della funzione Y4(x) nella base X4(x)

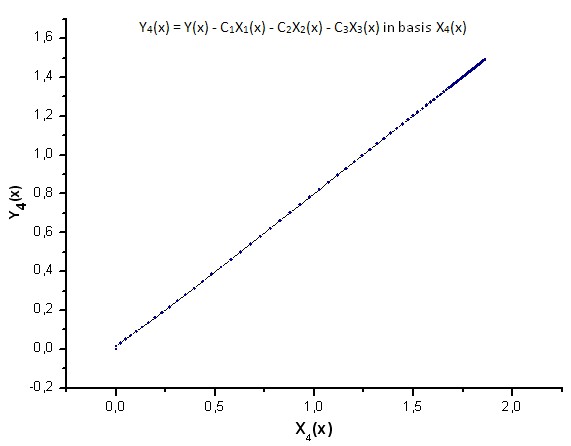
Fig.26. Rappresentazione della funzione Y4(x) nella base X4(x)


4. Se sembra un gatto... potrebbe non essere un gatto

La famiglia delle distribuzioni q-gaussiane è al centro della meccanica statistica non estensiva ed era quindi naturale aspettarsi che apparisse nel teorema del limite centrale generalizzato. Le considerazioni entropiche sono servite come principale argomento a suo favore [26].

Tuttavia, l'articolo [18, presentazione] ha mostrato che le distribuzioni come la q-gaussiana non sono universali, mettendo così in dubbio il loro ruolo speciale come distribuzioni limite.

Ad esempio, la funzione (soluzione analitica di uno dei problemi):

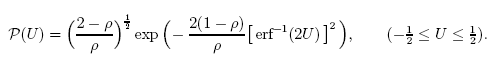
può essere descritta in modo molto accurato utilizzando la distribuzione q-gaussiana.

Fig.27. Un esempio tratto dall'articolo "A Note on q-Gaussians and Non-Gaussians in Statistical Mechanics"

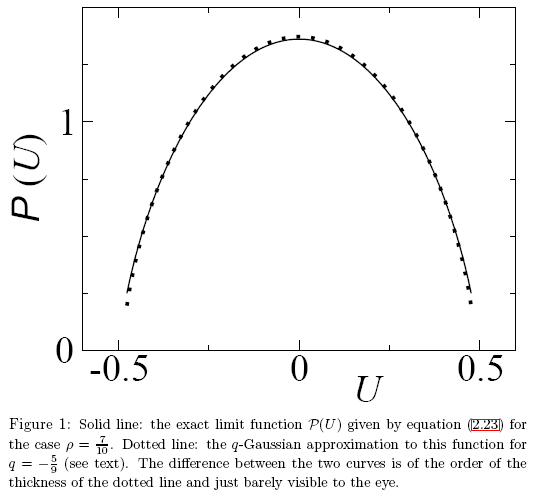
Fig.27. Un esempio tratto dall'articolo "A Note on q-Gaussians and Non-Gaussians in Statistical Mechanics"

In questo caso, funzioni analiticamente diverse hanno valori numerici simili e le differenze sono quindi appena visibili ad occhio nudo. È richiesto un metodo di identificazione della funzione accurato. Questo problema può essere risolto usando il metodo delle auto-coordinate.

Rivediamo un esempio dell'espansione in auto-coordinate della funzione P(U) e mostriamo cosa la rende esattamente diversa dalla q-gaussiana. Le funzioni appaiono molto simili all'occhio (Fig.27).

Generiamo un segnale (100 valori della funzione P(U)) e lo "proiettiamo" sul sistema delle auto-coordinate della funzione P2(x) tracciato nella Sezione 3.2.

Lo script Hilhorst-Schehr-problem.mq5 calcola la funzione P(U) e costruisce serie di dati che vengono salvati nel file MQL5\Files\test-data.csv. Questi dati vengono analizzati da EC_Example3_Test.mq5.

Fig.28. Funzione modello P(U), 100 punti

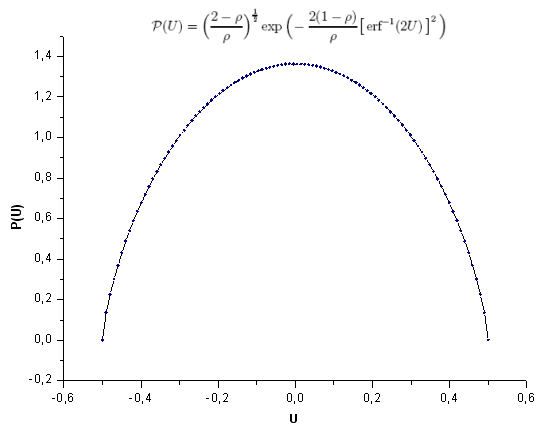
Fig.28. Funzione modello P(U), 100 punti

Fig.29. Forma generale della funzione Y(x) e delle auto-coordinate X1(x), X2(x), X3(x) e X4(x)

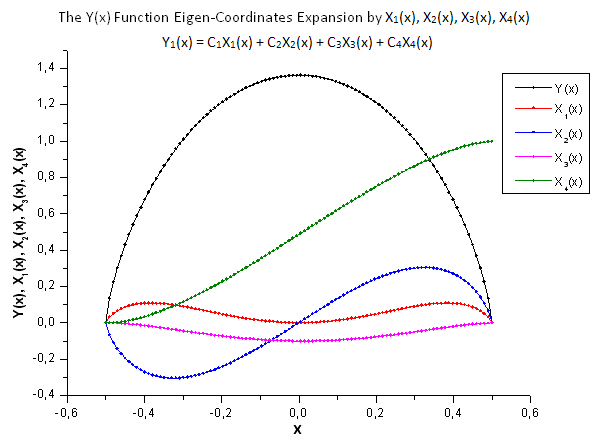
Fig.29. Forma generale della funzione Y(x) e delle auto-coordinate X1(x), X2(x), X3(x) e X4(x)

Fig.30. Rappresentazione della funzione Y1(x) nella base X1(x)

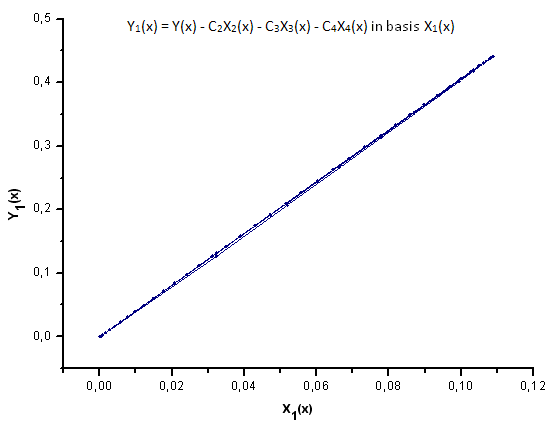
Fig.30. Rappresentazione della funzione Y1(x) nella base X1(x)

Fig.31. Rappresentazione della funzione Y2(x) nella base X2(x)

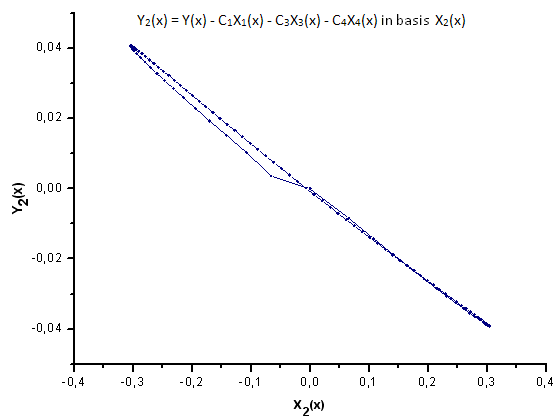
Fig.31. Rappresentazione della funzione Y2(x) nella base X2(x)

Fig.32. Rappresentazione della funzione Y3(x) nella base X3(x)

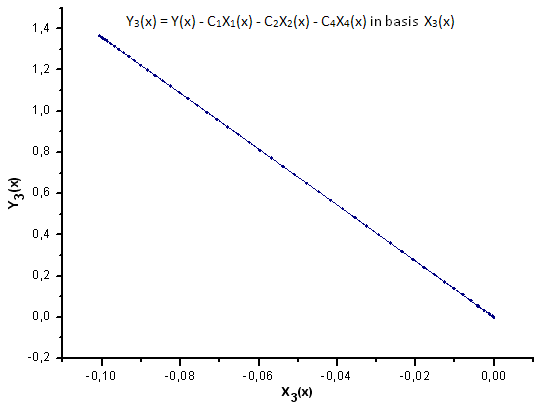
Fig.32. Rappresentazione della funzione Y3(x) nella base X3(x)

Fig.33. Rappresentazione della funzione Y4(x) nella base X4(x)

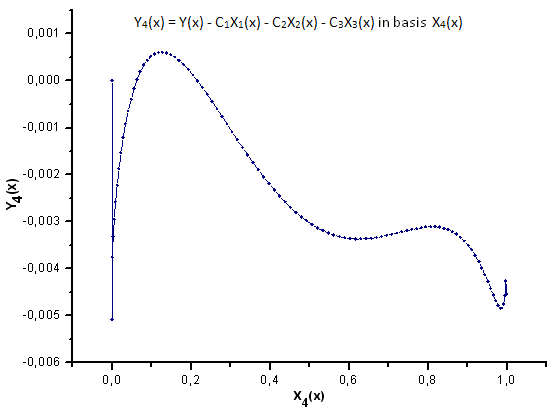
Fig.33. Rappresentazione della funzione Y4(x) nella base X4(x)


Come suggerisce la Fig.30-33, le funzioni P2(x) e P(U) sono molto simili in termini di coordinate X1(x), X2(x) e X3(x): si può osservare una buona dipendenza lineare tra Xi(x) e Yi(x). Una differenza significativa può essere vista nella componente X4(x) (Fig.33).

L'assenza della dipendenza lineare per la componente X4(x) prova il fatto che l'insieme di dati generato da P(U), nonostante appaia simile alla distribuzione q-gaussiana, in realtà non è q-gaussiana.

Possiamo dare uno sguardo diverso alle funzioni (Figure 34-37) tracciando insieme Xi(x) e Yi(x).

Fig.34. Forma generale delle funzioni X1(x) e Y1(x)

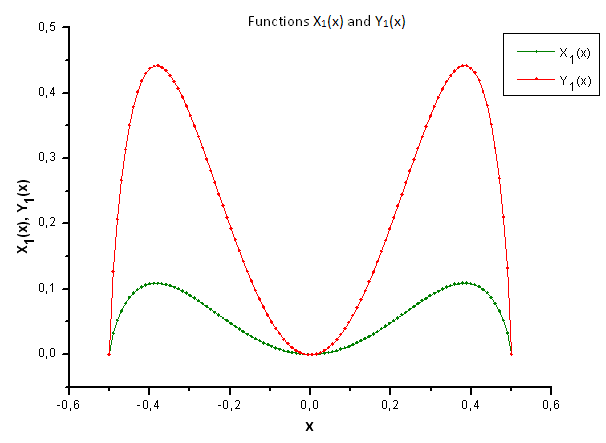
Fig.34. Forma generale delle funzioni X1(x) e Y1(x)

Fig.35. Forma generale delle funzioni X2(x) e Y2(x)

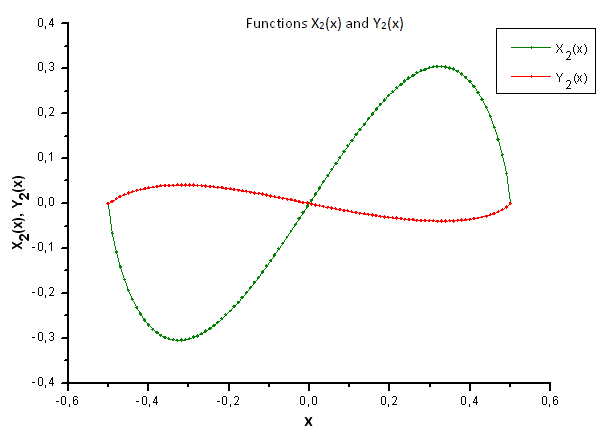
Fig.35. Forma generale delle funzioni X2(x) e Y2(x)

Fig.36. Forma generale delle funzioni X3(x) e Y3(x)

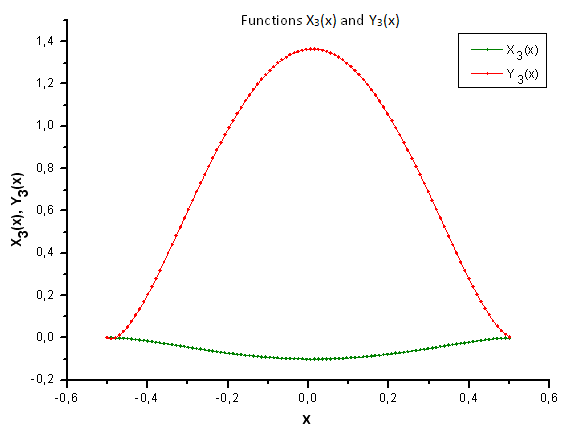
Fig.36. Forma generale delle funzioni X3(x) e Y3(x)

Fig.37. Forma generale delle funzioni X4(x) e Y4(x)

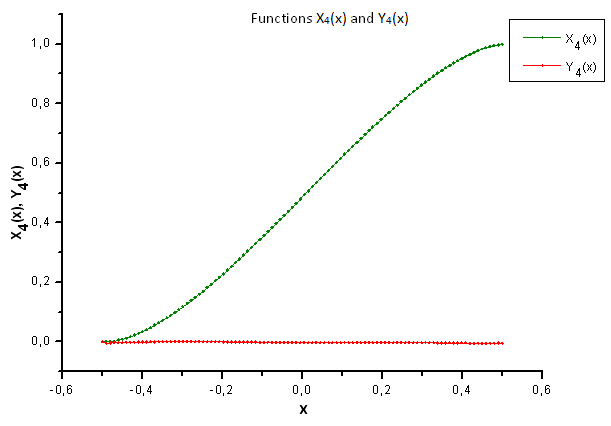
Fig.37. Forma generale delle funzioni X4(x) e Y4(x)

Come suggerisce la Fig.37, la differenza strutturale nella componente X4(x) è diventata evidente quando si proiettano i dati generati dalla funzione P(U) sulle auto-coordinate della funzione P2(x). Quindi, possiamo dire con certezza che i dati sperimentali non corrispondono alla funzione P2(x).

Il calcolo riportato di seguito (EC_Example3_test) parla a favore di questo fatto:

2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: theta=1.034054797050629
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: theta=-0.6736146397139184
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: a=199.3574440289263
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: a=-4.052181367572913
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: x0=-0.0003278538628371299
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: x0=0.0161122975924721
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C1=4.056448634458822
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C2=-0.1307174151339552
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C3=-13.57786363975563
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C4=-0.004451555043369697
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1  0.00465975 0.00000000 -0.00218260 0.02762761 0.04841405
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2  0.00000000 0.04841405 -0.00048835 0.06788438 0.00000001
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 3  -0.00218260 -0.00048835 0.00436149 -0.02811625 -0.06788437
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 4  0.02762761 0.06788438 -0.02811625 0.35379820 0.48337994

Ha anche alterato le relazioni tra i parametri.


Conclusione

Il metodo delle auto-coordinate è uno strumento unico per l'analisi delle proprietà strutturali delle relazioni funzionali e che consente di semplificare sostanzialmente l'analisi e l'interpretazione dei dati.

Il concetto alla base di questo metodo è quello di utilizzare set di dati sperimentali {xi,yi} per costruire nuove funzioni corrispondenti al modello proposto. La forma delle espansioni dell'operatore è determinata dalla struttura dell'equazione differenziale, la quale è soddisfatta dalla funzione che funge da "candidato" per la descrizione dei dati. Se la funzione è nativa, le espansioni della funzione calcolate utilizzando i dati {xi,yi} assumeranno in base alle auto-coordinate una forma lineare. Deviazioni dalla linearità in base alle auto-coordinate della "funzione candidata" suggeriscono che i dati {xi,yi} non potrebbero essere generati dalla funzione data e il modello costruito non è appropriato.

In alcuni casi complicati la funzione candidata e la funzione nativa possono apparire simili tanto che una parte maggiore delle espansioni calcolate risulta essere lineare. Tuttavia, il metodo delle auto-coordinate ci consente di identificare la differenza tra queste funzioni e rende nota la sua presenza per linearità alterata dell'espansione. L'esempio di Hilhorst e Schehr è servito da illustrazione della differenza che diventa evidente nell'ultimo membro di espansione, quando si proietta su X4(x).

Questa informazione può essere utile anche quando si ha a che fare con un'equazione differenziale (Sezione 3.2) soddisfatta dalla funzione P2(x): l'asta in questione corrisponde alla parte lineare rispetto a P2(x). Potrebbe non essere così interessante in caso di descrizione fenomenologica di dati sperimentali ("stiamo cercando una soluzione nella forma della q-gaussiana"). Tuttavia, se il modello è basato su equazioni differenziali (Fig.3), è possibile comprendere meglio il ruolo di ciascuno dei meccanismi presi in considerazione nei modelli dei processi fisici.


Fonti

  1. C. Tsallis, "Possible Generalization of Boltzmann-Gibbs Statistics", Journal of Statistical Physics, Vol. 52, Nos. 1/2, 1988.
  2. C. Tsallis, "Nonextensive Statistics: Theoretical, Experimental and Computational Evidences and Connections". Brazilian Journal of Physics, (1999) vol. 29. p.1.
  3. C. Tsallis, "Some Comments on Boltzmann-Gibbs Statistical Mechanics", Chaos, Solitons & Fractals Volume 6, 1995, pp. 539–559.
  4. Europhysics News "Special Issue: Nonextensive Statistical Mechanics: New Trends, New Perspectives", Vol. 36 No. 6 (November-December 2005).
  5. M. Gell-Mann, C. Tsallis, "Nonextensive Entropy: Interdisciplinary Applications", Oxford University Press, 15.04.2004, 422 p.
  6. Constantino Tsallis, the Official Website Nonextensive Statistical Mechanics and Thermodynamics.
  7. Chumak, O.V. "Entropy and Fractals in Data Analysis", М.-Izhevsk: RDC "Regular and Chaotic Dynamics", Institute for Computer Research, 2011. - 164 p.
  8. Qiuping A. Wang, "Incomplete Statistics and Nonextensive Generalizations of Statistical Mechanics", Chaos, Solitons and Fractals, 12(2001)1431-1437.
  9. Qiuping A. Wang, "Extensive Generalization of Statistical Mechanics Based on Incomplete Information Theory", Entropy, 5(2003).
  10. Lisa Borland, "Long-Range Memory and Nonextensivity in Financial Markets", Europhysics News 36, 228-231 (2005)
  11. T. S. Biró, R. Rosenfeld, "Microscopic Origin of Non-Gaussian Distributions of Financial Returns", Physica A: Statistical Mechanics and its Applications, Vol. 387, Nr. 7 (Mar 1, 2008) , p. 1603-1612 (preprint).
  12. S. M. D. Queiros, C. Anteneodo, C. Tsallis, "Power-Law Distributions in Economics: A Nonextensive Statistical Approach", Proceedings of SPIE (2005) Volume: 5848, Publisher: SPIE, Pages: 151-164, (preprint)
  13. R Hanel, S Thurner, "Derivation of Power-Law Distributions within Standard Statistical Mechanics", Physica A: Statistical Mechanics and its Applications (2005), Volume: 351, Issue: 2-4, Publisher: Elsevier, Pages: 260-268. (preprint)
  14. A K Rajagopal, Sumiyoshi Abe, "Statistical Mechanical Foundations of Power-Law Distributions", Physica D: Nonlinear Phenomena (2003), Volume: 193, Issue: 1-4, Pages: 19 (preprint)
  15. T. Kaizoji, "An Interacting-Agent Model of Financial Markets from the Viewpoint of Nonextensive Statistical Mechanics", Physica A: Statistical Mechanics and its Applications, Vol. 370, N. 1 (Oct 1, 2006) , p. 109-113. (preprint)
  16. V. Gontis, J. Ruseckas, A. Kononovičius, "A Long-Range Memory Stochastic Model of the Return in Financial Markets", Physica A: Statistical Mechanics and its Applications 389 (2010) 100-106. (preprint)
  17. H.E. Roman, M. Porto, "Self-Generated Power-Law Tails in Probability Distributions", Physical Review E - Statistical, Nonlinear and Soft Matter Physics (2001), Volume: 63, Issue: 3 Pt 2, Pages: 036-128.
  18. H. J. Hilhorst, G. Schehr, "A Note on q-Gaussians and Non-Gaussians in Statistical Mechanics" (2007, preprint, presentation).
  19. D. J. Hudson, "Lectures on Elementary Statistics and Probability", CERN-63-29, Geneva : CERN, 1963. - 101 p.
  20. D. J. Hudson, "Statistics Lectures II : Maximum Likelihood and Least Squares Theory", CERN-64-18. - Geneva : CERN, 1964. - 115 p.
  21. R. R. Nigmatullin, "Eigen-Coordinates: New Method of Analytical Functions Identification in Experimental Measurements", Applied Magnetic Resonance Volume 14, Number 4 (1998), 601-633.
  22. R.R. Nigmatullin, "Recognition of Nonextensive Statistical Distributions by the Eigencoordinates Method", Physica A: Statistical Mechanics and its Applications Volume 285, Issues 3–4, 1 October 2000, pp. 547–565.
  23. C. Antonini "q-Gaussians in Finance" (2010).
  24. C. Antonini, "The Use of the q-Gaussian Distribution in Finance" (2011).
  25. L. G. Moyano, C. Tsallis, M. Gell-Mann, "Numerical Indications of a q-Generalised Central Limit Theorem", Europhysics Letters 73, 813-819, 2006, (preprint).
  26. T. Dauxois, "Non-Gaussian Distributions under Scrutiny", J. Stat. Mech. (2007) N08001. (preprint)

Appendice. Analisi dei rendimenti giornalieri SP500 con Q-Gaussiana

Consideriamo l'esempio classico (Fig.4) di un approccio q-gaussiano di successo ai rendimenti giornalieri SP500 (funzione P2(x)).

Abbiamo utilizzato i dati giornalieri di: http://wikiposit.org/w?filter=Finance/Futures/Indices/S__and__P%20500 /

Fig.38. Prezzi di chiusura SP500 (giornaliero)

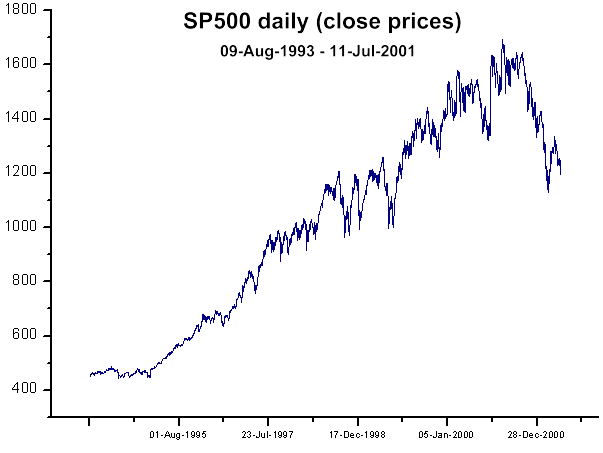
Fig.38. SP500 chiudi prezzi (giornaliero)

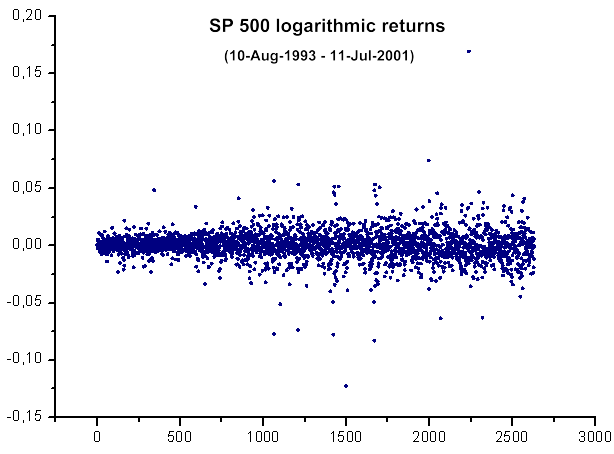
Fig.39. Rendimenti logaritmici SP500

Fig.39. Rendimenti logaritmici SP500

Fig.40. Distribuzione dei rendimenti logaritmici SP500

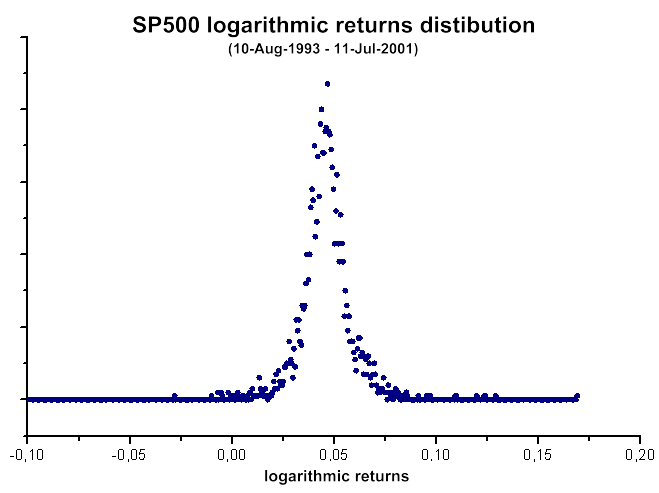
Fig.40. Distribuzione dei rendimenti logaritmici SP500

Fig.41. La funzione Y1(x) nella base X1(x)

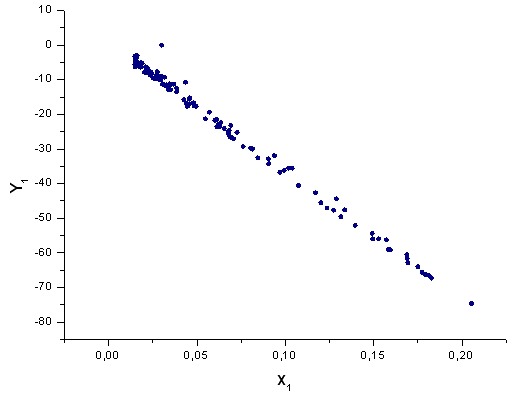
Fig.41. La funzione Y1(x) in base X1(x)

Fig.42. La funzione Y2(x) nella base X2(x)

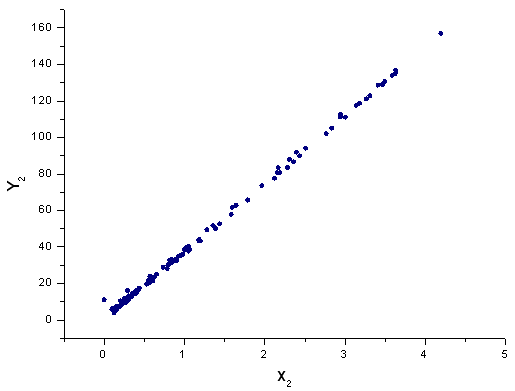
Fig.42. La funzione Y2(x) in base X2(x)

Fig.43. La funzione Y3(x) nella base X3(x)

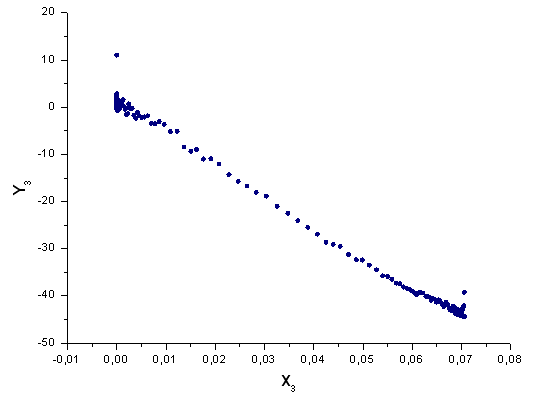
Fig.43. La funzione Y3(x) in base X3(x)

Fig.44. La funzione Y4(x) nella base X4(x)

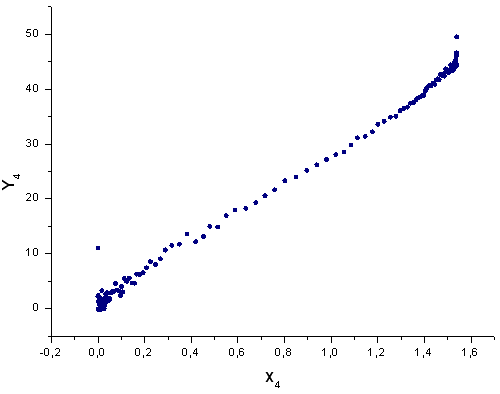
Fig.44. La funzione Y4(x) in base X4(x)

Per vedere come eseguire l'analisi nel tuo terminale, il file SP500-data.csv deve essere posizionato nella cartella \Files\.

Successivamente è necessario avviare due script:

  1. CalcDistr_SP500.mq5 (calcola la distribuzione).
  2. q-gaussian-SP500.mq5 (analisi delle coordinate Eigen)
I risultati sono:
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    2: theta=1.770125768485269
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    1: theta=1.864132228192338
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    2: a=2798.166930885822
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    1: a=8676.207867097581
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    2: x0=0.04567518783335043
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    1: x0=0.0512505923716428
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    C1=-364.7131366394939
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    C2=37.38352859698793
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    C3=-630.3207508306047
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    C4=28.79001868944634
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    1  0.00177913 0.03169294 0.00089521 0.02099064 0.57597695
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    2  0.03169294 0.59791579 0.01177430 0.28437712 11.55900584
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    3  0.00089521 0.01177430 0.00193200 0.04269286 0.12501732
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    4  0.02099064 0.28437712 0.04269286 0.94465120 3.26179090
2012.06.29 20:01:09    CalcDistr_SP500 (EURUSD,D1)    checking distibution cnt=2632.0 n=2632
2012.06.29 20:01:09    CalcDistr_SP500 (EURUSD,D1)    Min=-0.1229089015984444 Max=0.1690557338964631 range=0.2919646354949075 size=2632
2012.06.29 20:01:09    CalcDistr_SP500 (EURUSD,D1)    Total data=2633

Il valore stimato di q, derivato dal metodo delle auto-coordinate (q=1+1/theta): q~1,55

Il valore, riportato nel libro (Fig.4) q~1.4.

Conclusione: In generale, si può vedere che questi dati possono essere descritti dalla funzione q-gaussiana. Essa spiega la riuscita interpretazione mediante q-gaussiano, riportata nel libro.


Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/412

File allegati |
Scarica ZIP
cmatrix.mqh (4.1 KB)
ec_example1.mq5 (13.89 KB)
ec_example1-noise.mq5 (13.97 KB)
ec_example2.mq5 (12 KB)
ec_example3.mq5 (14.94 KB)
hilhorst-schehr-problem.mq5 (4.03 KB)
ec_example3_test.mq5 (15.07 KB)
Avvertimento: Tutti i diritti su questi materiali sono riservati a MetaQuotes Ltd. La copia o la ristampa di questi materiali in tutto o in parte sono proibite.

Altri articoli di questo autore

Vai alla discussione
Introduzione al metodo di decomposizione empirica Introduzione al metodo di decomposizione empirica
Questo articolo serve a far familiarizzare il lettore con il metodo di decomposizione empirica (EMD). È la parte fondamentale della trasformata di Hilbert-Huang ed è destinata all'analisi dei dati provenienti da processi non stazionari e non lineari. Questo articolo presenta anche una possibile implementazione software di questo metodo insieme a una breve considerazione delle sue peculiarità, oltre a fornire alcuni semplici esempi del suo utilizzo.
Ottieni 200 USD per il tuo articolo per il trading algoritmico! Ottieni 200 USD per il tuo articolo per il trading algoritmico!
Scrivi un articolo e contribuisci allo sviluppo del trading algoritmico. Condividi la tua esperienza nel trading e nella programmazione e ti pagheremo $200. Inoltre, la pubblicazione di un articolo sul popolare sito web MQL5.com offre un'eccellente opportunità per promuovere il proprio marchio personale in una comunità professionale. Migliaia di trader leggeranno il tuo lavoro. Puoi discutere le tue idee con persone che la pensano allo stesso modo, acquisire nuova esperienza e monetizzare le tue conoscenze.
MetaQuotes ID nel terminale mobile MetaTrader MetaQuotes ID nel terminale mobile MetaTrader
I dispositivi Android e iOS ci offrono molte funzionalità che non conosciamo nemmeno. Una di queste funzionalità sono le notifiche push che ci consentono di ricevere messaggi personali, indipendentemente dal nostro numero di telefono o dall'operatore di rete mobile. Il terminale mobile MetaTrader può già ricevere tali messaggi direttamente dal tuo robot di trading. Devi conoscere solo l'ID MetaQuotes del tuo dispositivo. L'hanno già ricevuto più di 9.000.000 di terminali mobile.
La stima kernel di densità della funzione di densità di probabilità La stima kernel di densità della funzione di densità di probabilità
L'articolo tratta la creazione di un programma che consenta di stimare la densità kernel della funzione di densità di probabilità incognita. Il metodo di stima kernel di densità è stato scelto per eseguire l'attività. L'articolo contiene i codici sorgente dell'implementazione del software del metodo, esempi del suo utilizzo e illustrazioni.