Нейросети — это просто (Часть 94): Оптимизация последовательности исходных данных

Введение

Общий подход при обработке временных рядов заключается в сохранении исходного расположения временных шагов нетронутыми. Предполагается, что исторический порядок является наиболее оптимальным. Однако большинство существующих моделей не имеет явных механизмов для исследования взаимосвязей между отдаленными сегментами внутри каждого временного ряда, которые на самом деле могут иметь сильные зависимости. Например, модели на основе сверточных сетей (CNN) для обучения временных рядов могут улавливать шаблоны только в пределах ограниченного временного окна. Как следствие, при анализе временных рядов, в которых важные закономерности охватывают более длительные временные окна, таким моделям сложно эффективно уловить эту информацию. Использование глубоких сетей позволяет увеличить размер рецептивного поля и частично решает проблему. Но количество сверточных слоев, необходимых для охвата всей последовательности, может оказаться слишком велико, а чрезмерное увеличение модели приводит к проблеме затухающих градиентов.

При использовании в моделях архитектуры Transformer, эффективность фиксации долгосрочных зависимостей сильно зависит от множества факторов. К ним можно отнести длину последовательности, различные стратегии позиционного кодирования и токенизации данных.

Подобные размышления привели авторов статьи "Segment, Shuffle, and Stitch: A Simple Mechanism for Improving Time-Series Representations" к вопросу оптимальности использования исторической последовательности. Может ли существовать лучшая организация временных рядов, которая позволила бы более эффективно обучать представлениям с учетом поставленной задачи?

В указанной статье авторы представляют простой и готовый к использованию механизм под названием Segment, Shuffle, Stitch (S3), предназначенный для обучения оптимизации представления временных рядов. Как следует из названия, S3 работает путем сегментирования временного ряда на несколько непересекающихся сегментов, перемешивания этих сегментов в наиболее оптимальном порядке, а затем объединения перетасованных сегментов в новую последовательность. Здесь стоит отметить, что порядок перестановки сегментов обучается для каждой конкретной задачи.

В дополнение к этому, S3 интегрирует исходный временной ряд посредством обучаемой операции взвешенной суммы с перетасованной версией, что позволяет сохранить ключевую информацию из исходной последовательности.

S3 действует как модульный механизм, предназначенный для плавной интеграции с любой моделью анализа временных рядов, и приводит к более плавной процедуре обучения с уменьшением ошибки. Поскольку S3 обучается вместе с магистральной сетью, параметры перетасовки обновляются целенаправленно, адаптируясь к характеристикам исходных данных и базовой модели, чтобы лучше отражать временную динамику. Кроме того, S3 может быть объединен в стек для создания более детальной перетасовки с более высоким уровнем детализации.

Предложенный алгоритм имеет очень мало гиперпараметров для настройки и требует незначительных дополнительных вычислительных ресурсов.

Для оценки эффективности предложенных подходов авторы метода интегрируют S3 в различные нейронные архитектуры, включая модели на основе CNN и Transformer. Оценка производительности в различных наборах данных задач классификации одномерного и многомерного прогнозирования демонстрирует, что внедрение S3 приводит к существенному улучшению эффективности обучаемой модели при прочих равных условиях. Результаты показывают, что интеграция S3 в современные методы может дать повышение производительности до 39,59% в задачах классификации. А в задачах одномерного и многомерного прогнозирования временных рядов эффективность модели может вырасти на 68,71% и 51,22%, соответственно.

1. Алгоритм S3

Предлагаю познакомиться с предложенным методом S3 более детально.

В качестве исходных данных используется многомерный временной ряд X, состоящий из T временных шагов и C каналов, который разбивается на N непересекающихся сегментов.

Мы рассматриваем общий случай многомерного временного ряда, хотя метод отлично работает и с одномерными временными рядами. По-существу, одномерный временной ряд можно рассматривать как частный случай многомерного ряда, когда количество каналов C равно 1.

Цель метода заключается в оптимальной перестановке сегментов для формирования новой последовательности X', которая позволит лучше уловить основные временные отношения и зависимости внутри временного ряда. Что, в свою очередь, приводят к улучшению представлений целевой задачи.

Авторы метода S3 предлагают решение вышеупомянутой проблемы в три этапа: «Сегментация», «Перемешивание» и «Объединение».

Модуль Segment разбивает исходную последовательность X на N непересекающихся сегментов, каждый из которых содержит τ временных шагов, где τ = T/N. Набор сегментов можно представить как S = {s1, s2, . . . , sn}.

Cегменты подаются в модуль Shuffle, который использует вектор перемешивания P = {p1, p2, . . . , pn} для перестановки сегментов в оптимальном порядке. Каждый параметр перетасовки pj в векторе P соответствует сегменту sj в матрице S. По сути, P — это набор обучаемых весов, оптимизированных с помощью сети, который контролирует положение и приоритет сегмента в переупорядоченной последовательности.

Процесс перетасовки довольно прост и интуитивно понятен: чем выше значение pj, тем выше приоритет сегмента sj в перетасованной последовательности. Перетасованную последовательность Sshuffled можно представить как:

Перестановка вектора S на основе порядка сортировки P не является дифференцируемой по умолчанию, поскольку она включает в себя дискретные операции и вносит разрывы. Методы мягкой сортировки аппроксимируют порядок сортировки, назначая вероятности, которые отражают, насколько больше каждый элемент по сравнению с другими. Хотя это приближение является дифференцируемым по своей природе, оно может вносить шум и неточности, делая сортировку не интуитивной. Чтобы добиться такой же точной и интуитивно понятной дифференцируемой сортировки и перестановки, как и традиционные методы, авторы метода вводят несколько промежуточных шагов. Эти шаги создают путь для прохождения градиентов через параметры перетасовки P.

Сначала мы получаем индексы, которые сортируют элементы P, используя σ = Argsort(P). У нас есть список тензоров S = {s1, s2, s3, ...sn}, которые мы хотим переупорядочить на основе списка индексов σ = {σ1, σ2, ..., σn} дифференцируемым способом. Затем создаем матрицу U размерностью (τ × C) × n × n, в которой повторяем каждый si N раз.

После чего формируем матрицу Ω размерностью n × n, в которой каждая строка j имеет один ненулевой элемент в позиции k = σj. Преобразуем матрицу Ω в двоичную, масштабируя каждый ненулевой элемент до 1 с помощью коэффициента масштабирования. Этот процесс создает путь для прохождения градиентов через P во время обратного распространения ошибки.

Выполняя Адамарное произведение U на Ω, мы получаем матрицу V, в которой каждая строка j имеет один ненулевой элемент k равный sk. Путем суммирования по последнему измерению и транспонирования результирующей матрицы, мы получаем окончательную перетасованную матрицу Sshuffled.

Использование многомерной матрицы P' позволяет ввести дополнительные параметры, которые позволяют модели улавливать более сложные представления. Поэтому авторы метода S3 вводят гиперпараметр λ для определения размерности матрицы P'. Затем выполняется суммирование P' по первым λ − 1 измерениям, чтобы получить одномерный вектор P, который затем используется для вычисления индексов перестановок σ = Argsort(P).

Такой подход позволяет увеличить количество параметров перетасовки, тем самым фиксируя более сложные зависимости в данных временных рядов, не влияя на операции сортировки.

На последнем этапе модуль Stitch объединяет перетасованные сегменты Sshuffled для создания одной перетасованной последовательности X'.

С целью сохранения информации, присутствующей в исходном порядке анализируемого временного ряда, выполняется взвешенное суммирование исходной и перемешенной последовательностей с параметрами w1 и w2, которые также оптимизируются в процессе обучения основной модели.

Рассматривая S3 как модульный уровень, мы можем последовательно складывать их в нейронную архитектуру. Определим ϕ как гиперпараметр, определяющий количество слоев S3. Для простоты и во избежание определения отдельного гиперпараметра сегмента, для каждого слоя S3 авторы метода определяют параметр θ в качестве множителя для количества сегментов в последующих слоях.

Когда несколько слоев S3 объединены в стопку, каждый уровень ℓ от 1 до ϕ сегментирует и перемешивает исходные данные на основе результатов работы предыдущего слоя.

Все обучаемые параметры S3 обновляются вместе с параметрами модели, и ни для одного из слоев S3 не вводится промежуточных потерь. Это гарантирует, что уровни S3 обучаются в соответствии с конкретной задачей и базовым уровнем.

В случаях, когда длина исходной последовательности X не делится на количество сегментов N, прибегаем к усечению первых T mod N временных шагов из входной последовательности. Чтобы гарантировать, что никакие данные не будут потеряны, а входные и выходные формы одинаковы, позже мы добавляем усеченные образцы обратно в начало выходных данных окончательного слоя S3.

Авторская визуализация метода представлена ниже.

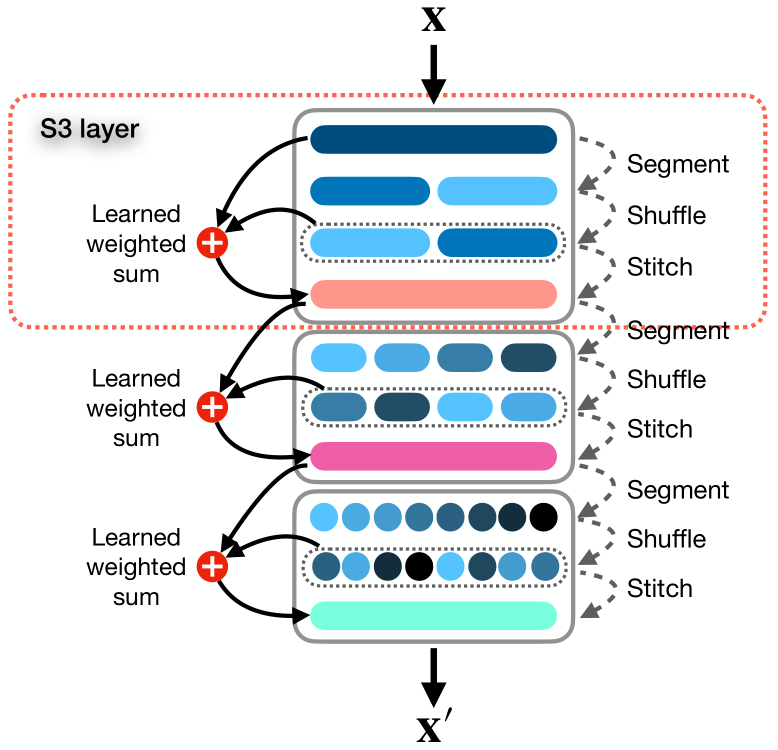
Здесь можно добавить, что по результатам экспериментов, представленных в авторской статье, параметры перестановки корректируются на начальном этапе обучения. После чего фиксируются и позже не изменяются.

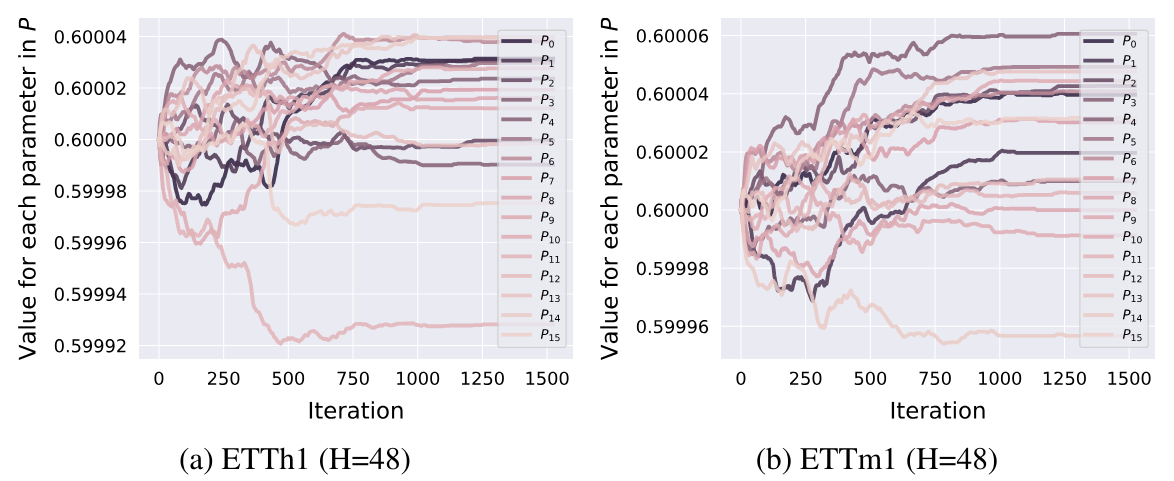
2. Реализация средствами MQL5

После рассмотрения теоретических аспектов метода S3 мы переходим к практической части нашей статьи, в которой рассмотрим один из вариантов практической реализации предложенных подходов средствами MQL5. Но прежде, чем приступить к написанию кода, давайте немного задумаемся об архитектуре построения предложенных подходов в свете имеющихся у нас наработок.

2.1 Архитектура построения

Для определения порядка сортировки данных авторы метода S3 используют вектор обучаемых параметров P. В нашей библиотеке обучаемые параметры существуют только в нейронных слоях. И в принципе, мы можем использовать нейронный слой, который бы генерировал нам приоритеты сегментов. При этом обучение параметров можно осуществлять готовыми средствами используемого нейронного слоя. Но есть один нюанс — на вход нейронного слоя нам необходимо подать исходные данные, которых не предусмотрено для обучаемых параметров. Из этой ситуации мы выходим довольно просто — на вход такого нейронного слоя мы подаем фиксированный вектор, заполненный "1".

Такой подход нам позволяет сразу решить и вопрос многомерной матрицы перестановок P'. Для изменения размерности этой матрицы (авторы метода S3 определили гиперпараметром λ), нам достаточно изменить размер вектора исходных данных. Остальной же функционал остается неизменным. Суммирование отдельных параметров для каждого сегмента уже реализовано в недрах нашего нейронного слоя. Размер результатов такого нейронного слоя равен количеству сегментов.

Для перевода приоритетов сегментов в область вероятностных значений, мы воспользуемся функцией SoftMax.

Аналогичный подход будем использовать и для параметров взвешивания влияния исходной и перетасованной последовательностей. Только на этот раз размер результатов слоя равен 2. А в качестве функции активации данного слоя воспользуемся сигмоидой.

С обучаемыми параметрами мы определились. А вот алгоритм сортировки сегментов в порядке возрастания или убывания вероятностей нам предстоит реализовать.

Теоретически порядок сортировки (возрастание или убывание) приоритетов отдельных сегментов не имеет значения. Ведь мы будем обучать порядок перестановки сегментов. Соответственно, в процессе обучения модель распределит приоритеты согласно заданному порядку сортировки. И здесь важно, чтобы порядок сортировки при обучении и эксплуатации модели оставался неизменным.

Следующий момент, для возможности распределения градиента ошибки на вектор приоритетов P авторы метода предложили довольно сложный алгоритм с созданием многомерных массивов и многократным дублированием исходных данных. Что ведет к дополнительным вычислительным расходам и повышенному потреблению памяти. Можем ли мы предложить более экономный вариант?

Давайте посмотрим на процесс, предложенный авторами метода S3, с анализом действий и результатов.

Вначале формируется матрица U, которая представляет собой многократное копирование исходных данных. Мне бы хотелось исключить данную процедуру, что позволит сократить расход памяти на хранение большой матрицы и вычислительных ресурсов, которые расходуются при копировании данных.

Вторая матрица Ω представляет собой двоичную матрицу, которая в большей части заполнена нулевыми значениями. Количество ненулевых значений равно количеству сегментов в анализируемой последовательности (N). При этом количество нулевых элементов в N - 1 раз больше. Здесь напрашивается использование разреженной матрицы, что позволит сократить как расход памяти, так и вычислительные расходы при умножении матриц.

Далее, согласно алгоритму S3, идет поэлементное умножение матриц, с последующим сложением по последнему измерению, и транспонирование результирующей матрицы.

В результате всех вышеуказанных операций мы просто получаем перемешанный исходный тензор. Обычная операция перестановки элементов тензора потребует меньше ресурсов и будет выполняться быстрее.

Столь "хитроумный" алгоритм перестановки был разработан авторами метода для организации распределения градиента ошибки до вектора приоритетов P. Отчасти это "ловушка" автоматического дифференцирования PyTorch, который использовали авторы метода при построении своего алгоритма.

Мы же сами строим алгоритмы прямого и обратного проходов. Это конечно увеличивает наши затраты на построение алгоритмов, но и дает нам большую гибкость в построении процессов. Поэтому при прямом проходе мы можем заменить вышеуказанные операции на прямую перестановку данных. Очевидно, что это более эффективный подход.

Но остается вопрос распределения градиентов ошибки. Думаю, ни у кого не вызывает сомнения, что при перестановке исходных данных каждый сегмент участвует в тензоре результатов только 1 раз. Следовательно и весь градиент ошибки передается на соответствующий сегмент. Иными словами, при распределении градиента ошибки на исходные данные, нам предстоит осуществить обратную перестановку сегментов. Только на этот раз мы будем работать с тензором градиентов ошибки.

Второй вопрос: распределение градиента ошибки на вектор приоритетов. Здесь алгоритм немного сложнее. При прямом проходе мы используем один приоритет для всего сегмента. Следовательно, при обратном проходе нам предстоит собрать градиент ошибки всего сегмента на одном приоритете. Для этого нам предстоит умножить вектор исходных данных нужного сегмента на соответствующий сегмент тензора градиентов ошибки.

Кроме того, при построении двоичной матрицы Ω использовались коэффициенты масштабирования для приведения ненулевых элементов до 1. Очевидно, что для приведения ненулевого числа до 1 нужно его разделить на это же число или умножить на обратное число. Следовательно, коэффициенты масштабирования равны обратным числам приоритетов. А значит полученное выше значение градиента ошибки необходимо разделить на приоритет сегмента.

Здесь следует обратить внимание, что приоритет сегмента не должен быть равен "0". Использование SoftMax позволяет исключить такой вариант. Но не исключает достаточно малых значений, деление на которые может привести к достаточно большим значениям градиента ошибки.

Кроме того, использование функции SoftMax при формировании вероятностей приоритетов сегментов гарантирует нам все значения в диапазоне (0, 1). И здесь становится очевидно, что сегменты с меньшим приоритетом получают больший градиент ошибки. Так как деление на число меньше 1 дает результат больше делимого.

Определившись с узкими моментами выстраиваемого алгоритма, мы можем перейти к непосредственному воплощению его в коде. И начнем мы с имплементации на стороне OpenCL контекста.

2.2 Построение кернелов OpenCL

Как всегда, мы начинаем работу с реализации алгоритмов прямого прохода. На стороне программы OpenCL первым мы создадим кернел FeedForwardS3.

Здесь я хочу напомнить, что генерацию вероятностей распределения сегментов и веса взвешенного суммирования исходной и перетасованной последовательности мы будем реализовывать во вложенных нейронных слоях. А значит, в данный кернел приходят уже готовые данные в виде параметров.

Поэтому наш кернел получает в параметрах указатели на 5 буферов данных и 2 константы. В 3 буферах содержатся исходные данные: исходная последовательность, вероятности сегментов и коэффициенты взвешивания. А еще 2 буфера предназначены для записи результатов работы кернела. В одном мы запишем результирующую последовательность, а во втором индексы перестановки сегментов, которые нам понадобятся при осуществлении операций обратного прохода.

В константах мы укажем размер окна одного сегмента и общее количество элементов в последовательности.

Здесь следует обратить внимание, что во второй константе мы указываем именно размер вектора исходных данных, а не количество сегментов или временных шагов. В размере окна сегментов мы также указываем количество элементов массива, а не временных шагов. Очевидно, что обе константы должны без остатка делиться на размер вектора одного временного шага.

__kernel void FeedForwardS3(__global float* inputs,
                            __global float* probability,
                            __global float* weights,
                            __global float* outputs,
                            __global float* positions,
                            const int window,
                            const int total
                           )
  {
   int pos = get_global_id(0);
   int segments = get_global_size(0);

Кернел мы планируем запускать в 1-мерном пространстве задач по числу сегментов в анализируемой последовательности. И в теле кернела мы сразу идентифицируем текущий поток, а также определяем общее количество сегментов по числу запущенных заданий.

Для случая, когда общий размер исходных не кратен размеру окна одного сегмента, мы уменьшаем общее количество сегментов на 1.

   if((segments * window) > total)
      segments--;

Следующим шагом нам необходимо отсортировать приоритеты сегментов для определения их последовательности. Однако мы не будем организовывать алгоритм сортировки в чистом виде. Вместо этого мы определим позицию анализируемого сегмента в последовательности. Возможно, это звучит как "игра слов", но для определения позиции 1 элемента нам достаточно 1 прохода по вектору вероятностей сегментов. При сортировке же вектора, нам потребуется несколько проходов по вектору вероятностей и синхронизация вычислительных потоков.

И тут мы разделяем алгоритм на 2 ветке, в зависимости от индекса текущего потока. Первая ветка является общим случаем и используется, если индекс текущего потока меньше количества сегментов. Учитывая, что индекс первого потока равен 0, приведенная формулировка условия может показаться странной. Но давайте вспомним, что выше для случая не кратности размера исходных данных к размеру окна сегментов мы уменьшили значение переменной числа сегментов. И в таком случае последний поток пойдет по 2 ветке алгоритма определения позиции сегмента.

В общем случае, для определения позиции сегмента, соответствующего текущему потоку операций, мы фиксируем в локальной константе его приоритет. И организовываем цикл от первого до текущего сегмента, в котором подсчитываем количество элементов с приоритетом меньше или равным текущему. Для случая сортировки по убыванию, определяем количество элементов с приоритетом больше или равным текущему сегменту.

Затем организовываем цикл от следующего сегмента до последнего, в котором добавляем количество элементов с приоритетом строго меньше (строго больше при сортировке по убыванию).

После завершения операций обоих циклов мы получим позицию текущего сегмента в общей последовательности.

   int segment = 0;
   if(pos < segments)
     {
      const float prob = probability[pos];
      for(int i = 0; i < pos; i++)
        {
         if(probability[i] <= prob)
            segment++;
        }
      for(int i = pos + 1; i < segments; i++)
        {
         if(probability[i] < prob)
            segment++;
        }
     }

Разделение прохода по вектору приоритетов на 2 цикла сделано для частного случая наличия 2-х и более элементов с одинаковым приоритетом. В таком случае приоритет отдается элементу, стоящему раньше в исходной последовательности. Конечно, возможно построение алгоритма и с одним циклом, но в таком случае перед сравнением приоритетов нам пришлось бы на каждой итерации проверять, стоит сегмент до или после текущего в исходной последовательности.

Во второй ветке алгоритма частного случая мы просто присваиваем номер сегмента его порядку в последовательности. Несложно догадаться, что в упомянутом выше частном случае, все полные сегменты будут перемешаны, а последний (не полный) останется на своем месте.

   else
      segment = pos;

Теперь, когда мы определили позицию сегмента в перемешанной последовательности, мы можем переместить его. Для этого определим смещения в буферах исходных данных и результатов.

   const int shift_in = segment * window;
   const int shift_out = pos * window;

Сразу сохраним определенную позицию в соответствующий буфер.

   positions[pos] = (float)segment;

И тут мы вспомним о взвешенном суммировании исходной и перемешанной последовательностей. Естественно, для исключения излишнего копирования данных в буфер результатов мы сохраним сразу взвешенную сумму 2 сегментов из исходной и перемешанной последовательностей. Для этого сохраним в локальные константы параметры взвешивания.

   const float w1 = weights[0];
   const float w2 = weights[1];

И организуем цикл с количеством итераций равным размеру окна одного сегмента, в котором суммируем элементы 2 последовательностей с учетом весовых коэффициентов и сохранением полученных значений в буфер результатов.

   for(int i = 0; i < window; i++)
     {
      if((shift_in + i) >= total || (shift_out + i) >= total)
         break;
      outputs[shift_out + i] = w1 * inputs[shift_in + i] + w2 * inputs[shift_out + i];
     }
  }

После построения кернела прямого прохода, мы переходим к работе над обратным проходом. И здесь мы начинаем работу с построения кернела InsideGradientS3, в котором распределим градиент ошибки до уровня предыдущего слоя и приоритетов сегментов. В параметрах указанного кернела к уже знакомым нам буферам добавляются указатели на буфера соответствующих градиентов ошибки.

__kernel void InsideGradientS3(__global float* inputs,
                               __global float* inputs_gr,
                               __global float* probability,
                               __global float* probability_gr,
                               __global float* weights,
                               __global float* outputs_gr,
                               __global float* positions,
                               const int window,
                               const int total
                              )
  {
   size_t pos = get_global_id(0);

Кернел планируется к запуску в 1-мерном пространстве задач по числу сегментов в анализируемой последовательности. В теле кернела мы сразу идентифицируем текущий поток операций. Определение общего числа сегментов в данном случае избыточное.

Далее загрузим из буферов данных константы, определенные при прямом проходе.

   int segment = (int)positions[pos];
   float prob = probability[pos];
   const float w1 = weights[0];
   const float w2 = weights[1];

После чего определим смещение в буферах данных.

   const int shift_in = segment * window;
   const int shift_out = pos * window;

И объявим локальные переменные для промежуточных данных.

   float grad = 0;
   float temp = 0;

На следующем этапе мы организуем цикл с числом итераций равным размеру окна сегмента, в котором мы соберем градиент ошибки для приоритета сегмента.

   for(int i = 0; i < window; i++)
     {
      if((shift_out + i) >= total)
         break;
      temp = outputs_gr[shift_out + i] * w1;
      grad += temp * inputs[shift_in + i];

И одновременно передадим градиент ошибки в буфер предыдущего слоя. Напомню, что при прямом проходе мы суммировали исходную и перемешанную последовательность. Следовательно, каждый элемент исходных данных должен получить градиент ошибки из 2 потоков с соответствующим весовым коэффициентом.

      inputs_gr[shift_in + i] = temp + outputs_gr[shift_in + i] * w2;
     }

Перед записью градиента ошибки приоритета сегмента в соответствующий буфер данных мы разделим полученное значение на вероятность текущего сегмента.

   probability_gr[segment] = grad / prob;
  }

В рассмотренном выше кернеле распределения градиента ошибки отсутствует один момент — распределение градиента ошибки на весовые коэффициенты исходной и перемешанной последовательностей. Для выполнения этого функционала мы создадим отдельный кернел WeightGradientS3.

Тут надо сказать, что используемый нами общий подход, когда в каждом отдельном потоке собирается градиент ошибки 1 элемента в данном случае мало эффективен. И это связано с малым количеством элементов в векторе весовых коэффициентов. Как можно заметить, здесь их всего 2. Но нам бы хотелось больше параллельных потоков для снижения общих затрат времени на обучения модели. Для достижения этого эффекта мы создадим 2 рабочих группы потоков, каждая из которых будет собирать градиент ошибки для своего параметра.

__kernel void WeightGradientS3(__global float *inputs,
                               __global float *positions,
                               __global float *outputs_gr,
                               __global float *weights_gr,
                               const int window,
                               const int total
                              )
  {
   size_t l = get_local_id(0);
   size_t w = get_global_id(1);

Соответственно, кернел планируется к запуску в 2-мерном пространстве задач. Первое измерение определяет количество параллельных потоков в одной группе. А второе измерение укажет на индекс параметра, для которого собирается градиент ошибки.

Затем мы объявим локальный массив, в элементы которого каждый поток рабочей группы будет сохранять свою часть работы.

   __local float temp[LOCAL_ARRAY_SIZE];

Так как количество рабочих потоков не может быть больше размера объявленного локального массива, то мы вынуждены ограничить количество "рабочих лошадок".

   size_t ls = min((uint)get_local_size(0), (uint)LOCAL_ARRAY_SIZE);

На первом этапе каждый поток собирает свою часть градиентов ошибки независимо от остальных потоков рабочей группы. Для этого мы организовываем цикл перебора элементов буфера градиентов ошибки на выходе текущего слоя от элемента с индексом текущего потока рабочей группы до последнего в массиве с шагом равным количеству "рабочих лошадок".

В теле цикла мы сначала определяем смещение до соответствующего элемента в буфере исходных данных. И надо сказать, это смещение зависит от индекса весового коэффициента, к которому мы собираем градиент ошибки. Для второго весового коэффициента смещение в буферах градиентов ошибки слоя и исходных данных одинаково.

   if(l < ls)
     {
      float val = 0;
      //---
      for(int i = l; i < total; i += ls)
        {
         int shift_in = i;

А вот для первого мы сначала определяем сегмент в буфере градиентов ошибки. Затем из вектора перестановок извлекаем соответствующий сегмент в исходной последовательности. И только потом мы можем вычислить смещение в буфере исходных данных до требуемого элемента.

         if(w == 0)
           {
            int pos = i / window;
            shift_in = positions[pos] * window + i % window;
           }

Имея индексы соответствующих элементов в обоих буферах данных, мы вычисляем градиент ошибки для весового коэффициента в данной позиции и добавляем в накопительную переменную.

         val += outputs_gr[i] * inputs[shift_in];
        }
      temp[l] = val;
     }
   barrier(CLK_LOCAL_MEM_FENCE);

После завершения всех итераций цикла накопленная сумма градиента ошибки записывается в соответствующий элемент массива локальной памяти и организовываем барьер синхронизации потоков рабочей группы.

На втором этапе мы суммируем значение элементов локального массива.

   int t = ls;
   do
     {
      t = (t + 1) / 2;
      if(l < t && (l + t) < ls)
        {
         temp[l] += temp[l + t];
         temp[l + t] = 0;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(t > 1);

И в завершении операций кернела первый поток рабочей группы переносит суммарный градиент ошибки в соответствующий элемент глобального буфера.

   if(l == 0)
      weights_gr[w] = temp[0];
  }

После распределения градиентов ошибки для всех элементов, в соответствии с их влиянием на общий результат, мы обычно переходим к работе над алгоритмами обновления параметров. Но в рамках данной статьи, все обучаемые параметры мы организовали в рамках вложенных нейронных слоев. Следовательно, алгоритмы обновления параметров уже прописаны в рамках упомянутых объектов. Поэтому на данном этапе мы завершаем работу на стороне OpenCL и переходим к работе с основной программой.

2.3.Создание класса CNeuronS3

Для реализации предложенных подходов на стороне основной программы мы создаём новый класс нейронного слоя CNeuronS3. Его структура представлена ниже.

class CNeuronS3   :  public CNeuronBaseOCL
  {
protected:
   uint              iWindow;
   uint              iSegments;
   //---
   CNeuronBaseOCL    cOne;
   CNeuronConvOCL    cShufle;
   CNeuronSoftMaxOCL cProbability;
   CNeuronConvOCL    cWeights;
   CBufferFloat      cPositions;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      feedForwardS3(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradientsS3(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronS3(void)   {};
                    ~CNeuronS3(void)   {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronS3;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual CLayerDescription* GetLayerInfo(void);
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

В нашем классе мы объявляем 2 переменные и 5 вложенных объектов. В переменных мы будем сохранять размер окна одного сегмента и общее количество сегментов в последовательности. А с назначением вложенных объектов мы познакомимся в процессе реализации методов нашего класса.

Все объекты класса объявлены статически, что позволяет нам оставить "пустыми" конструктор и деструктор класса. А инициализация всех вложенных объектов осуществляется в методе Init. Как всегда, в параметрах данного метода мы получаем от вызываемой программы основные параметры архитектуры создаваемого класса. И здесь следует обратить внимание на 2 параметра:

• window — размер окна 1 сегмента;
• numNeurons — количество нейронов в слое.

Особенностью использования указанных параметров является указание количества элементов массива, а не шагов временного ряда. При этом их значение должно быть кратно размеру вектора описания одного временного шага. Иными словами, для простоты реализации мы строим класс работы с одномерным временным рядом, а ответственность за сохранение целостности временных шагов многомерного временного ряда в рамках сегментов лежит на пользователе.

bool CNeuronS3::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                     uint window, uint numNeurons, 
                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch))
      return false;

В теле метода мы сразу вызываем одноименный метод родительского класса, в котором осуществляется контроль полученных параметров и инициализация унаследованных объектов. И конечно, мы не забываем логический результат работы вызываемого метода.

После успешной инициализации унаследованных объектов, мы сохраняем размер окна 1 сегмента и тут же определим общее количество сегментов.

   iWindow = MathMax(window, 1);
   iSegments = (numNeurons + window - 1) / window;

После чего мы приступаем к инициализации внутренних объектов класса. И первым мы инициализируем фиксированный нейронный слой единичных значений, который будет использоваться в качестве исходного для генерации приоритетов перестановки сегментов и параметров взвешенного суммирования последовательностей. Здесь мы сначала инициализируем нейронный слой, а затем принудительно заполняем буфер результатов единичными значениями.

   if(!cOne.Init(0, 0, OpenCL, 1, optimization, iBatch))
      return false;
   CBufferFloat *buffer = cOne.getOutput();
   if(!buffer || !buffer.BufferInit(buffer.Total(),1))
      return false;
   if(!buffer.BufferWrite())
     return false;

И тут следует обратить внимание на 2 момента. Первое, мы создаем слой из 1 нейрона. Как вы помните, во время проработки архитектуры построения нашей реализации мы говорили, что количество нейронов в данном слое укажет на размерность матрицы перестановок. Лично я не вижу целесообразности использования многомерной матрицы. С математической точки зрения без использования промежуточных функций активации линейная функция суммирования произведения нескольких переменных на константу вырождается в произведение одной переменной на используемую константу.

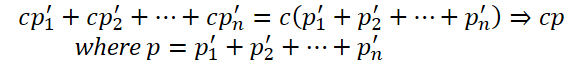
С этой точки зрения, увеличение параметров ведет только к росту вычислительной сложности с сомнительным влиянием на эффективность модели.

С другой стороны, это лишь мое мнение. И я предоставляю вам возможность проверить это экспериментальным путем.

Второй момент, на который стоит обратить внимание — это указание для данного вложенного слоя "0" исходящих связей. Напомню, что мы планируем использовать данный объект в качестве исходных данных для 2 нейронных слоев. Именно наличие 2 последующих слоев нас заставило прибегнуть к небольшой хитрости. Наш базовый нейронный слой построен таким образом, что содержит матрицу весовых коэффициентов только для 1 последующего слоя. Зато у нас есть класс сверточных нейронных слоев, который сам содержит матрицы весовых коэффициентов для входящих связей. Использование 1 элемента на входе и несколько приоритетов перестановок на выходе, мягко говоря, не совсем подходящий сценарий для использования сверточного слоя. Но не спешите.

Один элемент на входе гарантированно дает нам 1 обучаемый параметр в фильтре свертки. А размер вектора перестановок мы легко можем набрать, указав нужное количество фильтров свертки. При этом мы укажем всего лишь 1 элемент свертки. Таким образом мы перенесем обучаемые параметры в последующие нейронные слои.

   if(!cShufle.Init(0, 1, OpenCL, 1, 1, iSegments, 1, optimization, iBatch))
      return false;
   cShufle.SetActivationFunction(None);

Как и обсуждалось ранее, приоритеты перестановок мы переводим в область вероятностей с помощью функции SoftMax.

   if(!cProbability.Init(0, 2, OpenCL, iSegments, optimization, iBatch))
      return false;
   cProbability.SetActivationFunction(None);
   cProbability.SetHeads(1);

Аналогичным образом мы поступаем с объектом генерации параметров взвешенного суммирования последовательностей. Только здесь мы используем сигмоиду в качестве функции активации.

   if(!cWeights.Init(0, 3, OpenCL, 1, 1, 2, 1, optimization, iBatch))
      return false;
   cWeights.SetActivationFunction(SIGMOID);

И в завершении метода инициализации создадим буфер для записи индексов перестановки сегментов.

   if(!cPositions.BufferInit(iSegments, 0) || !cPositions.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Среди методов класса можно заметить 2 новых метода (feedForwardS3 и calcInputGradientsS3). В них организована постановка в очередь выполнения вышесозданных кернелов программы OpenCL. Несложно догадаться, что в первом методе осуществляется постановка в очередь выполнения кернела прямого прохода, а во втором — двух оставшихся кернелов распределения градиентов ошибки. В предыдущих статьях мы уже не раз описывали алгоритм постановки кернела в очередь выполнения. Данные методы построены по аналогичному алгоритму, и мы не будем сейчас останавливаться на их рассмотрении. Вы всегда можете самостоятельно ознакомиться с кодом данных методов во вложении. Там же представлен полный код всех классов и программ, используемых при подготовке статьи.

Алгоритм прямого прохода нашего класса построен в методе feedForward. Как и одноименный метод родительского класса, в параметрах он получает указатель на объект предыдущего нейронного слоя, содержащего исходные данные.

Хочу напомнить, что перед вызовом метода постановки кернела прямого прохода в очередь, нам предстоит подготовить приоритеты перестановок сегментов и параметры взвешивания суммы исходной и перемешанной последовательности. И тут следует обратить внимание, что в качестве исходных данных указанных процессов служит фиксированный вектор единичных значений. А следовательно, их значения не зависят от исходных данных и не меняются в процессе эксплуатации модели. Указанные значения могут лишь измениться при изменении обучаемых параметров в процессе обучения. А значит их пересчет необходим только в процессе обучения. Ну а непосредственный пересчет значений осуществляется путем вызова метода прямого прохода соответствующих вложенных объектов.

bool CNeuronS3::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(bTrain)
     {
      if(!cWeights.FeedForward(cOne.AsObject()))
         return false;
      if(!cShufle.FeedForward(cOne.AsObject()))
         return false;
      if(!cProbability.FeedForward(cShufle.AsObject()))
         return false;
     }

Далее мы осуществляем перемешивание исходной последовательности путем вызова метода постановки кернела прямого прохода в очередь выполнения.

   if(!feedForwardS3(NeuronOCL))
      return false;
//---
   return true;
  }

И, конечно, не забываем контролировать ход выполнения операций.

В алгоритме метод распределения градиентов отсутствуют "подводные камни". Сам метод вызывается только в процессе обучения и нам нет необходимости проверять текущий режим работы модели.

В параметрах метод получает указатель на объект предыдущего слоя, в который необходимо передать градиент ошибки, и мы сразу вызываем метод постановки в очередь вышесозданных кернелов распределения градиентов ошибки.

bool CNeuronS3::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!calcInputGradientsS3(NeuronOCL))
      return false;

Далее мы передаём градиент ошибки на слой параметров приоритетов перемешивания сегментов.

   if(!cShufle.calcHiddenGradients(cProbability.AsObject()))
      return false;

Передавать градиент ошибки далее до уровня фиксированного слоя не имеет смысла. Поэтому мы опустим эту процедуру. И нам остается лишь скорректировать полученный градиент ошибки на возможные функции активации.

   if(cWeights.Activation() != None)
      if(!DeActivation(cWeights.getOutput(), cWeights.getGradient(), cWeights.getGradient(), cWeights.Activation()))
         return false;
   if(NeuronOCL.Activation() != None)
      if(!DeActivation(NeuronOCL.getOutput(),NeuronOCL.getGradient(),NeuronOCL.getGradient(),NeuronOCL.Activation()))
         return false;
//---
   return true;
  }

Обратите внимание, что метод деактивации градиентов ошибки мы вызываем лишь в случае наличия таковой в соответствующем объекте.

После распределения градиента ошибки до всех элементов нашей модели в соответствии с их влиянием на общий результат, нам предстоит скорректировать параметры модели в сторону снижения общей ошибки. И здесь все довольно просто. Для корректировки параметров слоя CNeuronS3 нам достаточно лишь вызвать методы обновления параметров соответствующих вложенных объектов.

bool CNeuronS3::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cWeights.UpdateInputWeights(cOne.AsObject()))
      return false;
   if(!cShufle.UpdateInputWeights(cOne.AsObject()))
      return false;
//---
   return true;
  }

На этом мы завершаем рассмотрение методов нового класса. Объем статьи не позволяет описать алгоритм всех методов нашего нового класса, но вы можете самостоятельно ознакомиться с ними во вложении. Там представлен полный код данного класса и всех его методов.

2.4 Архитектура моделей

После создания класса нового слоя мы внедряем его в архитектуру нашей модели. И я думаю, очевидно, что класс CNeuronS3 мы добавим в архитектуру Энкодера состояния окружающей среды. В рамках данной статьи я не буду подробно останавливаться на архитектуре Энкодера, так как она полностью перенесена из предыдущей статьи. Остановимся лишь на добавленных нейронных слоях, которые мы поместили сразу за слоем исходных данных.

Напомню, что наши тестовые модели построены для анализа исторических данных  на таймфрейме H1. Для анализа мы используем последние 120 баров истории. Каждый из которых описывается 9 параметрами.

#define        HistoryBars             120           //Depth of history
#define        BarDescr                9             //Elements for 1 bar description

В процессе подготовки данной статьи мы внедрили в Энкодер 3 последовательных слоя перемешивания исходных данных. Для первого слоя мы использовали сегменты из 12 временных шагов (часов).

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronS3;
   descr.count = prev_count;
   descr.window = 12*BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Во втором слое мы уменьшили размер сегмента до 4 временных шагов.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronS3;
   descr.count = prev_count;
   descr.window = 4*BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

И в последнем мы перемешивали каждый временной шаг.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronS3;
   descr.count = prev_count;
   descr.window = BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

А далее полностью перенесена архитектура моделей из предыдущей статьи без каких-либо изменений. И следовательно, мы не вносили изменений в алгоритм программ взаимодействия с окружающей средой, обучения и тестирования моделей. С полным кодом всех программ, используемых при подготовке данной статьи, вы можете ознакомиться во вложении.

3. Тестирование

После завершения работы по построению алгоритмов предложенных подходов, мы переходим, наверное, к самому волнующему этапу — тестированию и оценке результатов проделанной работы.

Как уже было сказано выше, в процессе работы над данной статьей мы не вносили изменений в программы взаимодействия с окружающей средой. А значит, для обучения моделей мы можем воспользоваться ранее собранной выборкой обучающих данных.

Напомню, для обучения моделей используются записи проходов программы взаимодействия с окружающей средой в тестере стратегий MetaTrader 5 на реальных исторических данных инструмента EURUSD таймфрейм H1 за полный 2023 год.

На первом этапе мы осуществляем обучение Энкодера состояния окружающей среды. Данная модель обучается прогнозированию данных последующих 24 элементов анализируемого временного ряда.

#define        NForecast               24            //Number of forecast

Иными словами, наша модель пытается спрогнозировать движение цены на последующие сутки. Сразу скажу, что при построении политики поведения нашего Агента мы опираемся не на полученный прогноз, а на скрытое состояние Энкодера. Поэтому в процессе обучения модели нам не столько важен точный прогноз предстоящего движения, сколько способность Энкодера уловить и зашифровать в своем скрытом состоянии основные тренды и тенденции предстоящего ценового движения.

Модель Энкодера обучается только анализу рыночного состояния без учета состояния счета и открытых позиций. Поэтому в процессе обучения данной модели обновление обучающей выборки не даст дополнительной информации. Что позволяет обучать модель на ранее созданной выборке до получения желаемого результата.

И конечно, по результатам первого этапа обучения нам интересно влияние нашего нового слоя на исходные данные, получаемые моделью. Тут я должен отметить, что модель практически в равной степени уделяет внимание перемешанной и исходной последовательностям. Последней - немножко больше.

На первом слое коэффициент перемешанной последовательности составил 0.5039, а исходной последовательности 0.5679. В то же время, наблюдается практически полное перемешивание последовательности. Случайным образом только сегмент с индексом 7 остался на своей позиции. При этом перемешивание не является зеркальным. Нет ни одной пары элементов, которые бы просто поменялись местами.

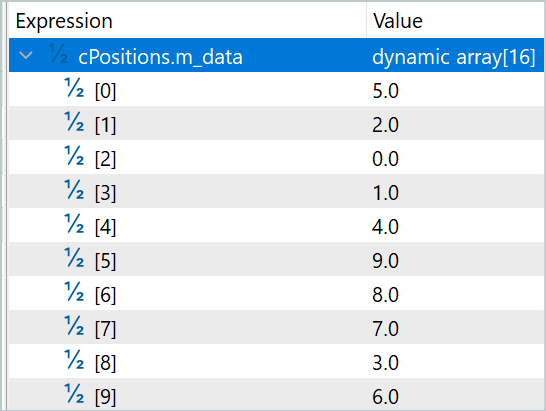
На следующем слое оба коэффициента немного увеличились до 0.6386 и 0.6574 соответственно. Список перестановок не привожу, так как он увеличился в 3 раза. Но в нем уже отсутствуют сегменты без перемещений.

В третьем слое больше внимания уделяется исходной последовательности, но коэффициент при перемешанной последовательности остается довольно высоким. Параметры изменились до 0.5064 и 0.7089, соответственно.

Можно по-разному оценивать полученные результаты. На мой взгляд, модель ищет рациональное зерно в попарном сопоставлении сегментов.

Полученный результат довольно интересен, но нас больше интересует влияние на финальную политику Агента. После обучения Энкодера мы переходим ко второму этапу обучения наших моделей. На этом этапе осуществляется обучение политики Актера и модели Критика. Работа данных моделей сильно зависит от состояния счета и открытых позиций в анализируемом моменте. Следовательно, процесс обучения наш будет итерационный с чередованием обучения моделей и сбора дополнительных данных взаимодействия с окружающей средой, которые позволят уточнить и оптимизировать политику поведения Агента.

В процессе обучения нам удалось обучить политику, способную генерировать прибыль как на обучаемом, так и на тестовом периоде. Результаты обучения приведены ниже.

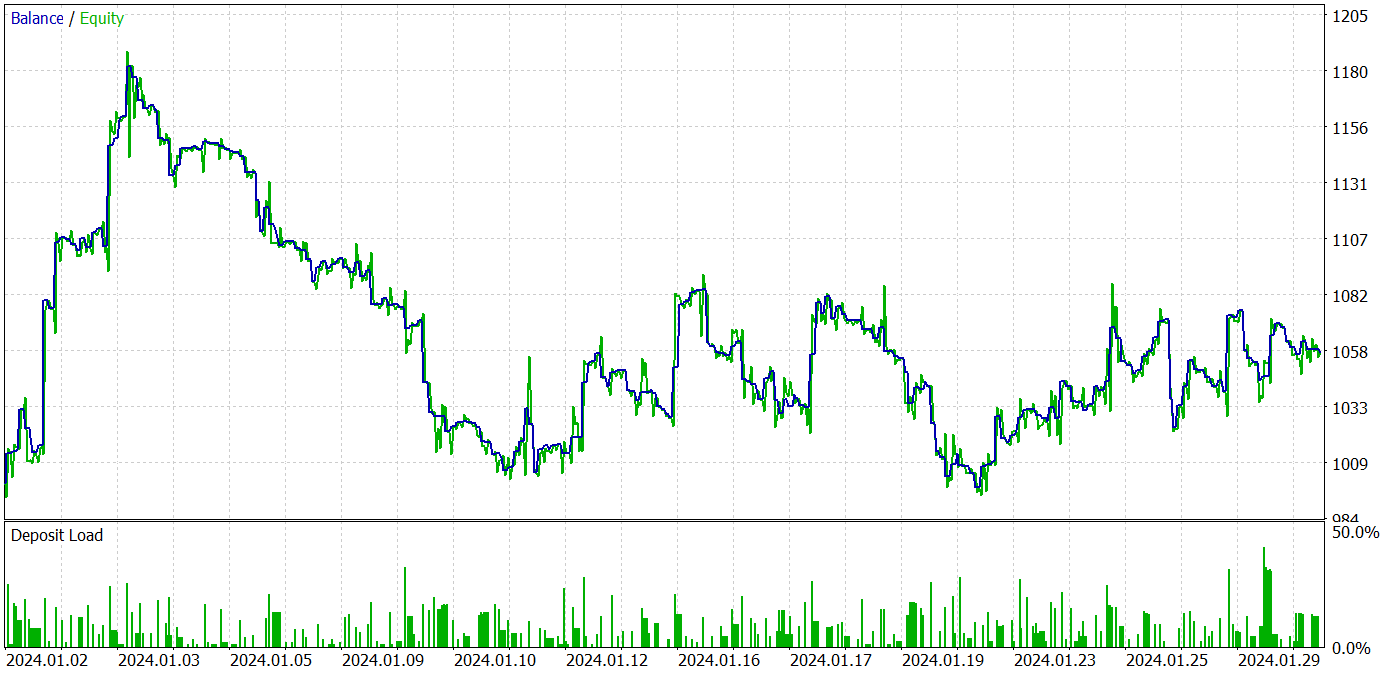
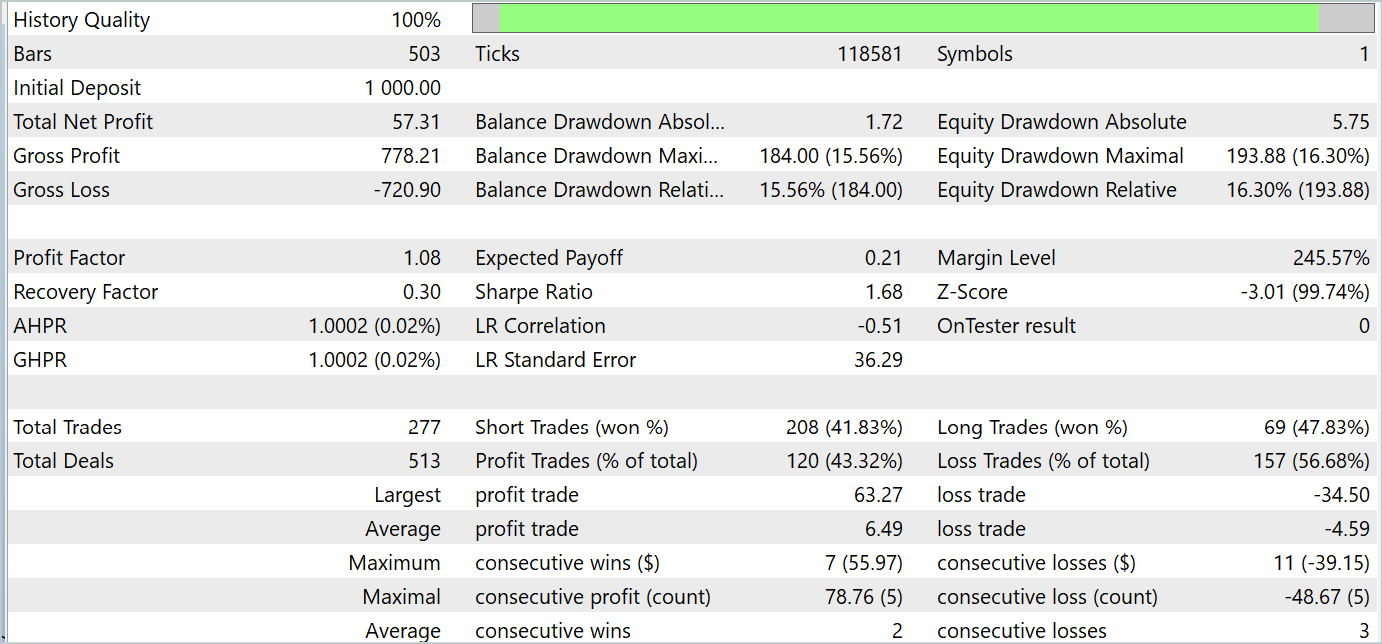
Несмотря на полученную прибыль, график баланса далек от желаемого. И модель еще требует доработок. И если более внимательно посмотреть на отчет тестирования, то можно выделить наиболее убыточные понедельник и пятницу. В среду же напротив, модель генерирует максимальную прибыль.

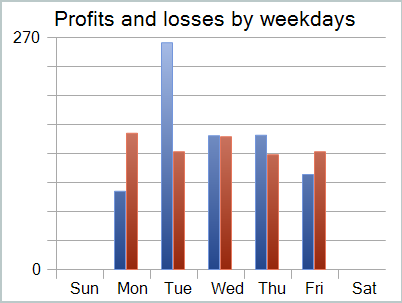
Следовательно, ограничение работы модели в отдельные дни недели позволит поднять общую доходность модели. Но эта гипотеза требует более детального тестирования на более репрезентативной выборке данных.

Заключение

В данной статье мы познакомились с довольно интересным методом оптимизации последовательности временных рядов S3, который был представлен в статье "Segment, Shuffle, and Stitch: A Simple Mechanism for Improving Time-Series Representations". Основная идея метода — повышение качества представления временных рядов. Применение S3 приводит к увеличению точности классификации и устойчивости моделей.

В практической части нашей статьи мы построили свое видение предложенных подходов средствами MQL5. Провели обучение и тестирование моделей с использованием предложенных подходов. И  результаты довольно интересные.

Ссылки

• Segment, Shuffle, and Stitch: A Simple Mechanism for Improving Time-Series Representations
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник обучения Моделей
4	StudyEncoder.mq5	Советник	Советник обучения Энкодера
5	Test.mq5	Советник	Советник для тестирования модели
6	Trajectory.mqh	Библиотека класса	Структура описания состояния системы
7	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
8	NeuroNet.cl	Библиотека	Библиотека кода программы OpenCL