Нейросети — это просто (Часть 91): Прогнозирование в частотной области (FreDF)
Введение
Прогнозирование временных рядов будущих цен имеет критическое значение в различных сценариях работы на финансовых рынках. И большинство существующих на данный момент методов построены на наличии автокорреляции в данных. Иными словами, мы эксплуатируем наличие зависимости между временными шагами, которая существует как в исходных данных, так и в прогнозируемых значениях.
В последнее время набирают популярность модели на основе архитектуры Transformer, использующие механизмы Self-Attention для динамической оценки автокорреляции. Одновременно наблюдается повышение интереса к использованию частотного анализа в модели прогнозирования. Представляя последовательность исходных данных в частотной области, можно обойти сложность описания автокорреляции, что повышает эффективность различных моделей.
Ещё одним важным аспектом является автокорреляция в последовательности прогнозируемых значений. Ведь очевидно, что прогнозируемые значения являются частью более крупного временного ряда, который включает анализируемую и прогнозируемую последовательности. Следовательно, прогнозные значения сохраняют зависимости анализируемых данных. Но это явление часто игнорируется в современных методах прогнозирования. В частности, современные методы преимущественно используют парадигму прямого прогнозирования (Direct Forecast — DF), которая генерирует многоэтапные прогнозы одновременно. А это неявно предполагает независимость шагов в последовательности прогнозных значений. Такое несоответствие между предположениями модели и характеристиками данных приводит к неоптимальному качеству прогнозов.
Одно из решений указанной проблемы было предложено в статье "FreDF: Learning to Forecast in Frequency Domain". В ней авторы предложили метод прямого прогнозирования с частотным усилением (FreDF). Он уточняет парадигму DF, выравнивая прогнозные значения и последовательность меток в частотной области. При переходе в частотную область, где основания ортогональны и независимы, влияние автокорреляции эффективно уменьшается. Таким образом, FreDF обходит несоответствие между предположением о DF и существованием автокорреляции меток, сохраняя при этом преимущества DF.
Авторы метода проверяют его эффективность в ряде экспериментов, которые демонстрируют существенное превосходство предложенного подхода над современными методами.
1. Алгоритм FreDF
Парадигма DF использует модель с несколькими выходами ɡθ для создания прогнозов на T шагов Ŷ = ɡθ(X). Пусть Yt — это t-й шаг Y, а Yt(n) будет n-м выборочным наблюдением. Параметры модели θ оптимизируются путем минимизации среднеквадратической ошибки (MSE):
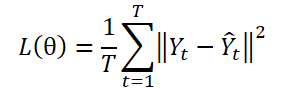
Парадигма DF вычисляет ошибку прогнозирования на каждом этапе независимо, рассматривая каждый элемент последовательности как отдельную задачу. Однако данный подход не учитывает автокорреляцию, присутствующую в Y, что противоречит наличию автокорреляции меток. И как следствие, это приводит к смещению правдоподобия и отклонению от принципа максимального правдоподобия во время обучения модели.
Одной из стратегий преодоления указанного ограничения является представление последовательности меток в преобразованном домене, образованном ортогональными базисами. В частности, это можно эффективно реализовать с помощью преобразования Фурье, которое проецирует последовательность на ортогональные базисы, связанные с разными частотами. Преобразуя последовательность меток в ортогональную частотную область, можно эффективно уменьшить зависимость от автокорреляции меток.

где i — мнимая единица, определяемая как √(-1),
exp(•) — это базис Фурье, связанный с частотой k, является ортогональным для различных значений k.
Благодаря ортогональности базиса, представление последовательности меток в частотной области обходит зависимость, возникающую в результате автокорреляции во временной области. Это подчеркивает потенциал обучения прогнозированию в частотной области.
При классическом использовании подходов DF, в заданную временную отметку n историческая последовательность Xn вводится в модель для генерации прогнозов на T шагов, обозначенных как Ŷn=ɡθ(Xn). И рассчитывается ошибка прогноза во временной области Ltmp.
В дополнение к каноническому подходу, авторы метода FreDF предлагают преобразовывать прогнозные значения и последовательности меток в частотную область. Тогда ошибка прогнозирования в частотной области рассчитывается по формуле:

Здесь каждый член суммирования представляет собой матрицу комплексных чисел A, |A| обозначает операцию вычисления и суммирования модуля каждого элемента в матрице. При этом модуль комплексного числа a = ar + i ai вычисляется как √(ar^2 + ai^2).
Обратите внимание, что из-за различных числовых характеристик последовательности меток в частотной области, авторы метода FreDF не используют форму квадрата потерь (MSE), как это типично для вычисления ошибки потерь во временной области. В частности, различные частотные компоненты часто имеют сильно различающиеся величины: более низкие частоты имеют больший объем – на несколько порядков, по сравнению с более высокими частотами, что делает методы квадратичных потерь нестабильными.
Ошибки прогнозирования во временной и частотной областях объединяются с использованием коэффициента α в диапазоне значений [0,1], который контролирует относительную силу выравнивания частотной области:
![]()
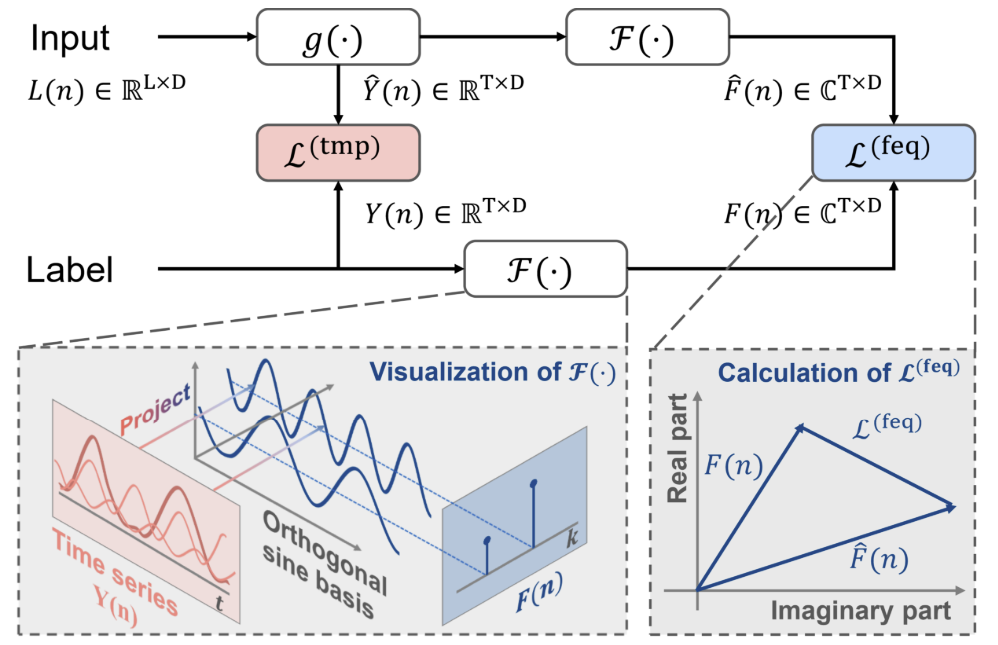
FreDF обходит эффект автокорреляции целевых значений путем выравнивания сгенерированных прогнозных значений и последовательности меток в частотной области. При этом сохраняются преимущества DF, такие как эффективный вывод и возможности многозадачности. Примечательное свойство FreDF заключается в его совместимости с различными моделями прогнозирования и преобразованиями. Эта гибкость значительно расширяет потенциальную сферу применения FreDF.
Авторская визуализация метода представлена ниже.
2. Реализация средствами MQL5
После рассмотрения теоретических аспектов предложенного метода FreDF, мы переходим к практической части нашей статьи, в которой реализуем свое видение предложенного подхода. Из представленного выше теоретического описания можно сделать вывод, что предложенный подход, по существу, не вносит каких-либо конструктивных особенностей в архитектуру модели. Более того, он не оказывает влияние на работу модели в процессе эксплуатации. Его действие можно заметить только в процессе обучения модели. Наверное, предложенный метод FreDF можно сравнить с некой сложной функцией потерь. И её мы будем использовать для обучения модели, целевые метки которой по нашим априорным знаниям имеют автокорреляционные зависимости.
И прежде, чем приступить к построению нового объекта для реализации предложенных подходов, стоит отметить, что для трансформации данных из временного ряда в частотную область авторы метода использовали преобразование Фурье. Надо сказать, что метод FreDF довольно гибкий. Он хорошо работает и с другими методами преобразования данных в ортогональный домен. Авторы метода проводят ряд экспериментов и демонстрируют его эффективность при использовании других преобразований. Результаты указанных экспериментов представлены ниже.

Как можно заметить, модели с использованием преобразования Фурье демонстрируют лучшие результаты.
Сразу хочу обратить внимание на коэффициент α. Его значение около 0.8 выглядит оптимальным по результатам проведенных экспериментов. Следует отметить, что прогнозирование только в частотной области (использование α равным 1) по результатам тех же экспериментов ведет к снижению точности работы модели.
Из этого можно сделать вывод, что для получения оптимальной модели прогнозирования временных рядов, в процессе обучения нам необходимо учитывать как временную, так и частотную области изучаемого сигнала. Различные представления позволяют получить больше информации о сигнале и, как следствие, обучить более эффективную модель.
Но вернемся к нашей реализации. По результатам экспериментов авторов метода, преобразование Фурье позволяет обучить модели с меньшей погрешностью прогнозирования. Напомню, что в предыдущей работе мы уже реализовали прямое и обратное быстрое преобразование Фурье. И в данной реализации мы можем воспользоваться этими наработками.
Для реализации подходов FreDF мы создадим новый класс CNeuronFreDFOCL, который унаследует основной функционал от базового класса нейронных слоев CNeuronBaseOCL. Структура нового класса представлена ниже.
class CNeuronFreDFOCL : public CNeuronBaseOCL { protected: uint iWindow; uint iCount; uint iFFTin; bool bTranspose; float fAlpha; //--- CBufferFloat cForecastFreRe; CBufferFloat cForecastFreIm; CBufferFloat cTargetFreRe; CBufferFloat cTargetFreIm; CBufferFloat cLossFreRe; CBufferFloat cLossFreIm; CBufferFloat cGradientFreRe; CBufferFloat cGradientFreIm; CBufferFloat cTranspose; //--- virtual bool FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false); virtual bool Transpose(CBufferFloat *inputs, CBufferFloat *outputs, uint rows, uint cols); virtual bool FreqMSA(CBufferFloat *target, CBufferFloat *forecast, CBufferFloat *gradient); virtual bool CumulativeGradient(CBufferFloat *gradient1, CBufferFloat *gradient2, CBufferFloat *cummulative, float alpha); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) { return true; } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); public: CNeuronFreDFOCL(void) {}; ~CNeuronFreDFOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint count, float alpha, bool need_transpose = true, ENUM_OPTIMIZATION optimization_type = ADAM, uint batch = 1); virtual bool calcOutputGradients(CArrayFloat *Target, float &error); //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual int Type(void) const { return defNeuronFreDFOCL; } virtual void SetOpenCL(COpenCLMy *obj); };
В представленной структуре нового класса можно заметить 2 особенности:
- внутренние объекты представлены только буферами данных и нет внутренних слоев;
- переопределение метода calcOutputGradients.
Сюда можно добавить еще одну неявную особенность, данный объект не содержит обучаемых параметров, что довольно редко встречается. И все указанные особенности связаны с назначением класса — мы создаем класс сложной функции потерь, а не обучаемого нейронного слоя. И метод calcOutputGradients в нашей архитектуре нейронных слоев отвечает за вычисление отклонений прогнозных значений от целевых. А с назначением внутренних объектов и переменных я предлагаю познакомиться в процессе реализации методов класса.
Все внутренние объекты были объявлены статично, что позволяет нам оставить "пустыми" конструктор и деструктор класса. При этом работу по очистке памяти мы оставим системе.
Инициализация объектов класса осуществляется в методе Init. Как обычно, в параметрах данного метода мы передаем основные константы, определяющие архитектуру класса. Здесь мы видим:
- окно описания одного элемента исходных данных (window),
- количество элементов в последовательности (count),
- коэффициент силы выравнивания частотной и временной областей (alpha),
- флаг указания необходимости транспонирования данных для частотного преобразования (need_transpose).
Первое, что следует сказать: данный объект мы планируем использовать на выходе модели. Следовательно на вход поступают прогнозные значения, сгенерированные нашей моделью. Данные должны поступать в формате, сопоставимом с целевыми результатами. И здесь параметры window и count соответствуют как прогнозным, так и целевым значениям. При этом мы предоставляем возможность пользователю осуществлять преобразование данных в частотную область в другой плоскости. Именно для этого мы ввели флаг need_transpose.
Здесь стоит привести результаты ещё одних экспериментов, проведенных авторами метода. Они проверили результативность моделей при проведении сравнения частотных характеристик в унитарных временных рядах многомерной последовательности (T), в разрезе отдельных временных шагов (D) и для совокупной последовательности (2D).

Наилучшие результаты продемонстрировала модель с представлением частотных характеристик общей совокупной последовательности. При этом сравнение частотных характеристик отдельных временных шагов оказалось аутсайдером эксперимента. А анализ частотных характеристик унитарных временных рядов занял почетное 2 место с незначительным отставанием от лидера.
Мы же, в своей реализации, предоставляем пользователю самостоятельно выбрать измерение для частотного преобразования путем указания соответствующего значения флага need_transpose. Для сравнения 2-мерных частотных характеристик достаточно указать размер всей последовательности в параметр window, а для остальных параметров указать следующие значения:
- count: 1,
- need_transpose: false.
bool CNeuronFreDFOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint count, float Alpha, bool need_transpose = true, ENUM_OPTIMIZATION optimization_type = ADAM, uint batch = 1) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * count, optimization_type, batch)) return false;
В теле метода мы сначала вызываем одноименный метод родительского класса и проверяем результат выполнения операций. Напомню, что в родительском классе реализован минимально-необходимый набор контролей, включая размер создаваемого нейронного слоя. И в качестве размера слоя мы указываем произведение переменных window и count. Очевидно, что стоит лишь в одном из них указать нулевое значение, как все произведение будет равно "0", и метод родительского класса завершится с ошибкой.
После успешного выполнения метода родительского класса, мы сохраняем полученные значения в локальные переменные.
bTranspose = need_transpose; iWindow = window; iCount = count; fAlpha = MathMax(0, MathMin(Alpha, 1)); activation = None;
Тут следует вспомнить, что для быстрого преобразования Фурье нам необходимы буферы размером со степенью 2. Рассчитаем размеры буферов данных:
//--- Calculate FFTsize uint size = (bTranspose ? count : window); int power = int(MathLog(size) / M_LN2); if(MathPow(2, power) != size) power++; iFFTin = uint(MathPow(2, power));
Следующим шагом мы инициализируем внутренние буферы данных. Первыми мы инициализируем буферы частотных характеристик прогнозных значений. Мы будем использовать конструкцию из 2 буферов данных. Один для записи данных вещественной составляющей, а второй — для мнимой.
//--- uint n = (bTranspose ? iWindow : iCount); if(!cForecastFreRe.BufferInit(iFFTin * n, 0) || !cForecastFreRe.BufferCreate(OpenCL)) return false; if(!cForecastFreIm.BufferInit(iFFTin * n, 0) || !cForecastFreIm.BufferCreate(OpenCL)) return false;
Далее мы создаем аналогичные буферы для частотных характеристик целевых значений:
if(!cTargetFreRe.BufferInit(iFFTin * n, 0) || !cTargetFreRe.BufferCreate(OpenCL)) return false; if(!cTargetFreIm.BufferInit(iFFTin * n, 0) || !cTargetFreIm.BufferCreate(OpenCL)) return false;
Ошибку прогнозирования запишем в буферы cLossFreRe и cLossFreIm:
if(!cLossFreRe.BufferInit(iFFTin * n, 0) || !cLossFreRe.BufferCreate(OpenCL)) return false; if(!cLossFreIm.BufferInit(iFFTin * n, 0) || !cLossFreIm.BufferCreate(OpenCL)) return false;
Здесь стоит отметить важность сравнения обоих составляющих частотных характеристик. Ведь для корректного прогнозирования временных рядов нам важны как амплитуды, так и фазы частотных характеристик временного ряда.
И обязательно создадим буферы для записи градиентов ошибки на уровне прогнозных значений временного ряда:
if(!cGradientFreRe.BufferInit(iFFTin * n, 0) || !cGradientFreRe.BufferCreate(OpenCL)) return false; if(!cGradientFreIm.BufferInit(iFFTin * n, 0) || !cGradientFreIm.BufferCreate(OpenCL)) return false;
Конечно, в целях экономии памяти мы можем отказаться от буферов cGradientFreRe и cGradientFreIm. Они безболезненно могут быть заменены, к примеру, на буферы cForecastFreRe и cForecastFreIm. Но их наличие делает код более читабельным. А используемый ими в нашем случае объем памяти не критичен.
В завершении мы создадим буфер временной для записи транспонированных значений, конечно, если это требуется:
if(!cTranspose.BufferInit(iWindow * iCount, 0) || !cTranspose.BufferCreate(OpenCL)) return false; //--- return true; }
После инициализации данных, мы обычно создаем метод прямого прохода. Выше уже было сказано, что объект данного класса не осуществляет операций с данными в процессе эксплуатации. А как вы знаете, метод прямого прохода описывает операции режима эксплуатации модели. Казалось бы, мы можем метод прямого прохода переопределить "пустышкой", но тогда становится вопрос передачи данных. При этом, мы бы хотели минимизировать процесс копирования данных, ведь объем данных может быть различным, и добавляются "накладные расходы" на организацию процесса. В этом контексте мы создали метод прямого прохода максимально простым, каким только можно было создать. В нем мы лишь проверяем соответствие указателей на буферы результатов в текущем и предыдущем слое. При необходимости мы заменяем указатель в текущем слое на буфер результатов предыдущего слоя.
bool CNeuronFreDFOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL || !NeuronOCL.getOutput()) return false; if(NeuronOCL.getOutput() != Output) { Output.BufferFree(); delete Output; Output = NeuronOCL.getOutput(); } //--- return true; }
Таким образом подмена указателя на один буфер заменяет нам процесс переноса данных вне зависимости от их объема. Обратите внимание, что контроль осуществляется на каждом проходе, а подмена буферов данных только при первом из них.
Основной функционал класса мы реализуем для обратного прохода. И здесь вначале мы проведем небольшую подготовительную работу. Для полноценной реализации требуемого функционала мы создадим 2 небольших кернела на стороне OpenCL программы.
Авторы метода FreDF рекомендуют использовать MAE в качестве функции потерь при оценке отклонений в частотной области и отмечают снижение стабильности обучения при использовании MSE. Напомню, что в нашем базовом нейронном слое CNeuronBaseOCL используется именно MSE для определения градиента ошибки. А значит, нам необходимо создать кернел для определения градиента ошибки прогнозных значений с помощью MAE. С математической точки зрения это довольно просто: нам достаточно из вектора целевых меток вычесть вектор прогнозных значений.
__kernel void GradientMSA(__global float *matrix_t, __global float *matrix_o, __global float *matrix_g ) { int i = get_global_id(0); matrix_g[i] = matrix_t[i] - matrix_o[i]; }
После определения градиента ошибки в частотной и временной областях, нам необходимо объединить градиенты ошибки с использованием коэффициента температуры. Этот функционал мы выполним в кернеле CumulativeGradient, понимание алгоритма которого, думаю, не вызовет труда.
__kernel void CumulativeGradient(__global float *gradient_freq, __global float *gradient_tmp, __global float *gradient_out, float alpha ) { int i = get_global_id(0); gradient_out[i] = alpha * gradient_freq[i] + (1 - alpha) * gradient_tmp[i]; }
Напомню, что для преобразования данных из временной области в частотную и обратно мы будем использовать алгоритм быстрого преобразования Фурье, который реализовали в предыдущей статье. Там же вы найдете описание используемого алгоритма и метода постановки кернела в очередь выполнения.
В данной статье мы не будем останавливаться на рассмотрении алгоритмов методов постановки кернелов в очередь выполнения. Они все построены по единой схеме, которая была уже не раз представлена в статьях данной серии, включая предыдущую.
Рассмотрим метод CNeuronFreDFOCL::calcOutputGradients, в котором реализован основной функционал нашего класса. Как вы знаете, по структуре наших моделей в данном методе определяется ошибка отклонения прогнозных значений модели от целевых меток. В параметрах метода мы получаем указатель на буфер целевых значений. А после выполнения операций метода, нам предстоит сохранить градиент ошибки в соответствующий буфер текущего слоя.
bool CNeuronFreDFOCL::calcOutputGradients(CArrayFloat *Target, float &error) { if(!Target) return false; if(Target.Total() < Output.Total()) return false;
В теле метода мы проверяем корректность полученного указателя на буфер целевых значений. А также его размер должен быть не менее тензора результатов нашей модели.
Так как полученный буфер может не иметь своей копии на стороне OpenCL контекста, то нам предстоит создать её там для последующих вычислений. Однако для более экономного использования ресурсов OpenCL-контекста, полученные данные мы перенесем в уже созданный буфер градиентов.
if(Target.Total() == Output.Total()) { if(!Gradient.AssignArray(Target)) return false; } else { for(int i = 0; i < Output.Total(); i++) { if(!Gradient.Update(i, Target.At(i))) return false; } } if(!Gradient.BufferWrite()) return false;
И здесь есть 2 варианта развития событий. Если размеры буферов целевых меток и прогнозных значений равны, то мы используем существующий метод копирования. В противном случае мы используем цикл для переноса требуемого числа значений. И в любом случае, после копирования данных мы переносим их в память OpenCL контекста.
Далее полученные данные используются для вычисления отклонений как во временной области, так и в частотной. И здесь стоит обратить внимание, что при вычислении отклонений во временной области, буфер градиентов ошибки нашего слоя будет перезаписан вычисленными отклонениями с полной потерей полученных целевых значений. Поэтому, перед вычислением отклонений во временной области, нам как минимум, необходимо разложить полученный временной ряд целевых меток на частотные составляющие.
И тут мы вспоминаем о возможности разложения временного ряда на частотные характеристики в двух измерениях. Выбор которого определяется по значению флага bTranspose. Если флагу присвоено значение true, то мы сначала транспонируем буфер результатов модели, а затем раскладываем его на частотные характеристики:
if(bTranspose) { if(!Transpose(Output, GetPointer(cTranspose), iWindow, iCount)) return false; if(!FFT(GetPointer(cTranspose), NULL, GetPointer(cForecastFreRe), GetPointer(cForecastFreIm), false)) return false;
Аналогичные операции выполняем для тензора целевых меток:
if(!Transpose(Gradient, GetPointer(cTranspose), iWindow, iCount)) return false; if(!FFT(GetPointer(cTranspose), NULL, GetPointer(cTargetFreRe), GetPointer(cTargetFreIm), false)) return false; }
Если значение флага bTranspose равно false, то выполняем разложение целевых и прогнозных значений на соответствующие частотные характеристики без предварительного транспонирования:
else { if(!FFT(Output, NULL, GetPointer(cForecastFreRe), GetPointer(cForecastFreIm), false)) return false; if(!FFT(Gradient, NULL, GetPointer(cTargetFreRe), GetPointer(cTargetFreIm), false)) return false; }
После определения частотных характеристик, мы можем рассчитать отклонения как во временной области, так и в частотной без боязни утраты целевых значений.
if(!FreqMSA(GetPointer(cTargetFreRe), GetPointer(cForecastFreRe), GetPointer(cLossFreRe))) return false; if(!FreqMSA(GetPointer(cTargetFreIm), GetPointer(cForecastFreIm), GetPointer(cLossFreIm))) return false; if(!FreqMSA(Gradient, Output, Gradient)) return false;
Здесь стоит обратить внимание, что в частотной области мы определяем отклонения как по вещественной, так и по мнимой части частотной характеристики. Ведь значение фазового сдвига не менее важно, чем амплитуда сигнала. Однако мы не можем на прямую обетонить градиенты ошибок временной и частотной областей. Ведь здесь очевидна несопоставимость данных. Поэтому, предварительно нам нужно вернуть градиенты ошибки частотных характеристик во временную область. Для этого мы воспользуемся обратным преобразованием Фурье.
if(!FFT(GetPointer(cLossFreRe), GetPointer(cLossFreIm), GetPointer(cGradientFreRe), GetPointer(cGradientFreIm), true)) return false;
После приведения градиентов ошибок временной и частотной областей в сопоставимый вид, следует вспомнить, что измерение извлечения частотных характеристик зависит от значения флага bTranspose. Следовательно, градиент ошибки частотной области нам необходимо трансформировать в соответствии со значением флага. И только потом мы можем определить совокупный градиент ошибки нашей модели.
if(bTranspose) { if(!Transpose(GetPointer(cGradientFreRe), GetPointer(cTranspose), iCount, iWindow)) return false; if(!CumulativeGradient(GetPointer(cTranspose), Gradient, Gradient, fAlpha)) return false; } else if(!CumulativeGradient(GetPointer(cGradientFreRe), Gradient, Gradient, fAlpha)) return false; //--- return true; }
Не забываем контролировать процесс выполнения операций на каждом шаге. И логическое значение выполненных операций возвращаем вызывающей программе.
После определения градиента ошибки на выходе модели, нам предстоит передать его на предыдущий слой. Как вы знаете, этот функционал мы выполняем в методе CNeuronFreDFOCL::calcInputGradients, который в параметрах получает указатель на объект предшествующего нейронного слоя.
Здесь стоит вспомнить, что наш слой не содержит обучаемых параметров. При прямом проходе мы осуществили подмену буфера данных, и в качестве результатов показываем значения предыдущего слоя. В чем же задача указанного метода? Все очень просто. Нам лишь предстоит скорректировать посчитанный выше совокупный градиент ошибки на функцию активации предыдущего слоя.
bool CNeuronFreDFOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false; //--- return DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), Gradient, NeuronOCL.Activation()); }
Ну а так как наш класс не содержит обучаемых параметров, то и метод updateInputWeights мы переопределяем "пустой заглушкой".
Отсутствие обучаемых параметров в классе накладывает отпечаток и на методы работы с файлами. Ведь нам нет необходимости сохранять внутренние объекты, данные которых не имеют ценности. Следовательно, при сохранении данных мы лишь вызываем одноименный метод родительского класса.
bool CNeuronFreDFOCL::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false;
И сохраняем значения переменных, описывающих конструктивные особенности объекта:
if(FileWriteInteger(file_handle, int(iWindow)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iCount)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iFFTin)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(bTranspose)) < INT_VALUE) return false; if(FileWriteFloat(file_handle, fAlpha) < sizeof(float)) return false; //--- return true; }
Немного сложнее выглядит алгоритм восстановления объекта из файла данных Load. Здесь мы сначала восстанавливаем элементы родительского класса:
bool CNeuronFreDFOCL::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false;
Затем загружаем данные переменных в порядке их сохранения, при этом не забывая проверять достижения конца файла данных:
if(FileIsEnding(file_handle)) return false; iWindow = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iCount = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iFFTin = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; bTranspose = bool(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; fAlpha = FileReadFloat(file_handle);
И далее нам предстоит инициализировать вложенные объекты в соответствии с загруженными параметрами архитектуры класса. Инициализация объектов осуществляется аналогично алгоритму инициализации нового экземпляра класса:
uint n = (bTranspose ? iWindow : iCount); if(!cForecastFreRe.BufferInit(iFFTin * n, 0) || !cForecastFreRe.BufferCreate(OpenCL)) return false; if(!cForecastFreIm.BufferInit(iFFTin * n, 0) || !cForecastFreIm.BufferCreate(OpenCL)) return false; if(!cTargetFreRe.BufferInit(iFFTin * n, 0) || !cTargetFreRe.BufferCreate(OpenCL)) return false; if(!cTargetFreIm.BufferInit(iFFTin * n, 0) || !cTargetFreIm.BufferCreate(OpenCL)) return false; if(!cLossFreRe.BufferInit(iFFTin * n, 0) || !cLossFreRe.BufferCreate(OpenCL)) return false; if(!cLossFreIm.BufferInit(iFFTin * n, 0) || !cLossFreIm.BufferCreate(OpenCL)) return false; if(!cGradientFreRe.BufferInit(iFFTin * n, 0) || !cGradientFreRe.BufferCreate(OpenCL)) return false; if(!cGradientFreIm.BufferInit(iFFTin * n, 0) || !cGradientFreIm.BufferCreate(OpenCL)) return false; if(bTranspose) { if(!cTranspose.BufferInit(iWindow * iCount, 0) || !cTranspose.BufferCreate(OpenCL)) return false; } else { cTranspose.BufferFree(); cTranspose.Clear(); } //--- return true; }
На этом мы завершаем рассмотрение методов нового класса CNeuronFreDFOCL. А с полным кодом данного класса вы можете познакомиться во вложении.
После построения методов нового класса, мы обычно переходим к описанию архитектуры обучаемых моделей. Но в данной статье мы построили не совсем обычный нейронный слой. Точнее, мы реализовали сложную функцию потерь в виде нейронного слоя. И по существу, мы можем добавить выше созданный объект к одной из обученных нами ранее модели, переобучить её и посмотреть на изменение результатов. Для своих экспериментов я выбрал модель FEDformer, архитектура которой описана здесь. И добавил к ней новый слой.
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- ........ ........ //--- layer 17 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Должен сказать, что немного подумав, я решил расширить эксперимент. Ведь авторы метода FreDF предложили свой алгоритм для учета зависимостей в прогнозируемых результатах. По большому счету, между отдельными параметрами результатов нашего Актера так же существует зависимость. К примеру, объемы сделок на покупку и продажу являются взаимоисключающими, ведь в любой момент времени у нас открыта позиция только в одном направлении. Параметры стоп-лосса и тейк-профита определяют силу наиболее вероятного предстоящего движения. Следовательно, тейк-профит длинной позиции должен в какой-то мере коррелировать со стоп-лоссом короткой позиции и наоборот. Аналогичными рассуждениями можно предположить зависимости и в прогнозных значениях Критика. А почему бы нам не расширить эксперимент и на указанные модели? Сказано — сделано. Добавляем новый слой в модели Актера и Критика:
bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; } //--- Actor ......... ......... //--- layer 17 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NActions; descr.count = 1; descr.step = int(false); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- Critic ......... ......... //--- layer 17 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NRewards; descr.count = 1; descr.step = int(false); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
Обратите внимание, что в данном случае мы анализируем частотные характеристики всей последовательности результатов, а не отдельных унитарных рядов.
Наша реализация подходов, предложенных методом FreDF, не требует внесения каких-либо корректировок в советники обучения моделей и взаимодействия с окружающей средой. А значит, в процессе тестирования полученных результатов мы можем использовать собранные ранее советники и обучающие выборки.
3. Тестирование
Мы провели довольно большую работу по реализации подходов, предложенных авторами метода FreDF средствами MQL5. И теперь переходим к заключительному этапу нашей работы — обучению и тестированию моделей.
Как было сказано выше, для обучения моделей мы будем использовать созданного ранее советника и предварительно собранные обучающие данные. Напомню, что обучение моделей осуществляется на исторических данных инструмента EURUSD тайм-фрейм H1 за весь 2023 год.
Вначале мы обучаем модель Энкодера состояния окружающей среды. Модель обучается прогнозированию последующих состояний окружающей среды на горизонт планирования, который определяется константой NForecast. В моем эксперименте это 12 последующих свечей. Прогноз осуществляется в разрезе всех анализируемых параметров описания состояния окружающей среды.
#define NForecast 12 //Number of forecast
В процессе обучения Энкодера можно отметить снижение ошибки прогнозирования по сравнению с аналогичной моделью без использования подходов FreDF. Однако мы не проводили графическое сравнение результатов прогнозирования. Поэтому сложно судить о реальном качестве прогнозных значений. Здесь стоит отметить что, как бы это не казалось странным, перед нами не стоит цель получения максимально точных прогнозов всех анализируемых показателей. Дело в том, что модель Актера для принятия решения об оптимальных действиях ориентируется на скрытое пространство Энкодера. И цель первого этапа обучения — получение максимально информативного скрытого пространства Энкодера, в котором было бы закодировано наиболее вероятное предстоящее ценовое движение.
Как и ранее, модель Энкодера анализирует только ценовое движение, поэтому в процессе первого этапа обучения нам нет необходимости обновлять обучающую выборку.
На втором этапе нашего процесса обучения мы осуществляем поиск наиболее оптимальной политики действий нашего Актера. И здесь мы уже осуществляем итерационное обучение моделей Актера и Критика, которое чередуется с обновлением обучающей выборки.
В результате нескольких итераций обучения политики Актера, нам удалось получить модель, способную генерировать прибыль. Результативность обученной модели мы проверяли в тестере стратегий MetaTrader 5 на реальных исторических данных за Январь 2024 года. При этом параметры тестирования полностью соответствовали параметрам обучающей выборки, включая инструмент, тайм-фрейм и параметры анализируемых индикаторов. Результаты тестирования представлены на скриншотах ниже.
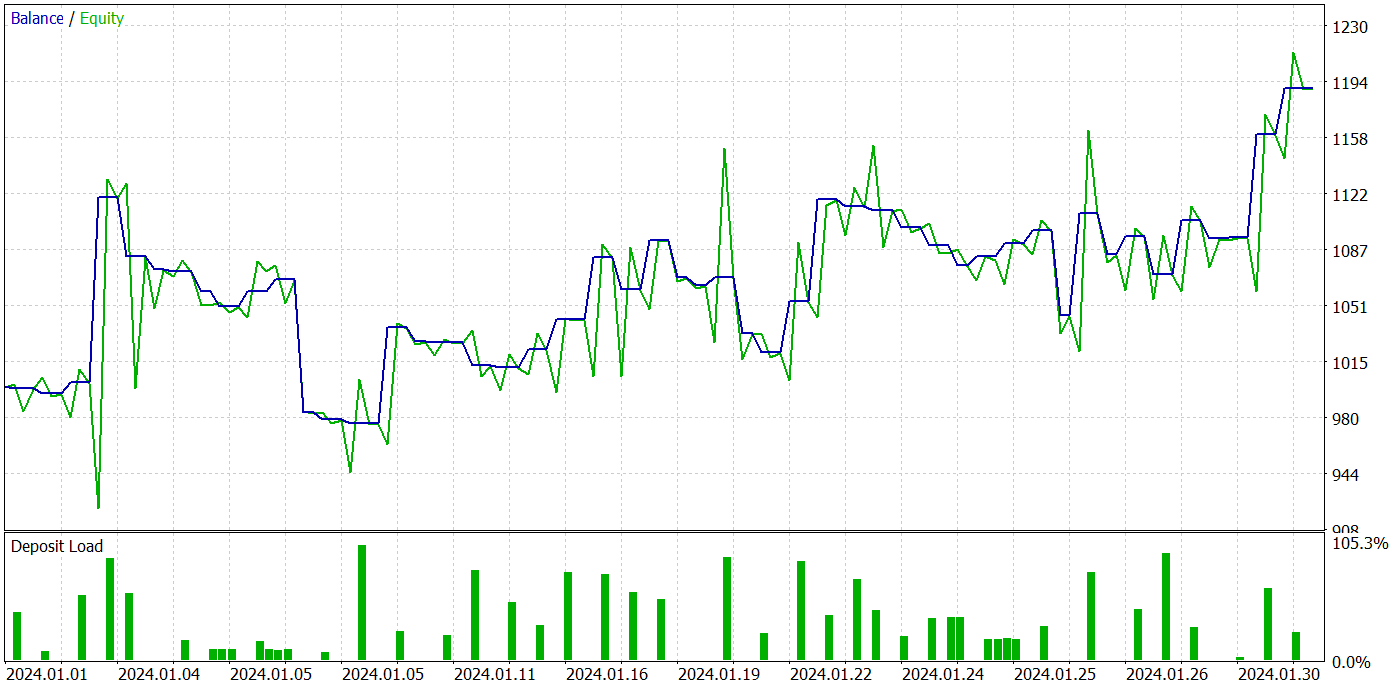
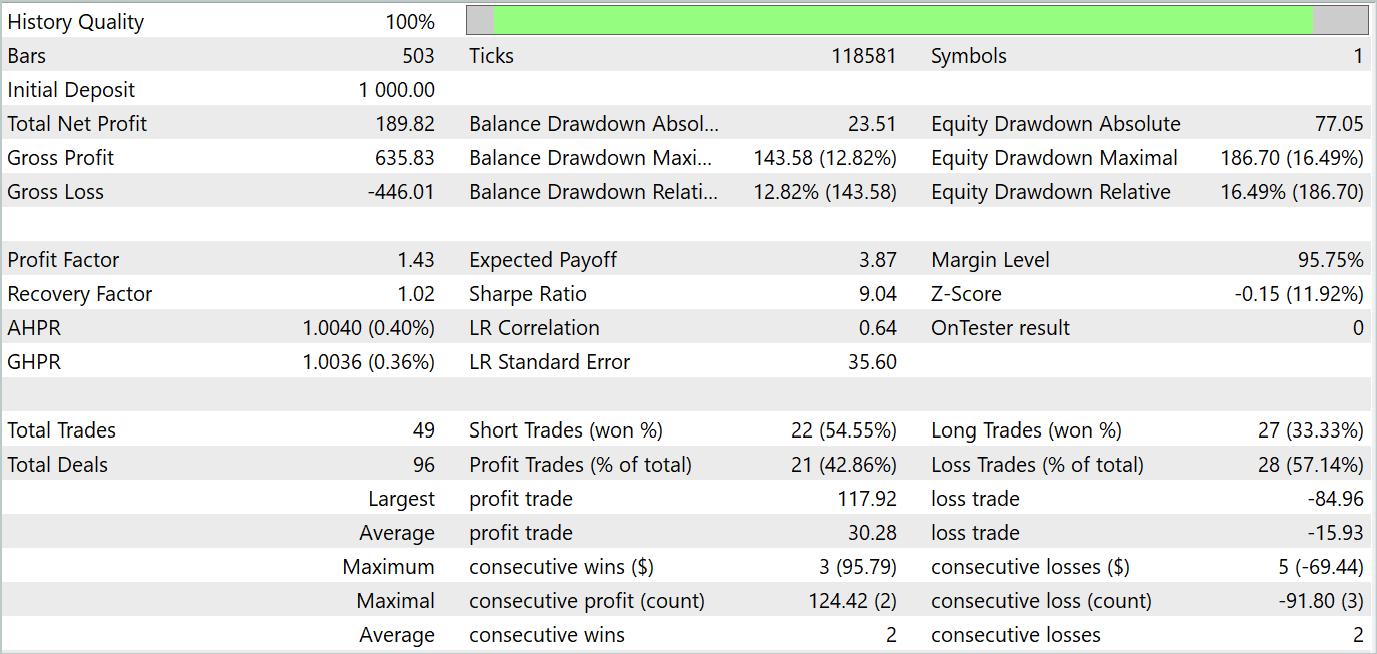
По результатам тестирования можно отметить явно выраженную тенденцию к росту баланса счета. За период тестирования модель совершила 49 сделок, 21 из которых были закрыты с прибылью. Да, прибыльных позиций меньше половины. Однако, средняя прибыльная сделка почти в 2 раза превышает среднюю убыточную. Как следствие, профит-фактор модели на тестовой выборке составляет 1.43 и совокупный доход за месяц около 19%.
Заключение
В данной работе мы познакомились с методом FreDF, который направлен на улучшение прогнозирования временных рядов. Авторы метода эмпирически обосновали, что игнорирование автокорреляции в последовательности меток приводит к смещению правдоподобия и ухудшению качества прогнозов в текущей парадигме DF. И была представлена простая, но эффективная модификация текущей парадигмы DF, которая учитывает автокорреляцию, выравнивая прогнозы и последовательности меток в частотной области. Метод FreDF совместим с различными моделями прогнозирования и преобразованиями, что делает его гибким и универсальным.
В практической части статьи мы реализовали свое видение предложенных подходов средствами MQL5. Мы дополнили ранее созданную модель FEDformer предложенными подходами и провели её обучение. Результаты тестирования обученной модели позволяют судить об эффективности предложенных подходов, так как добавление FreDF позволяет повысить эффективность модели при прочих равных условиях.
Хочется отметить гибкость метода FreDF, что позволяет его эффективно использовать с довольно широким кругом существующих моделей.
Ссылки
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Research.mq5 | Советник | Советник сбора примеров |
| 2 | ResearchRealORL.mq5 | Советник | Советник сбора примеров методом Real-ORL |
| 3 | Study.mq5 | Советник | Советник обучения Моделей |
| 4 | StudyEncoder.mq5 | Советник | Советник обучения Энкодера |
| 5 | Test.mq5 | Советник | Советник для тестирования модели |
| 6 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы |
| 7 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 8 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL |
 Алгоритм кодового замка (Сode Lock Algorithm, CLA)
Алгоритм кодового замка (Сode Lock Algorithm, CLA)
 Создаем простой мультивалютный советник с использованием MQL5 (Часть 6): Два индикатора RSI пересекают линии друг друга
Создаем простой мультивалютный советник с использованием MQL5 (Часть 6): Два индикатора RSI пересекают линии друг друга
 Разрабатываем мультивалютный советник (Часть 12): Риск-менеджер как для проп-трейдинговых компаний
Разрабатываем мультивалютный советник (Часть 12): Риск-менеджер как для проп-трейдинговых компаний
 Разработка и тестирование торговых систем Aroon
Разработка и тестирование торговых систем Aroon
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования