
Алгоритм докупки: математическая модель увеличения эффективности
Содержание
- Введение
- Методы уточнения торговых характеристик на основе алгоритма усреднения
- Помогите выйти из просадки
- Общие мысли про алгоритм усреднения
- Тонкости более точной оценки систем с докупкой
- Углубленное и универсальное понимание прибыльности
- Увеличение эффективности систем при диверсификации
- Полезные пределы
- Полезности в контексте использования параллельных инструментов
- Нормальный закон распределения случайной величины
- Красота кривой прибыли в рамках закона распределения случайной величины
- Заключение
Введение
Данный торговый прием очень широко используется в самых разнообразных советниках и более того — имеет много разновидностей и гибридов. Кроме того, если судить по количеству упоминаний о подобных системах, очевидно, что данная тема очень популярна не только на данной площадке, но и на любых других порталах. Во всех этих разновидностях присутствует общая концепция, при которой торговля ведется против движения рынка. Иначе говоря, можно сказать, что советник использует докупку для того, чтобы иметь возможность купить как можно дешевле и продать как можно дороже.
Это классическая схема торговли которая стара как мир, и в одной из прошлых статей я частично касался данной темы, но старался осветить возможные способы гибридизации подобных методов. Но в данной статье мне стало интересно максимально подробно разобрать данную концепцию, и, используя свои аналитические способности, копнуть поглубже, чем это делают господа форумчане. Однако статья будет скорее общей и гораздо более широкой, просто алгоритм докупки очень подходит для освещения некоторых очень интересных и полезных фишек, которые будет проще понять на примере алгоритма докупки.
Методы уточнения характеристик торговой системы на примере алгоритма усреднения
Помогите выйти из просадки "от создателей мой советник неплохо зарабатывает но иногда все сливает"
Очень у многих новичков алго трейдеров или ручных трейдеров возникают такие комичные вопросы. Например, в момент написания данной статьи у меня произошел разговор именно с таким человеком, но он так и не понял всю суть моих аргументов. И, как ни печально, почему-то мне кажется, что у него практически нет шансов когда-либо понять всю комичность подобной ситуации. Ведь я сам когда-то мог задать подобный вопрос самому себе, чисто теоретически, более старому и опытному, и я бы тоже скорее всего не понял, что мне хотят донести. Я даже знаю, какие чувства у меня бы вызвали правдивые ответы самому себе. Я бы подумал, что меня хотят унизить или отговорить от дальнейшего занятия алготрейдингом.
В реальности все гораздо проще. Просто у меня хватило терпения пройти определенный путь и обрести некоторую мудрость, если хотите, если так можно это назвать. Это вовсе не идеализация и самохвальство, это скорее необходимый минимум. Очень жаль, что это годы, а не недели и месяцы.
Здесь у нас целый мир грез и самообмана, и если честно, я уже начинаю уставать от простоты некоторых людей и могу прочитать между их строк, что "счастье в неведении". Господа, прекратите заниматься ерундой и думать, что вы короли рынка, лучше напишите знающему человеку и попросите подобрать робот под свой бюджет. Поверьте мне, вы так сохраните целый товарный состав времени и денег, не говоря уже о волосах на своей голове. Один из таких людей написал эту статью. А в доказательство вам — все что написано ниже.
Общие мысли про алгоритм усреднения
Если рассматривать алгоритм докупки или "усреднение", на первый взгляд может показаться, особенно начинающему разработчику советников (коим был и я когда-то) что эта система беспроигрышна. Более того, были моменты, когда я еще не знал ничего о подобных приемах и удивлялся огромным математическим ожиданиям, которые побеждают любые спреды. Сейчас понятно, что это лишь иллюзия, тем не менее в данном подходе есть рациональное зерно, но об этом позже. Для начала, чтобы иметь возможность объективно оценивать подобные системы, мы должны знать некоторые косвенные показатели, которые могут нам рассказать немного больше, чем просто картинка растущей прибыли.
Самые актуальные показатели в отчете тестера стратегий могут даже помочь понять, что система заведомо проигрышная, не смотря на тот факт, что кривая баланса выглядит прекрасно. Как уже поняли многие читатели, все дело на самом деле в кривой прибыльности. На самом деле все важные показатели торговой системы вторичны перед первыми и самыми основными математическими характеристиками, коими является, конечно же, математическое ожидание и первичные ему характеристики. Но стоит отметить, что математическое ожидание настолько гибкая величина, что всегда можно выдать желаемое за действительное.
На самом деле, чтобы правильно использовать такое понятие, как математическое ожидание, нужно в первую очередь понимать, что это терминология теории вероятностей, и любое вычисление данной величины должно осуществляться по правилам теории вероятностей, а именно:
- Вычисления тем точнее, чем больше анализируемая выборка, в идеале точное значение вычисляется по бесконечной выборке.
- Если разбить бесконечность на несколько частей, мы получим несколько бесконечностей
Кто-то подумает, как же вычислить точное математическое ожидание той или иной стратегии, если в нашем распоряжении лишь ограниченная выборка реальных котировок? А кто-то подумает, зачем нам вообще эти бесконечности? Все дело в том, что все оценки тех или иных усредненных величин, таких как математическое ожидание, имеют вес только на том участке, где производились данные вычисления, но не имеют ничего общего с другим участком. Любая математическая характеристика имеет вес только там, где она вычисляется. Тем не менее можно выделить некоторые приемы для уточнения характеристик прибыльности той или иной стратегии, которые позволят получить наиболее близкие значения к истинному значению требуемых показателей для вычисления.
К чему я это? Это имеет непосредственное отношение к нашей задаче. После понимания того, что мы не можем заглянуть в будущее стратегии длинной в бесконечность, что само по себе уже звучит как полная глупость. Тем не менее это является математическим фактом и необходимым и достаточным условием для вычисления истинных математических характеристик. Мы приходим к мысли о том, как сделать более близким число вычисленное по ограниченной выборке, к числу, которое могло быть вычислено по бесконечной выборке? Те, кто знаком с математикой, знают, что есть два математических понятия. которые могут быть применены для вычисления бесконечных сумм:
- Интеграл
- Сумма бесконечного ряда
Всем, я думаю понятно, что для вычисления интеграла, как и суммы ряда, необходимо получить либо все точки функции, интеграл которой нужно вычислить, в рамках рассматриваемой области интегрирования, либо все элементы последовательности чисел рассматриваемого ряда. Есть еще самый прекрасный вариант - получить соответствующие математические выражения для функции, которую мы собираемся интегрировать, и выражение для генерации элементов ряда. Во многих случаях если мы имеем соответствующие математические выражения, мы можем получить точные формулы для готового интеграла или суммы ряда, но в случае реальной торговли мы не сможем применять дифференциальное исчисление, да и в общем-то нам это не особо поможет, но это важно понимать.
Вывод из всего этого таков, что для прямой оценки любой системы у нас есть лишь ограниченная выборка и те или иные показатели, которые мы получаем в тестере стратегий, на самом деле их значимость сильно преувеличена. Встает вопрос о том, можно ли судить о прибыльности или убыточности той или иной стратегии, используя показатели тестера стратегий и достаточно ли данных показателей для однозначного ответа, а самое главное — как правильно использовать данные показатели и действительно ли вы используете их правильно?
Дополнительно что нужно уяснить, что для каждой стратегии тот или иной показатель, по которому мы можем корректно оценить реальную прибыльность и безопасность стратегии, может быть совершенно разным. Это имеет прямой отношение к оценке кривой прибыли. Чтобы это понять, давайте сначала изобразим примерный общий вид кривой торговли, которую мы получим при использовании алгоритма докупки:
Рис. 1
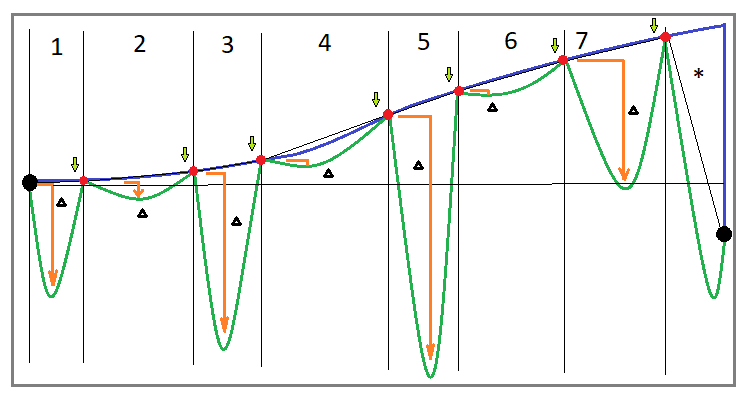
Начнем с реализации докупки для одного инструмента. Если вы верно реализуете данный алгоритм, то ваша торговля в любом случае будет состоять из циклов. Все циклы в идеале должны быть плюсовыми. Если некоторые циклы закрываются в минусовой зоне, то это значит что либо вы неправильно реализуете данный алгоритм, либо он уже не является чистым алгоритмом и в нем уже есть модификации. Но мы с вами рассмотрим классическую докупку. Давайте определим некоторые характерные параметры кривой торговли для обозначения классической докупки:
- Кривая баланса должна быть растущей и состоять из N циклов
- Все циклы имеют положительную прибыль
- При обрывании торговли мы скорее всего окажемся в последнем незавершенном цикле
- Незавершенный цикл имеет отрицательную прибыльность
- Циклы имеют характерные просадки по средствам.
Вроде бы по общему виду кривой должно быть понятно на первый взгляд, что такая система прибыльна, но не все так просто. Если вы посмотрите на последний незавершенный торговый цикл, закрытие которого я специально сделал ниже стартовой точки, чтобы показать что в некоторых случаях вам повезет и вы дождетесь успешного завершения цикла, а в некоторых вы можете либо вовсе не дождаться и уйти сильно в минус, либо вовсе слить депозит. Почему так происходит? Все дело в том, что по картинке может сложиться ложное впечатление, что величина просадки по средствам ограничена в своей абсолютной величине и, как вытекающее, должно быть ограниченным и время нахождения в данной просадке.
В реальности, чем более длительный участок тестирования, тем более продолжителен средний участок просадки, и предела здесь абсолютно не существует. Предел существует только в виде вашего депозита и грамотности вашего мани-менеджмента. Тем не менее, грамотный подход к настройке вашей системы, которая построена на данном принципе, может привести лишь к увеличению продолжительности жизни вашего депозита, перед тем как вы сольете ваш депозит, либо в лучшем случае получите очень небольшую прибыль.
Когда дело касается тестирования систем на основе алгоритма докупки или, как его еще называют "усреднение", для верной оценки его живучести, надежности и реальной прибыльности следует придерживаться особенной схемы тестирования. Почему стоит так поступать, я сейчас расскажу. Все дело в том, что ценность одиночного теста в данном подходе сведена к минимуму по одной простой причине, что при тесте любой "нормальной" стратегии, ваша прибыль за весь тест в тестере стратегий очень близка к "нормально" распределенной величине. Это означает, что при тесте любой среднестатистической стратегии без длительного удержания позиции, вы получите примерно равное количество прибыльных и убыточных участков тестирования, что очень быстро вам даст понять, что стратегия нестабильна, либо то, что стратегия имеет под собой верное понимание рынка и работает на всей истории.
Когда мы имеем дело со стратегией докупки, там это распределение может быть сильно деформировано, потому что для корректного тестирования данной системы нужно выставлять максимально возможный депозит. Кроме того, результат тестирования сильно зависит от длины участка тестирования. Ведь в данном подходе вся торговля построена на основе торговых циклов, и у каждой уникальной настройки данной системы может быть как совершенно разный показатель средней просадки, так и связанный с ним показатель средней длительности просадки. В зависимости от этих показателей, слишком короткие участки тестирования могут показать либо слишком завышенный, либо слишком заниженный результат теста. Как правило, таких тестов проводят немного, а это и может являться в большинстве случаев причиной излишней уверенности при эксплуатации данных систем.
Тонкости более точной оценки системы с докупкой
Давайте теперь научимся правильно оценивать работоспособность систем использующих алгоритм докупки, используя известные показатели торговых систем. В первую очередь при такой оценке я бы советовал использовать одну единственную характеристику - фактор восстановления. Давайте определимся как его считать:
- Recovery Factor = Total Profit / Max Equity Drawdown
- Total Profit - общая прибыль за участок торговли
- Max Equity Drawdown - максимальная просадка по средствам относительно предыдущей совместной точки для баланса и средств (пик баланса)
Как видно, это итоговая прибыль, деленная на максимальную просадку по средствам. Математический смысл данного показателя в классическом понимании таков, что по задумке он должен показывать способность системы восстанавливать свою просадку по средствам. Граничным условием прибыльности торговой системы при использовании подобной характеристики является следующий факт:
- Recovery Factor > 1
Если перевести на всем понятный человеческий язык, это будет означать что для получения прибыли, мы можем рискнуть не более чем такой же по модулю величиной депозита. Данный показатель, во многих случаях довольно близко к правде, говорит нам о том, какова реальность в отношении торговли для той или иной системы, пользуйтесь им, но очень аккуратно, ведь это довольно спорная величина относительно своей математической значимости.
Тем не менее, мне придется вскрыть и показать вам все его минусы, чтобы вы понимали, что этот показатель тоже весьма условен и уровень его математической значимости также весьма невысок. Конечно, вы будете правы, если скажете - критикуешь, значит предлагай. Так я и собираюсь поступить, но только после того как мы разберем этот показатель. Все дело в том, что данный показатель привязан к максимальной просадке, которая в свою очередь может быть привязана к любой точке кривой торговли, а это означает, что если мы пересчитаем данную просадку относительно стартового баланса и подставим ее вместо максимальной просадки, то мы получим практически всегда завышенный фактор восстановления. Давайте формализуем все это как положено:
- Recovery Factor Variation 1 = Total Profit / Max Equity Drawdown From Start
- Max Equity Drawdown From Start - максимальная просадка считая от стартового баланса (не от предыдущего максимума)
Конечно, это не классический фактор восстановления, но по своей сути на самом деле он гораздо более верно определяет прибыльность относительно общепринятого граничного условия. Давайте сначала визуально изобразим оба варианта вычисления данного показателя - классический и мой:
Рис. 2
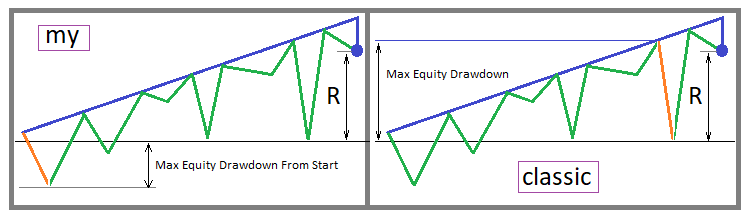
Видно что в первом случае данный показатель будет принимать более высокие значения, что для нас, конечно же, очень приятно. Но с точки зрения оценки прибыльности можно придерживаться двух подходов, вот как раз классический показатель более адаптирован к подходу, при котором длительность участка тестирования лучше брать как можно больше. В данном случае более высокое значение "Max Equity Drawdown" как бы компенсирует тот факт, что эта просадка начинается не с самого начала кривой торговли, и тем самым данный показатель в большинстве случаев близок к истинной оценке. Мой же показатель более эффективен при оценке множественных бектестов.
Иначе говоря, данный показатель тем точнее, чем больше тестов вашей стратегии вы провели. Тесты вашей стратегии должны быть по максимально разным участкам. Это означает, что точки начала и конца должны выбираться с максимальной вариативностью. Для корректной оценки необходимо выделить "N" максимально разных участков и произвести тестирование на них, после чего посчитать среднее арифметическое данного показателя по всем участкам тестирования. Данное правило позволит уточнить оба варианта фактора восстановления, как мой, так и классический, за той лишь поправкой, что для уточнения классического нужно будет произвести меньше независимых бектестов.
Тем не менее сказать, что таких уточняющих манипуляций мало, для уточнения данных показателей - ничего не сказать. Я продемонстрировал свой собственный аналог фактора восстановления для того чтобы показать, что любой человек может придумать свой подобный показатель, и его даже могут добавить в качестве одной из вычисляемых характеристик для бектеста в MetaTrader. Но любой из данных показателей не имеет никакого математического доказательства и более того, любой из подобных показателей имеет свои погрешности и границы применимости. Все это значит, что на данный момент не существует точного математического показателя для абсолютно точной оценки того или иного алгоритма использующего докупку, тем не менее, мой показатель будет стремиться к абсолютно точному, при увеличении количества разнообразных тестов. Следующий раздел вам многое объяснит.
Углубленное и универсальное понимание прибыльности
Универсальная оценка
Всем, я думаю, известно, что такие показатели, как математическое ожидание прибыли и фактор прибыли, существуют в любом отчете тестера стратегий или в характеристиках торгового сигнала, но, я думаю, никто вам не говорил, что данные характеристики можно использовать и для вычисления прибыльности таких торговых систем, где недостаточно анализа по сделкам. Так вот, можно использовать данные показатели, заменив единицу "позиция" на единицу "тест на участке". При вычислении данного показателя вам нужно будет произвести множество независимых тестов, но забыть о том, что внутри есть какая-то структура. Этот подход поможет вам, пользуясь лишь двумя самыми популярными показателями, оценивать реальную перспективность торговой системы. Кроме того, может привить вам крайне полезную привычку - множественные тесты. Для того чтобы использовать данный подход, необходимо лишь знать следующую формулу:
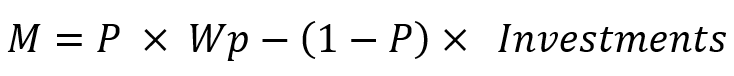
Где:
- M - математическое ожидание прибыли
- Wp - желаемая прибыль
- Investments - сколько вы готовы инвестировать для достижения требуемой прибыли
- P - вероятность, что нам хватит инвестиций до момента достижения прибыли
- (1-P) - вероятность, что нам не хватит инвестиций до достижения прибыли (потеря депозита)
Сразу приведу аналогичную формулу для фактора прибыли:
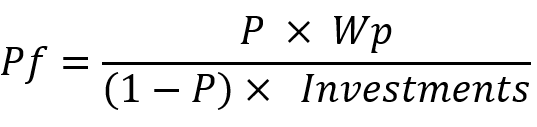
Все, что нужно знать, так это то, что при случайной торговле и отсутствии препятствующих факторов, таких как спред, комиссия и своп а также проскальзывание, данные величины абсолютно всегда и абсолютно для любой торговой системы будут принимать следующие значения:
Данные характеристики могут измениться в вашу сторону только при наличии предсказательного момента. Следовательно, вероятность, что мы получим прибыль, не потеряв депозита, примет следующее значение:
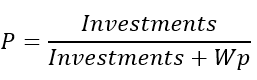
Если вы подставите данное выражение вместо вероятности в наши формулы, то вы получите те тождества, что я вам дал. А если учитывать спред комиссию и своп, то вовсе мы получаем следующее:
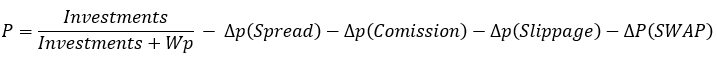
Думаю, всем понятно, что смысл таков, что спред, комиссия и своп уменьшают итоговую вероятность, что в итоге приводит к тому, что наши тождества теряют силу, а вместо них появляются следующие неравенства:
- M < 0
- Pf < 1
Так будет абсолютно с любой торговой системой, и алгоритм докупки здесь совершенно ничем не лучше любой другой системы. Просто при тестировании подобной системы или эксплуатации, он способен сильно деформировать функцию распределения случайной величины итоговой прибыли бектеста или сигнала, но, как правило, такой сценарий наиболее часто возникает при кратковременном тестировании или эксплуатации.
Все потому, что вероятность нарваться на большую просадку сильно меньше, если тестировать на коротком участке. Но как только вы начнете производить эти тесты на более длительных участках, то увидите, как правило то, что не видели раньше. Но я уверен, большинство сможет успокоить себя тем, что это лишь случайность, и просто надо как-то обходить данные опасные участки. То же самое в целом будет и при множественном тестировании на коротких участках. В принципе, что так что эдак, как говорят — то же самое, только в профиль.
Существует единственный способ побороть убыточность любой системы. Для этого добавим в формулу вычисления вероятностей дополнительное слагаемое:
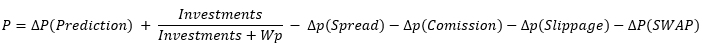
Как видно, в формуле появилось новое слагаемое "dP(Prediction)", оно со знаком плюс, что я специально сделал, чтобы показать, что только это слагаемое способно скомпенсировать эффект от спредов, комиссий и свопов. Тогда выходит для начала, чтобы побороть негативные эффекты и выйти к прибыли, нам однозначно необходимо достаточное качество предсказания:
![]()
Если мы обеспечиваем данное неравенство, то только тогда мы получим наши желанные неравенства:
- M > 0
- Pf > 1
Примеры уточняющих методов
В данном подразделе я хочу вам предложить некоторые дополнительные уточняющие манипуляции, которые позволят получить более корректное значение фактора восстановления. Я предлагаю вернуться к "рис 1" и посмотреть на пронумерованные сегменты. Для уточнения фактора восстановления необходимо представить, что эти сегменты — независимые тесты. Таким образом мы можем обойтись без множественного тестирования, считая, что мы уже провели эти тесты. Мы можем так сделать, потому что данные отрезки являются циклами, в которых имеется как точка старта, так и точка конца, именно это и обеспечивает эквивалентность бектесту.
В рамках данного раздела, я думаю, также стоит дополнить первый рисунок его эквивалентом, только учитывающий тот факт, что мы тестируем или торгуем сразу на нескольких инструментах одновременно. Так будет выглядеть кривая торговли с помощью алгоритма докупки для параллельной торговли на множественных инструментах:
Рис. 3
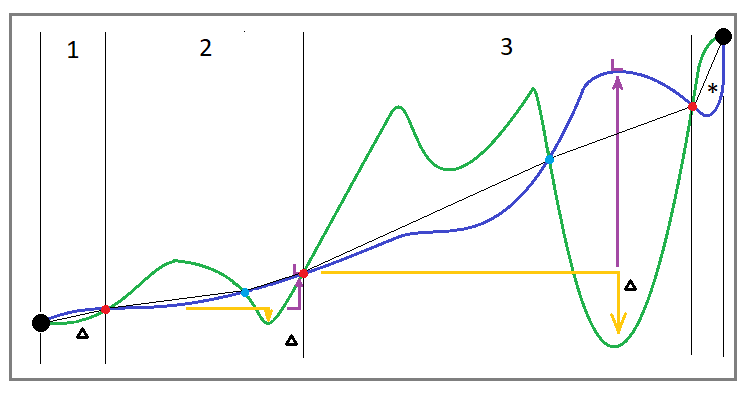
Видно, что данная кривая отличается по своему строению от кривой для докупки на одном инструменте, я здесь добавил промежуточные точки голубого цвета, которые означают, что перед просадкой могут присутствовать сегменты, которые имеют "просадку наоборот". Я не знаю, как назвать данные сегменты, называйте как хотите, не это является сутью, а тот факт, что мы не можем считать это просадкой. Но тем не менее, мы не имеем права считать данные сегменты вне анализа, потому они обязаны войти в состав какого-либо цикла.
Я думаю, более правильно было бы откладывать каждый новый цикл от конца предыдущего. Концом предыдущего цикла при этом следует считать точку восстановления последней просадки по средствам. На рисунке данные циклы отделяются красными точками. Но на самом деле мало данного определения цикла, важно также определить, что недостаточно просто зафиксировать просадку по средствам, а важно, чтобы она была ниже старта текущего цикла, иначе какая же это просадка?
После выделения данных циклов вы можете считать их отдельными независимыми тестами и посчитать для каждого из них фактор восстановления. Сделать это можно следующим образом:
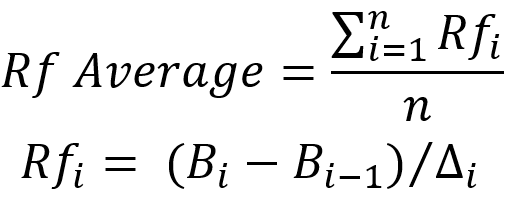
В данной формуле в качестве "B" используются соответствующие точки на кривой баланса (конечное значение баланса на участке и начальное), ну а дельта олицетворяет нашу просадку. Еще я бы хотел, чтобы читатель вернулся к последнему рисунку. На нем я откладывал дельту от красной точки старта каждого цикла, а не от синей как считается по классике, по тем причинам что я говорил выше, но если нужно уточнить оригинальный фактор восстановления то дельту следует откладывать от синей точки. В данном случае важен метод уточнения показателей а не сами показатели. В качестве усредняющего действия берется простое среднее арифметическое.
Тем не менее, даже после уточнения того или иного пользовательского или классического показателя не стоит принимать тот факт, что значение данного показателя больше единицы, или даже двух или трех, за признаки прибыльной торговой системы.
Точно ту же формулу нужно применять при множественных бектестах. Все дело в том, что любой бектест в данном случае равноценен циклу. Можно даже сначала посчитать средние показатели по циклам, а после всего этого посчитать среднее от среднего относительно бектестов. Либо можно поступить намного проще - максимально увеличить длительность участка тестирования. Данный подход избавит вас как минимум от множественного тестирования, за счет того, что количество циклов будет максимальным, а значит и средний фактор восстановления будет вычислен максимально точно.
Увеличение эффективности систем при диверсификации
Полезные пределы
После рассмотрения возможностей для уточнения тех или иных характеристик бектестов вы несомненно лучше вооружены, но вы все еще не знаете главного. Основа состоит в ответе на вопрос - почему нужно проводить все эти множественные тесты или дробления на циклы? Вопрос на самом деле комплексный, так что простому обывателю непонятно и не будет понятно до тех пор, пока вы не вложите столько же сил, сколько я вложил в свое время. Как ни печально, это необходимо, но с моей помощью вы сможете сильно сократить время, которое вам потребуется для этого.
Данный раздел позволит оценить объективность того или иного показателя, а почему, я покажу дальше. Я попробую объяснить как на пальцах, так и на формулах. Начну, наверное, с общей формулы:
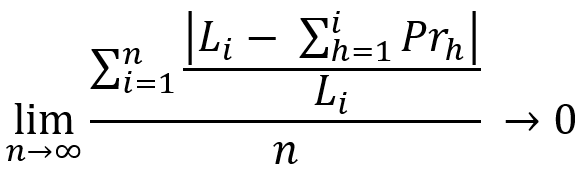
И сразу приведу аналогичную ей формулу, только немного в ином виде:
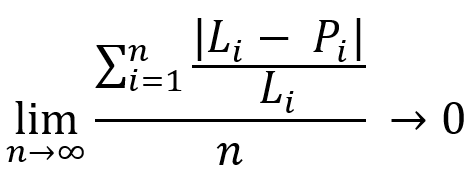
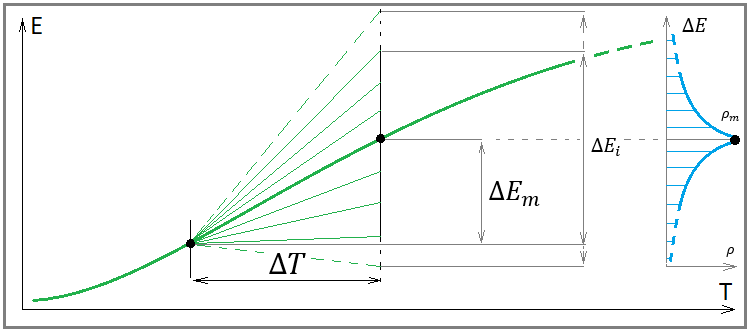
Суть этих формул одинакова. Данные формулы говорят о том, что в любой прибыльной торговой системе, при стремлении длительности участка тестирования к бесконечности мы получим полное слияние линий баланса и текущей прибыли, с некоей линией, олицетворяющей среднюю нашей прибыли. В большинстве случаев характер данной линии определяется выбранной нами стратегией. Давайте для более глубокого понимания посмотрим на следующую иллюстрацию:
Рис. 4
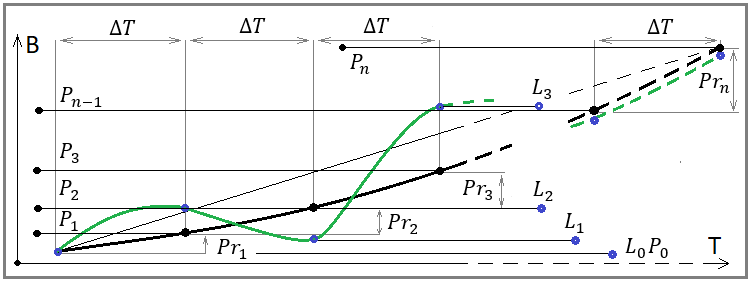
Если вы внимательно посмотрите на эту картинку, то увидите на ней все величины, которые присутствуют в наших формулах. В ней раскрыт геометрический смысл наших математических пределов. Единственное, чего нет в наших формулах, так это промежутка времени "dT". С помощью данного промежутка мы дискретизируем наши шаги по балансу и даем начало всем точкам наших числовых рядов для баланса и прибыли данных участков, а также вычисляем значения нашей средней линии в тех же точках. Данные формулы являются математическим эквивалентом следующего утверждения:
- При совмещении множественных тестов или кривых торговли воедино, тем больше они похожи на гладкую возрастающую линию (только в случае если система действительно прибыльна)
Иначе говоря, любая прибыльная торговая система тем более красиво выглядит в графической части тестера стратегий или сигнале, чем более длительный участок тестирования мы выберем. Я понимаю, что есть усатые дядьки, которые будут говорить, что никакая система не может достичь подобных показателей, тем не менее полно подобных примеров в Маркете, и отрицать это глупо, как минимум. А если серьезно, то все зависит от универсальности алгоритма и того, насколько хорошо вы понимаете физику рынка. Если вы знаете математику, которая всегда присуща рынку, на котором вы торгуете, то фактически вы и получаете в данном случае бесконечно растущую кривую прибыли, и вам не требуется ждать целую бесконечность, чтобы подтвердить эффективность системы. Конечно, понятно, что это крайне сложная задача, но тем не менее в рамках многих алгоритмов данная задача достижима.
Давайте завершим данное теоретическое вступление тем, что научимся правильно использовать полученные приемы. "Как же использовать данные приемы с бесконечными суммами, когда у нас лишь ограниченные выборки и соответственно, также неизбежные неполные суммы" — спросите вы, а я отвечу:
- Делим всю историю на отрезки
- Выделяем несколько отрезков с постоянно растущей длиной по длительности тестирования вплоть до отрезка во всю историю
- Выбираем методологию тестирования
- Тестируем
- Ищем улучшение фактора восстановления или/и относительной просадки
Суть данной хитрой схемы тестирования в том, чтобы определить косвенные признаки того, что наши пределы действительно стремятся к бесконечности и нулю соответственно. Для увеличения эффективности нашей схемы тестирования мы должны понимать, что самый длительный участок тестирования должен как минимум выглядеть красивее чем самый короткий, а в идеале каждый следующий участок должен быть одновременно больше и выглядеть красивее. Но понятие "красивее" я использую только для того чтобы всем было понятно что это на самом деле эквивалентно нашим пределам.
Тем не менее, наши пределы хороши лишь при теоретическом рассмотрении или подготовке(как вам угодно). В данной связи встает вопрос — а как же обнаружить данные факты не прибегая к "анализу на глаз"? Нам нужно как-то адаптировать наши пределы к тем показателям, что у нас есть в отчете тестера стратегий. Иными словами, нам нужны альтернативные пределы для некоторых показателей из отчета тестера стратегий или показателей сигнала, чтобы можно было воспользоваться нашей схемой тестирования. Давайте я вам покажу необходимую и достаточную совокупность альтернативных пределов:
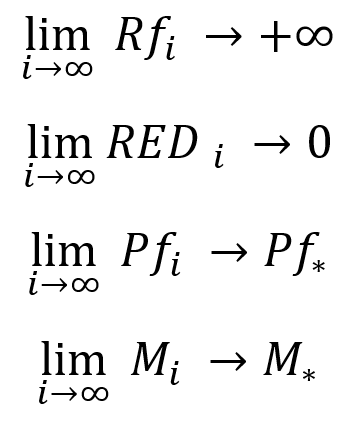
Что здесь стоит понимать:
- При бесконечном тесте, фактор восстановления (любой прибыльной стратегии) стремится к бесконечности
- При бесконечном тесте, относительная просадка по средствам (любой прибыльной стратегии), стремится к нулю
- При бесконечном тесте, профит фактор сделок (любой прибыльной стратегии) стремится к своему среднему значению и имеет конечный, действительный предел.
- При бесконечном тесте, математическое ожидание (любой прибыльной стратегии) без включенного авто лота (с фиксированным лотом) стремится к своему среднему значению и имеет конечный, действительный предел
Все это для бесконечных тестов, тем не менее полезно понять математический смысл данных пределов, прежде чем переходить к их адаптации к конечной выборке. Адаптация данных выражений к нашей методологии должна начаться с того факта, что мы должны выделить несколько отрезков тестирования, каждый из которых должен быть ощутимо больше чем предыдущий, желательно хотя бы в два раза. Нужно это для того, чтобы можно было заметить разницу показаний между более короткими и более длинными тестами. Если пронумеровать наши тесты таким образом, что при возрастании индекса растет его длина во времени, то мы получаем следующую адаптацию для случая конечных выборок:
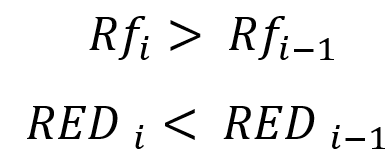
Иначе говоря, увеличение фактора восстановления и уменьшение относительной просадки по средствам и будет косвенным свидетельством, того что скорее всего при дальнейшем увеличении отрезка тестирования или времени жизни сигнала, наша кривая будет становиться визуально красивее. А это значит, что мы подтвердили выполнение наших бесконечных пределов. В противном случае, если кривая прибыли не становится прямее,то мы можем констатировать тот факт, что полученный результат очень близок к случайному и крайне высока вероятность слива в дальнейшем.
Многие конечно скажут, что можно просто почаще оптимизировать систему и все будет в порядке, в некоторых и крайне редких случаях это возможно, но для такого подхода потребуется совсем другая методология тестирования. Я же не советую никому прибегать к такому подходу, ведь в данном случае у вас нет никакой математики, а здесь у вас все четко и ясно.
Все эти нюансы должны убедить вас в том, что для тестирования алгоритма докупки тем более требуется применение данного подхода. В частности, можно даже упростить себе задачу и тестировать систему с докупкой сразу на участке максимальной длины. Можно пойти от обратного, если на самом долгом участке нам не нравятся показатели торговли, то даже более высокие показатели на коротких участках будут свидетельствовать о том, что наши неравенства уже не выполняются и система на данном этапе не готова к торговле.
Полезности в контексте параллельного использования множественных инструментов
При тестировании на ограниченной истории непременно встанет вопрос о том, а хватит ли нам истории для того чтобы правильно воспользоваться нашей методологией тестирования? Все дело в том, что во многих случаях стратегия имеет под собой вес, но ее качество недостаточно высокое для комфортного использования. Для начала нам бы хотя бы понять, действительно ли в ней есть предсказательное начало и можем ли мы начинать заниматься ее модернизацией? В некоторых случаях нам в прямом смысле не хватит доступной торговой истории. Как быть? Как многие уже догадались, судя по названию подраздела, нам следует использовать множественные инструменты для этой цели.
Казалось бы очевидный факт, но вот незадача, как всегда нигде нет никакой математики, и как всегда мы можем что-то чувствовать каким угодно местом, но только не головой. Суть тестирования на множественных инструментах эквивалентна той же сути, только для увеличения длительности тестирования. С единственной поправкой на то, что ваша система должна быть мультивалютной. Система может иметь разные настройки для различных торговых инструментов, но желательно, чтобы все настройки были похожи. Похожесть настроек будет олицетворять тот факт что система использует физические принципы, работающие на максимально возможном количестве торговых инструментов.
При данном подходе и правильной реализации подобных тестов, под индексом "i", следует уже понимать количество одновременно тестируемых инструментов, но уже на фиксированном отрезке для тестирования. Тогда данные выражения будут означать следующее:
- При увеличении количества торгуемых инструментов, чем больше инструментов, тем больше фактор восстановления
- При увеличении количества торгуемых инструментов, чем больше инструментов, тем меньше относительная просадка по средствам
Фактически, увеличение количества тестов можно для простоты интерпретировать как увеличение суммарной длительности тестов, как будто каждый тест для каждого инструмента мы считаем частью общего огромного теста. Данная абстракция лишь поможет с чего-то начать, чтобы понять, почему данный подход тоже имеет под собой ту же силу. Но если более точно рассмотреть данный вопрос и более глубоко понять, почему же линия, которая состоит из нескольких будет намного красивее, то следует воспользоваться следующими понятиями теории вероятностей:
- Случайная величина
- Дисперсия случайной величины
- Математическое ожидание случайной величины
- Закон нормального распределения случайной величины
Для полного объяснения того, зачем нам это все, нам сначала потребуется рисунок, который поможет нам немного иначе взглянуть на бектест или торговый сигнал:
Рис. 5
Я тут не рисую линию баланса, поскольку она здесь ничего не решает, а нам нужна лишь линия прибыли. Смысл данного рисунка в том, что для каждой линии прибыли, можно выделить бесконечно большое количество независимых участков фиксированной длины, в которых можно построить закон распределения случайной величины приращения линии прибыли. Наличие случайной величины означает тот факт, что в будущем приращение прибыли на выбранном участке может иметь абсолютно разные значения в самом широком диапазоне.
Звучит страшно, но на самом деле не так все страшно. Как правило, я думаю, многие слышали про нормальный закон распределения и якобы он описывает практически все случайные процессы в природе. Так вам говорят, чтобы вы не дай бог не посмели начать "думать". Тем не менее, если отбросить шутки, то на самом деле причины популярности данного закона распределения в том, что это искусственно составленная и очень удобная формула для описания симметричных распределений относительно математического ожидания случайной величины. Она нам пригодится для дальнейших математических преобразований и экспериментов.
Тем не менее, прежде чем начинать работать с данным законом, мы должны определить основное свойство для любого закона распределения случайной величины:
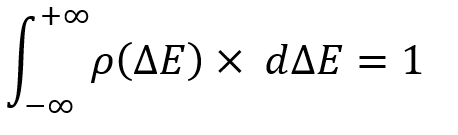
Любой закон распределения случайной величины не что иное, как аналог полной группы несовместных событий. Разница только в том, что у нас не фиксировано количество данных событий и мы в любой момент можем выбрать любое интересующее нас событие вот так:
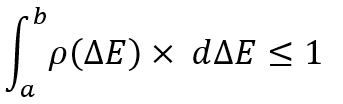
Строго говоря, данный интеграл считает вероятность нахождения случайной величины в обозначенном диапазоне случайной величины, и естественно, он не может быть больше единицы. Так как никакое суммарное событие из данного пространства событий не может иметь вероятность большую единицы, тем не менее, не это самое главное. Важно здесь только то, чтобы вы понимали, что событие в данном случае определяется лишь набором из двух чисел. Это примеры для случайных величин минимальной размерности.
Есть аналоги данных формул для размерности "N", когда событие может определяться "N*2" числами, и даже более сложными конструкциями (в рамках интегралов по многомерным областям). Это довольно сложные разделы математики, но здесь они избыточны, по этому не забивайте себе голову. Все полученные нами законы будут самодостаточны для одномерного варианта.
Прежде чем переходить к более сложным конструкциям, давайте напомним некоторые популярные показатели-характеристики законов распределения случайной величины:
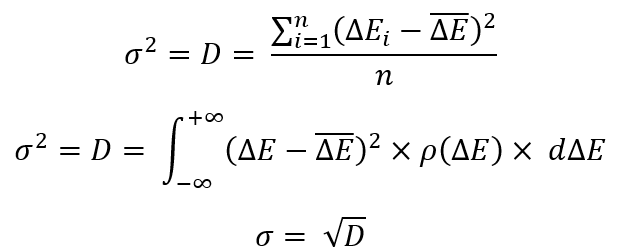
Для определения какой-либо из данной формулы нужно определить самое главное — это математическое ожидание случайной величины, в нашем случае это:
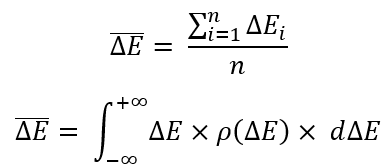
Что следует знать, так это то, что математическое ожидание это просто среднее арифметическое, просто математики любят давать очень умные названия простым вещам, чтобы никто ничего не понял. Я привел две формулы, их отличие лишь в том что первая формула работает по конечному количеству случайных величин (это когда у нас есть ограниченное количество данных), а во втором случае используется интеграл по "плотности вероятности".
Интеграл — это эквивалент суммы с тем лишь отличием что он суммирует бесконечное количество случайных величин. Закон распределения случайной величины, который находится под интегралом и содержит в себе всю бесконечность случайных величин. Есть некоторые отличия, но в целом суть та же самая.
Теперь давайте вернемся к предыдущим формулам. Это просто некоторые удобные для большинства математиков манипуляции с законами распределения случайных величин. Как и в последнем примере, есть две реализации, одна для конечного набора случайных величин, другая для бесконечного(закон распределения случайной величины). Там говорится, что "D" это усредненный квадрат разности между всеми случайными величинами и средней случайной величиной(математическое ожидание случайной величины). Данная величина получила название "дисперсия". Корень из данной величины называется "среднеквадратичным отклонением".
Нормальный закон распределения случайной величины
Общепринятым в математике случайных величин являются именно данные величины, и они считаются наиболее удобными для описания важнейших характеристик законов случайного распределения. Я же так не считаю, но тем не менее я обязан вам показать, как они считаются, в конечном итоге данные величины понадобятся для понимания нормального закона распределения. Вряд ли вы найдете данную информацию вот так просто, но я вам расскажу, что нормальный закон распределения был придуман искусственно, лишь с несколькими целями:
- Простой способ определения закона распределения симметричного относительно математического ожидания
- Возможность задания дисперсии и среднеквадратичного отклонения
- Возможность задания математического ожидания
Все эти опции позволяют получить готовую формулу закона распределения случайной величины, именуемую нормальным законом распределения:
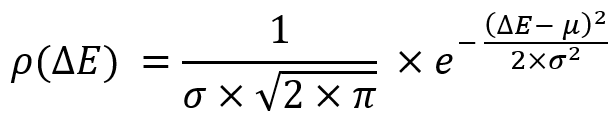
- Чем больше параллельно торгуемых инструментов для прибыльной системы, тем красивее и прямее наш график прибыли(частный случай диверсификации)
- Чем дольше выбранный участок для теста или торговли, тем красивее и прямее наш график прибыли
- Чем больше параллельно торгуемых систем с доказанной прибыльностью, тем прямее и красивее наш общий график прибыльности
- Комбинация всего вышесказанного рождает идеальную диверсификацию и максимально красивый график
Все что сказано относится только к прибыльным торговым системам, прибыльность которых доказана математически и практически (но никак не те, про которые кто-то когда-то сказал и все приняли это за истину). Начнем с того, что определим, что такое ''более красивый график" математическим языком. С этим нам может помочь "среднеквадратичное отклонение", формулу которого я уже показывал выше.
Если у нас имеется семейство кривых плотностей распределения случайной величины приращения прибыли с одинаковым математическим ожиданием, которые символизируют два отрезка, одинаковых по длительности во времени, для двух практических одинаковых графиков, то для нас желаннее будет та, у которой среднеквадратичное отклонение самое маленькое. Идеальной кривой в этом семействе могла быть та, у которой среднеквадратичное отклонение равно нулю. Данная кривая достижима лишь в том случае, когда мы знаем будущее на сто процентов, но понятно, что такого никогда не будет, тем не менее это нужно понимать для сравнения кривых из данного семейства.
Красота кривой прибыли в рамках закона распределения случайной величины
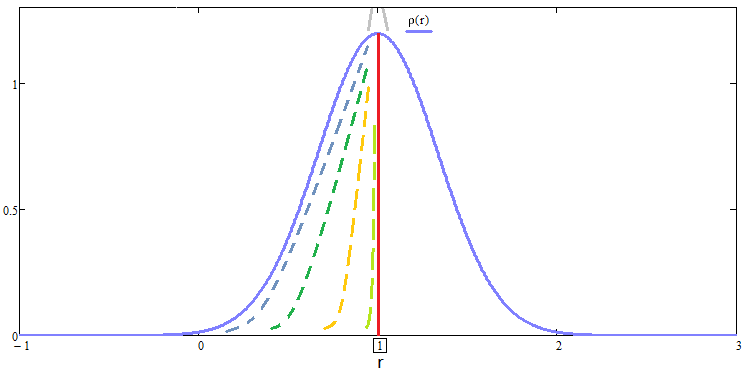
Данный факт понятен, когда мы имеем дело с семейством кривых, где одинаковые математические ожидания приращения прибыли на выбранном временном участке, но что делать, когда мы имеем дело с совершенно произвольными кривыми распределения? Непонятно как их сравнивать. В данной связи среднеквадратичное отклонение уже не является идеалом и нам необходима иная более универсальная величина сравнения, которая учитывает масштабирование, либо мы должны придумать некий алгоритм сведения данных законов распределения к некоей относительной величине, где все распределения будут иметь одинаковое математическое ожидание и следовательно ко всем кривым будут применимы классические критерии. Я разработал такой алгоритм. Одним из приемов в нем является следующее преобразование:
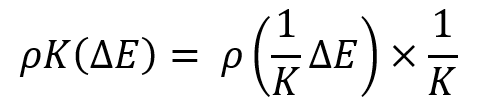
Семейство данных кривых будет выглядеть примерно так:
Рис. 6
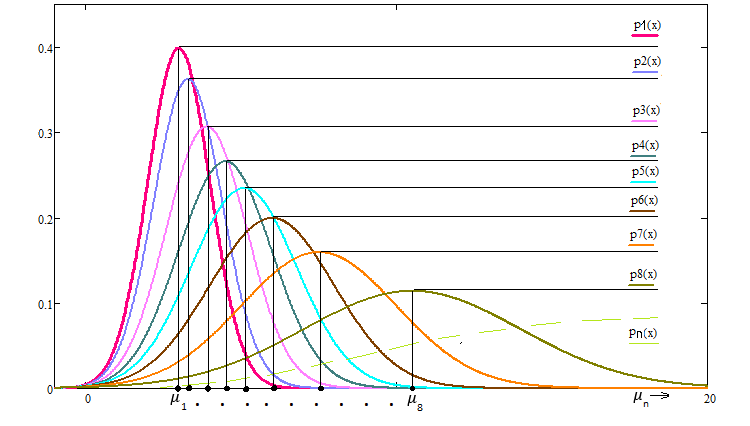
Очень интересным фактом является то, что если подвергнуть данному преобразованию закон нормального распределения то он инвариантен относительно данного преобразования и будет выглядеть вот так:
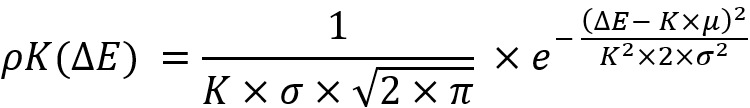
Инвариантность заключается в следующих заменах:
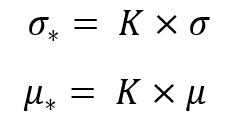
Если подставить данные замены в предыдущую формулу, то получится тот же закон распределения, только уже оперирующий соответствующими величинами со звездочками:
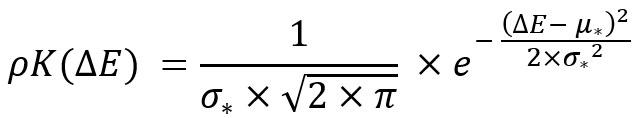
Данное преобразование нужно, чтобы обеспечить не только инвариантность закона преобразования, но еще для того, чтобы обеспечить инвариантность следующего показателя:
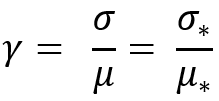
Мне пришлось выдумать данный показатель, потому что без его соблюдения невозможно правильное масштабирование нормального закона распределения, как и любого другого закона. Данный показатель будет инвариантен и для любого другого закона распределения, дело тут не только в нормальном законе, просто как пример его проще воспринимать и понимать. Смысл его таков, что его можно использовать для любых распределений, с разными математическими ожиданиями и его смысл будет аналогичен среднеквадратичному отклонению, только без требования, что все сравниваемые распределения должны иметь одно математическое ожидание. А наше преобразование, получается, предназначено для того, чтобы получать семейство распределений, где данный показатель имеет одинаковое значение, удобно — не правда ли?
Это один из способов определения так называемой красоты графика. Та система, которая будет иметь меньший данный показатель, и будет "самой красивой". Это все хорошо, но нам данный показатель был бы нужен с другой целью. Мы поставили задачу сравнить красоту двух систем. Представим, что у нас есть две системы которые торгуют независимо. Так вот, наша цель совершить слияние данных систем и понять, будет ли эффект от данного слияния, а если точнее, мы надеемся на следующее:
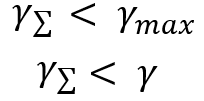
Я могу вам сказать, что данные соотношения будут соблюдаться при использовании любого закона распределения, а это автоматически означает, что имеет смысл заниматься диверсификацией, если наши параллельно торгуемые инструменты или системы имеют схожие показатели по прибыльности. Но доказывать данный факт мы будем немного иначе, я же говорил, что придумал алгоритм сведения всех распределений к относительной случайной величине. Им мы и воспользуемся, но сначала мы разберем общий процесс слияния нескольких линий, в рамках закона распределения случайной величины суммы двух дельт. Мы будем попарно производить слияние с помощью рекуррентной логики. Для этого мы положить, что у нас есть "n+1" кривых, у каждой из которых определено математическое ожидание. Но для того, чтобы перейти к случайной величине символизирующий слияние, нам следует понять что:
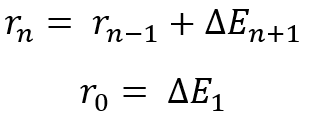
Фактически, это рекуррентное выражение, которое не несет математического смысла, но показывает логику слияния всех случайных величин из списка, каждая из которых в нашем списке. Если проще, то у нас есть "n+1" кривая, которые мы должны объединить с использованием "n" последовательных преобразований. Фактически это означает, что мы должны получить закон распределения суммарной случайной величины, на каждом из шагов, с помощью каких-то операторов преобразования.
Я не буду вас грузить "что, почему и зачем", а просто покажу данные операторы преобразования, а вы посмотрите на них и подумаете. Данные формулы реализуют слияние двух кривых прибыли, внутри выбранного временного отрезка, и считают вероятность того, что суммарная прибыль двух сегментов кривых "dE1 + dE2" будет меньше(Pl) и больше(Pm) выбранной величины "r", соответственно:
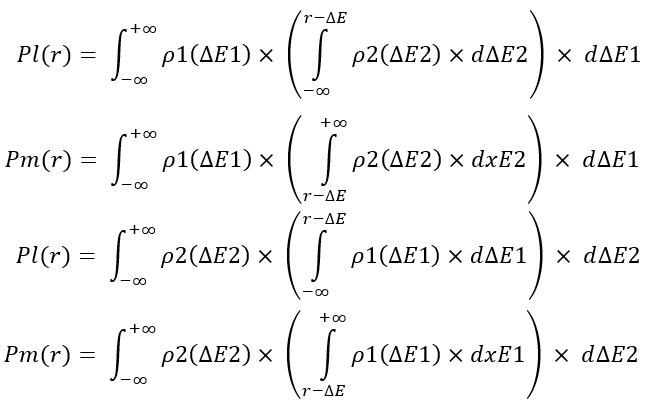
Здесь два варианта реализации данных величин, оба абсолютно эквивалентны. После вычисления данных величин их можно использовать для получения закона распределения случайной величины "r", что от нас и требуется для отработки всей рекуррентной цепочки слияния. По определению случайной величины, из данных формул можно получить соответствующие законы распределения следующим образом:
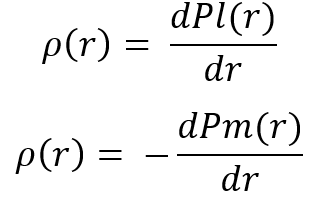
Как вы уже догадались, после получения закона распределения можно переходить к следующему шагу в рамках рекуррентной цепочки преобразований. После проработки всей цепочки мы получаем итоговое распределение, которое мы уже можем сравнивать с одним из распределений, которые мы использовали для рекуррентной цепочки слияния. Давайте создадим парочку распределений на основе полученных нами законов и проведем для примера один шаг слияния для демонстрации того факта, что каждое слияние "красивее предыдущего":
Рис. 7
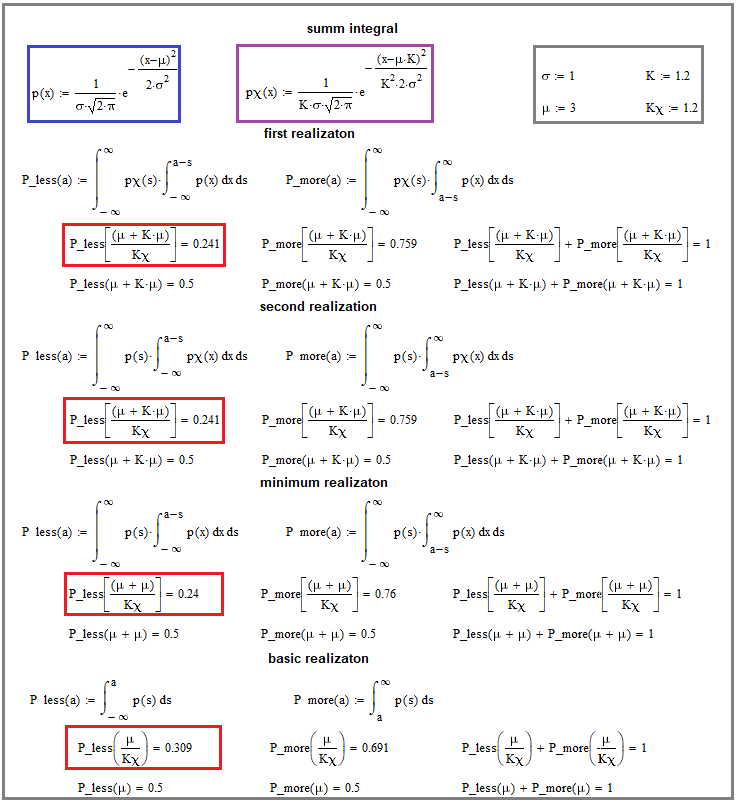
На рисунке математическое слияние, используя наши формулы для слияния, единственное, там не показано дифференцирование для преобразования интегралов в законы распределения случайной величины слияния. На результат дифференцирования мы посмотрим чуть позже, в рамках более общей идеи, а пока давайте разберемся с тем, что на данном рисунке.
Обратите внимание на красные прямоугольники, они тут основа. Самый нижний интеграл говорит о том, что мы берем интеграл по исходному закону распределения именно так, чтобы вычислить вероятность того, что случайная величина примет меньшее значение, чем математическое ожидание деленное на "Kx". А если вы посмотрите выше, то увидите аналогичные интегралы для слияний двух немного отличающихся распределений. Во всех случаях важно выдерживать данное соотношение(Kx) между математическим ожиданием и выбранным граничным значением интеграла, которое и выражено в соответствующем "Kx".
Заметьте, что там представлены оба варианта слияния, по формулам которые я вам дал выше, плюсом имеется слияние базового распределения с самим собой же, как бы представляя, что мы производим слияние двух одинаковых кривых прибыли. Одинаковых — не значит идентичных на картинке, но имеющих идентичные законы распределения случайной величины приращения кривой прибыли на выбранном временном отрезке. Фактом доказательства является то, что мы нашли более маленькую вероятность относительного отклонения случайной величины слияния, относительно исходной, это и означает то, что у нас имеется более "красивый" закон приращения случайной величины прибыли при любом слиянии. Конечно, есть и исключения, и более глубокое погружение в тему, но я считаю, что данного подхода достаточно в рамках данной статьи, да вы и не найдете скорее всего ничего лучше нигде, потому что это очень специфический материал.
Альтернативным способом сравнения красоты является преобразование всех, как исходных законов распределения, так и результата рекуррентной цепочки, которую мы рассмотрели выше. Для этого мы всего лишь должны воспользоваться нашим преобразованием, которое позволило получить семейство масштабируемых кривых распределения и сделать лишь так:
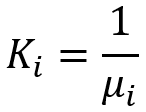
Хитрость данного преобразования в том, что при таком подходе все законы распределения, подвергнутые соответствующему преобразованию, будут иметь одинаковое математическое ожидание и, соответственно, мы сможем применять для оценки их "красоты" всего лишь среднеквадратичное отклонение, без необходимости выдумывания каких-либо экзотических критериев. Тем не менее, я показал вам два способа, какой из них лучше — выбирать только вам. Как вы уже догадались, законы распределения всех таких относительных кривых будут выглядеть так:
Я хочу вам сказать, что подобный подход абсолютно аналогично применим к удлиненным тестам. Под удлиненными тестами здесь понимается, когда мы тестируем по более длительному участку. Применение это годится только для подтверждения того факта, что чем длиннее тест, тем красивее график. Единственный прием для данного доказательства, который вы должны применить - принять, что если мы удлиняем длительность теста, то мы делаем это кратно целому числу, и кратно этому числу мы уже рассматриваем не 1 шаг а "n" и применяем формулы слияния. Данное слияние будет даже проще, поскольку рекуррентная цепочка слияния будет содержать лишь единственный элемент, который дублируется, да и сравнивать результат можно будет лишь с данным элементом, и все сильно упрощается.
Заключение
В статье мы рассмотрели даже скорее не сам алгоритм докупки, а гораздо более важную тему, которая дает вам необходимые математические формулы и методы для более точной и эффективной оценки торговых систем. А также, что еще более важно, вы получаете математическое доказательство того, что стоит заниматься диверсификацией и от чего же зависит ее эффективность, и как ее увеличить естественным и здоровым образом, будучи уверенным в том, что вы все делаете верно.
Также мы фактически доказали факт того, что график любой прибыльной системы тем красивее, чем более длительный участок торговли мы используем, а также, чем больше прибыльных систем торгуют параллельно на одном счете. Пока все оформлено в виде теории, но в следующей статье мы рассмотрим прикладные аспекты данной теории. Если проще, то мы построим работающую математическую модель симуляции цены и имитации мультивалютной торговли и подтвердим все наши теоретические выводы. Кроме того, данную теорию вы, скорее всего, не найдете нигде, так что постарайтесь вникнуть в данную математику поглубже или хотя бы понять ее суть.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования