Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
Não, não se pode usar um rastejador para avaliar o quanto o mercado mudou.
Você só pode avaliar o quanto os novos erros de previsão alteraram a previsão em relação aos erros antigos.
Ou seja, a SSA não diz nada sobre a exatidão da previsão, a diferença da SSA só nos diz sobre a diferença dos erros. Para onde o mercado irá, a SSA não se importa com isso de forma alguma.
Sem uma estimativa de erro de cada SSA, sua diferença está pendurada no ar, não tem nada com que contar.
Eu sei disso há muito tempo, mas tenho esperança, então estou pensando onde mais procurar :)) Quero fazer a matriz de covariância sobre a história e analisar quão grandes são as diferenças nela - e de repente dizem em teoria que o preço leva em conta tudo e assim por diante ))))
Não sei, parece-me que se Alexander ainda não chegou ao fim - nada pode salvar esta abordagem. É difícil prever a vagueação aleatória, e avaliar alguns estados imaginários :)
Aqui, além do meu posto acima, particularmente a parte da anedota... Para ser honesto, há alguma ilusão de que a regularidade nas tabelas de preços é simplesmente não repetir seus estados anteriores. Na SSA eu terei tempo, farei um conjunto de todas as matrizes de covariância possíveis e tentarei analisá-las para não repetição em estados próximos, ou seja, as matrizes devem alternar em ordem não repetitiva
talvez à noite eu limpe o código pela SSA e o poste, o código é apenas um porto de Matlab, eu não esperava, mas Alglib é muito útil para rapidamente portar essas coisas feitas como um exemplo para mim mesmo a fim de aprender, pode também ajudar alguém a entender, aqui está Matlab SSA anexo
Vou destacar a questão separadamente:
Em que função fazer uma regressão, para que seu último ponto esteja no centro do canal de preços?
Eu preciso de uma função, como um polinômio, que possa lidar com ziguezague e meio círculo (como você pode ver pelos exemplos, o polinômio não pode lidar com estes temas).
(A figura de Maxim Dmitrievsky ainda não pode ser considerada, não se enquadra na teoria de que o preço é um canal de comércio que segue uma determinada trajetória. esta figura é um canal de comércio com uma ejeção no final, ela pode ser considerada mais tarde).
Outros exemplos de funções não lineares são funções exponenciais, funções logarítmicas, funções trigonométricas, funções de potência, funções gaussianas e curvas de Lorenz.
Bem Smokchchy, você tem todo mundo irritado com suas fotos! ))
Bem e um pouco de psicologia para avaliar se a busca do Graal é bem sucedida, apreciou o vídeo, aparentemente a garota parece natural e convincente
E um pouco de psicologia para avaliar o sucesso da busca do Graal, eu gostei do vídeo, aparentemente a garota parece natural e convincente
Você poderia dar à luz uma lagarta à noite com esses olhos.
um pouco de psicologia para avaliar o sucesso da busca do Graal, gostou do vídeo, aparentemente a garota parece natural e convincente
A garota é esperta-jovem ela vê o invisível para muitos.
Bem, se a psicologia é interessante, a cereja no bolo...
bem, se a psicologia é interessante, a cereja no bolo, por assim dizer...
O 30º minuto do filme é o mais interessante), mas você tem que assistir a tudo para entendê-lo.
Já lhe foi dito que é um passatempo inútil.
até que você tenha passado seu tempo, você não entende.
Como fazer regressão em Excel.
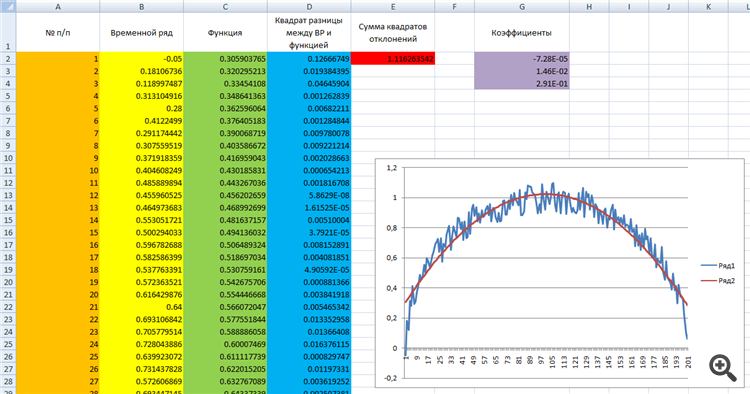
Usando a função Data/Solution Finder.
Na tabela anexa:
a primeira coluna é o número do n/a.
A segunda coluna é a série cronológica.
A terceira é uma função (neste caso, um polinômio).
O quarto é o ANC. o valor da série temporal menos o valor da função, e ao quadrado.
nas células vermelhas é a soma sobre a coluna azul, ou seja, a soma dos quadrados dos desvios.
nas células roxas são os coeficientes a serem ajustados.
A função polinomial é y=ax2+bx+c
onde x são os valores de coordenadas no eixo x. coluna laranja. de 0 a 201.
y são os valores de coordenadas no eixo y que o polinômio escolhido terá.
a,b,c são os coeficientes que nos serão ajustados.
No Excel, a fórmula será assim =a*A1^2+b*A1+c. Ou seja, substituímos os valores da coluna A em vez dos X (ver a coluna verde).
Para encontrar os coeficientes da função, clique em "Data" e depois em "Find Solution".

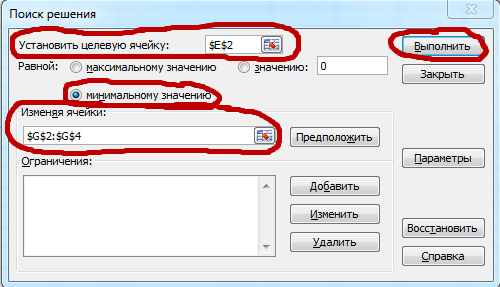
No menu que abre, selecione:
Definir célula alvo (a célula vermelha em nossa tabela),
a um valor mínimo,
Trocar células (células roxas em nossa mesa).
e depois clique em Executar.
Ou seja, minimizamos os quadrados dos desvios da série temporal em relação à função.
Tente colocar suas próprias funções na coluna verde.
funções exponenciais, funções logarítmicas, funções trigonométricas, funções de potência, função gaussiana, curvas de Lorenz, outras...
O problema continua o mesmo, é preciso encontrar uma função cujo último ponto estará no centro do canal de preços (tanto para números em ziguezague quanto em meio círculo).
...
Ou seja, minimizamos os quadrados de desvios da série temporal em relação à função.
Tente colocar suas próprias funções na coluna verde.
funções exponenciais, funções logarítmicas, funções trigonométricas, funções de potência, função gaussiana, curvas de Lorenz, outras...
O problema é o mesmo: você tem que encontrar uma função, cujo último ponto estará no centro do canal de preços (tanto para números em ziguezague quanto em meio círculo).
Interessante. Em primeiro lugar, é impreciso, não minimizamos "quadrados", mas "soma de quadrados". Em segundo lugar, se você quiser dar maior valor aos últimos pontos, isso é feito de forma simples, na soma minimizada não se tomam apenas quadrados, mas quadrados ponderados, que são multiplicados por alguns coeficientes de ponderação positivos. Seus valores no final da matriz devem ser maiores, e no início - menores. Por exemplo, para o número de pontos i de 1 a n, pesos iguais a q^(n-i) com q < 1, dê quadrados de multiplicadores de desvio semelhantes aos pesos dos cursos em uma média móvel exponencial. Muitas vezes sua soma também é igual a uma, se quisermos comparar diferentes aproximações pelo valor da soma mínima ponderada dos quadrados de desvio.
E qual é o "centro" de um canal curvilíneo cujos limites são descritos por diferentes tipos de fórmulas? Ou pelo menos para a primeira variante, por funções exponenciais?
Se for simplesmente o ponto médio do segmento desde o penúltimo valor da série até o último, então é suficiente para tornar os pesos de desvio nos dois últimos pontos da série muito grandes. Ou ainda mais simples, encontre este meio e pronto.
Você precisa de alguns outros requisitos para os desvios, caso contrário o problema é subestimado.
Qual é a utilidade de calcular o "centro" no último ponto?