Locatário - página 16
Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
É interessante ver como estes parâmetros afetam o resultado:
Por exemplo, para nossas condições de base, em diferentes posições de válvulas, obtemos estas interessantes imagens
.
.
.
Isso é para o quadro geral...
Estamos interessados na última dependência
(perfil da fase "a-da" -- o último gráfico é um caso especial dele)
Não funcionou muito bem. Não vou postar os cálculos aqui. Não há nada de belo neles.
Eu tentei usar a seguinte observação: 1+q-k = 1+epsilon, sendo o epsilon um valor pequeno. Depois expandi a derivada por k na série da Taylor, primeiro mantendo termos até a terceira ordem de pequenez. Então, após simplificações, obtivemos a equação cúbica. Eu descartei o menor termo de terceira ordem e tentei resolver o quadrático resultante. Eu falhei: o discriminante é positivo apenas em pequenos t.
Receio ter cometido um erro ao rejeitar o termo cúbico: embora seja um termo da terceira ordem de pequenez em epsilon, não é pequeno. Eu o tinha como segue: epsilon*epsilon*(epsilon-q)(t-1)(t-2)(t-3). Pode-se ver que para grandes pode ser bastante pequeno (mesmo que epsilon~0,01 seja uma suposição bastante realista). E não se quer resolver o cúbico.
Vamos ver o que Oleg consegue.
P.S. Assumindo epsilon*t = O(1) (ou q*t = O(1) ), você pode aproximar a função de potência por um expoente. Vamos tentar.
Há outra abordagem - sem a série Taylor, mas simplesmente pelo método tangente (Newton, acho). E também se pode chegar a uma solução analítica bastante exata.
A questão é que inicialmente as condições não contêm tempo contínuo, mas uma função de malha - ou seja, uma transformação adequada deve ser realizada primeiro. Somente então a introdução de um pequeno epsilon será válida. Estas são as propriedades das funções da malha.
A propósito, foi a tradução para a região do tempo contínuo que eu lidei no primeiro passo para resolver o problema, usando a transformação de Laplace na cadeia discreta --frequências-tempo. Para ser mais exato: também por isto...
Portanto, o objeto de nossa análise posterior é a função
.
E eu não quero resolver o cúbico.
Alexey, eu nunca vi uma expressão analítica para as raízes de uma equação cúbica (exceto para casos parcialmente simplificados). Você não tem tal expressão? Assim como para uma equação quadrática: x1=b/2+SQRT()... etc. Afixe isso se você o conhece. Eu não encontrei nada na Internet. Lembro-me da escola, que existe até mesmo uma representação das raízes através de funções harmônicas!
Há outra abordagem - sem a série Taylor, mas simplesmente pelo método tangente (Newton, eu acho). E também se pode chegar a uma solução analítica bastante exata.
É realmente possível obter uma solução aproximada em forma analítica desta maneira? Nunca ouvi falar disso. Muito interessante, eu gostaria de ver um exemplo do método.
Vamos para o estúdio!
Sim, você fala sobre a solução obtida para as grandes t. Isto também é de interesse prático como um caso de depósito "não matável". O que você conseguiu para obter uma aproximação? Talvez seja possível uma transição limite para t->inf. Então poderemos obter expressão analítica para a porcentagem de pagamento ótima, k, em função de apenas um parâmetro q - valor dos juros acumulados. Este seria um ótimo resultado.
avtomat:
A questão é que as condições iniciais não contêm tempo contínuo, mas uma função de malha - ou seja, uma conversão deve ser feita primeiro. Somente então a introdução de um pequeno epsilon seria válida. Estas são as propriedades das funções da malha.
A propósito, foi a tradução para a região do tempo contínuo que eu lidei no primeiro passo para resolver o problema, usando a transformação de Laplace na cadeia discreta --frequências-tempo. Para ser mais exato: incluindo este...
Oleg, por que você acha que a expressão analítica obtida acima para a soma dos meios deriváveis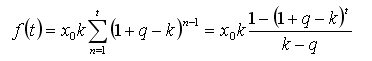
não é marginal para o tempo contínuo? Afinal, não estipulamos o limite mínimo de intervalo (etapa) da série cronológica original (forma iterada de escrita no primeiro post do tópico). Se assim for, basta que na transição limite em dt->0 tenhamos um certo df(t) e não há contradição...
Oleg, por que você acha que a expressão analítica acima para a soma dos derivados não é o limite para o tempo contínuo? Afinal, não estipulamos especificamente uma restrição ao intervalo mínimo (etapa) da série cronológica original (forma iterada de notação no primeiro post do tópico). Se assim for, então é suficiente que na transição limite em dt->0 tenhamos um df(t ) definido e não haja contradição...
Não é assim... Tente introduzir um pequeno epsilon aqui...
Sim, não estipulamos especificamente em nenhum lugar, mas a formulação do problema em si implica implicitamente no uso de uma função de malha.
Isto significa que a correspondência estará nos nós da malha. Além disso, para as funções da malha não há pontos intermediários - apenas os nós da malha. Portanto, todas as tentativas de construir valores intermediários levarão a resultados errôneos (a propósito, estas questões pertencem ao campo da quantização de sinais). Os valores intermediários podem ser construídos aumentando a taxa de amostragem, ou seja, introduzindo novamente uma função de malha com mais nós, o que não mudará fundamentalmente a essência do fenômeno. Isto significa, em particular, que são utilizados derivativos em primeiro, segundo, etc., em vez de primeiro, segundo, etc. diferenças. Em vez de integrais -- somas. ... etc. -- este é todo um campo de estudo.
Mas há maneiras de se mover de um campo para outro e voltar novamente.
Neste caso particular de nosso problema, esta abordagem não nos convém. Portanto, a primeira coisa que temos que fazer é passar do tempo discreto para o tempo contínuo.
A questão é que as condições iniciais não são de tempo contínuo, mas uma função de malha - ou seja, uma transformação deve ser realizada primeiro.
Eu nunca vi uma expressão analítica para as raízes de uma equação cúbica (exceto por simplificações parciais). Você não tem um? Assim como para uma equação quadrática: x1=b/2+SQRT()... etc. Afixe isso se você o conhece. Eu não consegui encontrar nada na Internet.
A fórmula de Cardano.
Lembro-me da escola que existe até mesmo uma representação das raízes através de funções harmônicas!
A fórmula trigonométrica do Viets
... Ou não para produzir, mas para usar o aparelho disponível da versão discreta da transformação Laplace, ou seja, a transformação Z. Você não acha que seria mais simples?
Esse não é o problema. Logo no início há um quadro tridimensional de "%crescimento - %rendimento - rendimento" - tudo já está calculado, e está no domínio discreto.
Agora a tarefa esportiva é apresentar tudo isso de uma forma analítica ;)
Fórmula Cardano
Fórmula trigonométrica do Vyet