Давайте начнем наш сегодняшний разговор со всем нам знакомого индикатора ЗигЗаг, который входит в стандартный комплект поставки терминала МТ4. Реализация индикатора из стандартной поставки далеко не самая лучшая и уж точно не самая быстрая, но нам сейчас это неважно. Давайте сначала вспомним, что представляет собой ЗигЗаг. Это не что иное как...
ウラジミールさん、こんにちは。
インターネット上には、量子物理学に関する彼の著作はない--すべて探した。残されたのは、老境に書かれたガラクタだけだ。どうしてこの擬似微分方程式に行き着いたのか、本当に理解したい...。信じられないかもしれませんが、彼の分析結果は私の実験データと完全に一致して いるのです。
https://www.mql5.com/ru/forum/221552/page158#comment_6392311 では、リンクを紹介しました。
オーバーショットというパラメータ、それを計算するMQLプログラム、適用方法、結果の解釈など、一般的に非エントロピーが持っていないものをすべて含んでいるのです。そして何より、トレンドとフラットの分離を直接的に証明するものです。非エントロピーとは異なり、その必要な性質において、私たちはあなたの伝統的な「そうだそうだ」によって、その代償として、すでにここであなたの確信、確実性の数々の例によって明らかにされています。絶対的なものも含めて。
そのメッセージ(記事)の作者に記念碑を立てる。
フラットからのトレンドは、どちらかというと、通常のハイ/ローの更新でうまく区切られています(ウラジミールが書いているオーバーショットに非常に近い意味です)。確かに、ジグザグは閾値が決まっていて、あまり好きではないのですが......)。
明確にしたいと思います。
レベルブレイクアウトでの取引とレベルリバウンドでの取引で、変動の性質が収益性に及ぼす影響を見るのは面白いと思います。それゆえ、トレンド/フロート分割とその目的があるのです。http://www.argolab.net/izuchaem-zigzagi.html では、この目的が直接的に反映されています。
「オーバーシュートの平均値が1よりはるかに大きい場合、ジグザグに形成されたニー(「ブレイクアウト」)の方向へ取引を開始することが有益であることを意味します。そして、それが1より大幅に小さい場合は、反対方向(「オンリバーサル」)の取引を開始すべきです」。
この目標が「通常のhai/loiの更新」にどう反映されるのか、まだ理解できていません。教えてもらえますか?
これはジグザグのように、例えばHigh(i, 30)-High(i+5, 30)のように単なるツールに過ぎない。ただ、その方が(おそらく)現在のボラティリティをより考慮しているので、私には近いです。ジグザグのように、更新値をチャンネルの高さ(幅?)で割るなど、何らかの指標を工夫することは可能です。ジグザグがオーバーシュートした場合、この測定器は高値/安値の更新を行います。
変動の性質については、資産全体の指標を平均化すると、トレンド性/フラット性が一日のうち特定の時間帯に集中するため、「病院の平均気温」のようなものです(日中の作業でいえば)。ただし、平均して他のペアより若干扁平率が高いクロスが2組(ご存知だと思いますが)あります。
横ばいとトレンドを見分けるためのパラメータについて。
このパラメータはハーストの係数ではありません。
あのね、このパラメータは非エントロピー https://en.wikipedia.org/wiki/Negentropy と呼ばれているんだ。
それを正しく計算し、アルゴリズムに使えるようになった最初の人は、感謝する人類から生涯に一度、記念碑をもらうべきだろう。それだ!
なでしこ
そのようにすることができます
ただ、ひとつだけ問題がある。
また、精度が落ちてしまう。
そして「1円玉は1円玉を貯める」。
えんまんか
それでいいんです。
が、ひとつだけ問題がある。
またしても精度が落ちてしまう。
と、"1円玉は1円玉を救う"。
いや、カッコいいんですよ。実際には、与えられたサンプルサイズに対する確率の増分とその対数の積の和である。ある時点の確率分布が、あるベンチマークとどの程度異なるかを示すものである。ハーストのようにテーブルを作ればいいだけですからね。
非対称度や尖度では物足りないので、この隠しパラメータをずっと探していたのです。私は涙ながらに、このフォーラムのトレーダーに探すのを手伝ってくれるように頼みました。このリクエストに応えてくれたのは、私が尊敬する2人のトレーダー、VladimirとDmitriy Skubだけでした。二人はそれぞれのバリエーションを提案した。私は何も理解していないし、何もわかっていない。どうして、何も知らずにここでお金を稼ぐ人がいるのでしょうか?パラドックスです!
過去2週間のAUDCADのチャートです。サンプルサイズは16900ティック、指数読み出しの時間です。
そう、何もかもが順調でいい感じなんだけど、何か気になるんだよね...。何を説明しよう。
まず、理論を少し。
この積F(x,t)が、目に見える増分の分布となる。
マクドナルドの機能は、私たちのプロセスの「記憶」を担っているのです。
そして、こんな感じです。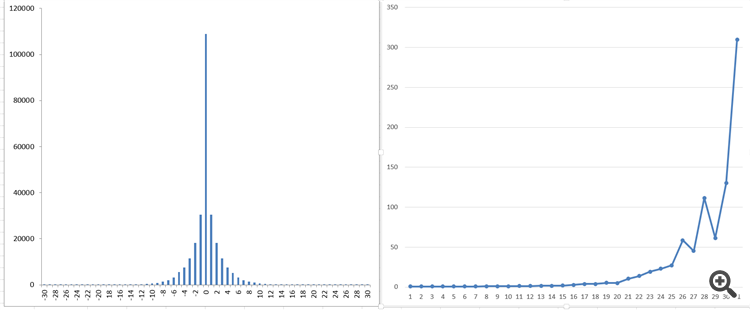
右の写真は、私がプロセスの「記憶」として得たものです。
これは、一般的なダニが25万匹以上いる状態での話です
残念なことに、修正ベッセル関数のような滑らかな関数は見当たりません。こんな「ジャンプ」はないはずなのに...。
そういうわけで、結局ティックデータの取り方が間違っているのだろうという結論になりかけています。
やはり一定期間ごとに飲む必要がありますね。とはいえ...実践でしか確認できない。
今のところ、良い結果と抑えきれない疑問が残っています...。
そして、こんな感じです。
右の写真は、私がプロセスの「記憶」として得たものです。
これは、一般的なダニが25万匹以上いる状態での話です
残念なことに、修正ベッセル関数のような滑らかな関数は見当たりません。こんな「ジャンプ」はないはずなのに...。
これが、「やっぱりティックデータの取り方が悪いんだろうな」という結論になりかけている理由です。
やはり一定期間ごとに飲む必要がありますね。とはいえ...実践でしか確認できない。
今のところ、良い結果と放漫な疑問が残っています...。
あなたのデータは正しい。誰もが持っている。平均の変化、分散の変化、テール、ARCH効果など、花束を持ったいつもの種類の不安定な増分であ る。すべてをモデル化する必要があるのです。
そして、何千何万という人々が、30年、40年と続けてきたのです。