なぜ正規分布は正規分布ではないのですか? - ページ 4 1234567891011...47 新しいコメント 削除済み 2009.12.01 19:25 #31 ひどいな そんな言葉を投げかける人たち、負け犬の私はここにふさわしくありません。 Петр 2009.12.01 19:31 #32 AlexEro >> : ホラー。そんな言葉を投げかける人たちは、私の居場所がない。 何を合意するつもりなのか、考えながら読んでいます。 タコにフリルを付けるのは、他の子羊が初めての試みだというなら、それもありでしょう。実用的なものであれば、参加します。 Mykola Demko 2009.12.01 19:40 #33 Mathemat >> : そこで、ニュートロンがやってきて、すべてを元の場所に戻してくれた。ちなみに、marketeerは、kurtosisとasymmetryについても話しています。 対応するガウス曲線は好きなようにプロットできますが、ここでは単純に標本分散を計算し、パラメータ0とシグマでガウス曲線をプロットするのが最も簡単です。その時、本物のヒストグラムとこのようなガウス曲線の違いがわかります。 ちなみに、このガウス近似は、曲線の中心(ゼロ点)で実際のヒストグラムよりかなり低くなるはずです。 ウライン、サンプルのS.C.O.はどのくらいかけたのでしょうか? 一方、強くファットテイルな分布に対するc.s.o.推定値はサンプルサイズに依存するので、ここではそれほど単純ではありません。 RMSは全く触らず、既成のグラフをヒストグラムの縦方向に合うようにスケーリングしているだけです。 ヒストグラムはClos差の分布であり(MOとRMSがある)、このMOとRMSを用いて上の式で赤い線を構成しますが、線はヒストグラムの底で失われるため、また比例yヒストグラムを構成するには絶対値が小さいため、各y線に乗算して比較しなければならないのでした。 Yurixx 2009.12.01 19:47 #34 Urain писал(а)>> ベンチマーク関数については、分散とMOをいくつかの相場から取り出して(そこでも計算)同じ値に設定しているが、操作はベンチマークの絶対値のみで、ここでは各項を係数に加算して頂点を結合することにしている。 私が理解する限り、リファレンス機能はHPの機能です。 もしそうなら、あなたはすべてを正しく行ったことになります。ただし、1つだけ、ドメイン取得はできません。頂点を結合したいという思いは、実際のグラフの位置とは関係ありません。また、ドメイン化すると、HP関数の正規化に違反する。確率 >1 はどうなんだろう? ドミネーションを外してもう一度絵を描くと、プロットの幅が多少なりともまともに合うようになります。しかし、ヒストグラムは中央とエッジで高くなり、これは2つの主要な問題、すなわちリターンが大きいことと、同時にテールが重いことを示しています。 こんな感じの絵でよければやってください。 追記 前の記事でお悩みがわかりました。HPのノルマに違反する必要はない。ヒストグラムに適したスケールを見つけるとよいでしょう。同じ配給から見つかります。ヒストグラムのすべてのバーの高さを合計し、この値でそれぞれのバーを割る必要があります。その結果、ヒストグラムも1に正規化される。 Mykola Demko 2009.12.01 19:48 #35 Svinozavr >> : 読書中 - 彼らが何に同意するのかを考えようとしている。 タコにフリルをつけるという、これまた初めての試みであれば、それはそれでアリなのですが。実用的なものであれば、参加します。 正規分布にない一連の引用符の最初の差に何があるかを見つけようとしている? Петр 2009.12.01 19:51 #36 Urain >> : 引用符系列の最初の差分には、正規分布には存在しないものがあるのか、調べようとしています。 そして、その目的は何なのか、ゴールは何なのか。異常」な部分を特定する?もう一度、なぜ? (今のところ"?????? "だけ))) Mykola Demko 2009.12.01 19:53 #37 Svinozavr >> : そして、その目的は何なのか、ゴールは何なのか。異常」な部分を特定する?もう一度言いますが、なぜですか? (今のところ1つの「??????」)) どのような法則で異常が現れるのかを探るために言ってみましょう。 Mykola Demko 2009.12.01 19:58 #38 Yurixx >> : リファレンス機能はHP機能であると理解しています。 もしそうなら、あなたはすべてを正しく行ったことになります。ただし、1つだけ、ドメイン取得はできません。頂点を結合したいという思いは、実際のグラフの位置とは関係ありません。また、ドメイン化すると、HP関数の正規化に違反する。確率 >1 はどうなんだろう? ドミネーションを外してもう一度絵を描くと、プロットの幅が多少なりともまともに合うようになります。しかし、ヒストグラムは中央と端で高くなり、これは2つの主要な問題を示しています:大きなリターンと、同時に重いテールです。 こんな感じの絵でよければやってください。 追記 前の記事でお悩みがわかりました。HPのノルマに違反する必要はない。ヒストグラムに適したスケールを見つけるとよいでしょう。同じ配給から見つかります。ヒストグラムのすべてのバーの高さを合計し、この値でそれぞれのバーを割る必要があります。その結果、ヒストグラムも1によって正規化されます。 まあ、そんな大げさなものではありません。やはり正規化する必要があります。 まあ、配給は全くないんですけどね。両者ともmultiplier=1.0/Pointに調整されており、それ以外の場合はインダクタがこのような小さな値を見ることはない。 Vladimir Gomonov 2009.12.01 20:14 #39 Neutron >> :.左下は確率分布密度、右は同じものを対数スケールで表示したものです。 分布が正規分布であれば、ここで放物線を描くはずですが、「太い」尾があるため、そうではありません。原理的には、ここに最小二乗法によるガウシアンを当てはめれば、すべてがうまくいくことになる。最適な装着感のための計算式を入れなければ......。 セルゲイさん、両対数についてはどうですか? ずっと考えていたんです...。 まだ謙遜してテストできないんです :) Neutron 2009.12.01 20:27 #40 MetaDriver >> : セルゲイさん、両対数についてはどうですか? 以前から考えていたのですが...。 私は控えめなので、チェックできませんが :) そう判明したのです。 ゼロ付近では正規分布に近く、その後、直線の形で漸近し、両対数スケールでは「テール」の分布が指数関数的であることを示すことがわかる。つまり、「重さ」についてです。 1234567891011...47 新しいコメント 取引の機会を逃しています。 無料取引アプリ 8千を超えるシグナルをコピー 金融ニュースで金融マーケットを探索 新規登録 ログイン スペースを含まないラテン文字 このメールにパスワードが送信されます エラーが発生しました Googleでログイン WebサイトポリシーおよびMQL5.COM利用規約に同意します。 新規登録 MQL5.com WebサイトへのログインにCookieの使用を許可します。 ログインするには、ブラウザで必要な設定を有効にしてください。 ログイン/パスワードをお忘れですか? Googleでログイン
ホラー。そんな言葉を投げかける人たちは、私の居場所がない。
何を合意するつもりなのか、考えながら読んでいます。
タコにフリルを付けるのは、他の子羊が初めての試みだというなら、それもありでしょう。実用的なものであれば、参加します。
そこで、ニュートロンがやってきて、すべてを元の場所に戻してくれた。ちなみに、marketeerは、kurtosisとasymmetryについても話しています。
対応するガウス曲線は好きなようにプロットできますが、ここでは単純に標本分散を計算し、パラメータ0とシグマでガウス曲線をプロットするのが最も簡単です。その時、本物のヒストグラムとこのようなガウス曲線の違いがわかります。
ちなみに、このガウス近似は、曲線の中心(ゼロ点)で実際のヒストグラムよりかなり低くなるはずです。
ウライン、サンプルのS.C.O.はどのくらいかけたのでしょうか?
一方、強くファットテイルな分布に対するc.s.o.推定値はサンプルサイズに依存するので、ここではそれほど単純ではありません。
RMSは全く触らず、既成のグラフをヒストグラムの縦方向に合うようにスケーリングしているだけです。
ヒストグラムはClos差の分布であり(MOとRMSがある)、このMOとRMSを用いて上の式で赤い線を構成しますが、線はヒストグラムの底で失われるため、また比例yヒストグラムを構成するには絶対値が小さいため、各y線に乗算して比較しなければならないのでした。
ベンチマーク関数については、分散とMOをいくつかの相場から取り出して(そこでも計算)同じ値に設定しているが、操作はベンチマークの絶対値のみで、ここでは各項を係数に加算して頂点を結合することにしている。
私が理解する限り、リファレンス機能はHPの機能です。
もしそうなら、あなたはすべてを正しく行ったことになります。ただし、1つだけ、ドメイン取得はできません。頂点を結合したいという思いは、実際のグラフの位置とは関係ありません。また、ドメイン化すると、HP関数の正規化に違反する。確率 >1 はどうなんだろう?
ドミネーションを外してもう一度絵を描くと、プロットの幅が多少なりともまともに合うようになります。しかし、ヒストグラムは中央とエッジで高くなり、これは2つの主要な問題、すなわちリターンが大きいことと、同時にテールが重いことを示しています。
こんな感じの絵でよければやってください。
追記
前の記事でお悩みがわかりました。HPのノルマに違反する必要はない。ヒストグラムに適したスケールを見つけるとよいでしょう。同じ配給から見つかります。ヒストグラムのすべてのバーの高さを合計し、この値でそれぞれのバーを割る必要があります。その結果、ヒストグラムも1に正規化される。
読書中 - 彼らが何に同意するのかを考えようとしている。
タコにフリルをつけるという、これまた初めての試みであれば、それはそれでアリなのですが。実用的なものであれば、参加します。
正規分布にない一連の引用符の最初の差に何があるかを見つけようとしている?
引用符系列の最初の差分には、正規分布には存在しないものがあるのか、調べようとしています。
そして、その目的は何なのか、ゴールは何なのか。異常」な部分を特定する?もう一度、なぜ?
(今のところ"?????? "だけ)))
そして、その目的は何なのか、ゴールは何なのか。異常」な部分を特定する?もう一度言いますが、なぜですか?
(今のところ1つの「??????」))
どのような法則で異常が現れるのかを探るために言ってみましょう。
リファレンス機能はHP機能であると理解しています。
もしそうなら、あなたはすべてを正しく行ったことになります。ただし、1つだけ、ドメイン取得はできません。頂点を結合したいという思いは、実際のグラフの位置とは関係ありません。また、ドメイン化すると、HP関数の正規化に違反する。確率 >1 はどうなんだろう?
ドミネーションを外してもう一度絵を描くと、プロットの幅が多少なりともまともに合うようになります。しかし、ヒストグラムは中央と端で高くなり、これは2つの主要な問題を示しています:大きなリターンと、同時に重いテールです。
こんな感じの絵でよければやってください。
追記
前の記事でお悩みがわかりました。HPのノルマに違反する必要はない。ヒストグラムに適したスケールを見つけるとよいでしょう。同じ配給から見つかります。ヒストグラムのすべてのバーの高さを合計し、この値でそれぞれのバーを割る必要があります。その結果、ヒストグラムも1によって正規化されます。
まあ、そんな大げさなものではありません。やはり正規化する必要があります。
まあ、配給は全くないんですけどね。両者ともmultiplier=1.0/Pointに調整されており、それ以外の場合はインダクタがこのような小さな値を見ることはない。
.左下は確率分布密度、右は同じものを対数スケールで表示したものです。
分布が正規分布であれば、ここで放物線を描くはずですが、「太い」尾があるため、そうではありません。原理的には、ここに最小二乗法によるガウシアンを当てはめれば、すべてがうまくいくことになる。最適な装着感のための計算式を入れなければ......。
セルゲイさん、両対数についてはどうですか? ずっと考えていたんです...。
まだ謙遜してテストできないんです :)
セルゲイさん、両対数についてはどうですか? 以前から考えていたのですが...。
私は控えめなので、チェックできませんが :)
そう判明したのです。
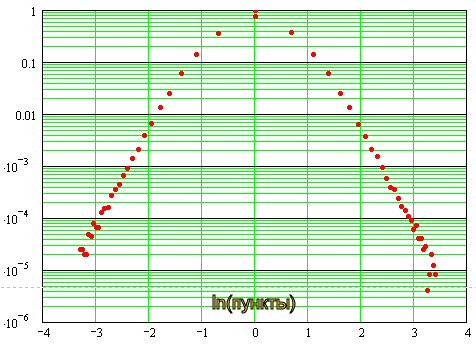
ゼロ付近では正規分布に近く、その後、直線の形で漸近し、両対数スケールでは「テール」の分布が指数関数的であることを示すことがわかる。つまり、「重さ」についてです。