ハーストの索引 - ページ 9 12345678910111213141516...46 新しいコメント Neutron 2009.02.02 05:48 #81 Prival писал(а)>> いいえ、そうではありません。この式によると、GVHは相関があるように見える。常にrはマイナス0.5程度である。 以下は、そのテストコードです。 確認しました。 セルゲイ、一歩一歩進んでいこうよ。 1.見積書と同じようなBPで仕事をします。このような系列は、CBをゼロMOで積分することで得られる。MOがゼロのCBの例。 dX=rnorm(n+1,0,10), ここで n+1 はガウス分布を持つ CB メンバーの数, 0 は私の場合はゼロに等しい MO, あなたの例では 10, 10 はこの分布の幅, あなたの場合は 100。価格と同じようなBPを構成するには、初期系列を積分する(可換和を求める)必要がある。 積分したCBの増分の分布はどのようになっているか(左図)と、BPを背景とした増分そのもの(右図の赤線と青線)である。 Sergeyさん、私たちはBP(青い方)の性質を研究しているのですが、あなたの投稿では、系列の最初の差の相関係数を計算する式に、一番最初の差(私の表記ではdX、あなたの表記ではX)を代入していますね。もちろん、R=0.5が得られるので、それ以上はないはずです(初歩的な証明です)。そこで、今、私が提案した式で、MOがゼロの積分型CB(右図の青い方)のrを計算すると、期待通りのゼロが得られます。 そして、もちろん、これはdXの一連の増分のrと同じである(ただし、別の式による)。 この点については、もうコンセンサスが得られているのでしょうか? 追伸:こんな方法もあるんですね。 というのは、もちろん、論点は変わりません。 Prival 2009.02.02 11:52 #82 よし、整理してみよう。 言われた通り、MOJ=0でCBを再統合してみました。これがすべてのコードです。 一見、大丈夫そうに見える。しかし、そこには落とし穴がある。数式の入力に相関配列を与えてみよう。トレンド+ノイズとして y=a*x+b+rnorm().これは、MOJ=0の代わりに0.5を設定することで簡単に行うことができる。 図から、曲線(青色)が明らかに相関していることがわかると思います。これを2つの配列A、Bに分割して相関係数を計算すると、0.993となる。あなたの計算式によると0.225です。 問題は、定義上、2つのアレイの間で相関係数(CC)がカウントされることです。同じものを使っているんですね。これは、配列と それ自身を比較することで実現できます。つまり、2つの配列Aを形成し、初期と、Aに対して時間的にシフトした2番目のBを形成し、相関係数のシフトに対する依存性というグラフを構築するのである。シフトがなければ、もちろんACF=1です。最後の青い曲線のACFプロットを示します。 これが近似値です。だから、この計算式で計算しているけれど、ACではない、という意見に今もこだわっています。数字が合わないんです。 しかし、私たちは横道にそれてしまった。まずはハーストを正しく計算し、QCとの違いを確認する必要があります。 削除済み 2009.02.02 11:56 #83 異なる時系列を分析した興味深い論文を紹介 します 。 ハースト社のインデックスを使用しています。 Neutron 2009.02.02 12:27 #84 Prival писал(а)>>図では、曲線(青色)が明らかに相関していることがわかる。これを2つの配列A、Bに分割して相関係数を求めると、0.993となる。あなたの計算式では0.225となります。 ここで私は完全に理解しているわけではありません。 トレンドBPはどのような配列に分けられたのでしょうか?直線のY=a*X+bと、MOが0のランダム成分に、両者の間に相関係数を求めるのですか? Aleku さんが書き込みました >>1 異なる時系列を分析した興味深い論文を紹介します 。 ハースト社のインデックスを使用して ありがとうございます。見てみよう。 Neutron 2009.02.02 12:38 #85 Neutron писал(а)>> ここではうまく伝わらなかった。 今ならわかるよ。 元の血圧(増分ではない)と、同じ血圧を500カウント右にずらしたものとの相関係数を求めているのである。つまり、常に正である2つのBPの相関係数を求めているのだ!もちろん、常にプラスで非常に大きな値(1程度)になりますね。 セルゲイ 理解できないわ!初期血圧と同じでずらしたときの相関係数、何をカウントしているのでしょうか?一体何のために必要なんだ!?初期値BPの最初の差の系列で、隣り合うサンプル間の 相関係数に興味があります。この係数は、予想される増分が以前の増分に依存することを示すものである。この係数こそ、Hurstを1/2にシフトしたものと同じである。 TheXpert 2009.02.02 13:00 #86 Neutron >> : >> ありがとうございました。>> 今にわかる。 ここには 真実があるように思います。 実装してみましたが、レートが1に近い状態になってしまいました。 ______________ 記事を読み直す -- 私は間違った側にいるようだ。 通貨ペアの場合、Hearst's indexはデリバティブで計算する必要がありますが、私は為替レートで計算しました。 Neutron 2009.02.02 13:34 #87 TheXpert писал(а)>>記事を読み直すと、熊手を踏んだようなものだ。 うん:-) 先走りすること。 SVとEURGBPレートの積算値の系列はどのように見えるか(左図)、そして、異なるTFでのそれらの増加の振幅を両対数スケールで示したのがこちら(右図)、横軸はTFの対数をプロットしたものです。 Hersは、これらの直線の傾斜角の正接は、ランダムな積分変数では1/2に等しく(このような商で取引するのは意味がない)、プルバック相場では1/2より小さく、トレンド相場では1/2より大きくなると主張する。この角度が、NEにとってどのような意味を持つのか見てみましょう。ここで、記事でアドバイスされているように、ISC線を引いてその傾きを求めることもできますが、ここでは局所的に、つまり2点ごとに線を引いてこの値を求めます。その結果が各TFのPCとなる。 ここでの円は、TFの横軸にCBのPC(赤)、EURGBPの商を青でminに表示したものです。十字は、オフセット1/2のオリジナルシリーズの最初の差分に対する近隣の測定値間の相関係数を示している。相関係数は、本ページの最初のメッセージにある計算式に従って算出しました。これら2つのBPの予測可能性の推定方法の一致は満足のいくものであることがわかりますが、私の場合の計算式ははるかに小さい(1つだけ)ものです。それが、実は、表示することが求められていたのです。 また、Random系列では、定義から次のようにPX=1/2、r=0(図では偏りがある)が与えられた。商については、ローリングトレンド(反存在)が明確に見られ、大きくなればなるほどTFは小さくなる。 削除済み 2009.02.02 13:49 #88 Neutron >> : ここでは、PCBはCB(赤)、EURGBPは青で横軸にTFを分単位でプロットしています。 乱数系列は定義から次のようにPX=1/2、r=0を与えた(図では偏りがある)。コチエの場合、ロールバック傾向(反存在)がはっきりと見られ、TFが大きいほど小さくなる。 だからpipsはユーロポンドが好きなのでしょう Neutron 2009.02.02 13:51 #89 Aleku писал(а)>> だからピップスマンはユーロポンドが好きなんだろうなぁ。 当たり前だ! 削除済み 2009.02.02 13:58 #90 Neutron >> : 当たり前だ! 好奇心旺盛な私は、非常に粘り強いペアを見つけたいと思っています。 または少なくとも永続性が発生する条件)。 12345678910111213141516...46 新しいコメント 取引の機会を逃しています。 無料取引アプリ 8千を超えるシグナルをコピー 金融ニュースで金融マーケットを探索 新規登録 ログイン スペースを含まないラテン文字 このメールにパスワードが送信されます エラーが発生しました Googleでログイン WebサイトポリシーおよびMQL5.COM利用規約に同意します。 新規登録 MQL5.com WebサイトへのログインにCookieの使用を許可します。 ログインするには、ブラウザで必要な設定を有効にしてください。 ログイン/パスワードをお忘れですか? Googleでログイン
いいえ、そうではありません。この式によると、GVHは相関があるように見える。常にrはマイナス0.5程度である。
以下は、そのテストコードです。
確認しました。
セルゲイ、一歩一歩進んでいこうよ。
1.見積書と同じようなBPで仕事をします。このような系列は、CBをゼロMOで積分することで得られる。MOがゼロのCBの例。
dX=rnorm(n+1,0,10), ここで n+1 はガウス分布を持つ CB メンバーの数, 0 は私の場合はゼロに等しい MO, あなたの例では 10, 10 はこの分布の幅, あなたの場合は 100。価格と同じようなBPを構成するには、初期系列を積分する(可換和を求める)必要がある。
積分したCBの増分の分布はどのようになっているか(左図)と、BPを背景とした増分そのもの(右図の赤線と青線)である。
Sergeyさん、私たちはBP(青い方)の性質を研究しているのですが、あなたの投稿では、系列の最初の差の相関係数を計算する式に、一番最初の差(私の表記ではdX、あなたの表記ではX)を代入していますね。もちろん、R=0.5が得られるので、それ以上はないはずです(初歩的な証明です)。そこで、今、私が提案した式で、MOがゼロの積分型CB(右図の青い方)のrを計算すると、期待通りのゼロが得られます。
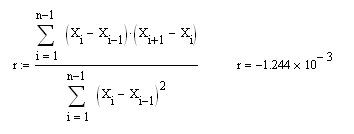
そして、もちろん、これはdXの一連の増分のrと同じである(ただし、別の式による)。
この点については、もうコンセンサスが得られているのでしょうか?
追伸:こんな方法もあるんですね。
よし、整理してみよう。
言われた通り、MOJ=0でCBを再統合してみました。これがすべてのコードです。
一見、大丈夫そうに見える。しかし、そこには落とし穴がある。数式の入力に相関配列を与えてみよう。トレンド+ノイズとして y=a*x+b+rnorm().これは、MOJ=0の代わりに0.5を設定することで簡単に行うことができる。
図から、曲線(青色)が明らかに相関していることがわかると思います。これを2つの配列A、Bに分割して相関係数を計算すると、0.993となる。あなたの計算式によると0.225です。
問題は、定義上、2つのアレイの間で相関係数(CC)がカウントされることです。同じものを使っているんですね。これは、配列と それ自身を比較することで実現できます。つまり、2つの配列Aを形成し、初期と、Aに対して時間的にシフトした2番目のBを形成し、相関係数のシフトに対する依存性というグラフを構築するのである。シフトがなければ、もちろんACF=1です。最後の青い曲線のACFプロットを示します。
これが近似値です。だから、この計算式で計算しているけれど、ACではない、という意見に今もこだわっています。数字が合わないんです。
しかし、私たちは横道にそれてしまった。まずはハーストを正しく計算し、QCとの違いを確認する必要があります。
異なる時系列を分析した興味深い論文を紹介 します 。
ハースト社のインデックスを使用しています。
図では、曲線(青色)が明らかに相関していることがわかる。これを2つの配列A、Bに分割して相関係数を求めると、0.993となる。あなたの計算式では0.225となります。
ここで私は完全に理解しているわけではありません。
トレンドBPはどのような配列に分けられたのでしょうか?直線のY=a*X+bと、MOが0のランダム成分に、両者の間に相関係数を求めるのですか?
異なる時系列を分析した興味深い論文を紹介します 。
ハースト社のインデックスを使用して
ここではうまく伝わらなかった。
今ならわかるよ。
元の血圧(増分ではない)と、同じ血圧を500カウント右にずらしたものとの相関係数を求めているのである。つまり、常に正である2つのBPの相関係数を求めているのだ!もちろん、常にプラスで非常に大きな値(1程度)になりますね。
セルゲイ 理解できないわ!初期血圧と同じでずらしたときの相関係数、何をカウントしているのでしょうか?一体何のために必要なんだ!?初期値BPの最初の差の系列で、隣り合うサンプル間の 相関係数に興味があります。この係数は、予想される増分が以前の増分に依存することを示すものである。この係数こそ、Hurstを1/2にシフトしたものと同じである。
>> ありがとうございました。>> 今にわかる。
ここには 真実があるように思います。
実装してみましたが、レートが1に近い状態になってしまいました。
______________
記事を読み直す -- 私は間違った側にいるようだ。
通貨ペアの場合、Hearst's indexはデリバティブで計算する必要がありますが、私は為替レートで計算しました。
記事を読み直すと、熊手を踏んだようなものだ。
うん:-)
先走りすること。
SVとEURGBPレートの積算値の系列はどのように見えるか(左図)、そして、異なるTFでのそれらの増加の振幅を両対数スケールで示したのがこちら(右図)、横軸はTFの対数をプロットしたものです。
Hersは、これらの直線の傾斜角の正接は、ランダムな積分変数では1/2に等しく(このような商で取引するのは意味がない)、プルバック相場では1/2より小さく、トレンド相場では1/2より大きくなると主張する。この角度が、NEにとってどのような意味を持つのか見てみましょう。ここで、記事でアドバイスされているように、ISC線を引いてその傾きを求めることもできますが、ここでは局所的に、つまり2点ごとに線を引いてこの値を求めます。その結果が各TFのPCとなる。
ここでの円は、TFの横軸にCBのPC(赤)、EURGBPの商を青でminに表示したものです。十字は、オフセット1/2のオリジナルシリーズの最初の差分に対する近隣の測定値間の相関係数を示している。相関係数は、本ページの最初のメッセージにある計算式に従って算出しました。これら2つのBPの予測可能性の推定方法の一致は満足のいくものであることがわかりますが、私の場合の計算式ははるかに小さい(1つだけ)ものです。それが、実は、表示することが求められていたのです。
また、Random系列では、定義から次のようにPX=1/2、r=0(図では偏りがある)が与えられた。商については、ローリングトレンド(反存在)が明確に見られ、大きくなればなるほどTFは小さくなる。
ここでは、PCBはCB(赤)、EURGBPは青で横軸にTFを分単位でプロットしています。
乱数系列は定義から次のようにPX=1/2、r=0を与えた(図では偏りがある)。コチエの場合、ロールバック傾向(反存在)がはっきりと見られ、TFが大きいほど小さくなる。
だからpipsはユーロポンドが好きなのでしょう
だからピップスマンはユーロポンドが好きなんだろうなぁ。
当たり前だ!
当たり前だ!
好奇心旺盛な私は、非常に粘り強いペアを見つけたいと思っています。
または少なくとも永続性が発生する条件)。