純粋数学、物理学、論理学(braingames.ru):貿易に関連しない頭脳ゲーム - ページ 125 1...118119120121122123124125126127128129130131132...229 新しいコメント --- 2012.09.03 20:18 #1241 GaryKa: 2つの重さですべてのオプションに対応するようです。 この絵は、何か宇宙人みたいだ...。 Vladislav Andruschenko 2012.09.03 20:30 #1242 sergeev: この絵は、何か宇宙人みたいだ...。 ネットにあった絵なんですけどね...。 GaryKa 2012.09.03 21:29 #1243 TheXpert: どうしてなのか、図がよくわからなかった。 変だな、もっとわかりやすいと思ったんだけどな、言葉より絵の 方がわかりやすいと思う。OK、少しコメントします。 最初の計量では、秤の各カップに2個のボールを置き、それぞれのカップに選んだ色のボール1個と、反対側のバスケットのボールの色とは異なる他の色のボール1個を入れます。(写真では赤い玉に緑の玉、赤い玉に青い玉)。1の計量結果は、オプション1.1)の秤がバランスしている場合と、オプション2)の秤がアンバランスで、カップの1つが2.1)を上回っている場合では、異なることがあります。つまり、解答の分岐が2つあるのです。 最初のバリエーションであれば、ボールを2つの同質なグループ(グループ 'とグループ ')に分け、1.2)両方のグループの重量(天秤のカップあたり3個のボール)を単純に測定して、どちらが重いかを判断します。以上、重い玉が見つかりました。 2つ目の選択肢は、2つの(一般的な)ケースで起こり得ます。各カップの最初の計量で出た色の玉が両方とも重いか軽い場合。(2.2)により、球をグループ(グループ'とグループ')に分けた後、重い球で一回計量することにより、どのグループが重いグループに属し、どのグループが軽いグループに属するかを決定することができます。 Vladon(ブラドン)。 これはネットにあった写真ですが...。 疑問は胸にしまっておいてください。打ち切り TheXpert 2012.09.03 21:45 #1244 GaryKa: OK、少しコメントします。これでパターンがはっきりしましたね。 2つ目の選択肢は、2つの(一般的な)ケースで起こり得ます。各カップの最初の計量で出た色の玉が、両方とも重いか軽いかのどちらかになったとき。 3つ目のケースとして、ヘビーグリーンとライトブルーがあります。カウントされない。 Vladislav Andruschenko 2012.09.03 22:03 #1245 GaryKa: 変だな、もっとわかりやすいと思ったんだけどな、言葉より絵の 方がわかりやすいと思う。OK、少しコメントします。 最初の計量では、秤の各カップに2個のボールを置き、それぞれのカップに選んだ色のボール1個と、反対側のカゴのボールの色とは異なる他の色のボール1個が入るようにします。(写真では赤い玉に緑の玉、赤い玉に青い玉)。1の計量結果は、オプション1.1)の秤がバランスしている場合と、オプション2)の秤がアンバランスで、カップの1つが2.1)を上回っている場合では異なる場合があります。つまり、解答の分岐が2つあるのです。 最初のバリエーションであれば、ボールを2つの同質なグループ(グループ 'とグループ ')に分け、1.2)両方のグループの重量(天秤のカップあたり3個のボール)を単純に測定して、どちらが重いかを判断します。以上、重い玉が見つかりました。 2つ目の選択肢は、2つの(一般的な)ケースで起こり得ます。各カップの最初の計量で出た色の玉が両方とも重いか軽い場合。(2.2)により、1回の計量で(グループ'とグループ')、どちらが重いか、どちらが軽いかを判断することができる。 疑問は胸にしまっておいてください。打ち切り悪気はないのですが...。選択肢1.1 内輪で提案した。冒頭がおかしい。 Sceptic Philozoff 2012.09.03 22:13 #1246 みんな、お祝いをありがとう!でも真実が一番だよ。要するに、2か3か?2つの場合は、私自身が3つ分知っているので、図を教えてください。 GaryKa 2012.09.03 22:30 #1247 TheXpert: 3つ目のケースとして、ヘビーグリーンとライトブルーもあるんですよ。考慮されていない。Right thanks, then the second branch of solution diverges into three options (option c is added). そして、2回目の計量は、1回目と同じボールから編成されますが、その配置は異なります。その結果、2回目の計量で3つの答えのうち1つを得ることができ、それによって1回目の計量でのボールの位置を復元することができ、1回目の計量で重かったボール(緑の重いボール)を知ることによって、他のボールの重さを決定することができます。 Vladon:悪気はないのですが...。 私は怒らないし、あなたは怒らない ) Sceptic Philozoff 2012.09.03 22:35 #1248 Andrei さん、3つのボールの解決策(各計量の初期レイアウトだけで十分です)は何ですか?解決策はいくつかあるという意見もあります。 TheXpert 2012.09.03 23:10 #1249 Mathemat:Andrei さん、ボールが3つある場合(各計量の初期レイアウトだけで十分です)、どのような解決策がありますか?選択肢はないのですが :) 上の解答が正しいようです。______________そして、お誕生日おめでとうございます :)もっと面白いパズルを作って、全部解けるようにしよう。 Sceptic Philozoff 2012.09.03 23:13 #1250 TheXpert:選択肢はないのですが :) 上の解決策が正しいようです。______________そして、お誕生日おめでとうございます :)面白いパズルをたくさん作って、全部解けるようになりますように。ありがとう、アンドリュー。 解いていないものは、もっと頻繁に投稿する必要がありそうですね。でも、緊急に解決してください!(自分で解決していないのに、他の人の解決策を読むのは嫌です。)追伸:53の問題は解決したのでしょうか? 1...118119120121122123124125126127128129130131132...229 新しいコメント 取引の機会を逃しています。 無料取引アプリ 8千を超えるシグナルをコピー 金融ニュースで金融マーケットを探索 新規登録 ログイン スペースを含まないラテン文字 このメールにパスワードが送信されます エラーが発生しました Googleでログイン WebサイトポリシーおよびMQL5.COM利用規約に同意します。 新規登録 MQL5.com WebサイトへのログインにCookieの使用を許可します。 ログインするには、ブラウザで必要な設定を有効にしてください。 ログイン/パスワードをお忘れですか? Googleでログイン
2つの重さですべてのオプションに対応するようです。
この絵は、何か宇宙人みたいだ...。
変だな、もっとわかりやすいと思ったんだけどな、言葉より絵の 方がわかりやすいと思う。OK、少しコメントします。
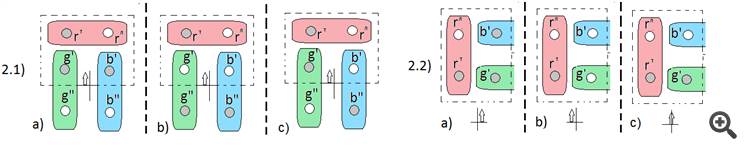
最初の計量では、秤の各カップに2個のボールを置き、それぞれのカップに選んだ色のボール1個と、反対側のバスケットのボールの色とは異なる他の色のボール1個を入れます。(写真では赤い玉に緑の玉、赤い玉に青い玉)。1の計量結果は、オプション1.1)の秤がバランスしている場合と、オプション2)の秤がアンバランスで、カップの1つが2.1)を上回っている場合では、異なることがあります。つまり、解答の分岐が2つあるのです。
最初のバリエーションであれば、ボールを2つの同質なグループ(グループ 'とグループ ')に分け、1.2)両方のグループの重量(天秤のカップあたり3個のボール)を単純に測定して、どちらが重いかを判断します。以上、重い玉が見つかりました。
2つ目の選択肢は、2つの(一般的な)ケースで起こり得ます。各カップの最初の計量で出た色の玉が両方とも重いか軽い場合。(2.2)により、球をグループ(グループ'とグループ')に分けた後、重い球で一回計量することにより、どのグループが重いグループに属し、どのグループが軽いグループに属するかを決定することができます。
これはネットにあった写真ですが...。
OK、少しコメントします。
これでパターンがはっきりしましたね。
2つ目の選択肢は、2つの(一般的な)ケースで起こり得ます。各カップの最初の計量で出た色の玉が、両方とも重いか軽いかのどちらかになったとき。
変だな、もっとわかりやすいと思ったんだけどな、言葉より絵の 方がわかりやすいと思う。OK、少しコメントします。
最初の計量では、秤の各カップに2個のボールを置き、それぞれのカップに選んだ色のボール1個と、反対側のカゴのボールの色とは異なる他の色のボール1個が入るようにします。(写真では赤い玉に緑の玉、赤い玉に青い玉)。1の計量結果は、オプション1.1)の秤がバランスしている場合と、オプション2)の秤がアンバランスで、カップの1つが2.1)を上回っている場合では異なる場合があります。つまり、解答の分岐が2つあるのです。
最初のバリエーションであれば、ボールを2つの同質なグループ(グループ 'とグループ ')に分け、1.2)両方のグループの重量(天秤のカップあたり3個のボール)を単純に測定して、どちらが重いかを判断します。以上、重い玉が見つかりました。
2つ目の選択肢は、2つの(一般的な)ケースで起こり得ます。各カップの最初の計量で出た色の玉が両方とも重いか軽い場合。(2.2)により、1回の計量で(グループ'とグループ')、どちらが重いか、どちらが軽いかを判断することができる。
疑問は胸にしまっておいてください。打ち切り悪気はないのですが...。
選択肢1.1 内輪で提案した。冒頭がおかしい。
みんな、お祝いをありがとう!でも真実が一番だよ。
要するに、2か3か?
2つの場合は、私自身が3つ分知っているので、図を教えてください。
Right thanks, then the second branch of solution diverges into three options (option c is added).
そして、2回目の計量は、1回目と同じボールから編成されますが、その配置は異なります。その結果、2回目の計量で3つの答えのうち1つを得ることができ、それによって1回目の計量でのボールの位置を復元することができ、1回目の計量で重かったボール(緑の重いボール)を知ることによって、他のボールの重さを決定することができます。Andrei さん、3つのボールの解決策(各計量の初期レイアウトだけで十分です)は何ですか?
解決策はいくつかあるという意見もあります。
Andrei さん、ボールが3つある場合(各計量の初期レイアウトだけで十分です)、どのような解決策がありますか?
選択肢はないのですが :) 上の解答が正しいようです。
______________
そして、お誕生日おめでとうございます :)もっと面白いパズルを作って、全部解けるようにしよう。
選択肢はないのですが :) 上の解決策が正しいようです。
______________
そして、お誕生日おめでとうございます :)面白いパズルをたくさん作って、全部解けるようになりますように。
ありがとう、アンドリュー。
解いていないものは、もっと頻繁に投稿する必要がありそうですね。でも、緊急に解決してください!(自分で解決していないのに、他の人の解決策を読むのは嫌です。)
追伸:53の問題は解決したのでしょうか?