微分とエントロピー解析によるGrokking市場の「記憶」

アプローチを使用した理由と簡単な背景

流動性の高い市場では、さまざまな投資領域で活動する多数の参加者が市場が大きな雑音を生み出しています。 従って、市場のシグナル対雑音比は低くなります。この状況は、整数時系列を微分する試みによって悪化する可能性があります。このような試みは、残りの記憶を消去し、相場を定常性を特徴とする級数に変換するからです。 

それぞれの値は長期にわたる過去の価格レベルに依存しているので、価格系列には記憶があります。例えば増分の対数などの時系列変換は、限られたウィンドウ長に基づいて作成されるため、記憶が切り取られます。 定常性への変換によって市場の記憶が削除されると、統計学者は複雑な数学的方法を使用して残りの記憶を抽出します。それが、関連する古典的な統計的アプローチの多くが誤った結果につながる理由です。

長期依存の概念

長期記憶または長期持続性とも呼ばれる長期依存性(LRD)は、金融時系列の分析で発生する可能性がある現象です。これは、2つの価格間の時間の増加(または価格間の距離)に伴う統計的依存関係の減衰率で表されます。依存性が指数関数的な減衰よりも低速で減衰する場合、現象には長期依存関係があると見なされます。長期依存性はまた、自己相似プロセスに関連していることがよくあります。LRD(Long-Range Dependence)についての詳細は、ウィキペディアの記事をご覧ください。

定常性と記憶の存在の問題

価格チャートの一般的な特徴は、非定常性です。価格チャートには、長期にわたる過去の価格レベルがあり、これが時間とともに平均価格をシフトさせます。統計分析を実行するためには、研究者は価格の増分(または増分の対数)、収益性またはボラティリティの変化に取り組む必要があります。これらの変換は、価格系列から記憶を削除することによって時系列を定常化します。定常性は統計的結論には必要な特性ですが、記憶はモデルの予測特性の基礎となるため、記憶全体を削除する必要は必ずしもありません。例えば、均衡(定常)モデルには、価格がその期待値からどれだけ離れているかを評価できるようにするために、ある程度の記憶を含める必要があります。

問題は、価格の増分は定常的であるが過去の記憶を含まないのに対し、価格系列は利用可能な記憶の全量を含むが非定常的であるということです。ここで、できるだけ多くのの記憶を保持させながら定常化するためにはどのように時系列を微分するかという問題が発生します。したがってすべての記憶が消去されるわけではない定常的な級数を考慮するための価格増分の概念を一般化したいと思います。この場合、他にも利用可能な方法があり、価格の増分は価格変換に最適な解決策ではありません。

この目的で、分数階微分の概念が紹介されます。2つの両極端(1と0の微分)の間には広範囲の可能性があります。一方の端には、完全に微分された価格があり、後一方の端には微分されていない価格があります。

分数階微分は十分に広い範囲で使用されています。例えば、機械学習アルゴリズムには通常微分された級数が入力されます。 問題は、機械学習モデルが認識できるように、利用可能な履歴に従って新しいデータを表示する必要があることです。非定常級数の場合、新しいデータは既知の値の範囲外にある可能性があり、これによってモデルが正しく動作しなくなる場合があります。

分数階微分の歴史

さまざまな科学論文に記載されている金融時系列の分析および予測のためのほとんどすべての方法では、整数階微分のアイデアが提示されています。

これに関連して、以下の質問が発生します。

• 整数階微分(例えば、単位遅れを持つ)が最適なのはなぜでしょうか。    
• そのような過微分は、経済理論が効率的な市場という仮説を立てやすい理由の1つではないでしょうか。

時系列分析と予測に適用される分数階微分の概念は、少なくともHoskingに遡ります。彼の記事では、ARIMAプロセスのファミリーは一般化され、微分化度が小数部分を持つことが可能になりました。分数階微分のプロセスは長期持続性または抗持続性を明らかにし、したがって標準のARIMAと比較して予測能力を高めたので、これは理にかなっていました。このモデルはARFIMA (autoregressive fractionally integrated moving average、自己回帰分数積分移動平均)またはFARIMAと呼ばれました。その後、分数階微分は、主に計算方法の加速に関連して、他の著者の論文に言及されることがありました。

そのようなモデルは、長期記憶の時系列をモデル化することにおいて、すなわち、長期減衰の平均からの偏差が指数関数なよりも低速な場合に有用であり得ます。

分数階微分の概念

実数値の行列{Xt}に適用されるバックシフト演算子(または遅れ演算子)Bを考察してみましょう。ここで、任意の整数k ≥ 0に対してB^kXt = Xt−kです。例えば、(1 − B)^2 = 1 − 2B + B^2です。ここでB^2Xt = Xt−2、よって(1 − B)^2Xt = Xt − 2Xt−1 + Xt−2です。 

(x + y)^n =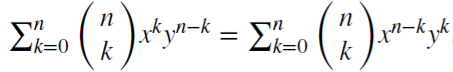はすべての正の整数nに対して当てはまります。実数dに対して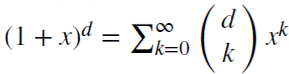は二項級数です。分数モデルでは、dは実数で、二項級数は次のように拡張される場合があります。

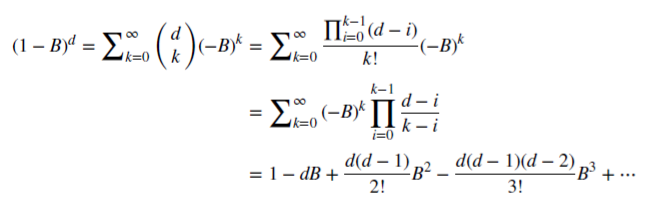
分数階微分の場合の市場の記憶の維持

非負有理数dがどのように記憶を維持できるかを見てみましょう。この算術級数は、スカラ積で構成されています。

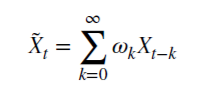
重み𝜔:

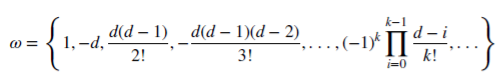
値X:

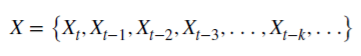
dが正の整数の場合、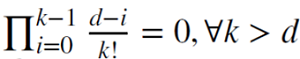で、記憶が切り取られます。

例えば、d = 1は、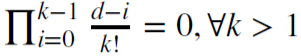及び𝜔 = {1,−1, 0, 0,…}の場合に増分を計算するために使用されます。

固定観測ウィンドウでの分数階微分

分数階微分は通常、時系列全体に適用されます。この場合、計算はより複雑ですが、変換された級数のシフトは負です。Marcos Lopez De Pradoは、著書のAdvances in Financial Machine Learning(金融機械学習の進歩)で、固定幅ウィンドウ法を提案しました。この方法では、モジュール(|𝜔k|) が指定された閾値値(𝜏)未満になると、係数のシーケンスは破棄されます。古典的なウィンドウ拡大法と比べて、この手順には、元の系列の任意のシーケンスに対して等しい重みを持つことを可能にし、計算の複雑さを軽減し、バックシフトを排除するという利点があります。この変換により、価格レベルと雑音に関する記憶を保存できます。この変換の分布は、記憶の存在、非対称性および過剰な尖度のために正規分布(ガウス分布)ではありませんが、定常的にはなり得ます。

分数階微分プロセスの実証

時系列の分数階微分から得られる効果を視覚的に評価できるようにするスクリプトを作成しましょう。2つの関数を作成します。1つは重み𝜔を取得するためのもので、もう1つは系列の新しい値を計算するためのものです。

//+------------------------------------------------------------------+
void get_weight_ffd(double d, double thres, int lim, double &w[]) {
    ArrayResize(w,1); 
    ArrayInitialize(w,1.0);
    ArraySetAsSeries(w,true);
    
    int k = 1;
    int ctr = 0;
    double w_ = 0;
    while (ctr != lim - 1) {
        w_ = -w[ctr] / k * (d - k + 1);
        if (MathAbs(w_) < thres) break;  
        ArrayResize(w,ArraySize(w)+1); 
        w[ctr+1] = w_;      
        k += 1;
        ctr += 1;
    }
}
//+------------------------------------------------------------------+
void frac_diff_ffd(double &x[], double d, double thres, double &output[]) {
   double w[];
   get_weight_ffd(d, thres, ArraySize(x), w);

   int width = ArraySize(w) - 1;
   
   ArrayResize(output, width);
   ArrayInitialize(output,0.0);
   ArraySetAsSeries(output,true);
   ArraySetAsSeries(x,true);
   ArraySetAsSeries(w,true);
   
   int o = 0;
   for(int i=width;i<ArraySize(x);i++) {
      ArrayResize(output,ArraySize(output)+1);
      
      for(int l=0;l<ArraySize(w);l++)       
         output[o] += w[l]*x[i-width+l];      
      o++; } 
   ArrayResize(output,ArraySize(output)-width);
}

パラメータ0<d<1に応じて変化するアニメーションチャートを表示しましょう。

//+------------------------------------------------------------------+
//| スクリプトプログラム開始関数                                   |
//+------------------------------------------------------------------+
void OnStart()
  {
   for(double i=0.05; i<1.0; plotFFD(i+=0.05,1e-5))     
  }
//+------------------------------------------------------------------+
void plotFFD(double fd, double thresh) {
   double prarr[], out[];
   CopyClose(_Symbol, 0, 0, hist, prarr);
   
   for(int i=0; i < ArraySize(prarr); i++)
      prarr[i] = log(prarr[i]);
    
   frac_diff_ffd(prarr, fd, thresh, out);
   GraphPlot(out,1); Sleep(500);
}

以下が結果です。

  

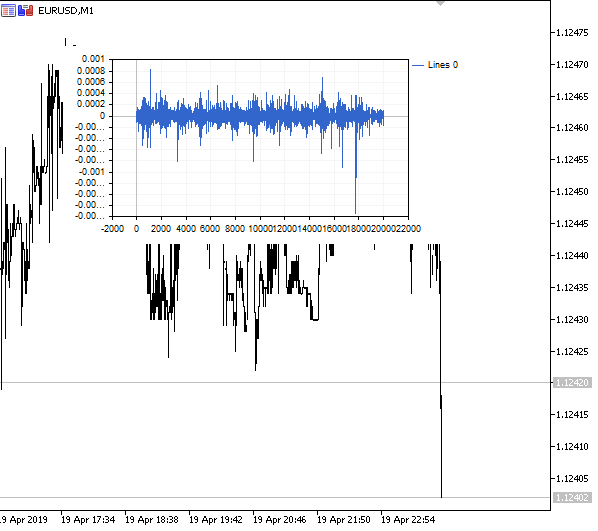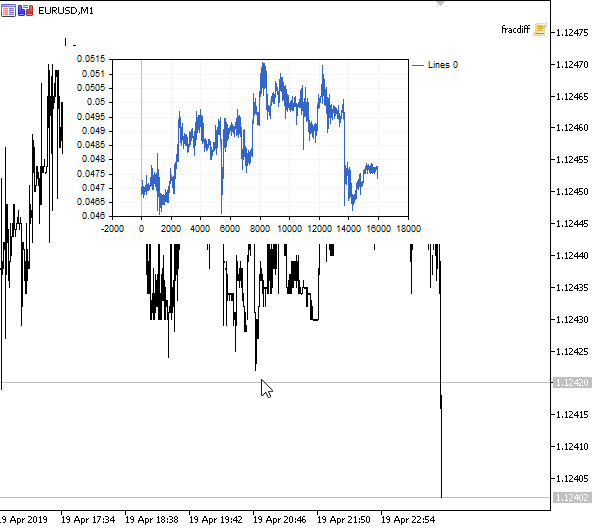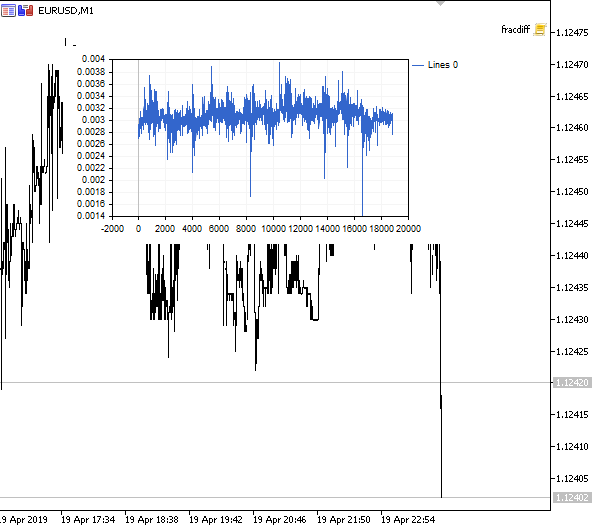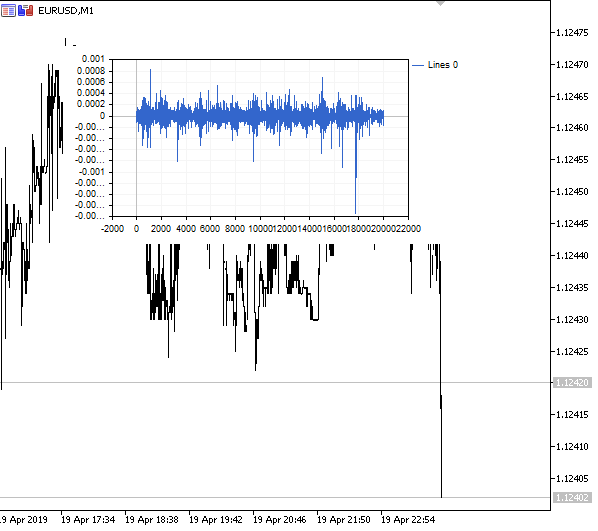
図1　分数階微分0<d<1

予想どおり、微分の次数が増すにつれて、過去のレベルの「記憶」を徐々に失いながら、チャートはより安定したものになります。系列の重み(価格による重みのスカラ積の関数)は、シーケンス全体を通じて変更されないため、再計算は不要です。

分数階微分に基づく指標の作成

エキスパートアドバイザーで便利に使用するために、さまざまなパラメータ(微分の次元、過剰な重みを除去するための閾値値のサイズ、表示される履歴の深さ)の指定を含めることができる指標を作成しましょう。完全な指標コードはここでは掲載しませんので、ソースファイルでご覧ください。

ここでは、単に重み計算関数が同じであることを示します。指標バッファ値を計算するためには以下の関数が使用されます。

frac_diff_ffd(weights, price, ind_buffer, hist_display, prev_calculated !=0);  

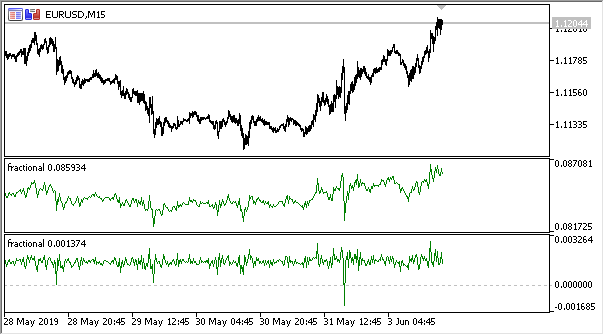
図2　0.3と0.9のべき乗による分数階微分

これで、情報量の変化のダイナミクスを時系列で非常に正確に説明する指標ができました。微分の次元が上がると、情報が失われ、級数がより定常的になります。ただし、価格レベルのデータのみは失われます。残っている可能性があるのは、予測の基準点となる周期的なサイクルです。よって、データ量の評価に役立つ情報理論手法、つまり情報エントロピーに近づくことになります。

情報エントロピーの概念

情報エントロピーは情報理論に関連する概念であり、イベントに含まれる情報量を示します。一般に、イベントがより具体的または決定論的であるほど、含まれる情報は少なくなります。より具体的には、情報は不確実性の増大と関連しています。この概念はクロード・シャノンによって紹介されました。

乱数のエントロピーは、有限個の値をとる、乱数Xの値の分布の概念を導入することで決定できます。

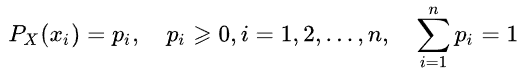
次に、イベント(または時系列)特定の情報が次のように定義されます。

エントロピー推定値は次のように書くことができます。

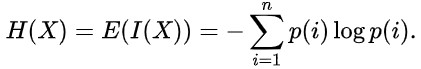
情報量とエントロピーの測定単位は、対数の底によって異なり、ビット、ナッツ、トリット、ハートレーなどです。

シャノンエントロピーについては詳しく説明しません。ただし、この方法は短くて雑音の多い時系列の評価にはあまり適していません。そこでSteve PincusとRudolf Kalmanは、金融時系列に関して「 ApEn 」(近似エントロピー)と呼ばれる方法を提案しました。この方法については、「Irregularity, volatility, risk and financial market time series(不規則性、ボラティリティ、リスクおよび金融市場の時系列)」稿で詳細に説明されています。

この記事では、根本的に異なる2つの形態の恒常性からの価格偏差(ボラティリティの説明)が検討されました。

• 1番目のものは大きな標準偏差を表します
• 2番目のものは極端な不規則性と予測不可能性を示します

これら2つの形式は完全に異なるため、このような分離が必要です。標準偏差は中心性の尺度からの偏差の優れた推定値であり、ApEnは不規則性の推定値を表します。さらに、変動の程度はそれほど重要ではありませんが、不規則性と予測不可能性は本当に問題です。

以下は2つの時系列を持つ簡単な例です。

• 10と20が交互になる系列(10,20,10,20,10,20,10,20,10,20,10,20...)
• 10と20が1/2の確率でランダムに選択される系列(10,10,20,10,20,20,20,10,10,20,10,20...)

平均や分散などの統計の瞬間は、2つの時系列間の違いを示しません。同時に、最初の級数は完全に規則的です。前の値を知っていれば、いつでも次の値を予測できます。2番目の級数は完全にランダムなので、予測しようとしても失敗します。

Joshua RichmanとRandall Moormanは「Physiological time-analysis analysis using approximate entropy and sample entropy(近似エントロピーとサンプルエントロピーを使った生理学的時間分析)」でApEn法を批判して、代わりに改善された「SampEn」法を提案しました。特に批判されたのは、エントロピー値のサンプル長への依存性、および異なるが関連した時系列に対する値の不一致でした。また、新しく提供された計算方法はそれほど複雑ではありません。この方法を使用し、そのアプリケーションの機能について説明します。

価格増分の規則性を決定するための「サンプルエントロピー」法

SampEnはApEn法を修正したもので、シグナル(時系列)の複雑さ(不規則性)を評価するために使用されます。指定されたmポイントのサイズ、許容されるr許容値、および計算されているN値に対して、SampEnはその対数です。長さmの2つの一連の同時点の距離がr未満の場合、2つの一連の長さm + 1の同時点の距離もr未満となります。 

の長さを持ち、それらの間に一定の時間間隔がある時系列のデータセットがあるとします。となるような長さmのベクトルテンプレートを定義して、距離関数(i≠j)の関係をChebyshevで定義すると、これは、これらのベクトルコンポーネント間の差の最大係数となります(ただし、これは別の距離関数になる可能性もあります)。すると、SampEnは次のように定義されます。

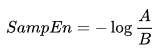
ここで、

• Aはテンプレートベクトルの数で、 
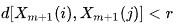
• Bはテンプレートベクトルのペアの数で、 

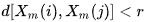
上記から、常にA <= Bであり、よってSampEnは常に0以上であることが明確です。値が小さいほど、データセットの自己相似は高く、雑音が少なくなります。

主に、m = 2とr = 0.2 * stdが使用されます。ここで、stdは非常に大きなデータセットに対して取るべき標準偏差です。

以下のコードで提案されたメソッドの迅速な実装を見つけ、それをMQL5で書き直しました。

double sample_entropy(double &data[], int m, double r, int N, double sd)
{
  int Cm = 0, Cm1 = 0;
  double err = 0.0, sum = 0.0;
  
  err = sd * r;
  
  for (int i = 0; i < N - (m + 1) + 1; i++) {
    for (int j = i + 1; j < N - (m + 1) + 1; j++) {      
      bool eq = true;
      //m - length series
      for (int k = 0; k < m; k++) {
        if (MathAbs(data[i+k] - data[j+k]) > err) {
          eq = false;
          break;
        }
      }
      if (eq) Cm++;
      
      //m+1 - length series
      int k = m;
      if (eq && MathAbs(data[i+k] - data[j+k]) <= err)
        Cm1++;
    }
  }
  
  if (Cm > 0 && Cm1 > 0)
    return log((double)Cm / (double)Cm1);
  else
    return 0.0; 
}

さらに、2つの系列(2つの入力ベクトル)のエントロピー推定値を取得する必要がある場合には、クロスサンプルエントロピー(cross-SampEn)を計算するためのオプションを提案します。ただし、これは、サンプルエントロピーの計算にも使用できます。

// Calculate the cross-sample entropy of 2 signals
// u : signal 1
// v : signal 2
// m : length of the patterns that compared to each other
// r : tolerance
// return the cross-sample entropy value
double cross_SampEn(double &u[], double &v[], int m, double r) {
    double B = 0.0;
    double A = 0.0;
    if (ArraySize(u) != ArraySize(v))
        Print("Error : lenght of u different than lenght of v");
    int N = ArraySize(u);
    
    for(int i=0;i<(N-m);i++)
      {
         for(int j=0;j<(N-m);j++)
           {   
               double ins[]; ArrayResize(ins, m); double ins2[]; ArrayResize(ins2, m);
               ArrayCopy(ins, u, 0, i, m); ArrayCopy(ins2, v, 0, j, m);
               B += cross_match(ins, ins2, m, r) / (N - m);
               ArrayResize(ins, m+1); ArrayResize(ins2, m+1);
               ArrayCopy(ins, u, 0, i, m + 1); ArrayCopy(ins2, v, 0, j, m +1);
               A += cross_match(ins, ins2, m + 1, r) / (N - m);
           }
      }
    
    B /= N - m;
    A /= N - m;
    return -log(A / B);
}
// calculation of the matching number
// it use in the cross-sample entropy calculation
double cross_match(double &signal1[], double &signal2[], int m, double r) {
    // return 0 if not match and 1 if match
    double darr[];
    for(int i=0; i<m; i++)
      {
         double ins[1]; ins[0] = MathAbs(signal1[i] - signal2[i]);
         ArrayInsert(darr, ins, 0, 0, 1);
      }    
    if(darr[ArrayMaximum(darr)] <= r)  return 1.0; else return 0.0;
}

最初の計算方法で十分なので、それをさらに使用します。

持続性および非整数ブラウン運動モデル

価格系列の増分値が現在増加している場合、次の瞬間に継続的な増加が見込まれる確率はどのくらいでしょうか。持続性について考えてみましょう。持続性の測定は非常に役立ちます。このセクションでは、スライディングウィンドウ内の増分の持続性の評価へのSampEn法の適用について考察します。この評価法については、前述の「Irregularity, volatility, risk and financial market time series(不規則性、ボラティリティ、リスクおよび金融市場の時系列)」稿で詳細に説明されています。

非整数ブラウン運動理論による微分級数はすでに存在します(これが「分数階微分」という用語の由来です)。粗粒度2進増分級数を定義します 

BinInci:= +1(di+1 – di > 0, –1の場合)。簡単に言えば、増分を+1、-1の範囲で2値化します。したがって、増分動作の4つの可能なバリアントの分布を直接推定します。

• 上昇、上昇
• 下降、下降
• 上昇、下降
• 下降、上昇

推定値の独立性と手法の統計的検出力は、ほとんどすべてのプロセスがBinlnci系列に対してSampEnエラーが非常に小さいという特徴と関連しています。より重要な事実は、見積もりがデータをマルコフ連鎖に対応させることを暗示することも要求することもせず、定常性以外の他の特性に関する事前知識を必要としないということです。データが一重マルコフ特性を満たす場合、SampEn(1) = SampEn(2)であり、追加の結論を引き出すことができます。

非整数ブラウン運動のモデルは、長期依存性または「記憶」と「ヘビーテール」の両方を示す現象をモデル化したBenoit Mandelbrotに遡ります。これはまた、ハースト指数やR/S分析のような新しい統計的応用の出現にもつながりました。すでにご存じのとおり、価格の上昇は時々長期にわたる依存性とヘビーテールを示します。

したがって、時系列の持続性を直接評価することができます。最小の SampEn値が最大の持続値に対応し、その逆も成り立ちます。

微分系列に対する持続性評価の実装

指標を書き換えて、持続性評価モードで実行する可能性を追加しましょう。エントロピー推定値は離散値に対して機能するため、増分値を最大2桁の精度で正規化する必要があります。

完全な実装は、添付の「非正数エントロピー」指標で利用可能です。指標の設定は以下のとおりです。

input bool   entropy_eval = true; // show entropy or increment values
input double diff_degree = 0.3;   // the degree of time series differentiation
input double treshhold = 1e-5;    // threshold to cut off excess weight (the default value can be used)
input int    hist_display = 5000; // depth of the displayed history
input int    entropy_window = 50; // sliding window for the process entropy evaluation

下の図は、2つのモードでの指標を示しています(上の部分はエントロピーを示し、下の部分は増分を標準化したものです)。

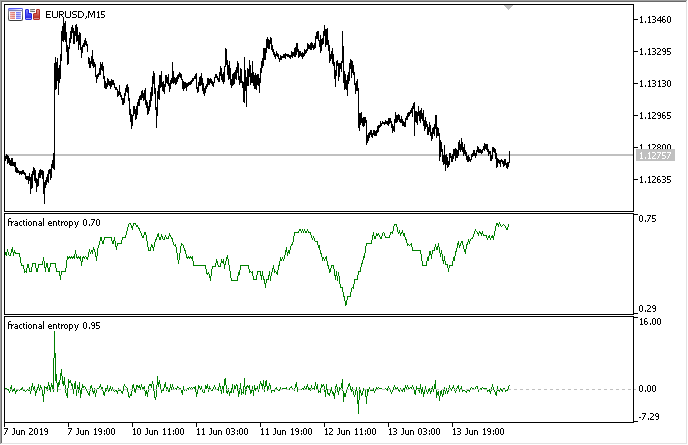
図3　スライディングウィンドウ50のエントロピー値(上)と0.8の次数による分数階微分

これら2つの推定値は相関していないことがわかります。これは、次のセクションで検討する機械学習モデル(多重共線性がないこと)にとって良い兆候です。

機械学習を用いたオンザフライのエキスパートアドバイザー最適化: ロジスティック回帰分析

よって、取引シグナルを生成するために使用できる適切な微分時系列が存在します。時系列はより定常的であり、機械学習モデルにとってより便利であることは上述しました。級数の持続性の評価もあります。今度は最適な機械学習アルゴリズムを選択する必要があります。EAはそれ自身の中で最適化されなければならないので、学習速度には、非常に高速でありながら最小限の遅れを持たなければならないという要件があります。これらの理由から、私はロジスティック回帰を選択しました。

ロジスティック回帰は、予測子または回帰子とも呼ばれる一連の変数 x1、x2、x3 ... xNの値に基づいてイベントの確率を予測するために使用されます。ここでの場合、変数は指標値です。従属変数yを導入することも必要です。これは通常0か1のどちらかです。このように、それは買うまたは売るための合図として役立ちます。回帰子の値に基づいて、従属変数が特定のクラスに属する確率を計算します。

y = 1の発生確率はであると仮定します。ここで、はそれぞれ独立変数1, x1, x2 ... xNの値のベクトルと回帰係数、f(z)はロジスティック関数またはシグモイド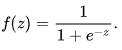です。その結果、与えられたx に対するy分布関数はとして書くことができます。

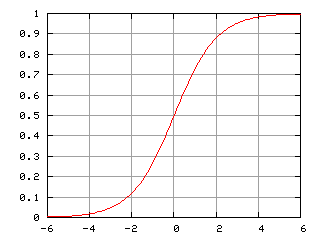
図4　ロジスティック曲線(シグモイド)出典: ウィキペディア

ロジスティック回帰アルゴリズムは広く知られているので、詳細には説明しません。Alglibライブラリの既製のCLogitModelクラスを使用しましょう。

自動オプティマイザクラスの作成

単純な仮想テスタとロジスティック回帰の組み合わせを表す別のCAuto_optimizerクラスを作成しましょう。

//+------------------------------------------------------------------+
//|Auto optimizer class                                              |
//+------------------------------------------------------------------+
class CAuto_optimizer
  {
private:
// Logit regression model |||||||||||||||
   CMatrixDouble     LRPM;
   CLogitModel       Lmodel;
   CLogitModelShell  Lshell; 
   CMNLReport        Lrep;
   int               Linfo;
   double            Lout[];
//||||||||||||||||||||||||||||||||||||||||
   int               number_of_samples, relearn_timout, relearnCounter;
   virtual void      virtual_optimizer();
   double            lVector[][2];
   int               hnd, hnd1;
   
public:
                     CAuto_optimizer(int number_of_sampleS, int relearn_timeouT, double diff_degree, int entropy_window) {                                      
                             this.number_of_samples = number_of_sampleS;
                             this.relearn_timout = relearn_timeouT;
                             relearnCounter = 0;
                             LRPM.Resize(this.number_of_samples, 5);
                             hnd = iCustom(NULL, 0, "fractional entropy", false, diff_degree, 1e-05, number_of_sampleS, entropy_window);
                             hnd1 = iCustom(NULL, 0, "fractional entropy", true, diff_degree, 1e-05, number_of_sampleS, entropy_window);
                            }
                     ~CAuto_optimizer() {};
   double            getTradeSignal();
  };

// Logit regression model//セクションには、xおよびy値の行列、ロジスティックモデル「Lmodel」、およびその補助クラスが作成されます。モデルを訓練した後、Lout[]配列はシグナルがクラスのいずれかに属する確率(0:1)を受け取ります。 

コンストラクタは、学習ウィンドウのサイズnumber_of_samples、その後モデルが再最適化される期間relearn_timout、およびdiff_degree指標の分数階微分の次数とともに、エントロピー計算ウィンドウentropy_windowを受け取ります。

virtual_optimizer()メソッドを詳しく考察しましょう。

//+------------------------------------------------------------------+
//|Virtual tester                                                    |
//+------------------------------------------------------------------+
CAuto_optimizer::virtual_optimizer(void) {
   double indarr[], indarr2[];
   CopyBuffer(hnd, 0, 1, this.number_of_samples, indarr);
   CopyBuffer(hnd1, 0, 1, this.number_of_samples, indarr2);
   ArraySetAsSeries(indarr, true); ArraySetAsSeries(indarr2, true);
   
   for(int s=this.number_of_samples-1;s>=0;s--) {
      LRPM[s].Set(0, indarr[s]);
      LRPM[s].Set(1, indarr2[s]);
      LRPM[s].Set(2, s);
     
      if(iClose(NULL, 0, s) > iClose(NULL, 0, s+1)) { 
         LRPM[s].Set(3, 0.0);
         LRPM[s].Set(4, 1.0);
      }
      else {
         LRPM[s].Set(3, 1.0);
         LRPM[s].Set(4, 0.0);
      }  
    }
     
    CLogit::MNLTrainH(LRPM, LRPM.Size(), 3, 2, Linfo, Lmodel, Lrep);
    
    double profit[], out[], prof[1];
    ArrayResize(profit,1); ArraySetAsSeries(profit, true); profit[0] = 0.0;
    int pos = 0, openpr = 0;
    
    for(int s=this.number_of_samples-1;s>=0;s--) {
      double in[3];
      in[0] = indarr[s]; in[1] = indarr2[s]; in[2] = s;
      CLogit::MNLProcess(Lmodel, in, out);
      
      if(out[0] > 0.5 && !pos) {pos = 1; openpr = s;};
      if(out[0] < 0.5 && !pos) {pos = -1; openpr = s;};
      
      if(out[0] > 0.5 && pos == 1) continue;
      if(out[0] < 0.5 && pos == -1) continue;
      
      if(out[0] > 0.5 && pos == -1) {
         prof[0] = profit[0] + (iClose(NULL, 0, openpr) - iClose(NULL, 0, s)); 
         ArrayInsert(profit, prof, 0, 0, 1); pos = 0; }
         
      if(out[0] < 0.5 && pos == 1) {
         prof[0] = profit[0] + (iClose(NULL, 0, s) - iClose(NULL, 0, openpr)); 
         ArrayInsert(profit, prof, 0, 0, 1); pos = 0; }
    }
 GraphPlot(profit);
}

このメソッドは明らかに非常に単純であり、したがって迅速です。LRPM行列の最初の列は、指標値+線形トレンド値(追加)でループでで埋められます。次のループでは、売買の可能性を明確にするために、現在の終値が前の終値と比較されます。現在の値が前の値よりも大きい場合は、あったのは買いシグナルで、それ以外の場合は、売りシグナルです。したがって、次の列は値0と1で埋められます。

これは非常に単純なテスターで、シグナルの選択の最適化を目的とするかわりに単に各バーでシグナルを読み取ります。テスターはメソッドのオーバーロードによって改善できますが、これは本稿の範囲外です。

その後、ロジスティック回帰は、行列、そのサイズ、変数の数x(各場合に対して1つの変数のみがここで渡されます)、訓練されたモデルを保存するLmodelクラス、補助クラスを受け入れるMNLTrain()メソッドを使用して訓練されます。

訓練後、モデルはテストされ、バランスチャートとしてオプティマイザウィンドウに表示されます。これは視覚的に効率的であり、モデルが学習サンプルでどのように訓練されたかを示すことができます。しかし、パフォーマンスはアルゴリズムの観点から分析されていません。

仮想オプティマイザは次のメソッドから呼び出されます。

//+------------------------------------------------------------------+
//|Get trade signal                                                  |
//+------------------------------------------------------------------+
double CAuto_optimizer::getTradeSignal() {
   if(this.relearnCounter==0)
      this.virtual_optimizer();
   relearnCounter++;
   if(this.relearnCounter>=this.relearn_timout) this.relearnCounter=0;
   
   double in[], in1[];
   CopyBuffer(hnd, 0, 0, 1, in); CopyBuffer(hnd1, 0, 0, 1, in1);
   double inn[3]; inn[0] = in[0]; inn[1] = in1[0]; inn[2] = relearnCounter + this.number_of_samples - 1;         
   CLogit::MNLProcess(Lmodel, inn, Lout);
   return Lout[0];
}

前回の訓練以降に経過したバーの数を確認します。値が指定された閾値値を超える場合は、モデルを再訓練する必要があります。その後、最後の訓練から経過した時間の単位とともに指標の最終値がコピーされます。これはMNLProcess()メソッドを使用してモデルに入力され、値がクラス0:1(取引シグナル)に属するかどうかを示す結果を返します。

ライブラリ操作をテストするためのエキスパートアドバイザの作成

ここで、ライブラリを取引エキスパートアドバイザーに接続し、シグナルハンドラを追加する必要があります。

#include <MT4Orders.mqh>
#include <Math\Stat\Math.mqh>
#include <Trade\AccountInfo.mqh>
#include <Auto optimizer.mqh>

input int       History_depth = 1000;
input double    FracDiff = 0.5;
input int       Entropy_window = 50;
input int       Recalc_period = 100;
sinput double   MaximumRisk=0.01;
sinput double   CustomLot=0;
input int       Stop_loss = 500;           //Stop loss, positions protection
input int       BreakEven = 300;           //Break even
sinput int      OrderMagic=666;

static datetime last_time=0;

CAuto_optimizer *optimizer = new CAuto_optimizer(History_depth, Recalc_period, FracDiff, Entropy_window);
double sig1;

エキスパートアドバイザーの設定は簡単で、ウィンドウサイズHistory_depth(自動オプティマイザの訓練例の数)が含まれています。微分の次元FracDiffと、越すとモデルが再訓練される、受け取られたバーの数Recalc_periodです。また、エントロピー計算ウィンドウを調整するためのEntropy_window設定が追加されています。

最後の関数では、訓練されたモデルからシグナルを受け取り、取引操作を実行します。

void placeOrders(){
   if(countOrders(0)!=0 || countOrders(1)!=0)   {
      for(int b=OrdersTotal()-1; b>=0; b--)
         if(OrderSelect(b,SELECT_BY_POS)==true) {
          if(OrderType()==0 && sig1 < 0.5) if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {};
          if(OrderType()==1 && sig1 > 0.5) if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {};
      }
    }
   
   if(countOrders(0)!=0 || countOrders(1)!=0) return;
   if(sig1 > 0.5 && (OrderSend(Symbol(),OP_BUY,lotsOptimized(),SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN)>0)) { return; }
   if(sig1 < 0.5 && (OrderSend(Symbol(),OP_SELL,lotsOptimized(),SymbolInfoDouble(_Symbol,SYMBOL_BID),0,0,0,NULL,OrderMagic,INT_MIN)>0)) {}
  }

 買いの確率が0.5より大きい場合、これは買いシグナルおよび/または売りポジションを閉じるシグナルです。その反対も同じです。

自己最適化EAのテストと結論

テストで最も興味深い部分であるi8.eに進みましょう。 

エキスパートアドバイザーは、遺伝的最適化なし、すなわち15分の時間枠を持つEURUSDペアで、始値で、指定されたハイパーパラメータで実行されました。

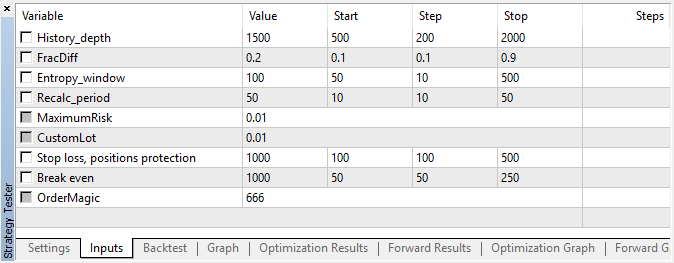
図5　テストされたエキスパートアドバイザー設定

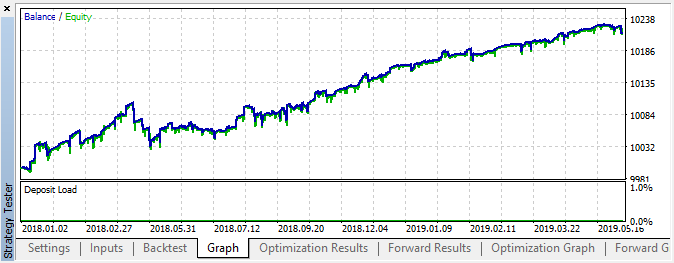
図6　指定の設定でのテストの結果

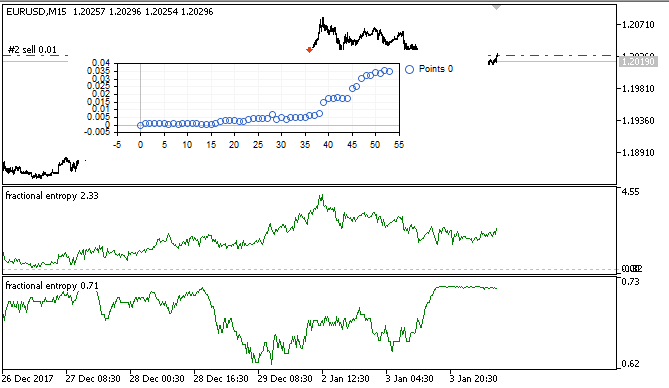
図7　訓練サンプルでの仮想テスター結果

この間に、実装は安定した成長を示しました。これは、このアプローチがさらなる分析にとって興味深いものである可能性があることを意味しています。

その結果、1つの記事で次の3つの目標を達成しようとしました。

• 市場の「記憶」の理解、
• エントロピーによる記憶の評価
• 自己最適化エキスパートアドバイザーの開発