リプレイシステムの開発 - 市場シミュレーション（第14回）：シミュレーターの誕生(IV)

はじめに

前回の「リプレイシステムの開発 - 市場シミュレーション（第13回）：シミュレーターの誕生(III)」では、ティックとその処理をよりよく表現するためにサービスファイルに加えられた変更を示しました。前回の記事の主な目的は、サービスからデータを取得するために、これがどのように可能で、どこのコードを変更追加する必要があるかを示すことでした。これにより、このデータを別の場所（この場合はファイル）に移動することができます。このファイルが手元にあれば、プログラム（今回はEXCELの使い方を紹介）を使って、シミュレーターが生成するデータを分析することができます。

このような作業は、些細なことのように思えるかもしれませんが、この記事でやろうとしていることにとって最も重要です。シミュレーターが生成するデータの分析方法を理解しなければ、何を実装する必要があるのかを理解することはできませんが、最も重要なことは、なぜこれから紹介する方法で実装するのかを理解することです。前回の本題に加えて、バーを約1分で正確に作成し、すべてを現実に近づけるためにコードを変更する必要があるいくつかの点についても説明しました。しかし、それにもかかわらず、この記事でやろうとしていることを理解するためには、あと１つのことについて考える必要があります。前回すでに多くの情報があったので、ここで最後の詳細を説明することにしました。添付のコードで見ることができます。

フリーランダムウォークを試す

以下に、このルーチンの最も基本的なバージョンを示しますが、これはフリーランダムウォークを作成しようとするものです。

inline void Simulation(const MqlRates &rate, MqlTick &tick[])
                        {
#define macroRandomLimits(A, B) (int)(MathMin(A, B) + (((rand() & 32767) / 32767.0) * MathAbs(B - A)))

                                long il0, max;
                                double v0, v1;
                                int p0;
                                
                                ArrayResize(m_Ticks.Rate, (m_Ticks.nRate > 0 ? m_Ticks.nRate + 3 : def_BarsDiary), def_BarsDiary);
                                m_Ticks.Rate[++m_Ticks.nRate] = rate;                           
                                max = rate.tick_volume - 1;     
                                v0 = 4.0;
                                v1 = (60000 - v0) / (max + 1.0);
                                for (int c0 = 0; c0 <= max; c0++, v0 += v1)
                                {
                                        tick[c0].last = 0;
                                        tick[c0].flags = 0;
                                        il0 = (long)v0;
                                        tick[c0].time = rate.time + (datetime) (il0 / 1000);
                                        tick[c0].time_msc = il0 % 1000;
                                        tick[c0].volume_real = 1.0;
                                }
                                tick[0].last = rate.open;
                                tick[max].last = rate.close;
                                for (int c0 = (int)(rate.real_volume - rate.tick_volume); c0 > 0; c0--)
                                        tick[macroRandomLimits(0, max)].volume_real += 1.0;
                                for (int c0 = 1; c0 < max; c0++)
                                        tick[c0].last = macroRandomLimits(rate.low, rate.high);                                 
                                il0 = (long)(max * (0.3));
                                tick[macroRandomLimits(il0, il0 * 2)].last = rate.low;
                                tick[macroRandomLimits(max - il0, max)].last = rate.high;                                         
                                for (int c0 = 0; c0 <= max; c0++)
                                {
                                        ArrayResize(m_Ticks.Info, (m_Ticks.nTicks + 1), def_MaxSizeArray);
                                        m_Ticks.Info[m_Ticks.nTicks++] = tick[c0];
                                }
                        }
                        
#undef macroRandomLimits

次にやることを理解するためには、上記のコードを理解することが非常に重要です。このコードをそのまま実行すると、非常にわかりにくいグラフになってしまいます。この非常に基本的な機能がどのように働くかを知ることは、より複雑な機能がどのように働くかを理解する上で重要です。マクロの定義から始めましょう。ここで質問です。このマクロは何をするのでしょうか。読者は、これを見て、「これは一体何の狂気だろうか？そんな奇妙なものが本当に必要なのか？」と考えていらっしゃるかもしれません。この質問に対する答えははいといいえです。

はいなのは、特定の範囲内で乱数値を生成する必要があるからです。そのためには、何らかの制約を設定する必要があります。いいえなのは、ランダムウォークを生成するためには、この計算自体が必要ないからです。ただし、繰り返しになりますが、より複雑な他のシステムを理解するためには、この単純なシステムがどのように機能するかを理解しなければなりません。

つまり、AND演算をするときに、値をある範囲に限定するのです。これが最初のポイントです。この値をレンジの上限で割れば、0から1の範囲の値が得られます。そして、0と1の間になるこの値に、上限と下限の差を掛けます。こうして、0から最大値までの範囲の値が得られます。これが私たちの範囲になります。さて、この範囲を最小値に加えれば、実際に必要な値が得られます。これが使用されるべき値です。こうすれば、他のチェックを実行する心配はありません。マクロ自体が、値が許容範囲内であることを保証してくれるからです。このクレイジーなマクロの背後にあるアイデアはおわかりでしょうか。これは純粋な数学であり、それ以上のものではありません。

次に、関数内にある4つのFORループの最初のループに移りましょう。ループそのものに入る前に、関数の残りの部分で役立つ簡単な計算をいくつかおこなう必要があります。まず最初に、実際にシミュレーションするティックの数を知る必要があります。次に、各ティックの長さ、より正確にはいつ表示されるかを知る必要があります。物事をシンプルにするため、両者間の時間は一定とします。これでループに入り、1分足の範囲内でティックを分散させることができます。ティックが離れている場合もあれば、近くにある場合もありますが、今は関係ありません。何が必要で何が欲しいのか、それが私たちにとって本当に重要なことなのです。それぞれのティックが存在し、ユニークであるということです。これは、異なる時点にティックを配置することで実現できます。

お気づきかもしれませんが、各シミュレーションティックは最初に最小ボリューム値を持つように設定しました。この点は次のステップでも重要です。さて、次のループに入ります。ここが興味深いところです。最初におこなうのは、1分足の始値と終値がいくらになるかを決定することだからです。本当に興味深いのは、ループの中で何が起こっているかということです。使用するティック数から総ボリュームを引きます。これにより、まだ割り当てられていないボリュームを表す値が得られます。このボリュームは、最後のティックで直接割り当てることも、他のティックで割り当てることもできます。しかし、これはボリュームの急激な変化を引き起こすことになり、実際の市場ではあまり起こりません。したがって、残りのティックを分配し、その結果出来高が1分足バーの値で表されるようにする別の方法が必要です。この分布を可能な限りスムーズでランダムな方法で作成するために、マクロを使用します。マクロが呼び出されるたびに、一定の範囲内の値が生成されます。そしてこの瞬間に、ボリュームに存在する価値が1増加します。言い換えれば、総ボリュームはランダムかつ滑らかに分布し、あたかも実際の市場に近いデータであるかのような印象を与えます。

最後に、最後の2つのループを見てみましょう。最初のループは、ティックシステムにランダム性を生み出すものです。努力は必要ありません。私たちがおこなうことは、使用する最小価格と最大価格をシステムに伝えることだけです。したがって、各ティックはランダムに選択された価格を持つことになります。この選択にはマクロを使っています。そうしたら、最大値ポイントと最小値ポイントの両方が存在することを確認する必要があります。これは、ランダム生成の際に作成されなかった可能性があるためで、これらのポイントが見つかる位置もランダムに選ばれます。

最後のループは、実際のティックであるかのように値をティックシステムに渡すだけです。出力をファイルに保存し、その出力をグラフのデータとして使用すれば、結果を目で見て理解することができます。通常、エクセルなどのプログラムでこれをおこないます。しかし、これはMetaTrader 5でカスタム銘柄を使って直接おこなうこともできます。今はその詳細は考えません。シミュレーションが実際に期待通りにおこなわれることを理解することが重要です。

前の記事で始めた説明に基づいて、今は動きのランダム化を優先していることがわかるでしょう。他の記事で見られるような、ストラテジーテスターにあるような方法とよく似た方法でシミュレーションをおこなうのとは異なり、下図にあるようなジグザグの動きを使いました。

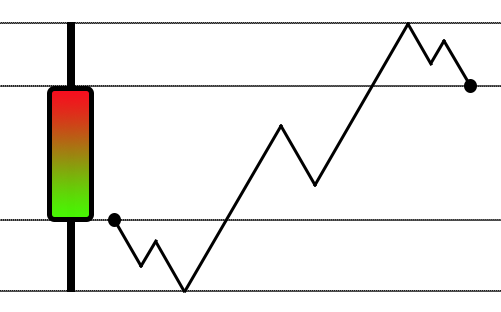
これはストラテジーテスターで使うには素晴らしいアイデアですが、リプレイ/シミュレーションシステムではこのアプローチはまったく適切ではありません。もう少し創造的で、同時に複雑な、別のアプローチが必要です。こうして今説明したシステムが生まれました。そこで、1分足バー内の動きを単純に「ランダム化」し始めます。しかし、液体に浮遊する物体の動きに非常に似たスタイルの動きを意図するのであれば、このアプローチは完全には適切ではありません。この方法を理解するためには、一連のデータをグラフ上で見えるように変換する方法を知ることが重要です。最も簡単な方法は、EXCELを使って変換することです。繰り返しになりますが、この方法を知っていることが重要です。

前回の「リプレイシステムの開発 - 市場シミュレーション（第13回）：シミュレーターの誕生(III)」には説明付きのビデオがありました。この記事で起こることを本当に理解したいのであれば、この方法を知っておくことは非常に重要です。というのも、ここではランダムウォークのような動作シミュレーションをおこなうからです。シミュレーターで作成されたチャートを見ると、その動きが銘柄取引段階で観察される動きと非常に似ていることにすぐに気づくでしょう。このようなアプローチには何のメリットもないと思うので、この記事では数式などは含めません。読者が本当に興味があるのは、コードそのものと、それが生み出すものです。使用される数式は何の足しにもならないし、多くの人にとって何の知識にもなりません。なぜなら、多くの人は検討されている抽象的な問題を理解していないからです。その結果、問題を説明するどころか、むしろ複雑にしてしまうことになります。しかし、得られる結果はきっと誰もが理解するでしょう。

この記事では、図01を図02に変換する最も簡単な方法を紹介します。                   

                       

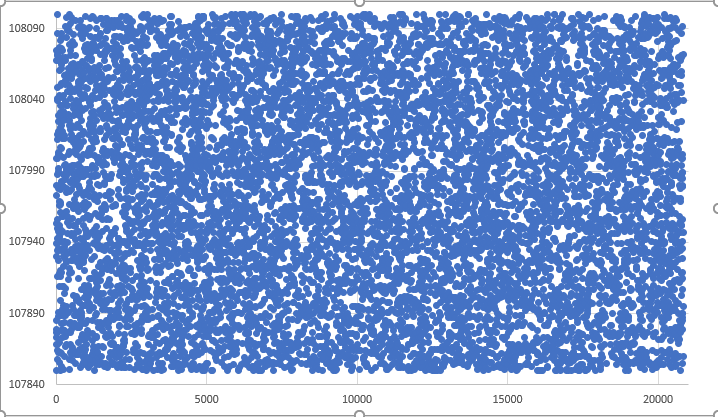
図01：ジャンプでおこなわれるランダムな動き

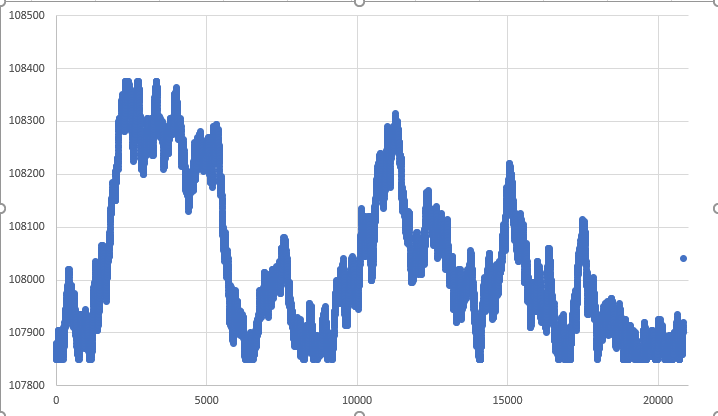
図02：ステップでおこなわれるランダムな動き

どちらの図も同じデータベースを使用して作成されています。

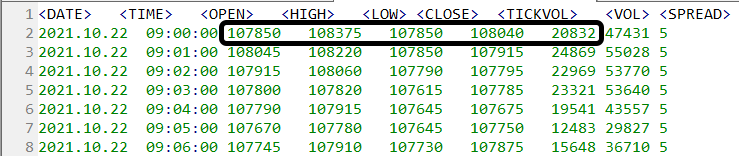
図03：両方の動きで使用されたデータベース

ただし完全にランダムなシステムとは異なる問題があり、それを修正する必要があります。それでも、99％以上のケースで本当に適切なシステムがすぐにできるわけではなく、残りの1％は何らかの偶然によるものです。しかし、それは稀なことでしょう。したがって、それ以外のケース、つまり99％を解決するためには、いくつかのコツが必要です。

実際にどのような仕組みになっているのか見てみましょう。しかしその前に、もし前回の「リプレイシステムの開発 - 市場シミュレーション（第13回）：シミュレーターの誕生(III)」をお読みでない場合、まずお読みになることを強くお勧めします。というのも、ここでは必要な変更とその実施方法のみに焦点を当てるからです。前回までの説明は繰り返しません。従って、先の内容を理解することが重要です。特に、エクセルでデータをグラフに変換する部分です。

さて、次は実装の話題に移りましょう。

完全に自由な動きを持つランダムウォークを実施

ランダムジャンプをランダムステップに変換するために必要なのは、シミュレーション機能の動作方法を変更することだけです。そのために、そのコードを見てみましょう。

inline void Simulation(const MqlRates &rate, MqlTick &tick[])
                        {
#define macroRandomLimits(A, B) (int)(MathMin(A, B) + (((rand() & 32767) / 32767.0) * MathAbs(B - A)))

                                long il0, max;
                                double v0, v1;
                                
                                ArrayResize(m_Ticks.Rate, (m_Ticks.nRate > 0 ? m_Ticks.nRate + 3 : def_BarsDiary), def_BarsDiary);
                                m_Ticks.Rate[++m_Ticks.nRate] = rate;
                                max = rate.tick_volume - 1;     
                                v0 = 4.0;
                                v1 = (60000 - v0) / (max + 1.0);
                                for (int c0 = 0; c0 <= max; c0++, v0 += v1)
                                {
                                        tick[c0].last = 0;
                                        tick[c0].flags = 0;
                                        il0 = (long)v0;
                                        tick[c0].time = rate.time + (datetime) (il0 / 1000);
                                        tick[c0].time_msc = il0 % 1000;
                                        tick[c0].volume_real = 1.0;
                                }
                                tick[0].last = rate.open;
                                tick[max].last = rate.close;
                                for (int c0 = (int)(rate.real_volume - rate.tick_volume); c0 > 0; c0--)
                                        tick[macroRandomLimits(0, max)].volume_real += 1.0;
                                for (int c0 = 1; c0 < max; c0++)
                                        tick[c0].last = macroRandomLimits(rate.low, rate.high);
                                        tick[c0].last = tick[c0 - 1].last + (m_PointsPerTick * ((rand() & 1) == 1 ? 1 : -1));
                                il0 = (long)(max * (0.3));
                                tick[macroRandomLimits(il0, il0 * 2)].last = rate.low;
                                tick[macroRandomLimits(max - il0, max)].last = rate.high;
                                for (int c0 = 0; c0 <= max; c0++)
                                {
                                        ArrayResize(m_Ticks.Info, (m_Ticks.nTicks + 1), def_MaxSizeArray);
                                        m_Ticks.Info[m_Ticks.nTicks++] = tick[c0];
                                }
#undef macroRandomLimits
                        }                       

注意してほしいのは、関数の働き方を変えているだけで、負荷は変わらないということです。こうすることで、同じティック数を使うことができます。強調表示された部分に注目してください。削除されたコードは削除され、強調表示されたコードがその場所に挿入されなければなりません。この変更だけを実行すれば、ランダムウォークを作ることができますが、これは適切な動きではありません。なぜなら、たとえ稀な瞬間に1分足バー内にとどまる動きがあったとしても、言い換えれば、高値と安値が合致し、その振幅内にとどまるのであれば、このコードでは、それ以上の信頼性もコントロールもできないからです。これを実行し、結果のグラフをチェックすればわかります。

添付のファイルを使用し、設定ファイルを変更しない場合、リプレイ/シミュレーションサービスは最初のパネルでのみ動作し、下の画像で強調表示されているパネルが使用されます。

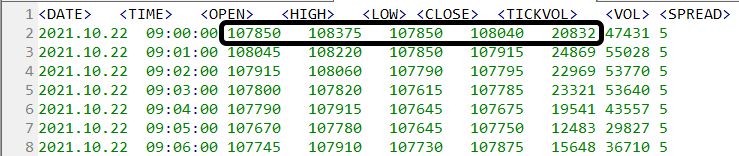
範囲に注意してください。 上限 => 108375、下限 => 107850です。 そして、これらはグラフで見ることができる範囲ではありません。ざっと見ただけでも、この範囲が尊重されていないことがわかります。以下に示すある実行のデータグラフ画像をご覧ください。

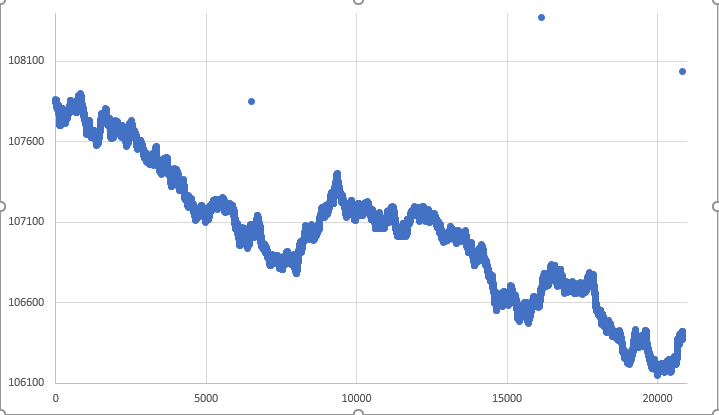
図04：完全に自由なランダムウォークのグラフ

ご覧の通り、下限は尊重されているとは言い難いです。繰り返しになりますが、ある特定の時点で、境界線が尊重されることがあります。上のグラフに見られるように、孤立点にはもう一つ問題がありますが、徐々に進みましょう。これらの点は、私たちが解決しなければならないもう1つの問題です。しかし、まずは範囲に対処しましょう。動きのシミュレーションを作るのであれば、受け入れられるものもあるかもしれません。しかし、ここではそれを受け入れません。というのも、私たちは過去に得られた何らかのデータに基づいてシミュレーションを行っており、提供されたものを尊重しなければならないからです。

この範囲の問題を解決するためには、自由なシステムを制限付きのシステムに変えなければなりません。多くの人はこのやり方を認めませんが、何としても制限を守るために何らかのチェック機能を作るしかありません。したがって、前回の記事を読んで、EXCELやその他のプログラムを使って、シミュレーションシステムによって生成されたグラフを分析する方法を理解することが重要です。データを鵜呑みにして、それが正しいと思ってはいけません。グラフで見る必要があります。

図01に示すように、MetaTrader 5グラフィックシステムの使用が完全に不可能な、完全にランダムなジャンピングベースのシステムを使用している場合に起こることとは異なり、図02や図04に示されているものを取得する場合には、同じことは起こりません。しかし、どちらの場合も、グラフ上の孤立点が奇妙なバーを生成するという問題があります。しかし、シミュレーションデータをEXCELに転送したくない場合は、各ティックがMetaTrader 5チャートに直接表示されるようにコードを変更することができます。しかし、これでは情報量が多くなり、チャートの理解が難しくなります。覚えておいてください。棒グラフではなく、チャート上にティックごとに配置する必要があります。やり方がわからない場合は、「一からの取引エキスパートアドバイザーの開発（第13部）：Time and trade (II)」をご覧ください。シミュレーターで生成したティックをプロットする方法をそこで説明しています。Times And Tradeは実際の銘柄のティックを表示することに重点を置いていますが、シミュレーターで生成されたティックを表示するために使用することもできます。Times And Tradeに表示されているコードを適応させることがすべてです。

これはそれほど難しい作業ではありませんが、変更が必要になり、それを元に戻さなければならなくなります。やり方は紹介しません。ここでの目標は、1分バーの中で可能な動きを、ジャンプではなく連続した形でシミュレーションできるように、システムに動きを生成させる方法を非常にシンプルな方法で示すことです。皆さんの多くは、MQL5を使ったこれらのプログラミング方法について深い知識をお持ちでないと思います。個人的な満足のためだけにアプローチを変えることは、この連載や他の記事の範囲を完全に超えています。よって、作業を続けましょう。次に、図03で強調表示されている1分バーに含まれる情報によって決定される制限に一致するように、コードに何かを追加しましょう。

移動制限のあるランダムウォークの実施

前のトピックで見たことに基づけば、何を更新する必要があるかはすぐにわかります。以下のコードの変更点を参照してください。

inline void Simulation(const MqlRates &rate, MqlTick &tick[])
                        {
#define macroRandomLimits(A, B) (int)(MathMin(A, B) + (((rand() & 32767) / 32767.0) * MathAbs(B - A)))

                                long    il0, max;
                                double  v0, v1;
                                bool    bLowOk, bHighOk;
                                
                                ArrayResize(m_Ticks.Rate, (m_Ticks.nRate > 0 ? m_Ticks.nRate + 3 : def_BarsDiary), def_BarsDiary);
                                m_Ticks.Rate[++m_Ticks.nRate] = rate;
                                max = rate.tick_volume - 1;     
                                v0 = 4.0;
                                v1 = (60000 - v0) / (max + 1.0);
                                for (int c0 = 0; c0 <= max; c0++, v0 += v1)
                                {
                                        tick[c0].last = 0;
                                        tick[c0].flags = 0;
                                        il0 = (long)v0;
                                        tick[c0].time = rate.time + (datetime) (il0 / 1000);
                                        tick[c0].time_msc = il0 % 1000;
                                        tick[c0].volume_real = 1.0;
                                }
                                tick[0].last = rate.open;
                                tick[max].last = rate.close;
                                for (int c0 = (int)(rate.real_volume - rate.tick_volume); c0 > 0; c0--)
                                        tick[macroRandomLimits(0, max)].volume_real += 1.0;
                                bLowOk = bHighOk = false;
                                for (int c0 = 1; c0 < max; c0++)
                                {                               
                                        v0 = tick[c0 - 1].last + (m_PointsPerTick * ((rand() & 1) == 1 ? 1 : -1));
                                        if (v0 <= rate.high)
                                                v0 = tick[c0].last = (v0 >= rate.low ? v0 : tick[c0 - 1].last + m_PointsPerTick);
                                        else
                                                v0 = tick[c0].last = tick[c0 - 1].last - m_PointsPerTick;
                                        bLowOk = (v0 == rate.low ? true : bLowOk);
                                        bHighOk = (v0 == rate.high ? true : bHighOk);
                                }                                       
                                il0 = (long)(max * (0.3));
                                if (!bLowOk) tick[macroRandomLimits(il0, il0 * 2)].last = rate.low;
                                if (!bHighOk) tick[macroRandomLimits(max - il0, max)].last = rate.high;
                                for (int c0 = 0; c0 <= max; c0++)
                                {
                                        ArrayResize(m_Ticks.Info, (m_Ticks.nTicks + 1), def_MaxSizeArray);
                                        m_Ticks.Info[m_Ticks.nTicks++] = tick[c0];
                                }
#undef macroRandomLimits
                        }                       

何の変化もないように見えるかもしれませんし、すべてのラベルに少し戸惑いを感じるかもしれません。ここで2つの新しい変数が追加され、状況をよりうまくコントロールできるようになりました。これらのポイントは初期化されているので、もしポジションが正しくアクセスされなければ、チャート上にこれらのポイントを配置しなければなりません。そして、これらのポイントはランダムに選ばれます。必要なチェックは、範囲を分析するシステムの枠組みの中でおこなわれます。したがって、私たちが集中できるのは1つのことだけです。ランダムウォークを1分バーによって以前に設定された範囲内に維持することです。最初にチェックするのは、上限に違反したか上限が尊重されたかです。違反が発生した場合、直ちにその動きを制限の範囲内に戻します。尊重された場合、下限が破られたかどうかをチェックします。破られていれば、すぐにその動きを制限の範囲内に戻します。破られていなければ、その値が受け入れられます。

コードに大きな変更はありませんが、結果は大きく変わりました。実行結果をご覧ください。

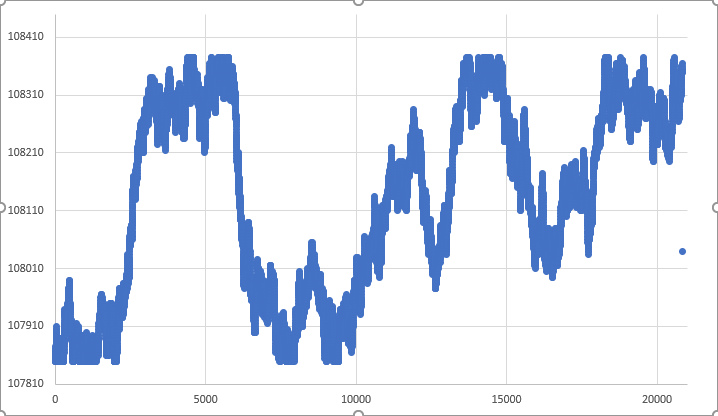
図05：一定の範囲内でのランダムウォーク

実際、この動きがすべてのルーズポイントをカバーしたのは全くの幸運でした。ただし、まだチャート上のポイントが緩くなっています。このポイントは1分足の終値を表しています。ランダムウォークの性質やその方法を考えると、これを正確に達成するのは実はかなり難しいことです。制限を満たせなかった図04とは異なり、図05では制限を満たしており、1分バー全体が事前に設定された制限内に収まるため、動きはほぼ完璧です。そして「ほとんど」と言ったのは、図05の結果はまったくの運だったからです。ほとんどの場合、以下の図06のような結果が得られるでしょう。

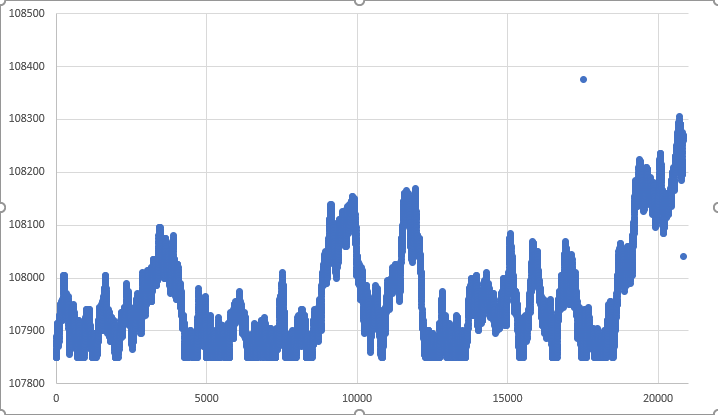
図06：限界内の典型的な移動グラフ

図06でも、ランダムムーブメントシステムによって、クロージングポイントが望ましい時間に到達していないことに注意してください。しかし、極めて稀なケースでは、図07のような結果が得られることもあります。ここで、クロージングポイントはランダムな動きによって到達したことがわかります。

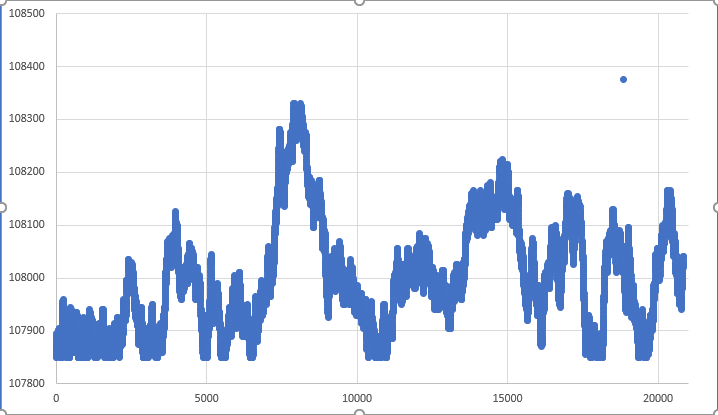
図07：クロージングポイントに達した稀な動き

しかし、このような動きは非常に稀であり、期待することはできません。ほとんどの場合、クロージング前のティックはクロージングポイントから離れています。これにより、MetaTrader 5に表示されるリプレイ/シミュレーション資産のグラフに急激な動きが生じます。この影響が気にならないのであれば、システムは使えるようになったということでいいのですが、それ以外にも気づいてほしいことがあります。これはそれほど珍しいことではありませんが、様々な場面で、高値も安値も実際には影響を受けていません。つまり、2つ目か3つ目のポイントでは、資産プロットシステムで別の急激な動きが見られるということです。ある意味、少なくともほとんどの場合でこれは大きな問題ではありません。現実の市場でも実際、そのような動きがあるからです。この場合、このような動きが頻繁に起こらないようなシステムを作りたいとしても、他の対策を講じなければなりません。言い換えれば、シミュレーションシステムにさらなる変更を加えなければなりませんが、この変更には困難が伴います。それどころか、一部の人々にとっては理解しがたいことでしょう。さらに、図07のようなグラフにしたい場合は、以下のような変更が必要になります。

このバージョンで発表された結果には、すでに多くの方が満足していると思いますが、まだこのすべてを改善することができます。これで十分だと思う方は、今後の記事は必要ないと思われるかもしれませんが、完璧主義者のために、もうひとつ提案があります。これで、ルーズポイントのないランダムなウォークができます。こうすることで、すべてのポイントを訪れることができます。でも、今日はここまでにします。この記事の知識を消化する時間を差し上げます。さまざまな種類の資産を使用してシステムを数回テストする必要があります。そうして初めて、1分足内で起こり得る動きが適切であるかどうか、また、制限付きのランダムウォークの概念を使用して利用したい市場の起こり得る現実を反映しているかどうかを真に知ることができます。

最終的な検討事項

複雑な数式をほとんど使わず、簡単な言葉で、読者の皆さんに、非常に興味深く、市場に存在するコンセプトをお伝えできたと思います。これがいわゆるランダムウォークです。この記事で紹介したシステムは、複雑な概念を理解しなくてもどこまで行けるかを示しています。もちろん、知識を得ることは常に良いことですが、かなりシンプルで楽しい方法で説明できるのに、複雑にする必要はないと思います。

添付のファイルは、現在の開発段階のシステムを提供するものです。リプレイ/シミュレーターでオーダーシステムを実際に使い始めるのはいつになるのだろうと、おそらく多くの方が思われているでしょう。ご心配なく。オーダーシステムはすぐに追加し始めます。ただし、その前にもうひとつやらなければならないことがあります。これは、オーダーシステムがかなり興味深い問題になるため、必要なことなのです。しかし、まずはリプレイ/シミュレーションサービスの実装を完了させる必要があります。現時点でその準備はほぼ整っています。あとは細部を追加するだけです。この後、オーダーシステムの開発に取りかかることができます。こうすることで、リプレイ/シミュレーターを実際の市場で取引するように使用することが可能になります。使い始める前に、いくつか変更する必要があるかもしれませんが。後で決めましょう。いずれにせよ、経験豊富なプログラマーになるには練習と訓練が必要です。私が読者に説明しようとしていることは、その助けとなるでしょう。それではまた次回、この「ランダムウォーク」でお会いしましょう。この段階はまだ完了していません。