开发回放系统 — 市场模拟(第 14 部分):模拟器的诞生(IV)
概述
在上一篇文章 “开发回放系统 — 市场模拟(第 13 部分):模拟器的诞生(III)” 中,我展示了针对服务文件所做的修改,以便能更好地表述跳价,及其处理流程。 上一篇文章的主要目标是展示如何做到这一点,以及哪处代码需要修改和添加,才能从服务获取数据。 这令我们能将此数据转至另一个位置,在本例中是转到文件。 文件在手,我们就可在程序里使用它,在本例中,我展示了如何利用 EXCEL 来分析模拟器生成的数据。
这种类型的任务,虽然看起来微不足道,但对于我们即将在本文中的所作所为至关重要。 如果不明白如何分析模拟生成的数据,我们就无法理解需要实现的内容;但最重要的是,我们就不会理解为什么它要以我将展示的方式来实现。 上一篇文章的主题之外,我们还解释了代码中需要修改的一些要点,使之能在大约 1-分钟内创建柱线,并且具有良好的精准度,如此一切都非常接近现实。 不过,尽管如此,为了明白我们将在本文中做什么,我们需要考虑另一件事。 由于上一篇文章中已提供了很多信息,我决定在此解释最后一个细节。 您可以在随附的代码中查看它。
尝试自由的随机游走
在下面,您可以看到该例程的最基本版本,它将尝试创建自由随机游走。
inline void Simulation(const MqlRates &rate, MqlTick &tick[]) { #define macroRandomLimits(A, B) (int)(MathMin(A, B) + (((rand() & 32767) / 32767.0) * MathAbs(B - A))) long il0, max; double v0, v1; int p0; ArrayResize(m_Ticks.Rate, (m_Ticks.nRate > 0 ? m_Ticks.nRate + 3 : def_BarsDiary), def_BarsDiary); m_Ticks.Rate[++m_Ticks.nRate] = rate; max = rate.tick_volume - 1; v0 = 4.0; v1 = (60000 - v0) / (max + 1.0); for (int c0 = 0; c0 <= max; c0++, v0 += v1) { tick[c0].last = 0; tick[c0].flags = 0; il0 = (long)v0; tick[c0].time = rate.time + (datetime) (il0 / 1000); tick[c0].time_msc = il0 % 1000; tick[c0].volume_real = 1.0; } tick[0].last = rate.open; tick[max].last = rate.close; for (int c0 = (int)(rate.real_volume - rate.tick_volume); c0 > 0; c0--) tick[macroRandomLimits(0, max)].volume_real += 1.0; for (int c0 = 1; c0 < max; c0++) tick[c0].last = macroRandomLimits(rate.low, rate.high); il0 = (long)(max * (0.3)); tick[macroRandomLimits(il0, il0 * 2)].last = rate.low; tick[macroRandomLimits(max - il0, max)].last = rate.high; for (int c0 = 0; c0 <= max; c0++) { ArrayResize(m_Ticks.Info, (m_Ticks.nTicks + 1), def_MaxSizeArray); m_Ticks.Info[m_Ticks.nTicks++] = tick[c0]; } } #undef macroRandomLimits
理解上面的这段代码对于理解我们接下来要做什么非常重要。 如果您运行这段代码,您最终会得到一个非常混乱的图形。 重点是了解这个非常基本的函数是如何运作的,如此您就能明白更复杂的函数将如何运作。 我们从宏定义开始。 问:这个宏有做什么的? 您也许正在看并思考:这是什么疯狂的举动? 我们真的需要这么奇怪的东西吗? 这个问题的答案是肯定的和否定的。
肯定的,是因为我们所需生成的随机值应当在非常特定的范围之内。 为此,我们需要设置某种约束。 否定的,则是因为为了生成随机游走,我们不需要这个计算本身。 但再次,我们必须明白这个更简单的系统是如何运作的,以便理解其它更复杂的。
那么,当我们进行“与(AND)“运算时,我们将数值限定在一个范围内。 这是第一个要点。 如果我们将此值除以范围的上限,我们会得到一个介于 0 到 1 之间的数值。 然后,我们将这个介于 0 和 1 之间的数值乘以上限与下限之间的差值。 由此,我们就得到一个介于 0 到范围最大值的数值。 现在,如果我们在范围里加上最小值,我们就得到了实际需要的数值。 这就是应当采用的数值。 以这种方式,我们就不必担心运行任何其它检查:宏本身将确保该值在可接受的范围内。 您有没有想到这个疯狂的宏背后的思路? 这是纯粹的数学,无它尔。
接下来,我们转到函数内部四个 FOR 循环中的第一个。 在我们进入循环本身之前,我们需要做少量简单的计算,这将有助于我们完成函数的其余部分。 首先,我们需要知道我们实际模拟的跳价有多少。 接着,我们需要知道每个跳价的时长,或者更准确地说,它们应该何时出现。 出于行事简单,我们将在它们之间采用恒定时长。 现在我们能进入循环,并在 1-分钟柱线范围内派发跳价。 在某些情况下,跳价会相距更远,而在其它情况下,它们会彼此靠近。 但现在这都不算啥。 我们的所需和所想才是我们真正在意的。 这就是每个跳价都要存在、且是唯一的。 这可由在不同的时间点放置跳价来达成。
您也许已经注意到,我设置的每个模拟跳价,最初均具有最小交易量值。 这一点对于下一步也很重要。 现在我们进入下一个循环。 这就是事情变得有趣的所在,因为我们要做的第一件事就是判定 1-分钟柱线的开盘价和收盘价。 真正有趣的是循环内部发生的事情。 我们将从用到的跳价数量中减去总交易量。 这为我们提供了一个数值,表示尚未分配的交易量。 我们可以把该交易量直接分配给最后一次跳价,或其它跳价。 然而,这会导致交易量的尖锐变化,而这在实际市场中并不经常发生。 故此,我们需要另一种方法来派发剩余的跳价,如此结局交易量就能以 1-分钟柱线值来表达。 为了能以最平滑和最随机的方式创建此分布,我们将使用宏。 每次调用宏时,它都会生成一个确定限制内的数值。 正是在这一刻,交易量中存在的数值加 1。 换言之,总交易量将随机平滑地分布,给人的印象是数据与真实市场的数据相似。
最后,我们看一下最后两个循环,其中第一个循环将在我们的跳价系统中创建随机性。 请注意,我们不必付出任何努力:我们所做的只是告诉系统所要用的最低和最高价格是多少。 因此,每个跳价都会有一个随机选择的价格。 注意,我们用宏来执行此选择。 一旦此操作完成,我们需要确保最大值点和最小值点两者都存在。 这是因为它们也许不是在随机生成过程中创建的,并且这些点的位置也是随机选取的。
至于最后一个循环,它只是简单地将数值传递到跳价系统之中供使用,就如同它们是真实的跳价。 如果您将输出保存到文件,然后依据输出数据作图,您就能看清并理解结果。 我们通常在某些程序中执行此操作,譬如 Excel。 不过,直接在 MetaTrader 5 中利用一些自定义交易品种也能做到。 然而,我们现在不去考虑这些细节。 重点是要明白模拟会如实按预期发生。
基于我们在上一篇文章中开始的讲解,您能看出现在我们正优先研究走势随机化。 不同于其它文章中所见,那些创建模拟所采用的方法都与策略测试器中的非常相似,我们所用是的与下图所示非常相似的锯齿形走势:
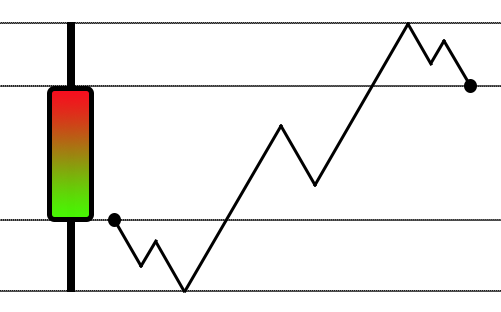
虽然如策略测试器一样是个好主意,但这种方式对于回放/模拟系统来说并不完全足够。 需要一种不同的方式,更有创意,但与此同时更复杂。 我刚才讲解的系统就是这样诞生的。 在当中,我们在 1-分钟柱线内开始非常简单地“随机化”走势。 但如果我们的意图是让走势风格与悬浮在液体中的物体运动相类似,那么这种方式就并不完全足够。 为了帮助您理解这是如何完成的,重要的是要知道如何将一系列数据转换为图表上可见的内容。 最简单的方法是利用 EXCEL 进行转换。 再有,重点是您知道如何做到这一点。
上一篇文章 开发回放系统 — 市场模拟(第 13 部分):模拟器的诞生(III) 中有一个视频进行了解释。 如果您真的想搞明白本文中会发生什么,那么知道如何去做非常重要。 这是因为在此我们将创建一个看起来像随机游走的走势模拟。 查看由模拟器创建的图表,您会立即注意到该走势与品种交易阶段观察到的走势非常相似。 我不会在本文中囊括数学公式或类似的东西,因为我没有看出这种方式有任何益处。 每个人真正感兴趣的是代码本身,以及它产生的结果。 用到的数学公式根本没有增加任何实质益处,也不能为大众提供任何知识,因为大众不理解所研究的抽象问题。 故而,越解释牵扯越多、越复杂。 但可以肯定的是,每个人都会理解得到的结果。
在本文中,您将看到把图例 01 转换为图例 02 的最简单途径:
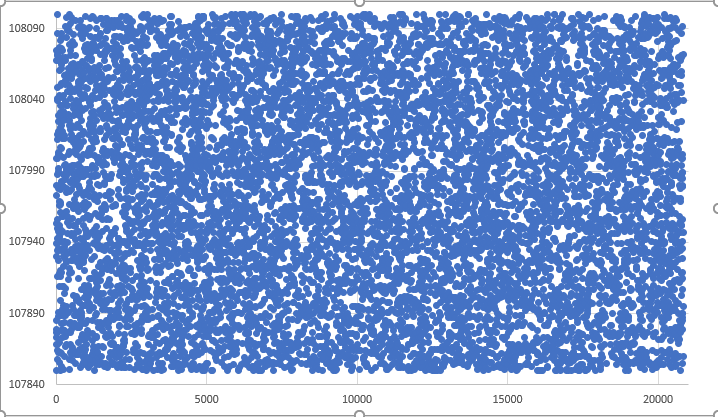
图例 01 — 跳跃执行的随机走势
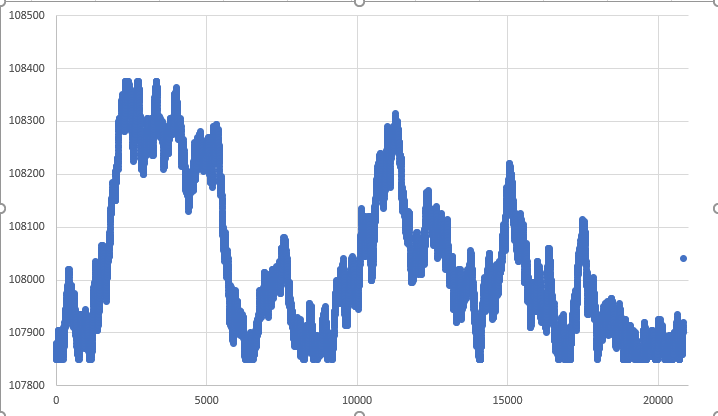
图例 02 — 步进执行的随机走势
这两个图例都基于相同的数据库创建:
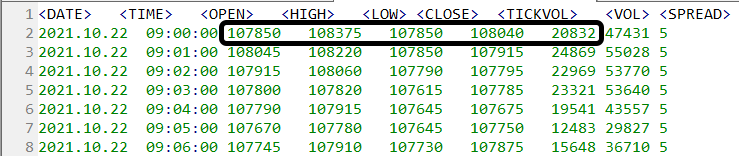
图例 03 — 两种走势所依据的数据库
但是,有些问题与完全随机系统不同,我们需要纠正。 即便如此,在超过 99% 的情况下,我们不会立即拥有一个真正合适的系统,而剩余的 1% 会由于一些机会,令模拟很理想。 但这是比较罕见的。 因此,我们需要实现一些技巧来解决所有其它情况,即 99%。
我们看看这个系统是如何实际运作的。 但在此之前,如果您还没有看过上一篇文章 “开发回放系统 — 市场模拟(第 13 部分):模拟器的诞生(III)”,我强烈建议您先停下来,先回头阅读上一篇文章。 这里的原因在于,我们将只关注必要的修改,以及如何实现它们。 我们不会重复上一篇文章中给出的解释。 因此,了解上述内容很重要。 尤其是涉及在 Excel 中将数据转换为图形的部分。
现在我们转入实现的主题。
以绝对自由的走势实现随机游走
为了将随机跳跃转换为随机步进,我们需要做的就是改变模拟函数的运作方式。 为此,我们看看它的代码:
inline void Simulation(const MqlRates &rate, MqlTick &tick[]) { #define macroRandomLimits(A, B) (int)(MathMin(A, B) + (((rand() & 32767) / 32767.0) * MathAbs(B - A))) long il0, max; double v0, v1; ArrayResize(m_Ticks.Rate, (m_Ticks.nRate > 0 ? m_Ticks.nRate + 3 : def_BarsDiary), def_BarsDiary); m_Ticks.Rate[++m_Ticks.nRate] = rate; max = rate.tick_volume - 1; v0 = 4.0; v1 = (60000 - v0) / (max + 1.0); for (int c0 = 0; c0 <= max; c0++, v0 += v1) { tick[c0].last = 0; tick[c0].flags = 0; il0 = (long)v0; tick[c0].time = rate.time + (datetime) (il0 / 1000); tick[c0].time_msc = il0 % 1000; tick[c0].volume_real = 1.0; } tick[0].last = rate.open; tick[max].last = rate.close; for (int c0 = (int)(rate.real_volume - rate.tick_volume); c0 > 0; c0--) tick[macroRandomLimits(0, max)].volume_real += 1.0; for (int c0 = 1; c0 < max; c0++) tick[c0].last = macroRandomLimits(rate.low, rate.high); tick[c0].last = tick[c0 - 1].last + (m_PointsPerTick * ((rand() & 1) == 1 ? 1 : -1)); il0 = (long)(max * (0.3)); tick[macroRandomLimits(il0, il0 * 2)].last = rate.low; tick[macroRandomLimits(max - il0, max)].last = rate.high; for (int c0 = 0; c0 <= max; c0++) { ArrayResize(m_Ticks.Info, (m_Ticks.nTicks + 1), def_MaxSizeArray); m_Ticks.Info[m_Ticks.nTicks++] = tick[c0]; } #undef macroRandomLimits }
请当心,我们只是改变了函数的运作方式,但我们仍然保持相同的加载方式。 这样的话,我们就能使用相同数量的跳价。 注意高亮部分。 现在请注意以下事实:删划线 覆盖的代码必须删除,并其位置由插入的高亮代码替换。 通过实现这样的修改,我们就能创建随机游走,但这并非一个正确的走位。 还不是,因为即使在极少时刻,在 1-分钟柱线内仍有剩余走位,换言之,如果已满足高点和低点,并保持在该幅度之内,则依靠这段代码,我们对此不能确保或控制上述举动。 如果您运行它,并查看生成的图形,就可以看到这一点。
如果您使用附带文件,并且不更改配置文件,则回放/模拟服务仅在第一根柱线上操作,该柱线如下图高亮所示:
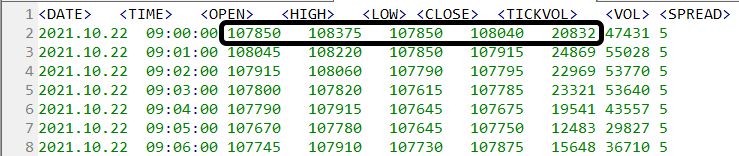
请注意限制:上限 => 108375 和 下限 => 107850。然在图形上看到的却不是这些界限。 即便快速扫一眼,您也能看出这些界限并未得到遵守。 查看如下所示的其中一个执行的数据图形画面。
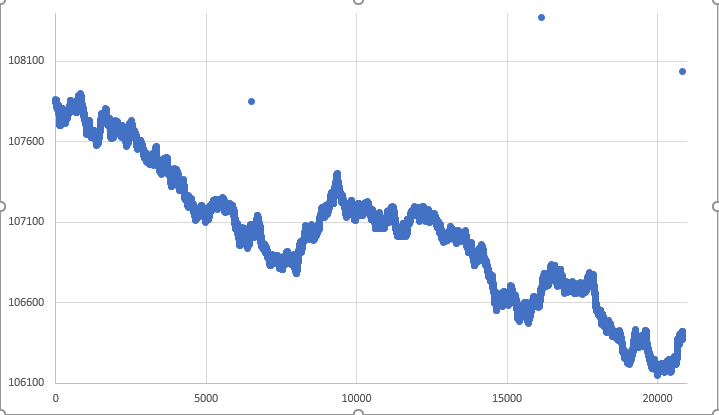
图例 04 — 完全自由的随机游走图形
如您所见,下限远未得到遵守。 再有,在某个非常非常特殊的时刻,也许会发生遵守边界的情况。 还有另一个问题,即孤立点,如上图所见,但我们要逐步前进。 这些孤立点代表了我们必须解决的另一个问题。 不过,我们先来应对界限。 好吧,当我们创建走势模拟时,有些事情也许是可接受的。 但在此我们不会接受它们。 原因是我们正在根据先前获得的某种数据进行模拟,我们必须遵守提供给我们的数据。
为了解决这个界限问题,我们必须把一个自由系统转变为一个受限系统。 尽管许多人不赞成这种方式,但我们别无选择,只能不惜一切代价创建某种检查来遵守限定。 因此,阅读上一篇文章,从而了解如何利用 EXCEL,或任何其它程序来分析模拟系统生成的图形非常重要。 不要只依赖数据,并认为它就是正确的。 您真的需要在图表上看看它们。
当我们有一个完全基于随机跳转的系统时,发生的一切与图例 01 所示不同,于其中使用 MetaTrader 5 图形系统完全不可行,同样不可能发生如我们在图例 02、甚或图例 04 中所描绘的内容。 尽管在这两种情况下,我们都会遇到图形上孤立点的问题,这将产生一根奇怪的柱线。 不过,如果您不打算将模拟数据传输到 EXCEL,您可以修改一些代码,如此即可在 MetaTrader 5 图表上直接显示每个跳价。 但由于图表包含的信息量,令图表更难理解。 请记住:您需要在图表上逐个放置跳价,而不是在柱线上。 如果您不知道如何做这些,请阅读这篇文章:“从头开始开发智能系统(第 13 部分):时间和交易(II)”,因为在其内我已解释了如何在模拟器中绘制我们于此处生成的跳价。 虽然 “时间和交易” 专注于观察真实品种跳价,但我们也能用它来观察模拟器中生成的跳价。 这一切都适合 “时间与交易” 当中所示的代码。
这项任务不太困难,但它需要一些修改,之后还需撤消这些修改。 所以我不会展示如何做到这一点。 此处的目标是以一种非常简单的方式展示如何令系统生成走势,如此我们可以模拟 1-分钟柱线内可能的走势,但是按连续的形式,而非跳跃式。 我想你们中的许多人针对这些东西如何利用 MQL5 编程没有深度的认知。 仅仅为了满足个人而改变您的方式,完全超出了本文或本序列任何其它文章的范畴。 故此,我们继续我们的工作。 现在,我们要在代码中添加一些内容,如此即可与限定匹配,如图例 03 中高亮显示的 1-分钟柱线中检测到的包含信息。
实现受限走势的随机游走
基于我们在上一个主题中看到的内容,我们能轻易地注意到我们需要更新的内容。 请参见以下代码中的更改:
inline void Simulation(const MqlRates &rate, MqlTick &tick[]) { #define macroRandomLimits(A, B) (int)(MathMin(A, B) + (((rand() & 32767) / 32767.0) * MathAbs(B - A))) long il0, max; double v0, v1; bool bLowOk, bHighOk; ArrayResize(m_Ticks.Rate, (m_Ticks.nRate > 0 ? m_Ticks.nRate + 3 : def_BarsDiary), def_BarsDiary); m_Ticks.Rate[++m_Ticks.nRate] = rate; max = rate.tick_volume - 1; v0 = 4.0; v1 = (60000 - v0) / (max + 1.0); for (int c0 = 0; c0 <= max; c0++, v0 += v1) { tick[c0].last = 0; tick[c0].flags = 0; il0 = (long)v0; tick[c0].time = rate.time + (datetime) (il0 / 1000); tick[c0].time_msc = il0 % 1000; tick[c0].volume_real = 1.0; } tick[0].last = rate.open; tick[max].last = rate.close; for (int c0 = (int)(rate.real_volume - rate.tick_volume); c0 > 0; c0--) tick[macroRandomLimits(0, max)].volume_real += 1.0; bLowOk = bHighOk = false; for (int c0 = 1; c0 < max; c0++) { v0 = tick[c0 - 1].last + (m_PointsPerTick * ((rand() & 1) == 1 ? 1 : -1)); if (v0 <= rate.high) v0 = tick[c0].last = (v0 >= rate.low ? v0 : tick[c0 - 1].last + m_PointsPerTick); else v0 = tick[c0].last = tick[c0 - 1].last - m_PointsPerTick; bLowOk = (v0 == rate.low ? true : bLowOk); bHighOk = (v0 == rate.high ? true : bHighOk); } il0 = (long)(max * (0.3)); if (!bLowOk) tick[macroRandomLimits(il0, il0 * 2)].last = rate.low; if (!bHighOk) tick[macroRandomLimits(max - il0, max)].last = rate.high; for (int c0 = 0; c0 <= max; c0++) { ArrayResize(m_Ticks.Info, (m_Ticks.nTicks + 1), def_MaxSizeArray); m_Ticks.Info[m_Ticks.nTicks++] = tick[c0]; } #undef macroRandomLimits }
看似并无变化发生,或者您也许会对所有标签感到一点困惑。 于此加入了两个新的变量,这将有助于我们更好地控制局势。 它们的初始化方式是,如果它们所代表的位置没有被正确存放,我们肯定要将这些点放置到图表上。 且这些点是随机选择的。 所需的检查是在分析限定的系统框架内完成的。 由此,我们就仅需专注一件事:在之前由 1-分钟柱现设置的限定范围内保持随机游走。 我们首先要检查是否违反了上限,以及它是如何遵守上限的。 如果发生违反,我们要立即将走势退回到限定范围内。 如果已遵守,我们就检查是否违反了下限。 若是,我们要立即将走势退回到限定范围内。 否则,接受该数值。
我们并未在代码中改动太多。 然而,结果发生了重大变化。 参见其中一个的执行结果。
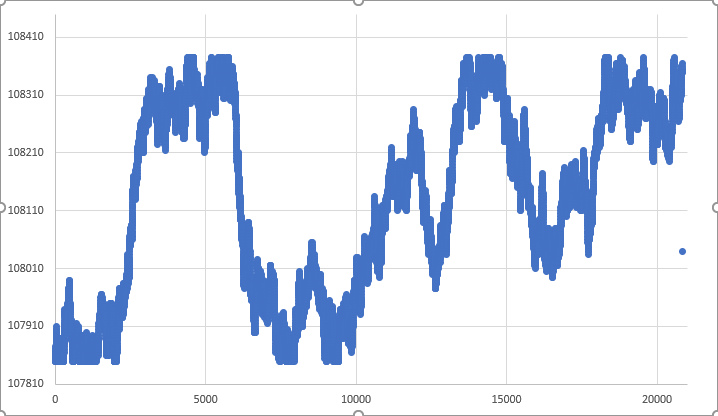
图例 05 — 确定限定内的随机游走
事实上,走势覆盖了所有松散点纯粹是运气使然。 但我们在图表上仍然有一个松散点。 该点代表 1-分钟柱线的收盘跳价。 实际上很难达到这样的精准度,这是随机游走的本质、以及我们如何做到这一点所决定的。 不像图例 04,其中未满足限定;在图例 05 中,这些限定均已满足,且整根 1-分钟柱线将在先前设置的限定范围内,故走势几乎完美无缺。 我说“几乎”是因为图例 05 的结果纯粹是运气使然。 在大多数情况下,我们将得到类似于如下图例 06 所示的结果。
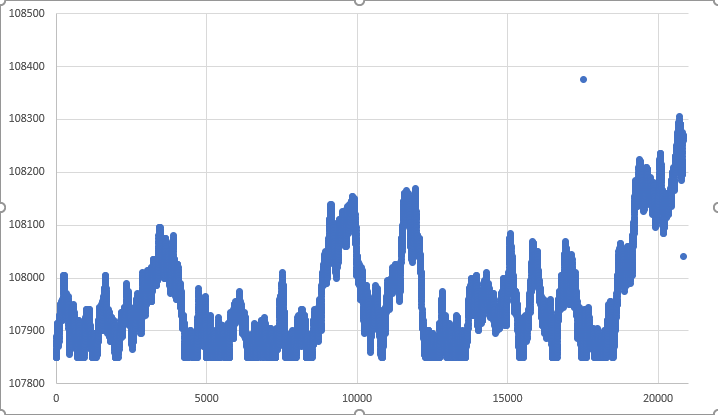
图例 06 — 限定范围内的典型走势图形
注意,同样在图例 06 中,随机走势系统没有在期待时刻抵达收盘点。 不过,在极端罕见情况下,您可以得到类似于图例 07 的结果。 于此,我们能注意到,收盘点是经由随机走势达到的。
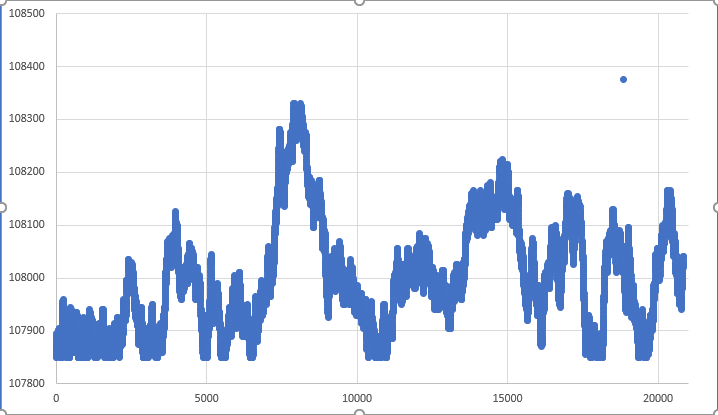
图例 07 — 达到收盘点的罕见走势
但这种类型的走势非常罕见,我们并不指望它。 在大多数情况下,收盘前的跳价与收盘点相距甚远。 这将导致 MetaTrader 5 显示的回放/模拟资产图表有一处尖锐走位。 如果您不介意这种效果,太好了,系统现在就可使用了,但您还应注意到其它的东西。 在不同的时间,这并不少见,高点或低点实际上并没有受到影响。 这意味着在第二点或第三点,我们会看到资产绘图系统的另一次突然移动。 按某种意义来说,这并非一个大问题,至少是在大多数情况下,因为在真实市场里,事实上,在某些时刻我们确有这种走势。 即便若在这种情况下,我们打算创建一个系统,这样的走势在其中不会如此频繁,我们就必须采取其它措施。 换言之,我们不得不对模拟系统进行更多修改,但这些修改不会一帆风顺。 对比而言,这种实现对于某些人来说更加难以理解。 此外,如果我们想要一个与图例 07 中所示的图形非常相似的图形,就需要进行这样的修改。
我想很多人已经对这个版本中呈现的结果感到很满意了。 不过,所有这些我们仍然有改进余地。 对于那些认为这已经足够的人来说,下面的文章看似没有必要。 但对于完美主义者,我还有一个建议要做。 这就是创建一个没有松散点的随机游走。 这样的话,所有点都会走访到。 但今日这些已经足够了。 我会给您时间消化本文中的知识。 您需要利用不同类型的资产对系统进行多次测试,只有这样,您才能真正知道仅据受限随机游走的概念,1-分钟柱线内的可能走势是否合适,且能反映出您想象当中的真实市场。
后记
亲爱的读者们,几乎没有复杂的数学公式,且以简单的语言,我想我已经成功地向你们传达了一个非常有趣且存在于市场上的概念。 这就是所谓的随机游走。 本文讲述的系统表明,如果不理解复杂的概念,我们能走多远,当然,获得更多知识总是好的。 但若您能以一种相对简单和愉快的方式解释它时,为什么要把事情复杂化,对吧?
附带文件提供当前开发状态的系统。 你们当中的许多人可能想知道我们什么时候才能真正开始在我们的回放/模拟器中使用订单系统。 不要担心,我们很快就会开始添加订单系统,但在此之前,我们还需要做一件事。 这是必要的,因为订单系统会变成一个要解决的有趣问题。 但首先我们需要完成回放/模拟服务的实现,现在看来它几乎已经准备就绪了。 我们只需要再添加少量细节。 此后,我们就可以起始开发订单系统了。 这样的话,就可以如同在真实市场上交易一样使用回放/模拟器。 尽管在开始使用它之前,您也许需要更改一些内容。 但我们稍后决定。 无论哪种方式,您都需要练习和训练才能成为一名经验丰富的程序员。 我正尝试向您讲解的内容会帮到您。 期待在下一篇文章中与您相见,我们将完成这个随机游走。 该阶段尚未完成。
本文由MetaQuotes Ltd译自葡萄牙语
原文地址: https://www.mql5.com/pt/articles/11058